Translate this page into:
Analysis of buoyancy assisting and opposing flows of colloidal mixture of titanium oxide, silver, and aluminium oxide nanoparticles with water due to exponentially stretchable surface
⁎Corresponding author. sayed.eldin22@fue.edu.eg (Sayed M Eldin),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Energy is essential for a nation's economic growth. Energy is recognized in contemporary society as being crucial to the development of quality of life and sustainability. The environment transforms/absorbs heat and sunlight in a variety of ways. Some of these transitions lead to the flow of renewable energy sources like wind and biomass. Solar energy has become one of the promising alternative energy sources in the future because to the improvements made to enhance its performance. In this context, the impact of solar radiation on modified nanofluid flow over an exponential stretching sheet is examined. Using the proper similarity transformations, the governing equations for the flow assumptions are reduced to ordinary differential equations. The numerical simulation of these simplified equations is then performed using the Runge-Kutta Fehlberg method and the shooting methodology. With the aid of graphs and tables, the effects of numerous parameters on the involved fields are described. Results reveal that the modified nano liquid shows increased heat transport for opposing flow situation than the assisting flow situation for incremented values of porosity parameter and volume fraction. The modified nanoliquid shows increased heat transport for opposing flow situation with respect to augmented values of radiation parameter.
Keywords
Ternary nanofluid
Thermal radiation
Exponentially stretching sheet
Buoyancy assisting and opposing flow
Nomenclature
-
Temperature
-
Wall temperature
-
Far-field temperature
-
Reference temperature
-
Thermal radiation heat flux
-
Mean absorption coefficient
-
Permeability of porous medium
-
Porous permeability parameter
-
Velocity
-
Nusselt number
-
Dimensionless velocity profile
-
length
-
Thermal Conductivity
-
Specific Heat
-
Prandtl number
-
Radiation parameter
- and
-
Velocity components
- and
-
Coordinates
-
Skin friction
-
Local Reynolds number
Symbols
-
Stream function
-
Thermal expansion
-
Kinematic Viscosity
-
Stefan-Boltzmann constant
-
Dynamic Viscosity
-
Mixed convection parameter
-
Dimensionless temperature profile
-
Similarity variable
-
Solid volume fraction
-
Density
Greek Symbols
-
Modified nanofluid
-
Nanofluid
-
Solid particles
-
Hybrid nanofluid
-
Fluid
Subscripts
1 Introduction
A nanofluid (NF) is a fluid that contains nanosized particles in addition to the base fluid. Colloidal suspensions of nanosized particles in a base fluid yields NFs. The thermal performance of NFs is predicted to be better than that of conventional fluids due to the suspended nanoparticles (NPs) presence high thermal conductivity. In this reference frame, Choi and Eastman (Choi and Eastman, 1995) investigated the usage of NPs to advance the thermal conductivity of liquids in 1995. The various applications of nanofluid involve solar energy (Mahian et al., 2013), evaporating system and condensing system (Rashidi et al., 2018; Ezaier et al., 2022; Ezaier et al., 2022), and heat transfer devices (Sajid and Ali, 2019; Ezaier, 2022). Recently, numerous researchers discussed the flow, heat and mass transport behaviour of diverse liquid streams by considering different NPs suspension under the impact of several influencing factors over different geometries (Saleem et al., 2022; Anantha Kumar et al., 2022; Sandeep et al., 2022; Zaydan et al., 2020; Awan et al., 2020; Ashraf et al., 2022). In this era of rapidly developing technology, a new subclass of nanofluids known as hybrid NFs has been produced. This subclass is a modified version of the original nanofluids. In contrast to traditional NFs, hybrid NFs are made up of more than one metallic nanoparticle. Recently, a number of researchers have discussed the flow, heat and mass transport behavior of various liquid streams by considering dual NPs suspension under the influence of a number of different influencing factors over a variety of geometries (Cao et al., 2022; Shah et al., 2022; Song et al., 2021; Saleh, 2022; Gowda et al., 2021; Ashwinkumar et al., 2022; Awan et al., 2022). These researchers considered the impact of several influencing factors on the flow of the dual NPs suspension.
Nowadays, researchers are taking steps to add different NPs to the hybrid NF mixture and the resulting mixture is known as a modified NF. Two-particle NFs were used in hybrid NF research in the beginning, but more recently, a new class of functioning liquids has been developed and is being intensively studied. Three dissimilar types of nanoparticles were suspended in a base fluid subsequently by scientists and academics in order to create a new class of nanofluid. A ternary hybrid nanofluid (THNFs) is one of the innovative types of nanofluids. Researchers were drawn to change the existing nano liquid as a result of the amplified need for cooling agents combined with high thermal capability at the industrial level, which led to the outline of trihybrid nanofluid with upgraded thermal properties. With this reason more experimental studies have been carried out to advance the thermal properties of an existing hybrid nanofluid by suspending three dissimilar types of solid nanoparticles in carrier liquid to form Trihybrid nanofluids. Recently, Yogeesha et al. (Yogeesha et al.) investigated the physical effects of blowing, Soret, and Dufour on an unstable surface occupied in a permeable medium containing a THNF. The impact that the various dimensionless limitations have had on the important profiles is shown pictorially here. Abbas et al. (Abbas et al., 2021) swotted the transport of a modified NF flow with time-dependent viscosity on an exponential Riga plate. The primary objective of this study was to investigate the heat transport efficiency that gains greater in comparison to HNF and NF systems. Xiu et al. (Xiu et al., 2022) swotted the forced convection stream of THNFs due to dual stretching on wedge surfaces when NPs volume is large and small. In this scenario, the researchers came to the conclusion that as time went on, in all of the four cases of water at various temperatures as well as in the case of four THMF flows, the same thing happened. Kumar et al. (Naveen Kumar et al., 2022) conferred the water based THNF flow over a surface with magnetic dipole effect. The influence that the various dimensionless limitations have had on the important profiles is shown here. Elnaqeeb et al. (Elnaqeeb et al., 2021) swotted the three-dimensional flow of THNF with water conveying NPs by considering suction and dual-stretching. In this particular instance, they came to the conclusion that an increase in suction and stretching ratio led to an increase in the vertical velocity of the motion along the x-direction, as well as an increase in the Nusselt number.
A porous media can be considered as a solid structure containing passages through which fluids can flow. Porous media has numerous applications in engineering, agriculture, building, and geothermal sciences. Lately, energy conversion and energy storage are two key ongoing domains of application for porous materials, where porous materials are necessary for supercapacitors, fuel cells, and batteries. Xia (Xia et al., 2021) explored the stream and heat transport in a Taylor-Couette streams of second-grade liquids subject to Lorentz and Darcy-Forchheimer quadratic drag forces. Rasool et al. (Rasool et al., 2022) investigated the influence of radiation and magnetic field on convection flow across a riga pattern with porous media. A comparative investigation of the LTNE condition for NF flow through porous media was conducted by Prasannakumara (Prasannakumara, 2022). Gowda et al. (Punith Gowda et al., 2021) investigated the impact of radiation and heat production on second grade fluid flow in a permeable medium. Madhukesh et al. (Madhukesh et al., 2021) investigated the impact of particle deposition on Casson hybrid NF flow in a permeable medium.
Thermal radiation is one of the three main kinds of heat transport and it is a basic feature of matter that depends on its temperature. From a microcosmic perspective, thermal radiation is caused by random particle motion (caused by the material's temperature), which accelerates the charge or induces the electrons and protons to oscillate in a dipole. Wakif (Wakif, 2020) studied the dynamics of thermal conductivity and temperature-dependent viscosity on steady convective flows of radiative Casson liquids over a sheet. Wakif et al. (Wakif et al., 2021) explored how heat radiation affected Walters-b fluid flow across a surface due to mixed convection. The effects of thermal radiation on flow of a NF over a surface was studied by Ganesh et al. (Vishnu Ganesh et al., 2018). Wang et al. (Wang, 2022) investigated the effect of thermal radiation on heat transport in stream of NF. Alhadhrami et al. (Alhadhrami, 2021) investigated the effect of thermal radiation on heat transport in plane wall jet stream of Casson NF with suction.
Buoyancy forces occur as a result of density fluctuations in a fluid subject to gravity, and they create a wide range of important phenomena in many fields of fluid mechanics. Progress in this field has generally been driven by a desire to find solutions to very real issues, like those in hydraulic engineering or meteorology sectors. Khan et al. (Khan et al., 2021) swotted the buoyant effect on the flow of hybrid NPs along a vertical plate using the Darcy Brinkman model. Guderi et al. (Mohammed Alshehri et al., 2021) imposed the Cattaneo Christov model to investigate the thermal transfer rate of an SWCNT/MWCNT nanofluid including micropolar fluid via a partly slipped vertical riga plate. Sandeep et al. (Sandeep et al., 2022) examined the convective phenomenon with a buoyancy effect in a nanofluid flow. Samrat et al. (Samrat et al., 2022) analyzed the radiation effects of the stream of an unstable non-Newtonian fluid. Li et al. (Li et al., 2022) swotted the flow of a Maxwell micropolar hybrid NF in an exponentially stretched/shrunk vertical sheet approaching a stagnation point comprising buoyant assisting and opposing flow.
It is not always necessary for the stretching surface to be linear, as in situations involving stretching plastic sheets. Due to its usage in the manufacture of plastic films, polymer sheets, metal wires, paper, glass fiber and other materials, the heat transfer analysis of boundary layer flow across an exponentially extending surface with specified temperature or heat flux has drawn a lot of interest. Neethu et al. (Neethu et al., 2022) conducted research using an exponentially extending sheet to investigate multiple linear regression on a bioconvective hybrid NF flow. Guderi et al. (Guedri et al., 2022) investigated the three-dimensional flow and thermal transport of a third-grade fluid across an exponentially stretched sheet. Awan et al. (Awan et al., 2020) numerically investigated the chemical effects on the second-grade fluid flow across an oscillatory stretched sheet. Krishnamurthy et al. (Krishnamurthy et al., 2015) explored the role of viscous dissipation and magnetic field on the flow and heat transport of a NF using an exponentially stretched sheet. Sandhya et al. (Sandhya et al., 2021) investigated the impact of buoyant forces and activation energy on a hydromagnetic radioactive flow along an exponentially stretched surface.
In view of the above-served literature, no work is carried out on an exponentially stretching sheet in assisting and opposing the behavior of ternary nanofluid including thermal radiation and porous medium. Here, we considered suspension of three different NPs in the base liquid water. According to the available research, one of the key aspects of channel flows is water dynamics. This applies regardless of the amount of the water. Water is commonly used in commercial settings due to the fact that it can be obtained without much trouble, is very inexpensive, and may be dissolved to produce a solution, suspension, or colloidal suspension. Because of this, the incorporation of nanoparticles is required in order to alter the attributes of water's poor thermal conductivity, which is caused by the fact that water naturally has a pH of 7 and may exist in three different states while maintaining a high surface tension (Animasaun et al., 2022).
Based on the aforementioned accessible literature analysis. No work is conducted to study the impact of assisting and opposing flow behavior with porous and thermal radiation in the combination of ternary nanofluid over an exponential stretched surface. The present investigation is carried out to investigate assisting and opposing the behavior of ternary nanofluid over an exponential stretched surface including thermal radiation and porous medium. The governing equations that represent momentum and temperature equations are reduced to ODEs using similarity constraints. The results are numerically tackled with RKF-45 and the shooting procedure. The analysis of the results and important engineering coefficients are discussed in brief. Finally, the purpose of this article was to answer the relevant research questions:
-
●
What effect do several significant factors have on the dynamics of flow, mass, and heat transfer behavior?
-
●
What is the impact of thermal radiation factor on temperature profile.
-
●
What effect do several significant factors have on both assisting and opposing flows?
-
●
What impact does increase of different parameters have on skin friction and heat transfer rate?
2 Mathematical background of the study
Let us consider the two-dimensional ternary hybrid NF flow through an exponentially stretched sheet with subject to mixed convection and thermal radiation. The sheet's stretching direction is considered as the
axis, and the
axis is normal to the
axis (see Fig. 1(a)). The sheet is further extended while maintaining its fixed origin. The surface is elastic in nature and stretching in the direction of
with velocity
. The sheet is having the temperature of
variable and it is given by
. The far field temperature is denoted as
and the reference temperature is
. All over the liquid motion, liquid properties are assumed to be constant.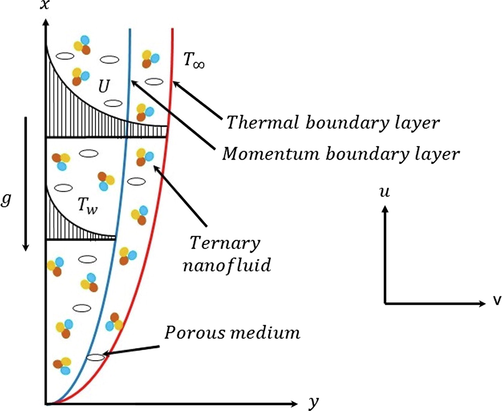
Geometric representation of the problem.
The governing equations for the presented issue are as follows based on the aforementioned assumption (see (Ferdows et al., 2012; Mukhopadhyay and Gorla, 2012; Sajid and Hayat, 2008; Manzur et al., 2018):
The boundary conditions (Madhukesh et al., 2021) are
From equation (3) the thermal radiation heat flux is considered according to Rosseland approximation (see (Rosseland, 1931) such that . Where is the mean absorption coefficient and is called the Stefan-Boltzmann constant. It is believed that the fluid-phase temperature variations within the flow are negligibly small, allowing to be stated as a linear function of temperature i.e. . Now substituting the equation of the radiation heat flux is reduced. Hence, we get and this is the reduced form of radiation heat flux.
The following suitable similarity variables are introduced (see (Mukhopadhyay and Gorla, 2012):
Using equation (6) in equation (2) and (3), one obtains the form as:
along with reduced boundary conditions:
where
is called the mixed convection parameter. Further, for
indicates the opposing flow and
indicates the assisting flow. Also,
,
, and
denote the Prandtl number, the radiation parameter and the porous permeability parameter, respectively. In above equations, the other mathematical symbols use for the ternary hybrid nanofluid and for the convenient it is demarcated as:
The following expressions provide the relation between thermophysical properties of nanoparticles with base liquid (see (Ashwinkumar et al., 2022).
These equations (10d) to (10p) represent the thermophysical properties of the ternary hybrid nanofluid, hybrid nanofluid and nanofluid, respectively.
In the present study, the major engineering aspects like
and
are stated as (see (Madhukesh et al., 2022). So, the expression for
(skin friction) is given as
The expression for
(Nusselt number) is given as
In the above expressions, the terms
and
are stated as,
By using (13) in (11–12) the expression simplified to
where is called the local Reynolds number.
3 Methodology and validation of the code
The RKF-45 strategy and shooting techniques (see refs. (Rehman et al., 2019; Ur Rehman et al., 2017; Rehman et al., 2017; Rehman et al., 2019; Rehman et al., 2017) are utilised to solve the governing equations (7 and 8) and simplified boundary conditions using well-known computational tools. We convert the modified equations into a system of first-order.
To convert the system of equations into first order, let us choose,
,
,
,
and
. The equations become
And the boundary conditions are
The IVP from equations (16 to 17) and (18) is quantitatively evaluated using the RKF-45 order approach, and unknown values are discovered using a shooting procedure with error tolerance and step size set to 10-6 and
correspondingly, meeting the boundary conditions at the infinity level. The numerical estimates are derived by applying the MATLAB built-in program bvp4c by substituting the values of the parameters
and utilizing the material characteristics of base liquid and NPs (see Table 1). The graphical results of each restriction are achieved by altering one parameter while holding the other parameters constant. The numerical validation of the code for
values between the current study and the published research is shown in Table 2 and Table 3, and there is a fair level of agreement between both.
Material
Aluminium oxide
3970
765
40
0.85
Silver
6500
540
18
1.89
Titanium Oxide
4250
686.2
8.9538
0.9
Water
997.1
4179
0.613
21
(Bidin and Nazar)
(Abd El-Aziz, 2009)
(Magyari and Keller, 1999)
(Mukhopadhyay and Gorla, 2012)
(Ishak, 2011)
Present study
1
0.9547
0.954785
0.954782
0.9547
0.9548
0.954955
2
1.4714
1.4714
1.4715
1.4714207
3
1.8691
1.869074
1.869075
1.8691
1.8691
1.8690440
5
2.500132
2.500135
2.5001
2.5001
2.5001089
10
3.660372
3.660379
3.6603
3.6604
3.6603543
(Khan et al., 2011)
(VIPM)
(Kameswaran et al., 2012)
(RKF)
Present study
(RKF-45)
−1.28138
−1.281809
−1.281805
The algorithm of the RKF −45 is given below (see (Mathews and Fink, 2004):
RK 4th order:
RK 5th order:
The six steps of the methodology as follows:
The flow chart of the numerical procedure is shown in the Fig. 1(b).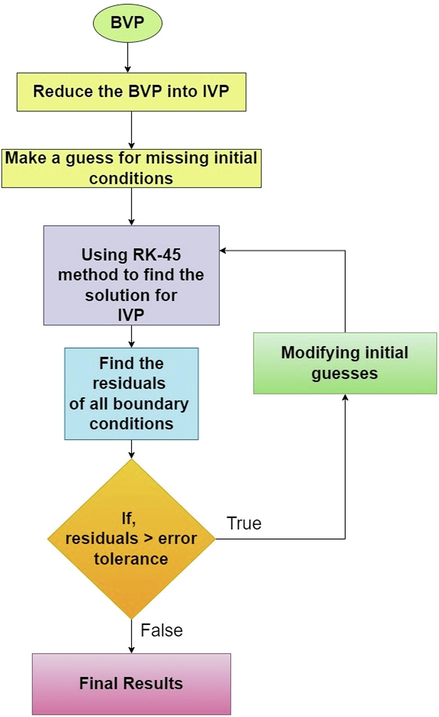
Numerical procedure algorithm.
4 Results and discussion
The current work investigates the THNF flow over an exponential stretching sheet with porous medium. The modelling also takes thermal radiation into account. By utilizing a suitable collection of similarity variables, the simulated issue is reduced to a dimensionless form for the current analysis. Some significant factors were found throughout this procedure, and the impact of these relevant parameters on the involved profiles is shown graphically and briefly described. The graphs and tables illustrate the heat transfer rates and friction factors for various value of different parameters. In the figures, the solid lines indicate assisting flow condition whereas, the dashed lines indicate opposing flow condition.
The impact of
on
for both opposing and assisting flow cases is displayed in Fig. 2. Here, increase in
value decreases the
for both flow conditions. The resistance of the system is improved by raising values of the porosity component. The larger frictional force causes the fluid flow to decrease. The resistance of the surface to liquid mobility in this situation is enhanced by increasing porosity. The increased resistance reduces liquid velocity. Moreover, the
declines faster for opposing flow case than the assisting flow case for incremented values of
.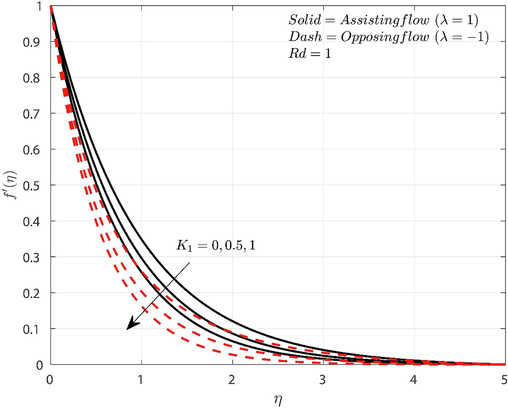
Influence of
on
The effect of
on
for both flow cases is displayed in Fig. 3. Here, upsurge in
value increases the
for both flow conditions. It is clear that the presence of a porous medium reasons for an advanced restriction to fluid flow, which leads to a decline in fluid velocity and an increase in the thickness of the thermal boundary layer and enhances
. Furthermore, the modified nanoliquid shows increased heat transport for opposing flow situation than the assisting flow situation for incremented values of
.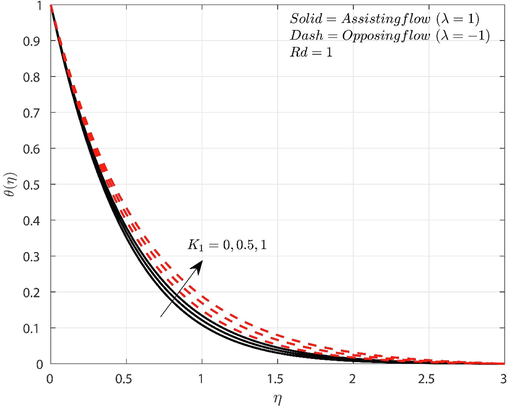
Influence of
on
The upshot of
on
for both flow cases is showed in Fig. 4. Here, upsurge in
value increases the
for both flow situations. The mean absorption coefficient is inversely related to
and decreases as
increases. Due to conductive heat transmission which is more effective than radiative heat transfer, the buoyancy force has decreased. In fact, a higher
effectively transports more heat to operating fluids, increasing thermal dispersion. The fluid becomes more heated when the
is set to a high value. The heat transmission thereafter considerably rises. Moreover, the modified nanoliquid shows increased heat transport for opposing flow situation than the assisting flow situation for incremented values of
.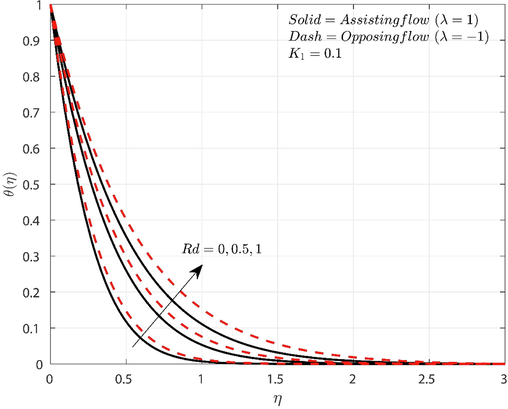
Influence of
on
Impact of
and
on
for both flow cases is displayed in Fig. 5. Here, augmented values of
and
improve the
in opposing flow and reverse behaviour is observed for assisting flow situation. This is due to the fact that improvement in the porous parameter will opposes the motion of the liquid also improvement in the solid volume fraction will enriches the momentum boundary layer as a result surface drag force increases Moreover, the modified nanoliquid show improved friction factor for opposing flow case than the assisting case with respect to increased
and
values. Figs. 6(a) and 6(b) represents the three-dimensional representation of friction factor for both assisting and opposing flow conditions.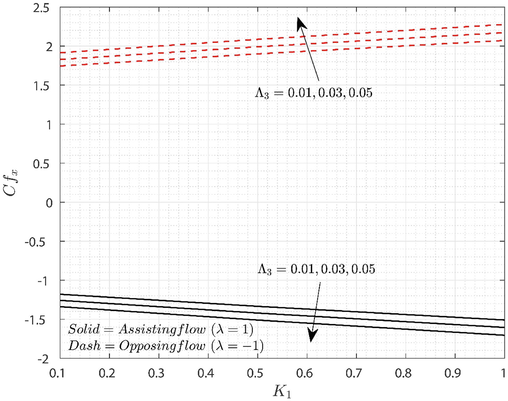
Influence of
and
on
.
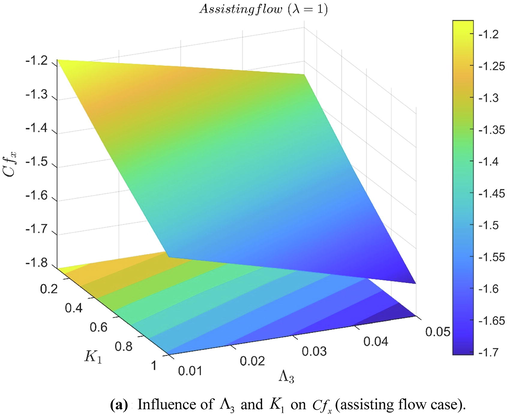
Influence of
and
on
(assisting flow case).
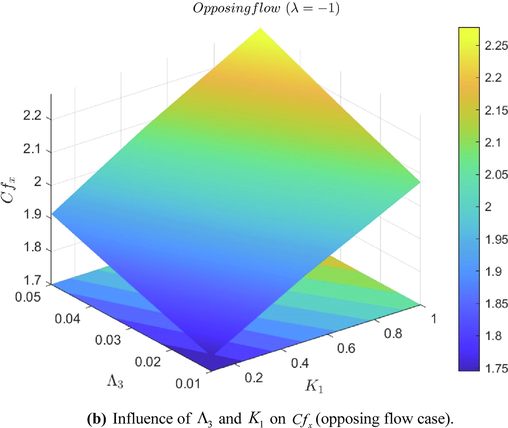
Influence of
and
on
(opposing flow case).
Impact of
and
on
for both flow cases is displayed in Fig. 7. Here, improved values of
advances the
for both flow situations but opposing trend is seen for increased
values. This is due to the fact that, increases in the values of
which leads to decrease
The radiative thermal flux indices and radiative heat transfer rates into the liquid will enhance as a consequence. The thickness of the thermal boundary layer is noticed due to improvement in
and enhanced radiative thermal transmission. Moreover, the modified nanoliquid show improved heat transport rate for assisting flow case than the opposing case with respect to increased
and
values. Figs. 8(a) and 8(b) represents the three-dimensional representation of heat transport rate for both assisting and opposing flow conditions. Computational values of
and
for dimensionless constraints is tabulated in Table 4 keeping
Here, the rise in values of
and
increases the
for both flow situations. Whereas, the
has negative impact on
for assisting flow case and positive impact
for opposing flow case. Finally, the rise in
,
and
declines the
for opposing flow case.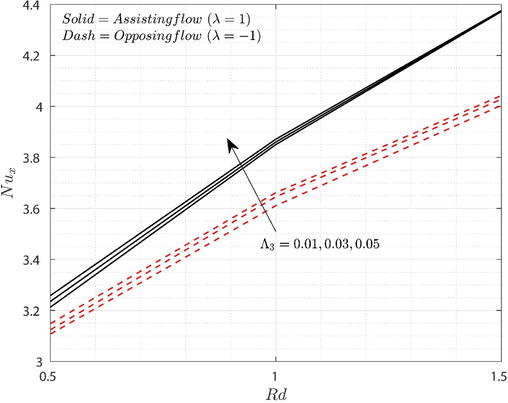
Influence of
and
on
.
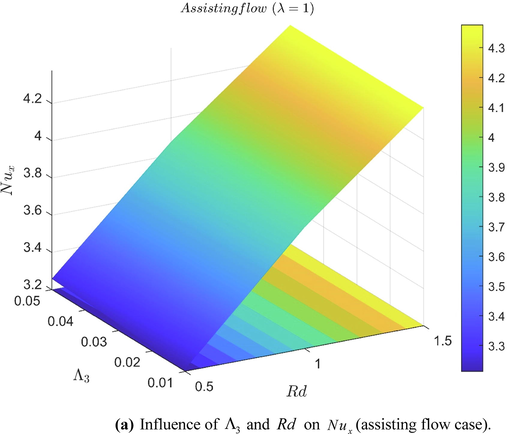
Influence of
and
on
(assisting flow case).
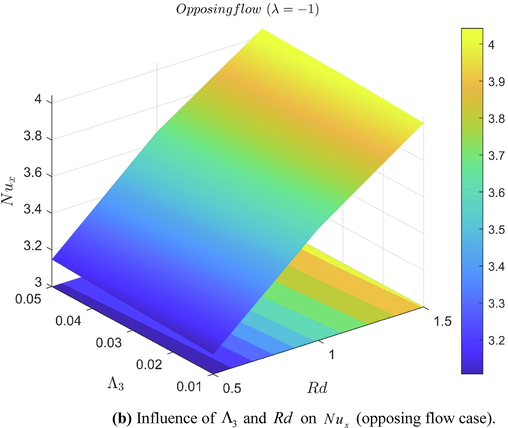
Influence of
and
on
(opposing flow case).
Parameters
Assisting flow
Opposing flow
0.01
0.1
1
1.272510067
1.893916857
1.428568475
1.861824562
0.03
1.272510070
1.893916868
1.428568480
1.861824558
0.05
1.272510070
1.893916868
1.428568480
1.861824558
0.01
0.1
1
1.272510067
1.893916857
1.425161820
1.812303724
0.5
1.412462391
1.858980580
1.564306516
1.775536556
1.0
1.572160912
1.818845927
1.722411822
1.733515855
0.01
0.1
0.5
1.284222776
2.385390279
1.414105182
2.277281476
1
1.272510022
1.893916483
1.425161760
1.812304283
1.5
1.263480468
1.603316161
1.433959327
1.531010992
5 Final remarks
The current study will examine the effects of thermal radiation and the porous medium when modified nanofluid flow is present across an exponential stretching sheet. Additionally, the work investigates two distinct scenarios of modified nanofluid flow, namely (i) assisting flow case and (ii) opposing flow case. Using similarity variables, the set of governing equations are converted into ODEs. Furthermore, the RKF-45 and shooting methods are used to numerically solve these equations. Graphs are used to illustrate the significant dimensionless constraints on flow and thermal profiles. Using tables and graphs the significant engineering coefficients are described. The key points are the following as
-
●
The declines faster for opposing flow case than the assisting flow case for incremented values of .
-
●
The modified nanoliquid shows increased heat transport for opposing flow situation than the assisting flow situation for advanced values of .
-
●
The modified nanoliquid shows increased heat transport for opposing flow situation than the assisting flow situation for augmented values of .
-
●
The modified nanoliquid show improved friction factor for opposing flow case than the assisting case with respect to increased and values.
-
●
The modified nanoliquid show improved heat transport rate for opposing flow case than the assisting case with respect to increased and values.
The current investigation is useful in the applications like supercapacitors, fuel cells, batteries, nanodevices and energy storage. The present work is conducted to investigate the ternary nanofluid flow across an exponential stretched surface with thermal radiation, porous medium and buoyancy effects. The current work can be extended to investigate concentration and bioconvection using different non-Newtonian fluids.
CRediT authorship contribution statement
J.K. Madhukesh: Conceptualization, Methodology, Software, Formal analysis, Validation, Writing – original draft. R. Naveen Kumar: Conceptualization, Methodology, Software, Formal analysis, Validation, Writing – original draft. Umair Khan: Conceptualization, Methodology, Software, Formal analysis, Validation, Writing – original draft. Rana Gill: Writing – original draft, Data curation, Investigation, Visualization, Validation. Zehba Raizah: Writing – original draft, Data curation, Investigation, Visualization, Validation. Samia Elattar: Conceptualization, Writing – original draft, Writing – review & editing, Supervision, Resources. Sayed M Eldin: Validation, Investigation, Writing – review & editing, Formal analysis. S.H.A.M. Shah: Provided significant feedback and assisted in the revised version of manuscript. Further, he also assisted us in revising the manuscript critically for important intellectual content. B. Rajappa: Writing – review & editing, Software, Data curation, Validation, Resources. Ahmed M. Abed: Writing – review & editing, Software, Data curation, Validation, Resources.
Acknowledgments
The author (Z. Raizah) extend her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP.2/154/43). Also, this work was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Moreover, this work is also supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
References
- Transportation of modified nanofluid flow with time dependent viscosity over a Riga plate: Exponentially stretching. Ain Shams Eng. J.. 2021;12:3967-3973.
- [Google Scholar]
- Viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Can. J. Phys.. 2009;87:359-368.
- [Google Scholar]
- Impact of thermophoretic particle deposition on Glauert wall jet slip flow of nanofluid. Case Studies in Thermal Engineering. 2021;28:101404
- [CrossRef] [Google Scholar]
- Effect of electromagnetic induction on the heat transmission in engine oil-based hybrid nano and ferrofluids: A nanotechnology application. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 2022 09544089221139569
- [CrossRef] [Google Scholar]
- Ratio of momentum diffusivity to thermal diffusivity: introduction, meta-analysis, and scrutinization. CRC Press; 2022.
- A generalized differential quadrature algorithm for simulating magnetohydrodynamic peristaltic flow of blood-based nanofluid containing magnetite nanoparticles: A physiological application. Numer. Methods Partial Differential Equations. 2022;38(3):666-692.
- [CrossRef] [Google Scholar]
- Convective heat transfer in MHD Cu-TiO2-H2O cross nanofluid flow over three diverse surfaces. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. Oct. 2022;236(5):1800-1807.
- [CrossRef] [Google Scholar]
- Theoretical study of unsteady oblique stagnation point based Jeffrey nanofluid flow over an oscillatory stretching sheet. Adv. Mech. Eng.. 2020;12(11) 1687814020971881
- [CrossRef] [Google Scholar]
- Magnetohydrodynamic oblique stagnation point flow of second grade fluid over an oscillatory stretching surface. Results Phys.. Sep. 2020;18:103233
- [CrossRef] [Google Scholar]
- Significance of nanoparticles aggregation and Coriolis force on the dynamics of Prandtl nanofluid: The case of rotating flow. Chin. J. Phys.. Oct. 2022;79:264-274.
- [CrossRef] [Google Scholar]
- Bidin, B., Nazar, R. Numerical Solution of the Boundary Layer Flow Over an Exponentially Stretching Sheet with Thermal Radiation, 8.
- Yogeesha, K.M., Megalamani, S.B., Gill, H.S., Umeshaiah, M., Madhukesh, J.K., The physical impact of blowing, Soret and Dufour over an unsteady stretching surface immersed in a porous medium in the presence of ternary nanofluid, Heat Transfer.
- Cao, W., A. I.l., S.-J. Yook, O. V.a., and X. Ji, “Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid,” International Communications in Heat and Mass Transfer, vol. 135, p. 106069, Jun. 2022, doi: 10.1016/j.icheatmasstransfer.2022.106069.
- Choi, S.U.S., Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles, Argonne National Lab. (ANL), Argonne, IL (United States), 1995.
- Ternary-hybrid nanofluids: significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with various shapes and densities. Zeitschrift für Naturforschung A. Mar. 2021;76(3):231-243.
- [CrossRef] [Google Scholar]
- Significance of deposition and diffusion retention on the performance of the composite membrane. Waves Random Complex Media May 2022:1-14.
- [CrossRef] [Google Scholar]
- Morphological properties of the interfaces growth of composite membranes. Mater. Today:. Proc. May 2022
- [CrossRef] [Google Scholar]
- Breaking process of composite membranes used in desalination phenomenon. Multidiscipline Modeling in Materials and Structures. Jan. 2022;18(2):249-261.
- [CrossRef] [Google Scholar]
- MHD Mixed Convective Boundary Layer Flow of a Nanofluid through a Porous Medium due to an Exponentially Stretching Sheet. Math. Probl. Eng.. 2012;2012:1-21.
- [Google Scholar]
- Theoretical analysis of SWCNT- MWCNT/H2OH2O hybrid flow over an upward/downward moving rotating disk. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems. Sep. 2021;235(3–4):97-106.
- [CrossRef] [Google Scholar]
- Insight into the heat transfer of third-grade micropolar fluid over an exponentially stretched surface. Sci Rep. Sep. 2022;12(1) Art. no. 1
- [CrossRef] [Google Scholar]
- MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana. 2011;40:391-395.
- [Google Scholar]
- On radiation effects on hydromagnetic Newtonian liquid flow due to an exponential stretching sheet. Boundary Value Problems. Oct. 2012;2012(1):105.
- [Google Scholar]
- A New Analytical Approach To Solve Exponential Stretching Sheet Problem In Fluid Mechanics By Variational Iterative Pade Method. The Journal of Mathematics and Computer Sciences. Aug. 2011;3:135-144.
- [Google Scholar]
- Buoyancy effect on the stagnation point flow of a hybrid nanofluid toward a vertical plate in a saturated porous medium, Case Studies. Therm. Eng.. 2021;27:101342
- [Google Scholar]
- Effect of viscous dissipation on hydromagnetic fluid flow and heat transfer of nanofluid over an exponentially stretching sheet with fluid-particle suspension. Cogent Mathematics.. 2015;2:1050973.
- [Google Scholar]
- Heat Transfer of Hybrid Nanomaterials Base Maxwell Micropolar Fluid Flow over an Exponentially Stretching Surface. Nanomaterials. Jan. 2022;12(7) Art. no. 7
- [CrossRef] [Google Scholar]
- Physical insights into the heat and mass transfer in Casson hybrid nanofluid flow induced by a Riga plate with thermophoretic particle deposition. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 2021 09544089211039305
- [CrossRef] [Google Scholar]
- Evaluation of heat and mass transfer characteristics in a nanofluid flow over an exponentially stretchable sheet with activation energy. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. 2022 095440892210748
- [Google Scholar]
- Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D: Appl. Phys.. 1999;32:577-585.
- [Google Scholar]
- A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf.. 2013;57:582-594.
- [Google Scholar]
- Mixed convection heat transfer to cross fluid with thermal radiation: Effects of buoyancy assisting and opposing flows. Int. J. Mech. Sci.. 2018;138–139:515-523.
- [Google Scholar]
- Numerical methods using MATLAB (4th ed.). Upper Saddle River, N.J: Pearson; 2004.
- Buoyancy Effect on a Micropolar Fluid Flow Past a Vertical Riga Surface Comprising Water-Based SWCNT–MWCNT Hybrid Nanofluid Subject to Partially Slipped and Thermal Stratification: Cattaneo-Christov Model. Math. Probl. Eng.. 2021;2021:e6618395.
- [Google Scholar]
- Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presence of thermal radiation. Heat Mass Transfer.. 2012;48:1773-1781.
- [Google Scholar]
- Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B Jul. 2022:2250170.
- [CrossRef] [Google Scholar]
- Multiple linear regression on bioconvective MHD hybrid nanofluid flow past an exponential stretching sheet with radiation and dissipation effects. Int. Commun. Heat Mass Transfer. 2022;135:106115
- [Google Scholar]
- Assessment of the local thermal non-equilibrium condition for nanofluid flow through porous media: a comparative analysis. Indian J Phys. Jul. 2022;96(8):2475-2483.
- [CrossRef] [Google Scholar]
- Impact of Binary Chemical Reaction and Activation Energy on Heat and Mass Transfer of Marangoni Driven Boundary Layer Flow of a Non-Newtonian Nanofluid. Processes. Apr. 2021;9(4) Art. no. 4
- [CrossRef] [Google Scholar]
- Numerical study of heat transfer enhancement in mixed convection flow along a vertical plate with heat source/sink utilizing nanofluids. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:4318-4334.
- [CrossRef] [Google Scholar]
- Numerical study of heat transfer enhancement in mixed convection flow along a vertical plate with heat source/sink utilizing nanofluids. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:4318-4334.
- [Google Scholar]
- Applications of nanofluids in condensing and evaporating systems. J. Therm. Anal. Calorim.. 2018;131:2027-2039.
- [Google Scholar]
- Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: application of passive control strategy and generalized transfer laws. Waves Random Complex Media May 2022:1-20.
- [CrossRef] [Google Scholar]
- Magneto-nanofluid numerical modelling of chemically reactive Eyring-Powell fluid flow towards both flat and cylindrical an inclined surface: A comparative study. AIP Adv.. Jun. 2017;7(6):065103
- [CrossRef] [Google Scholar]
- Numerical analysis subject to double stratification and chemically reactive species on Williamson dual convection fluid flow yield by an inclined stretching cylindrical surface. Chin. J. Phys.. Aug. 2017;55(4):1637-1652.
- [CrossRef] [Google Scholar]
- Group theoretical analysis for MHD flow fields: a numerical result. J Braz. Soc. Mech. Sci. Eng.. Mar. 2019;41(3):156.
- [CrossRef] [Google Scholar]
- Symmetry analysis on thermally magnetized fluid flow regime with heat source/sink. Case Studies in Thermal Engineering. Sep. 2019;14:100452
- [CrossRef] [Google Scholar]
- Astrophysik und atom-theoretische Grundlagen. Berlin: Springer; 1931. p. :41-44.
- Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev.. 2019;103:556-592.
- [Google Scholar]
- Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transfer. 2008;35:347-356.
- [Google Scholar]
- Insight into the motion of water conveying three kinds of nanoparticles shapes on a horizontal surface: Significance of thermo-migration and Brownian motion. Surf. Interfaces. Jun. 2022;30:101854
- [CrossRef] [Google Scholar]
- Aspects of magnetic dipole and heat source/sink on the Maxwell hybrid nanofluid flow over a stretching sheet. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 2022 09544089211056243
- [CrossRef] [Google Scholar]
- Effect of exponential heat source on parabolic flow of three different non-Newtonian fluids. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering. Oct. 2022;236(5):2131-2138.
- [CrossRef] [Google Scholar]
- Flow and heat transfer in radiative MHD dusty-hybrid ferrofluids. Waves Random Complex Media Feb. 2022:1-14.
- [CrossRef] [Google Scholar]
- Transpiration effect on Falkner-Skan bioconvective mixed nanoliquid flow above a poignant wedge. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022 09544062221134387
- [CrossRef] [Google Scholar]
- Buoyancy forces and activation energy on the MHD radiative flow over an exponentially stretching sheet with second-order slip. Heat Transfer.. 2021;50:784-800.
- [Google Scholar]
- Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO) Case Studies in Thermal Engineering. Jul. 2022;35:102046
- [CrossRef] [Google Scholar]
- Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Studies in Thermal Engineering. Aug. 2021;26:101050
- [CrossRef] [Google Scholar]
- A comparative study of nanofluids flow yields by an inclined cylindrical surface in a double stratified medium. Eur. Phys. J. Plus. Oct. 2017;132(10):427.
- [CrossRef] [Google Scholar]
- “Magneto-Marangoni nano-boundary layer flow of water and ethylene glycol based γ Al2O3 nanofluids with non-linear thermal radiation effects”, Case Studies. Therm. Eng.. Sep. 2018;12:340-348.
- [CrossRef] [Google Scholar]
- A Novel Numerical Procedure for Simulating Steady MHD Convective Flows of Radiative Casson Fluids over a Horizontal Stretching Sheet with Irregular Geometry under the Combined Influence of Temperature-Dependent Viscosity and Thermal Conductivity. Math. Probl. Eng.. May 2020;2020:e1675350.
- [Google Scholar]
- Dynamics of radiative-reactive Walters-b fluid due to mixed convection conveying gyrotactic microorganisms, tiny particles experience haphazard motion, thermo-migration, and Lorentz force. Phys. Scr.. Oct. 2021;96(12):125239
- [CrossRef] [Google Scholar]
- Aspects of Uniform Horizontal Magnetic Field and Nanoparticle Aggregation in the Flow of Nanofluid with Melting Heat Transfer. Nanomaterials. 2022;12(6) Art. no. 6
- [CrossRef] [Google Scholar]
- Gear-generalized differential quadrature analysis of oscillatory convective Taylor-Couette flows of second-grade fluids subject to Lorentz and Darcy-Forchheimer quadratic drag forces. Int. Commun. Heat Mass Transfer. Jul. 2021;126:105395
- [CrossRef] [Google Scholar]
- Dynamics of ternary-hybrid nanofluids due to dual stretching on wedge surfaces when volume of nanoparticles is small and large: forced convection of water at different temperatures. Int. Commun. Heat Mass Transfer. Oct. 2022;137:106241
- [CrossRef] [Google Scholar]
- Significances of blowing and suction processes on the occurrence of thermo-magneto-convection phenomenon in a narrow nanofluidic medium: A revised Buongiorno’s nanofluid model. Case Studies in Thermal Engineering. Dec. 2020;22:100726
- [CrossRef] [Google Scholar]







