Translate this page into:
Insight into the significance of nanoparticle aggregation and non-uniform heat source/sink on titania–ethylene glycol nanofluid flow over a wedge
⁎Corresponding author. sayed.eldin22@fue.edu.eg (Sayed M Eldin),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The properties of nanoparticles in the working fluid are affected by many external factors and it further influences the effective properties of the resulting nanofluid. To study the heat transference mechanism in nanofluids, the inclusion of such factors is quite important as it provides the exact illustration of the mechanism. One such factor is the nanoparticle aggregation effect. Authors have studied the titania–ethylene glycol nanofluid (TiO2/EG NF) flow over a wedge with nanoparticle aggregation effect. Through this communication, authors have attempted to make a development on the Falkner-Skan problem. The flow is developed in the presence of the suction/injection effects, mixed convection, thermal radiation, porous medium, and non-uniform heat source/sink. To account for the influence of nanoparticle aggregation, revised forms of the Maxwell and Bruggeman models and the Krieger-Dougherty model are employed to estimate the effective thermal conductivity and viscosity of TiO2/EG NF, respectively. The aforementioned modified models developed for TiO2/EG NF gave a soundly close agreement with the experimental data. The governing equations are numerically solved employing the “bvp4c function in MATLAB”. The effect of the primary relevant parameters on the velocity, temperature, and heat transmission rate is depicted graphically. The heat transmission rate at the surface is higher with aggregated nanoparticles in comparison to its absence. The higher NPs volume fraction and the aggregation effect enhance the effective viscosity, the fluid becomes denser, and as a result, the velocity decreases. The outcomes of this study will be useful in many fields that utilize applications of flow over wedge such as in raw oil extraction, storage of nuclear waste, insulating heat exchangers, etc.
Keywords
TiO2/EG nanofluid
Falkner–Skan problem
Nanoparticle aggregation
Porous medium
Thermal radiation
Non-uniform heat source/sink
Nomenclature
- ,
-
Heat source/sink parameter
-
Skin friction
- D
-
Fractal (constant) index
-
Dimensionless stream function
-
Dimensionless velocity
-
Local Grashof number
- g
-
Acceleration due to gravity (m/s2)
- k
-
Thermal conductivity (W/mK)
- k*
-
Mean absorption coefficient (m−1)
- Ko(x)
-
Permeability of the porous medium (m2)
- m
-
Angle
-
Nusselt number
- Pr
-
Prandtl number
-
Non-uniform heat source/sink term
- qr
-
Radiative heat flux (W/m2)
- Rd
-
Thermal radiation parameter
- Rex
-
Local Reynolds number
- ra
-
Radius of nanoparticles aggregates
- rp
-
Radius of individual nanoparticles
- S
-
Suction/injection parameter
- T
-
Temperature (K)
-
Temperature of the surface (K)
-
Free stream temperature (K)
-
Components of velocity (m/s)
-
Stretching/shrinking velocity (m/s)
-
Free stream velocity (m/s)
-
Velocity of mass transfer
-
Cartesian coordinates (m)
-
Porosity parameter
- λ
-
Stretching/shrinking parameter
-
Mixed convection parameter
-
Thermal expansion (K−1)
-
Hartree pressure gradient parameter
-
Volume fraction of individual nanoparticles
-
Volume fraction of nanoparticles aggregates
-
Kinematic viscosity (m2/s)
-
Dynamic viscosity (kg m−1 s−1)
-
Density (kg/m3)
-
Stream function
-
Stefan–Boltzmann constant (W. m−2. K−4)
-
Total angle of the wedge
-
Heat capacity (J/m3K)
-
Intrinsic viscosity constant
-
Similarity variable
-
Dimensionless temperature
-
Constants
Greek symbols
- f
-
Base fluid
- nf
-
Nanofluid
- p
-
Individual nanoparticle
- a
-
Nanoparticle aggregates
Subscripts
- ′
-
Derivative w.r.t
Superscripts
1 Introduction
Heating and cooling applications of working fluids are critical in nuclear and chemical reactors, electronic devices, etc. Effective cooling procedures are necessary for cooling high-energy structures. The thermal performance of some common coolants (water, oil, ethylene glycol, etc.) is not significant and hence they are not able to perform as an efficient coolant. The last two decades have seen progressive research on enhancing the thermal efficiency of various fluids. More than two decades ago, it was discovered that the suspension of nanoparticles (NPs) in a working fluid contributes to increasing the thermal performance of the resultant fluid and these resultant fluids were named nanofluids (NFs) (Choi, 1995). The variation in size (diameter), substance (oxides of metal, nonmetal, metal, etc.), and dispersion of NPs, the different features of the NFs may be adjusted (Kumar et al., 2020; Sumithra and Sivaraj, 2022; Indumathi et al., 2022, and Ibrahim et al., 2021c). Because of this remarkable property, NFs are used in both traditional industries and solar technologies (Kumar et al., 2021; Vijayalakshmi and Sivaraj, 2022; Abdul Hakeem et al., 2016; Chu et al., 2021a; Madhukesh et al., 2021). Ibrahim et al. (Ibrahim et al., 2021a) studied the effect of SiO2 NPs on the thermal conductivity of different base fluids. They concluded that for ethylene glycol and glycerol base fluid, SiO2 NPs improve thermal conductivity by 12% and 6%, respectively.
The NF flows in various contexts are theoretically studied using the two-phase model (see Buongiorno, 2006) and the single-phase model (see Tiwari and Das, 2007). The NFs flow in various contexts is investigated using these models. Numerous authors have investigated different NFs flow over various geometries using various combinations of NPs and base fluid (BF). Santhosh et al. (Santhosh et al., 2023) explicated the thermal efficiency of Cu/water and Al2O3/water NF flow in a porous rectangular cavity with heat source/sink and Joule heating. Ganga et al. (Ganga et al., 2016) investigated the influence of heat source/sink and radiation on the magnetohydrodynamics flow of a nanofluid over a vertical plate. Mishra and Kumar (Mishra and Kumar, 2020) analyzed the flow of Ag/water over a stretching cylinder with self-heating and velocity slip effects. (Ragupathi et al. (Ragupathi et al., 2019) expounded on the heat transference mechanism of an NF flow with Fe3O4 and Al2O3 NPs with different base fluids past a Riga plate with a non-uniform heat source/sink. Shafiq et al. (Shafiq et al., 2020) explicated the thermal performance of three-dimensional NF flow in a rotating frame with convective heating and thermal slip effects. Adnan et al. (Adnan et al., 2020) studied the impacts of freezing temperature and the diameter of NPs on the heat transfer rate (HTR) over a curved Riga surface. Reddy et al. (Reddy et al., 2021) investigated the water-based NF flow with molybdenum disulfide and ferro sulfate NPs over a rotating disk with a magnetic field. Thirumalaisamy and Ramachandran (Thirumalaisamy and Ramachandran, 2023) analyzed the Fe3O4/water NF and Fe3O4-Cu/water hybrid NF flow in a square porous cavity with heat source/sink effects. Ganesh Kumar (Ganesh Kumar, 2022) and Gnaneswara Reddy et al. (Gnaneswara Reddy et al., 2020) expounded on the HTR of the water-based NF with AA7072-AA7075 alloys NPs over a stretching sheet and semi-infinite heated plate, respectively. Prakasha et al. (Prakasha et al., 2023) explicated the applications of non-linear radiation on ethylene glycol-based heat transfer rate of hybrid NF (Graphene, Magnesium oxide) and ternary hybrid NF (Graphene, Zirconium oxide, Magnesium oxide) over a plate. Nayak et al. (Nayak et al., 2019) studied the influence of a non-uniform heat source/sink and the Cattaneo-Christov heat flux model of third-grade nanofluid over an inclined and stretching Riga plate. Chu et al. (Chu et al., 2021b) studied the free convective flow of the Cu-Al2O3/H2O NF in a microchannel. Khan et al. (Khan et al., 2021) investigated the bioconvection aspects in non-Newtonian nanofluid over periodically moving surface with chemical reaction and activation energy effects. Some other remarkable studies regarding the NF flow and their thermal performance can be referred to from Refs. (Hakeem et al., 2018; Ibrahim et al., 2021b; Khan et al., 2020; Puneeth et al., 2022; Thirumalaisamy et al., 2022).
The suspension of NPs in a working fluid is affected by various physical phenomena. The NPs behavior in the suspension and hence the properties of NFs are significantly affected by these physical factors. One such important factor in the suspension is the NPs aggregation. The resilient covalent and metallic bond between the NPs is the reason NPs aggregation occurs (Chen et al., 2007, 2020; Motevasel et al., 2018). The covalent and metallic bonds tend to hold the NPs together and hence they form the cluster known as NPs aggregates. As a result, rather than being present as individuals in a BF, NPs are present in clusters (see Fig. 1). Many studies (Chen et al., 2007, 2020; Motevasel et al., 2018) have experimentally validated the claim that the NPs aggregation severely affects the thermal performance and properties of NFs. Motevasel et al. (Motevasel et al., 2018) expounded on the significance of NPs aggregation effect on thermal conductivity (TC). They demonstrated that NPs aggregation has a significant impact on the physical features, thermal proficiency, rheology, and heat transference of BFs. They strenuously argued for the inclusion of the NPs aggregation effect even at low concentrations. Chen et al. (Chen et al., 2020) published a study based on experimental results to explicate the NPs aggregate influence on the thermal radiative properties of NFs. In their study, they also provided the theoretical models and correlations for the inclusion of NPs aggregation and validated the theoretical models and correlations with the experimental data. Chen et al. (Chen et al., 2007) published an experimental study that presents the rheology of ethylene glycol (EG) based NF with spherical Titania (TiO2) NPs with NPs aggregates. They found from their experiments that the Maxwell model underrates thermal conductivity. Furthermore, they suggested that the Maxwell model could be modified to include the NPs aggregate influence on TC. For the modification, they suggested that the Bruggeman model can be used to calculate the TC of NPs aggregates and the value be substituted back in the Maxwell model for predicting the TC of NFs. They also validated that the shear viscosity of the NFs strongly depends on the NPs aggregates. Their modified models and correlations for TC and shear viscosity of the TiO2/EG NF gave a soundly close precision with the data obtained through the experiment. In the second half of the last decade, few authors (Mackolil and Mahanthesh, 2021a, 2021b; Madhukesh et al., 2022; Mahanthesh and Thriveni, 2021a, 2021b; Rana et al., 2021; Wang et al., 2022) have studied the NPs aggregation effect on the NFs flows. Mackolil and Mahanthesh (Mackolil and Mahanthesh, 2021a, 2021b) studied the boundary layer flow of TiO2/EG NF in presence of Marangoni convection and NPs aggregation effects. Rana et al. (Rana et al., 2021) investigated the influence of NPs aggregates on the HTR of TiO2/EG NF flow over a plate with considerable buoyancy force. Madhukesh et al. (Madhukesh et al., 2022) explicated the significance of NPs thermophoretic deposition on the TiO2/water NF over a rotating sphere with NPs aggregation effect. Wang et al. (Wang et al., 2022) expounded on the influence of chemical reactions on the HTR of TiO2/EG NF flow over a rotating disk. Mahanthesh and Thriveni (Mahanthesh and Thriveni, 2021a, 2021b) studied the HTR of TiO2/EG NF flow over a vertical cylinder with thermal radiation and the HTR of TiO2/EG NF flow over a cylinder with heat generation and NPs aggregation effect, respectively. Some other remarkable investigations regarding the HTR of NF and their thermal performance with NPs aggregation effect can be referred from Refs. (Ali et al., 2022; Yaseen et al., 2022; Yu et al., 2022).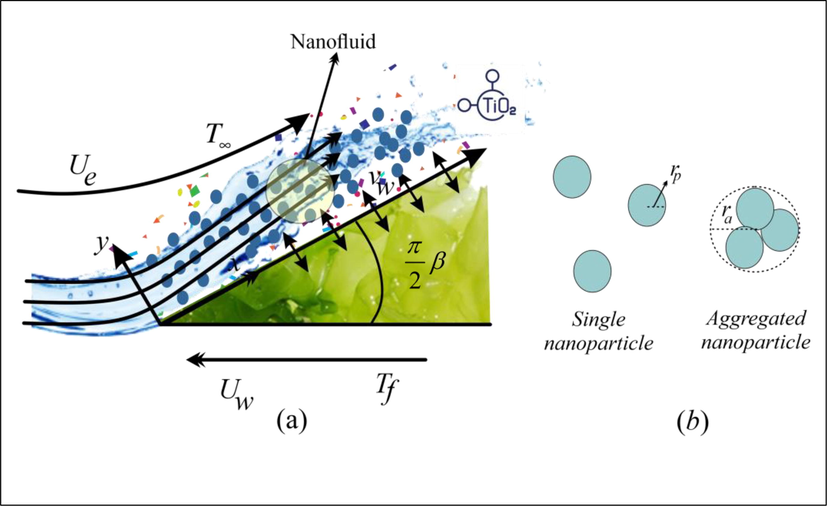
Physical Representation.
NFs flow towards a wedge is an interesting topic to study due to the entrancing applications in engineering, such as in geothermal systems, raw oil extraction, storage of nuclear waste, insulating heat exchangers, etc. These applications have prompted scholars to investigate the NF flow across a wedge. Falkner and Skan (Falkner and Skan, 1931) were the first to use a wedge to configure fluid flow. Since then various researchers (Bano et al., 2020; Ibrahim and Tulu, 2019; Kudenatti and L., 2021; Mishra and Kumar, 2021; Raju and Sandeep, 2016; Sandeep and Reddy, 2017) have made many developments on the flow towards/over a wedge. The focus of the aforementioned studies was to study the HTR of a viscous or NFs but they have ignored the kinematics of NPs aggregation effect. Some studies (Ellahi et al., 2016; Rehman et al., 2022; Yaseen et al., 2022) have been published to investigate the NFs flow over a wedge with NPs aggregation effect, but the investigations have been done ignoring the various body and surface forces. Hence, the influence of NPs aggregation and the rheology of NPs aggregation kinematics on NF flow over a wedge needs resolute attention. TiO2 NPs suspended in the base fluid (to increase their thermal characteristics) is a worthy combination because TiO2 NPs have a more stable chemical nature compared to their other metallic state. Furthermore, TiO2 has a relatively cheap manufacturing cost, and TiO2 NPs are manufactured on a big scale in industries. Authors of the present study have made a development on the Falkner-Skan problem and studied the NPs aggregation influence on the HTR of TiO2/EG NF flow over a wedge (refer to Fig. 1). As a novelty, authors have considered the influence of mixed convection, thermal radiation, porous medium, and non-uniform heat source/sink together with the suction/injection effect. The author's goal with this investigation was to thoroughly analyze the influence of NPs aggregation. Furthermore, the following are the primary goals of the current study:
-
Development of Falkner-Skan problem with NPs aggregation effect and important body and surface forces.
-
Influence of NPs aggregation on the thermal field.
-
Analyzing the HTR of TiO2/EG NF flow with and without NPs aggregation.
The authors have specifically considered the TiO2/EG NF for this investigation and modeling of the flow with NPs aggregation effect. Appropriate models for viscosity and TC were required to include the NPs aggregation effect and Chen et al. (Chen et al., 2007) have experimentally studied the values of viscosity and TC for the TiO2/EG NF with NPs aggregation effect and have also provided the theoretical models for the same. Their modified models and correlations for TC and shear viscosity of the TiO2/EG NF gave a soundly close agreement with the experimental data.
2 Mathematical model
Consider the TiO2/EG flow (ethylene glycol-based NF with Titania NPs) and heat transference towards a wedge in a porous medium with permeability under the influence of buoyancy force. The surface of the wedge is coincident with the x-axis and the y-axis is delineated normal to it (see Fig. 1). The free stream velocity of TiO2/EG NF flow is where ue is constant. In addition, the wedge is moving with velocity , where uw is constant and the stretching and shrinking wedge are denoted by uw > 0, and uw < 0; and uw = 0 for a stationary wedge. Here, m is the angle and , where is the Hartree pressure gradient parameter. The total angle of the wedge is and . Moreover, the flow over a wedge is modeled when . In addition, the flow past a flat surface along a horizontal axis is denoted by, , and denotes the stagnation point flow past a vertical flat surface. The HTR is analyzed in presence of thermal radiation and a non-uniform heat source/sink. The temperature of the surface is assumed as and the free stream temperature of TiO2/EG NF flow is considered as . The boundary layer flow is subjected to suction/injection with as mass transfer velocity at the surface. Moreover, the last term in the energy equation (Eqn. (3)) stands for the non-uniform heat source/sink term and it is explained later.
The governing equations of the TiO2/EG nanofluid flow over a wedge are written as follows (see Refs. (Anuar et al., 2021; Khan et al., 2022; Mishra and Kumar, 2021; Waini et al., 2020; Yaseen et al., 2022):
Continuity Equation:
Momentum Equation:
Energy Equation:
Boundary Conditions (BCs) (see Refs. Mishra and Kumar, 2021; Yaseen et al., 2022):
2.1 Modeling of nanofluid properties with nanoparticles aggregation effect
The properties of TiO2/EG NF are modeled credibly by considering the kinematics of NPs aggregation. Chen et al. (Chen et al., 2007) in their published study reported the models to consider for TiO2/EG NF to employ the NPs aggregation influence. Their theoretical models and correlations were in brilliant agreement with the experimental findings. The traditional models of NFs that do not consider the NPs aggregation influence and the models proposed by Chen et al. (Chen et al., 2007) are thoroughly summarized and compared in Table 1.
Properties
Without aggregation
With aggregation
Dynamic viscosity
Density
Thermal conductivity
Thermal expansion coefficient
Heat capacitance
2.1.1 Volume fraction of TiO2 nanoparticles aggregates
The aggregates of NPs are not uniform throughout the aggregate structure, it is anticipated that the density varies with the radial position according to the power law. The volume fraction of NPs aggregates
is determined by the following relation (Chen et al., 2007):
2.1.2 Viscosity of TiO2/EG nanofluid with nanoparticles aggregates
The effective viscosity of TiO2/EG with NPs aggregates is given by revising the Krieger-Dougherty model and the revised model gives the precise estimation of TiO2/EG NF viscosity. The revised model for viscosity is as follows (Chen et al., 2007):
2.1.3 Thermal conductivity of TiO2/EG nanofluid with nanoparticles aggregates
The thermal conductivity for various NFs or homogeneous mixtures is most of the time estimated by the traditional Maxwell equation as follows:
Other models used in this study are summarized in Table 1 (see (Mackolil and Mahanthesh, 2021a)). The physical properties of TiO2 NPs and ethylene glycol are summarized in Table 2 (see (Madhukesh et al., 2022; Yaseen et al., 2022)).
ρ(Kg/m3)
Cp(J/KgK)
k(W/mK)
Ethylene glycol
1114
2415
0.252
57
TiO2
4250
686.2
8.9538
1.05
0.0157
2.2 Similarity transformations
The following similarity variables are applied to the system of Eqns. (1)–(3), and BCs (4) (see Refs. (Anuar et al., 2021; Yaseen et al., 2022)):
Here, is the stream function and is similarity variable, is the dimensionless temperature and f is the dimensionless stream function, and for this study. After computations, the Eqns. (1)–(3), and BCs (4) are transformed as:
Reduced momentum Equation:
Reduced energy Equation:
Reduced BCs:
The dimensionless parameters in aforementioned Eqns. (12)–(14) are as follows:
are constants, is mixed convection parameter, where is the local Grashof number and is the local Reynolds number. Furthermore, symbolizes the porosity parameter, represents the thermal radiation parameter, represents the Prandtl number, represents the stretching/shrinking parameter (of the wedge), denotes the suction/injection parameter, and are heat source/sink parameter.
To have the similarity solution of the Eqns. (12)–(13) with the BCs (Eqn. (14)), the term of × must vanish from these equations. It is noticed that the mixed convection parameter appearing in the Eqn. (9) when computed in the simplified form will be written as . Further simplification will lead to the value of the parameter as . Therefore, a similar solution will exist only when because the term × will vanish. For a similar solution to exist and for computations of results of this study, the value of parameter m is strictly restricted .
3 Engineering parameter
The physical quantity of significance in this study is the skin friction Cf and Nusselt number Nux (Yaseen et al., 2022):
Using Eqns. (11) and (16), the skin friction and Nusselt number in equation (15) is written as:
4 Methodology of numerical approach
This section focuses on the methodology used for deducing solutions as well as code validation. The equations are at first modeled as PDEs and later, altered into ODEs via similarity variables. The solution of the Eqns. (12)–(13) along with BCs (14) is deduced with the “bvp4c function” (a built-in package in MATLAB), the more specific details of the bvp4c function can be referred from the Shampine et al. (Shampine et al., 2003). The “bvp4c function” uses a finite difference scheme together with a precision of fourth order with the help of the “3-stage Lobatto IIIA formula” (Khan et al., 2020). The appropriate thickness of the boundary layer, point depicting the far field
, and initial guess must be selected relying on the parameters applied, to obtain accurate solutions. To deduce the solution of the model, the ODEs obtained after similarity transformation are reduced into first-order ODEs by the following substitution (Yaseen et al., 2022):
Utilizing the new variables, the Eqns. (12)–(13) are reduced to first-order ODEs and the following MATLAB syntax is used:
The following MATLAB syntax is used for BCs at the surface and far-field:
Then, the numerical solutions are obtained by coding Eqns. (18)–(20) into the bvp4c solver. The output of bvp4c is a structure called “sol”. The syntax of the solver is given by “sol = bvp4c (@OdeBVP, @OdeBC, solinit, options)” which consists of several functions (Yaseen et al., 2022). The “@OdeBVP” function is where the Eqns. (18)–(19) are coded. The “@OdeBC” function is employed to code the BCs (20). The “solinit” function is used to code the initial mesh points and the initial solution approximation at the mesh points (Khan et al., 2020). Meanwhile, the “options” function is an optional argument for integration. The solver will then run and the outcomes will be printed out as numerical solutions and graphs. Furthermore, the values of missing conditions are guessed to initiate the process of finding the solution and other parameters present in the Eqns. (19) and (20) are set to find the desired solution. The process of iteration is repeated and the solution is accepted only when the conditions in Eqn. (20) are satisfied asymptotically. The process of finding the solution is shown via a flow chart in Fig. 2. To validate the model and the code used to find the numerical solution, an assessment in Table 3 is outlined with the published computations of Yacob et al. (Yacob et al., 2011) and Anuar et al. (Anuar et al., 2021) as a limiting case to validate the numerical code utilized to solve the current model. The comparative results are quite consistent, ensuring that the current conclusions are valid.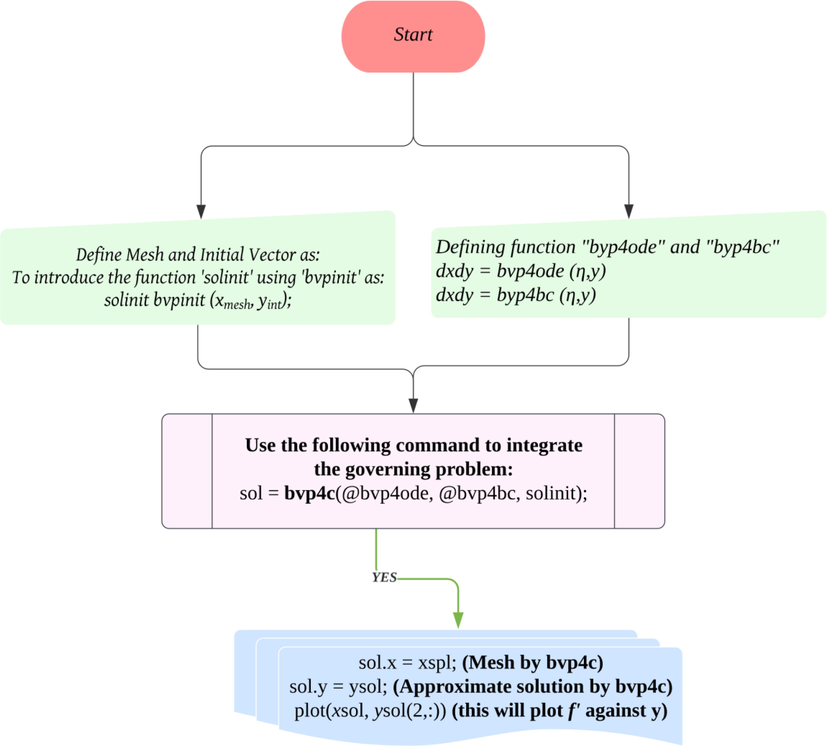
Flow chart.
m
Yacob et al. (Yacob et al., 2011)
Anuar et al. (Anuar et al., 2021)
Present Results
0
0.4696
0.4696
0.46960055
1/11
0.655
0.655
0.65499374
1/5
0.8021
0.8021
0.80212722
1/3
0.9277
0.9277
0.92768008
1/2
1.0389
1.0389
1.03890348
1
1.2326
1.2326
1.23258766
5 Results and discussion
This communication explores the impact of NPs aggregation on the flow of TiO2/EG NF over a wedge. This section of the paper deals with the results and their analysis. The results are depicted graphically and through tabular values for TiO2/EG NF over the wedge for two cases: with and without NPs aggregation. The discussion is focused on the velocity , temperature , skin friction, and Nusselt number of TiO2/EG NF on the surface of the wedge. In the figures, the dotted lines depict the solution for TiO2/EG NF without aggregation and solid lines depict the solution for TiO2/EG NF flow with aggregation. During the derivation of the solution, authors have used the following general values of the parameters (present in Eqns. (19) and (20)) during the numerical computations: , , , , , , and .
5.1 Discussion of velocity profiles
Figs. 3-7 visualize the impact of emerging parameters on the velocity profile
. Fig. 3 displays the velocity
for different estimates of mixed convection parameter
. The negative values
and positive values
of the mixed convection parameter
denote the case of opposing flow and assisting flow, respectively. Fig. 3 demonstrates that TiO2/EG NF velocity
increases with an increment in parameter
. The findings indicate that the velocity
of the TiO2/EG NF rises for assisting flow and the magnitude of resistive forces escalates for opposing flow, hence the velocity
is low for the negative value of the parameter
. The convection phenomenon is the mechanism of transportation of heat. This phenomenon causes motion because of variation in fluid density, which occurs due to temperature gradients. An increment in the parameter
correlates to the increased buoyancy forces and indicates a favorable pressure gradient scenario throughout the flow, increasing the velocity profiles. Fig. 4 displays the velocity
for deviation in the porosity parameter
. The findings indicate that the velocity
rises with an increment in the parameter
. The increase in velocity is due to less resistance experienced by the TiO2/EG NF during its movement in the boundary layer region. The increasing porosity parameter corresponds to a fall in the magnitude of surface resistive forces, and consequently, the velocity rises. Fig. 5 displays the velocity
for diverse estimates of suction/injection parameter S. The negative
and positive
values of parameter S symbolize the injection and suction, respectively. Furthermore
symbolizes the non-existence of both. The graph demonstrates that the velocity of TiO2/EG NF increases when parameter S is increased. The findings indicate that applying suction at the surface aids the velocity of the TiO2/EG NF. The application of suction involves the removal of the layers with zero velocity. The removal of such layers reduces the friction provided to layers in motion. Consequently, the velocity rises. It confirms that the application of suction in the present model helps delay the boundary layer separation.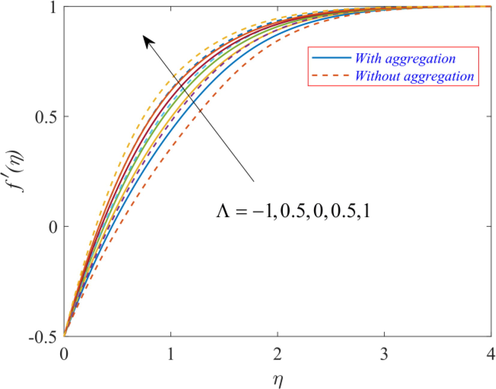
Effect of
on
.
Effect of
on
.
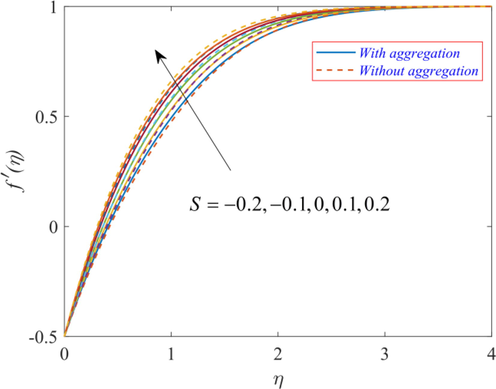
Effect of S on
.
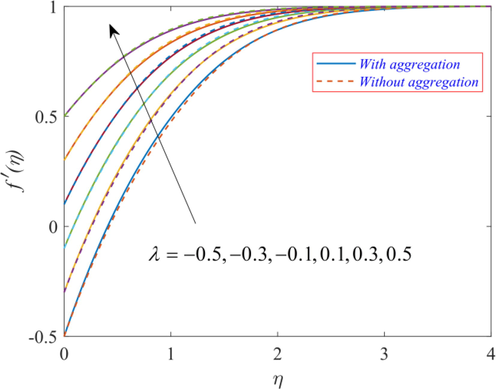
Effect of
on
.
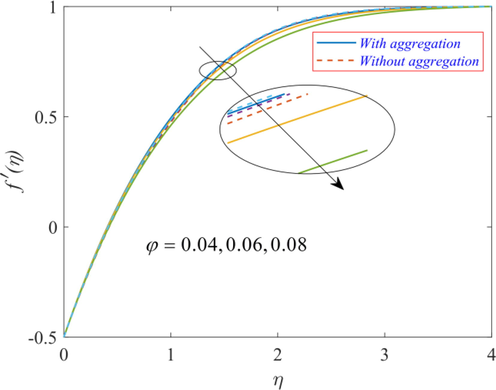
Effect of
on
.
Fig. 6 displays the velocity
with deviation in the stretching/shrinking parameter (of wedge)
. The negative
and positive values
of
symbolize the shrinking and stretching of the wedge, respectively. In addition,
symbolizes the static wedge. The findings indicate that the velocity
of TiO2/EG NF is aided by the increase in the magnitude of stretching of the wedge and the flow is resisted by the increase in the shrinking of the wedge. Fig. 7 displays the velocity
for w.r.t volume fraction
of TiO2 NPs in EG, which is the BF. Adding more TiO2 NPs to the base fluid increases the effective viscosity of TiO2/EG NF. That being the case, the effective fluid is now denser and it restricts the movement of NF. Hence, the velocity
of TiO2/EG NF decreases. Fig. 8 displays the 3-D visualization of velocity profile with NPs aggregation with variation in parameter
and
. The trends in Fig. 8 are the same as seen in Figs. 4 and 6. Furthermore, for opposing flow
(see Fig. 3), the velocity
of TiO2/EG NF with NPs aggregation is higher whereas, for assisting flow
the velocity
of TiO2/EG NF without NPs aggregation is higher. For assisting flow, it is clear that the velocity boundary layer pattern and boundary layer thickness becomes denser and thinner in the presence of the nanoparticle aggregation effect. This is due to an increase in the effective viscosity caused by aggregate formation. Hence for assisting flow, the velocity decreases with the formation of NPs aggregates.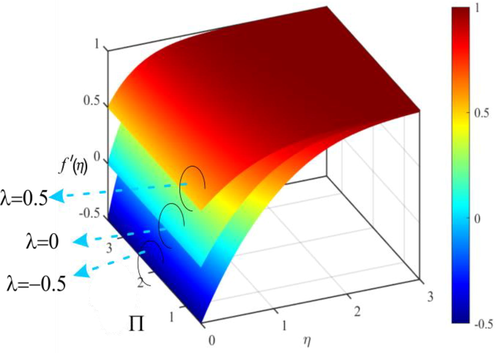
3D visualization of influence of
and
on
.
5.2 Discussion of temperature profiles
Fig. 9 displays the temperature
for variation in the mixed convection parameter
. The findings indicate that the temperature
of TiO2/EG NF drops with an increment in the parameter
. The findings indicate that the temperature of the TiO2/EG NF flow is aided by the opposing flow. The magnitude of resistive forces increases in case of opposing flow, hence the friction force increases, and the loss of energy increases due to friction. Thus the temperature
rises. Fig. 10 displays the temperature
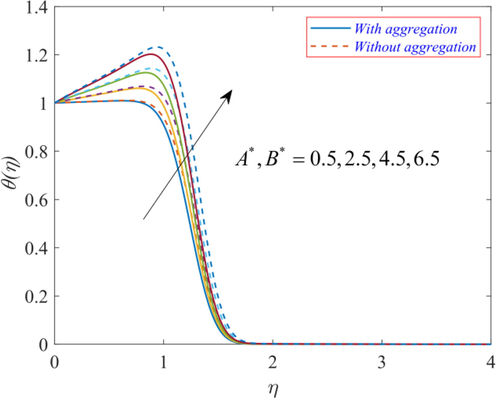
for variation in heat source parameters
. The findings indicate that the thermal profile rises upon increasing the values of heat source parameters
and
. The heat source case denotes the generation of heat and hence it leads to a rise in temperature
. It is inferred that for higher heat source parameters, the thermal profile near the surface is higher than that at the surface; and this phenomenon is observed only for heat source parameters. Fig. 11 displays the temperature profile
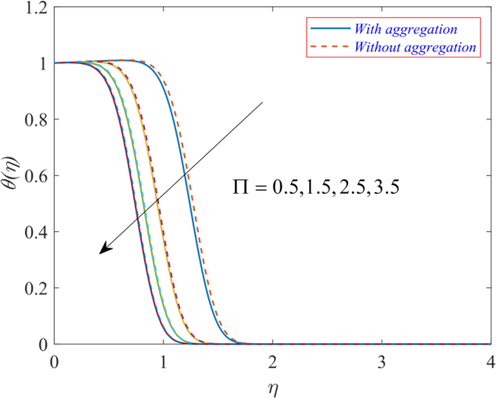
for variation in the porosity parameter
. The higher estimates of the porosity parameter
lead to a reduction in the magnitude of resistive forces, which further reduces the loss of energy, and hence the temperature
falls.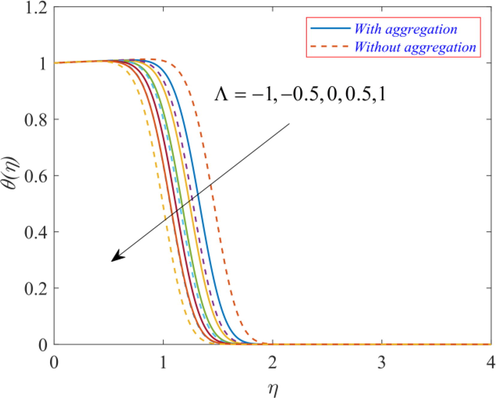
Effect of
on
.
Effect of A* and B* on
.
Effect of
on
.
Fig. 12 displays the temperature
for changes in the radiation parameter Rd. The findings indicate that the temperature display transitioning behavior with radiation parameter Rd. Near the surface, the temperature falls for higher estimates of parameter Rd but after a reflection point, it rises for larger values of radiation parameter Rd. The higher values of the radiation parameter correspond to a higher amount of heat released in the medium. The energy released in the system with a rise in the radiation parameter is absorbed by the particles. Hence, the temperature of the nanofluid increases. The rising temperature
is accredited to the increased amount of radiation in the flow region. Fig. 13 displays the temperature profile
for variation in the stretching/shrinking parameter (of wedge)
. The results demonstrate that temperature
falls with an increment in parameter
. The findings indicate that the thermal profile is aided by the increase in the shrinking. The reason for this outcome is the resistance provided by the shrinking of the wedge to the flow. Fig. 14 displays the temperature profile
for changes in the volume fraction
of TiO2 NPs in EG, which is the BF. Adding more TiO2 NPs in the BF increases the effective TC of the TiO2/EG NF. That being the case, the operating fluid becomes highly conductive and the temperature of TiO2/EG NF is enhanced. Furthermore, for opposing flow
(see Fig. 9), the temperature
of TiO2/EG NF without NPs aggregation is higher whereas, for assisting flow
the temperature
of TiO2/EG NF with NPs aggregation is higher. For opposing flow, the resistive force dominates and it reduces the interaction of the nanoparticle aggregates in the nanofluid and consequently, it acts to reduce the thermal conductivity of nanoparticles. Thus, with opposing flow the formation of nanoparticle aggregates reduces the thermal conductivity of the nanofluid, and hence the temperature of the nanofluid decreases. Figs. 15 and 16 display the 3-D visualization of the thermal profile with NPs aggregation for different values of the parameter
and
; and
and
. The trends in Figs. 15 and 16 are the same as seen in Figs. 9, 10, and 12.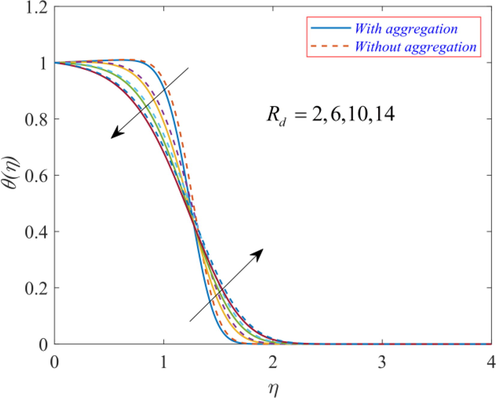
Effect of Rd on
.
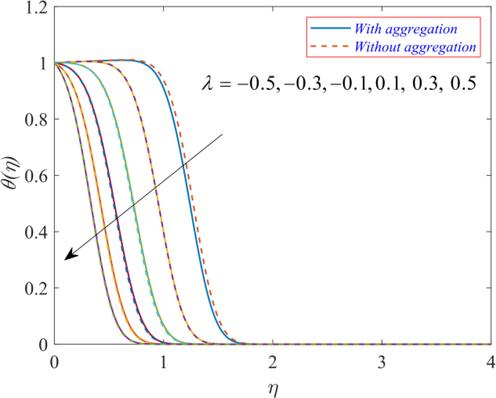
Effect of
on
.
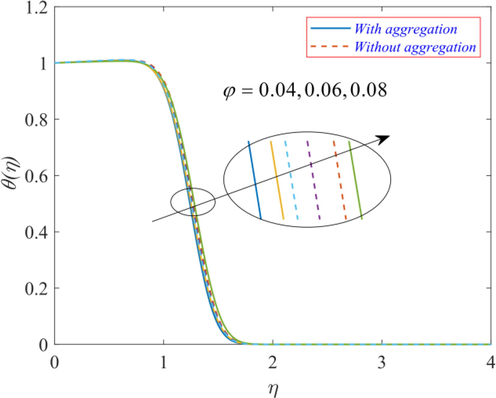
Effect of
on
.
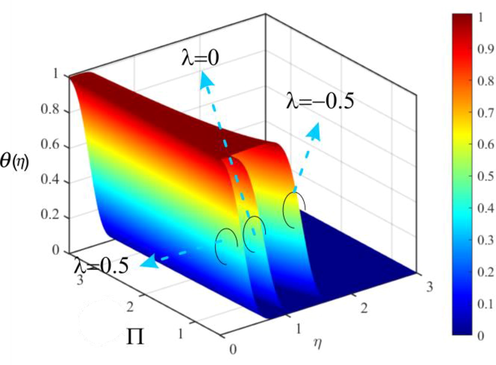
3D visualization of influence of
and
on
.
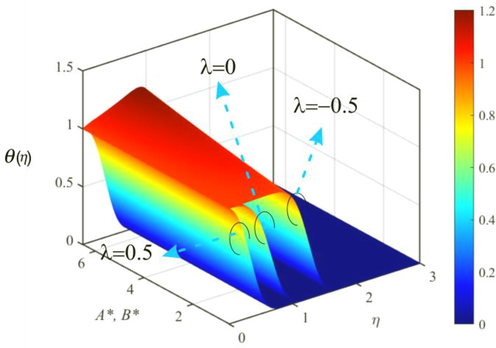
3D visualization of influence of A* &B* and
on
.
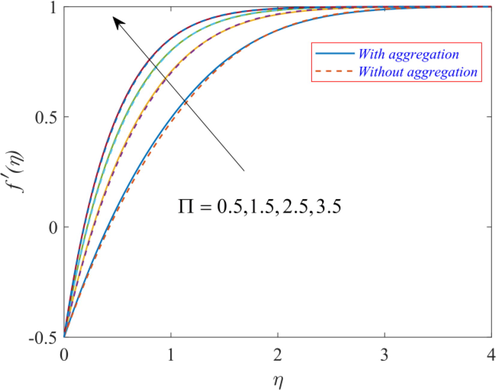
5.3 Discussion of streamlines and Nusselt number
Fig. 17 visualizes the effect of the shrinking wedge
, static wedge
, and stretching wedge
on streamlines of TiO2/EG NF flow with NPs aggregation. The streamlines represent the path followed by particles and their movement along the stream. The streamline provides the velocity direction at any point with the help of tangent. The streamlines depict that the movement of the TiO2/EG NF is restricted by the shrinking, whereas the stretching of the wedge aids the movement of the flow. Table 4 and Figs. 18-20 visualize the effect of emerging parameters (porosity parameter
, mixed convection parameter
, stretching/shrinking parameter
, volume fraction
, heat source parameters
, and radiation parameter Rd) on the skin friction and Nusselt number. The Nusselt number signifies the heat transmission rate on the surface of the wedge. The findings indicate that the increasing values of the mixed convection parameter
, porosity parameter
, and radiation parameter Rd act to enhance the heat transmission rate at the surface of the wedge. Furthermore, the increasing values of the stretching/shrinking parameter
and heat source parameters
act to reduce the heat transmission rate. From Fig. 20, it is clear that the Nusselt number values are higher when NPs aggregation is taken into account. The reason for this outcome is that the thermal conductivity of aggregated NPs is greater than that of independent NPs. Hence, the heat transmission rate is higher for TiO2/EG NF flow with aggregated NPs. It is observed that the increasing values of the radiation parameter Rd, porosity parameter
, mixed convection parameter
, and volume fraction
act to enhance the skin friction at the surface of the wedge. In addition, the increasing values of the heat source parameters
and stretching/shrinking parameter
act to reduce the skin friction at the surface of the wedge. It is seen that skin friction values are higher when NPs aggregation is taken into account. This is due to an increase in the effective viscosity caused by aggregate formation. Hence the skin friction at the surface rises with NPs aggregation effect.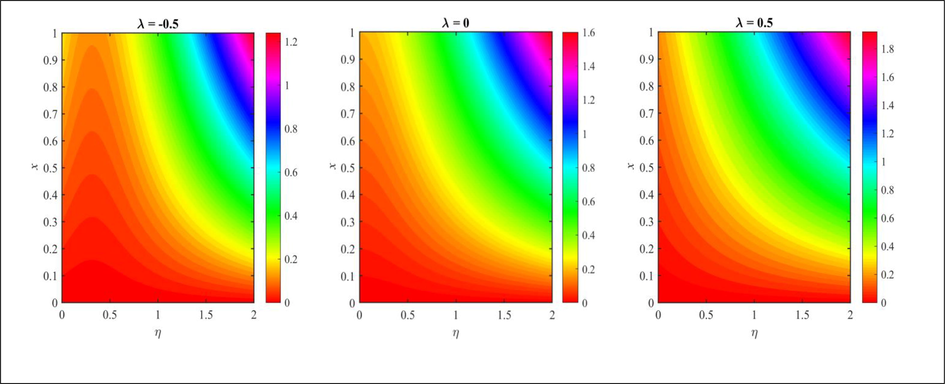
Streamlines.
With aggregation
Without aggregation
Rd
A*, B*
Cf*
Cf*
2
0.5
0.5
−0.5
−0.5
0.04
2.0269458
−0.05595535
1.31005339
−0.05851778
6
2.03075675
−0.08674277
1.31442874
−0.09873223
10
2.03478659
0.11739075
1.31915591
0.07715161
2
2.5
2.0204786
−0.28150822
1.30181487
−0.29443944
4.5
2.01349328
−0.50979444
1.29280331
−0.53333156
0.5
1.5
3.13255333
−0.05580724
2.06601183
−0.05864476
2.5
3.95035702
−0.05227681
2.62025833
−0.05574282
0.5
0
2.19631079
−0.05606718
1.50406111
−0.05872106
1
2.50606328
−0.05617506
1.84048704
−0.05876718
−0.5
0
1.57641145
0.02554052
1.04198727
0.01584842
0.5
0.87447484
1.12159882
0.57952216
1.07844696
−0.5
0.06
2.81265879
−0.05178458
1.39485217
−0.06251167
0.08
4.2030547
−0.04281347
1.48466707
−0.06651996
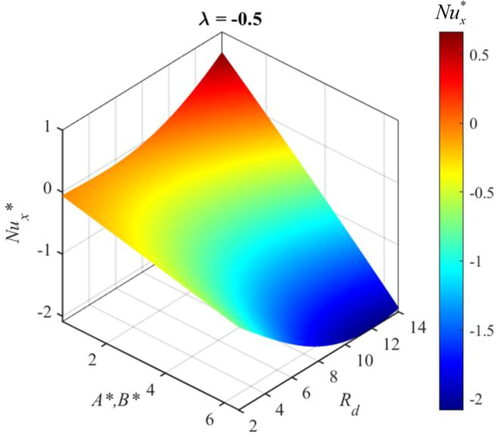
3D visualization of influence of A* &B* and Rd on
.
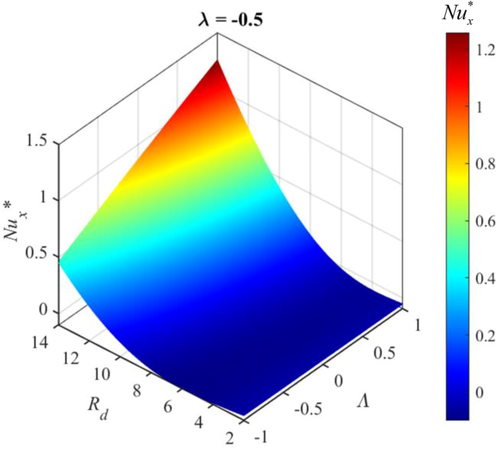
3D visualization of influence of
and Rd on
.

Effect of (a)
, (b)
, (c) A* & B*, and (d) Rd on
.
6 Conclusions
This communication presents a development on the Falkner–Skan problem for a wedge with the influence of NPs aggregation in the presence of the non-uniform heat source/sink, porous medium, mixed convection, radiation, and suction/ injection effects. This model was developed using the combination of modified Maxwell and Bruggeman models for the inclusion of NPs aggregation influence in the flow of TiO2/EG NF, which are already tested experimentally and predict true values for properties of TiO2/EG NF. The mathematical model is solved via the “bvp4c function which is accessible by MATLAB software”. The outcomes of this study will be useful in many fields that utilize applications of flow over wedge such as in raw oil extraction, storage of nuclear waste, insulating heat exchangers, etc. The important results of this investigation are:
-
The velocity of the TiO2/EG nanofluid increases due to the stretching of the wedge and assisting flow.
-
The temperature of the TiO2/EG nanofluid increases due to the shrinking of the wedge and opposing flow.
-
For assisting flow, the velocity is lower for nanofluid with nanoparticle aggregation due to an increase in the effective viscosity.
-
For opposing flow, the formation of nanoparticle aggregates reduces the thermal conductivity of the nanofluid, and hence the temperature of the nanofluid decreases.
-
Thermal profile rises due to increment in the heat source parameters.
-
The Nusselt number and skin friction values are higher when NPs aggregation is taken into account.
-
The Nusselt number is directly proportional to radiation and porosity parameters.
Acknowledgement
The author would like to extend his appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this work through the Research Group Program under grant No. RGP.2/218/44. Also, this work received support from Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. In addition, this study is further supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Second law analysis for radiative MHD slip flow of a nanouid over a stretching sheet with non-uniform heat source effect. Sci. Iran.. 2016;23:1524-1538.
- [CrossRef] [Google Scholar]
- Adnan, Zaidi, S.Z.A., Khan, U., Ahmed, N., Mohyud-Din, S.T., Chu, Y.M., Khan, I., Nisar, K.S., 2020. Impacts of Freezing Temperature Based Thermal Conductivity on the Heat Transfer Gradient in Nanofluids: Applications for a Curved Riga Surface. Molecules 25, 2152. https://doi.org/10.3390/MOLECULES25092152
- The crucial features of aggregation in TiO2-water nanofluid aligned of chemically comprising microorganisms: A FEM approach. Comput. Math. with Appl.. 2022;123:241-251.
- [CrossRef] [Google Scholar]
- Analysis of Al2O3-Cu nanofluid flow behaviour over a permeable moving wedge with convective surface boundary conditions. J. King Saud Univ. - Sci.. 2021;33:101370
- [CrossRef] [Google Scholar]
- MHD heat transfer flow of casson fluid with velocity and thermal slips over a stretching wedge in the presence of thermal radiation. Diffus. Found.. 2020;26:1-22.
- [CrossRef] [Google Scholar]
- Rheological behaviour of ethylene glycol based titania nanofluids. Chem. Phys. Lett.. 2007;444:333-337.
- [CrossRef] [Google Scholar]
- Effect of nanoparticle aggregation on the thermal radiation properties of nanofluids: an experimental and theoretical study. Int. J. Heat Mass Transf.. 2020;154:11-14.
- [CrossRef] [Google Scholar]
- Enhancing thermal conductivity of fluids with nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. FED. 1995;231:99-105.
- [Google Scholar]
- Examining rheological behavior of MWCNT-TiO2/5W40 hybrid nanofluid based on experiments and RSM/ANN modeling. J. Mol. Liq.. 2021;333:115969
- [CrossRef] [Google Scholar]
- Influence of hybrid nanofluids and heat generation on coupled heat and mass transfer flow of a viscous fluid with novel fractional derivative. J. Therm. Anal. Calorim.. 2021;144:2057-2077.
- [CrossRef] [Google Scholar]
- Aggregation effects on water base Al2O3—nanofluid over permeable wedge in mixed convection. Asia-Pacific J. Chem. Eng.. 2016;11:179-186.
- [CrossRef] [Google Scholar]
- Falkneb, V.M., Skan, S.W., 1931. LXXXV. Solutions of the boundary-layer equations. London, Edinburgh, Dublin Philos. Mag. J. Sci. 865–896.
- Impact of magnetic dipole on flow and heat transfer of AA7072-AA7075/water based nanofluid over a stretching sheet using Koo and Kleinstreuer model. Eur. Phys. J. Plus. 2022;137:1-13.
- [CrossRef] [Google Scholar]
- Ganga, B., Mohamed Yusuff Ansari, S., Vishnu Ganesh, N., Abdul Hakeem, A.K., 2016. MHD flow of Boungiorno model nanofluid over a vertical plate with internal heat generation/absorption. Propuls. Power Res. 5, 211–222. https://doi.org/10.1016/j.jppr.2016.07.003
- A static and dynamic approach of aluminum alloys (AA7072-AA7075) over a semi-infinite heated plate. Phys. Scr.. 2020;95:125201
- [CrossRef] [Google Scholar]
- Effect of entropy generation in viscoelastic fluid over a stretching surface with non-uniform heat source / sink and thermal radiation. Int. J. Appl. Eng. Res.. 2018;13:16485-16493.
- [Google Scholar]
- Study of capabilities of the ANN and RSM models to predict the thermal conductivity of nanofluids containing SiO2 nanoparticles. J. Therm. Anal. Calorim.. 2021;145:1993-2003.
- [CrossRef] [Google Scholar]
- Using artificial neural networks to predict the rheological behavior of non-Newtonian graphene–ethylene glycol nanofluid. J. Therm. Anal. Calorim.. 2021;145:1925-1934.
- [CrossRef] [Google Scholar]
- Comprehensive study concerned graphene nano-sheets dispersed in ethylene glycol: Experimental study and theoretical prediction of thermal conductivity. Powder Technol.. 2021;386:51-59.
- [CrossRef] [Google Scholar]
- Magnetohydrodynamic (MHD) boundary layer flow past a wedge with heat transfer and viscous effects of nanofluid embedded in porous media. Math. Probl. Eng.. 2019;2019
- [CrossRef] [Google Scholar]
- Magnetohydrodynamics boundary layer flow past a wedge of Casson CuO-TiO2/EG embedded in non-darcian porous media: viscous dissipation effects. J. Nanofluids. 2022;11:906-914.
- [CrossRef] [Google Scholar]
- Significance of temperature-dependent viscosity and thermal conductivity of Walter’s B nanoliquid when sinusodal wall and motile microorganisms density are significant. Surfaces and Interfaces. 2021;22:100849
- [CrossRef] [Google Scholar]
- Hybrid nanofluid on mixed convective radiative flow from an irregular variably thick moving surface with convex and concave effects. Case Stud. Therm. Eng.. 2020;21:100660
- [CrossRef] [Google Scholar]
- Impact of irregular heat sink/source on the wall jet flow and heat transfer in a porous medium induced by a nanofluid with slip and Buoyancy effects. Symmetry (Basel). 2022;14:2212.
- [CrossRef] [Google Scholar]
- Kudenatti, R.B., L., S., 2021. Local Thermal Nonequilibrium Analysis of Boundary Layer Flow of Carreau Fluid Over a Wedge in a Porous Medium. J. Heat Transfer 143, 1–9. https://doi.org/10.1115/1.4051128
- Kumar, K.G., Reddy, M.G., Vijaya kumari, P., Aldalbahi, A., Rahimi-Gorji, M., Rahaman, M., 2020. Application of different hybrid nanofluids in convective heat transport of Carreau fluid. Chaos, Solitons & Fractals 141, 110350. https://doi.org/10.1016/J.CHAOS.2020.110350
- A novel approach for investigation of heat transfer enhancement with ferromagnetic hybrid nanofluid by considering solar radiation. Microsyst. Technol.. 2021;27:97-104.
- [CrossRef] [Google Scholar]
- Sensitivity analysis of Marangoni convection in TiO2–EG nanoliquid with nanoparticle aggregation and temperature-dependent surface tension. J. Therm. Anal. Calorim.. 2021;143:2085-2098.
- [CrossRef] [Google Scholar]
- Inclined magnetic field and nanoparticle aggregation effects on thermal Marangoni convection in nanoliquid: a sensitivity analysis. Chinese J. Phys.. 2021;69:24-37.
- [CrossRef] [Google Scholar]
- Madhukesh, J.K., Prasannakumara, B.C., Khan, U., Madireddy, S., Raizah, Z., Galal, A.M., 2022. Time-Dependent Stagnation Point Flow of Water Conveying Titanium Dioxide Nanoparticle Aggregation on Rotating Sphere Object Experiencing Thermophoresis Particle Deposition Effects. Energies 2022, Vol. 15, Page 4424 15, 4424. https://doi.org/10.3390/EN15124424.
- Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: a non-Fourier heat flux model approach. J. Mol. Liq.. 2021;335
- [CrossRef] [Google Scholar]
- Mahanthesh, B., Thriveni, K., 2021a. Nanoparticle aggregation effects on radiative heat transport of nanoliquid over a vertical cylinder with sensitivity analysis. Appl. Math. Mech. 2021 423 42, 331–346. https://doi.org/10.1007/S10483-021-2687-7.
- Mahanthesh, B., Thriveni, K., 2021b. Effects of aggregation on TiO2–ethylene glycol nanoliquid over an inclined cylinder with exponential space-based heat source: sensitivity analysis. J. Therm. Anal. Calorim. 2021 1472 147, 1835–1848. https://doi.org/10.1007/S10973-020-10516-1.
- Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl. Sci.. 2020;2
- [CrossRef] [Google Scholar]
- Numerical analysis of MHD nanofluid flow over a wedge, including effects of viscous dissipation and heat generation/absorption, using Buongiorno model. Heat Transf. 2021
- [CrossRef] [Google Scholar]
- The effect of nanoparticles aggregation on the thermal conductivity of nanofluids at very low concentrations: Experimental and theoretical evaluations. Heat Mass Transf. und Stoffuebertragung. 2018;54:125-133.
- [CrossRef] [Google Scholar]
- Influence of non-uniform heat source/sink and variable viscosity on mixed convection flow of third grade nanofluid over an inclined stretched Riga plate. Int. J. Thermofluid Sci. Technol.. 2019;6:19060401.
- [CrossRef] [Google Scholar]
- Comparative study of hybrid (graphene/magnesium oxide) and ternary hybrid (graphene/zirconium oxide/magnesium oxide) nanomaterials over a moving plate. Int. Commun. Heat Mass Transf.. 2023;140:106557
- [CrossRef] [Google Scholar]
- Perspective of multiple slips on 3D flow of Al2O3–TiO2–CuO/H2O ternary nanofluid past an extending surface due to non-linear thermal radiation. Waves Random Complex Media 2022
- [CrossRef] [Google Scholar]
- Non-uniform heat source/sink effects on the three-dimensional flow of Fe3O4 /Al2O3 nanoparticles with different base fluids past a Riga plate. Case Stud. Therm. Eng.. 2019;15:100521
- [CrossRef] [Google Scholar]
- Falkner-Skan flow of a magnetic-Carreau fluid past a wedge in the presence of cross diffusion effects. Eur. Phys. J. Plus. 2016;131
- [CrossRef] [Google Scholar]
- Nanofluid flow past a vertical plate with nanoparticle aggregation kinematics, thermal slip and significant buoyancy force effects using modified Buongiorno model. Waves Random Complex Media. 2021;1–25
- [CrossRef] [Google Scholar]
- Magnetohydrodynamic flow and heat transfer of a hybrid nanofluid over a rotating disk by considering Arrhenius energy. Commun. Theor. Phys.. 2021;73:045002
- [CrossRef] [Google Scholar]
- Aggregation effects on entropy generation analysis for nanofluid flow over a wedge with thermal radiation: a numerical investigation. J. Nanomater.. 2022;2022
- [CrossRef] [Google Scholar]
- Heat transfer of nonlinear radiative magnetohydrodynamic Cu-water nanofluid flow over two different geometries. J. Mol. Liq.. 2017;225:87-94.
- [CrossRef] [Google Scholar]
- Computational study of MHD mixed convective flow of Cu/Al2O3-water nanofluid in a porous rectangular cavity with slits, viscous heating, Joule dissipation and heat source/sink effects. Waves Random Complex Media. 2023;1–34
- [CrossRef] [Google Scholar]
- Significance of thermal slip and convective boundary conditions in three dimensional rotating darcy-forchheimer nanofluid flow. Symmetry (Basel). 2020;12:1-21.
- [CrossRef] [Google Scholar]
- Shampine, L.F., Gladwell, I., Thompson, S., 2003. Solving ODEs with MATLAB, Solving ODEs with MATLAB. Cambridge University Press, Cambridge. https://doi.org/10.1017/cbo9780511615542.
- Impact of exothermic chemical reaction on MHD unsteady mixed convective flow in a rectangular porous cavity filled with nanofluid. Waves Random Complex Media 2022
- [CrossRef] [Google Scholar]
- Comparative heat transfer analysis on Fe3O4–H2O and Fe3O4–Cu–H2O flow inside a tilted square porous cavity with shape effects. Phys. Fluids. 2023;35:022007
- [CrossRef] [Google Scholar]
- Comparative heat transfer analysis of electroconductive Fe3O4–MWCNT– water and Fe3O4–MWCNT– kerosene hybrid nanofluids in a square porous cavity using the non-Fourier heat flux model. Phys. Fluids. 2022;34:122016
- [CrossRef] [Google Scholar]
- Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf.. 2007;50:2002-2018.
- [CrossRef] [Google Scholar]
- Heat transfer analysis on micropolar alumina–silica–water nanofluid flow in an inclined square cavity with inclined magnetic field and radiation effect. J. Therm. Anal. Calorim.. 2022;148:473-488.
- [CrossRef] [Google Scholar]
- MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge. Appl. Math. Mech. (English Ed.). 2020;41:507-520.
- [CrossRef] [Google Scholar]
- Wang, F., Kumar, R.N., Prasannakumara, B.C., Khan, U., Zaib, A., Abdel-Aty, A.H., Yahia, I.S., Alqahtani, M.S., Galal, A.M., 2022. Aspects of Uniform Horizontal Magnetic Field and Nanoparticle Aggregation in the Flow of Nanofluid with Melting Heat Transfer. Nanomater. 2022, Vol. 12, Page 1000 12, 1000. https://doi.org/10.3390/NANO12061000.
- Falkner-Skan problem for a static or moving wedge in nanofluids. Int. J. Therm. Sci.. 2011;50:133-139.
- [CrossRef] [Google Scholar]
- Falkner-Skan problem for a stretching or shrinking wedge with nanoparticle aggregation. J. Heat Transfer. 2022;144:1-9.
- [CrossRef] [Google Scholar]
- Yu, Y., Madhukesh, J.K., Khan, U., Zaib, A., Abdel-Aty, A.H., Yahia, I.S., Alqahtani, M.S., Wang, F., Galal, A.M., 2022. Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet. Nanomater. 2022, Vol. 12, Page 977 12, 977. https://doi.org/10.3390/NANO12060977.







