Translate this page into:
Electro-magnetic radiative flowing of Williamson-dusty nanofluid along elongating sheet: Nanotechnology application
⁎Corresponding author. wasiktk@hotmail.com (Wasim Jamshed)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The flowing of nanomolecules in Williamson nanoliquids via a stretched sheet has a significant influence, and its demand in the manufacturing, therapeutic disciplines, medication, and cooking supplies is enormous and frequently reported. However, 2-dimensional (2-D) combined convective flowing of Williamson-dusty nanofluid (WDNF) via a stretchable sheet in the presence of a magneto force and the porous medium remains unidentified. Hence, this report inspects the combined influence of Brownian and thermophoretic diffusion preserved in magneto WDNF modeling in the occurrence of radiative flowing. The Runge-Kutta Fehlberg approach (RKFA) is used to numerically study the problem of an ordinary differential system employing shooting techniques. The table also addresses the frictional force factor, heat, and mass transmission rate, as well as validates the current findings with earlier available results in the scheduled manner. The acquired outcomes demonstrate that a larger magnetic field decreases the rapidity and thickening of the impetus boundary layer of nanofluids. The momentum dust parameter and the fluid interaction parameter are shown to enhance the heat transmission rate. The rapidity and temperature fields of the liquid and dusty phases improved as the radiation parameter was raised on the contrary of magnetism force which causes dwindling in two phases. Consequently, the examined model's heat transference is reduced in the opposite direction of the Weissenberg number by the magnetic force. Additionally, it is found that higher thermophoresis parameters show an increasing trend in temperature for both phases.
Keywords
Williamson Dusty fluid
Nanofluidics
MHD
Mixed convection
Thermal radiation
Nanomaterials
Nomenclature:
-
reference temperature
-
reference Concentration
-
strength of magnetic field ( )
-
fluid Concentration at wall
-
ambient concentration
-
skin friction coefficient
-
specific heat of fluid ( ))
-
specific heat of nanoparticles
-
specific heat of dust particles
-
Brownian diffusion coefficient
-
thermophoretic diffusion coefficient
-
Eckert number
-
Grashof numbers
-
gravitational force due to acceleration
-
porosity parameter
-
porousness of penetrable material
-
thermal conductance ( )
-
mean absorption coefficient
-
Lewis number
-
mass concentration of dust particles
-
magnetic parameter
-
buoyancy forces ratio
-
thermophoretic variant
-
Brownian factor
-
local Nusselt quantity
-
Prandtl quantity
-
radioactive heat fluxing
-
wall heat fluxing
-
wall mass fluxing
-
chemically reactive variant
-
radiative variant
-
Reynolds quantity
-
local Sherwood quantity
-
convective liquid temperature
-
temperature
-
ambient temperature
-
rapidity elements ( )
-
stretchable sheet speed ( )
-
Weissenberg number
-
coordinate axes
-
thermal diffusion
-
volumetric thermal expansion
-
momentum dust parameter
-
fluid interaction parameter
-
specific heat ratio
-
similarity variable
-
heat generation parameter
-
relaxation time
-
combined convective variant
-
liquid dynamical viscidness ( )
-
kinematic viscosity ( )
-
fluid Density ( )
-
density of dust phase
-
dimensionless nanoparticle size
-
streaming function
-
electric conductance
-
Stefan Boltzmann value
-
heat capacitance ratio
-
recreation time of dusty molecules
-
thermal balance time
-
surface shearing stress
-
nondimensional temperature
Greek letters
-
constraint at ambient
-
constraint at surface
Subscripts
1 Introduction
Nanofluid is the next-generation fluid that contains the predominant thermo-physical properties which empower it valuable in heat transport applications, including fusion power engines, cooling systems, heat exchangers, underground water cable systems, and many chemical processes (Esfe et al., 2014; Mashayekhi et al., 2018; Bazdar et al., 2020; Hassan et al., 2022). The new progressions in nanotechnology prompt the creation of a new group of liquids with advanced heat transport characteristics. Now the question comes to mind what is nanofluid? Nanofluid is the uniform and homogeneous combination of nanometer-scale-sized solid particles (oxide, silica, polymers, metals, non-metals, and carbon nanotubes) and conventional fluids (water, oils, alcohols, etc.) (Al-Kouz et al., 2021). In order to create improved heat transfer fluids with much greater thermal conductivities from an energy-saving and environmental cleansing point of view, a noble and novel technique that calls for the mixing of nanoparticles and the base fluid was devised. Nanoparticles possess high thermo-physical assets as linked to conventional liquids that accordingly upgrade the thermal transportation characteristics of the standard liquid. In 1995, the idea of suspension of nanoparticles was firstly coined by Choi and Eastman (Choi and Eastman, 1995) to root out the issues of Maxwell's work (Maxwell, 1873). The size range of nanoparticles is limited to 0 to 0.04 vol fraction because if the size of the nanoparticles surpasses this limit, sedimentation and clogging difficulties would occur. It is essential to specify here that nanofluids are not made by just embedding the nanoparticles in the base fluid but involve a specific chemical procedure to develop a homogenous mixture with effective and stable applications. Due to their potential implementation in the motion of dust-ladder air, fluid motion, gas-cooling strategies to improve heat transport, environmental degradation, powder innovation, geothermal power, nuclear reactor refrigeration, dust compendium, soil erosion, solid propellant nozzles, fossil fuel industry, crude oil sanitization, and so on, analyses of two-phase flowing in which solid sphere-shaped molecules are dispersed in base fluids are of great interest. Various specialists engaged in these technologies have worked on researching the momentum and heat transmission properties of a dusty liquid.
In laboratories, there are two techniques for preparing nanofluid: a one-step approach and a two-step method. In the scientific field, the two-step process for preparing nanofluid is commonly used. In the two steps method, primarily the raw material is converted to powder form through the physical or chemical procedure. Secondly, the powder is mixed with the regular fluid with highly extreme magnetic force, ultrasonic agitation, or homogenizing (Mukherjee and Paria, 2013). Nanofluid has improved characteristics such as increased heat capacitance, enhanced viscosity, higher thermal conductive, and advanced thermal transmit rate as linked to the conventional liquid. Using different nanofluids, Kavusi and Toghraie (Kavusi and Toghraie, 2017) created a two-dimensional numerical model to replicate the operation of a heat pipe. Through the use of the finite volume approach, the impact of various nanofluids at various concentrations and particle sizes on the functionality of heat pipes were also investigated. These important characteristics led Toghraie et al. (Toghraie et al., 2020) to examine the impact of heat fluxing profile in a concentric annulus utilizing H2O-Al2O3 nanoliquid. By taking into account the radiative impact using single- and two-phase techniques with defined wall temperature circumstances and prescribed surface heat fluxing parameters, Mostafazadeh et al. (Mostafazadeh et al., 2019) analyzed heat transference and laminar flowing of a nanoliquid in a vertical pipe. Li et al. (Li et al., 2019) explored a non-Newtonian nanoliquid's two-phase mixed convection in a porousness h-shaped hole. They took four revolving cylinders and used the Boussinesq approximation to produce mixed convective within the enclosure. Najafabadi et al. (Najafabadi et al., 2022) discussed the mixed convection flow of nanofluid through a vertical channel. In another paper, Sarkar and Das (Sarkar and Das, 2022) discussed the heat transfer in a Cross nanofluid through a horizontal cylinder in the existence of magnetism force and chemical reaction. Ali et al. (Ali et al., 2022) reported the impact of Arrhenius activation energy in the electrical conductance flowing of nano liquid over a stretching cylinder. Some other important regarding applications of nanofluids can be seen in (Das et al., 2021; Ali et al., 2021; Ali et al., 2023; Jamshed et al., 2021; Najafabadi et al., 2022; Zangooee et al., 2022).
Dust granules and base fluid are combined to create the dusty fluid. As it has numerous uses in industry, engineering, and the field of medicine, including power technology, cooling nuclear reactors, recovering crude oil, the sedimentation process, treating wastewater, the formation of raindrops, environmental pollution, fluid-particle suspension past an elongated surface has received a great deal of research attention. In a variety of technological fields, the study of dusty fluids is of tremendous interest. Fluidization (flow of fluid through packed beds), flow in rocket tubes (when the metallic and carbon fuel particle is present together), the coalescing of small droplets (the process of formation of raindrops), extraction of matter from the fluid through a centrifugal separator, polymerization, fluid droplets sprays, purification of crude oil and cooling system are the areas having great technical importance. A noteworthy investigation of the complex plasma has been done by Fortov et al. (Fortov et al., 2005). They have reviewed the main types of experimental complex plasma, and many elementary operations, like the charging of grain in various regimes, the influence of change particles upon each other, and the exchange of momentum of various species are investigated. Time-dependent electro-hydro-dynamic flowing of a dusty liquid flowing on a stretchable plate has been discussed by Ramesh et al. (Ramesh et al., 2012). The authors also took the cause of non-uniformly heat generating in their analysis. In alkaline anion exchange membranes, Grew et al. (Grew and Chiu, 2010) employed the dusty fluid model to predict hydroxyl anion thermal conduction study. Dusty fluid flow with time-dependent viscosity and conductivity between two parallel plates has been inspected by Makinde and Chinyoka (Makinde and Chinyoka, 2010). 2-D hybrid dusty fluid flow through non-Darcian material under the effect of Cattaneo-Christov thermal fluxing has been assessed by Reddy et al. (Reddy et al., 2020). Some other exciting and significant industrial applications of dusty fluid flow and thermal radiation influence can be seen in (Radhika et al., 2020; Kaneez et al., 2020; Ahmadi et al., 2020; Dadsetani et al., 2020; Safaei et al., 2020; Abuldrazzaq et al., 2020; Abu-Hamdeh et al., 2021; Khosravi et al., 2021; Safaei et al., 2021; Reddy and Ferdows, 2021).
The flowing and thermal exchange of a power-law liquid over a stretchable plate is an impressive standard problematic in rheology, with many implementations in a variety of manufacturing fields; instances incorporate chemical manufacturing polymer fluids, the coolant of an endless metal surface in a freezing immersion, crystal growing, hot rolling, exotic lubricants, and suspension solutions (Megahed, 2012; Gulzar et al., 2020; Attar et al., 2022; Faghiri et al., 2022; Alali and Megahed, 2022). Non-Newtonian materials play a significant role in many mechanical and chemical processes as well as engineering implementations. These compounds have an important use in medications, surfactants, petroleum engineering, blood, and numerous other areas. Williamson fluid, which is a type of pseudoplastic fluid, is one of the non-Newtonian fluids. Williamson originally created the Williamson liquid in his pioneering study on pseudo-plastic materials flow. He developed a modeling approach to explain the flowing of shear-thinning liquids and tested this theory with experimentation. Several more investigators have applied the Williamson liquid since then. Keeping in view the characteristics of Williamson fluid, Hashim et al. (Hashim and Khan, 2018) probed the time-dependent combined convective flowing of Williamson nanofluid. The authors considered variable conductivity and magnetic field in their study. Impact of dual chemically reactive flowing along with the influence of active energy on Williamson nanoliquid has been evaluated by Hamid et al. (Hamid and Khan, 2018). In another paper, Hamid et al (Hamid et al., 2018) investigated the stagnating point flowing of Williamson liquid created by stretchable plate together with the impact of Ohmic heat. The phenomenon of thermal radiation and viscous dissipation in Williamson liquid flowing generated results in the stretchable wall has been reported by Megahed (Megahed, 2019). Reddy et al. (Reddy et al., 2022) discussed quantitatively the thermal radiation implications of Williamson nanoliquid flow alongside a stretched plate with porosity media while accounting for velocity and thermal slippage via the Keller box method. Other concerned and significant work on Williamson nanofluid can be found in (Hamid et al., 2019; Hamid et al., 2019; Hamid et al., 2019).
We discovered that the mixed convection Williamson dusty nanoliquid flowing produced by a stretchy plate in a porousness medium has never been investigated before. To close this gap, research is done on the 2-D mixed convection flowing of Williamson dusty nanofluid on a stretchy plate in the existence of a cross-cut magnetism force and radiative flowing. The goal of the current problem is to analyze the impact of thermal radiative fluxing on the electrical conductance flowing of Williamson's dusty nanofluid through a porous medium. The controlling PDEs are converted to non-linear ODEs using suitable similarity transform variables and then solved numerically. Plots are generated and thoroughly analyzed to provide insight into the ramifications of entered dimensionless parameters.
2 Mathematical formulation
Consider combined convective flowing of WDNF initiated by stretchable plate. The surface is expanded with the rapidity of
, wherein
is constant. The
axis is measured via the surface axis, whereas the
axis is measured in the path of flowing (Fig. 1(a)).
Physical model and Coordinate system.
In the present problem, we made the following assumptions.
In the perpendicular direction, a transverse magnetic field of intensity is applied.
It is presumed that the plate's surface is warmed by the temperature in which being reference temperature and concentration is , where shows the source concentricity.
The temperature and concentricity at the ambient are and , correspondingly.
The nanofluid is non-Newtonian, laminar, electrically conducting, and incompressible.
For steady laminar flow, the Boussinesq approximation is used.
The principal equalities for impetus, energy, and mass along with the continuity equation are given as (Ramesh et al., 2012; Makinde and Chinyoka, 2010; Kaneez et al., 2020):
2.1 For fluid Phase:
2.2 For dust phase:
In the previous equations, and labeled the quickness elements in and trends correspondingly, is dynamic viscidness, is the relaxation time, is the fluid consistency, is the consistency of the dust phase, is the consistency of nanoliquid, is the gravitational force due to acceleration, is the porousness of the penetrable material, is the relaxation time of dusty molecules, is the thermal expansion amount, signifies the thermal diffusion of a liquid, denotes the thermal conductance, signifies the relative amount of heat capacitances wherein symbols of the liquid heat capacitance and signifies the nanomolecules heat capacitance, signifies the Brownian motion factor, denotes the thermophoretic variable, symbols of the radiation heat fluxing, implies the thermal balance time and signifies the specific heat of dusty particles.
The subsequent bounder constraints are created as next (Megahed, 2012)
The Rosseland guesstimate is applied to represent the radioactive heat fluxing
in energy equality (Gulzar et al., 2020);
where
symbols the Stefan Boltzmann value and
is the mean absorbing amount.
may be represented as a temperature-dependent linearly function. We dilate
in a Taylor series about
and ignoring larger bounds, acquired
Now propose the streaming function
, a similarity parameter
, and the similarity modifications shown below (Attar et al., 2022)
By using the above transformations, the systematic of equalities (2–7) will get
The associated bounder constraints conditions are given as
Where
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
and
are the Weissenberg number, magnetic parameter, porosity constraint, mass concentricity of dusty molecules, momentum dusty variable, mixed convection factor, buoyancy forces ratio, fluid interaction constraint, Prandtl amount, radiative variable, thermophoresis parameter, Brownian diffusion factor, Eckert quantity, Lewis amount, specific heat ratio and Grashof numbers, and are defined as
The surface drag force, surface heat fluxing, and wall mass fluxing, separately, are described as
The non-dimensional skin friction coefficient
, the local Nusselt number
and local Sherwood number
on the sheet alongside x- orientation, local Nusselt quantity
and Sherwood quantity
are provided as
where is the Reynold quantity.
3 Results and discussion
The 4th order Runge-Kutta based shooting procedure is used to solve the coupled ordinary differential Eqs. (13–17) concerning the boundary conditions (18) and (19) (Fig. 1(b)).
Flow Chart of 4th order Runge Kutta with shooting procedure.
For computational outcomes, we considered
,
,
,
,
,
,
,
,
,
. Except for the varying values indicated in the individual figures, these values are kept consistent throughout the study. Table 1 and Table 2 show a comparison of the skin friction coefficient and the Nusselt number, respectively, which were found to be in excellent agreement.
f″ (0)
Ref. (Akbar et al., 2013)
Ref. (Ali, 2006)
Present results
1
−1.41421
−1.41421
−1.41421
5
−2.44948
−2.44948
−2.44949
10
−3.31662
−3.31662
−3.31662
50
−7.14142
−7.14142
−7.14141
500
–22.3830
–22.3830
–22.38301
1000
−31.6386
−31.6386
−31.63857
Ref. (Ali, 2006)
Ref. (Chen, 1998)
Present results
1
−0.5801
−0.58199
−0.58222
3
−1.1599
−1.16523
−1.16522
5
–
–
−1.56802
10
−2.2960
−2.30796
−2.30797
100
–
–
−7.76562
Moreover, Table 3 demonstrates the influence of different factors on the frictional force coefficient, Nusselt, and Sherwood numbers.
0
0.5
0.5
0.5
0.5
1
−0.954866
−0.647637
−0.628831
0.1
−0.979693
−0.646592
−0.622475
0.3
−1.046023
−0.642499
−0.625030
0.1
0.0
0.5
0.5
0.5
1
−0.906574
−0.654557
−0.638399
0.5
−0.979693
−0.646592
−0.622475
1.0
−1.027364
−0.640390
−0.619932
0.1
0.5
0.0
0.5
0.5
1
−1.013378
−0.396491
−2.471301
0.5
−0.979693
−0.646592
−0.622475
1.0
−0.963116
−0.791605
−0.504067
0.1
0.5
0.5
0.4
0.5
1
−0.900352
−0.822992
−1.570139
0.8
−1.092792
−0.317124
−2.811889
1.0
−1.125097
−0.200458
−3.089430
0.1
0.5
0.5
0.5
0.4
1
−1.027824
−0.627917
−1.132522
0.8
−0.8658207
−0.665138
−0.978264
1.0
−0.809900
−0.654170
−1.877018
0.1
0.5
0.5
0.5
0.5
0
−0.600820
−0.647875
−1.044207
0.5
−0.796787
−0.647773
−0.818533
1.0
−0.979693
−0.646592
−0.622475
Figs. 2(a) and 2(b) depict the influence of
on quickness and energy profiles in both liquid and dust phases. The Weissenberg quantity is a measurable relationship between the fluid's recreation and a particular procedure time. The mounting values of the Weissenberg number cause an upsurge in the recreation on time of liquid molecules, which causes the viscosity to be more important and produces an impedance to a liquid flowing, resulting in a dwindle in liquid speed. The rapidity outline and related boundary layer thickening for the liquid phase reduce and the dust phase increases as the
grows, however temperature boundary layer thickening increases for liquid and dust phases as
increases.
Variation of
and
for
.

Variation of
for
.
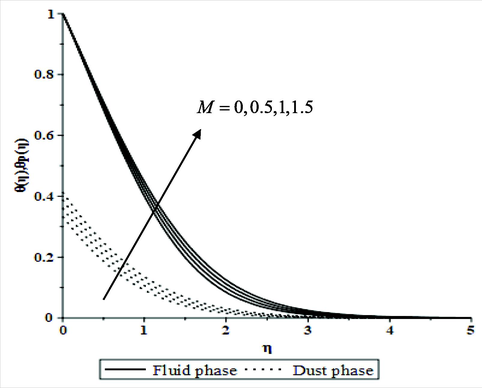
Figs. 3(a) and 3(b) demonstrate how the magnetic parameter affects the velocity and temperature profiles in together liquid and dusty phases. The graphs show that increasing the magnetic parameter diminishes the velocity field whilst increasing temperature outlines for together liquid and dusty phases. Because of the Lorentz force, which is the polar opposite of the flow when the magnetic field parameter is increased, which in turn upsurges the energy stored inside the fluid molecules and thus rises the temperature. This force tends to diminish the thickener of the quickness bounder-layer while growing the thickener of the thermal bounder-layer. As a result, the temperature profiles of a flow have risen. A similar effect is noticed for the variation of porosity parameter
with rapidity and energy fields for together liquid and dusty phases, as shown in Figs. 4(a) and 4(b). This behavior is explained physically by the porous medium's inertial imparting resistance to the fluid flow mechanisms, causing the fluid to travel at a slower rate and at a lower velocity. Furthermore, as the number of dusty molecules in a liquid rose, a drag force increased, creating more impedance to a liquid flowing and, eventually, a reduction in the quickness field and a growth in an energy field. This effect is due to the physical explanation which considers the augmented pores to be the reason behind this.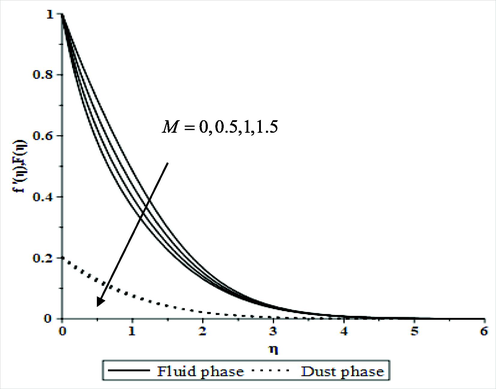
Variation of
and
for
.
Variation of
and
for
.

Variation of
and
for
.

Variation of
and
for
.
Figs. 5(a) and 5(b) portray the impact of momentum dust variable on quickness and energy outlines for liquid and dusty phases. It's worth noting that when
increases, the rapidity of a liquid phase decreases while the speed of a dusty phase increases, as illustrated in Fig. 5(a). Since the fluid-particle phase contact is so strong, the particle phase exerts an opposing force on a liquid phase up to the molecule's rapidity and approaches a liquid swiftness. Increasing the
value improves the temperature outline of the liquid and dusty stages, as shown in Fig. 5(b). This is consistent with the common fact that contact among a liquid and molecules stages improves flow thermal conductance. Furthermore, an increase in
causes the internal opponent power to the flowing to developing until the rapidity of a nanofluid phase is reached by the dust phase.
Variation of
and
for
.

Variation of
and
for
.
Figs. 6(a) and 6(b) illustrate the variation of
on rapidity and energy outlines of liquid and dusty stages. It has been observed that the liquid and dusty stage velocities boosted with growth
and the liquid and dusty phase temperatures decreased. Because of greater
, buoyancy force takes precedence over viscous force. Following this, the buoyancy force parameter improves liquid flowing, which manages to boost fluid velocity and the corresponding boundary layer thickening. Further, this might happen when high buoyant values obtained enable the liquid to waste thermal and kinetic energy from dusty particle collisions, leading both numbers to drop at the top edge. Moreover, the mixed convection parameters combine the flow and heat fields. This represents the ability of the liquid to expand thermally. This is the underlying concept of liquid-in-glass thermometers. A rise in temperature causes the liquid to expand, causing it to ascend the glass. Figs. 7(a) and 7(b) exhibit the effect of
on the rapidity and temperature outlines for together liquid and dusty phases. Fig. 7(a) shows that as
value increases, the rapidity of the fluid and dusty phases decline. On the other hand, the temperature of the fluid phase tends to decrease as the
increases and the temperature of the dusty phase rise as demonstrated in Fig. 7(b). Result the dusty elements generate frictional force in the liquid, slowing it down. This might be owing to enhanced contact between the nanoparticle phase and the dust particle phase, which allows for more conduction heat transfer in the dusty phase. Also, up until the dust phase reaches the fluid phase's rapidity, the fluid phase and flow are opposed internally as the liquid particles interface parameter increases. Moreover, this may happen because the liquid and particle phases interact strongly, leading to the particle phase developing an opposing force to the liquid phase until the particle speed reaches the liquid rapidity. Figs. 8(a) and 8(b) show the effect of
on the rapidity and temperature outlines of both the liquid and dust phases. The relationship between momentum and thermal conductivity is expressed in Prandtl number. The increase in
has a greater effect on the decrease in thermal bounder-layer thickener than on the impetus bounder-layer thickener. In a heat transport situation, the Prandtl number is utilized to govern the relative impetus and thickening of the temperature bounder-layer. The rate of thermal diffusivity slows as
rises, resulting in a decline in thermal bounder- layer thickener. Physically, the fluid with a lesser Prandtl quantity has greater thermal conductance and a bigger thermal bounder-layer structure, allowing heat to permeate from the plate more quickly than the liquid with a greater Prandtl quantity, which has a thinner boundary layer.
Variations of
and
for
.

Variations of
for
.

Variations of
and
for
.

Variation of
and
for
.

Variation of
and
for
.

Variation of
and
for
.
Figs. 9(a) and 9(b) are plotted to visualize the appearance of
on quickness and temperature outlines of liquid and dusty phases. Interestingly, the quickness and energy fields of both liquid and dusty stages rise with growing amounts of
. The following behaviour can be explained physically by the fact that large warming rates of solely viscous nanofluids can also be predicted using the thermal radiation phenomenon. Another possible reason could be because the Stefan–Boltzmann value dominates, and the mean absorbing factor has less influence in the Rosseland approximation. Also, higher radiation parameter values increase the heating of the fluid, improving the energy outline and the thickener of the thermal bounder-layer between the liquid and dusty stages. Radiation enhances a conductive effect and tends to expand the thermal bounder-layer. This will improve the rapidity and temperature at any point away from the sheet metal surface. The excess radiation upsurges the turbulence of the fluid particles' movement, including dust particles as well, which surges internal collisions and increases the stored energy, raising the fluid's velocity and improving temperatures.
Variation of
and
for
.

Variations of
and
for
.
Figs. 10(a) and 10(b) elucidate the variation of
on rapidity and temperature of the liquid and dusty phases. It can be seen that rapidity and temperature outlines for both liquid and dusty phases enhance with increasing values of
. A high Brownian motion parameter value represents that nanoparticles and base fluid particles collide frequently. As a result, there is an enhancement in heat transference qualities within the system, resulting in enhanced temperature and velocity fields. Figs. 11(a) and 11(b) describe the variation of rapidity and temperature profiles for increasing values of
for together liquid and dusty phases. The thermophoretic force between the particles grows as the temperature difference in the system increases, causing the dusty nanofluid to heat up and the temperature of the nanofluid and dusty nanofluid to rise. Furthermore, this force can move suspended particles from a warm to a cold state, boosting the nanoparticle's strength in the fluid.
Variations of
and
for
.

Variation of
and
for
.

Variation of
and
for
.

Variation of
for
.
4 Conclusion
The flowing of a Williamson-dusty nanoliquid across a stretched plate has been studied using magnetohydrodynamic (MHD) mixed convection. The similarity solutions are achieved by applying the Runge Kutta Fehlberg technique and Maple software's algebraic code. The following are significant findings:
-
The increment in diminishes the velocity of the nanofluid while the dusty phase improved.
-
The temperature of both the nanoliquid and the dusty phase are enlarged with the upsurge in .
-
A rise in increased the fluid temperature while decreasing the fluid velocity.
-
The influence of on the temperature field of the dust phase is more profound than the rapidity of the dusty phase.
-
The improvement of cause an augmentation in the quickness and energy of the dust phase.
-
has an opposing influence on the temperature field of both fluid and dust phases.
-
Increasing has a significant impact on the temperature field of both phases.
-
Velocity and thermal fields show the same behavior of an improvement with the growing amounts of .
-
An expansion in the leads to a growth in both the temperature and velocity of both phases.
-
Higher values of and were shown to cause a drop in the heat transfer coefficient.
In the future, the existing method might be used to a number of physical and technical obstacles (Jamshed and Aziz, 2018; Jamshed, 2021; Jamshed and Nisar, 2021; Jamshed et al., 2021; Jamshed, 2021; Jamshed et al., 2022; Islam et al., 2022; Pasha et al., 2022; Rasool et al., 2022; Rasool et al., 2022; Rasool et al., 2022).
CRediT authorship contribution statement
Imran Ullah: Conceptualization. Farhad Ali: Formal analysis. Sharena Mohamad Isa: Methodology. Saqib Murtaza: Software. Wasim Jamshed: Validation, Investigation. Mohamed R. Eid: Investigation, Validation, Writing - original draft, Writing - review & editing. Ayesha Amjad: Writing – review & editing.
Acknowledgment
The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- A detailed hydrothermal investigation of a helical micro double-tube heat exchanger for a wide range of helix pitch length. Case Stud. Therm. Eng.. 2021;28:101413
- [Google Scholar]
- Heat transfer improvement in a double backward-facing expanding channel using different working Fluids. Symmetry.. 2020;12(7):1088.
- [Google Scholar]
- Configuration and optimization of a minichannel using water–alumina nanofluid by non-dominated sorting genetic algorithm and response surface method. Nanomaterials. 2020;10(5):901.
- [Google Scholar]
- Numerical solutions of Magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J Phys.. 2013;87(11):1121-1124.
- [Google Scholar]
- MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev.. 2022;11(1):463-472.
- [Google Scholar]
- The effect of variable viscosity on mixed convection heat transfer along a vertical moving surface. Int J Therm Sci.. 2006;45(1):60-69.
- [Google Scholar]
- Investigation of cattaneo–christov double diffusions theory in bioconvective slip flow of radiated magneto-cross-nanomaterial over stretching cylinder/plate with activation energy. Int. J. Appl. Comput. Math. 2021;7(5):208.
- [Google Scholar]
- A report on entropy generation and Arrhenius kinetics in magneto-bioconvective flow of Cross nanofluid over a cylinder with wall slip. Int. J. Amb. Ener.. 2022;15:1-6.
- [Google Scholar]
- Bioconvective chemically reactive entropy optimized Cross-nano-material conveying oxytactic microorganisms over a flexible cylinder with Lorentz force and Arrhenius kinetics. Math. Comput. Simul.. 2023;205:1029-1051.
- [Google Scholar]
- Galerkin finite element analysis of magneto two-phase nanofluid flowing in double wavy enclosure comprehending an adiabatic rotating cylinder. Sci. Rep.. 2021;11(1):1-15.
- [Google Scholar]
- Analytical solution of fractional differential equations by Akbari–Ganji’s method. Partial Differ. Equations Appl. Math.. 2022;6:100450
- [Google Scholar]
- numerical investigation of turbulent flow and heat transfer of nanofluid inside a wavy microchannel with different wavelengths. J Therm Anal Calorim.. 2020;139(3):2365-2380.
- [Google Scholar]
- Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transf.. 1998;33(5–6):471-476.
- [Google Scholar]
- Choi, S. U. S., Eastman, J. A. 1995. Enhancing Thermal Conductivity of Fluids with Nanoparticles. Proc. 1995 ASME Int. Mech. Engi- neering Congr. Expo. SanFrancisco, USA, ASME, FED231/MD66 99–105.
- Cooling enhancement and stress reduction optimization of disk-shaped electronic components using nanofluids. Symmetry.. 2020;12(6):931.
- [Google Scholar]
- Darcy-Forchheimer flow of a magneto-radiated couple stress fluid over an inclined exponentially stretching surface with Ohmic dissipation. World J. Eng.. 2021;18(2):345-360.
- [Google Scholar]
- Effect of nanofluid variable properties on mixed convection flow and heat transfer in an inclined two-sided lid-driven cavity with sinusoidal heating on sidewalls. Heat Transfer Research.. 2014;45(5):409-432.
- [Google Scholar]
- Hydrothermal analysis of non-Newtonian fluid flow (blood) through the circular tube under prescribed non-uniform wall heat flux Theor. Appl. Mech. Lett.. 2022;12(4):100360
- [Google Scholar]
- Complex (dusty) plasmas: Current status, open issues, perspectives. Phys. Rep.. 2005;421(1–2):1-103.
- [Google Scholar]
- A dusty fluid model for predicting hydroxyl anion conductivity in alkaline anion exchange membranes. J Electrochem Soc.. 2010;157(3):B327.
- [Google Scholar]
- A nonlinear mathematical analysis for magneto-hyperbolic-tangent liquid featuring simultaneous aspects of magnetic field, heat source and thermal stratification. Appl. Nanosci.. 2020;10:4513-4518.
- [Google Scholar]
- Unsteady stagnation-point flow of Williamson fluid generated by stretching/shrinking sheet with Ohmic heating. Int J Heat Mass Transf.. 2018;126:933-940.
- [Google Scholar]
- Impacts of binary chemical reaction with activation energy on unsteady flow of magneto-Williamson nanofluid. J. Mol. Liq.. 2018;262:435-442.
- [Google Scholar]
- An investigation of thermal and solutal stratification effects on mixed convection flow and heat transfer of Williamson nanofluid. J Mol Liq.. 2019;284:307-315.
- [Google Scholar]
- Heat transport features of magnetic water–graphene oxide nanofluid flow with thermal radiation: Stability Test. Eur J Mech-B/Fluids.. 2019;76:434-441.
- [Google Scholar]
- Numerical simulation for transient flow of Williamson fluid with multiple slip model in the presence of chemically reacting species. Int J Numer Meth Heat Fluid Flow.. 2019;29(11):4445-4461.
- [Google Scholar]
- Unsteady mixed convective flow of Williamson nanofluid with heat transfer in the presence of variable thermal conductivity and magnetic field. J Mol Liq.. 2018;260:436-446.
- [Google Scholar]
- Thermal energy and mass transport of shear thinning fluid under effects of low to high shear rate viscosity. Int. J. Thermofluids.. 2022;15:100176
- [Google Scholar]
- On Powell-Eyring hybridity nanofluidic flow based Carboxy-Methyl-Cellulose (CMC) with solar thermal radiation: A quadratic regression estimation. Int. Commun. Heat Mass Transfer. 2022;138:106413
- [Google Scholar]
- Numerical Investigation of MHD Impact on Maxwell Nanofluid. Int. Commun. Heat Mass Transfer. 2021;120(5):683.
- [Google Scholar]
- Finite element method in thermal characterization and streamline flow analysis of electromagnetic silver-magnesium oxide nanofluid inside grooved enclosure. Int. Commun. Heat Mass Transfer. 2021;130:105795
- [Google Scholar]
- Entropy Analysis of TiO2-Cu/EG Casson Hybrid Nanofluid via Cattaneo-Christov Heat Flux Model. Applied Nanosciences. 2018;08:01-14.
- [Google Scholar]
- Partial velocity slip effect on working magneto non-Newtonian nanofluids flow in solar collectors subject to change viscosity and thermal conductivity with temperature. PLoS One. 2021;16(11):e0259881.
- [Google Scholar]
- Experimental and TDDFT materials simulation of thermal characteristics and entropy optimized of Williamson Cu-methanol and Al2O3-methanol nanofluid flowing through solar collector. Sci. Rep.. 2022;12:18130.
- [Google Scholar]
- Computational single phase comparative study of Williamson nanofluid in parabolic trough solar collector via Keller box method. Int. J. Energy Res.. 2021;45(7):10696-10718.
- [Google Scholar]
- Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: a solar thermal application. J. Mater. Res. Technol.. 2021;14:985-1006.
- [Google Scholar]
- An enhancement in transportation of heat energy in yield stress dusty fluid via mono and hybrid nanoparticles. Phys Scr.. 2020;95(8):085216
- [Google Scholar]
- A comprehensive study of the performance of a heat pipe by using of various nanofluids. Adv. Powder Technol.. 2017;28(11):3074-3084.
- [Google Scholar]
- Entropy generation of graphene–platinum hybrid nanofluid flow through a wavy cylindrical microchannel solar receiver by using neural networks. J. Therm. Anal. Calorim.. 2021;145:1949-1967.
- [Google Scholar]
- Mixed convection of non-Newtonian nanofluid in an H-shaped cavity with cooler and heater cylinders filled by a porous material: Two phase approach. Adv. Powder Technol.. 2019;30(11):2666-2685.
- [Google Scholar]
- MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comput Math Appl.. 2010;60(3):660-669.
- [Google Scholar]
- CFD analysis of thermal and hydrodynamic characteristics of hybrid nanofluid in a new designed sinusoidal double-layered microchannel heat sink. J. Therm. Anal. Calorim.. 2018;134(3):2305-2315.
- [Google Scholar]
- A treatise on electricity and magnetism. Vol Vol. 1. Oxford: Clarendon Press; 1873.
- Variable viscosity and slip velocity effects on the flow and heat transfer of a power-law fluid over a non-linearly stretching surface with heat flux and thermal radiation. Rheol Acta. 2012;51(9):841-847.
- [Google Scholar]
- Williamson fluid flow due to a nonlinearly stretching sheet with viscous dissipation and thermal radiation. J Egy Math Soc.. 2019;27(1):1-10.
- [Google Scholar]
- Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single- and two-phase approaches. J. Therm. Anal. Calorim.. 2019;138(1):779-794.
- [Google Scholar]
- Preparation and stability of nanofluids-a review. IOSR J Mech Civil Eng.. 2013;9(2):63-69.
- [Google Scholar]
- Hydrothermal study of nanofluid flow in channel by RBF method with exponential boundary conditions. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022 09544089221133909
- [Google Scholar]
- Investigation of nanofluid flow in a vertical channel considering polynomial boundary conditions by Akbari-Ganji's method. Theor. Appl. Mech. Lett.. 2022;12(4):100356
- [Google Scholar]
- Statistical analysis of viscous hybridized nanofluid flowing via Galerkin finite element technique. Int. Commun. Heat Mass Transfer. 2022;137:106244
- [Google Scholar]
- The flow of fluid-particle suspension between two rotating stretchable disks with the effect of the external magnetic field. Phys Scr.. 2020;96(1):015214
- [Google Scholar]
- MHD flow of a dusty fluid near the stagnation point over a permeable stretching sheet with non-uniform source/sink. Int J Heat Mass Transf.. 2012;55(17–18):4900-4907.
- [Google Scholar]
- Darcy-Forchheimer Flow of Water Conveying Multi-Walled Carbon Nanoparticles through a Vertical Cleveland Z-Staggered Cavity Subject to Entropy Generation. Micromachines. 2022;13:744.
- [CrossRef] [Google Scholar]
- Significance of Rosseland’s Radiative Process on Reactive Maxwell Nanofluid Flows over an Isothermally Heated Stretching Sheet in the Presence of Darcy-Forchheimer and Lorentz Forces: Towards a New Perspective on Buongiorno’s Model. Micromachines. 2022;13:368.
- [CrossRef] [Google Scholar]
- Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022
- [CrossRef] [Google Scholar]
- Species and thermal radiation on micropolar hydromagnetic dusty fluid flow across a paraboloid revolution. J Therm Anal Calorim.. 2021;143(5):3699-3717.
- [Google Scholar]
- Radiation, velocity and thermal slips effect toward mhd boundary layer flow through heat and mass transport of Williamson nanofluid with porous medium. Arab. J. Sci. Eng.. 2022;21:1-5.
- [Google Scholar]
- Hybrid dusty fluid flow through a Cattaneo-Christov heat flux model. Physica A: Stat Mech Appl.. 2020;551:123975
- [Google Scholar]
- Thermal analysis of a binary base fluid in pool boiling system of glycol–water alumina nano-suspension. J. Therm. Anal. Calorim.. 2020;143(3):2453-2462.
- [Google Scholar]
- An innovative design of a high strength and low weight sudden micro expansion by considering a nanofluid: Electronic cooling application. Case Stud. Therm. Eng.. 2021;28:101637
- [Google Scholar]
- Magneto-thermo-bioconvection of a chemically sensitive Cross nanofluid with an infusion of gyrotactic microorganisms over a lubricious cylindrical surface: Statistical analysis. Int. J. Model. Simul.. 2022;13:1-22.
- [Google Scholar]
- Two-phase investigation of water-Al2O3 nanofluid in a micro concentric annulus under non-uniform heat flux boundary conditions. Int. J. Numer. Methods Heat Fluid Flow.. 2020;30(4):1795-1814.
- [Google Scholar]
- Hydrothermal analysis of Hybrid nanofluid flow on a vertical plate by considering slip condition. Theor. Appl. Mech. Lett.. 2022;12(5):100357
- [Google Scholar]







