A comprehensive approach in perceiving the chelation of Cu(II) and Zn(II) with Alizarin Red S using pH-oscillotitrimetric and volumetric-oscillographic methods

3.1.1 pH-oscillotitrimetric (pHOT) and volumetric-oscillographic (VOG) methods

3.1.1.1

3.1.1.1 The general effect of the light on the ligands

The 4x10^-3M stock solutions of ARS, Calmagite, PEG (400, 2000 and 4000g/mol), CuCl₂, SnCl₂ and ZnCl₂ have been prepared to always start with them in various experiments. Therefore, the stability of those solutions has been studied in terms of unsuitable preservation conditions, the light exposure along with the temperature in specific, to get the limitations signs of those solutions endurance, where the change in the solutions’ colours, especially the dyes’ colours, has not been observed as an indication to the structures’ stability of those compounds as it is shown in Figs. 1 and 2. The solutions have been exposed to the light beams for 20 hours in which Calmagite and PEG (400, 2000 and 4000g/mol) have been used as a comparison between different organic compounds, consequently those beams heated the samples up to 55-60°C at the distance of 40cm from the light source, which has the temperature of ∼150°C at its center (see Figs. 1, 2 and 3). TIS60 Thermal Imager Camera (Model No. FLUKE TIS60 9HZ) has been used as a temperature detector for this experiment, where it was located adjacent to the light source to measure temperature degrees of both; the samples and the light source.

Close

Fig. 1

The solutions colors before the exposure to the light. 1: The solution of [4x10^-3M PEG(4000) 0.5ml + 75ml DI water], 2: The solution of [4x10^-3M PEG(2000) 0.5ml + 75ml DI water], 3: The solution of [4x10^-3M PEG(400) 0.5ml + 75ml DI water], 4: The solution of [4x10^-3M ARS 0.5ml + 75ml DI water], 5: The solution of [4x10^-3M Calm 0.5ml + 75ml DI water].

Export to PPT

Close

Fig. 2

The solutions colors after the exposure to the light for 20 hours. 1: The solution of [4x10^-3M PEG(4000) 0.5ml + 75ml DI water], 2: The solution of [4x10^-3M PEG(2000) 0.5ml + 75ml DI water], 3: The solution of [4x10^-3M PEG(400) 0.5ml + 75ml DI water], 4: The solution of [4x10^-3M ARS 0.5ml + 75ml DI water], 5: The solution of [4x10^-3M Calm 0.5ml + 75ml DI water].

Export to PPT

Close

Fig. 3

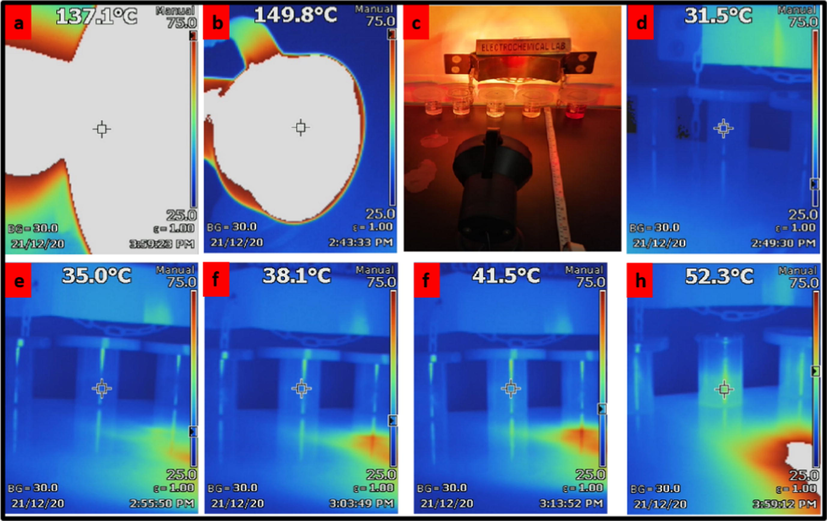
The process of exposing the samples to the light; a: the temperature around the center of the light source. b: the temperature of the center of the light source. c: the exact setup of the sample for the exposure process to the light. d-h: the gradual increase in the temperature of the samples.

Export to PPT

The data in Table 1 show unsignificant differences in the pH values and consequently the electrode potential (EP), and that indicates again to the stability of the solutions in case they are exposed to bearable conditions such as light and heat, whilst the data exhibit the differences between the temperature and conductivity values before and after the exposure to the light and after cooling down the samples naturally for 3 hours on the second day. Basically, when the temperature of a liquid increases, the conductivity also increases. Hence, to know better about the relationship between both factors, the concern is to identify the difference range that the temperature makes for the same solution. For example, for Calm., the assumption can be as in equation (1).

(1)

[The conductivity/temperature change (CTC)(Calm.)/1 °C](CTC_Calm)=ΔCond./ΔT=(Cond.₂-Cond.₁)/(T₂–T₁)=(159.5-27.11)/(27.3-24.3)=44.13 μS.cm⁻¹.°C⁻¹

Table 1 The measured values of pH, EP (electrode potential), Conductivity (Cond.) and temperature of the ARS, Calm., PEG (400, 2000 and 4000g/mol) solutions before and after the exposure to the light for 20h.

Solution	Before the light exposure		After the light exposure for 20h
4x10-3M Calm 0,5ml + 75ml DI water	pH  =  5,97	T  =  24.3˚C	pH  =  6.18	T  =  27.3˚C
	EP  =  84.1mV	Cond.  =  27.11 μS/cm	EP  =  89.4mV	Cond.  =  159.5 μS/cm
4x10-3M ARS 0,5ml + 75ml DI water	pH  =  5,43	T  =  24.1˚C	pH  =  5,36	T  =  28.2˚C
	EP  =  92.0mV	Cond.  =  25.48 μS/cm	EP  =  97.4mV	Cond.  =  134.4 μS/cm
4x10-3M PEG(400) 0,5ml + 75ml DI water	pH  =  5,44	T  =  24.2˚C	pH  =  5,36	T  =  28.2˚C
	EP  =  91.3mV	Cond.  =  25.71 μS/cm	EP  =  97.4mV	Cond.  =  134.4 μS/cm
4x10-3M PEG(2000) 0,5ml + 75ml DI water	pH  =  5,57	T  =  24.2˚C	pH  =  5,64	T  =  27.1˚C
	EP  =  84.1mV	Cond.  =  11.68 μS/cm	EP  =  84.1mV	Cond.  =  83.19 μS/cm
4x10-3M PEG(4000) 0,5ml + 75ml DI water	pH  =  5,61	T  =  24.1˚C	pH  =  5,62	T  =  26.4˚C
	EP  =  81.7mV	Cond.  =  57.27 μS/cm	EP  =  81.5mV	Cond.  =  123.5 μS/cm

The same for all solutions has been done and the calculations are expressed in equation (2).

(2)

$$\mathrm{C}\mathrm{T}{\mathrm{C}}_{\mathrm{A}\mathrm{R}\mathrm{S}}\approx 26.566\mathrm{\mu }\mathrm{S}.\mathrm{c}{\mathrm{m}}^{-1}{.}^{°}{\mathrm{C}}^{-1},\mathrm{C}\mathrm{T}{\mathrm{C}}_{\mathrm{P}\mathrm{E}\mathrm{G}(400)}\approx 27.173\mathrm{\mu }\mathrm{S}.\mathrm{c}{\mathrm{m}}^{-1}{.}^{°}{\mathrm{C}}^{-1},\mathrm{C}\mathrm{T}{\mathrm{C}}_{\mathrm{P}\mathrm{E}\mathrm{G}(2000)}\approx 23.837\mathrm{\mu }\mathrm{S}.\mathrm{c}{\mathrm{m}}^{-1}{.}^{°}{\mathrm{C}}^{-1},\mathrm{C}\mathrm{T}{\mathrm{C}}_{\mathrm{P}\mathrm{E}\mathrm{G}(4000)}\approx 33.115\mathrm{\mu }\mathrm{S}.\mathrm{c}{\mathrm{m}}^{-1}{.}^{°}{\mathrm{C}}^{-1}$$

The average rate (AR) of the 1°C variations in the conductivity can be referred to as in equation (3), where CTC_OC is the conductivity/temperature change of an organic compound.

(3)

$$\mathrm{A}\mathrm{R}=\frac{\sum {\mathrm{C}\mathrm{T}\mathrm{C}}_{\mathrm{O}\mathrm{C}}}{{\mathrm{n}}_{\mathrm{C}\mathrm{T}\mathrm{C}\mathrm{O}\mathrm{C}}}=154.\frac{821}{5}\approx 30.964\mathrm{\mu }\mathrm{S}.{\mathrm{c}\mathrm{m}}^{-1}{.}^{°}{\mathrm{C}}^{-1}$$

Given that, the 1°C increase can practically increase the solutions’ conductivity by approximately 5-15 times comparing to the conductivity of DI water, which realistically varies from 2 μS/cm to 6 μS/cm as an acceptable value.

3.1.2 The indications of the pH values on the solutions and mixtures of ARS and zinc chloride

Zinc chloride is very soluble in water, and its solutions cannot be considered to contain simply solvated Zn²⁺ ions and Cl⁻ ions, where ZnCl_xH₂O_(4−x) species are also present (Irish et al., 1963; Yamaguchi et al., 1989; Pye et al., 2006). Aqueous solutions of ZnCl₂ are acidic, where 6M aqueous solution has pH =1 (Holleman and Wiberg, 2001). As it is shown in Fig. 4, for the first solution that consists of 100% ZnCl₂, the solution is acidic. That can be interpreted as the solution can afterward react with the water molecules as in reaction (4).

Close

Fig. 4

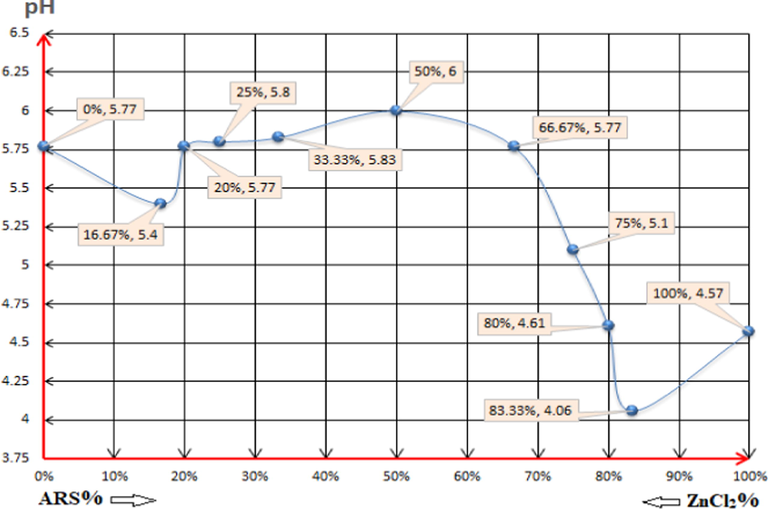
The pH values of the following solutions: (0%, 5.77): 4x10^-3M ZnCl₂ 0.5ml + 79.5ml DI water. (16.67%, 5.4) (1:5): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2.5ml + 77ml DI water. (20%, 5.77) (1:4): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2ml + 77.5ml DI water. (25%, 5.8) (1:3): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1.5ml + 78ml DI water. (33.33%, 5.83) (1:2): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1ml + 78.5ml DI water. (50%, 6) (1:1): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 0.5ml + 79ml DI water. (66.67%, 5.77) (2:1): 4x10^-3M ARS 1ml + 4x10^-3M ZnCl₂ 0.5ml + 78.5ml DI water. (75%, 5.1) (3:1): 4x10^-3M ARS 1.5ml + 4x10^-3M ZnCl₂ 0.5ml + 78ml DI water. (80%, 4.61) (4:1): 4x10^-3M ARS 2ml + 4x10^-3M ZnCl₂ 0.5ml + 77.5ml DI water. (83.33%, 4.06) (5:1): 4x10^-3M ARS 2.5ml + 4x10^-3M ZnCl₂ 0.5ml + 77ml DI water. (100%, 4.57): 4x10^-3M ARS 0.5ml + 79.5ml DI water.

Export to PPT

Reaction (4) reveals that the medium is acidic in its nature more than being alkali or neutral, which means pH < 7.

For the first mixture (ARS 1:5 ZnCl₂), the pH value goes down comparing to the 100% ZnCl₂ solution and goes up when it is compared with the 100% ARS solution. At this point the reagent displaces for the first (-OH)-group since the mixture has a weak acidity (Ali et al., 2016). According to that, the elucidation of that process happening in the mixture is according to reaction (5).

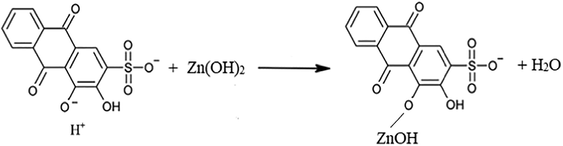
The formation of the water molecules in reaction (5) is the reason behind the increase in the pH of the first mixture, diluting it consequently. Therefore, the situation remains as per this reaction for the next three mixture (1:4), (1:3) and (1:2) until having the mixture of (1:1) with pH=6. This bids the most sufficient stoichiometry of the reactions as it gives the largest amount of water molecules to increase the pH of the mixture. Given that and at this point, the assumption is that the reagent starts to chelate with zinc ion via forming the covalent bond, formed by the oxygen atom in the near ketone group as in reaction (6).

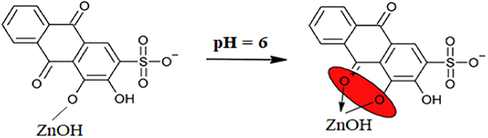
For the rest of the mixtures, ARS ions continue to liberate protons into the solutions without any further chelation process with Zn ions as long as the concentration increases, and this allows the pH value to be dropped rather than being increased. Thus, in these mixtures the dominant reaction is expressed in reaction (7), where pK_a = 6.17 (Ali et al., 2016).

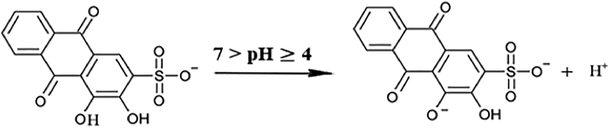
3.1.3 The indications of the pH-titrimetric and pH-oscillotitrimetric (pHOT) graphs of the solutions and mixtures of ARS and zinc chloride

The pH-titrimetric curves in Fig. 5. bid what exactly happens in the solutions and mixtures. For curve 1 and 2, it can demonstrate the precise understanding of the titration processes that are of the weak diprotic (polyprotic) acids (pH > 4.5) after dissolving in DI water and do not exhibit full titration leaps of the first displacements. That appears by examining the pH-titration curves’ offsets. In curve 1, ARS starts as a half leap that indicates that the first hydroxyl-group has been already titrated, and the half way to the second hydroxyl-group is not the real pKa₂. In such cases, the half way is just pKa₁, and pKa₂ can be approximately determined using the following equation: 2pKa₁ ± 1. Up to this point, ARS displaces according to reaction (7) by adding the first two drops of the hydroxide. By that, the hydroxide is consumed for the titration of the second displacement of the second hydroxyl group. pKa₁ is, therefore, the half way to the second equivalence point (at pH ≈ 8.7), which means pKa₁  =  (pH at V_eq,2/2)  =  [pH at (9.62/2  =  4.8mL)] ≈ 6.35 ± 0.1. pKa₂  =  2pKa₁ ± 1 ≈ 12.7 ± 1. However, the first derivative shows more accurate value of the second equivalence point, which is 9.5mL, and the pH-Oscillotitrimetric graph gives even more precise value, which is 9.267mL as in Fig. 7. Hence, pKa₁ and pKa₂ would change accordingly, where pKa₁ ≈ 6.3 and pKa₂ ≈ 12.6 ± 1. For curve 3 and 4 in Fig. 5, ZnCl₂ takes considerably longer buffer region to be completely titrated, and that is because the hydroxide is consumed to titrate a strong acid as a result of ZnCl₂ being dissolved in DI water according to reaction (4), and it is as per reaction (8).

Close

Fig. 5

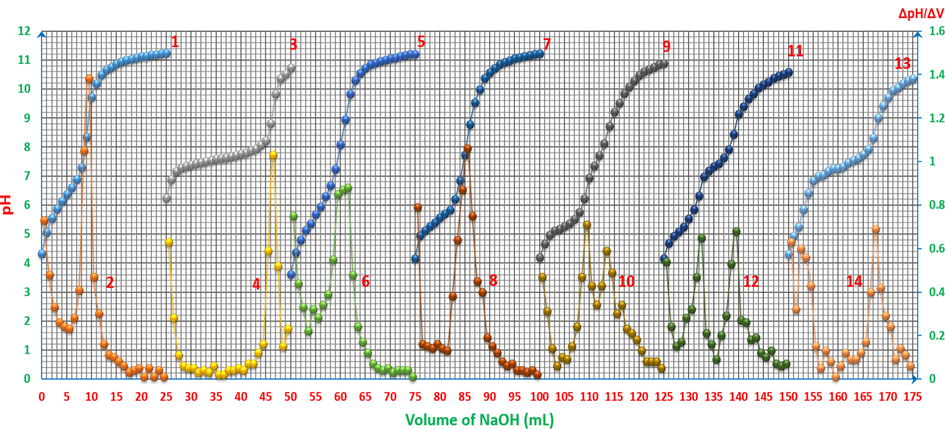
pH-titrimetric curves of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH with the first derivatives: 1 and 2: 4x10^-3M ARS 25ml. 3 and 4: 4x10^-3M ZnCl₂ 25ml. 5 and 6: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 7 and 8: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 9 and 10: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 11 and 12: 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 13 and 14: 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. The curves (3-14) are extracted after adding 25 to each value of horizontal axis (volume axis) consecutively.

Export to PPT

Close

Fig. 6

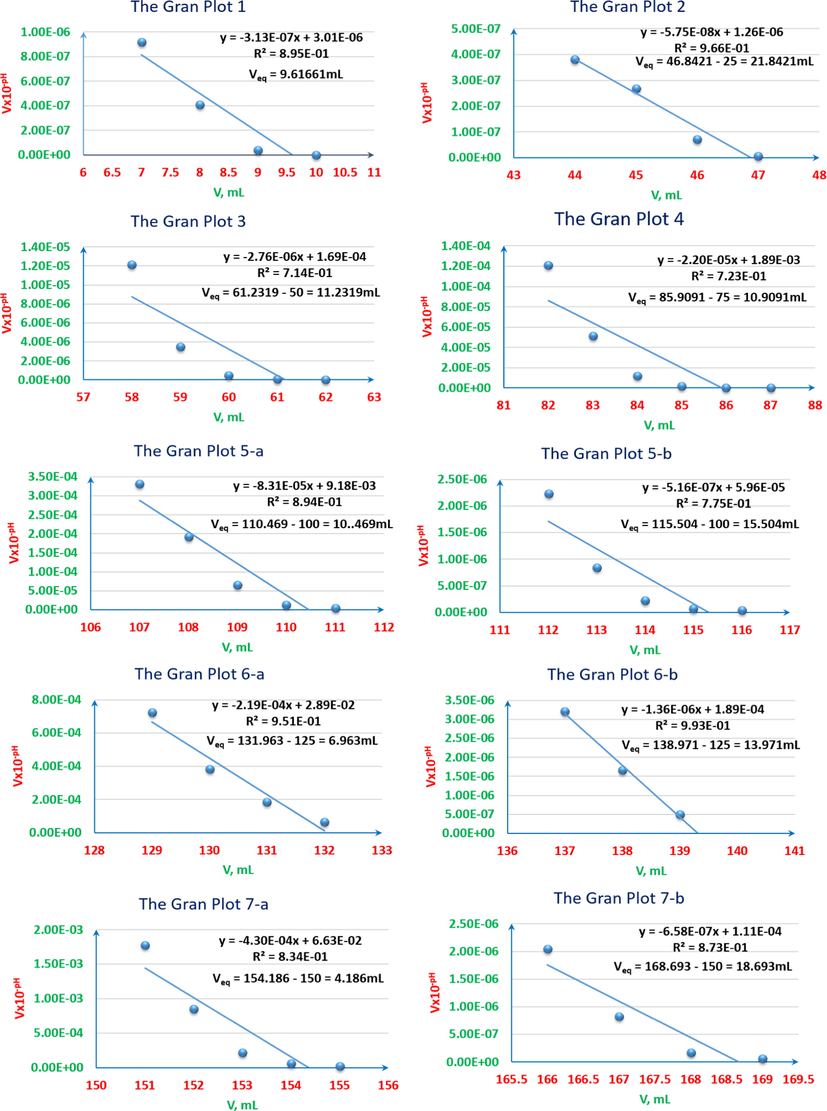
pH-titrimetric Gran plots of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH. 1: 4x10^-3M ARS 25ml. 2: 4x10^-3M ZnCl₂ 25ml. 3: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 4: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 5-a: first equivalence point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 5-b: second equivalent point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 6-a: first equivalence point of 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 6-b: second equivalence point of 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 7-a: first equivalent point of 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. 7-b: second equivalence point of 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml.

Export to PPT

Close

Fig. 7

pH-oscillotitrimetric graphs (pHOT) of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH: 1: 4x10^-3M ARS 25ml. 2: 4x10^-3M ZnCl₂ 25ml. 3: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 4: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 5: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 6: 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 7: 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. The curves (2-7) are extracted after adding 25 to each value of horizontal axis (volume axis) consecutively.

Export to PPT

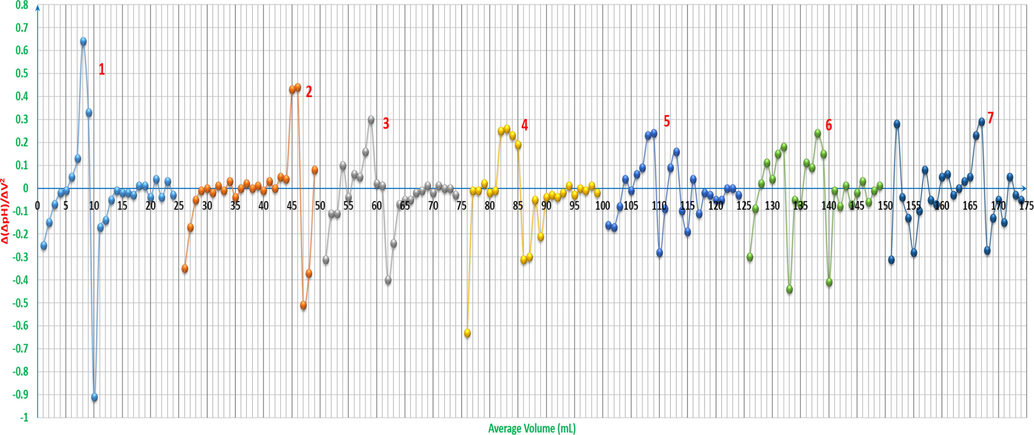
The equivalence point is referred to be ≈ 21.84mL, while the first derivative refers to 21.5mL, and the pH-oscillotitrimetric graph’s Gran plot 2 in Fig. 8 refers to ≈ 21.4mL. It is worth mentioning that for considering the fluctuation in the pHOT plot to be as a sign referring to a chemical process happening during the titration, the difference between two positive and negative points has to be Δ(ΔpH)/ΔV² ≥ 0.35, otherwise it does not refer to any change or to a point that can be taken into account.

Close

Fig. 8

pH-oscillotitrimetric graphs’ Gran plots (VOGs’ Gran plots) of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH. 1: 4x10^-3M ARS 25ml. 2: 4x10^-3M ZnCl₂ 25ml. 3: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 4: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 5-a: first equivalence point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 5-b: second equivalence point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 6-a: first equivalence point of 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 6-b: second equivalence point of 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. 7-a: first equivalence point of 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. 7-b: second equivalence point of 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml.

Export to PPT

From the next titration curves, when the metal salts’ solutions are mixed with the organic compound’s solutions in different ratios, the concentrations are as in Table 2.

It has been noticed that 18mL and 6mL of the hydroxide are required to reach the offset of the peak in the first derivative curve when titrating 25mL of ZnCl₂ and 25mL of ARS respectively, and the required volumes to titrate each total bulk of the materials are as in Table 3.

As per it is shown in Table 3, neither the usual pH-titrimetric nor the first derivative or the pHOT graphs can sense and separate the two pH hops of the mixtures unless the difference is dV_off-Veq(1,2) ≥ 6mL between the offsets of the leaps according to (12.5:12.5 v/v) ratio, where the two leaps start to be separated. For curves 5-6 in Fig. 5, reaction (9) is deployed at the beginning and before starting the titration.

Reaction (9) shows that ARS is not displaced for the first hydroxyl-group as the ambient pH is unsuitable for that. The reaction seems to be more displaced to the right side to form more hydrochloric acid, where zinc hydroxide is more stable in these conditions. HCl concentration in this case is equal to 5x10^-4M and Zn(OH)₂ concentration is 25x10^-5M. That means that HCl concentration is higher, which gives the acidic properties to the overall solution. By starting the pH-titrimetric process with adding the first mL of the hydroxide, reactions (10) and (11) carry out.

(11)

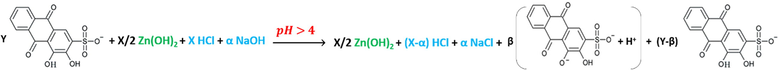
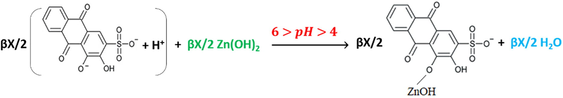
Reactions (10) and (11) continue to be the dominant ones until reaching the pH leaps, but by dropping the sixth mL of the hydroxide, the last reaction turns to be as reaction (12), where the pH value is suitable to form the complex. The same is proposed for curves 7 and 8 in Fig. 5 by adding the seventh mL of the hydroxide as in reaction (12).

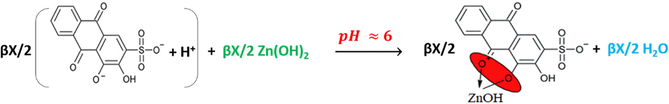
As it can be noticed from Table 3, HCl is titrated completely before the complete titration of ARS for the first ratio (5:20 v/v), and the hydroxide starts to be consumed first to titrate ARS for all next ratios. That is because the required volume of the hydroxide to titrate HCl is less than that are required to titrate it for the remaining ratios. However, as long as the difference is inappropriate to distinguish the two leaps of titrating HCl and ARS, and both leaps are overlapped for the first two ratios; (5:20 v/v, 10:15 v/v), pH-titrimetric method and even with the help of the first derivative and pHOT graphs cannot sense the difference to separate those two leaps. Instead, only the overall volume that is required to titrate both HCl and ARS can be determined. In most cases, the first derivatives are more accurate than the normal pH-titrimetric curves in determining the equivalence point. However, if there is an overlapping process, neither the pH-titrimetric curves nor the first derivatives are accurate enough in comparison with the pHOT graphs in determining the overall equivalence point of overlapped leaps. Hence, the Gran plots 3 and 4 in Fig. 6 of the pH-titrimetric curves 5 and 7 in Fig. 5 refer to V_{eq, overall(5)} ≈ 11.23mL and V_{eq, overall(7)} ≈ 10.91mL respectively, while the first derivatives in Fig. 5 and the Gran plots 3 and 4 of the pHOT graphs in Fig. 8 refer to [V_{eq, overall(6)} ≈ 11.5mL, V_{eq, overall(8)} ≈ 10.5mL] and [V_{eq, overall(3)} ≈ 10.2mL, V_{eq, overall(4)} ≈ 10.7mL] respectively.

After passing the overall equivalence points of (5:20 v/v, 10:15 v/v) ratios, as their curves 5 and 7 indicate in Fig. 5, the pH curves start to tend to be more stabilized at approximately pH ≈ 10.5, and the final products in the solution are supposed to be as in reactions (13) and (14).

(14)

An interesting fact can be noticed when different species start to have the same concentrations, or when having a weak organic acid’s (ARS) concentration lesser than that of an added salt (ZnCl₂) which, by dissolving it in the same aqueous solution, results a formation of a strong inorganic acid (HCl). This fact has at least three factors to be taken into account to prognosticate the results prior to the titration of the mixtures. The first factor is the length of the buffer regions of both materials when titrated individually with the same concentration against the same concentration of a standard solution, the second is the strength of both acidic materials and their products after dissolving in eques solutions and the third is the number of the displacements appeared as leaps on the titration curves that both materials have when titrated individually. According to the previous discussion, the added hydroxide is consumed to titrate the components that are of lesser concentrations, which means in the current case that ARS is titrated first and its leap is appeared before the titration leap of HCl resulted from ZnCl₂ which was previously dissolved in the solution as a precursor.

For the rest of the pH-titrimetric curves; 9, 11 and 13 in Fig. 5, depending on what has been discussed earlier on, there is no complex formation, and also the titration of the weak acid, which is of equal or less concentration, carries on indirectly with the help of titrating the strong acid. The following explanations exhibit the mechanism of what carries on before and during the titration. Before titrating the mixtures, as it is shown from the initial pH value of the solution, ARS is already displaced for the first hydroxyl-group, and that means that the solution already has the formation of the salt which forms between Zn(OH)₂ and ARS^- in accordance with reaction (15).

As it can be seen from the curves of these last three mixtures, the first leaps start from pH ≈ [5.25-5.5]. Therefore, the pH values are not suitable for the formation of the complex. Thereafter, the reactions remain as the same as reactions (13) and (14) with only the difference of having some of HCl concentration gets titrated before and after the second displacement of ARS to form the salts in reaction (14) until finishing the titration of the entire species of HCl which is expressed by the second leaps of those three curves.

α.3- The indications of the electro-conductivity values on the solutions and mixtures of ARS and zinc chloride:

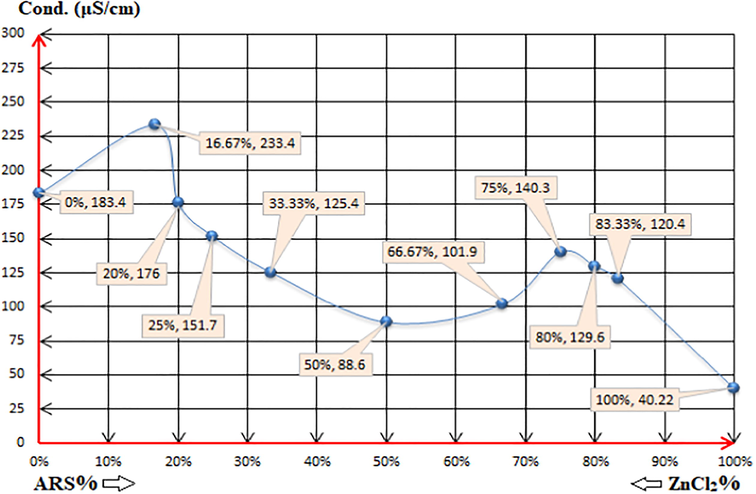
Fig 9 as electro-conductivity method reveals more accuracy than pH-metric method to either interpret the reasons behind the statuses of the mixtures at some points or to confirm the same. For the first five mixtures namely (1:5), (1:4), (1:3), (1:2) and (1:1), the conductivity decreases with the decrease of the zinc chloride percentage and with the increase of ARS per cent. This process confirms reactions (4) and (5) until (1:1) stoichiometry at which reaction (6) is provided to be the dominant one in this case. Thereafter, ARS contributes more to the conductivity value of the mixture with the increase of its percentage, which causes the increase in the conductivity as long as there is no more sufficient molecules of zinc hydroxide to react with. Hence, ARS ions confer more protons from the first displacement of their (-OH)-groups according to reaction (7), increasing the conductivity of (2:1) and (3:1) mixtures. The accuracy is revealed when studying the following-up mixtures; (4:1) and (5:1). The conductivity starts to decrease again although the percentage of ARS increases, and this is the proof of the suppression of the first displacement of ARS in which it begins to initiate its functionality partially. This implementation of that partial inhibition is due to the unsuitability of the pH value, which is intrinsically required to induce that displacement reaction further. In other words, reaction (7) is likely to be a reversible reaction (16).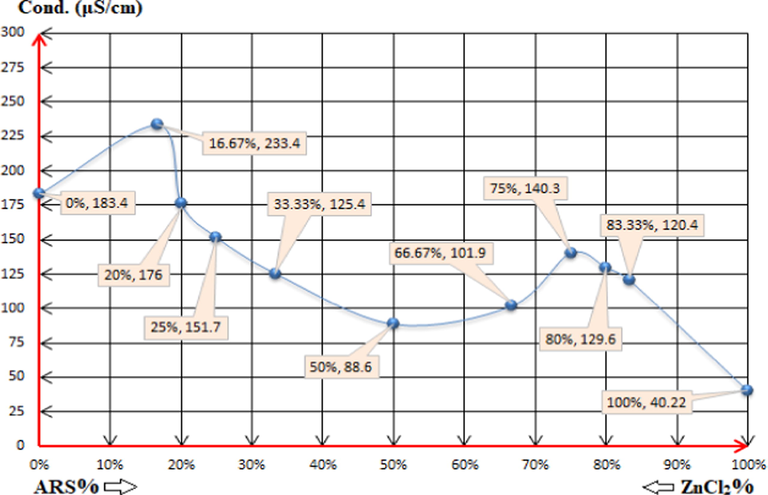

Close

Fig. 9

The electro-conductivity values of the solutions: (0%, 5.77): 4x10^-3M ZnCl₂ 0.5ml + 79.5ml DI water. (16.67%, 5.4) (1:5): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2.5ml + 77ml DI water. (20%, 5.77) (1:4): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2ml + 77.5ml DI water. (25%, 5.8) (1:3): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1.5ml + 78ml DI water. (33.33%, 5.83) (1:2): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1ml + 78.5ml DI water. (50%, 6) (1:1): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 0.5ml + 79ml DI water. (66.67%, 5.77) (2:1): 4x10^-3M ARS 1ml + 4x10^-3M ZnCl₂ 0.5ml + 78.5ml DI water. (75%, 5.1) (3:1): 4x10^-3M ARS 1.5ml + 4x10^-3M ZnCl₂ 0.5ml + 78ml DI water. (80%, 4.61) (4:1): 4x10^-3M ARS 2ml + 4x10^-3M ZnCl₂ 0.5ml + 77.5ml DI water. (83.33%, 4.06) (5:1): 4x10^-3M ARS 2.5ml + 4x10^-3M ZnCl₂ 0.5ml + 77ml DI water. (100%, 4.57): 4x10^-3M ARS 0.5ml + 79.5ml DI water.

Export to PPT

3.1.4 The indications of the electroconductivity titrimetric and volumetric-oscillographs (VOG) (fingerprint spectrums) of the solutions and mixtures of ARS and zinc chloride

As it can be seen from Figs. 10a and 10b, when there is Zn(OH)₂ in the solution, the fluctuations of the mixtures’ electroconductivity increases depending on the concentrations of the both species; ARS and Zn(OH)₂. Also, when both species are close in concentration to each other, there are clear fluctuations at the equivalence points. That means ARS restrains the fluctuations when it has more concentration in the solution, and even when it has less concentrations, it prevents the electroconductivity from being disturbed the way it is when having only ZnCl₂ solution. This is a good sign that ARS firstly increases the conductivity and secondly plays a stabilization role. On the other hand, comparing the fluctuations when both species have the same concentration as in curves 9 and 10 with other curves, the strength of these two curves’ fluctuations is due to the clear start of the separation between two equivalence points as it is shown from curve 10 in Fig. 5, but they are still close to each other. Another reason for that, as it has been discussed earlier from curves 9, 11 and 13 in Fig. 5, is that there is no complex formation before or near the two equivalence points along with having these two points still close to each other. Forming a complex gives more stability to the curve in such cases.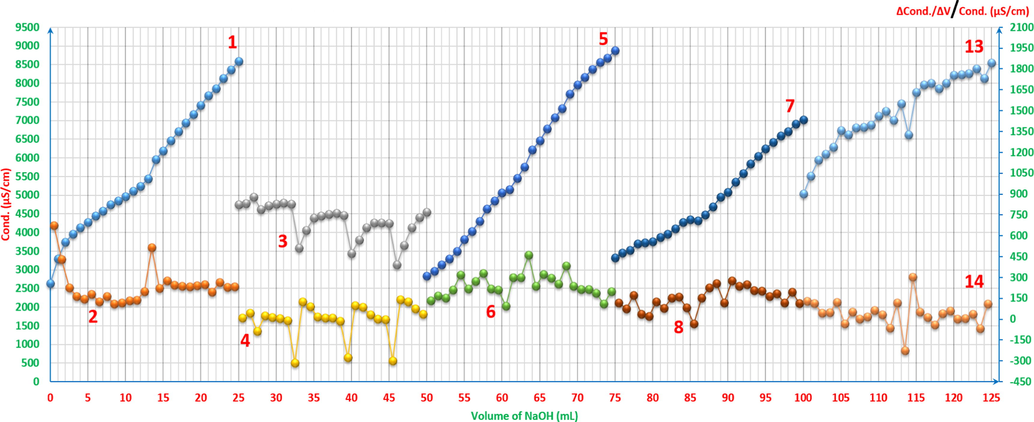

Close

Fig. 10a

Electroconductivity titrimetric graphs of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH with the first derivatives: 1 and 2: 4x10^-3M ARS 25ml. 3 and 4: 4x10^-3M ZnCl₂ 25ml. 5 and 6: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 7 and 8: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 13 and 14: 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. The curves (3-8, 13, 14) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively. The curves 3 and 13 are of the secondary axis on the right.

Export to PPT

Close

Fig. 10b

Electroconductivity titrimetric curves of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH with the first derivatives: 9 and 10: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 11 and 12: 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. The curves (11, 12) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively.

Export to PPT

For a complete study of what happens in the solutions while electroconductotitrating against the hydroxide, the second derivatives offer stunning information that push towards higher level of interpretations. The peaks areas have been marked and named to start the analysis process as it is shown in Figs. 11a and 11b. Some rules have been set to understand the plots and to explain the line-graphs in clear and stable way. The small peaks (fluctuations) have to be more than 300 as a difference between the bottom values of the peaks and their top values; Δ(ΔCond.)/ΔV² > 300, to be considered as either a new formation of a new species that can affect the conductivity in obvious way or as an equivalence point, otherwise; Δ(ΔCond.)/ΔV² ≤ 300, it is indicated as pKa for weak acids or the start of forming new species that can be formed in different stages or forms later on, or it is the finish of the titration when the solution has accumulated amount of the hydroxide and the pH value is above 10. Curve 1 shows three significant areas of changes, where a is indicated at approximately 4-6mL of the hydroxide to be the pKa of ARS, the second area b is where ARS is completely titrated and c is where the titration finishes due to the accumulation of hydroxide species. Curve 2 has four areas. Starting with area a, this indicates to the initiation stage of Zn(OH)_x which slightly drops the electroconductivity and makes small fluctuations in the curve. Hence, when it reaches to area b and c, here comes the stage of the clear Zn chemistry to form the hydroxide in different forms, where white gelatinous zinc hydroxides precipitate as in Fig. 12.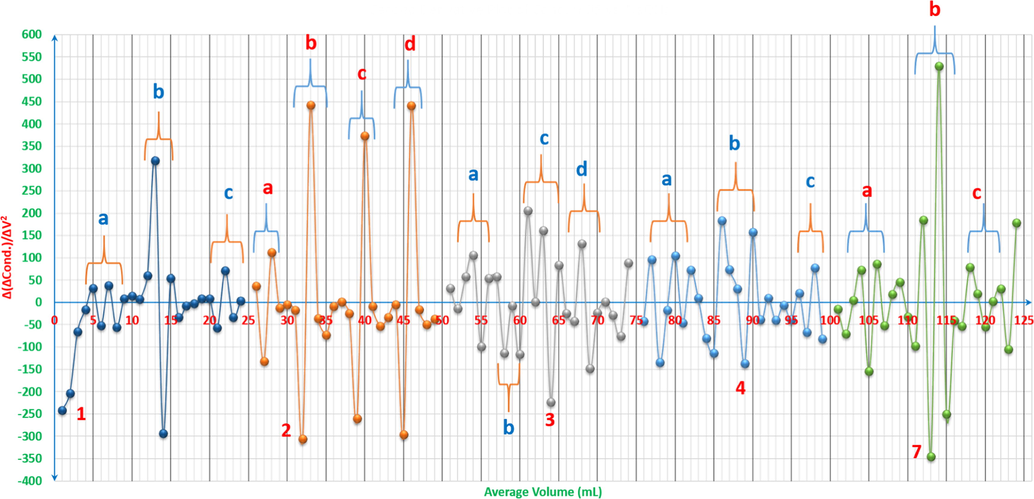

Close

Fig. 11a

Volumetric-oscillographs (VOGs) (fingerprint spectrums) of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH: 1: 4x10^-3M ARS 25ml. 2: 4x10^-3M ZnCl₂ 25ml. 3: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. 4: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml. 7: 4x10^-3M ZnCl₂ 20ml with 4x10^-3M ARS 5ml. The curves (3-4, 7) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively.

Export to PPT

Close

Fig. 11b

Volumetric-oscillographs (VOG) (fingerprint spectrum) of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH: 5: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M ARS 12.5ml. 6: 4x10^-3M ZnCl₂ 15ml with 4x10^-3M ARS 10ml. The curve 6 is extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively.

Export to PPT

Close

Fig. 12

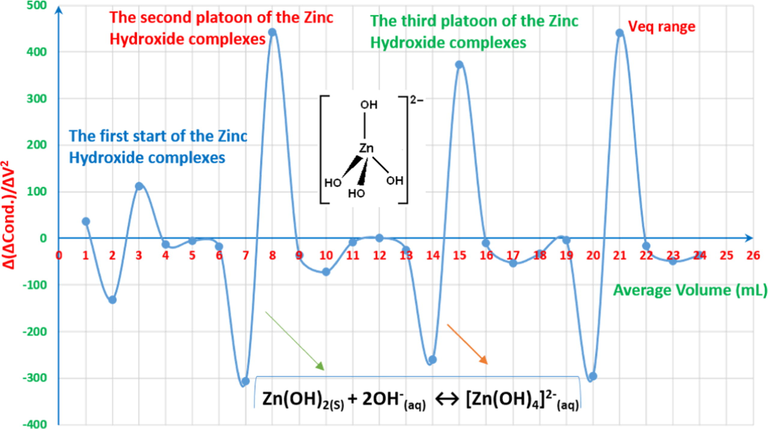
Interpretation of volumetric-oscillograph (VOG) (fingerprint spectrum) of 4x10^-3M ZnCl₂ 25ml vs. 0.01M NaOH.

Export to PPT

It is assumed that the reaction with the increase of the hydroxide concentration has two formation paths according to reaction (17).

The final area d is for the complete titration of HCl resulted from dissolving ZnCl₂ in DI water.

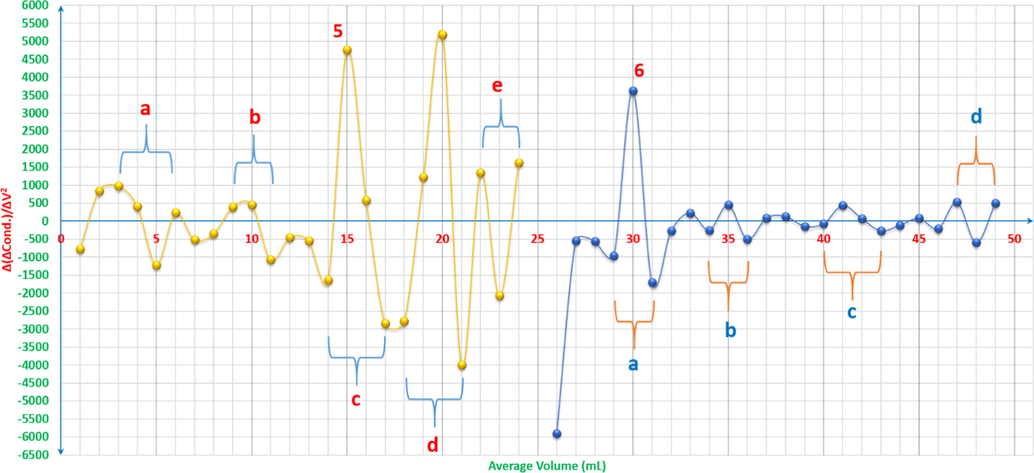
Curve 3 has four regions, where area a refers to the pKa of ARS in which the salt ARSZnOH is formed, whereas area b is where the initiation stage of Zn(OH)_x and ARSZnOH complexes nearer to the neutral medium are preferable. Thereafter, area c is indicated to be the area of the complete titration of the mixture; both HCl and ARS. With increasing the concentration of the hydroxide, area d shows where [Zn(OH)₄]^2- complexes and the salt ARSZn are formed. Area a of curve 4 that has three regions indicates to the pKa of ARS in which the salt ARSZnOH is formed, beside the initiation stage of Zn(OH)_x and ARSZnOH complexes nearer to the neutral medium, whilst area b is assumed to be the area of the complete titration of the mixture; both HCl and ARS, where also the salt ARSZn starts to be formed. Up to area c, [Zn(OH)₄]^2- complexes and the accumulation of NaOH access at the end of the titration are the major species. pKa of ARS, the formation of the salt ARSZnOH and the initiation stage of Zn(OH)_x complexes are indicated to be at the area a in curve 4, whereas the complete titration of the mixture; both HCl and ARS, is assumed to be at the area b. [Zn(OH)₄]^2- complexes and the accumulation of NaOH access at the end of the titration are the major species where it is indicated as area c. In curve 7, area a is the region in which ARS is completely titrated, the initiation stage of Zn(OH)_x complexes and the formation of the salt ARSZn, while area b is of the complete titration of HCl and the formation of [Zn(OH)₄]^2- complexes and the salt ARSZn. The accumulation of [Zn(OH)₄]^2- complexes and NaOH access are referred to be at are c.

As it is shown in Fig. 11b, curves 5 and 6 are divided to five and four areas respectively, where areas a refer to pKa of ARS and the formation of the salt ARSZnOH in higher concentrations than those of other curves and that is the reason behind Δ(ΔCond.)/ΔV² > 300, and this applies on all areas in curves 5 and 6, whilst areas b are of the complete titration of ARS, and areas c are referred to be the complete titration of HCl. Clear formation of [Zn(OH)₄]^2- complexes with higher concentrations at area d in curve 5 is exhibited, whilst the accumulation of [Zn(OH)₄]^2- complexes and NaOH access are referred to be at areas e and d in curves 5 and 6 respectively.

As it can been seen from Fig. 13, the temperature titrimetric curves can interpret what happens in the solutions. These are some examples of the temperature-oscillotitrimetric curves. However, from method to another, the details and information provided differ in their amounts.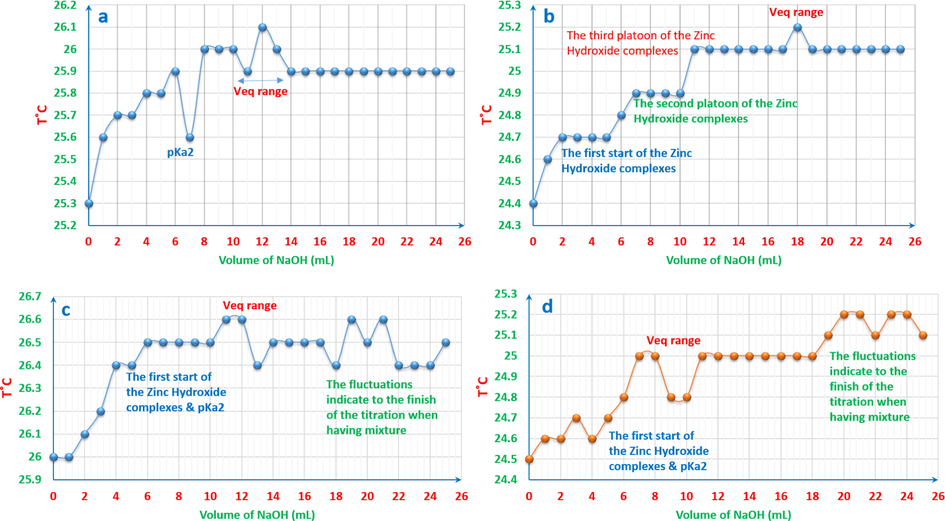

Close

Fig. 13

Temperature-oscillotitrimetric graphs of ARS, ZnCl₂ and their mixtures vs. 0.01M NaOH: a: 4x10^-3M ARS 25ml. b: 4x10^-3M ZnCl₂ 25ml. c: 4x10^-3M ZnCl₂ 5ml with 4x10^-3M ARS 20ml. d: 4x10^-3M ZnCl₂ 10ml with 4x10^-3M ARS 15ml.

Export to PPT

3.1.5 The indications of the pH values in studying the competition between copper and zinc ions to chelate with ARS simultaneously

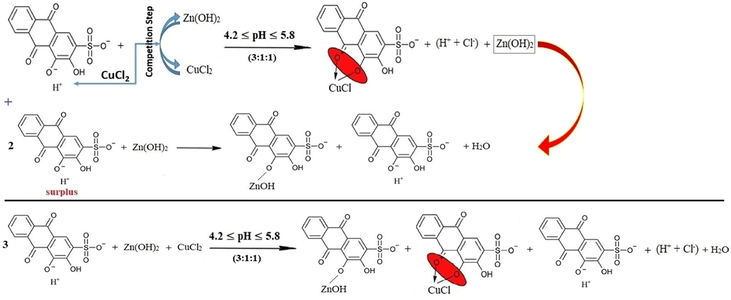
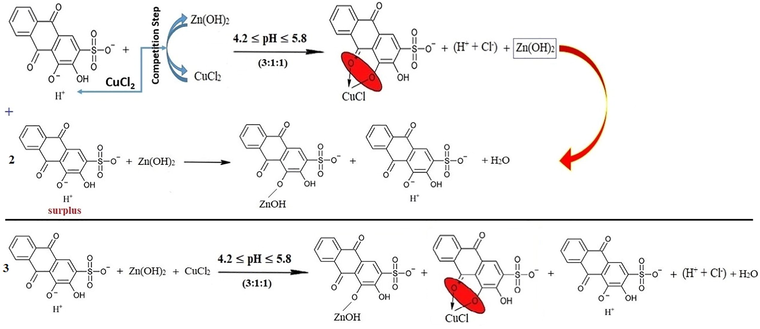
For the first three mixtures (1:5:5), (1:4:4) and (1:3:3), the predominant reaction could be elicited as follows:

The range of the pH values of all the mixtures is [4.37-5.32] as it is shown in Fig. 14, and that is suitable for the first displacement of the first (-OH)-group of ARS where the range [4.2-5.8] of pH is the considered one for this reaction. Also, since the pH value debilitates for the first bunch of mixtures, it seems that copper chloride ions react with ARS^- to form the complex rather than zinc chloride ions. The overall reaction is, therefore, as per reaction (18).

Close

Fig. 14

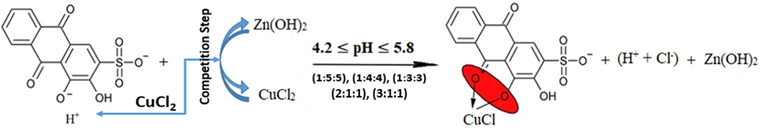
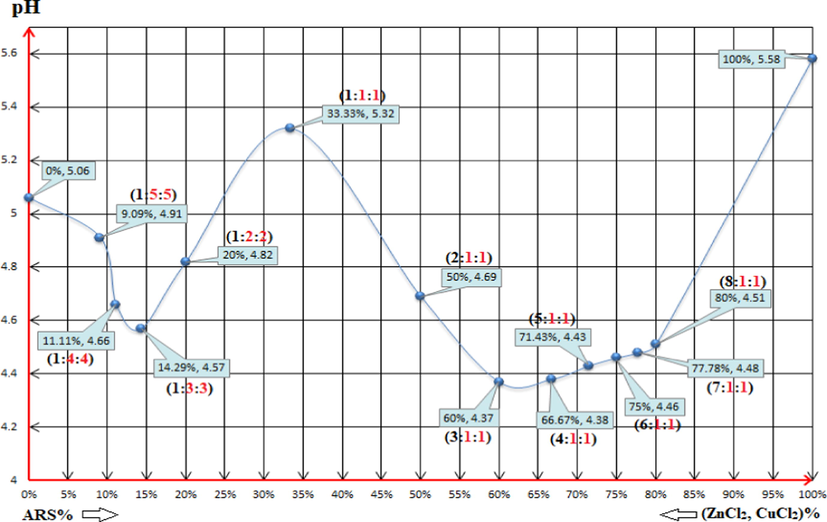
The pH values of the following solutions: (0%, 5.06): 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 79ml DI water. (9.09%, 4.91) (1:5:5): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2.5ml + 4x10^-3M CuCl₂ 2.5ml + 74.5ml DI water. (11.11%, 4.66) (1:4:4): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2ml + 4x10^-3M CuCl₂ 2ml + 75.5ml DI water. (14.29%, 4.57) (1:3:3): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1.5ml + 4x10^-3M CuCl₂ 1.5ml + 76.5ml DI water. (20%, 4.57) (1:2:2): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1ml + 4x10^-3M CuCl₂ 1ml + 77.5ml DI water. (33.33%, 5.32) (1:1:1): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 78.5ml DI water. (50%, 4.69) (2:1:1): 4x10^-3M ARS 1ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 78ml DI water. (60%, 4.37) (3:1:1): 4x10^-3M ARS 1.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 77.5ml DI water. (66.67%, 4.38) (4:1:1): 4x10^-3M ARS 2ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 77ml DI water. (71.43%, 4.43) (5:1:1): 4x10^-3M ARS 2.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 76.5ml DI water. (75%, 4.46) (6:1:1): 4x10^-3M ARS 3ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 76ml DI water. (77.78%, 4.48) (7:1:1): 4x10^-3M ARS 3.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 75.5ml DI water. (80%, 4.51) (8:1:1): 4x10^-3M ARS 4ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 75ml DI water. (100%, 5.58): 4x10^-3M ARS 0.5ml + 79.5ml DI water. Where (L:M:M)  =  (ARS:Zn:Cu).

Export to PPT

For the following two mixtures (1:2:2) and (1:1:1), the pH values are again suitable for the first displacement of the first (-OH)-group of ARS. However, since the pH value increases for these two mixtures and the pH values are not suitable for the formation of the complex between zinc and ARS, zinc chloride ions react with ARS^- to form the salt and not the complex rather than having copper chloride ions reacting instead. The overall reaction is, therefore, as per reaction (19).

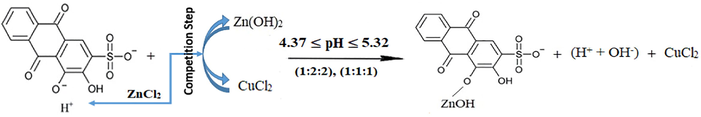
For the following two mixtures (2:1:1) and (3:1:1), the pH values are still suitable for the first displacement of the first (-OH)-group of ARS. However, since the pH value decreases for these two mixtures and the pH values are suitable for the complex formation between copper and ARS, copper ions again intervene the competition step to outdo zinc ions and react with ARS^- to form the complex. The overall reaction is, thus, as per reaction (18).

On the other hand, the surplus ions of ARS can in this case have another overall suggested reaction. First, after the reaction of copper ions with ARS^-, the competition step is stopped and it is the time for zinc ions to react with the surplus ions of ARS^- to form the salt ARSZnOH. Hence, the process can be written as in reaction (20).

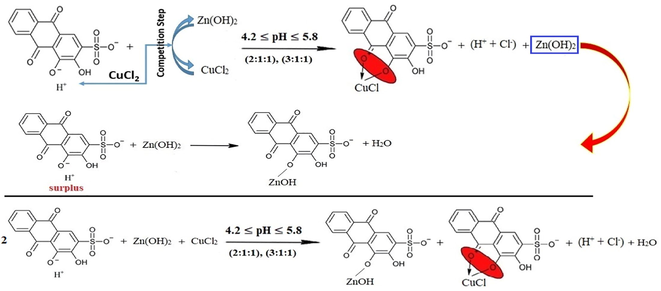
As the competition process supposes its own conditions, different than normal conditions that are required for chelation step, the suggestions of the stoichiometry can be also different. Therefore, beginning from the added stoichiometry (3:1:1) to form the mixture, the ultimate or secondary triumphant reactions might be different as well. To this point, in accordance with the decrease or increase of the pH value of a certain bunch of mixtures, it can be pointed out which one is the preponderant reaction that takes place at first. For further explication, the stoichiometry (3:1:1) has the overflowing ions of ARS. Therefore, there are many suggestions to this case. First, the surplus of ARS reacts with ARSCuCl as a complex with the stoichiometry of (2:1):(L:M). Hence, the suggested reaction can be written as in reaction (21).

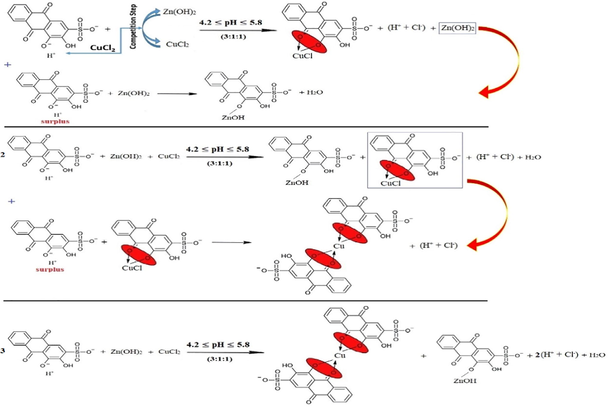
Second, the surplus of ARS reacts with ARSZnOH as a salt with the stoichiometry of (2:1):(L:M) since the pH value is not sufficient to form a complex. This can be expressed as in reaction (22).

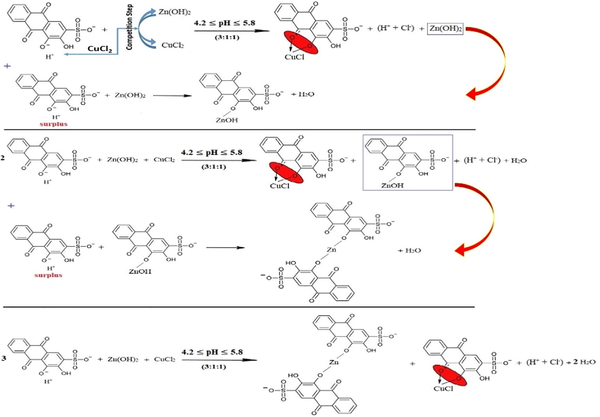
Third, the surplus of ARS reacts with both ARSCuCl and ARSZnOH equally with the stoichiometry of (2:1) for the half of ions of each kind of the metals as in reaction (23).

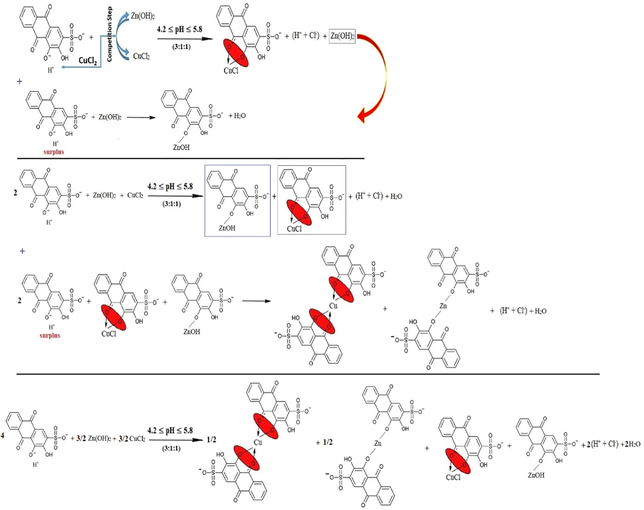
Fourth, the stoichiometry (1:1:1) is stable and fixed for each kind of metals, and the excess of ARS ions only displaces the first (-OH)-group as in reaction (24).

The mixtures (4:1:1), (5:1:1), (6:1:1), (7:1:1) and (8:1:1) confirm that the last suggestion is the correct one since the increase in the ARS volume tries to shift the pH value of these mixtures to the pH value that is sufficient for the first displacement of the first (-OH)-group. Hence, the pH shifts to a value that is related to the case when considerably having only ARS ions in the solution as their volume increases each time. Therefore, the reactions can be referred to as in reaction (25) with respect to the stoichiometry accordingly.

3.1.6 The indications of the electro-conductivity values in studying the competition between copper and zinc ions to bond with ARS simultaneously

As it is exhibited in Fig. 15, for the first five mixtures; (1:5:5) - (1:1:1), the amount of both CuCl₂ and ZnCl₂ decreases and causes the decrease in the electroconductivity value as the number of the electrolytic-active ions is reduced. As normally the fact has been justified as per the previous reasons, the indication of the electro-conductivity remains away from explaining the reactions apparently happening in the mixtures. The competition process starts to appear for the next mixtures. Beginning with looking at (2:1:1) and (3:1:1) mixtures, the electroconductivity increases, and this indicates that the competition process now takes place in which copper is bound with ARS since the products are HCl ions that are responsible for the increase of the electroconductivity. That is fully compatible with what has been found in pH-metery and showing the efficacious reaction to the value of the electroconductivity, and that is as in reaction (18). Although the suggested reactions as in pH-metery remain the same, the before mentioned reaction and the first displacement of ARS are the responsible reactions of the increase in the electroconductivity value. At the conclusion, the reaction is as per reaction (25).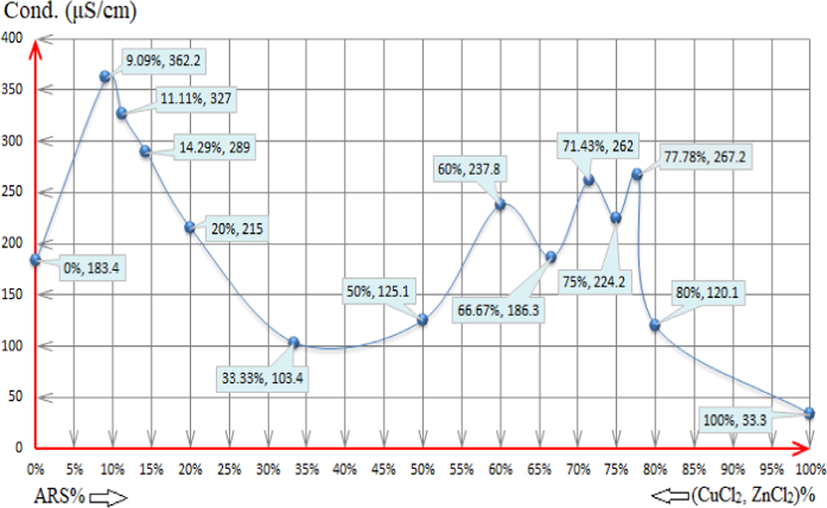

Close

Fig. 15

The electro-conductivity values of the following solutions: (0%, 183.4): 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 79ml DI water. (9.09%, 362.2) (1:5:5): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2.5ml + 4x10^-3M CuCl₂ 2.5ml + 74.5ml DI water. (11.11%, 327) (1:4:4): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 2ml + 4x10^-3M CuCl₂ 2ml + 75.5ml DI water. (14.29%, 289) (1:3:3): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1.5ml + 4x10^-3M CuCl₂ 1.5ml + 76.5ml DI water. (20%, 215) (1:2:2): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 1ml + 4x10^-3M CuCl₂ 1ml + 77.5ml DI water. (33.33%, 103.4) (1:1:1): 4x10^-3M ARS 0.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 78.5ml DI water. (50%, 125.1) (2:1:1): 4x10^-3M ARS 1ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 78ml DI water. (60%, 237.8) (3:1:1): 4x10^-3M ARS 1.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 77.5ml DI water. (66.67%, 186.3) (4:1:1): 4x10^-3M ARS 2ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 77ml DI water. (71.43%, 262) (5:1:1): 4x10^-3M ARS 2.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 76.5ml DI water. (75%, 224.2) (6:1:1): 4x10^-3M ARS 3ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 76ml DI water. (77.78%, 267.2) (7:1:1): 4x10^-3M ARS 3.5ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 75.5ml DI water. (80%, 120.1) (8:1:1): 4x10^-3M ARS 4ml + 4x10^-3M ZnCl₂ 0.5ml + 4x10^-3M CuCl₂ 0.5ml + 75ml DI water. (100%, 33.3): 4x10^-3M ARS 0.5ml + 79.5ml DI water. Where (L:M:M)  =  (ARS:Zn:Cu).

Export to PPT

The next volumetric stoichiometries; (4:1:1), (5:1:1), (6:1:1), (7:1:1) and (8:1:1), show the competition again. In these mixtures, new phenomenon starts to take place in which copper and zinc compete each other differently according to whether there is odd volumetric stoichiometry of ARS or even. Given that, for even stoichiometries; (4:1:1), (6:1:1) and (8:1:1), zinc competes copper to bond with ARS, and the only suggestion that can interpret this case of having these values of the electroconductivity is as in reaction (22). Copper competes zinc for odd stoichiometries; (5:1:1) and (7:1:1), in which this case turns the scale to have the suggested reaction (21) due to having more (H⁺ + Cl^-) in the solution which can explicate having higher electro-conductivity values.

Obviously, the insulations given in the electroconductivity method are different than those in pH-metric method, especially for the last five mixtures as presented lately. The reason beyond that is that the latter does not seem to sense the difference between having more (H⁺ + Cl^-) besides (H⁺) and having (H⁺) only in terms of low concentrations, whilst the electroconductivity method sensed those nuances and to some extent suggested certain reactions for each later and particular mixtures.

3.1.7 The indications of the pH-titrimetric, pH-oscillotitrimetric (pHOT) and volumetric-oscillo graphs (VOG) in studying the competition between copper and zinc ions to chelate with ARS simultaneously

As it is shown in Fig. 16, the pH curve exhibits two leaps. To examine the reason behind these two leaps, reactions (26) and (27) are taken into consideration.

Close

Fig. 16

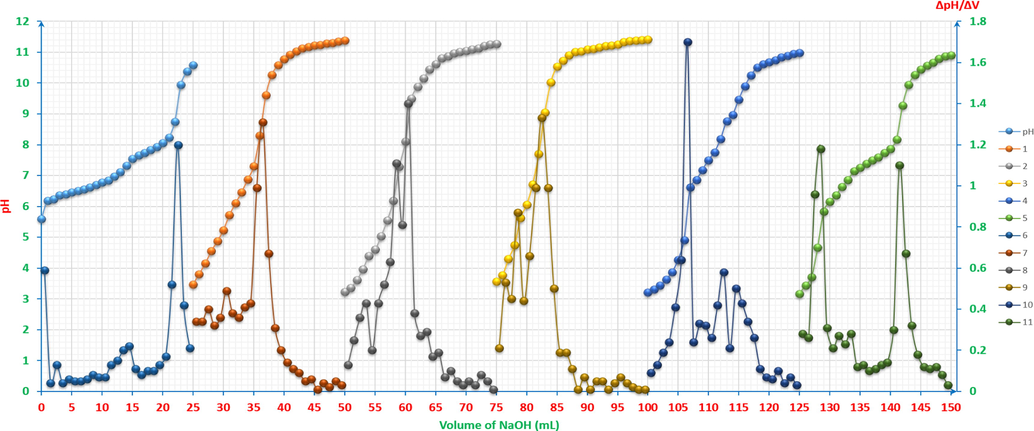
pH-titrimetric curves of ARS, ZnCl₂, CuCl₂ and their mixtures vs. 0.01M NaOH with the first derivatives: pH and 6: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M CuCl₂ 12.5ml. 1 and 7: 4x10^-3M ZnCl₂ 2.5ml and 4x10^-3M CuCl₂ 2.5ml with 4x10^-3M ARS 20ml. 2 and 8: 4x10^-3M ZnCl₂ 5ml and 4x10^-3M CuCl₂ 5ml with 4x10^-3M ARS 15ml. 3 and 9: 4x10^-3M ZnCl₂ 6.25ml and 4x10^-3M CuCl₂ 6.25ml with 4x10^-3M ARS 12.5ml. 4 and 10: 4x10^-3M ZnCl₂ 7.5ml and 4x10^-3M CuCl₂ 7.5ml with 4x10^-3M ARS 10ml. 5 and 11: 4x10^-3M ZnCl₂ 10ml and 4x10^-3M CuCl₂ 10ml with 4x10^-3M ARS 5ml. The curves (2-11) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively.

Export to PPT

Even in case when CuCl₂ reacts with water as hydrolysis reaction as follows: (Cu²⁺ + 2Cl^-) + H₂O ↔ (Cu²⁺ + 2OH^-) + HCl, and then the products react with NaOH as the following: HCl + NaOH → NaCl + H₂O, the overall assumption would be having either the chloride salts with the products of neutralisation reactions resulting in from the reaction between hydrochloric acid and sodium hydroxide or only the products of neutralisation reactions. That most probably leads to that the neutralisation reaction of HCl is the prevalent one in this medium. Therefore, the expected leaps’ number of the titrimetric curve must be only one. From another angle, the Gran plot of the first heap cannot be accurate at any calculations as it is shown in Fig. 17, Gran plot 1-a, and having 1-2 points as a neck of leap is not sufficient to be considered as a valuable leap. From these perspectives, it has been discovered throughout this study that there could be Pseudo-leaps in such cases when having a mixture to be titrated. The second leap is the expected actual one, as it is shown in Fig. 17, Gran plot 1-b. According to the previous observations, and by taking into account the first derivative, the new rule for the leap to be considered is that the following condition has to be fulfilled: ΔpH ≥ 0.4, between the pervious point, that is the nearest to the peak climax, and the utmost point itself. Also, in case of any doubt about the peaks, that are adjacent, to be considered in any first derivative curve, the previous and sequence mixtures curves in the studied samples series have to be taken into account. Therefore, if the previous and next curves have peaks get to be separated in the latest one, these overlapped peaks has to be considered as two peaks, e. g. the peaks in curves 8 and 9 in Fig. 16, they are considered as one peak otherwise, e.g. the second overlapped peaks in curve 10 in Fig. 16.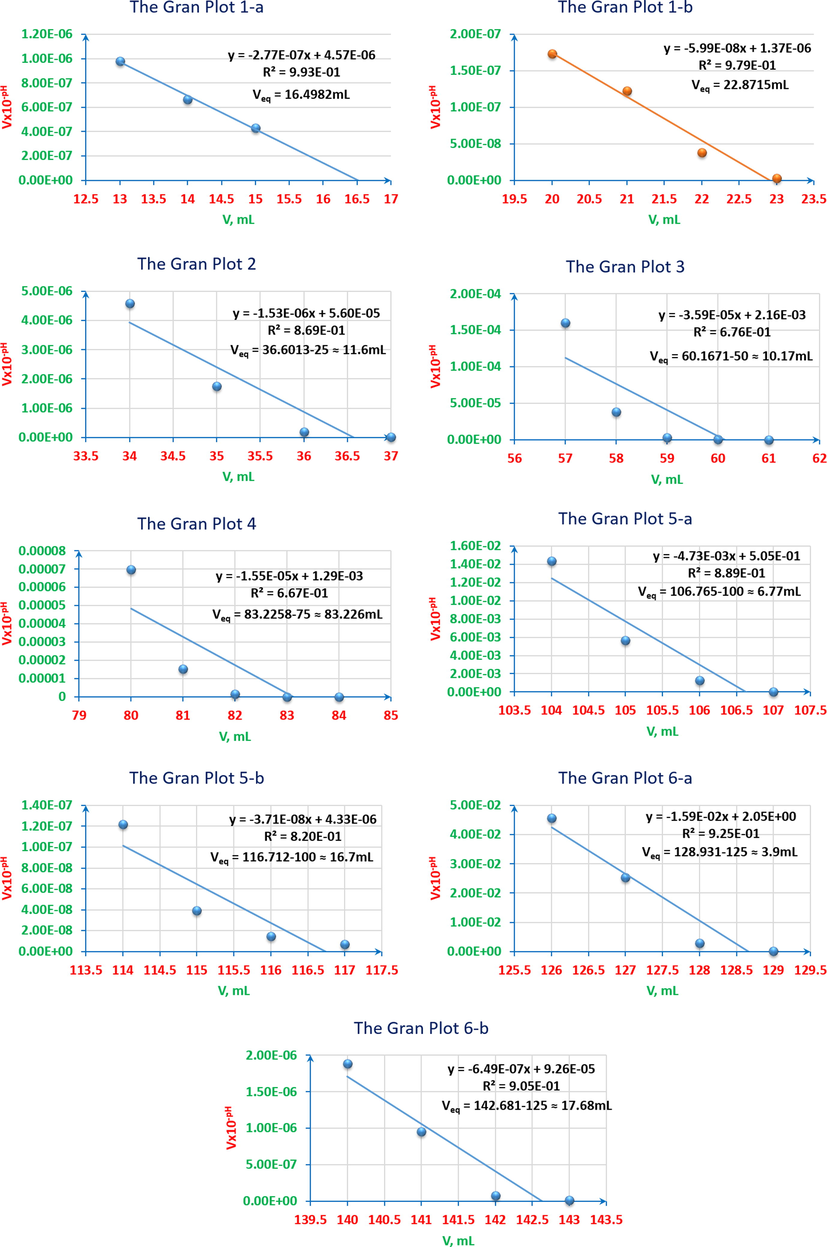

Close

Fig. 17

pH-titrimetric curves’ Gran plots of ARS, ZnCl₂, CuCl₂ and their mixtures vs. 0.01M NaOH. 1-a: the first equivalence point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M CuCl₂ 12.5ml (pseudo-leap). 1-b: the second equivalence point of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M CuCl₂ 12.5ml. 2: 4x10^-3M ZnCl₂ 2.5ml and 4x10^-3M CuCl₂ 2.5ml with 4x10^-3M ARS 20ml. 3: 4x10^-3M ZnCl₂ 5ml and 4x10^-3M CuCl₂ 5ml with 4x10^-3M ARS 15ml. 4: 4x10^-3M ZnCl₂ 6.25ml and 4x10^-3M CuCl₂ 6.25ml with 4x10^-3M ARS 12.5ml. 5-a: the first equivalent point of 4x10^-3M ZnCl₂ 7.5ml and 4x10^-3M CuCl₂ 7.5ml with 4x10^-3M ARS 10ml. 5-b: the second equivalent point of 4x10^-3M ZnCl₂ 7.5ml and 4x10^-3M CuCl₂ 7.5ml with 4x10^-3M ARS 10ml. 6-a: the first equivalent point of 4x10^-3M ZnCl₂ 10ml and 4x10^-3M CuCl₂ 10ml with 4x10^-3M ARS 5ml. 6-b: the second equivalent point of 4x10^-3M ZnCl₂ 10ml and 4x10^-3M CuCl₂ 10ml with 4x10^-3M ARS 5ml.

Export to PPT

The reactions in accordance with the different pH mediums; pH < 4, 4.6 > pH > 4, 5.8 > pH > 4.6, 6.6 > pH > 5.8, 13 > pH > 7.5, are as per reactions (28), (29), (30), (31) and (32).

(29)

(30)

(31)

(32)

In order to understand the analysis of these graphs, Fig. 18 represents pHOT graphs that show more precision in the determination of the number of titration leaps. For graphs 1 and 2, there is only one leap for each (a and b respectively), whereas there are two leaps (a and b) for each graph of 3, 4, 5 and 6. Therefore, as a mixture solution of two metals and a dye, some distinguished rules have to be conceived, knowing that the anterior established rules are considered. First, the leap’s direction has to start from the positive section to the negative one; for example, the start of graph 3. Second, the graph cannot be read as a taken into account leap at its start; for instance, as in graph 4. Third, taking into account the subsequent graph and comparing the numbers of the concerned-graph’s leaps with those of the other; for example, the last leap of graph 5 seems to be as two leaps, it is rather one leap when compared with the posterior graph, which is graph 6.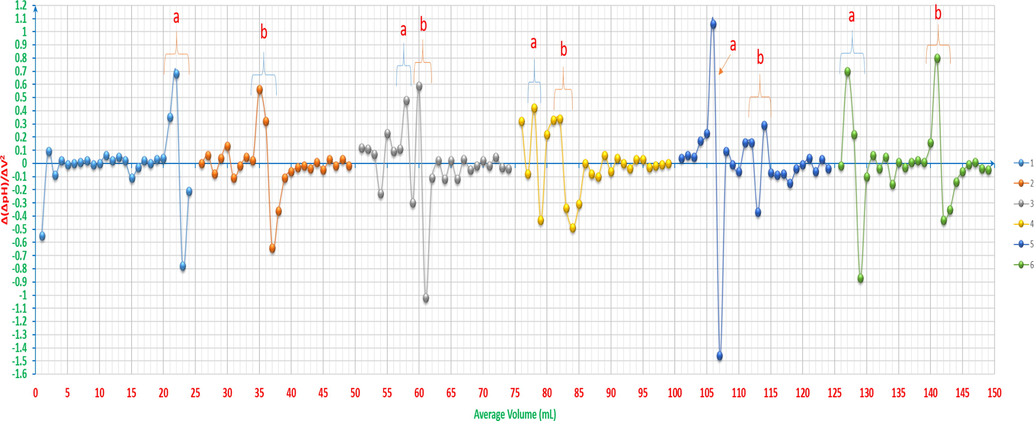

Close

Fig. 18

pH-oscillotitrimetric graphs of ARS, ZnCl₂, CuCl₂ and their mixtures vs. 0.01M NaOH: 1: 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M CuCl₂ 12.5ml. 2: 4x10^-3M ZnCl₂ 2.5ml and 4x10^-3M CuCl₂ 2.5ml with 4x10^-3M ARS 20ml. 3: 4x10^-3M ZnCl₂ 5ml and 4x10^-3M CuCl₂ 5ml with 4x10^-3M ARS 15ml. 4: 4x10^-3M ZnCl₂ 6.25ml and 4x10^-3M CuCl₂ 6.25ml with 4x10^-3M ARS 12.5ml. 5: 4x10^-3M ZnCl₂ 7.5ml and 4x10^-3M CuCl₂ 7.5ml with 4x10^-3M ARS 10ml. 6: 4x10^-3M ZnCl₂ 10ml and 4x10^-3M CuCl₂ 10ml with 4x10^-3M ARS 5ml. The curves (2-6) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively.

Export to PPT

For more complicated solutions that contain a dye as an organic compound and more than one metal, when using VOGs, the graphs can be informative to know their fluctuation and strength diagrams (VOGFSD). As it can be seen from Fig. 19, the fluctuations give the possible ratios that can be focused on to know the exact and correct correlation ratio. As it is shown, VOGFSD tends to be in a medial status for the suitable ratio, and the reason is that the formation of the complexes; for both Zn⁺² and Cu⁺², with ARS increases when the ratio is suitable for higher concentrations of these two formed complexes, where these formations influence the conductivity of the solution and force it to fluctuate in comparison with the previous and later ratios (1:1:3 and 1.5:1.5:2). On the other hand, the first and last ratios (1:1:8 and 2:2:1) have more fluctuation strength due to either the higher concentration of ARS or metals in the solution. It is worth mentioning that the first 25ml from the volume axis have been deleted for the mixture of 4x10^-3M ZnCl₂ 12.5ml with 4x10^-3M CuCl₂ 12.5ml in order to indicate that the device couldn’t measure the high conductivity of it during the titration.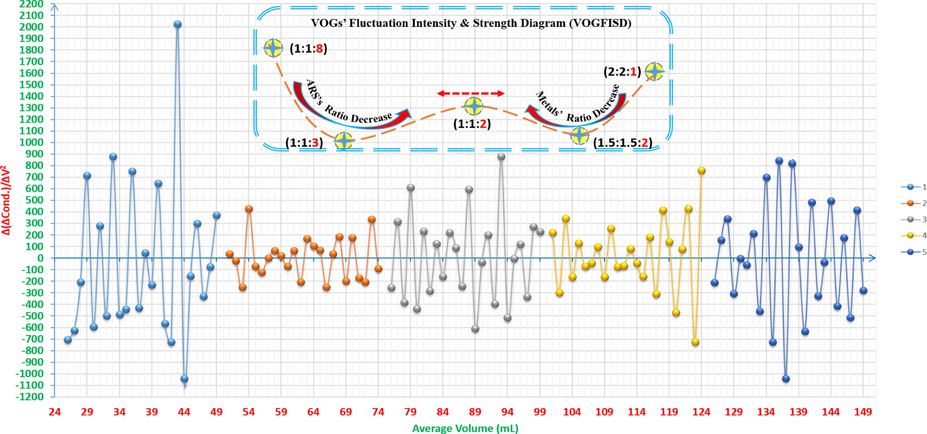

Close

Fig. 19

Volumetric-oscillographs (VOGs) of the mixtures of ARS, ZnCl₂ and CuCl₂ vs. 0.01M NaOH and their VOGs’ fluctuation intensity & strength diagram (VOGFISD): 1: 4x10^-3M ZnCl₂ 2.5ml and 4x10^-3M CuCl₂ 2.5ml with 4x10^-3M ARS 20ml. 2: 4x10^-3M ZnCl₂ 5ml and 4x10^-3M CuCl₂ 5ml with 4x10^-3M ARS 15ml. 3: 4x10^-3M ZnCl₂ 6.25ml and 4x10^-3M CuCl₂ 6.25ml with 4x10^-3M ARS 12.5ml. 4: 4x10^-3M ZnCl₂ 7.5ml and 4x10^-3M CuCl₂ 7.5ml with 4x10^-3M ARS 10ml. 5: 4x10^-3M ZnCl₂ 10ml and 4x10^-3M CuCl₂ 10ml with 4x10^-3M ARS 5ml. The curves (1-5) are extracted after adding 25 to each value of the horizontal axis (volume axis) consecutively

Export to PPT

4.1.1 Studying the correlation ratio between Zn(II) and ARS using pH/conductivity diagrams (pHCD) method

Fig 20 shows the percentage of ZnCl₂ and ARS in a series of samples as mixtures of 6x10^-5M ARS and 6x10^-5M Zn(II) and indicates to both graphs of pH and electroconductivity of the correct ratio in which Zn(II) and ARS are chelated. For the pH graph, the range is [5.58-5.97] and it is quite convenient for Zn⁺² to bond with ARS forming the complex according to reaction (6). This means that Zn(II), when it is chelated at its most ratio, produces the largest amount of protons (H⁺) that can in its turn increase the acidity (lowers the pH value) of the solution to reach the lowest value (5.58) of the above mentioned pH range. Paradoxically, the electroconductivity seems to increase when the percentage reaches its correct ratio. That is justifiable as the protons increases to its utmost concentration resulted from the chelation process between ARS and Zn(II), where these protons are obviously electroactive species.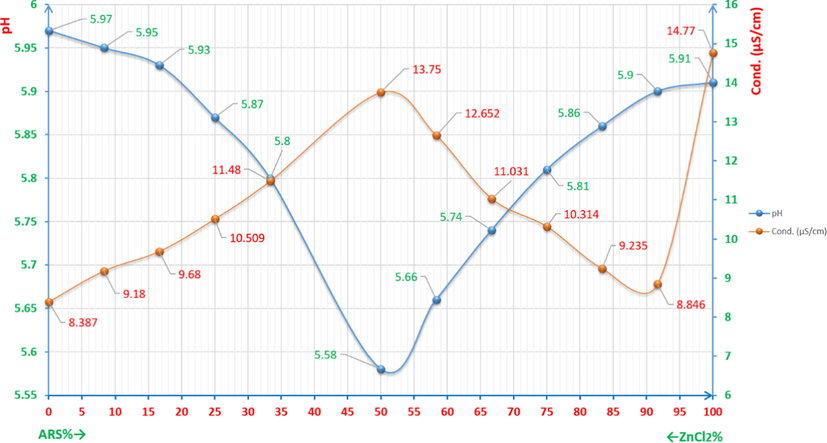

Close

Fig. 20

pH/conductivity diagrams (pHCD) for studying the correlation ratio between Zn(II) and ARS.

Export to PPT

The interstitial obstruction (IO) has been presented in Fig. 21 when the concentration plays a major role for accurate readings of the conductivity. In addition, larger concentration than 6x10^-5M would provide more acidity of the solution, which leads to the use of a buffer solution in order to maintain the pH value suitable for the chelation. However, IO cannot be eliminated even if a buffer solution is used.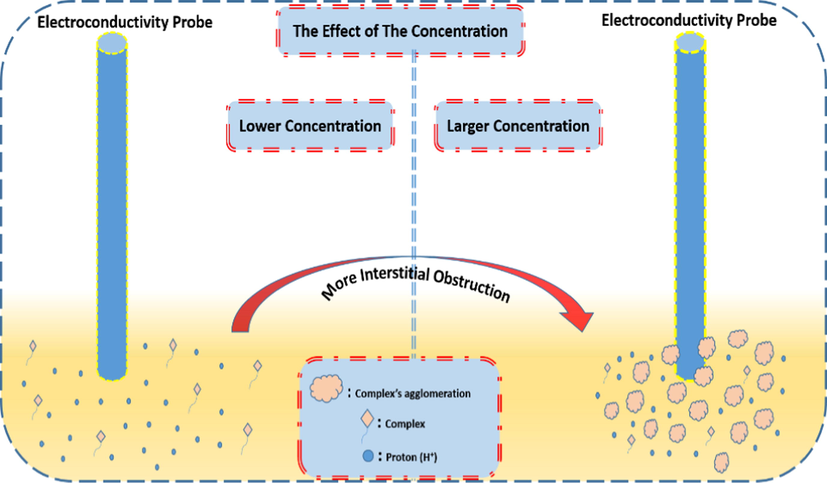

Close

Fig. 21

The effect of the concentration on the acidity and readings due to the formation of the agglomerations in case of higher concentrations than 6x10^-5M.

Export to PPT

4.1.2 Studying the correlation ratio between Zn(II) and ARS using electroconductivity diagrams (ECD) method

4.1.2.1

4.1.2.1 The effects of the additives’ order (EAO) on ECD

4.1.2.1.1

4.1.2.1.1 Adding 6x10^-5M Zn(II) to 6x10^-5M ARS

To determine the reaction stoichiometry, 6x10^-5M ZnCl₂ 24ml has been consecutively added to 6x10^-5M ARS 12ml dropwise, 1ml in each batch. The observed conductivities have been corrected using equation (33) (Ali et al., 2016) as it is shown in Fig. 22a.

(33)

[(V_ml(ARS) + V_ml(CuCl2)) ∕ V_ml(ARS)] × observed conductivity (mS/cm)  =  corrected conductivity (mS/cm)

Close

Fig. 22

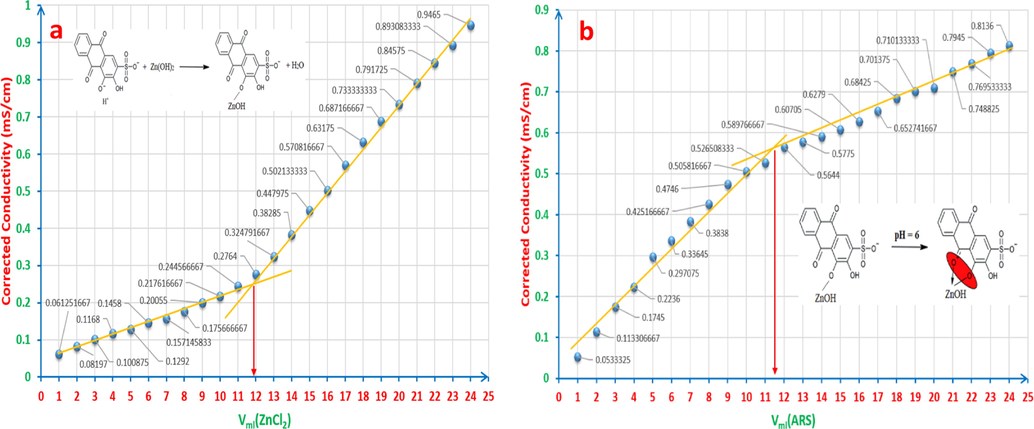
a: The correlation ratio when adding 6x10^-5M ZnCl₂ 24ml to 6x10^-5M ARS 12ml. b: The correlation ratio when adding 6x10^-5M ARS 24ml to 6x10^-5M ZnCl₂12ml.

Export to PPT

For accurate observations and readings, pH values of ARS solution have been measured for every added ml of ZnCl₂, where the range was [3.41-5.4]. This pH range confirms that the resulted reaction stoichiometry is not for the formation of the complex. It is rather for the formation of the salt as in reaction (5), which is (1:1).

4.1.2.1.2

4.1.2.1.2 Adding 6x10^-5M ARS to 6x10^-5M Zn(II)

In this experiment, the addition way has been reversed, where 6x10^-5M ARS 24ml has been consecutively added to 6x10^-5M ZnCl₂ 12ml, 1ml in each batch. Also, the observed conductivities have been corrected using equation (33) as it is exhibited in Fig. 22b. The pH range was [5.69-5.9] during carrying out this experiment, and this confirms the suitable medium for the complex to be formed as expressed in reaction (6), where the correlation ration is (1:1).

4.1.3 Studying the correlation ratio between Zn(II), Cu(II) and ARS using pH/conductivity diagrams (pHCD) method

Two series of solutions have been prepared in order to find out the correlation ration. The first one included ZnCl2 and CuCl2 with a concentration of 6x10^-5M for each, whereas the second one included 6x10^-5M ARS. Fig. 23 shows both pH and conductivity diagrams, which confirms the reaction stoichiometry of (1:1) for the formation of Cu and Zn salts because the medium is convenient for that kind of bonding. That means that the competition process between Cu(II) and Zn(II) to bond with ARS is in fact a sharing process as long as the solution has an amount of ARS that can be shared equally between these two metals. Therefore, this is very useful for different purposes. For example, the electrodeposition of brass that requires bonds between both metals with the dye at the same time. For obtaining the complexes instead of the salts, the solutions can be diluted more so that the pH value can be at 5.7 or 5.8. In this case, both Zn and Cu complexes can be formed for better organizing effect on the electrodeposition process.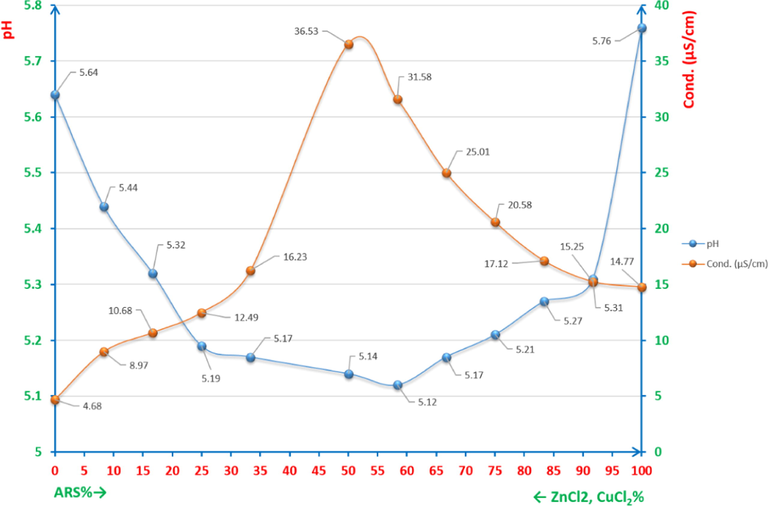

Close

Fig. 23

pH/conductivity diagrams (pHCD) for studying the correlation ratio between Zn(II), Cu(II) and ARS.

Export to PPT