A comprehensive physical insight of inclined magnetic field on the flow of generalized Newtonian fluid within a conduit with Homogeneous-heterogeneous reactions

Hashim; Sohail Rehman; Sultan Alqahtani; Sultan Alshehery; Sana Ben Moussa

doi:10.1016/j.arabjc.2023.104633

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

05 2023

:16;

104633

doi:

10.1016/j.arabjc.2023.104633

A comprehensive physical insight of inclined magnetic field on the flow of generalized Newtonian fluid within a conduit with Homogeneous-heterogeneous reactions

Hashim^{^a}, Sohail Rehman^{^b,⁎}, Sultan Alqahtani^{^c}, Sultan Alshehery^{^c}, Sana Ben Moussa^{^d}

aDepartment of Mathematics & Statistics, The University of Haripur, Haripur 22620, Pakistan

bDepartment of Mechanical Engineering, School of Material Sciences and Engineering, Georgia Institute of Technology, Atlanta, GA, USA

cCollege of Engineering, Mechanical Engineering Department, King Khalid University, Abha, Saudi Arabia

dFaculty of Science and Arts, Mohail Asser, King Khalid University, Saudi Arabia

⁎Corresponding author. srehman34@gatech.edu (Sohail Rehman)

Received: 2022-11-29, Accepted: 2023-1-26,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Modern nanomaterials and their flow dynamism processes promote complex chemical reactions that are necessary for the accurate synthesis of bespoke geometries at high temperatures. Such flow processes are very intricate and involve viscous behavior along with mass and heat transfer. Such flows mechanism can be controlled by external magnetic fields. Mathematical models offer an inexpensive opening into the fundamental properties of these dynamical processes. The homogeneous-heterogeneous reactions for nanofluids flow are established by invoking the Buongiorno's nanofluid model, in which the homogeneous reactions are regulated by first order kinetics occurring in the flowing liquid and the heterogeneous reactions are given by isothermal cubic autocatalytic kinetics. To testify the feasibility of this model, the steady, laminar Jaffrey-Hamel flow problem in the converging conduit is extended to rheological model. The system steady states are evaluated under the scenario where the reactant and the catalyst's diffusion coefficients are equivalent. In order to investigate heat and mass transfer analysis, viscous dissipation affirmation, Joule heating, and homogeneous-heterogeneous reactions are incorporated. The mathematical model prevailing the dimensionless function, velocity for flow, temperature for heat, and nanoparticles volume fraction for concentration are simulated numerically by means of Runge-Kutta method. The numerical algorithm has been validated in comparison to previously published research with extremely good agreement. The acquisition and detailed discussion of distributions of flow structure, heat, concentrations, and average Nusselt, Sherwood number at a wide range of critical characteristics. The fluid velocity in the conduit center increases significantly as the Reynolds number rises. By intensifying the magnetic field, the flow reversal control is accomplished. Applications in the allied domains have enormous promise since the ratio of Brownian and thermophoretic diffusivity has a significant impact on the transport mechanisms of homogeneous-heterogeneous processes. Chemical species $A^{*}$ and $B^{*}$ behave in fundamentally distinct ways in the reduced concentrations.

Keywords

Jeffery-Hamel problem

Two-phase model

Carreau model

Inclined magnetic field

Heat source

Homogeneous-heterogeneous reactions

Show Related Articles from PubMed

Nomenclature

$U (r, θ)$: Radial velocity, ( $m s^{- 1})$
$(r, θ)$: Polar coordinates
$\frac{D}{Dt} = \frac{\partial}{\partial t} + V ∙ \nabla$: The material derivative
$Ω$: Relaxation parameter (s)
$n$: Power-indexed
$T$: The temperature of the fluid, ( $K$ )
$C$: Fluid concentration, ( $kg m^{- 3}$ )
$p$: Pressure $(N m^{- 2})$
$k_{f}$: Thermal conductivity $(W m^{- 1} K^{- 1})$
$J$: Current density $(A . m^{- 2})$
$ρ_{f}$: Fluid density, ( $kg / m^{3}$ )
$μ_{0}$: Dynamic viscosity $(k g m^{- 1} s^{- 1})$
$α_{1} = \frac{k_{f}}{{(ρ c)}_{f}}$: Thermal diffusivity ( $m^{2} / s$ )
$D_{A}$ , $D_{B}$: Brownian diffusion $(m^{2} s^{- 1})$
$a, b$: Concentrations of chemical species $A^{*}$ and $B^{*}$
$K_{1}$ , $K_{s}$: Rate constant
$\nabla T$: Temperature gradient
$q_{w}$: Wall heat flux $(W m^{- 2})$
$Re$: Reynold number
$\Pr$: Prandtl number
$We$: Weissenberg number
$Sh$: Sherwood number
$C_{f}$: The skin friction
$K$: Homogenous reaction strength
$N_{AB}$: Ratio of Brownian and thermophoretic diffusivity
$Δ$: Heat generation parameter
$τ = \frac{{(ρ c_{p})}_{p}}{{(ρ c_{p})}_{f}}$: Ratio of heat capacities
$f$: Normalized velocity
$U_{m a x}$: Maximum velocity, ( $m s^{- 1})$
$\nabla$: Gradient operator $\frac{\partial}{\partial r} \hat{i} + \frac{1}{r} \frac{\partial}{\partial} \hat{j} + \frac{\partial}{\partial z}$
$I$: Identity tensor
$\dot{γ}$: The strain tensor
$Q^{″'}$: Heat generation $(W m^{- 2})$
$T_{w}$: The temperature of the wall, ( $K$ )
$C_{w}$: Fluid concentration at the wall, ( $kg m^{- 3}$ )
$c_{p}$: Specific heat at constant pressure, ( $j {. k g}^{- 1} K^{- 1}$ )
$σ$: Electrical conductivity $(S / m)$
$B_{0}$: Magnetic field ( $W m^{2}$ )
$ρ_{p}$: Nanoparticle's density ( $kg / m^{3}$ )
$ν_{f}$: Kinematic viscosity ( $m^{2} s^{- 1}$ )
${(ρ c_{p})}_{f}$: Fluid heat capacitance
$D_{T}$: Thermophoresis diffusion $(m^{2} / s)$
$a_{w}$ , $b_{w}$: Concentrations of chemical species $A^{*}$ and $B^{*}$ at the wall
$q_{w}$: Wall heat flux $(W m^{- 2})$
$q_{m}$: Wall mass flux $(k g m^{- 2} s^{- 1})$
$α$: Channel angle
$η = \frac{θ}{α}$: Dimensional variable
$M$: Magnetic number
$Ec$: Eckert number
$Sc$: Schmidt number
$Nu$: Nusselt number
$δ$: Strength parameter due to heterogeneous reaction
$N_{AB}$: Ratio of Brownian and thermophoretic diffusivity
$Δ$: Heat generation parameter
$ψ$: Normalized concentration
$β$: Normalized temperature

1 Introduction

The science of the interaction amongst flowing, conducting fluids and magnetic fields is termed as magnetohydrodynamics (MHD). Magnetohydrodynamic (MHD) channel flows have substantial theoretic and pragmatic importance because of the extensive applications in channel designing, cooling structures with fluid metals, MHD generators, nuclear reactors, accelerators, blood flow capacities, pumps and flow meters. Due to its potential applications in biology, the study of magnetohydrodynamic (MHD) flow of blood through arteries has attracted a lot of attention recently. Numerous significant benefits in engineering and industries are found for studies on non-Newtonian fluid MHD flow and heat transfer within channels. For instance, the channel expansion during the extrusion of a polymer sheet from a die. The final products characteristics are heavily influenced by the cooling rate. It is possible to control the rate of cooling and produce a final product with the desired properties by drafting such a sheet in a viscoelastic electrically conducting fluid under the influence of a magnetic field. In the industrial setting, they are frequently employed to heat pump, stir, and levitate liquid metals. There are three different kinds of magnetic fields: a galactic magnetic field that affects star formation, a solar magnetic field that produces sunspots and solar flares, and a terrestrial magnetic field that is maintained by fluid motion in the earth core. The Lorentz force that results when a constant current is applied to a fluid while it is subject to a magnetic field usually causes motion. One of the first MHD applications was the use of electromagnetic pumps, which were widely employed in a variety of sectors. The analysis of electrically conducting non-Newtonian fluid flowing through convergent-divergent channels while being affected by an external magnetic field is fascinating on a theoretical level, but it also has practical applications in the mathematical modelling of various industrial and biological systems. In the area of industrial metal casting, the regulation of molten metal flows, the theory we envision may find in practical application. A number of researchers (Fraenkel and Squire, 1962), (Makinde and Mhone, 2006), (Sadeghy et al., 2007), (Makinde, 2008), (Alam et al., 2017), (Raza et al., 2020), (Krishna and Chamkha, 2020), (Ameer Ahamad et al., 2020), (Veera Krishna et al., 2020), (Veera Krishna et al., 2021), (Hamid et al., 2021), (Rehman et al., 2022a), employed the MHD to the conventional flows of ordinary fluid mechanics. An exterior magnetic field functions as a control parameter for both convergent and divergent channel flows in the MHD solution.

Modern engineering fields such as aerospace, chemical, civil, environmental, mechanical, and biomechanical and the flow through rivers and canals are the few examples of the notion of flow along convergent-divergent channels extensively. Due to its significance in numerous domains, including mechanical, industrial, biological, and physical applications, the fluid flow between two inclined plates is an essential and vital component of the physical model. Examples of converging/diverging channels include the flow of blood via arteries and capillaries, flows through canals, flows through cavities, and river flow. The Jeffery-Hamel flow is a category of flows that was initially recognized by (Jeffery, 1915) and subsequently by (Hamel, 1917). These flows describe the discharge and inflow of a viscous, incompressible fluid in a wedge-shaped channel that is linearly expanding and has a specific angle between the walls. The wedge angle between its walls is conventionally inclined at $2 α$ . Thus, we are thinking about a source or sink flow in two dimensions that behaves self-similarly and has no-slip boundary requirements at the walls. In the specific scenario of two-dimensional flow through a channel with inclined plane walls intersecting at a vertex with a source or sink, these conservation equations actually have a precise similarity solution. In 1940, (Rosenhead and Taylor, 1940) discovered and thoroughly detailed the universal solution to the issue of the steady-two-dimensional radial flow of a viscous fluid across non-parallel plane walls. (Millsaps and Pohlhausen, 1953) thorough analysis is another noteworthy example. The reader is recommended to more significant books and the references within, where distinctions of this subject have been addressed: (Berrehal and Makinde, 2021) (Banerjee et al., 2021), (James and Roos, 2021), (Bég et al., 2022), (Asghar et al., 2022), (Rehman et al., 2022b), (Nazeer et al., 2022).

The nanofluids are quite beneficial in crude oil extraction, thermal energy storage devices, piping heat loss, heat exchangers, ground water systems, boilers, etc. are all used in engineering, civil, chemical, and mechanical engineering processes. A nanofluid is a substance that contains nanosized (less than 100 nm) substances, such as nanoparticles or nanofibers. In recent years, nanofluid composites comprised of nanoparticles or nanofibers dissolved in common liquids like water, triethylene glycol, refrigerants, bio liquids, toluene, and engine oil have become more and more popular. Among the many uses for nanoparticles, there are the cooling of a new class of portable computers, the condensation of extremely powerful and other electronic devices for use in military paradigms, the cooling of vehicles and transformers, the construction of waste heat expulsion equipment, and significant process industries like substances and chemicals, gas and oil, lubricants, and cancer therapy. In general, it can be demonstrated that nanofluid have a remarkable capacity to improve the thermal performance and conductivity of ordinary fluids (Das et al., 2007). According to (Khanafer and Vafai, 2011), the two most significant thermophysical properties of nanofluids that affect the convective heat transport phenomenon are their thermal conductivity and dynamic viscosity. (Buongiorno, 2005) provided a thorough analysis of the role that nanoparticles play in the convective transport of common fluids. (Hamad and Pop, 2011) examined the laminar flow of a viscous liquid in a porous medium containing nanoparticles. A well renewed studies can be found in the literature [See Refs (Das et al., 2015), (Das et al., 2020), (Ali et al., 2020), (Ali et al., 2021), (Ashraf et al., 2022), (Ali et al., 2022), (Shahid et al., 2022), (Kiranakumar et al., 2022)].

Several chemically reacting processes concede heterogeneous and homogeneous reactions, where the homogeneous reactions take place in the main body of the fluid and the heterogeneous reactions happen on the catalytic surfaces. Catalysis, combustion, and biochemical systems are characteristics of chemical reacting systems where both heterogeneous and homogeneous reactions occur. While heterogeneity reactions take place on a catalyst surface, homogeneous reactions happen in a fluid. Some processes can only take place in the presence of a catalyst or have no chance of happening on their own. These reactions have a variety of broad uses, including the production of ceramics, hydrometallurgical industry, polymers, dispersion and fog generation, and food preparation. Chaudhary and Merkin developed a mathematical model of two-dimensional flow across a flat sheet with a stagnation point and chemical reaction (Chaudhary and Merkin, 1995a), (Chaudhary and Merkin, 1995b). They predicated an isothermal cubic autocatalytic reaction. The rates of heat and mass transfer in forced convection flow can be greatly increased by chemical reaction, or the other way around. The overall rate of reactant consumption is impacted by transportation phenomena. Due to the performance of various factors on the transport effects, addition of both homogeneous and heterogeneous reactions is extremely desirable in a combined flow regime. Surface reactions were found to predominate close to the plate in (Merkin, 1996) analysis of viscous liquid flow with heterogeneous-homogeneous reactions. (Makinde et al., 2018) examined the hydro magnetic chemical reactions and unsteady mixed convection Blasius flow via surface flat in a porous media. Some recent development in the same subject through various geometries assuming different physical phenomena can be found in the Refs. (Saif et al., 2020), (Waqas et al., 2021), (Yazdi Sotoude et al., 2022), (Abbas et al., 2023).

In many industrial and biological processes, non-Newtonian fluid motion over accelerating geometries is often seen. Because they are found in human bodily fluids, industrial chemicals, crude oils, food items, and other things, shear-thinning fluids demand special consideration. It is well established that Navier Stokes equations are incapable of adequately convey the characteristics of non-Newtonian fluids because of the intricate interaction amongst shear and strain rates. Non-Newtonian fluids response to the deployment of shear stress as a function of strain rate significantly, according to experimental observations. Relying on this correlation, non-Newtonian liquids are categorized into shear thinning and thickening liquids. This categorization have heightened the significance of non-Newtonian fluids in a multitude of engineering, technological, and everyday activities. To illustrate the physical explanation of these fluids, several fluid models are provided. Carreau fluid is one of these models that is particularly helpful for comprehending the flow characteristics of shear thinning and thickening liquids. This model also demonstrates the behavior of materials that are shear thinning at low and high shear rates. Carreau liquid has a wide range of uses in the production of polymers, capillary electrophoresis, gas turbine engines, crystal development, mud drilling, the manufacture of gels and shampoos, powder technology, and biological applications. The references [(Akbar et al., 2014), (Khan and Hashim, 2015), (Khan et al., 2016b), (Malik et al., 2017), (Eid et al., 2018), (B. et al., 2018), (Bilal and Shah, 2022)] compile some recent developments addressing the evaluation of Carreau fluid flow in various physical configurations and features.

1.1

1.1 Objective and originality

The converging channel flow pattern in an intersecting channel originates from the complicated interaction of numerous factors such as inertia, viscosity, buoyancy, and surface tension. Because of the morphological and physical differences across flow regimes, the flow regime has a significant impact on pressure drop and heat transmission. As a result, a great number of studies have focused on capturing the fundamental physics for each flow regime and developing a flow regime map that can reliably forecast flow patterns. Recent interest in the development of miniaturized devices for converging channel flow applications has underlined the importance of producing consistent flow regime maps capable of predicting flow patterns in convergent divergent channels. The current study aims to investigate the effects passive control parameters to simulate the combined interactions between rheological fluid flow rates and heat, mass transfer related with geometric shape, and Lorentz force effects. The augmented or lessened heat transfer capabilities of non-Newtonian fluids due to varying shear stress in shear-thinning and shear-thickening domains are an important feature. The ever-increasing need for non-Newtonian fluids is mostly due to their significant contribution to energy transport in terms of thermal transport. Only a few numerical analyses have been carried out to explore the flow and heat transfer properties of non-Newtonian fluids in intersecting channel walls, with no experimental data to back up the findings. The problem has been solved in the entire geometrical setting, namely converging, and diverging channel sections in the geometry under discussion. A mass flow rate via the channel, the fluid flow diodicity, and the flow field both inside the channel and in the regions converging stream and diverging stream have been computed across a wide range of fluid rarefaction. Some of the several chemical processes that heavily rely on homogeneous-heterogeneous (HH) reactions include biochemical processes, fermentation, electrochemical catalysis, semiconducting films, and analysis of these reactions containing iron manufacturing in blast furnaces. The objective of this study is to investigate and determine the commencement and development of magnetohydrodynamic flow, as well as the region for heat transfer augmentation in a horizontal divergent or convergent channel. The results of flow visualization from the channel side or end by injecting fluid at the intake, as well as heat transfer measurements along the adiabatic wall, are provided. The computation results are compared to data for the channel with a constant cross-section.

2 Computational model

2.1

2.1 Problem description

A fluid flow penetrates the channel and escapes to the ambient after crossing through it. The isothermal wall is inclined and kept under an inclined Lorentz force intensity. The opposite wall of the diverging (convergent) channel has a divergence (convergence) angle of $2 α$ to the horizontal plane. We describe the velocity field when a non-Newtonian fluid is stationary moving in a channel created by two plane walls inclined to each other, implying that the temperature and fluid property fluctuation ranges are such that a change in heat-transfer characteristics with temperature can be ignored. We suppose that gravity is negligible, velocity has just a radial component $U (r, θ)$ , and fluid clings to the channel walls. This two-dimensional flow is widely recognized in scientific literature as the solution to the (Hamel, 1917) problem. The geometry of interest, which is depicted in Fig. 1 as a two-dimensional converging/diverging channel.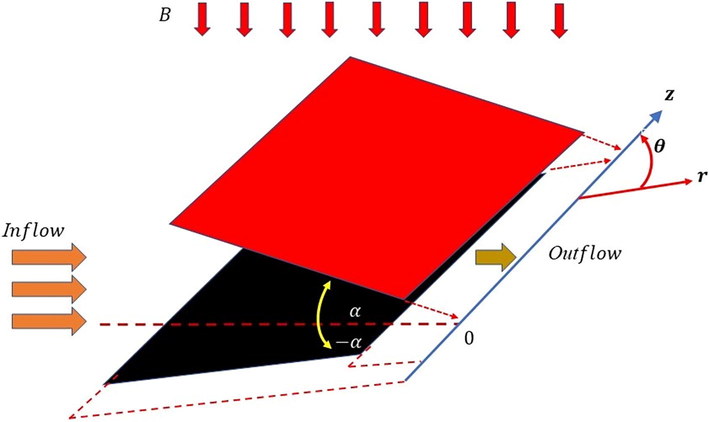

Physical model for the channel driven flow.

2.2

2.2 Problem assumptions

The flow has been assumed to be two-dimensional, steady, incompressible, and laminar across the entire domain, with the working fluid assumed to be a non-Newtonian Carreau model with constant properties.
The presumption of laminar flow is justified by the fact that the maximum Reynolds number of inlet flow is less than 2100 (Maharudrayya et al., 2004).
The flow operates within the walls in isothermal condition.
The cross section of the considered channel is small, the inlet flow stoichiometry coefficient is high, thus the temperature differential within the channel is not significant, and the isothermal condition is justified.
Under the suppositions of extremely tiny particles (100 nm), no slip velocity between the nanoparticles dispersed phase and the continuous liquid, and local thermal equilibrium between both.
The fluid is migrating in the radial direction and is subjected to a persistent magnetic field of strength $B$ in transverse direction.
Two additional chemical species, $A^{*}$ and $B^{*}$ , are taken into consideration for homogeneous and heterogeneous reactions, respectively.

2.3

2.3 Flow, heat and mass transfer governing equations

The constitutive equations for the assumed flow problem are (Bhandari and Tripathi, 2023), (Ayub et al., 2022):

(1)

\nabla ∙ q = 0,

(2)

ρ [q ∙ (\nabla q)] = - \nabla p + \nabla ∙ σ + J \times B,

(3)

(ρ c_{p}) (q ∙ \nabla T) = \nabla ∙ (k \nabla T) + μ Φ + \frac{J ∙ J}{σ} + Q^{'''} .

Here, $q = (U (r, θ), 0, 0)$ is the velocity field, $ρ$ the density of the fluid, $ρ c_{p}$ is the heat capacitance, $p$ is the pressure term, $k$ the thermal conductivity, $Q^{″'}$ is the corresponding heat generating source in energy equation.

The stress tensor for Carreau model is (Shahzad et al., 2023)

(4)

σ_{ij} = 2 μ (\dot{γ}) A_{ij} .

In above expression, the rate of strain tensor $A_{ij}$ is given as (Kefayati and Tang, 2018a):

(5)

A_{ij} = \frac{1}{2} (\frac{\partial u_{i}}{\partial r_{j}} + \frac{\partial u_{j}}{\partial r_{i}}) .

However, the generalized viscosity $μ (\dot{γ})$ for Carreau model takes the form:

(6)

μ (\dot{γ}) = μ_{\infty} + (μ_{0} - μ_{\infty}) ({[1 + {(Ω \dot{γ})}^{2}]}^{\frac{n - 1}{2}}), \dot{γ} = \sqrt{2 A_{ij} A_{ij}} .

Where $Ω$ is the time constant, $n$ is the power-law index, and $μ_{0}$ and $μ_{\infty}$ are the viscosities corresponding to zero and infinite-shear rates; the difference between $n$ and unity represents the degree of divergence from Newtonian behavior. The above equation depicts a dilatant fluid for ( $n > 1$ ) and a pseudoplastic fluid for ( $0 < n < 1$ ), respectively. Recall that by setting $n = 1$ and $Ω = 0$ , a Newtonian fluid may be recovered as a special case of the current Carreau fluid, and by assuming a large, a power-law fluid can be obtained. The fluid breaking down is typically linked with the infinite shear viscosity, $μ_{\infty} = 0$ , which is frequently noticeably less (times less $10^{3} - 10^{4}$ ) than $μ_{0}$ . As a result, the ratio $\frac{μ_{\infty}}{μ_{0}}$ is set at 0.001 (see (Kefayati and Tang, 2018b)).

The viscous dissipation term $Φ$ in the context of velocity field $q$ is:

(7)

Φ = [(2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})] .

The vectorial variant of Ohmic's current law regarding body force

(8)

J \times B = σ (E + q \times B) .

Allow a homogeneous, inclined magnetic field of strength $B_{0}$ to influence the flow of the fluid on inclined channel. The magnetic field has the form $B = (0, 0, B_{0})$ on the assumption that the magnetic Reynolds number is very low (Ayub et al., 2022). Hence, the Lorentz force becomes:

(9)

J \times B = - σ (B_{0}^{2} U (r, θ) {(c o s θ)}^{2}, B_{0}^{2} U (r, θ) (c o s θ) (s i n θ), 0) .

The homogeneous-heterogeneous reaction model is incorporated into the current model. We rely on the assumption that the reaction in the bulk is isothermal cubic autocatalytic in accordance with (Xu et al., 2018), which is given by

(10)

A^{*} + 2 B^{*} \to 3 B^{*}, r a t e = K_{1} a b^{2} .

Whereas the solitary, isothermal, first-order reaction on the catalyst surface is regulated by

(11)

A^{*} \to B^{*}, r a t e = K_{s} a .

Where $A^{*}$ and $B^{*}$ are two distinct types of autocatalysts, $a$ and $b$ are the concentrations of each, and $K_{1}$ and $K_{s}$ are constants related to homogeneous and heterogeneous reactions, respectively. The assumption is made that the species $B^{*}$ does not exist in the far fluid to meet the criteria of a real-world scenario. To make things simple, it is presumptively true that the species $A^{*}$ has a steady concentration in the ambient field. Since all chemical reactions take place in the boundary layer, it follows from Eq. (10) that none takes place at the far field. (Buongiorno, 2005), found that heat transfer resulting from nanoparticle dispersion is negligible in comparison to heat conduction and convection. In order to account for the additional contribution caused by the nanoparticles motion in relation to the fluid, we thus take his recommendation and eliminate the element relating to nanoparticle diffusion from the energy equation. We also disregard the part related to heat transfer from the energy equation because we believe that the heat released by chemical processes is minuscule. We further deliberate that the walls of the inclined channel are impervious as a result no-slip condition holds and there is a constant temperature $T_{w}$ for the up and down horizontal walls. Additionally, the bottom and top walls of the channel are kept insulated $(\frac{\partial T (r, θ)}{\partial θ} = 0)$ , where $T$ is the temperature of the nanofluid. On both walls, the mass flux of the nanoparticles is taken to be zero, i.e., $J_{p} = [- ρ_{p} (D_{B} \nabla C + \frac{D_{T}}{T_{0}} \nabla T)]$ , where $D_{B}$ is the Brownian motion diffusion coefficient and $D_{T}$ is the thermophoretic diffusion coefficient, and $ρ_{p}$ is the density of the nanoparticles.

Based on these arguments, the governing equations for the Jaffrey-Hamel flow problem of a Carreau nanofluid in the existence of homogeneous-heterogeneous processes can be expressed as

(12)

\frac{\partial}{\partial r} (r U (r, θ)) = 0,

(13)

U (r, θ) \frac{\partial U (r, θ)}{\partial r} = - \frac{1}{ρ_{f}} \frac{\partial p (r, θ)}{\partial r} + v_{f} [\frac{\partial^{2} U (r, θ)}{\partial r^{2}} + \frac{1}{r} \frac{\partial U (r, θ)}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} U (r, θ)}{\partial θ^{2}} - \frac{U (r, θ)}{r^{2}}] {[{(1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}}))}^{2}]}^{\frac{n - 1}{2}} + v_{f} Ω^{2} (n - 1) {[1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})]}^{\frac{n - 3}{2}} [4 {(\frac{\partial U (r, θ)}{\partial r})}^{2} \frac{\partial^{2} U (r, θ)}{\partial r^{2}} + \frac{6}{r^{2}} (\frac{\partial U (r, θ)}{\partial r}) (\frac{\partial U (r, θ)}{\partial θ}) (\frac{\partial^{2} U (r, θ)}{\partial r \partial θ}) - \frac{2}{r^{2}} (\frac{\partial U (r, θ)}{\partial θ}) {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{4 U (r, θ)}{r^{2}} {(\frac{\partial U (r, θ)}{\partial r})}^{2} - \frac{4 U^{2} (r, θ)}{r^{3}} \frac{\partial U (r, θ)}{\partial r} + \frac{2}{r^{4}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} \frac{\partial^{2} U (r, θ)}{\partial θ^{2}} + \frac{4 U (r, θ)}{r^{4}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2}] - σ B_{0}^{2} U (r, θ) {(c o s θ)}^{2},

(14)

- \frac{1}{ρ_{f} r} \frac{\partial p (r, θ)}{\partial θ} = \frac{2 v_{f}}{r^{2}} {[1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})]}^{\frac{n - 1}{2}} \frac{\partial U (r, θ)}{\partial θ} + v_{f} Ω^{2} \frac{(n - 1)}{2 r} {[1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})]}^{\frac{n - 3}{2}} [4 (\frac{\partial U (r, θ)}{\partial r}) (\frac{\partial U (r, θ)}{\partial θ}) (\frac{\partial^{2} U (r, θ)}{\partial r^{2}}) + \frac{2}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} (\frac{\partial^{2} U (r, θ)}{\partial r \partial θ}) - \frac{2}{r^{3}} {(\frac{\partial U (r, θ)}{\partial θ})}^{3} + \frac{4 U (r, θ)}{r^{2}} (\frac{\partial U (r, θ)}{\partial r}) (\frac{\partial U (r, θ)}{\partial r}) - \frac{4 U (r, θ)}{r^{3}} (\frac{\partial U (r, θ)}{\partial θ}) + 8 U (r, θ) (\frac{\partial U (r, θ)}{\partial r}) (\frac{\partial^{2} v (r, θ)}{\partial r \partial θ}) + \frac{4 U (r, θ)}{r^{2}} (\frac{\partial U (r, θ)}{\partial θ}) (\frac{\partial^{2} U (r, θ)}{\partial θ^{2}}) + \frac{8 U^{2} (r, θ)}{r^{2}} \frac{\partial U (r, θ)}{\partial θ}] - σ B_{0}^{2} U (r, θ) (c o s θ) (s i n θ),

(15)

v (r, θ) \frac{\partial T (r, θ)}{\partial r} = α_{1} [\frac{1}{r} \frac{\partial T (r, θ)}{\partial r} + \frac{\partial^{2} T (r, θ)}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} T (r, θ)}{\partial θ^{2}}] + \frac{μ_{0}}{{(ρ c_{p})}_{f}} {[{(1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}}))}^{2}]}^{\frac{n - 1}{2}} [(2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})] + \frac{Q_{0} T}{{(ρ c_{p})}_{f} r^{2}},

(16)

U (r, θ) \frac{\partial a (r, θ)}{\partial r} = D_{A} (\frac{1}{r} \frac{\partial a (r, θ)}{\partial r} + \frac{\partial^{2} a (r, θ)}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} a (r, θ)}{\partial θ^{2}}) + \frac{D_{T}}{T_{0}} (\frac{1}{r} \frac{\partial T (r, θ)}{\partial r} + \frac{\partial^{2} T (r, θ)}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} T (r, θ)}{\partial θ^{2}}) - K_{1} \frac{a b^{2}}{r^{2}},

(17)

U (r, θ) \frac{\partial b (r, θ)}{\partial r} = D_{B} (\frac{1}{r} \frac{\partial b (r, θ)}{\partial r} + \frac{\partial^{2} b (r, θ)}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} b (r, θ)}{\partial θ^{2}}) + \frac{D_{T}}{T_{0}} (\frac{1}{r} \frac{\partial T (r, θ)}{\partial r} + \frac{\partial^{2} T (r, θ)}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} T (r, θ)}{\partial θ^{2}}) + K_{1} \frac{a b^{2}}{r^{2}} .

The boundary conditions due to geometrical structure (Khan and Puneeth, 2021), (Rehman et al., 2023):

At the channel central line, where $θ = 0$ :

(18)

U (r, θ) = U_{m a x}, \frac{\partial U (r, θ)}{\partial θ} = 0, \frac{\partial T (r, θ)}{\partial θ} = 0, \frac{\partial a (r, θ)}{\partial θ} = \frac{K_{s}}{D_{A}} a, \frac{\partial b (r, θ)}{\partial θ} = - \frac{K_{s}}{D_{B}} a .

At the wall where $θ = α$ :

(19)

U (r, θ) = 0, T = T_{w}, a = a_{w}, b = 0 .

The flow, heat, and mass transfer rate properties of a nanofluid interacting with a boundary are quantified using physical parameters such as skin friction coefficient ( $C_{f}$ ), Nusselt number ( $Nu$ ).

(20)

C_{f} = \frac{σ_{r θ}}{ρ_{f} U_{\max}^{2}}, N u = - \frac{r q_{w}}{k_{f} T_{w}} .

Where

(21)

σ_{r θ} = {{[1 + Ω^{2} (2 {(\frac{\partial U (r, θ)}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial U (r, θ)}{\partial θ})}^{2} + \frac{2 U {(r, θ)}^{2}}{r^{2}})]}^{\frac{n - 1}{2}} \frac{1}{r} (\frac{\partial U (r, θ)}{\partial θ})|}_{θ = α},

(22)

q_{w} = - k {\frac{1}{r} (\frac{\partial T}{\partial θ})|}_{θ = α} .

To enables the deployment of one Schmidt number in the computation for both species $A^{*}$ and $B^{*}$ , even though the species concentrations, hare not quantitatively the identical due to the difference in the polarization of the heterogeneous- homogeneous catalytic reaction expressions, i.e., the last terms on the left side of Eqs. (16), (17). In the context of species $A^{*}$ , the terminology is destructive, whereas when referred to species $B^{*}$ , it is constructive and positive.

(23)

{Sh}_{A^{*}} = - \frac{r q_{m (A^{*})}}{D_{A} C_{w}}, {Sh}_{B^{*}} = - \frac{r q_{m (B^{*})}}{D_{B} C_{w}} .

3 Non-dimensional analysis

Introducing non-dimensional variables (Khan et al., 2016a), (Al-Saif and Jasim, 2019), (Rehman et al., 2022b)

(24)

f (η) = \frac{F (θ)}{f_{\max}}, F (θ) = r U (r, θ), η = \frac{θ}{α}, β (r, θ) = \frac{T (r, θ)}{T_{w}}, ψ (r, θ) = \frac{a (r, θ)}{a_{w}}, χ (r, θ) = \frac{b (r, θ)}{b_{w}}, f_{\max} = r U_{\max} .

With the aid of Eq. (25), the governing Eqs. (13)–(17) are reduced to dimensionless equation. Eliminating the pressure gradient term from Eqs. (13) and (14) using $F (θ) = r U$ , the reduced equation in the view of Eq. (25) takes the following form.

(25)

(f^{″'} (η) + 4 α^{2} f^{'} (η)) {(1 + {We}^{2} (4 α^{2} f^{2} (η) + {f^{'}}^{2} (η)))}^{\frac{n - 1}{2}} + 2 α R e f (η) f^{'} (η) - M^{2} R e (f^{'} (η) \cos^{2} (α η) - α f (η) s i n (2 α η)) + (n - 1) {We}^{2} {(1 + {We}^{2} (4 α^{2} f^{2} (η) + {f^{'}}^{2} (η)))}^{\frac{n - 3}{2}} ({3 f}^{'} (η) f^{″ 2} (η) + {32 α^{2} f (η) f}^{'} (η) f^{″} (η) + f^{' 2} {(η) f}^{″'} (η) + 64 {α^{4} f}^{'} (η) f^{2} (η)) + (n - 1) (n - 3) {({We}^{2})}^{2} {(1 + {We}^{2} (4 α^{2} f^{2} (η) + {f^{'}}^{2} (η)))}^{\frac{n - 5}{2}} (f^{' 3} (η) f^{″ 2} (η) + 16 α^{2} f {(η) f}^{' 3} (η) f^{″} (η) + {32 {α^{4} f}^{3} (η) f}^{'} (η) f^{″} (η) + 16 {α^{4} f}^{2} (η) f^{' 3} (η) + 64 {α^{6} f}^{4} (η) f^{'} (η) - 4 {α^{2} f}^{' 5} (η)) = 0,

(26)

β^{″} (η) + P r E c [{1 + {We}^{2} (4 α^{2} f^{2} (η) + {f^{'}}^{2} (η))}^{\frac{n - 1}{2}}] (4 α^{2} f^{2} (η) + {f^{'}}^{2} (η)) + α^{2} Δ β (η) = 0,

(27)

(ψ^{''} (η) + \frac{1}{N_{AB}} β^{''} (η)) - α^{2} K S c_{a} ψ (η) χ^{2} (η) = 0,

(28)

(∊ χ^{''} (η) + \frac{1}{N_{AB}} β^{''} (η)) + α^{2} K S c_{b} ψ (η) χ^{2} (η) = 0,

subject to the dimensionless boundary conditions

(29)

\begin{matrix} f (0) = 1, f^{'} (0) = 0, β^{'} (0) = 0, ψ^{'} (0) = δ α ψ (0), χ^{'} (0) = - \frac{δ}{λ} α ψ (0) \\ f (1) = 0, β (1) = 1, ψ (1) = 1, χ (1) = 0, \end{matrix}\} .

Here, $W e (= \sqrt{\frac{Ω^{2} U_{\max}^{2}}{r^{2} α^{2}}}) :$ Local Weissenberg number. $R e (= \frac{α r U_{\max}}{ν}) :$ Local Reynolds number. $M (= \sqrt{\frac{σ {B_{0}}^{2}}{ρ ν}}) :$ The Magnetic number. $P r (= \frac{μ C_{p}}{k}) :$ The Prandtle number. $E c (= \frac{U_{\max}^{2}}{T_{w} c_{p}}) :$ The Eckert number. $[S c_{a} (= \frac{ν}{D_{A}}), S c_{b} (= \frac{ν}{D_{B}})]$ : Are the Schmidt numbers, $∊ = \frac{D_{B}}{D_{A}}$ : is the ratio of the diffusion coefficients, $K = \frac{K_{1} b_{w}^{2}}{ν}$ : is the coefficient of the homogenous reaction strength, $δ = \frac{k_{s}}{D_{A}}$ : is the strength parameter due to heterogeneous reaction, $N_{AB} = \frac{D_{A} a_{w}}{(\frac{D_{T}}{T_{0}}) T_{w}}$ : is the ratio of Brownian and thermophoretic diffusivity, $Δ (= \frac{Q_{0}}{κ_{f}})$ : where $\frac{Q_{o}}{κ_{f}} > 0$ , is the heat generation parameter and, $Δ = \frac{Q_{o}}{κ_{f}} < 0,$ is the heat absorption parameter.

It is important to note that $A^{*}$ and $B^{*}$ are expected to be of identical extent in this case. As an outcome of this lucidity, we must adopt that the $D_{A}$ and $D_{B}$ are comparable, i.e., $∊ =$ 1, and $S c_{a} = S c_{b} = S c$ . Hence, the two equations

(30)

ψ (η) + χ (η) = 1 .

Incorporating above assumption, using Eq. (31), in Eq. (28) and Eq. (29), we have

(31)

(ψ^{''} (η) + \frac{1}{N_{AB}} β^{''} (η)) - α^{2} K S c ψ (η) {(1 - ψ (η))}^{2} = 0 .

Along with the boundary condition

(32)

ψ^{'} (0) = δ α ψ (0), ψ (1) = 1 .

Skin friction coefficients along direction and local Nusselt number are the measures of industrial interest designated quantities in the dimensionless form as:

(33)

C_{f} = \frac{1}{Re} [[{(1 + {We}^{2} (4 α^{2} f^{2} (1) + {f^{'}}^{2} (1)))}^{\frac{n - 1}{2}}] f^{'} (1)], N u = - \frac{1}{α} β^{'} (1), S h = - \frac{1}{α} ψ^{'} (1) .

4 Solution methodology

The shooting technique, which incorporates the Runga-Kutta (fourth order) method and the Newton's iteration approach, is used to find solutions for Eqs. (25), (26), (29) and the accompanying boundary conditions (29) and (32). The shooting strategy is more adjustable, and the convergence criteria are controlled by the initial predictions. The integration distance of $η_{\infty} = 20$ is settled to be sufficient to maintain the stability of many solutions. For different values, the step size $Δ η$ is changed in order to maintain the required precision and stability of solutions. After experimenting with a few numbers in the [0.001, 0.1] range, we found that $Δ η =$ 0.005 works well to maintain mesh independence. To confirm the precision of the solutions for all taken examples, a convergence threshold of $1 \times 10^{- 8}$ is adopted. In substitute of the HAM (homotopy analysis method) and ADM approach, we employ the Runge-Kutta Fehlberg fourth-fifth order method in combination with the shooting technique. This is because the method provides quick convergence and iterations. Without the requirement for higher derivative calculations, the Runge-Kutta approach can approximate a Taylor series with a reasonable degree of accuracy. The foundational form of other procedures can be thought of as being this one. One-step methods with adaptive step sizes, such as the Runge-Kutta Fehlberg method (RKF), provide superior error estimation than one-step methods with constant step sizes, such as the Runge-Kutta method.

5 Solutions justification

To confirm the precision of our MATLAB code, we compare the numerical values generated in present study to those reported in research for different values of $η = [- 1, 1]$ for $We = 0$ and $n = 1$ . The dimensionless governing Eq. (27) change to match those of (Turkyilmazoglu, 2014), (Dogonchi and Ganji, 2017) and (Ahmad et al., 2022) for $We = 0$ and $n = 1$ . It can be shown that, as shown in Table 1, the data generated by the MATLAB algorithm and those from the research are in perfect agreement. A comparative investigation for the dimensionless velocity $f (η)$ with (Sari et al., 2016) is carried out in Table 2 using two different numerical methodologies, namely the RK-4 routine and shot methodology, to further validate our numerical results. The solutions derived using the approach are found to be in very good agreement up to the fifth decimal point, as can be seen from the table. As a result, we can assume that all of the numerical results are accurate and trustworthy. This table also enables us to define skin friction as an increasing function of suction parameter.

Table 1 Nusselt number

Nu = - \frac{1}{α} β^{'} (1)

comparison with earlier research for specific values while maintaining

We = 0

and

n = 1

$α$	(Turkyilmazoglu, 2014)	(Dogonchi and Ganji, 2017)	(Ahmad et al., 2022)	Present study
${- 5}^{0} 5^{0}$	0.04214811723 0.03999321083	0.0421517243 0.0399820121	0.0421520009 0.0399841412	0.04215 0.03998

Table 2 Dimensionless velocity

f (η)

for various values of

η = [- 1, 1]

, when

We = 0

and

n = 1

$η$	$Re = 50$ , ${α = 3}^{0}$		$Re = 50$ , ${α = - 3}^{0}$
$η$	(Sari et al., 2016)	Present results	(Sari et al., 2016)	Present results
$- 1$	0	0	0	0
– 0.75	0.34617891945024026	0.34175932	0.9568619246104294	0.95862988
– 0.5	0.6693201741166637	0.66929111	0.8114573769442529	0.81146278
– 0.25	0.9097653427408956	0.90978112	0.5158279952776336	0.51582911
0.0	1.00000000000	1.00000000	1.00000000000	1.00000000
0.25	0.9097653427408956	0.90980111	0.5158279952776336	0.51579910
0.5	0.6693201741166637	0.66931012	0.8114573769442529	0.81145017
0.75	0.34617891627424824	0.34617239	0.9568619246104294	0.95890181
1.0	0.000000000000	0.00000000	0.00000000000	0.00000000

6 Results and discussion

We consider the heat and mass transmission of power-law nanofluids in a converging diverging conduit. The numerical solutions obtained for velocity, temperature and concentration to investigate the energy effectiveness of the system. The inclined magnetic field, which primarily affects the channel flow, and heat mass transmission mechanism. Two scenarios with magnetic effects and no magnetic effects are primarily focused here. Due to the large number of governing parameters included in the study, all computations are carried out by maintaining the $We = 2$ (Izbassarov et al., 2021), $Ec = 0.5, (P r = 10,$ of the water base solutions). To better understand the underlying physical processes, non-dimensional estimates of the velocity profile, temperature profile, and concentration profile in the conduit have been estimated in MATLAB for a variety of non-dimensional contributing parameters. The range of the emerging parameters are $(100 \leq R e \leq 200)$ , $1.2 \leq n \leq 1.8$ , $0 \leq M \leq 10$ , $(1 \leq Δ \leq 3)$ , $(0.2 \leq N_{AB} \leq 0.8)$ , $(0.2 \leq K \leq 0.8)$ , $(0.2 \leq δ \leq 0.8)$ , $(0.2 \leq S c \leq 0.8)$ kept fixed.

The variation of the inertial term $Re$ on dimensionless velocity $f (η)$ is displayed in Fig. 2. It has been found that greater values of Reynolds number ( $Re$ ) are caused by a rise in mainstream velocity rather than by strong values of $Re$ , which lead to reduced viscous forces. The flow velocity is decreased by the backflow that is caused by the larger values of $Re$ in the regions close to the wall (Fig. 2). Furthermore, the separation near channel walls may result from the larger values of $Re$ . The Reynold number $Re$ is defined as the ratio of momentum forces to viscous forces, it follows that a rise in $Re$ will likely result in an increase in momentum forces, which would then produce more heat, leading to an observed rise in the velocity of the nanofluid. Increasing values of $Re$ enable the fluid flow velocity in the diverging channel to drop, which leads to the accumulation of mass and an increase in the concentration of fluid (Fig. 3). In this case, bear in mind that the flow rate is kept constant according to the boundary conditions. The existence of flow reversal or a backflow/inflow area in the case of a diverging conduit is indicated by a negative value for the non-dimensional velocity. Physically, as the inflow region experiences an increase in velocity, the outflow region also experiences an increase in velocity. The magnitude of the outflow velocity increases with a corresponding magnitude increase in the inflow velocity at the center, which can be explained by the fact that the pressure gradient needed to maintain the same flow rate increases as viscosity increases. (Garimella et al., 2022) obtains a similar trend for velocity for the case of the Naiver–Stokes equations. Additionally, it can be concluded that for inertial forces focusing in an intersecting wall channel of non-Newtonian fluids, the equilibrium position does not strongly depend on the $Re$ number. Even though there are nearly no inertial forces at the channel center, this position cannot be regarded as a stable equilibrium position because weak up and downward pressures still easily propel the particle. The particle tends to migrate toward its equilibrium location when starting from the channel center ( $θ = 0$ ), hence, the overall inertial force is positive (dominant region of the shear gradient forces). The inertial forces strength decreases as the particle gets closer to its equilibrium point. A total negative inertial force is applied to the particle as it advances from the equilibrium point to the channel wall (dominant region of wall-induced lift forces). Due to powerful wall-induced forces, the magnitude of this negative lift force rapidly increases as the particle approaches the wall. 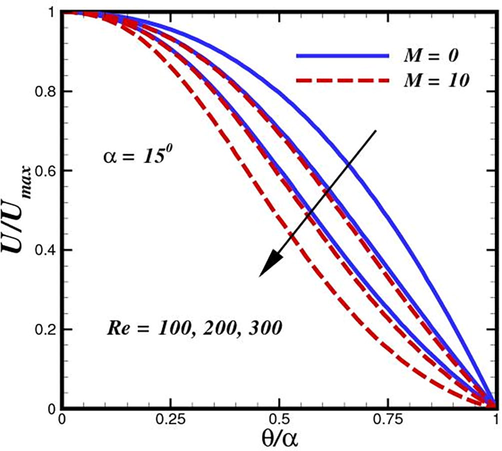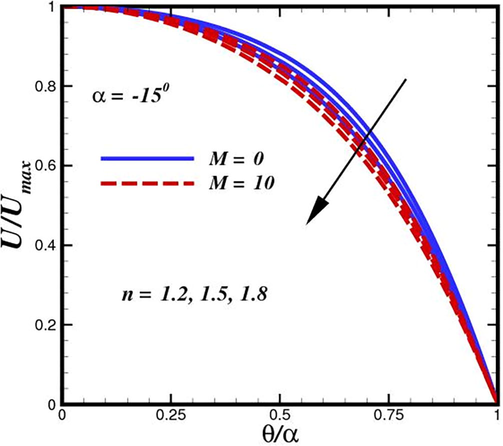Both graphics demonstrate how the velocity profile variation for a convergent and divergent channel with increasing $Re$ number demonstrates that as the magnetic field increases, the velocity profile flattens out and the thickness of the boundary layer diminishes. In actuality, the magnetic field produces a force that acts in the opposite direction of the momentum and stabilizes the velocity profile. Figs. 4 and 5 depict the predicted velocity with a power-law index $n$ in various conduit regions. The Carreau model accurately describes the viscosity across the whole range of shear rates, in contrast to the power-law model, which, as expected, cannot accurately capture the viscosity at low and high shear rates. In more detail, the power-law model theoretically overestimates and underestimates viscosity in the low and high shear-rate zones, respectively. The graphs illustrates how shear-thickened fluid behaves as power law $n$ values change. The decrease in fluid boundary layer thickness and velocity is indicated by the enhancement in $n$ for thickening. The power law is the cause of the increase in fluid viscosity, and higher viscosity results in less fluid velocity. It demonstrates that the increase in $n$ lowers the field and stops fluid momentum. Additionally, it appears that a dimensionless radial velocity profile promotes its incidence in diverging channels. With the power-law index and channel width, the momentum boundary layer thickness increases. As a result of power indexing, the fluid velocity is increased. Fig. 5 illustrates the case of converging channel, or $α = - 15^{0}$ . 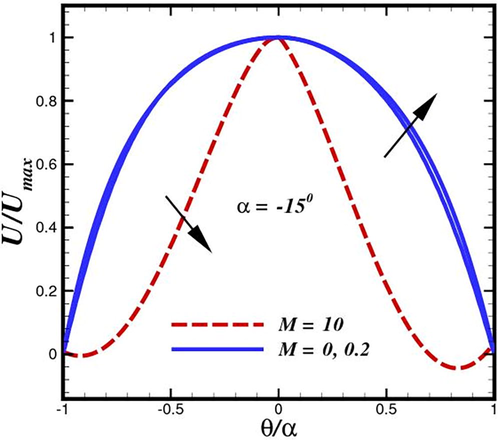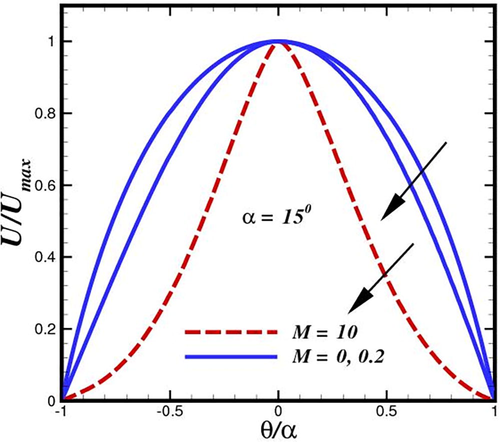In a convergent channel, the flow field does not invert near the walls; instead, when the magnetic Reynolds number increases, the fluid velocity around the channel centerline section also rises. The fluid radial velocity profile for diverging channels against various intensity of magnetic field strength at semi-angles is illustrated in Fig. 6. For divergent channels with outsized semi-angles, the existence of flow reversal close to the channel wall is seen. A general drop in fluid velocity is seen around the channel centerline region as the divergent semi-angle shrinks, and flow reversal near the walls is reduced. The fluid velocity near the channel's centerline region generally decreases as the magnetic field strength increases, which is an interesting observation. Furthermore, we observed that the Jeffery–Hamel flow, which corresponds to the case of $M = 0$ (no magnetic field), exhibits flow reversal near both walls, i.e. internal boundary layer separation. For $M = 0.2$ , the flow reversal has already been initiated as the magnetic number ( $M$ ) rises. For $M = 10$ , the profile becomes distinctly convex. We can observe that low values of $M$ are adequate to prevent the typical flow reversal of common fluids in divergent channels Fig. 7.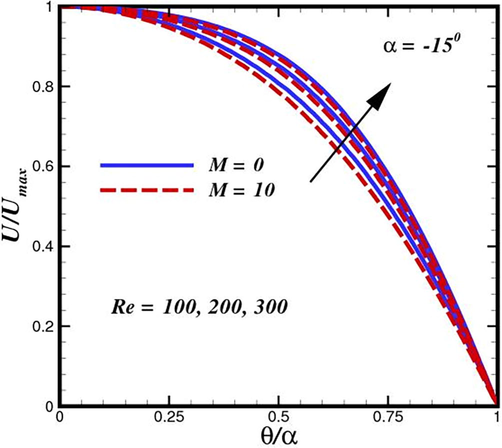

Tracking the flow structure inside converging conduit for different inertial force Re phases.

Tracking the flow structure inside diverging conduit for different inertial force Re phases.

Tracking the flow structure inside converging conduit for different power-indexed n phases.

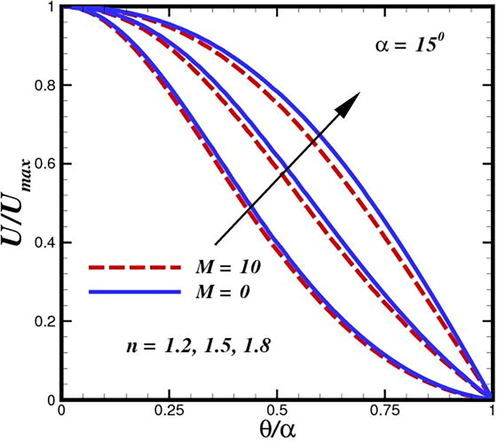
Tracking the flow structure inside diverging conduit for different power-indexed n phases.

Tracking the flow structure inside converging conduit (lower and upper section ( - α ≤ θ ≤ α ) or - 1 ≤ η ≤ 1 for different Lorentz forces M phases.

Tracking the flow structure inside diverging conduit (lower and upper section ( - α ≤ θ ≤ α ) or - 1 ≤ η ≤ 1 for different Lorentz forces M phases.

The influence of the heat generation parameter ( $Δ$ ) on temperature distributions in case of convergent and divergent conduit is depicted in Fig. 8 and Fig. 9, respectively. The heat transfer mechanism is significantly impacted by the heat source distribution. There are notable differences in the thermal distribution of the internal heat transfer process and the thermodynamic effectiveness of heat transfer systems with various heat source distributions from a thermodynamic point of view. To enhance various energy usage applications, it is crucial to clarify the mechanism by which the distribution of the heat source affects the system thermal efficiency and discover the best heating technique. A new combustion technology has also been created recently to provide a uniform heat source, but its impact on the heat transfer system and how it differs from conventional combustion techniques have not been studied. These figures indicate that the temperature and its associated thermal function are the heat generation parameter boosting functions for both shear thinning and shear thickening fluids. It is evident that the thermal boundary layer thicknesses and temperature profiles of the nanoparticles are larger in the heat generation scenario than in the heat absorption case. An interesting scenario is observed in case of diverging conduit in the presence of Lorentz forces. The application of inclined magnetic field make difference for controlling thermal boundary layer expansion. We have notice the depletion of nanofluid temperature in the existence of magnetic field strength. A slight reduction of approximately 6 % is perceived. According to Figs. 10 and 11, raising channel width $α$ has an impact on the fluid temperature in such a way that the temperature at the channel centerline rises dramatically because of the higher flow rate. The characteristic behavior of the nanofluid temperature in the diverging channel is very varied, as shown in Fig. 11. The nature of the fluids under study determines whether oscillations are present. The lowest temperature in the convergent channel instance is seen through the channel axis, whereas the maximum temperature is seen close to the plates. Similar behavior for temperature was observed by (Alam et al., 2017), (Saifi et al., 2020).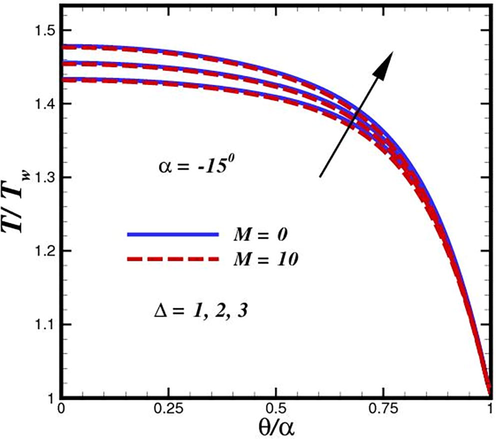

Flow temperature inside converging conduit for different heat source Δ intensities.

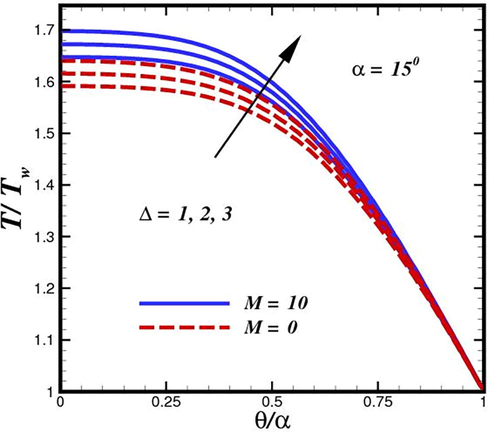
Flow temperature inside diverging conduit for different heat source Δ intensities.

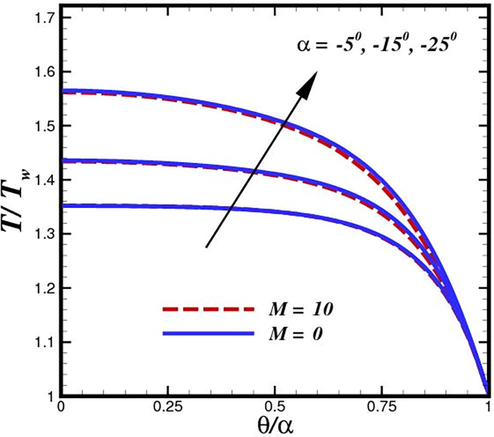
Flow temperature inside convergent conduit for different opening angles α configurations.

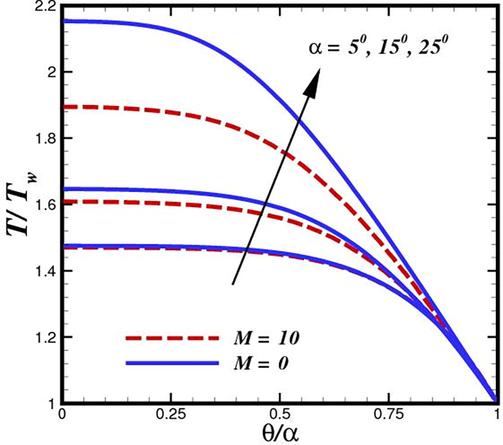
Flow temperature inside divergent conduit for different opening angles α configurations.

Figs. 12 and 13 exhibit the variation of dimensionless concentration for various values of $N_{AB}$ , respectively. The ratio of Brownian and thermophoretic diffusivities highlights the characteristics of nanofluids in our investigation. We thus consider how it may affect the distribution of autocatalysis $A^{*}$ and $B^{*}$ . As we approach $We = 0$ or $n = 1$ , it should be noticed from Eqs. (24) and (25) that fluids exhibit Newtonian fluid behaviour. In this limiting situation, tiny temperature gradients rather than Brownian diffusion are what primarily drive the movements of minuscule species. With this information, we explore how the fixed value of affects both curves with $K$ developing. The hysteresis point is visible on the smaller critical value of $K$ as it reduces, as shown in the figures, indicating that nanofluids are beneficial for preserving the stability of chemical reactions. The chemical reactions is prolonged and sufficiently reacted. 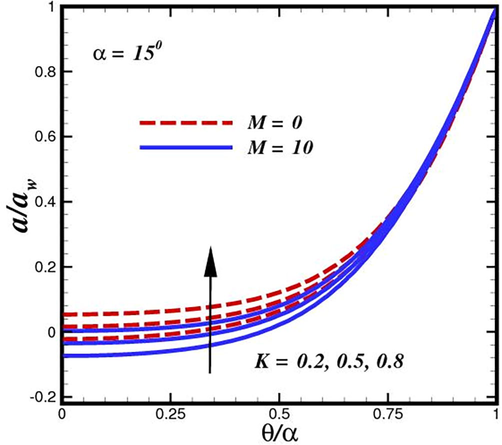The hysteresis point begins to emerge as $N_{AB}$ rises sufficiently. This serves as further evidence that nanofluids can maintain the stability of chemical processes. It is infer from both conduit that concentration is dramatically higher in the absence of magnetization. An elevation in the homogeneous reaction parameter $K$ , is accompanied by a concentration $ψ (η)$ (Fig. 14 and Fig. 15). This parameter is introduced in equation species $A^{*} / B^{*}$ . coupling term Eqs. (27) and (28). In the equation (27) for the species $B^{*}$ boundary layer, there is a corresponding cross-link term $α^{2} K$ , i.e. However, these concepts polarities are obviously diametrically opposed. The term is destructive (negative) ${- α}^{2} K$ when used to species ${(A}^{*})$ , whereas it is constructive when applied to species ${(B}^{*})$ (positive). 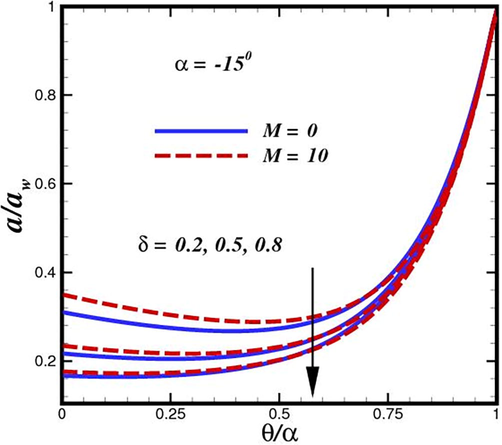Since species ${(A}^{*})$ concentration magnitudes upsurge with increasing distance from the channel surface, a rapid rise in species ${(A}^{*})$ concentration profiles are seen with rising $K$ , as previously indicated. As the heterogenous reaction parameter ( $δ$ ) is elevated, there is a noticeable destruction in concentration magnitudes, as seen in Fig. 16 and Fig. 17. It emerges in the conditions along the wall edge Eq. (32). According to the description of the autocatalytic reaction Eq. (10), $A^{*} + 2 B^{*} \to 3 B^{*}$ , rate $=$ $K_{1} a b^{2}$ , it is connected to the first order, isothermal catalytic reaction at the (channel) surface. Therefore, the channel surface has the lowest concentrations of this heterogeneous destructive reaction since this is where the greatest amount of species $A^{*}$ conversion to new species occurs. From the channel wall to the main stream, where they naturally reach their maximum distance from the cylinder surface, species $A^{*}$ concentrations rise. Since more and more species $A^{*}$ are being wiped out as $δ$ rises, species $A^{*}$ concentration magnitudes are reduced. All profiles asymptotically converge to the free stream, demonstrating that the simulations were run with an adequate-sized infinity boundary condition. 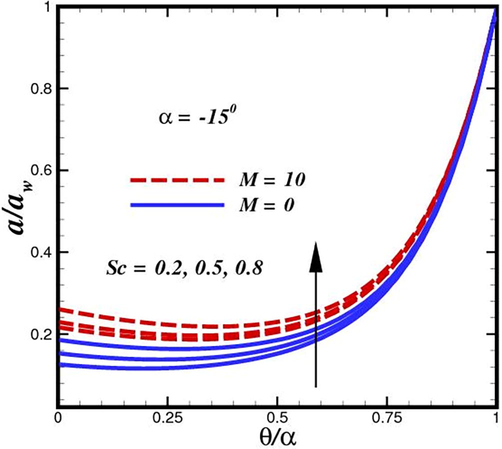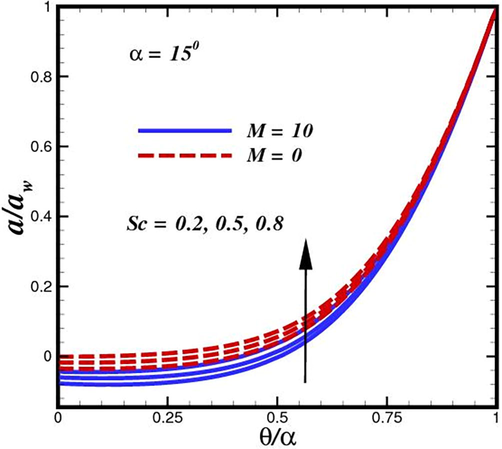The magnitude of the species $A^{*}$ concentration dramatically rises with an increase in Schmidt number ( $Sc$ ), as shown in Fig. 18 and Fig. 19. All profiles increase consistently as they move from the channel walls to the free stream. However, for very low $Sc$ values (0.2), which may represent diffusing in a lower-viscosity, highly aqueous functional polymer, the ascent is linear in nature, whereas for higher $Sc$ (0.3 $-$ 0.8), which represent diffusing in a magnetic nanofluid, the profiles adopt a parabolic monotonic growth disposition. The Schmidt number represents the proportion of species $B^{*}$ momentum to mass diffusivity. It is clear that rising Schmidt numbers have a tendency to boost concentration magnitudes noticeably, and this tendency persists across the boundary layer parallel to the channel surface. When gaseous diffusion occurs in non-Newtonian fluid, ( $A^{*} < 1)$ and the species diffusion rate exceeds the momentum diffusion rate, resulting in greater concentration magnitudes being calculated. In contrast, when $Sc > 1$ , the momentum diffusion rate outpaces the species diffusion rate, leading to a decrease in concentration values. The diffusion rates of momentum and nanoparticle species as well as the thicknesses of the boundary layer are comparable for the case of $Sc = 1$ . Species $A^{*}$ $Sc$ rises from 0.2 to 0.8, a concentration boundary layer thickness is evidently enhanced. Therefore, the ability of oxygen to travel through the reaction rates and functional polymer depend on the diffusivity of molecular species $A^{*}$ in the nanofluid.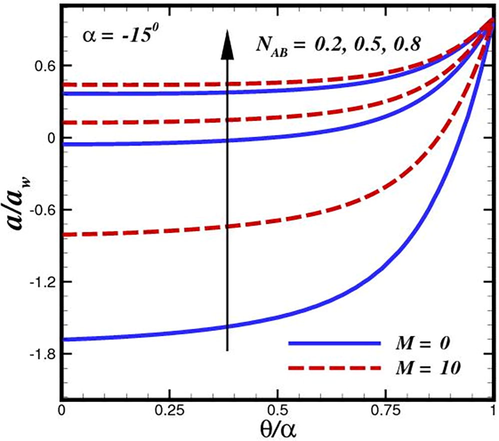

Fluid concentration inside convergent conduit featured by the ratio of Brownian and thermophoretic diffusivities N AB .

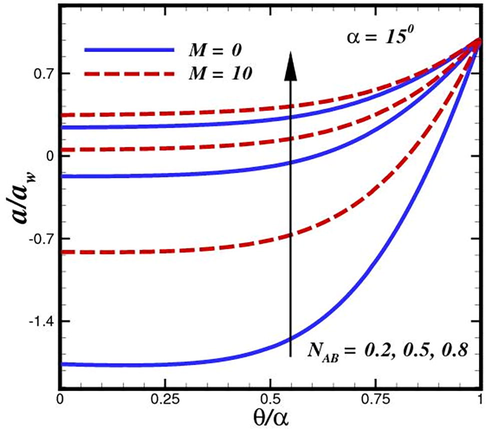
Fluid concentration inside divergent conduit featured by the ratio of Brownian and thermophoretic diffusivities N AB .

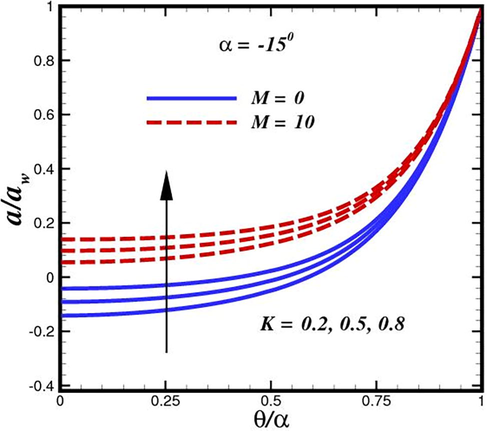
Fluid concentration inside convergent conduit for various strength of homogenous reaction K .

Fluid concentration inside divergent conduit for various strength of homogenous reaction K .

Fluid concentration inside convergent conduit for various strength of heterogenous reaction δ .

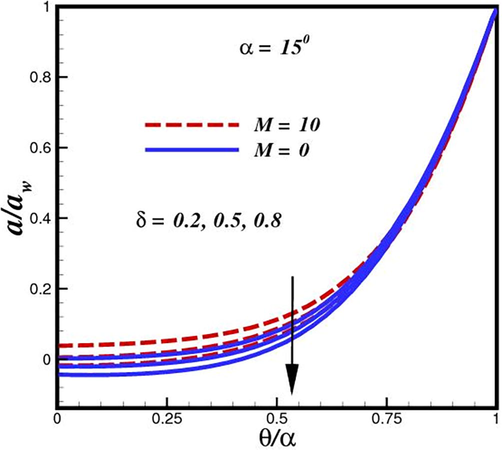
Fluid concentration inside divergent conduit for various strength of heterogenous reaction δ .

Fluid concentration inside convergent conduit for various strength of Schmidt number Sc .

Fluid concentration inside divergent conduit for various strength of Schmidt number Sc .

Tables 3 and 4 show local heat transfer and mass transfer contour topologies with different thermophysical, geometric, magnetic, and nanoscale characteristics. The computations shown in the tables are carried out using MATLAB. The analyses revealed that the Nusselt number depleted significantly with increasing magnetic parameter, however significant ascent with increasing Prandtl number is achieved. Eckert (viscous heating) number and heat source, which are both accountable for heat transmission to the boundary layer, both reduce the rate at which heat is transferred to the wall. As a result, the heat transmitted to the channel walls decreases while the heat transported away from the channel walls to the nanofluid increases. The increase in Eckert number also assists with the nanofluids Ohmic dissipation, or electromagnetic heating, which slackens the amount of heat that is transported to the channel surface. Furthermore, a depletion in Nusselt number is correlated with a larger heat source ( $Δ$ ) impact. Heat source raises the temperatures in the coating nanofluid while reducing the amount of heat that fluids transfer to the wall. A reduction in the Nusselt number. In contrast, as the Prandtl number rises, heat is successfully transferred to the channel surface by the cooling of the nanofluid, thus increasing Nusselt number magnitudes. According to estimates, the Nusselt number rises in divergent channels as the solid volume fraction rises, and the rate of increase consequently quickens. Nanofluid accelerates the pace of heat transfer qualities inside the flow region, as indicated in numerous related textbooks and studies. The evolution of the Sherwood number $Sh$ , for species $A^{*}$ and $B^{*}$ with different parameters is shown in Tables 3 and 4. Simulated contour topologies related to mass transfer are included. The simulation demonstrates that increasing the Schmidt number causes the local Sherwood number $Sh$ to increase significantly. Overall, it can be inferred that as $K$ , the first order homogeneous chemical reaction parameter, improves, the mass transfer rate of species $B^{*}$ to the channel wall diminishes while species $A^{*}$ mass transfer rate to the boundary increases. The ability to alter the functional nanofluid properties and the molecular diffusivity of the diffusing reactive species can be specifically highlighted in order to orchestrate various reactions in the transport phenomena. In contrast, a rise in the density of the nanofluid or the molecular (mass) diffusivity of the species ( $A^{*}$ , $B^{*}$ ) will result in a decrease in the Schmidt number, which is a measure of the dynamic viscosity of the functional coating material (nanofluid). Future research can study more species that may be considered in complex chemical synthesis and deposition processes.

Table 3 Computational values of heat

Nu

and mass transfer rate

Sh

against pertinent parameters in a convergent channel.

$\Pr$	$Ec$	$We$	$n$	$M$	$Re$	$N_{AB}$	$δ$	$K$	$Sc$	$Δ$	$- \frac{1}{α} β^{'} (1) α = - 1 5^{0}$	$- \frac{1}{α} ϕ^{'} (1) α = {- 15}^{0}$
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.51409600	0.07803444
13											−3.64170989	0.47101234
16											−5.98369808	0.23881231
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.39801341	0.15922343
10											−0.9802213	0.11946722
10											−0.39802134	0.23882446
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.09001345	0.47081233
10											−2.39242781	0.69655567
10											−3.38695780	0.91606780
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.84730082	0.47083360
10	0.2										−1.34678990	0.69658999
10	0.3										−1.12661345	0.47793678
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.96549678	0.49173679
10		1.2									−1.19509567	0.50500987
10		1.4									−2.84178978	0.47087890
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.78434566	0.52901235
10			1.2								−2.88164578	0.59589075
10			1.3								−3.94307841	0.10026688
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.25053456	0.10299065
10				12							−1.27124586	0.10565788
10				14							−1.38452256	0.09257900
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−2.27339456	0.08594629
10					150						−1.23126908	0.08022565
10					200						−0.20034567	0.10022344
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.25045677	0.10054563
10						0.2					−1.25093467	0.10074566
10						0.3					−2.25135531	0.18719088
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−3.27789001	0.21437890
10							0.3				−4.61541233	0.24341234
10							0.4				−5.97631334	0.09629023
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.40551233	0.18711234
10								0.3			−0.33851230	0.23081234
10								0.4			−0.30760877	0.09620998
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−2.40551234	0.14221233
10									0.3		−3.37051236	0.18711234
10									0.4		−4.33851345	0.09629023
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.96631334	0.02356889
10										1.4	−3.97639035	0.01356299
10										1.6	−4.986466I9	0.07803444

Table 4 Computational values of heat

Nu

and mass transfer rate

Sh

against pertinent parameters in a divergent channel.

$\Pr$	$Ec$	$We$	$n$	$M$	$Re$	$N_{AB}$	$δ$	$K$	$Sc$	$Δ$	$- \frac{1}{α} β^{'} (1) α = 1 5^{0}$	$- \frac{1}{α} ϕ^{'} (1) α = 15^{0}$
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.14090699	0.23444084
13											−1.23456610	0.17100753
16											−2.34566799	0.13886789
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.92201341	0.15922343
10											−0.67022134	0.11946722
10											−0.16021345	0.23882446
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.99078999	0.47081233
10											−1.88247817	0.69655309
10											−2.94672278	0.91606756
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.00753082	0.87083367
10	0.2										−0.08123990	0.69658999
10	0.3										−0.13451345	0.47793678
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.16549678	0.39173578
10		1.2									−0.99589567	0.50502345
10		1.4									−1.14178978	0.67087890
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.78434566	0.52901235
10			1.2								−2.88164578	0.59589075
10			1.3								−3.94307841	0.10026688
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.25053456	0.10299065
10				12							−1.27124586	0.10565788
10				14							−1.38452256	0.09257900
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.07339456	0.19465645
10					150						−0.83126908	0.60225690
10					200						−0.67034523	0.92457788
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.02504590	0.12023466
10						0.2					−1.05093478	0.17451086
10						0.3					−1.54622345	0.28719907
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.02256001	0.21437890
10							0.3				−2.22565433	0.24341234
10							0.4				−3.43789034	0.09629023
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.87190339	0.18711234
10								0.3			−0.38512301	0.23081234
10								0.4			−0.07607890	0.09620998
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−1.87117234	0.14221233
10									0.3		−2.39629023	0.18711234
10									0.4		−3.33854567	0.09629023
10	0.1	1.0	1.1	10	100	0.1	0.2	0.2	0.2	1.2	−0.10054563	0.02356889
10										1.4	−1.45778835	0.01356299
10										1.6	−2.081236I9	0.07803444

7 Conclusion

Establishing a deeper understanding of the channel fluid dynamics of innovative multifunctional subject to magnetic of significant interest in nuclear, aeronautical, marine, and medical engineering is the motivating factor behind this study. A novel mathematical model has been presented for renovated Jaffrey-Hamel problem by invoking Homogeneous and heterogeneous reactions internal and heat source. To establish a thermal analysis that is more physically accurate, Ohmic dissipation and Joule heating are invoked. In the unique situation in which the equivalent mass diffusivities of both species are combined into a single concentration equation. Two-phase nanoscale model is deployed. The non-linear constitutive equations for mass, momentum, energy, and species diffusion (species $A^{*}$ and $B^{*}$ ) are turned into a system of non-linear linked multi-degree ordinary differential equations (ODEs) using the appropriate scaling variables. Using a shooting method in MATLAB, the evolving nonlinear ordinary differential boundary value problem is solved. An effective, quickly convergent has been used to verify the MATLAB computations. Key electromagnetic, thermophysical, nanoscale, and geometric aspects were studied for their effects. It has used in a variety of ways in the aerodynamic extrusion of plastic sheet. Since capillaries and arteries are the best examples of convergent/divergent channels, the findings presented here are novel and significant because Carreau fluid has been proposed as the model that most accurately describes blood rheology in these channels. The computed findings lead to the following deductions:

The effect the inertial term $Re$ and apex angle $α$ has a higher velocity magnitude in a converging conduit, while presence of flow reversal region in a diverging conduit is gained. In all these cases momentum where flow dynamic upshot the (hydrodynamic) thickness of the boundary layer is increased in the flowing liquid.
High $Re$ number triggers the volume flux to concentrate at the channel center in divergent channel flow. In these situations, the boundary layer thickness increases by increasing the $Re$ number. Under the circumstances of a strong adverse pressure gradient, the backflow phenomena in divergent channels may occur for greater quantities of channel half-angle ( $α$ ).
With intensifying the magnetic field, it is possible to regulate the flow reversal and thermal distribution.
We observe that flow reversal is possible for the same volumetric flux of the fundamental Navier-Stokes equation of ordinary fluid, which is consistent with the findings for the Carreau liquid. Additionally, we see that the non-dimensional variables controlling the flow have an impact on the number of regions where the flow is reversed.
Due of the rapid flow rate, the temperature along the channel centerline significantly increases.
Presence of internal heat source influence the temperature significantly, while existence of external magnetic strength result in degradation of additional heat transmission.
In contrast to increasing for heterogeneous reaction parameters, the concentration profile drops for homogeneous reaction parameters.
With an elevation in magnetic field or homogeneity, concentration diminishes. It improves for the Schmidt number and $N_{AB}$ the ratio of Brownian and thermophoretic diffusivities.
Heat transport rate is surpassed by the magnetic field inclination. For the slow flow, a strong magnetic field dispersed the nanoparticles.

This computational model can be expanded to include the channel flow irreversibility mechanism. By selecting the appropriate physical and thermal parameters, this study will assist in increasing the system efficiency. The results could be useful for thermal processing applications requiring power-law nanofluids in the presence of heat-solutal capillary and natural convection phenomena, including food sterilization, protein crystal growth, polymer transformation, and many others. A typical physical system thermal efficiency might be improved by incorporating the entropy minimization mechanism by minimizing the temperature differential parameter, which would result in reduced energy loss.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, KSA, for funding this work through Research Group under grant number (R.G.P-1/3/43).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Abbas Z., Mehdi I., Hasnain J., Alzahrani A.K., Asma M., . Homogeneous-heterogeneous reactions in MHD mixed convection fluid flow between concentric cylinders with heat generation and heat absorption. Case Studies Thermal Eng.. 2023;102718
[CrossRef] [Google Scholar]
Ahmad S., Sheriff S., Anjum A., Farooq M., . Analysis of hydromagnetically modulated multiple slips motion of hybrid-nanofluid through a converging/diverging moving channel. Proc. Inst. Mech. Eng., Part E: J. Process Mech. Eng.. 2022;236:1377-1391.
[CrossRef] [Google Scholar]
Akbar N.S., Nadeem S., Haq R.U., Ye S., . MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions. Ain Shams Eng. J.. 2014;5:1233-1239.
[CrossRef] [Google Scholar]
Alam M.S., Khan M.A.H., Makinde O.D., . Magneto-Nanofluid Dynamics in Convergent-Divergent Channel and its Inherent Irreversibility. Defect and Diffusion Forum. 2017;377:95-110.
[CrossRef] [Google Scholar]
Ali F.H., Hamzah H.K., Hussein A.K., Jabbar M.Y., Talebizadehsardari P., . MHD mixed convection due to a rotating circular cylinder in a trapezoidal enclosure filled with a nanofluid saturated with a porous media. Int. J. Mech. Sci.. 2020;181:105688
[CrossRef] [Google Scholar]
Ali B., Hussain S., Nie Y., Hussein A.K., Habib D., . Finite element investigation of Dufour and Soret impacts on MHD rotating flow of Oldroyd-B nanofluid over a stretching sheet with double diffusion Cattaneo Christov heat flux model. Powder Technol.. 2021;377:439-452.
[CrossRef] [Google Scholar]
Ali B., Khan S.A., Hussein A.K., Thumma T., Hussain S., . Hybrid nanofluids: Significance of gravity modulation, heat source/ sink, and magnetohydrodynamic on dynamics of micropolar fluid over an inclined surface via finite element simulation. Appl. Math Comput.. 2022;419:126878
[CrossRef] [Google Scholar]
Al-Saif A.-S.-J.-A., Jasim A.M., . New analytical study of the effects thermo-diffusion, diffusion-thermo and chemical reaction of viscous fluid on magneto hydrodynamics flow in divergent and convergent channels. Appl. Math.. 2019;10:268-300.
[CrossRef] [Google Scholar]
Ameer Ahamad N., Veera Krishna M., Chamkha A.J., . Radiation-Absorption and Dufour effects on magnetohydrodynamic rotating flow of a nanofluid over a semi-infinite vertical moving plate with a constant heat source. J. Nanofluids. 2020;9:177-186.
[CrossRef] [Google Scholar]
Asghar Z., Saif R.S., Ali N., . Investigation of boundary stresses on MHD flow in a convergent/divergent channel: an analytical and numerical study. Alex. Eng. J.. 2022;61:4479-4490.
[CrossRef] [Google Scholar]
Ashraf M.Z., Rehman S.U., Farid S., Hussein A.K., Ali B., Shah N.A., Weera W., . Insight into significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics. 2022;10:2592.
[CrossRef] [Google Scholar]
Ayub A., Sabir Z., Shah S.Z.H., Wahab H.A., Sadat R., Ali M.R., . Effects of homogeneous-heterogeneous and Lorentz forces on 3-D radiative magnetized cross nanofluid using two rotating disks. Int. Commun. Heat Mass Transfer. 2022;130:105778
[CrossRef] [Google Scholar]
Banerjee A., Mahato S.K., Bhattacharyya K., Chamkha A.J., . Divergent channel flow of Casson fluid and heat transfer with suction/blowing and viscous dissipation: existence of boundary layer. Partial Differential Eq. Appl. Math.. 2021;4:100172
[CrossRef] [Google Scholar]
Bég O.A., Bég T., Khan W.A., Uddin M.J., . Multiple slip effects on nanofluid dissipative flow in a converging/diverging channel: a numerical study. Heat Transfer. 2022;51:1040-1061.
[CrossRef] [Google Scholar]
Berrehal H., Makinde O.D., . Heat transfer analysis of CNTs-water nanofluid flow between nonparallel plates: approximate solutions. Heat Transfer. 2021;50:4978-4992.
[CrossRef] [Google Scholar]
Bhandari D.S., Tripathi D., . Alteration in membrane-based pumping flow with rheological behaviour: a mathematical model. Comput. Methods Programs Biomed.. 2023;229:107325
[CrossRef] [Google Scholar]
Bilal S., Shah I.A., . A comprehensive physical insight about thermo physical aspects of Carreau fluid flow over a rotated disk of variable thickness by implementing finite difference approach. Propul. Power Res.. 2022;11:143-153.
[CrossRef] [Google Scholar]
Buongiorno J., . Convective Transport in Nanofluids. J. Heat Transfer. 2005;128:240-250.
[CrossRef] [Google Scholar]
Chaudhary M.A., Merkin J.H., . A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dyn. Res.. 1995;16:311-333.
[CrossRef] [Google Scholar]
Chaudhary M.A., Merkin J.H., . A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. II Different diffusivities for reactant and autocatalyst. Fluid Dyn. Res.. 1995;16:335.
[CrossRef] [Google Scholar]
Das S.K., Choi S.U., Yu W., Pradeep T., . Nanofluids: Science and Technology. John Wiley & Sons; 2007.
Das S., Mandal H.K., Jana R.N., Makinde O.D., . Magneto-nanofluid flow past an impulsively started porous flat plate in a rotating frame. J Nanofluids. 2015;4:167-175.
[CrossRef] [Google Scholar]
Das S., Ali A., Jana R.N., . Insight into the dynamics of magneto-casson hybrid nanoliquid caused by a plate rotation. World J. Eng.. 2020;18:66-84.
[CrossRef] [Google Scholar]
Dogonchi A.S., Ganji D.D., . Analytical solution and heat transfer of two-phase nanofluid flow between non-parallel walls considering Joule heating effect. Powder Technol.. 2017;318:390-400.
[CrossRef] [Google Scholar]
Eid M.R., Mahny K.L., Muhammad T., Sheikholeslami M., . Numerical treatment for Carreau nanofluid flow over a porous nonlinear stretching surface. Results Phys.. 2018;8:1185-1193.
[CrossRef] [Google Scholar]
Fraenkel L.E., Squire H.B., . Laminar flow in symmetrical channels with slightly curved walls, I. On the Jeffery-Hamel solutions for flow between plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1962;267:119-138.
[CrossRef] [Google Scholar]
Garimella S.M., Anand M., Rajagopal K.R., . Jeffery-Hamel flow of a shear-thinning fluid that mimics the response of viscoplastic materials. Int. J. Non Linear Mech.. 2022;144:104084
[CrossRef] [Google Scholar]
Hamad M.A.A., Pop I., . Scaling transformations for boundary layer flow near the stagnation-point on a heated permeable stretching surface in a porous medium saturated with a nanofluid and heat generation/absorption effects. Transp. Porous Med.. 2011;87:25-39.
[CrossRef] [Google Scholar]
Hamel G., . Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresber. Deutsch. Math.-Verein.. 1917;25:34-60.
[Google Scholar]
Hamid M., Usman M., Ul Haq R., Tian Z., . A Galerkin approach to analyze MHD flow of nanofluid along converging/diverging channels. Arch. Appl. Mech.. 2021;91:1907-1924.
[CrossRef] [Google Scholar]
Izbassarov D., Rosti M.E., Brandt L., Tammisola O., . Effect of finite Weissenberg number on turbulent channel flows of an elastoviscoplastic fluid. J. Fluid Mech.. 2021;927:A45.
[CrossRef] [Google Scholar]
James D.F., Roos C.A.M., . Pressure drop of a Boger fluid in a converging channel. J. Nonnewton. Fluid Mech.. 2021;293:104557
[CrossRef] [Google Scholar]
Jeffery G.B., . L. The two-dimensional steady motion of a viscous fluid. The London, Edinburgh, and Dublin Philosophical Mag. J. Sci.. 1915;29:455-465.
[CrossRef] [Google Scholar]
Kefayati G.H.R., Tang H., . Double-diffusive laminar natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part II: Entropy generation) Int. J. Heat Mass Transf.. 2018;120:683-713.
[CrossRef] [Google Scholar]
Kefayati G.H.R., Tang H., . Double-diffusive natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part I: Heat and mass transfer) Int. J. Heat Mass Transf.. 2018;120:731-750.
[CrossRef] [Google Scholar]
Khan U., Ahmed N., Tauseef Mohyud-Din S., . Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels. Chem. Eng. Sci.. 2016;141:17-27.
[CrossRef] [Google Scholar]
Khan M., Alshomrani A.S., . MHD stagnation-point flow of a carreau fluid and heat transfer in the presence of convective boundary conditions. PLoS One. 2016;11:e0157180.
[Google Scholar]
Khan M.I., Puneeth V., . Isothermal autocatalysis of homogeneous–heterogeneous chemical reaction in the nanofluid flowing in a diverging channel in the presence of bioconvection. Waves Random Complex Media 2021:1-21.
[CrossRef] [Google Scholar]
Khanafer K., Vafai K., . A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf.. 2011;54:4410-4428.
[CrossRef] [Google Scholar]
Khan M., Hashim,, . Boundary layer flow and heat transfer to Carreau fluid over a nonlinear stretching sheet. AIP Adv.. 2015;5:107203
[CrossRef] [Google Scholar]
Kiranakumar H.V., Thejas R., Naveen C.S., Khan M.I., Prasanna G.D., Reddy S., Oreijah M., Guedri K., Bafakeeh O.T., Jameel M., . A review on electrical and gas-sensing properties of reduced graphene oxide-metal oxide nanocomposites. Biomass Conv. Bioref. 2022
[CrossRef] [Google Scholar]
Krishna M.V., Chamkha A.J., . Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int. Commun. Heat Mass Transfer. 2020;113:104494
[CrossRef] [Google Scholar]
Maharudrayya S., Jayanti S., Deshpande A.P., . Pressure losses in laminar flow through serpentine channels in fuel cell stacks. J. Power Sources. 2004;138:1-13.
[CrossRef] [Google Scholar]
Makinde O.D., . Effect of arbitrary magnetic Reynolds number on MHD flows in convergent-divergent channels. Int. J. Numer. Meth. Heat Fluid Flow. 2008;18:697-707.
[CrossRef] [Google Scholar]
Makinde O.D., Eegunjobi A.S., Shuungula O., Neossi-Nguetchue S.N., . Hydromagnetic chemically reacting and radiating unsteady mixed convection Blasius flow past surface flat in a porous medium. Int. J. Computing Sci. Math.. 2018;9:525-538.
[CrossRef] [Google Scholar]
Makinde O.D., Mhone P.Y., . Hermite-Padé approximation approach to MHD Jeffery-Hamel flows. Appl. Math Comput.. 2006;181:966-972.
[CrossRef] [Google Scholar]
Malik M.Y., Khan M., Salahuddin T., . Study of an MHD flow of the carreau fluid flow over a stretching sheet with a variable thickness by using an implicit finite difference scheme. J Appl Mech Tech Phy. 2017;58:1033-1039.
[CrossRef] [Google Scholar]
Merkin J.H., . A model for isothermal homogeneous-heterogeneous reactions in boundary-layer flow. Math. Comput. Model.. 1996;24:125-136.
[CrossRef] [Google Scholar]
Millsaps K., Pohlhausen K., . Thermal distributions in Jeffery-Hamel flows between nonparallel plane walls. J. Aeronautical Sci.. 1953;20:187-196.
[CrossRef] [Google Scholar]
Nazeer M., Hussain F., Khan M.I., Khalid K., . Theoretical analysis of electrical double layer effects on the multiphase flow of Jeffrey fluid through a divergent channel with lubricated walls. Waves Random Complex Media 2022:1-15.
[CrossRef] [Google Scholar]
Ramadevi B., Sugunamma V., Kumar A., JV R.R., . MHD flow of Carreau fluid over a variable thickness melting surface subject to Cattaneo-Christov heat flux. Multidiscip. Model. Mater. Struct.. 2018;15:2-25.
[CrossRef] [Google Scholar]
Raza J., Mebarek-Oudina F., Ram P., Sharma S., . MHD flow of non-newtonian molybdenum disulfide nanofluid in a converging/diverging channel with rosseland radiation. Defect and Diffusion Forum. 2020;401:92-106.
[CrossRef] [Google Scholar]
Rehman S., Hashim, Ali Shah S.I., Galal A.M., . Multiple aspects of heat generation/absorption on the hydromagnetic flow of Carreau nanofluids via nonuniform channels. Proc. Inst. Mech. Engineers, Part E: J. Process Mech. Eng.. 2022;09544089221133343
[CrossRef] [Google Scholar]
Rehman S., Alqahtani S., Alshehery S., . Modeling a non-Newtonian nanofluid flow between intersecting planes with slip mechanism. Continuum Mech. Thermodyn. 2022
[CrossRef] [Google Scholar]
Rehman S., Alqahtani S., Hassine S.B.H., Eldin S.M., . Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel. Arab. J. Chem.. 2023;16:104475
[CrossRef] [Google Scholar]
Rosenhead L., Taylor G.I., . The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1940;175:436-467.
[CrossRef] [Google Scholar]
Sadeghy K., Khabazi N., Taghavi S.-M., . Magnetohydrodynamic (MHD) flows of viscoelastic fluids in converging/diverging channels. Int. J. Eng. Sci.. 2007;45:923-938.
[CrossRef] [Google Scholar]
Saif R.S., Muhammad T., Sadia H., Ellahi R., . Boundary layer flow due to a nonlinear stretching curved surface with convective boundary condition and homogeneous-heterogeneous reactions. Physica A. 2020;551:123996
[CrossRef] [Google Scholar]
Saifi H., Sari M.R., Kezzar M., Ghazvini M., Sharifpur M., Sadeghzadeh M., . Heat transfer through converging-diverging channels using Adomian decomposition method. Eng. Applications Computational Fluid Mech.. 2020;14:1373-1384.
[CrossRef] [Google Scholar]
Sari M.R., Kezzar M., Adjabi R., . Heat transfer of copper/water nanofluid flow through converging-diverging channel. J. Cent. South Univ.. 2016;23:484-496.
[CrossRef] [Google Scholar]
Shahid M., Javed H.M.A., Ahmad M.I., Qureshi A.A., Khan M.I., Alnuwaiser M.A., Ahmed A., Khan M.A., Tag-ElDin E.S.M., Shahid A., Rafique A., . A brief assessment on recent developments in efficient electrocatalytic nitrogen reduction with 2D non-metallic nanomaterials. Nanomaterials. 2022;12:3413.
[CrossRef] [Google Scholar]
Shahzad F., Ashiq M., Waqas M., Pasha A.A., Islam N., Zubair M., . Chemically reactive Carreau nanoliquid radiative flow induced by exponentially extending surface capturing variable liquid characteristics: a three-dimensional analysis. Int. Commun. Heat Mass Transfer. 2023;140:106313
[CrossRef] [Google Scholar]
Turkyilmazoglu M., . Extending the traditional Jeffery-Hamel flow to stretchable convergent/divergent channels. Comput. Fluids. 2014;100:196-203.
[CrossRef] [Google Scholar]
Veera Krishna M., Ameer Ahamad N., Chamkha A.J., . Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alex. Eng. J.. 2020;59:565-577.
[CrossRef] [Google Scholar]
Veera Krishna M., Ameer Ahamad N., Chamkha A.J., . Hall effects on unsteady magnetohydrodynamic flow of a nanofluid past an oscillatory vertical rotating flat plate embedded in porous media. J. Nanofluids. 2021;10:259-269.
[CrossRef] [Google Scholar]
Waqas H., Khan S.U., Khan M.I., Alzahrani F., Qayyum S., . Study of homogeneous–heterogeneous reactions in bioconvection stagnation pointslip flow of Walter’s-B nanofluid with nonlinear thermal radiation and activation energy. Int. Commun. Heat Mass Transfer. 2021;129:105729
[CrossRef] [Google Scholar]
Xu N.-L., Xu H., Raees A., . Homogeneous-heterogeneous reactions in flow of nanofluids near the stagnation region of a plane surface: the Buongiorno’s model. Int. J. Heat Mass Transf.. 2018;125:604-609.
[CrossRef] [Google Scholar]
Yazdi Sotoude M., Rahimi Nadaf M.A., Hosseini Imeni S.Z., Maghsoudi P., Bidabadi M., . Analysis of steady and oscillating flames fueled by biomass particles and syngases considering two-step pyrolysis and heterogeneous and homogeneous reactions. Int. J. Hydrogen Energy. 2022;47:21841-21862.
[CrossRef] [Google Scholar]

Introduction

Objective and originality

Computational model

Problem description
Problem assumptions
Flow, heat and mass transfer governing equations

Non-dimensional analysis

Solution methodology

Solutions justification

Results and discussion

Conclusion

Fulltext Views
12

PDF downloads
9

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abbas Z., Mehdi I., Hasnain J., Alzahrani A.K., Asma M., . Homogeneous-heterogeneous reactions in MHD mixed convection fluid flow between concentric cylinders with heat generation and heat absorption. Case Studies Thermal Eng.. 2023;102718
[CrossRef] [Google Scholar]

[2] Ahmad S., Sheriff S., Anjum A., Farooq M., . Analysis of hydromagnetically modulated multiple slips motion of hybrid-nanofluid through a converging/diverging moving channel. Proc. Inst. Mech. Eng., Part E: J. Process Mech. Eng.. 2022;236:1377-1391.
[CrossRef] [Google Scholar]

[3] Akbar N.S., Nadeem S., Haq R.U., Ye S., . MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions. Ain Shams Eng. J.. 2014;5:1233-1239.
[CrossRef] [Google Scholar]

[4] Alam M.S., Khan M.A.H., Makinde O.D., . Magneto-Nanofluid Dynamics in Convergent-Divergent Channel and its Inherent Irreversibility. Defect and Diffusion Forum. 2017;377:95-110.
[CrossRef] [Google Scholar]

[5] Ali F.H., Hamzah H.K., Hussein A.K., Jabbar M.Y., Talebizadehsardari P., . MHD mixed convection due to a rotating circular cylinder in a trapezoidal enclosure filled with a nanofluid saturated with a porous media. Int. J. Mech. Sci.. 2020;181:105688
[CrossRef] [Google Scholar]

[6] Ali B., Hussain S., Nie Y., Hussein A.K., Habib D., . Finite element investigation of Dufour and Soret impacts on MHD rotating flow of Oldroyd-B nanofluid over a stretching sheet with double diffusion Cattaneo Christov heat flux model. Powder Technol.. 2021;377:439-452.
[CrossRef] [Google Scholar]

[7] Ali B., Khan S.A., Hussein A.K., Thumma T., Hussain S., . Hybrid nanofluids: Significance of gravity modulation, heat source/ sink, and magnetohydrodynamic on dynamics of micropolar fluid over an inclined surface via finite element simulation. Appl. Math Comput.. 2022;419:126878
[CrossRef] [Google Scholar]

[8] Al-Saif A.-S.-J.-A., Jasim A.M., . New analytical study of the effects thermo-diffusion, diffusion-thermo and chemical reaction of viscous fluid on magneto hydrodynamics flow in divergent and convergent channels. Appl. Math.. 2019;10:268-300.
[CrossRef] [Google Scholar]

[9] Ameer Ahamad N., Veera Krishna M., Chamkha A.J., . Radiation-Absorption and Dufour effects on magnetohydrodynamic rotating flow of a nanofluid over a semi-infinite vertical moving plate with a constant heat source. J. Nanofluids. 2020;9:177-186.
[CrossRef] [Google Scholar]

[10] Asghar Z., Saif R.S., Ali N., . Investigation of boundary stresses on MHD flow in a convergent/divergent channel: an analytical and numerical study. Alex. Eng. J.. 2022;61:4479-4490.
[CrossRef] [Google Scholar]

[11] Ashraf M.Z., Rehman S.U., Farid S., Hussein A.K., Ali B., Shah N.A., Weera W., . Insight into significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics. 2022;10:2592.
[CrossRef] [Google Scholar]

[12] Ayub A., Sabir Z., Shah S.Z.H., Wahab H.A., Sadat R., Ali M.R., . Effects of homogeneous-heterogeneous and Lorentz forces on 3-D radiative magnetized cross nanofluid using two rotating disks. Int. Commun. Heat Mass Transfer. 2022;130:105778
[CrossRef] [Google Scholar]

[13] Banerjee A., Mahato S.K., Bhattacharyya K., Chamkha A.J., . Divergent channel flow of Casson fluid and heat transfer with suction/blowing and viscous dissipation: existence of boundary layer. Partial Differential Eq. Appl. Math.. 2021;4:100172
[CrossRef] [Google Scholar]

[14] Bég O.A., Bég T., Khan W.A., Uddin M.J., . Multiple slip effects on nanofluid dissipative flow in a converging/diverging channel: a numerical study. Heat Transfer. 2022;51:1040-1061.
[CrossRef] [Google Scholar]

[15] Berrehal H., Makinde O.D., . Heat transfer analysis of CNTs-water nanofluid flow between nonparallel plates: approximate solutions. Heat Transfer. 2021;50:4978-4992.
[CrossRef] [Google Scholar]

[16] Bhandari D.S., Tripathi D., . Alteration in membrane-based pumping flow with rheological behaviour: a mathematical model. Comput. Methods Programs Biomed.. 2023;229:107325
[CrossRef] [Google Scholar]

[17] Bilal S., Shah I.A., . A comprehensive physical insight about thermo physical aspects of Carreau fluid flow over a rotated disk of variable thickness by implementing finite difference approach. Propul. Power Res.. 2022;11:143-153.
[CrossRef] [Google Scholar]

[18] Buongiorno J., . Convective Transport in Nanofluids. J. Heat Transfer. 2005;128:240-250.
[CrossRef] [Google Scholar]

[19] Chaudhary M.A., Merkin J.H., . A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dyn. Res.. 1995;16:311-333.
[CrossRef] [Google Scholar]

[20] Chaudhary M.A., Merkin J.H., . A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. II Different diffusivities for reactant and autocatalyst. Fluid Dyn. Res.. 1995;16:335.
[CrossRef] [Google Scholar]

[21] Das S.K., Choi S.U., Yu W., Pradeep T., . Nanofluids: Science and Technology. John Wiley & Sons; 2007.

[22] Das S., Mandal H.K., Jana R.N., Makinde O.D., . Magneto-nanofluid flow past an impulsively started porous flat plate in a rotating frame. J Nanofluids. 2015;4:167-175.
[CrossRef] [Google Scholar]

[23] Das S., Ali A., Jana R.N., . Insight into the dynamics of magneto-casson hybrid nanoliquid caused by a plate rotation. World J. Eng.. 2020;18:66-84.
[CrossRef] [Google Scholar]

[24] Dogonchi A.S., Ganji D.D., . Analytical solution and heat transfer of two-phase nanofluid flow between non-parallel walls considering Joule heating effect. Powder Technol.. 2017;318:390-400.
[CrossRef] [Google Scholar]

[25] Eid M.R., Mahny K.L., Muhammad T., Sheikholeslami M., . Numerical treatment for Carreau nanofluid flow over a porous nonlinear stretching surface. Results Phys.. 2018;8:1185-1193.
[CrossRef] [Google Scholar]

[26] Fraenkel L.E., Squire H.B., . Laminar flow in symmetrical channels with slightly curved walls, I. On the Jeffery-Hamel solutions for flow between plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1962;267:119-138.
[CrossRef] [Google Scholar]

[27] Garimella S.M., Anand M., Rajagopal K.R., . Jeffery-Hamel flow of a shear-thinning fluid that mimics the response of viscoplastic materials. Int. J. Non Linear Mech.. 2022;144:104084
[CrossRef] [Google Scholar]

[28] Hamad M.A.A., Pop I., . Scaling transformations for boundary layer flow near the stagnation-point on a heated permeable stretching surface in a porous medium saturated with a nanofluid and heat generation/absorption effects. Transp. Porous Med.. 2011;87:25-39.
[CrossRef] [Google Scholar]

[29] Hamel G., . Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresber. Deutsch. Math.-Verein.. 1917;25:34-60.
[Google Scholar]

[30] Hamid M., Usman M., Ul Haq R., Tian Z., . A Galerkin approach to analyze MHD flow of nanofluid along converging/diverging channels. Arch. Appl. Mech.. 2021;91:1907-1924.
[CrossRef] [Google Scholar]

[31] Izbassarov D., Rosti M.E., Brandt L., Tammisola O., . Effect of finite Weissenberg number on turbulent channel flows of an elastoviscoplastic fluid. J. Fluid Mech.. 2021;927:A45.
[CrossRef] [Google Scholar]

[32] James D.F., Roos C.A.M., . Pressure drop of a Boger fluid in a converging channel. J. Nonnewton. Fluid Mech.. 2021;293:104557
[CrossRef] [Google Scholar]

[33] Jeffery G.B., . L. The two-dimensional steady motion of a viscous fluid. The London, Edinburgh, and Dublin Philosophical Mag. J. Sci.. 1915;29:455-465.
[CrossRef] [Google Scholar]

[34] Kefayati G.H.R., Tang H., . Double-diffusive laminar natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part II: Entropy generation) Int. J. Heat Mass Transf.. 2018;120:683-713.
[CrossRef] [Google Scholar]

[35] Kefayati G.H.R., Tang H., . Double-diffusive natural convection and entropy generation of Carreau fluid in a heated enclosure with an inner circular cold cylinder (Part I: Heat and mass transfer) Int. J. Heat Mass Transf.. 2018;120:731-750.
[CrossRef] [Google Scholar]

[36] Khan U., Ahmed N., Tauseef Mohyud-Din S., . Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels. Chem. Eng. Sci.. 2016;141:17-27.
[CrossRef] [Google Scholar]

[37] Khan M., Alshomrani A.S., . MHD stagnation-point flow of a carreau fluid and heat transfer in the presence of convective boundary conditions. PLoS One. 2016;11:e0157180.
[Google Scholar]

[38] Khan M.I., Puneeth V., . Isothermal autocatalysis of homogeneous–heterogeneous chemical reaction in the nanofluid flowing in a diverging channel in the presence of bioconvection. Waves Random Complex Media 2021:1-21.
[CrossRef] [Google Scholar]

[39] Khanafer K., Vafai K., . A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf.. 2011;54:4410-4428.
[CrossRef] [Google Scholar]

[40] Khan M., Hashim,, . Boundary layer flow and heat transfer to Carreau fluid over a nonlinear stretching sheet. AIP Adv.. 2015;5:107203
[CrossRef] [Google Scholar]

[41] Kiranakumar H.V., Thejas R., Naveen C.S., Khan M.I., Prasanna G.D., Reddy S., Oreijah M., Guedri K., Bafakeeh O.T., Jameel M., . A review on electrical and gas-sensing properties of reduced graphene oxide-metal oxide nanocomposites. Biomass Conv. Bioref. 2022
[CrossRef] [Google Scholar]

[42] Krishna M.V., Chamkha A.J., . Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int. Commun. Heat Mass Transfer. 2020;113:104494
[CrossRef] [Google Scholar]

[43] Maharudrayya S., Jayanti S., Deshpande A.P., . Pressure losses in laminar flow through serpentine channels in fuel cell stacks. J. Power Sources. 2004;138:1-13.
[CrossRef] [Google Scholar]

[44] Makinde O.D., . Effect of arbitrary magnetic Reynolds number on MHD flows in convergent-divergent channels. Int. J. Numer. Meth. Heat Fluid Flow. 2008;18:697-707.
[CrossRef] [Google Scholar]

[45] Makinde O.D., Eegunjobi A.S., Shuungula O., Neossi-Nguetchue S.N., . Hydromagnetic chemically reacting and radiating unsteady mixed convection Blasius flow past surface flat in a porous medium. Int. J. Computing Sci. Math.. 2018;9:525-538.
[CrossRef] [Google Scholar]

[46] Makinde O.D., Mhone P.Y., . Hermite-Padé approximation approach to MHD Jeffery-Hamel flows. Appl. Math Comput.. 2006;181:966-972.
[CrossRef] [Google Scholar]

[47] Malik M.Y., Khan M., Salahuddin T., . Study of an MHD flow of the carreau fluid flow over a stretching sheet with a variable thickness by using an implicit finite difference scheme. J Appl Mech Tech Phy. 2017;58:1033-1039.
[CrossRef] [Google Scholar]

[48] Merkin J.H., . A model for isothermal homogeneous-heterogeneous reactions in boundary-layer flow. Math. Comput. Model.. 1996;24:125-136.
[CrossRef] [Google Scholar]

[49] Millsaps K., Pohlhausen K., . Thermal distributions in Jeffery-Hamel flows between nonparallel plane walls. J. Aeronautical Sci.. 1953;20:187-196.
[CrossRef] [Google Scholar]

[50] Nazeer M., Hussain F., Khan M.I., Khalid K., . Theoretical analysis of electrical double layer effects on the multiphase flow of Jeffrey fluid through a divergent channel with lubricated walls. Waves Random Complex Media 2022:1-15.
[CrossRef] [Google Scholar]

[51] Ramadevi B., Sugunamma V., Kumar A., JV R.R., . MHD flow of Carreau fluid over a variable thickness melting surface subject to Cattaneo-Christov heat flux. Multidiscip. Model. Mater. Struct.. 2018;15:2-25.
[CrossRef] [Google Scholar]

[52] Raza J., Mebarek-Oudina F., Ram P., Sharma S., . MHD flow of non-newtonian molybdenum disulfide nanofluid in a converging/diverging channel with rosseland radiation. Defect and Diffusion Forum. 2020;401:92-106.
[CrossRef] [Google Scholar]

[53] Rehman S., Hashim, Ali Shah S.I., Galal A.M., . Multiple aspects of heat generation/absorption on the hydromagnetic flow of Carreau nanofluids via nonuniform channels. Proc. Inst. Mech. Engineers, Part E: J. Process Mech. Eng.. 2022;09544089221133343
[CrossRef] [Google Scholar]

[54] Rehman S., Alqahtani S., Alshehery S., . Modeling a non-Newtonian nanofluid flow between intersecting planes with slip mechanism. Continuum Mech. Thermodyn. 2022
[CrossRef] [Google Scholar]

[55] Rehman S., Alqahtani S., Hassine S.B.H., Eldin S.M., . Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel. Arab. J. Chem.. 2023;16:104475
[CrossRef] [Google Scholar]

[56] Rosenhead L., Taylor G.I., . The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1940;175:436-467.
[CrossRef] [Google Scholar]

[57] Sadeghy K., Khabazi N., Taghavi S.-M., . Magnetohydrodynamic (MHD) flows of viscoelastic fluids in converging/diverging channels. Int. J. Eng. Sci.. 2007;45:923-938.
[CrossRef] [Google Scholar]

[58] Saif R.S., Muhammad T., Sadia H., Ellahi R., . Boundary layer flow due to a nonlinear stretching curved surface with convective boundary condition and homogeneous-heterogeneous reactions. Physica A. 2020;551:123996
[CrossRef] [Google Scholar]

[59] Saifi H., Sari M.R., Kezzar M., Ghazvini M., Sharifpur M., Sadeghzadeh M., . Heat transfer through converging-diverging channels using Adomian decomposition method. Eng. Applications Computational Fluid Mech.. 2020;14:1373-1384.
[CrossRef] [Google Scholar]

[60] Sari M.R., Kezzar M., Adjabi R., . Heat transfer of copper/water nanofluid flow through converging-diverging channel. J. Cent. South Univ.. 2016;23:484-496.
[CrossRef] [Google Scholar]

[61] Shahid M., Javed H.M.A., Ahmad M.I., Qureshi A.A., Khan M.I., Alnuwaiser M.A., Ahmed A., Khan M.A., Tag-ElDin E.S.M., Shahid A., Rafique A., . A brief assessment on recent developments in efficient electrocatalytic nitrogen reduction with 2D non-metallic nanomaterials. Nanomaterials. 2022;12:3413.
[CrossRef] [Google Scholar]

[62] Shahzad F., Ashiq M., Waqas M., Pasha A.A., Islam N., Zubair M., . Chemically reactive Carreau nanoliquid radiative flow induced by exponentially extending surface capturing variable liquid characteristics: a three-dimensional analysis. Int. Commun. Heat Mass Transfer. 2023;140:106313
[CrossRef] [Google Scholar]

[63] Turkyilmazoglu M., . Extending the traditional Jeffery-Hamel flow to stretchable convergent/divergent channels. Comput. Fluids. 2014;100:196-203.
[CrossRef] [Google Scholar]

[64] Veera Krishna M., Ameer Ahamad N., Chamkha A.J., . Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alex. Eng. J.. 2020;59:565-577.
[CrossRef] [Google Scholar]

[65] Veera Krishna M., Ameer Ahamad N., Chamkha A.J., . Hall effects on unsteady magnetohydrodynamic flow of a nanofluid past an oscillatory vertical rotating flat plate embedded in porous media. J. Nanofluids. 2021;10:259-269.
[CrossRef] [Google Scholar]

[66] Waqas H., Khan S.U., Khan M.I., Alzahrani F., Qayyum S., . Study of homogeneous–heterogeneous reactions in bioconvection stagnation pointslip flow of Walter’s-B nanofluid with nonlinear thermal radiation and activation energy. Int. Commun. Heat Mass Transfer. 2021;129:105729
[CrossRef] [Google Scholar]

[67] Xu N.-L., Xu H., Raees A., . Homogeneous-heterogeneous reactions in flow of nanofluids near the stagnation region of a plane surface: the Buongiorno’s model. Int. J. Heat Mass Transf.. 2018;125:604-609.
[CrossRef] [Google Scholar]

[68] Yazdi Sotoude M., Rahimi Nadaf M.A., Hosseini Imeni S.Z., Maghsoudi P., Bidabadi M., . Analysis of steady and oscillating flames fueled by biomass particles and syngases considering two-step pyrolysis and heterogeneous and homogeneous reactions. Int. J. Hydrogen Energy. 2022;47:21841-21862.
[CrossRef] [Google Scholar]

A comprehensive physical insight of inclined magnetic field on the flow of generalized Newtonian fluid within a conduit with Homogeneous-heterogeneous reactions

Abstract

Keywords

Jeffery-Hamel problem

Two-phase model

Carreau model

Inclined magnetic field

Heat source

Homogeneous-heterogeneous reactions

Nomenclature

1 Introduction

1.1 Objective and originality

2 Computational model

2.1 Problem description

2.2 Problem assumptions

2.3 Flow, heat and mass transfer governing equations

3 Non-dimensional analysis

4 Solution methodology

5 Solutions justification

6 Results and discussion

7 Conclusion

Acknowledgments

Declaration of Competing Interest

References

Suggested read for related articles: