Translate this page into:
Analytical solution for thermal-diffusion induced stress model and numerical simulation of battery structure during charging-discharging process
⁎Corresponding author at: School of Mechanics and Civil Engineering, China University of Mining and Technology, China. qiliu@cumt.edu.cn (Qi Liu)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University. Production and hosting by Elsevier.
Abstract
During the course of thousands of charging and discharging cycles, batteries commonly undergo capacity fade and resistance growth, known as electrode aging. This phenomenon is attributed to local inhomogeneous deformation, as well as the possibility of fracture within electrode particles due to complex multi-physical couplings. To mitigate electrode aging and slow down the rate of fading, it is crucial to develop protective designs and tailored battery management strategies. However, accurately predicting potential fracturing and conducting precise battery simulations remain open challenges. This study presents a battery aging simulation model that incorporates multiphysical couplings of heat, concentration, stress, electric, and phase fields to assess battery performance at both the structural and electrode particle levels. Initially, an analytical solution is derived to determine stress distribution at the particle level within the thermal-concentration-mechanical deformation coupling, enabling quick calculation of stress distribution. Subsequently, a comprehensive battery structure is constructed to simulate discharge performance. Furthermore, the model computes the stress levels and fracture potential of the electrodes, thereby identifying locations prone to aging. Analytical and numerical findings indicate that tensile stress on the surface of an individual electrode acts as the driving force for fracture during lithium intercalation. Moreover, electrodes in close proximity to the electrolyte generate higher heat, while those near the electrode current collector are more susceptible to fracturing.
Keywords
Battery aging
Analytical solution
Phase field fracture
Crack distribution
1 Introduction
Lithium-ion battery (LIB) is an effective energy storage technology serving as a solution to rapid decarbonization (Liu et al., 2023, Xiao et al., 2023, Xu et al., 2023). Owing to its exceptional performance, LIB assumes a crucial function in energizing everyday electronic devices and appliances. However, LIB exhibits a convoluted internal microstructure and operates within intricate application environments, rendering the detection of its health state arduous and thereby potentially concealing certain safety hazards (Du et al., 2023, Wang et al., 2023).
An intricate analysis of the internal working state of the battery is imperative. A succinct model is anticipated to accurately assess this internal state and has strong guiding significance on detection of state of health of the battery (Pradhan and Chakraborty 2022). Such a model should effortlessly account for the couplings in the forward calculation predicated on electrochemical mechanisms (Deshpande and McMeeking 2023, Zhou et al., 2023) or the backward calculation based on experimental data (Deshpande and McMeeking 2023, Zhou et al., 2023). Among multiphysical coupling analyses (Miranda et al., 2023, Xiao et al., 2023, Zhang et al., 2023), forward models have been proposed for the detection of the LIB. LIBs typically comprise electrodes submerged in an electrolyte, with a separator to prevent direct contact between the negative and positive electrodes. Over thousands of cycles, power fading and capacity loss are typical characteristics of the aging and failure of batteries (Zhang et al., 2023). Previous investigations on multiphysical coupling analysis for LIBs have identified five main streams, delineated by their principal physical fields: Firstly, temperature detection and thermal runaway analysis (Ding et al., 2023, Zhang et al., 2023); Secondly, the optimization of mechanical properties to avert local stress concentrations (Estevez et al., 2023, Pistorio et al., 2023); Thirdly, the prediction of internal crack growth and dendrite formation utilizing the phase field method (Arguello et al., 2023, Yang and Wang 2023); Fourthly, the measurement of electrical parameters to monitor battery health (Li et al., 2023, Yu et al., 2023); and lastly, the determination of lithium ion concentration to ascertain the battery's charge state (Geetha et al., 2023, Zhuo et al., 2023). The steps mentioned above are complex systems and need to be simplified. During the running time of LIB, the electrode experiences moisture change and thermal expansion / contraction, ascribing to the uptake and removal of lithium ion in response to the heat in the electrochemical reaction process. Simultaneously, the transmission of ions between electrodes causes a part of ohmic heat and contributes to thermal runaway and thermal expansion. The dramatic temperature change is responsible for the dendrite growth and thermal cracking at low and high operating temperatures. Therefore, the aging process is related to the physical fields of heat, phase, concentration, electricity, and stress and needs complicated FEA simulations.
The investigation of the aging process and performance of batteries has been advanced through the application of multiphysical coupling methods. In the pioneering work of Prussin (Prussin 1961), a diffusion-induced stress (DIS) model was initially formulated to delve into the concentration-induced deformation of electrodes in lithium-ion batteries. Building upon this foundation, Clerici et al. (Clerici et al., 2020) provided an analytical solution for the coupled DIS model, examining the distribution of stress and concentration and elucidating the coupling effects on hydrostatic stress. Likewise, the research conducted by Sauerteig et al. (Sauerteig et al., 2018) led to the development of an electrochemical-mechanical coupling model, wherein a parametric formulation of interconnected equations was presented. Being similar to the concentration effect, the temperature is another cause for battery deformation and has similar impact effects as the DIS (Christensen, 2010). Temperature affects a battery system through the deformation of electrode materials and the speed of internal electrochemical reactions. A thermo-mechanical coupling model was proposed by Suo to analyze the thermal radiation effect in the cylindrical LIB and to develop a bridge between the stress field and thermal field (Suo and Liu 2021). Duan et al. (Duan et al., 2018) extended this line of inquiry by presenting an electrochemical-thermal–mechanical coupling model specifically designed for spiral-wound LIBs, encompassing comprehensive descriptions of electrochemical performance, thermal behaviors, and battery stress. Moreover, an electrochemical–thermal–mechanical model derived by Ai et al. (Ai et al., 2019) on the lithium-ion pouch cells and found that the simulated voltage, temperature, and stress are in good agreement with their experimental results. The battery's electricity field contains voltage, current, charge state information, and so on. Many of the experiments on the LIB aim to measure and predict the electricity parameters for monitoring the state of work and health. Due to the highly correlated impact with work environment, Wu et al. (Wu et al., 2022) set up a thermal-electric model within the full range of charge state to fit the non-linear relationship between voltage and temperature. A stochastic methodology based on random lattice spring theory was developed to describe the failure of electrode materials driven by diffusion induced stress (Barai and Mukherjee 2013). Failure analysis under mechanical abuse is a multiphysical process on electricity, deformation, and temperature fields. The phase field method is a computational approach to describe the distribution of the microstructure of materials and has been widely used to investigate the aging process and lithium dendrite that influenced the interaction among the multiphysical fields. Computed tomography imaging was employed by Boyca et al. (Boyce et al., 2022) to visualize micro-scale electrode details, and an electro-chemo-mechanical-phase field framework was developed, enabling accurate predictions of internal crack growth. In low temperature environment, the dendrite process of lithium ions near the separator is the leading cause of battery failure. An electrochemical-mechanical phase field model was proposed by Zhang et al. (Zhang et al., 2021), revealing that compressive stress acts as the driving force behind dendrite formation. Therefore, multiphysical coupling analysis is an effective tool for investigating the processive aging of LIB. However, all the theories mentioned above have no analytical solution for coupled thermal-diffusion induced stress of spherical electrodes. This analytical solution can fast predict the stress distribution in addition to tedious simulation.
The multiphysical coupling analysis presents a profound perspective of battery structure design for aging speed reduction. Through simulations, core–shell structures, special-shaped electrodes, and new material electrodes have been developed to improve the life and performance of an electrode. In manufacturing, protective coating outside the electrode is an effective technique for extending battery life and maintaining stability. In experiments, new structure electrodes made from various novel materials exhibited adequate protection and improved the battery performance. For instance, a yolk-shell structure with silicon nanoparticles encapsulating in the carbon/TiO2 double shells shows superior structural stability and a higher delivery capacity at a specific current density (Wang et al., 2021). Through mechanical simulation optimization, the electrode is designed in the form of film, tube, cellulose, and so on, and can effectively improve the stability of the electrode (Ko and Yoon 2022). Numerous new materials have also been developed in the laboratory to overcome traditional materials' shortcomings, such as Na2TiSiO5 anode with a high energy density and enhanced safety (He et al., 2019). Therefore, a well-designed multiphysical coupling framework combined with battery simulation can provide effective guidance for battery system optimization. However, only some relatively complete multiphysical coupling analyses have been conducted for the whole structure of the battery.
This paper aims to construct a comprehensive battery structure comprising electrodes, a separator, and an electrolyte, and develop a sophisticated multiphysical coupling model for numerical simulations of the battery structure's operational performance. The performance analysis is conducted through numerical simulations employing COMSOL Multiphysics, a finite element method-based partial differential equation solver. The organization of this paper is as follows: Section 2 presents the derivation of theoretical models encompassing the internal aging process of batteries across five distinct physics fields. In Section 3, the modeling methodology and the parameters of the models for numerical simulations are discussed. The evaluation of the constructed model's work performance is presented in Section 4. Finally, the conclusions drawn from the study are summarized in Section 5.
2 Mathematical principles and methods
2.1 Aging process and electrochemical mechanism in battery
The aging and failure of LIB are generally ascribed to irregular abuse, operation environment, and local damage of the battery composite. A multiphysical coupling theory can describe the cracking distribution, thermal generation, and concentration change and quantify the whole structure's operation status. Fig. 1 describes the aging and electrochemical mechanisms and their corresponding equations. In the mechanical analysis of this paper, the deformation is assumed to be elastic; thus, the plastic behavior is ignored. Further, the battery is simulated by a pseudo-two-dimensions (P2D) model; thus, a classic computational model is sued for battery analysis. The governing equations, and initial and boundary conditions for this problem are presented below.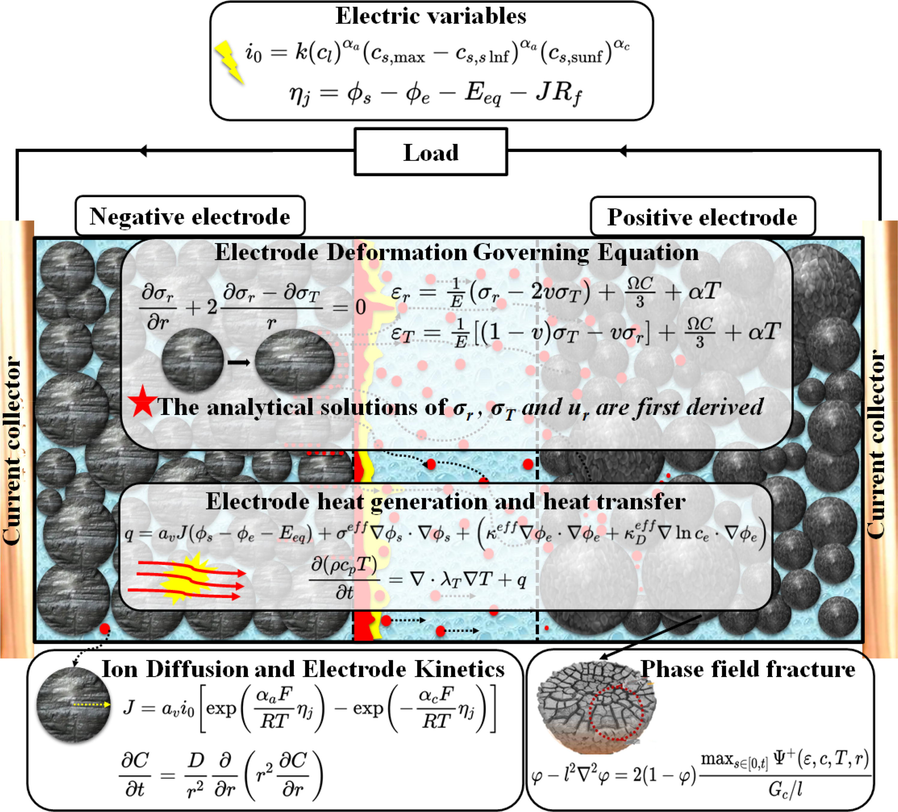
The equations describing the aging and electrochemical mechanism.
2.2 Heat generation and temperature distribution inside battery
The P2D model is established with basic LIB components, including electrodes (cathode, anode), separators, electrolytes, and current collectors. The ionic migration between positive and negative electrodes occurs in the lithiation / delithiation process over thousands of charging and discharging cycles. The uptake and removal of lithium-ion is accompanied by decalescence and discharge heat as a result of electrochemical reactions and current thermal effects. Electrochemical reaction occurs at the interface between the electrolyte and electrode, which is governed by the Bulter-Volmer equation as (Newman and Tobias 1962, FuQian Yang 2016)
Eq. (4) describes the heat generation in various parts of the battery. The heat for the internal temperature increment of the battery comes from the internal heat source and ambient heat transfer. The temperature distribution is attained by the differential equations of heat transfer as (Kumaresan et al., 2008)
2.3 Deformation of electrodes inside the battery
Commercial battery electrodes are made from various materials, including silicon, graphite, oxide and so on. As the most potential electrode material, silicon can change its volume by 400% upon the uptake and removal of lithium. This volume change leads to inhomogeneous deformation, even pulverization. This decrepitation of electrodes declines battery capacity and accelerates the aging process. Heat conduction and concentration variation result in an additive strain term in the constitutive equation for the deformation of each particle inside the electrode. The strain–displacement relationship in spherically symmetrical form is (Timoshenko and Gudyer 1970)
The constitutive equation for the deformation-concentration-thermal coupling in spherically symmetrical electrode particles is
The particle's radius is set to a and the displacement at the sphere's center is assumed to be zero. The stress on the surface is zero if the interaction at the free surface is ignored. The ambient temperature is Ts and the surface concentration is cs. Thus, the boundary conditions for the charging process are
For discharging processing, the boundary condition of concentration is c = cs at the whole domain. The rest condition is the same as charging process.
Eq. (7) is firstly substituted into Eq. (9) and then Eq. (8) to obtain the differential equation of displacement. The solution of displacement is obtained as
This is a pure functional analytical solution of displacement ur and C1/C2 is an integration constant to be determined by specific boundary conditions. The relationships between the Lame constant and the elastic constant are μ = E/2(1 + υ) and λ = υE/(1-2υ)(1 + υ). Substituting Eq. (11) into Eq. (7) and then Eq. (9) attains the radial and hoop stresses as
Eq. (12) displays that radial stress can reach zero at the free surface and hoop stress gains with increased r for given integration constants. By substituting boundary conditions of Eq. (10) into Eq. (11) and Eq. (12), the constants C1 and C2 are determined and analytical solutions are obtained. Lithium diffusion in the electrode follows Fick's second law, and the ionic concentration gradient is the driving force for lithium transmission. Therefore, the governing equation is (Han et al., 2023)
Eq. (13) indicates that lithium follows the mass conservation law. With the boundary condition of Eq. (10), the analytical solution of lithium concentration is obtained as (Cheng and Verbrugge 2009)
Eq. (14), Eq. (12) and Eq. (5) are the analytical solutions for the thermal-concentration-mechanical deformation system of battery electrodes. The hoop stress σT acts as a driving force to the crack growth on the particle's surface.
2.4 Crack distribution of electrodes inside the battery
The interaction of multi-physical fields inside the battery triggers the inhomogeneous deformation of electrode particles and leads to the appearance and distribution of internal fractures. Hygroscopic expansion, thermal expansion and current effect are the main driving forces for crack propagation. As shown in Fig. 2 (Ryu et al., 2018), throughout charge and discharge cycles, crack propagation and bifurcation occur inside the electrode particles and result in capacity and power loss.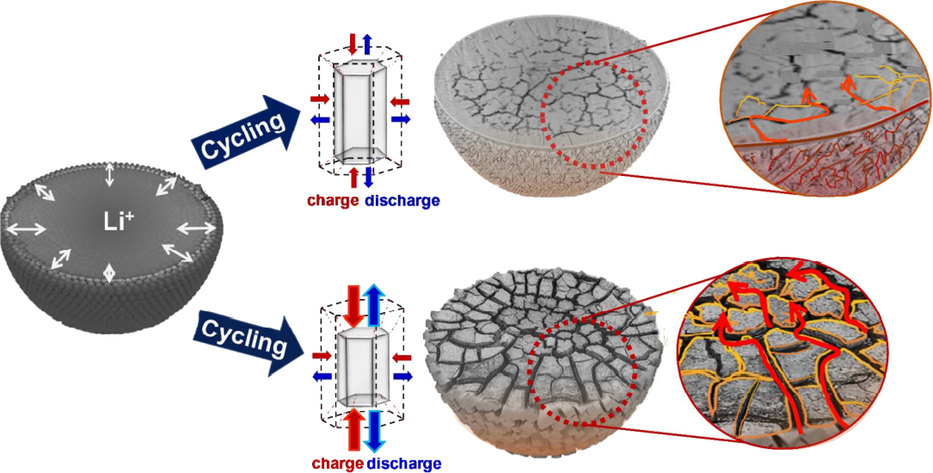
Internal crack distribution of electrode particle (Ryu et al., 2018).
Griffith’s fracture theory in 1920 is based on the energy conservation principle and can avoid the deficiency of strength theory. A crack is initiated or propagated only when a process causes the system energy to be reduced or kept constant. When the crack propagates forward, the total energy does not change. In the equilibrium state, with a crack propagation dA, the Griffith energy balance theory is expressed as (Alessi and Ulloa 2023)
Eq. (15) shows that the total energy is equal to the system's potential energy. The total energy comprises the internal strain energy and the work required to generate the superficial crack. Its integral form is (Alessi and Ulloa 2023)
The Griffith theory can analyze the distribution of crack whose cracked surface is Γ in the arbitrary domain Ω. The system’s free energy consists of elastic strain energy and fracture surface energy. That is the integral of the strain energy density at the electrode Ω plus the integral of the fracture energy at the crack surface Γ. It is difficult to accurately trace the trajectory of the actual crack surface, thus the calculation of fracture energy may fail. Francfort and Marigo (Francfort and Marigo 1998) proposed a variational fracture model based on the Griffith energy theory. They used an auxiliary field variable φ to describe the fractured interface. Here, the φ is a damage parameter to characterize the attenuation of material stiffness with the appearance of cracks through Edam=(1-φ)•E. Further, the stress is still calculated as σ = Edam•ε. The second term in Eq. (16) is the area integral along the crack extension surface that can be converted into bulk integral as (Klinsmann et al., 2016)
The elastic strain energy density Ψ is contributed by tensile and compressive stresses and is denoted by Ψ=(1-d)2Ψ++Ψ-. To catch the trace of crack, Eq. (18) is reformulated into a Lagrangian energy functional as (Klinsmann et al., 2016)
The Euler-Lagrange equation of Eq. (19) is obtained by finding a stationary point with algorithm δL = 0. The distribution of crack is described by phase field as (Klinsmann et al., 2016)
The first term on the right side of Eq. (21) represents tensile stress, which will be decayed to zero when the particle is wholly fractured (φ = 1). As tensile stress changes, the stiffness of the material gradually decays until complete failure. The compressive stress has no decaying effect on the stiffness of the material.
3 Simulation experiments and battery materials
The 3D geometry of P2D battery structure is built in Fig. 3. This section describes the modeling process details and presents computation parameters. The model will be verified with experimental data available from the literature.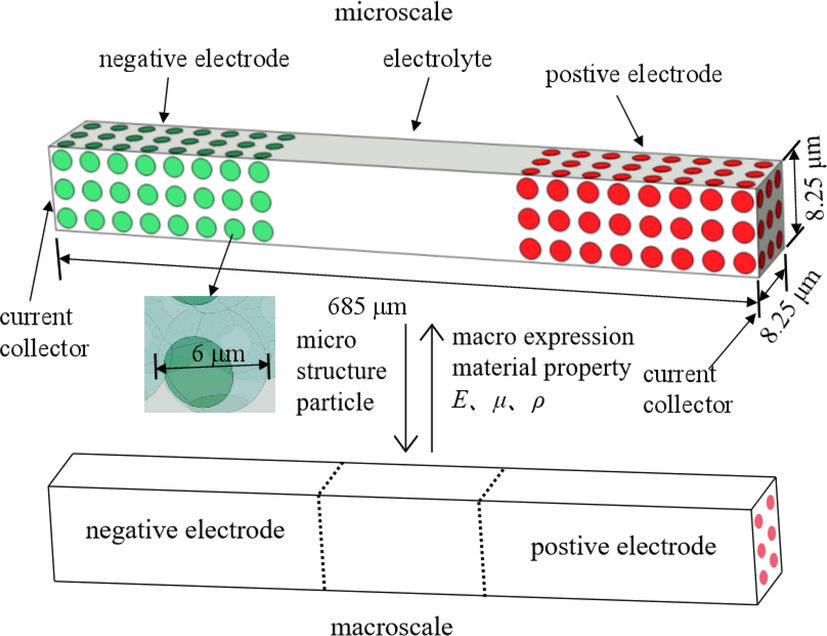
The geometry of the P2D battery model and connection between macro and micro structures.
3.1 Modeling methodology and computation parameters
The negative and positive electrodes are composed of 72 spherical particles with a radius of 3 mm, respectively. In order to observe the microscopic distribution of parameters during charging and discharging, the structure and the particles are set at the same scale. The fade of capacity is the macroscopic expression of electrode particle cracks in the aging process. The property changes of battery materials, such as elasticity modulus E, Poisson’s rate μ and density ρ, reflect the health condition of microstructures. In this model, the negative electrode is set to graphite and the positive electrode is set to lithium cobaltite (LiCoO2). The rest of the space inside the cuboid is full of electrolytes set as lithium Hexafluorophosphate solution (LiPF6). In order to reduce the perplexity of the simulation, the separator is neglected because it has little impact on the performance analysis.
The battery simulations with five coupling physical fields are implemented through the following 5 steps: (1) Initialize the current distribution at a specific discharge current; (2) Calculate the lithium ion concentration distribution inside the electrode particles by overvoltage; (3) Calculate heat generation to obtain the temperature distribution by the current and lithium concentration; (4) Calculate the stress distribution through the coupling of temperature and concentration; (5) Calculate the electrode elastic strain energy regarding stress and phase variable distribution.
After the geometry of the battery is set up, boundary conditions, initial values and electrochemical reactions are set in the specific domain and surface. Firstly, according to the sequence of simulation steps, a discharge current of 1 μA is set on the positive electrode current collector while electrical grounding is set on the negative electrode current collector. Eq. (1)–(3) are applied to the electrode–electrolyte contact interface and the distribution of current and potential is calculated. Secondly, the charge state is 50% in the initial state, and the lithium concentration is 15000 mol/m3. Eqs. (13) and (14) are applied to the electrode domain and the distribution of lithium concentration is calculated. Thirdly, the boundary of the battery is set to thermal insulation and the ambient temperature is 293.15 K. After calculating Eq. (4), the temperature is obtained by Eq. (5) and applied to the whole domain. The negative current collector is fully fixed and the rest of the structure is freely deformable. Eqs. (7)–(12) act on the electrode domain to acquire the stress. The critical energy release rate is set to 2300 J/m2, within a rational electrode damage standard. The computation parameters are listed in Table 1.
Parameter in electrode model
Value
Cation
Faraday constant, Fa (A•s/mol)
96485.3145
(Liu et al., 2023)
Gas constant, R (J/mol•K)
8.314
(Liu et al., 2023)
Diffusion coefficient, D (m2/s)
7.08 × 10-15
(Clerici et al., 2020)
Ambient temperature, T (K)
293.15
(Clerici et al., 2020)
Partial molar volume of ions in the electrode, Ω (m3)
3.50 × 10-6
(Liu et al., 2023)
Discharging current, i (μA)
1
(Liu et al., 2023)
Solid electrode radius, Rsradius (μm)
3
Estimated
The length of the battery structure, ls (μm)
685
Estimated
Partial molar volume of ions in the spherical shell, Ωs (m3)
5.3 × 10-6
Estimated
Initial state of charge, SOC
50%
Estimated
Width and height of the battery structure lwh (μm)
8.25
Estimated
Initial electrolyte concentration, cl (mol/m3)
1000
Estimated
Critical energy of interface debonding, Γd (J·m−2)
40
(Wu and Lu 2017)
Critical energy release rate of the material, Gc (J/m2)
2300
(Wu and Lu 2017)
4 Result and discussion
The battery performance and anti-aging effect induced by thermal, mechanical, electrochemical and fracture results are discussed by numerical simulations here. The effects of multiphysical coupling on battery performance are explored. In this paper, the analysis of the whole battery structure is presented based on the P2D model. All physical fields are calculated on the same dimensional scale. In order to verify the correctness of the simulation model, the stress results as selected parameters are compared the corresponding results in the literature.
4.1 Validation of the model
The numerical model is verified by the ccomputional data published in references (Clerici et al., 2020, Liu et al., 2023). This literature calculated the lithium insertion condition under galvanostatic control and lithium extraction condition under galvanostatic control, which is suitable for single electrode particles. The simulated structures are different from those in the literature; thus, the boundary conditions of particles in our model are slightly different from those in the literature. In the experiment, the fixed constraint was at the electrode center, while the particles in this paper do not have free surface and contact with adjacent particles. The dimensionless concentration and hoop stress along the radius direction are chosen to validate our model and presented in Fig. 4. Obviously, the fluctuations of variables along the dimensionless radius direction have the same trend.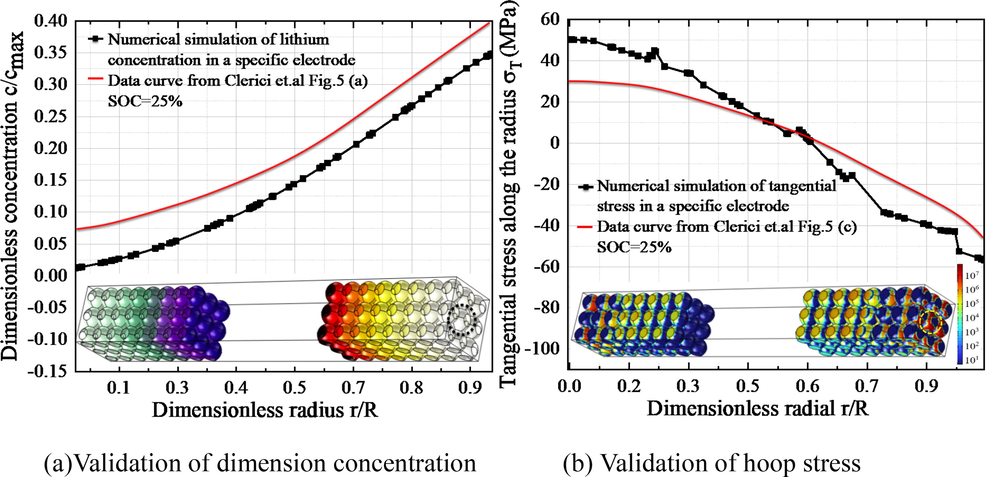
The model geometry and model validations. (a) the dimensionless concentration of a specific electrode and in literature; (b) hoop stress of a specific electrode and in literature.
4.2 Electrochemistry performance analysis during discharging
At a microscopic scale, porous electrodes have complex geometries to provide a larger specific surface area where the electrode materials participate in chemical reactions with the electrolyte. The positive and negative electrodes in this section use spherical particles as a porous electrode to characterize the compact structure of the electrode. The negative current collector of the battery is electrically grounded, and the positive current collector is discharged with a small current of 0.001C for the 90 s. The z-x plane of the cell is connected to the current collector, so there is a charge flux which can result in an uneven distribution of potential and ion concentration in the y-axis direction. The model sets the outer y-z and y-x surfaces as insulation to ensure zero charges and concentration flux at the boundary. During discharging, the negative electrode gives up electrons to the external circuit while lithium-ion travels toward the positive electrode. To maintain charge conservation, negatively charged ion moves toward the negative electrode in the electrolyte, where the solution supplies a medium for internal ionic transfer.
Fig. 5 shows the distribution of electrochemistry parameters, including ionic concentration, current density and potential distribution. Fig. 5(a) sows the distribution of lithium-ion transmission from negative electrode to negative electrode and the direction of diffusion flux. At the 90 s of charging, the positive side of electrodes gather a higher concentration of ions. At the same time, the electrolyte negative ions diffuse toward the negative electrode and the direction of flux is shown in Fig. 5(b). Eq. (3) indicates that the exchange current density is related to the concentration of lithium and electrode. Fig. 5(c) shows that the electrode reaction is more intense on the side close to the electrolyte, where the ability gaining / losing electrons is more robust, and the highest area is on the current collector.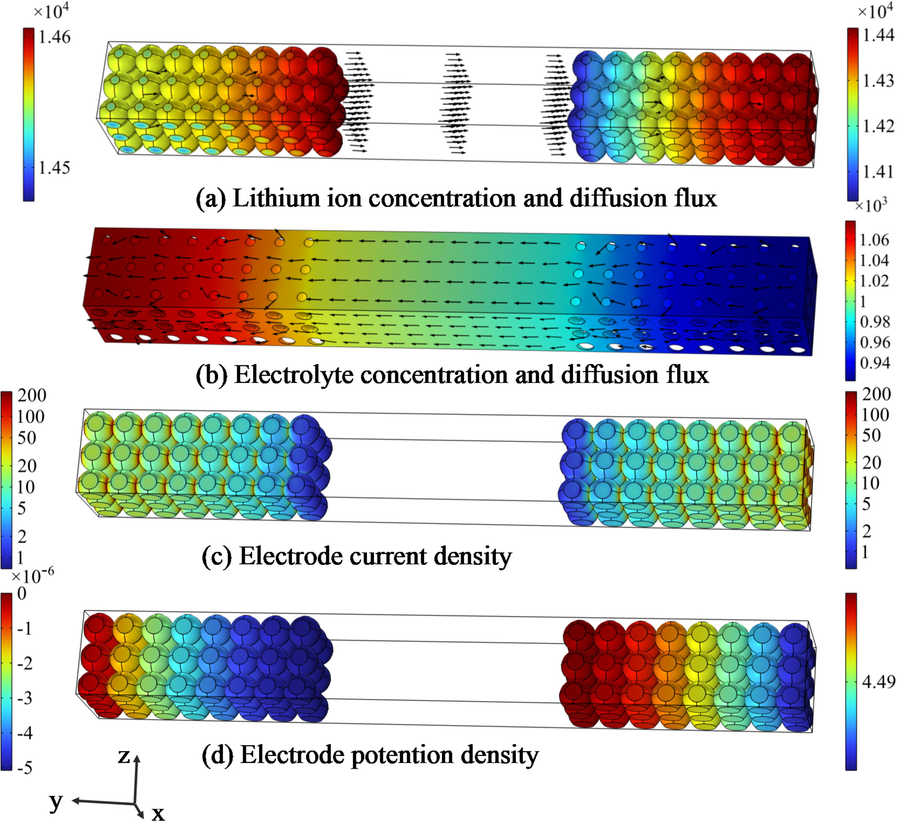
Parameter distribution map.
There are two dimensions of ion diffusion inside a battery: (1) the radial direction inside a single particle; (2) the direction between electrodes. Fig. 6 depicts the lithium-ion diffusion inside the battery at four time points. The diffusion is calculated by Eq. (13). During the charging process, along the radial direction, the lithium element loses electrons and is deintercalated from the negative electrode. At this moment, the concentration of lithium ions on the surface of the particle is higher than that in the center of the particle. Then, lithium ions diffuse from the negative electrode particles through the electrolyte to the positive electrode particles and intercalate into the positive electrode lattice. As the charging time increases, more lithium ions are deintercalated from the negative electrode and a higher concentration is detected.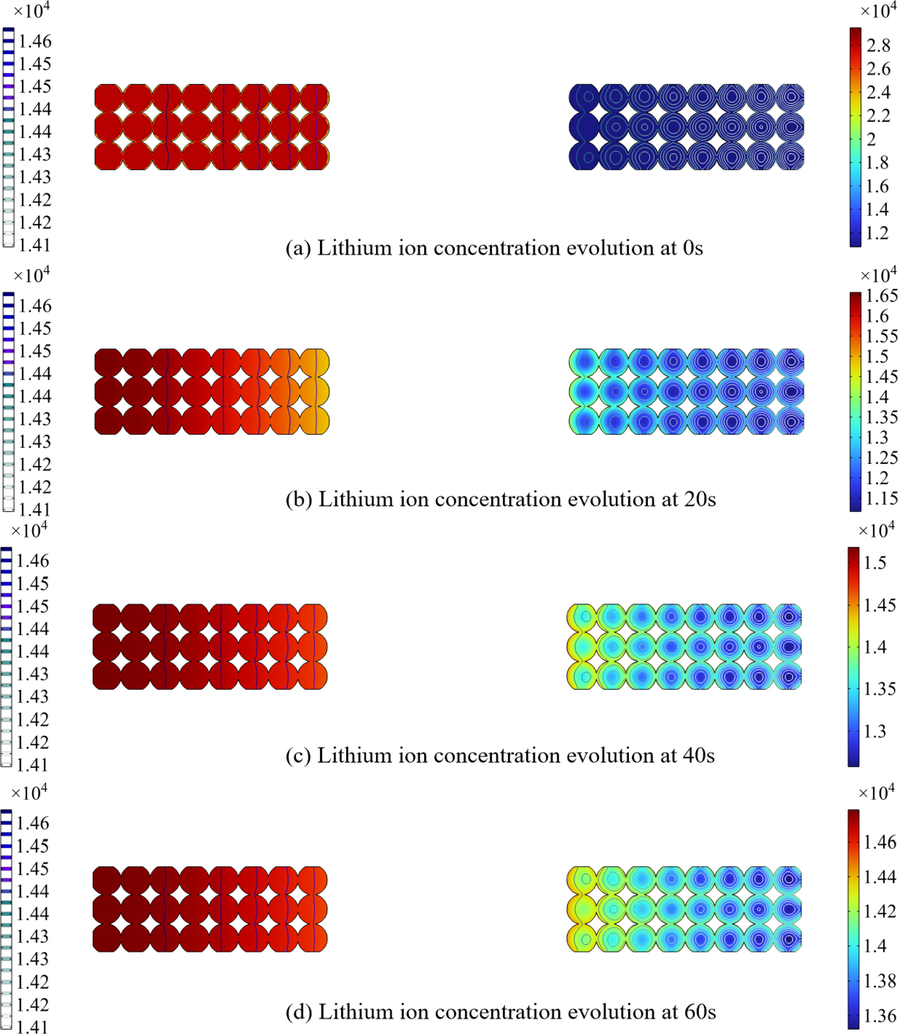
Lithium concentration distribution at 0 s, 20 s, 40 s and 60 s.
4.3 Thermal performance analysis during discharging
The temperature has a significant influence on battery performance. At low temperatures, the ion diffusion and migration rate slow down, and the local accumulation at the electrode causes harmful side reactions such as dendrites. At high temperatures, the electrochemical reaction rate inside the battery increases until thermal runaway occurs. Therefore, the simulations on the heat generation and temperature change inside a battery are essential to improve the safety of the battery. Eq. (4) shows that the internal heat source of the battery mainly comes from the electrochemical reaction heat and current heating effect inside the electrode and electrolyte. The heat generation induces thermal stress inside the electrode with an incidental concentration stress, which mechanically leads to the deformation and aging of the electrode. Fig. 7 plots the thermal and mechanical parameters of the P2D model. The heat transfer and stress of the battery are at the macro- and micro-scales, respectively. Fig. 7(a) indicates that the heat generation power is higher at the contact of the electrode and the electrolyte. When the battery is discharged, the heat generation at the positive electrode is higher than that at the negative electrode. This corresponds to the higher ion concentration of the positive electrode in Fig. 6. During cycling, the increase in internal resistance and capacity fading mainly occurred at the positive electrode, and the increase in internal resistance resulted in heat generation and temperature increase of the positive electrode. Fig. 7(b) shows the temperature distribution of the battery. The temperature in the positive electrode is slightly higher than that in the negative electrode distribution. At the positive current collector, the temperature is higher due to higher current density.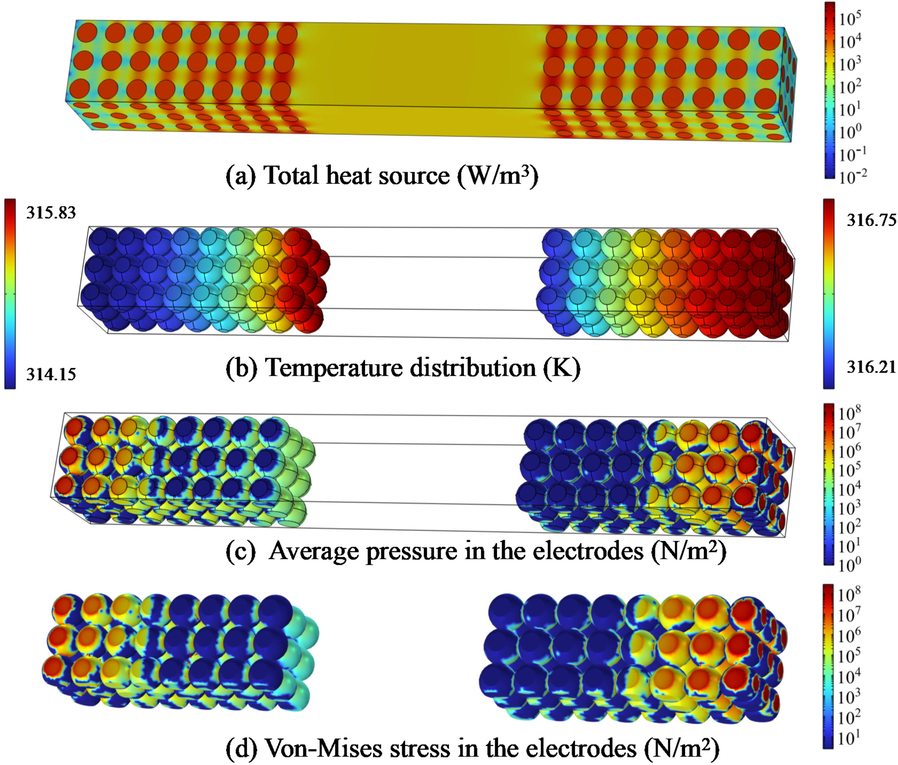
The distribution of thermal and mechanical parameters. (a) total heat resource; (b) temperature distribution; (c) average pressure; (d) Von-Mises stress.
4.4 Mechanical and yielding failure analysis during discharging
Stress analysis of electrodes can be done at two scales: battery structure and individual particles. Eq. (7) suggests that both temperature and lithium-ion concentration affect the deformation of the electrode. For the battery structure, the Von-Mises stress can intuitively indicate the location for easy yielding. That is, a ductile material begins yielding when the shape-changed ratio of a specific point reaches a critical value. Fig. 7(c) and Fig. 7(d) plot the average stress (average of maximum and minimum stress) and Von-Mises stress distribution. The yielding and failure are most likely to occur near the electrode current collector and the outer surface of the battery, where the boundary limits the electrode deformation.
For single particles, the force analysis of electrodes is based on the interaction between ion and electrode materials. The negative electrodes are mostly made of layered material, and the process of ionic uptake / removal causes expansion / contraction and inhomogeneous deformation. Lithium ions are transported to the positive electrode through the electrolyte and become a part of the positive electrode. This process is accompanied by the cathode material's phase transition, whose force analysis has more complicated material science and crystallographic principles. For simplicity, the model sets the reaction of lithium ions with electrodes as the intercalation / deintercalation principle. To further elucidate thermal-concentration coupling-induced stress, Fig. 8 combines of schematic diagrams and numerical graphs. Fig. 8(a) shows that the heat source generated by the electrodes and the electrolyte makes the temperature of the positive electrode slightly higher than that of the negative electrode. Since the temperature gradient inside the electrode particles is almost zero, the thermal stress at different particle points is almost unchanged, thus having little effect on the deformation. Fig. 8(b) depicts the change of lithium-ion concentration in anode particles and electrolytes under five different discharge times.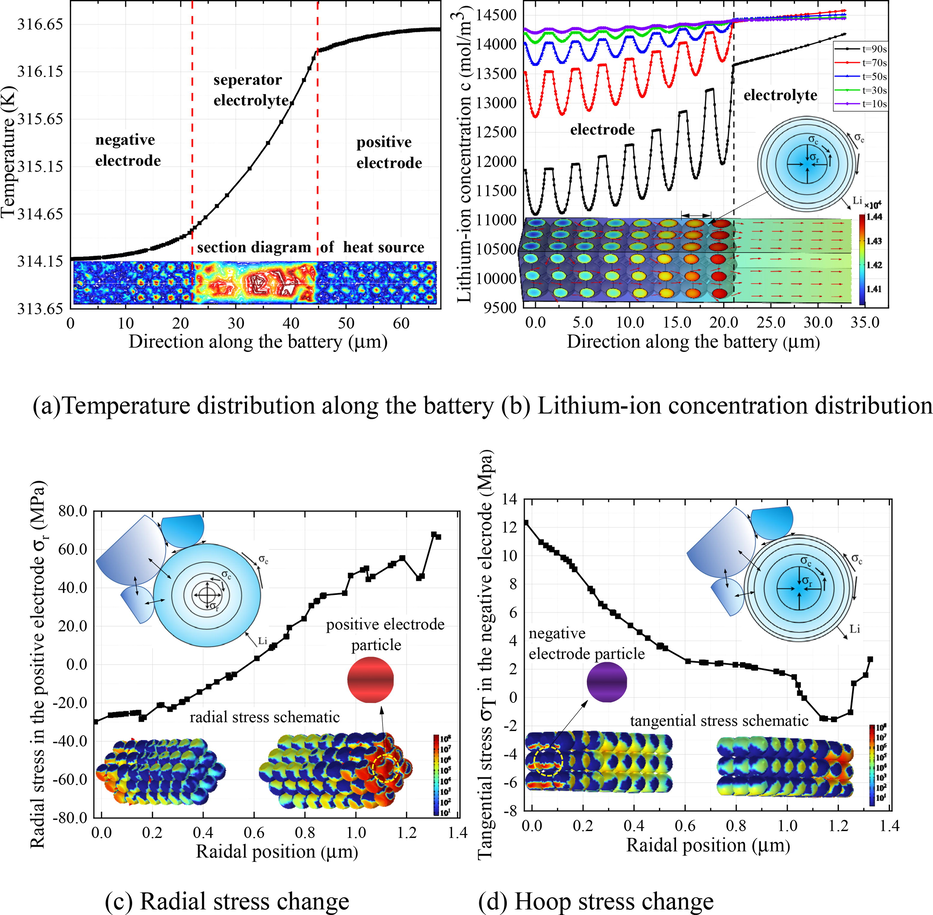
Thermal-concentration coupled stress diagram. (a) temperature distribution along the battery and cross-sectional view of heat source distribution; (b) lithium-ion concentration distribution in the negative electrode / electrolyte and ion flux map; (c) radial stress change in the positive electrode particle and the mechanics of the lithiation process; (d) hoop stress change in the negative electrode particle and the mechanics of the delithiation process.
In delithiation, lithium atoms inserted into the layered material lose electrons and diffuse toward the positive electrode through the electrolyte. In the particle, a lithium-ion concentration gradient is formed along the radial direction. Due to the deintercalation of ions, the intermolecular force in the negative electrode material is reduced and the space between the intercalation layers is reduced, which is macroscopically manifested as particle contraction. This contraction of spherical particles results in internal radial compressive stress (arrows pointing away from each other) and surficial hoop compressive stress. A zero-shear stress plane is where hoop tensile stress near the inner layer maintains equilibrium. The particles are subjected to radial compressive stress, where the outer surface is in contact with other particles. Fig. 8(c) depicts that Li-ion intercalation process of the positive particles (the reaction mechanism setting is the same as that of the anode) and radial pressure values. Similarly, lithium ions in lithiation diffuse from the positive electrode to the negative electrode and then combine with electrons to form lithium atoms and embedded in the layered material. Due to the intercalation of lithium atoms, the increase of the molecular force between the layered materials leads to a larger interlayer spacing, and the macroscopic manifestation is particle expansion. Mechanically, the intercalation process of lithium atoms creates a concentration gradient along the radial direction, with the outer layer having a higher concentration than the inner layer. The concentration gradient leads to internal radial tension stress (arrows pointing toward each other) and surficial hoop tensile stress. Fig. 8(d) depicts that Li-ion deintercalation process of the negative particles (the reaction mechanism setting is the same as that of the anode) and hoop stress value along the radius. The hoop tensile stress during expansion is the driving force of surficial fracture, while the radial compressive stress is beneficial to maintain structural stability.
4.5 Damage and fracture analysis during discharging
The hoop tensile stress is the driving force of particle fracture. In phase field theory, the elastic strain energy Ψ (ε, c, T, r) in the local tensile state of particles is the driving force of crack growth. The crack propagates when the Ψ affected by concentration and temperature exceeds the critical strain energy density Ψc. When Ψ gradually approaches the critical Ψc, φ grows from 0 to 1, representing the total crack. In the process of expansion and contraction, stress concentration exists in the cracks and defects inside particles, leading to the cracks' expansion and distribution. Fig. 9 shows the application of the phase field method in the electrode fracture problem. In Fig. 9(a), the elastic strain energy density of the electrode near the current collector is higher than that of the rest of the electrode. This result is consistent with the average pressure in Fig. 7(c). Due to the crack-driving effect of elastic strain energy, higher Ψ means more severe decay of material modulus and the more likely occurrence of fracture. Fig. 9(b) depicts the distribution of φ which is the same as the elastic strain energy density. When φ at one specific area reaches 1, that area cracks and exposes the crack surface. When φ is between 0 and 1, the modulus of the corresponding region is attenuated. Fig. 9 (c)(d) depict the material damage corresponding to the two sets of φ value.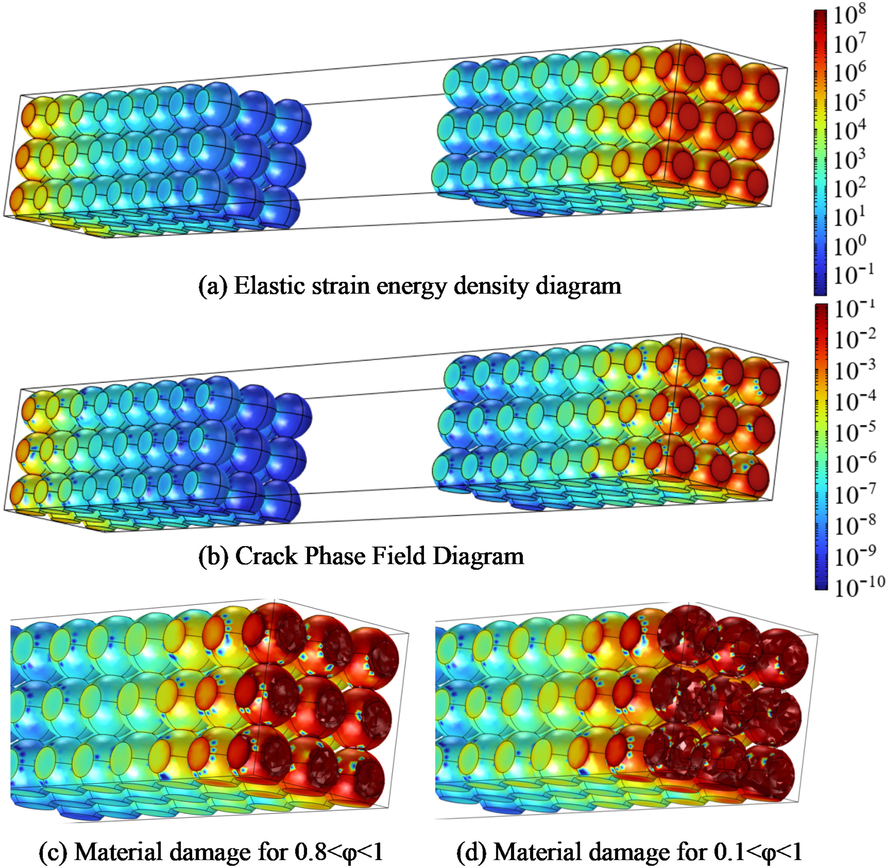
Phase field method in electrode fracture. (a) electrode elastic strain energy density distribution; (b) distribution of the phase field variable φ in the electrode; (c) the degree of material damage 0.8 < φ < 1; (d) the degree of material damage 0.1 < φ < 1.
Fig. 10 shows the distribution of phase variables along the radius of one specific positive particle. In the simulation, the elastic strain energy density Ψ (ε, c, T, r) coupled concentration and temperature does not reach the fracture threshold Ψc, reflected in Fig. 10(b), the phase variable φ does not reach 1. That means the operation causes material aging but does not induce material fracturing. This is related to the model scale. Further research should be based on a multi-scale battery model to more realistically calculate the fracture potential of the mosdel.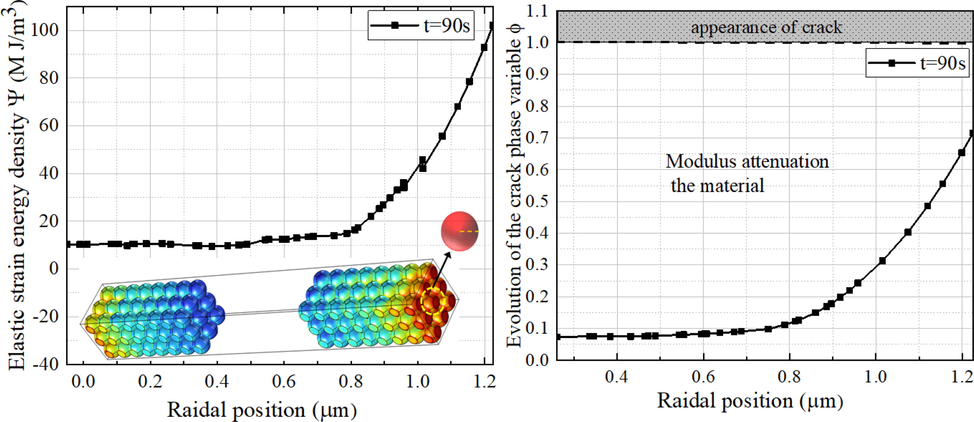
Distribution of phase field variables. (a) The distribution of elastic strain energy density in one particle; (b) The distribution of φ in one particle.
5 Conclusions
This study derived an analytical solution of stress in the spherical electrode particle based on coupled thermal-diffusion induced stress model. A battery structure model was constructed with electrodes, electrolytes and current collectors and a multiphysical coupling analysis was conducted for electrode aging and fracturing at both the structure and particle level. The model performance was numerically evaluated by the current distribution, ion diffusion, heat generation, stress distribution and electrode fracture during battery charge and discharge. A phase field fracture model was proposed for the thermal-electrochemical-mechanical coupling and an analytical solution for deformation and stress was obtained. For example, the positive, negative, and electrolyte materials were set to lithium cobaltite, graphite, and specific LiPF6 solution, respectively. The model was validated with experimental data available from the literature. Finally, heat generation, stress distribution and aging fracture were comparatively evaluated through numerical simulations. From these investigations, the following conclusions can be made:
First, more lithium ions are accumulated at the positive electrode during battery discharging. The heat release rate is higher at the positive electrode than at the negative electrode. The temperature of the positive electrode particles is higher than that of the negative electrode and the temperature of the electrode near the current collector is higher.
Second, the tensile stress on the particle surface is the driving force for fracturing during the lithium intercalation and expansion of the electrode. The stress of the electrode near the current collector can easily reach its peak, and thus the electrode is more prone to fracture. At small scales, the effect of thermal stress is not obvious.
Third, the elastic strain energy density of the electrode near the current collector is the highest and the material decay is the highest. The phase field fracture algorithm can conveniently simulate such a distribution and identify the potential risk location in a battery.
Acknowledgments
The authors are grateful for the National Key R&D Program of China (Grant No. 2022YFE0129100), the Natural Science Foundation of Jiangsu Province for the Youth Foundation (Grant No. BK20220232), the National Natural Science Foundation of China (Grant No. 52204113, 52174091, 51674246, 42174048), the Open Foundation of the Key Laboratory of Deep Earth Science and Engineering (Grant No. DESE 202205).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Electrochemical Thermal-Mechanical Modelling of Stress Inhomogeneity in Lithium-Ion Pouch Cells. J. Electrochem. Soc.. 2019;167
- [CrossRef] [Google Scholar]
- Endowing Griffith's fracture theory with the ability to describe fatigue cracks. Eng. Fract. Mech.. 2023;281
- [CrossRef] [Google Scholar]
- Three-dimensional experimental-scale phase-field modeling of dendrite formation in rechargeable lithium-metal batteries. J. Storage Mater.. 2023;62
- [CrossRef] [Google Scholar]
- Stochastic Analysis of Diffusion Induced Damage in Lithium-Ion Battery Electrodes. J. Electrochem. Soc.. 2013;160:A955-A967.
- [CrossRef] [Google Scholar]
- Cracking predictions of lithium-ion battery electrodes by X-ray computed tomography and modelling. J. Power Sources. 2022;526
- [CrossRef] [Google Scholar]
- C., Y., Wang, et al., 1998. Micro-macroscopic coupled modeling of batteries and fuel cells. Journal of the Electrochemical Society. 145, 3407-3417. https://10.1149/1.1838820.
- Evolution of stress within a spherical insertion electrode particle under potentiostatic and galvanostatic operation. J. Power Sources. 2009;190:453-460.
- [CrossRef] [Google Scholar]
- Modeling Diffusion-Induced Stress in Li-Ion Cells with Porous Electrodes. J. Electrochem. Soc.. 2010;157:A366-A380.
- [CrossRef] [Google Scholar]
- Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies. 2020;13:20.
- [CrossRef] [Google Scholar]
- Models for the Interplay of Mechanics, Electrochemistry, Thermodynamics, and Kinetics in Lithium-Ion Batteries. Appl. Mech. Rev.. 2023;75
- [CrossRef] [Google Scholar]
- A Review of Battery Thermal Management Methods for Electric Vehicles. Journalof Electrochemical Energy Conversion and Storage.. 2023;20
- [CrossRef] [Google Scholar]
- Research progress towards the corrosion and protection of electrodes in energy-storage batteries. Energy Storage Mater.. 2023;57:371-399.
- [CrossRef] [Google Scholar]
- A coupled electrochemical-thermal-mechanical model for spiral-wound Li-ion batteries. J. Mater. Sci.. 2018;53:10987-11001.
- [CrossRef] [Google Scholar]
- Aging estimation of lithium ion cells under real-world conditions through mechanical stress measurements. J. Storage Mater.. 2023;64
- [CrossRef] [Google Scholar]
- Revisiting brittle fracture as an energy minimization problem. J.mech.phys.solids.. 1998;46:1319-1342.
- [CrossRef] [Google Scholar]
- Influence of Electrode Parameters on the Performance Behavior of Lithium-Ion Battery. J. Electrochem. Energy Convers. Storage. 2023;20
- [CrossRef] [Google Scholar]
- Evolution of electrochemically induced stress and its effect on the lithium-storage performance of graphite electrode. Science China-Technological Sciences.. 2023;66:1784-1796.
- [CrossRef] [Google Scholar]
- Novel Na2TiSiO5 anode material for lithium ion batteries. Chem. Commun.. 2019;55:2234-2237.
- [CrossRef] [Google Scholar]
- Modeling Crack Growth during Li Extraction in Storage Particles Using a Fracture Phase Field Approach. J. Electrochem. Soc.. 2016;163:A102-A118.
- [CrossRef] [Google Scholar]
- Modeling crack growth during Li insertion in storage particles using a fracture phase field approach. J. Mech. Phys. Solids. 2016;92:313-344.
- [CrossRef] [Google Scholar]
- Lithium phosphorus oxynitride thin films for rechargeable lithium batteries: Applications from thin-film batteries as micro batteries to surface modification for large-scale batteries. Ceram. Int.. 2022;48:10372-10390.
- [CrossRef] [Google Scholar]
- Thermal Model for a Li-Ion Cell. J. Electrochem. Soc.. 2008;155:A164-A171.
- [CrossRef] [Google Scholar]
- Data-driven state-of-health estimation for lithium-ion battery based on aging features. Energy. 2023;274
- [CrossRef] [Google Scholar]
- Progressive Damage Analysis for Spherical Electrode Particles with Different Protective Structures for a Lithium-Ion Battery. ACS Omega 2023
- [CrossRef] [Google Scholar]
- Advances and Prospects in Improving the Utilization Efficiency of Lithium for High Energy Density Lithium Batteries. Adv. Funct. Mater. 2023
- [CrossRef] [Google Scholar]
- Overview on Theoretical Simulations of Lithium-Ion Batteries and Their Application to Battery Separators. Adv. Energy Mater.. 2023;13
- [CrossRef] [Google Scholar]
- Theoretical Analysis of Current Distribution in Porous Electrodes. J. Electrochem. Soc.. 1962;109:1183-1191.
- [CrossRef] [Google Scholar]
- Review on the numerical modeling of fracture in active materials for lithium ion batteries. J. Power Sources. 2023;566
- [CrossRef] [Google Scholar]
- Battery management strategies: An essential review for battery state of health monitoring techniques. J. Storage Mater.. 2022;51
- [CrossRef] [Google Scholar]
- Generation and Distribution of Dislocations by Solute Diffusion. J. Appl. Phys.. 1961;32:1876-1881.
- [CrossRef] [Google Scholar]
- Capacity Fading of Ni-Rich Li[NixCoyMn1–x–y]O2 (0.6 ≤ x ≤ 0.95) Cathodes for High-Energy-Density Lithium-Ion Batteries: Bulk or Surface Degradation? Chem. Mater.. 2018;30
- [CrossRef] [Google Scholar]
- Electrochemical-mechanical coupled modeling and parameterization of swelling and ionic transport in lithium-ion batteries. J. Power Sources. 2018;378:235-247.
- [CrossRef] [Google Scholar]
- Thermo-mechanical coupling analysis of a cylindrical lithium-ion battery with thermal radiation effect in generalized plane strain condition. Int. J. Energy Res.. 2021;45:1988-1998.
- [CrossRef] [Google Scholar]
- Timoshenko, S. P. and J. Gudyer, Elasticity theory.
- Dual confinement of carbon/TiO2 hollow shells enables improved lithium storage of Si nanoparticles. Electrochim. Acta. 2021;372
- [CrossRef] [Google Scholar]
- Exploring thermal hazard of lithium-ion batteries by bibliometric analysis. J. Storage Mater.. 2023;67
- [CrossRef] [Google Scholar]
- Dimensionless normalized concentration based thermal-electric regression model for the thermal runaway of lithium-ion batteries. J. Power Sources. 2022;521
- [CrossRef] [Google Scholar]
- Mechanical Modeling of Particles with Active Core-Shell Structures for Lithium-Ion Battery Electrodes. J. Phys. Chem. C. 2017;121:19022-19030.
- [CrossRef] [Google Scholar]
- Comprehensive investigation on Lithium batteries for electric and hybrid-electric unmanned aerial vehicle applications. Thermal Science and Engineering Progress.. 2023;38
- [CrossRef] [Google Scholar]
- Review of mechanical abuse related thermal runaway models of lithium-ion batteries at different scales. J. Storage Mater.. 2023;64
- [CrossRef] [Google Scholar]
- High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications. Energy & Environmental Materials 2023
- [CrossRef] [Google Scholar]
- Generalized Butler-Volmer relation on a curved electrode surface under the action of stress. Science China Physics, Mechanics & Astronomy. 2016
- [CrossRef] [Google Scholar]
- Effects of pressure, temperature, and plasticity on lithium dendrite growth in solid-state electrolytes. J. Solid State Electrochem. 2023
- [CrossRef] [Google Scholar]
- OCV-SOC-Temperature Relationship Construction and State of Charge Estimation for a Series-Parallel Lithium-Ion Battery Pack. IEEE Trans. Intell. Transp. Syst.. 2023;24:6362-6371.
- [CrossRef] [Google Scholar]
- Understanding of thermal runaway mechanism of LiFePO4 battery in-depth by three-level analysis. Appl. Energy. 2023;336
- [CrossRef] [Google Scholar]
- An Electrochemical-Mechanical Phase Field Model for Lithium Dendrite. J. Electrochem. Soc.. 2021;168
- [CrossRef] [Google Scholar]
- Multiscale modeling of the SEI of lithium-ion batteries. Energy Storage Science and Technology.. 2023;12:366-382.
- [CrossRef] [Google Scholar]
- Lithium-ion battery calendar aging mechanism analysis and impedance-based State-of-Health estimation method. J. Storage Mater.. 2023;64
- [CrossRef] [Google Scholar]
- Construction and simulation analysis of thermoelectric coupling model of lithium battery based on digital twin. Energy Storage Science and Technology.. 2023;12:536-543.
- [Google Scholar]
- Diffusion-aware voltage source: An equivalent circuit network to resolve lithium concentration gradients in active particles. Appl. Energy. 2023;339
- [CrossRef] [Google Scholar]







