Behaviour of electrical conductivity in CsI–Al₂O₃ and CsI–TiO₂ systems

1 Introduction

Composite electrolytes are multiphase (mostly two phase) solid systems in which two or more materials are mixed together to achieve some desirable material properties namely enhancement in the ionic conductivity at room temperature. Composite electrolytes are also called heterogeneously doped materials or dispersed solid electrolyte. Conductivity enhancement in two-phase composite systems was known for about many years (Jander, 1929). However, the research activity in this area gained impetus only after 1973, when Liang (1973) reported approximately 50 times enhancement in Li⁺ ion conductor at room temperature simply by dispersing ultrafine particle of inert Al₂O₃ in LiI. Since then a large number of two phase composite systems have been investigated with the conductivity enhancement of about one-third order of magnitude compared with those of constituent phases (Przluski et al., 1992; Wieczorek, 1992; Wagner, 1980; Poulsen, 1985). Two phase composite electrolyte systems were prepared in general, by dispersing semi micrometre size particles of insulating chemical inert materials (called second phase dispersoid) into a moderate-ionic conducting solid (called first phase host matrix). The conductivity increases with increasing dispersoid concentration, attains a peak value and then decreases. The peak is generally sharp, except for few systems, such as AgI–Al₂O₃ (Pack, 1979).

Further more, the conductivity maxima may be different in different composite systems and depend on the nature of the second phase dispersoid (Shahi and Wagner, 1982; Singh and Srivastava, 1992). Interface plays an important role for the transport properties of polycrystalline and polyphase (composite) materials. C. Wagner first used the space-charge layer concept to explain conductivity effects in the semiconducting two phase materials (Wagner, 1972). The importance of space-charge layer for the ionic conduction was first revealed by Liang (1973). After these initial studies, the conductivity enhancement in multiphase materials was confirmed for numerous ceramic composites, including dispersion of fine insulator particles in the ionic conductor matrix and mixture of two different ionic conductors, with a major contribution by Wagner (1989). In particular, the added oxides led to desirable mechanical properties and enhancement of ionic conductivity at room temperature (Mhiri and colomban, 1991; Uvarov et al., 1992, 1994; Ponomareva et al., 1994). He gave a quantitative description of the conductivity enhancement based on the concept of space-charge layer near the phase boundaries.

Heterogeneous doping has been employed to enhance the conductivity of solid electrolyte. In all cases the conductivity was found to go through a maximum as a function of concentration of the insulating component. It has been shown that if the particle size of the inert component is sufficiently small the heterogeneous doping causes a noticeable change in the bulk properties of the ionic salt. In particular new unusual phases of ionic salt were found in Li₂SO₄–Al₂O₃ (Chen et al., 1985) and RbNO₃–Al₂O₃ (Uvarov et al., 1996).

X-ray diffraction pattern of cesium iodide taken at room temperature up to the melting point gives no evidence of any transition from simple cubic to fcc structure in contrast to the cesium chloride where transition occurs at 469 °C and in cesium iodide at the melting point as a part of fusion process. The transition accompanied by the sharp decrease in conductivity is due to the mechanism of ionic transport and the presence of phase transition. When an aqueous solution of cesium iodide is evaporated slowly, the rhombic dodecahedral form (1 1 0) is obtained and at a high rate of evaporation, the cubic form (1 0 0) is obtained. CsI is strongly polarisable and has the CsCl-type lattice (Kern, 1952). We have used electrical conductivity measurements, XRD, DSC, to identify the existence of separate phases at CsI–Al₂O₃ and CsI–TiO₂ in the presence of high conducting space-charge region and interactions have also been suggested as the reason of conductivity enhancement in composite systems.

2 Experimental

CsI was used from sigma Aldrich with the stated purity of 99.9%. Alumina and titania were taken from BDH LABORATARY with a stated purity of 99.9%. Alumina and Titania were first ground for 2 h and mixed with acetone followed by drying at 150 °C for 3 h. The material was then ground again for an hour and sieved with 200 mesh. The required amounts of this material and CsI were mixed thoroughly using an agate motor and pestle to produce the series (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂, x = 0–0.7. These mixtures were then heated in an electrical furnace at 200 °C for 3 h with intermittent grinding. The final mixtures were crushed to fine powders and kept in glass tubes. X-ray diffractograms for the material were recorded using a “BRUKER ADVANCED D8” diffractometer with Cuka radiations. DSC traces were taken by heating in the temperature range 25–650 °C using a Perkin–Elmer instrument with Alumina powder as a reference. The heating rate was kept constant at 10 °C/min. Impedance spectroscopy was performed using a hightester HIOKI-353250 LCR METER in the frequency range 42 Hz–5 MHz for circular pellets pressed under 4 tonnes/cm² pressures. The two opposite surfaces of the pellet were coated with carbon paint and annealed between the electrodes for 2 h at 150 °C to increase the electrical connectivity between the samples and the electrodes. SEM micrographs were taken for the pelletized samples, and SEM was performed using “STEREO-SCAN 360”.

3 Result and discussion

3.1

3.1 X-ray-diffraction

X-ray diffractograms of the samples taken at room temperature are presented in Fig. 1a and b shows the presence of a prominent phase which is cubic CsI mixed with Al₂O₃ and TiO₂, respectively. The phase of CsI was confirmed by analysing the prominent peak using PDF#772185. X-ray Diffractograms of pure CsI and CsI doped with alumina did not show any characteristic peak associated with the alumina, indicating the two phases are completely mixed due to cubic phase nature of both CsI and alumina. Similar observations were made in NaCl–Al₂O₃, NaNO₃–Al₂O_3, KCl–Al₂O₃ and CsCl–Al₂O₃ solid electrolyte systems (Kumar and Shahi, 1992, 1994, 1996). However, in the case of CsI doped with titania, a new peak was observed which is attributed to anatase phase of titania. This has been observed to transfer to the rutile phase if titania is sintered at high temperatures or mixed with other impurities (Madhava Rao et al., 2005). It is worthy to mention that the strong X-ray absorbtion of CsI causes the intensities of alumina and titania to drop rapidly upon increasing the amount of CsI in the system.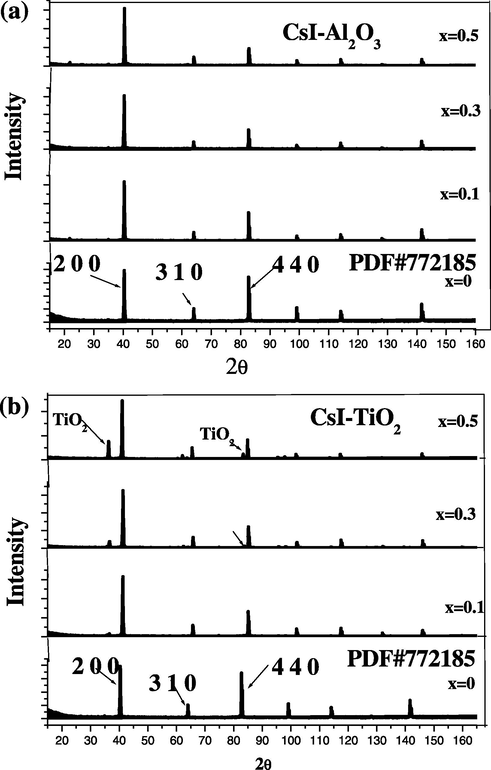

Close

Figure 1

(a and b) Room temperature X-ray diffractograms of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples.

Export to PPT

3.2

3.2 Differential scanning calorimetry

Fig. 2a and b shows the heating mode of DSC curve of the sample (pure CsI and CsI doped with different mole percent of alumina and titania) taken in the temperature range 25–650 °C. Pure cesium iodide does not give evidence of any transition and give its melting peak at 620 °C, whereas on increasing the amount of alumina (∼40%) a small hump appears towards the lower side of melting peak at about 257 °C indicating that the increase in the concentration of the dopant makes the transition shift towards the high temperature side. This peak attributed to interface-interaction between CsI and Al₂O₃. The increase in mole percent of alumina results in the growth of the hump and broadening of the melting peak there by slightly lowering the melting point. This hump could be due to the formation of an amorphous phase within the space-charge layer that is expected to form between the host material and the dispersoid particles (Madhava Rao et al., 2005). The mixture samples show no appreciable effect on the temperature of the phase transition as reported earlier in case of RbNO₃–Al₂O₃ (Uvarov et al., 1996), CsCl–Al₂O₃ (Uvarov et al., 1994), Cs₂H₃{(SO₄)₄–SO₂} (Lavrova et al., 2005) and TlI–TiO₂ (Sultana and Rafiuddin, 2009). In Fig. 2b, only melting peak of CsI was observed and titania does not show any phase transition.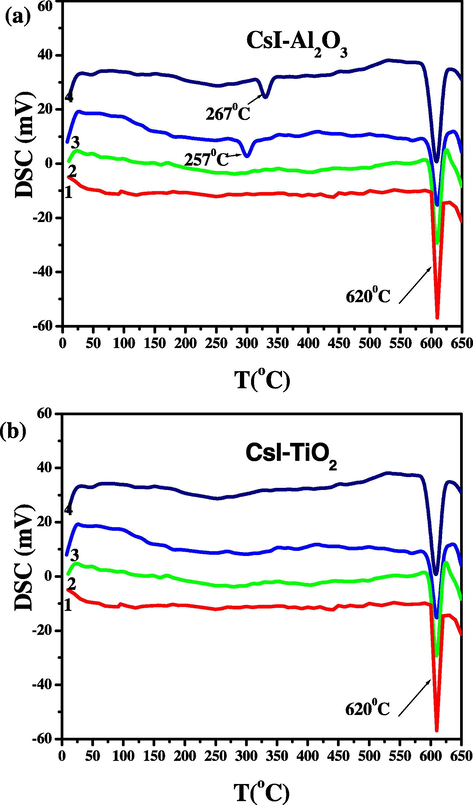

Close

Figure 2

(a and b) DSC curves of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples: (1) x = 0, (2) x = 0.1, (3) x = 0.3 and (4) x = 0.5.

Export to PPT

3.3

3.3 Scanning electron microscopy

Fig. 3a and b shows the SEM micrographs of two samples, the first is for pure titania after the process of its grinding with acetone and then sieving with 200 mesh. The micrograph shows reasonable homogeneity with average particle size in the range 200–400 nm. The second SEM micrograph is for the mixture contains 0.3 mol fraction of alumina and titania. It shows distribution of alumina and titania particles between the particles of cesium iodide which has higher average grain size. This distribution of alumina and titania layers between the grains of ionic salt is favoured from local thermodynamic equilibrium due to wetting of alumina and titania particles by CsI grains during the preparation of the mixture (Desvals and Knauth, 1997). This type of distribution is very important in creating a great number of surfaces which in turn act as additional sources of point defects. This new region between the ionic salt and the added oxide is called space-charge layer which strongly alters the bulk properties of the ionic salt (Uvarov and vanek, 2000). It is also clear that low density and a large number of pores are observed in the mixture sample. This is due to the two phase nature of the sample and the particle size difference between the salt and the added oxide.

Close

Figure 3

(a and b) SEM micrographs of (1 − x)CsI–xAl₂O₃ samples: (1) pure Al₂O₃ and (2) x = 0.3.

Export to PPT

3.4

3.4 Electrical conductivity

3.4.1

3.4.1 Impedance spectroscopy

AC impedance spectroscopy has become a powerful tool for the investigation of the ionic conductivity. Fig. 4a and b shows the impedance spectra of pure CsI and its mixture with alumina and titania. In this graph we plotted the imaginary impedance component (Z″) at each against the real impedance component (Z′) at each excitation frequency. It is observed that at high frequencies the impedance of the Randles cell was almost entirely created by the ohmic resistance. The frequency reaches its high limit at the left most end of the semicircle. It has been found that the idealized impedance plot of such material consists of a semicircle attributed to grain and grain boundary as well as low frequency inclined spike due to the ionic polarization and electrochemical reactions, occurring at the electrode interface (Dygas et al., 2005; Godinho et al., 2003).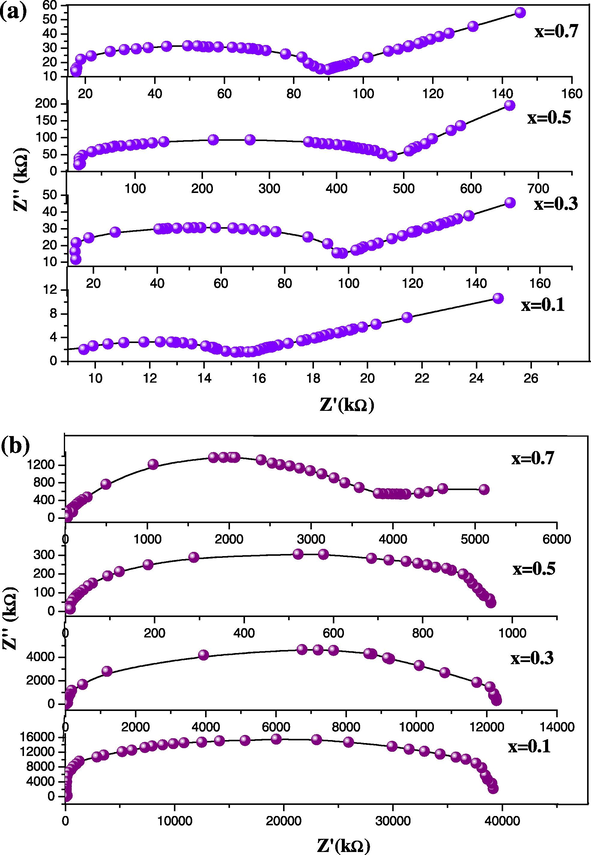

Close

Figure 4

(a and b) Impedance spectra of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples.

Export to PPT

It is well known that the complex impedance (Z^∗(ω)) is defined as the sum of its real (Z″) and imaginary part:

(1)

$$(Z^{\ast }(\omega )=Z^{\prime }+{\mathit{jZ}}^{″}\text{;}j=\sqrt{-1})$$ For our modeled equivalent circuit, Z″ and Z′ are given as follows:

(2)

$$Z^{\prime }=\frac{R_g}{1+{\omega }_g^2{C}_g^2{R}_g^2}$$

(3)

$$Z^{″}=\frac{R_g^2{\omega }_g{C}_g}{1+{\omega }_g^2{C}_g^2{R}_g^2}$$ where the resistance of grain (R_g)can be directly obtained from the intercept of the Z′-axis (Kezionis et al., 1999). The angular frequency of grain (ω_g) is obtained at the maxima of the semicircles.

3.4.2

3.4.2 Conductivity

Figs. 5a and b illustrates the behaviour of conductivity with the composition of the system at different temperatures. The conductivity increases with the alumina and titania content in the materials and passes through a threshold value after which it starts to decrease with further increase in the mole fraction of alumina and titania. This threshold value estimated from Fig. 5a and b is found to be x = 0.3 (i.e., 30%). The enhancement of ionic conductivity in these types of materials is observed for two reasons; first, the interface region itself is a disordered region where defect formation and migration enthalpies are notably reduced. This leads to the enhancement of ionic conductivity within the interface region (grain boundary diffusion), and second, the disordered region induces concentration profiles of point defect in the region adjacent to the interface in the ionic material (space-charge layers) (Knauth, 2000) These two factors lead to the enhancement of ionic conductivity with increasing amount of dispersoid alumina and titania in the material.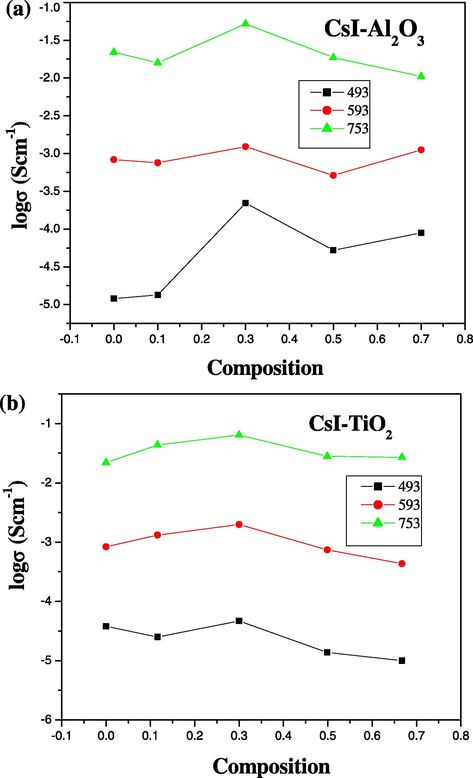

Close

Figure 5

(a and b) Electrical conductivity as a function of composition of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples at different temperatures.

Export to PPT

Fig. 6a and b shows the variation of conductivity as a function of concentration (mole percent) of Al₂O₃ and TiO₂ at different temperatures. The result shows that the maximum enhancement of conductivity occurred at 30% in both cases, thereafter the conductivity shows a remarkable drop (similar results were obtained from Fig. 5). This is because, when the concentration of the dispersoid exceeds the threshold value in the system (x = 0.3), blocking of conduction pathways by the alumina and titania particles was observed leading to a fall in conductivity (Uvarov et al., 1994). CsI is the Schottky disordered material in which anion vacancies are mobile than the cation vacancies. However, very little enhancement is observed due to the addition of alumina and in any case the maximum enhancement is observed at x < 0.4 alumina.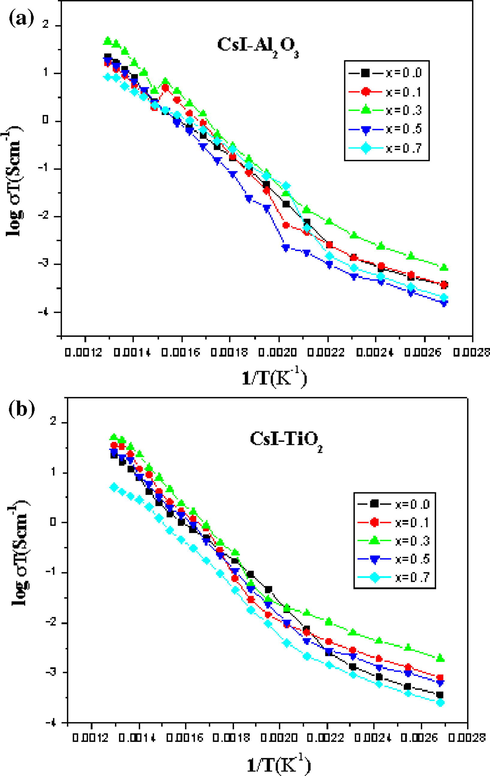

Close

Figure 6

(a and b) Electrical conductivity as a function of temperature at different composition of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples.

Export to PPT

A continuous increase in the contribution of grain boundary to the total resistivity of the samples is also observed with increasing the content of alumina and titania in the system. This is due to the increase in the phase boundary as has been seen in SEM micrographs above. CsI have a bcc crystal structure but in the case of CsCl the sharp fall in conductance occurs at the transition bcc-fcc. CsI shows a similar increase in activation energy on approaching the melting point.

The temperature dependence of ionic conductivity is given by the Arrhenius expression,

(4)

$$\sigma T={\sigma }_0\exp \left(\frac{-E_a}{\mathit{kT}}\right)$$ where σ₀ is the pre-exponential factor and E_a is the activation energy of ionic motion. The conductivity data in Fig. 6b were fitted well to the above equation to obtain the activation energy values of conduction. As it is shown, two regions are observed in the samples containing alumina and titania up to x ⩽ 0.3 after which the abrupt change in the conductivity disappeared and the curves tend to be straightened along the whole temperature region under study (Fig. 6a and b). The activation energies in the temperature range 100–500 °C were calculated using Line fittings and tabulated in Table 1. These values followed the opposite trend of ionic conductivity with composition, i.e. as the conductivity increases the activation energy decreases. The activation energy for pure CsI is calculated as 0.714 eV which is in good agreement found in value in another work (Hartmonova et al., 1981). Generally, conductivity enhancement in composites is most probably caused by a large increase in the point defect concentration inside the solid electrolyte after its heterogeneous doping with a dispersed additive. Such an increase might have been caused by different factors characteristic of each particular composite.

Table 1 Activation energies of conduction in the temperature range 100–500 °C of (1 − x)CsI–xAl₂O₃ and (1 − x)CsI–xTiO₂ samples.

Mole fraction	Activation energy (eV) Al2O3	Activation energy (eV) TiO2
0	0.714	0.714
0.1	0.721	0.715
0.3	0.713	0.677
0.5	0.785	0.706
0.7	0.720	0.670

According to the Maier’s space-charge model (Maier, 1995) the solid electrolyte is enriched with defects in the interface space-charge region, especially if the surface interaction between the phases of a composite takes place. Space-charge layers that are formed around dislocations and inner intergrain boundaries of the solid electrolyte (Dudney, 1988, 1989), also give rise to the point defect concentration. The space-charge model is applicable for many systems where the crystal structure and thermodynamic parameters of the ionic component do not change markedly after its heterogeneous doping. However, it is not the case in all composites. Thermodynamic properties of both the components in AgI–Al₂O₃ (Chen, 1986) differ from those of pure substances, silver iodide being likely in amorphous state (Uvarov et al., 1990).

4 Conclusion

Electrical conductivity has enhanced and activation energy of conduction has decreased remarkably in the systems CsI–Al₂O₃ and CsI–TiO₂ compared to the pure CsI. The highest ionic conductivity was observed in both the systems at x = 0.3 mol fraction of dispersoid (alumina and titania). XRD and DSC ruled out the formation of solid solutions between the host material and the dispersoid. The experimental data indicating higher conductivity in dispersed system are interpreted in terms of the formation of space-charge layer between the host material and the dispersoid in which defect concentration increases and that is believed to be the possible mechanism of conductivity enhancement. The material is found to be in a binary phase system with alumina and titania particles distributed between the grains of cesium iodide. The enhancement of electrical conductivity in comparison with pure cesium iodide can be interpreted with the space-charge layer model. The behaviour is explained in terms of disordering phenomena at interface regions and space-charge layers formed in the bulk grains of cesium iodide.