Translate this page into:
Computational study on the encapsulation of glucosamine anomers by cucurbit[6]uril and cucurbit[8]uril in aqueous solution
⁎Corresponding authors. musab@hu.edu.jo (Musa I. El-Barghouthi), Khaleel.assaf@bau.edu.jo (Khaleel I. Assaf)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Recently, we have investigated the cucurbit[7]uril (CB7) recognition of the α- and β-anomers of neutral, protonated, and acetylated forms of glucosamine in water. In the present work, we employed molecular dynamics (MD) and thermodynamic integration methods (TI) to investigate the recognition of these molecules by cucurbit[6]uril (CB6) and cucurbit[8]uril (CB8). MD revealed the formation of stable 1:1 inclusion complexes by all studied molecules with cucurbit[n]urils (CBn), and 2:1 complex by the α-anomer of the acetylated form of glucosamine with the large homologue CB8. CB6 forms roughly twice as many hydrogen bonds with the guest molecules as CB8. MM-PBSA results indicated that the electrostatic contribution to the binding free energy of each guest:CB complex was larger for CB6 than for CB8, and that CB6 and CB8 have lower affinity toward the different forms of glucosamine compared to CB7. Furthermore, TI was used to estimate the relative affinities of CB6 and CB8 toward the α- and β-anomers for each form of the studied glucosamine and compare with CB7.
Keywords
Cucurbiturils
Glucosamine
Molecular Dynamics
Thermodynamic Integration
MM-PBSA
1 Introduction
The molecular recognition of saccharides by synthetic receptors, mimicking their complexation with proteins, has potential applications in drug sensing and delivery (Arnaud, Audfray, & Imberty, 2013; Mazik, 2012; Davis, 2020). The hydrophilic nature of saccharides complicates their recognition in water. Boronic acid derivatives represent the most promising receptors for carbohydrates, via covalent bonding (Striegler, 2003; Williams, Kedge, & Fossey, 2021). Other synthetic receptors prepared for selective recognition of saccharides showed weak to modest binding affinities (Ferrand et al., 2009; Francesconi, Gentili, & Roelens, 2012; Klein, Ferrand, Auty, & Davis, 2007; Mazik, Cavga, & Jones, 2005; Palanichamy et al., 2018).
Glucosamine, a naturally occurring amino monosaccharide, is present in the connective and cartilage tissues, and plays an essential role in maintaining their strength, flexibility and elasticity (Matheson & Perry, 2003). It is also a prominent precursor in the biochemical synthesis of glycosylated proteins and lipids, and is part of the structure of two polysaccharides, chitosan and chitin (Lopes, Tanabe, & Bertuol, 2020). The molecular recognition of glucosamine by organic receptors has been limited to those operating based multi-hydrogen bonding interactions, and mostly functioning in organic solvents (Tamaru, Yamamoto, Shinkai, Khasanov, & Bell, 2001).
Recently, cucurbit[n]urils (CBn, Fig. 1) have emerged as molecular receptors for saccharides, despite their hydrophobic cavity (Bodoor, El-Barghouthi, Alhamed, Assaf, & Alrawashdeh, 2022; Jang, Natarajan, Ko, & Kim, 2014; Lee & Kim, 2018; Lee et al., 2016; Yin and Wang, 2018). CBn are a class of water soluble macrocyclic hosts that are capable of forming stable host–guest complexes with a variety of guest molecules through noncovalent interactions, such as hydrogen bonding, dipole–dipole, ion–dipole and dispersion interactions (Assaf & Nau, 2015; Barrow, Kasera, Rowland, del Barrio, & Scherman, 2015; Masson, Ling, Joseph, Kyeremeh-Mensah, & Lu, 2012). In addition, their hydrophobic cavity acts as a microenvironment for hydrophobic moieties (Assaf et al., 2017; Assaf & Nau, 2015; Florea & Nau, 2011). In 2014, Jang et al. found that CB7 binds amino saccharides (in their protonated states) in aqueous solution with exceptional affinity (Ka > 103 M−1), and their 1H NMR experiments indicated that they are encapsulated inside the hydrophobic cavity of CB7 (Jang et al., 2014). Other studies showed that CB7 preferentially binds the α-anomer of D-glucosamine hydrochloride,(Mazik et al., 2005) which was further supported by single-crystal structure analysis (Wang et al., 2016). Furthermore, quantum mechanical calculations and molecular dynamics simulations carried out in gas phase and water indicated, respectively, preferential binding of CB7 to the β- and α-anomer; the latter agrees with experiment and indicates the importance of solvation effects (Wang et al., 2016).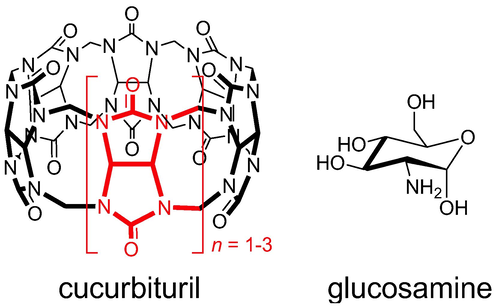
Chemical structure of cucurbiturils (glycoluril repeating unit are highlighted in red) and glucosamine.
Recently, we studied the host–guest complexation between CB7 and the α- and β-anomers of glucosamine in its neutral (GN), protonated (GP), and acetylated (GA) forms (Bodoor et al., 2022). Fluorescence dye displacement titrations were used to determine the binding affinities in aqueous solution, which revealed higher binding for the protonated glucosamine over the neutral and acetylated forms. Molecular dynamics simulations confirmed the formation of inclusion complexes with CB7, and MM-PBSA analysis showed that CB7 preferentially binds the β-anomers of the protonated and acetylated glucosamine over the α-anomers, and the α-anomer of the neutral form of glucosamine. In addition, thermodynamic integration analysis indicated that CB7 binds the α-anomers of neutral and acetylated glucosamine with higher affinity, while the opposite is true for the protonated form.
Herein, we extend our previous work(Bodoor et al., 2022) to study the complexation of α- and β-anomers of glucosamine (protonated and neutral) and its acetylated derivative with smaller and larger CBn homologues (CB6 and CB8) using molecular dynamics (MD) simulations and thermodynamic integration (TI). Our initial evaluation of the formation of host–guest complexes between GA (in its protonated form) and CB6/CB8 in aqueous solution was obtained based on dye displacement experiments, which indicated that GA can form supramolecular complexes with both hosts, however, with lower binding affinity compared to CB7.
2 Computational methods
MD simulations were carried out with AMBER 16.0 program,(Case, 2016) using GLYCAM06 force field(Kirschner et al., 2008) for glucosamine and General Amber Force Field parameters(Junmei Wang, Wolf, Caldwell, Kollman, & Case, 2004) for the host molecules. The restrained electrostatic potential (RESP) charges(Bayly, Cieplak, Cornell, & Kollman, 1993) were used for CBn, with their initial structures obtained from published X-ray(Freeman, Mock, & Shih, 1981; Kim et al., 2000). TIP3P water model(Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983) was used for solvation of each system with a spacing of 12 Å. Each system was equilibrated for 20 ns followed by 100 ns production run at 298.15 K and 1 atm. More details on the MD protocol can be found in our recent work(Bodoor et al., 2022). MM-PBSA(Homeyer & Gohlke, 2012; Miller et al., 2012) method was employed to estimate the binding free energies using a procedure described elsewhere(Dadou, El-Barghouthi, Antonijevic, Chowdhry, & Badwan, 2020; El-Barghouthi, Abdel-Halim, Haj-Ibrahim, & Assaf, 2015; El-Barghouthi, Abdel-Halim, Haj-Ibrahim, Bodoor, & Assaf, 2015; Malhis, Bodoor, Assaf, Al-Sakhen, & El-Barghouthi, 2015). Thermodynamic integration (TI) was performed based on the thermodynamic cycle shown in Scheme 1. A total of 11 values of the coupling parameter, λ, were used. Simulations were carried out for each λ, using 500 ps and 5 ns for equilibration and production, respectively. TI calculations were carried out via three steps: decharging of the H1C1O1H moiety of the α-anomer (ΔG1); mutarotation of the O1H from α- to β-anomer (ΔG2), applying soft-core potentials(Beutler, Mark, van Schaik, Gerber, & van Gunsteren, 1994); and recharging of the H1C1O1H moiety of the β-anomer (ΔG3).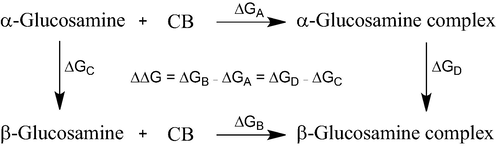
The TI cycle used in this work.
3 Results and discussion
100-ns MD simulations were conducted for the α- and β- anomers of the studied glucosamines complexes with CB6 and CB8. The computed average structures of the 1:1 complexes (Fig. 2) revealed that all molecules were encapsulated within CB6 and CB8 for the whole duration of the simulations, with some guest molecules exhibiting distorted structures. Several dihedral angles were monitored to get a better picture of the fluctuations of the structures of glucosamines during the simulations, and the data for the O1-C1-O5-C5 dihedral angle are shown in Figure S1 (Supplementary Material). During the simulations, glucosamines adopt the 4C1 conformation in the free and bound states, except for β-GN and β-GP in their complexes with CB6 cavity, in which they adopted roughly boat conformations, with the O1H group forming intramolecular hydrogen bond (HB) with O6H group (Figure S2). The complex of β-GA with CB8 showed ring distortion in 9.0% of the sampled snapshots. Unlike its complexes with CB7, no ring-flipping occurred from 4C1 to 1C4 conformation in the complexes of β-GA with CB6 and CB8(Bodoor et al., 2022).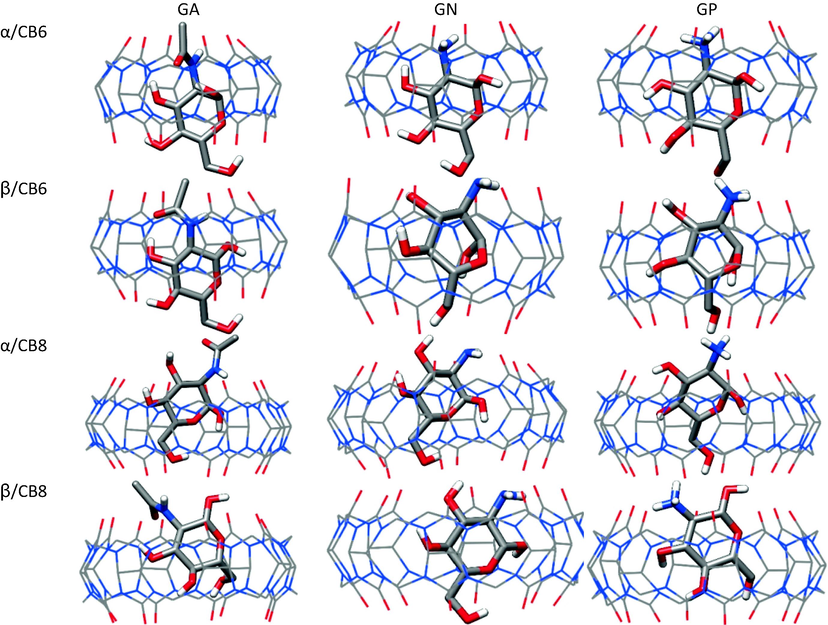
Average structures of the CB6 and CB8 complexes with glucosamines.
The distances during the simulation of O1H and O3H groups from the upper carbonyl portal are shown in Figs. 3 and 4. The two groups in CB6 complexes were encapsulated, except for O3H in β-GN and β-GP complexes, where it remained near the portal, probably due to ring distortion. For CB8 complexes, O1H in α-GA and α-GP was included, but not as deeply as in CB6 complexes; whereas it fluctuated above and below the portal in the remaining complexes. The O3H in CB8 complexes appeared to be excluded/included when O1H is included/excluded.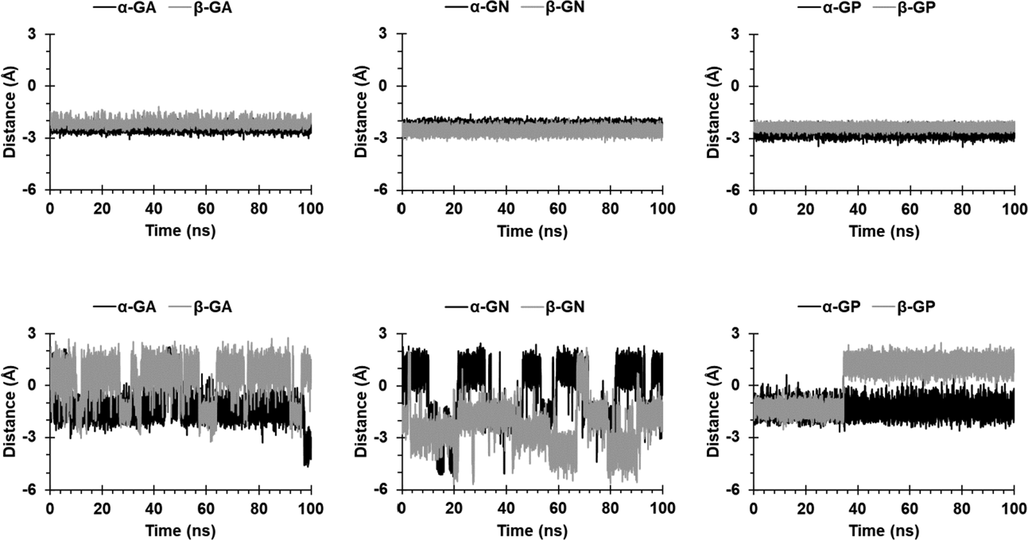
Distance between the O1H group and the upper carbonyl portals of CB6 (first row) and CB8 (second row).
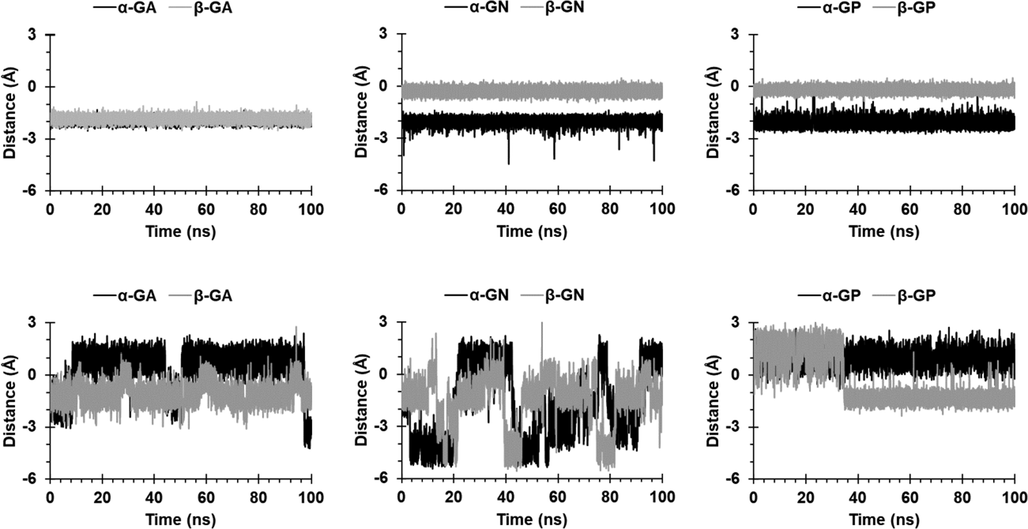
Distance between the O3H group and the upper carbonyl portals of CB6 (first row) and CB8 (second row).
Fig. 5 displays the probability distribution curves for the distances between the centers of mass of the host and the glucose ring, which revealed limited guest movement within the cavity in the case of CB6 compared to CB8, which is expected due to the smaller cavity size of the CB6.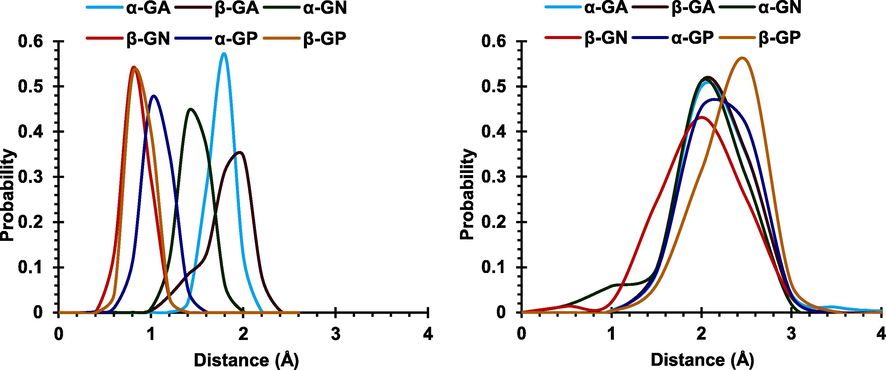
Probability distribution curves for the distances between the centers of mass of CB6 (left) and CB8 (right) and the glucose ring in each guest.
Fig. 6 displays positions of the nitrogen atom in the studied complexes as extracted from snapshots at 100 ps intervals, revealing for CB6 complexes limited movement of the nitrogen atom for α- and β- anomers, with the nitrogen atom sampling positions similar to those in the corresponding average structures. The observed lack of rotational symmetry for α-GA and β-GA around the axis of CB6 may be due to the strong hydrogen bonds formed between the NH group with the nitrogen atoms in CB6 (discussed below). Guests in CB8 complexes exhibited larger freedom within the cavity, with approximate rotational symmetry around the axis of CB8. The neutral glucosamine appeared to undergo flipping within the cavity, switching the position of the amine group from near the upper to near the lower carbonyl portal during the simulation.
Top and side views of the positions of the nitrogen atom in the studied complexes with CB6 (first and second rows) and CB8 (third and fourth rows).
The average numbers of host–guest, guest-water, and host-water intermolecular hydrogen bonds (HBs) are shown in Table 1. Upon complexation, a reduction of ∼ 8 and ∼ 4 in the guest-water HBs and ∼ 4–6 and ∼ 2–3 in the host-water HBs was observed for CB6 and CB8, respectively. CB8 complexes retained ∼ 3 water molecules within the CB8 cavity, while CB6 retained none; this explained the greater loss of guest-water HBs in the case of CB6. The total numbers of HBs for CB6 and CB8 complexes were ∼ 3.3–4.7 and ∼ 1.5–2.2, respectively; the smaller number in the case of CB8 is due to the larger donor–acceptor distances. The amine group and the hydroxyl groups significantly contribute to the HB network in both host molecules. As shown in Table 1, the O1H group in CB6 complexes, which is encapsulated within CB6, formed HBs with the nitrogen atoms of CB6. Table 2 shows that free guest intramolecular HBs were insignificant, but became substantial when included in CB6, possibly due to the large extent of desolvation of the guest (and ring distortion in β-GN and β-GP). The presence of water molecules in the cavity of CB8 in the bound states interfered with the process of forming intramolecular HBs, explaining the smaller increase compared to CB6.
Guest-Host
HBs with water
O1H
NH
O3H
O4H
O6H
Total
Bound
Free Guestb
Guest
CB
CB6
α-GA
0.01
1.01
0.22
1.10
0.99
3.33
2.41
12.42
10.55
β-GA
1.26
0.27
0.21
1.11
1.06
3.91
2.48
12.49
10.87
α-GN
1.06
0.85
0.26
1.12
0.88
4.17
1.04
12.67
10.52
β-GN
0.01
2.29
0.51
0.88
0.51
4.20
2.26
13.35
10.53
α-GP
1.13
2.03
0.90
0.32
0.29
4.67
1.80
10.95
9.60
β-GP
0.01
2.22
0.86
1.01
0.35
4.45
1.91
10.68
9.60
CB8
α-GA
0.12
0.29
0.22
0.51
0.32
1.46
5.68
20.30
β-GA
0.65
0.63
0.41
0.29
0.17
2.15
5.41
20.13
α-GN
0.22
1.00
0.19
0.30
0.32
2.03
6.28
19.57
β-GN
0.31
1.03
0.21
0.27
0.23
2.05
6.31
19.68
α-GP
0.00
0.91
0.62
0.27
0.27
2.07
5.84
18.88
β-GP
0.05
1.29
0.06
0.30
0.04
1.74
6.32
19.07
α-GA
β-GA
α-GN
β-GN
α-GP
β-GP
Free
0.06
0.04
0.06
0.04
0.01
0.02
CB6
1.16
1.07
0.38
1.13
0.60
1.06
CB8
0.30
0.17
0.13
0.06
0.10
0.01
Table 3 shows that electrostatic (ΔEELE) and van der Waals (ΔEvdW) interactions contribute favourably to complex stability. For GP complexes, ΔEELE ≫ ΔEvdW due to ion–dipole forces in the cationic guest complexes, whereas the opposite was seen for the neutral guests. Aside from GP, CB6 complexes exhibited larger electrostatic interactions compared to the CB8 complexes, while the difference in ΔEvdW values was not significant. The non-polar solvation free energy (ΔGNP) was favorable, and more or less close in values for all complexes due to the similarity in size among the studied guest molecules. The solvation energy (ΔGsolv = ΔGNP + ΔGPB) was found to be unfavourable for all complexes, due to the desolvation of the hydrophilic guest upon complexation. The ΔGsolv values for CB8 complexes with GA and GN were much lower than CB6 complexes and this is expected, due to lower values of ΔEELE in CB8 complexes. Table 3 indicates that a strong preference of CB6 for α-GA over its β-GA (ΔΔG = 5.8 kcal mol−1), while the opposite is seen in the case of CB8. β-GP seems to interact more favourably with CB6 and CB8 than α-GP. The small difference in ΔΔG between GN anomers (∼0.5 and 0.0 kcal mol−1 for CB6 and CB8, respectively) indicates that the anomeric state of GN has no significant effect on its affinity toward CB6 or CB8. Fig. 7 shows the binding free energies of the studied glucosamines with CB6, CB7 (computed previously(Bodoor et al., 2022)) and CB8, which shows that CB7 has the highest affinity toward the different forms of glucosamine; the trend can be understood in term of size complementarity. ΔEELE and ΔEVDW: electrostatic and van der Waals energies as calculated from the MM force field; ΔGNP: non-polar contribution to the solvation free energy; ΔGPB: electrostatic contribution to the solvation free energy; ΔGSOLV: sum of non-polar and polar contributions to solvation (ΔGNP + ΔGPB); ΔG: estimated binding free energy as sum of the ΔEELE, ΔEVDW and ΔGSOLV.
ΔEELE
ΔEvdW
ΔGNP
ΔGPB
ΔGSOLV
ΔG
CB6
α-GA
−20.7
−27.3
−3.3
35.5
32.2
−15.8
β-GA
−16.0
−22.5
−3.4
31.9
28.5
−10.0
α-GN
−11.9
−24.1
−2.9
24.4
21.4
−14.6
β-GN
−17.1
−22.5
−3.0
28.4
25.5
−14.1
α-GP
−66.6
−22.7
−3.0
81.7
78.8
−10.5
β-GP
−77.5
−19.5
−3.0
84.6
81.6
−15.4
CB8
α-GA
−7.2
−25.7
−3.3
22.1
18.9
−14.0
β-GA
−8.6
−27.2
−3.3
22.5
19.2
−16.6
α-GN
−8.7
−24.2
−3.1
20.9
17.8
−15.1
β-GN
−8.6
−24.7
−3.1
21.3
18.2
−15.1
α-GP
−65.1
−22.0
−3.1
75.9
72.8
−14.3
β-GP
−67.0
−22.9
−3.1
77.4
74.3
−15.6
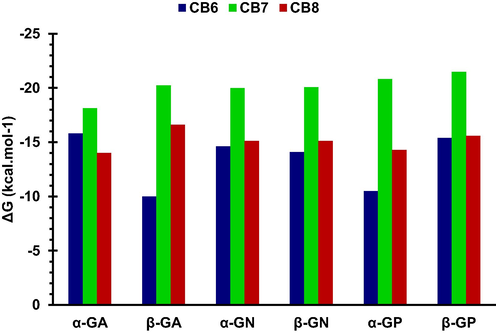
The binding free energies (ΔG) of the studied glucosamines with CB6, CB7, and CB8.
TI was performed to obtain better estimates of the relative free energies of binding (ΔΔG = ΔGβ − ΔGα) than those obtained from the MM-PBSA method. The thermodynamic cycle employed is shown in Scheme 1 and the results are listed in Tables 4 and Table S1-2, as well as Fig. 8. CB6 was found to preferentially bind to β-GA and α-GP anomers, with only a slight preference for α-GN. CB8 showed a clear preference only for α-GN. Our previous results for CB7 showed its preference for α-anomers of GA and GN. ΔΔGvdW for the α → β mutation was unfavorable(Bodoor et al., 2022), with the values for complexes of GN and GA with CB6 higher by ∼ 2 and ∼ 4 kcal mol−1, respectively, than for CB8 complexes. As shown in Table 4, ΔΔGELE was more significant for CB6 complexes.
Mutation
ΔΔGvdW
ΔΔGELE
ΔΔG
α-GA → β-GA
CB6
5.15
−7.85
−2.69
CB8
0.93
−0.26
0.69
α-GN → β-GN
CB6
4.05
−4.57
0.52
CB8
2.01
1.80
1.61
α-GP → β-GP
CB6
0.13
2.32
2.64
CB8
0.42
−0.53
−0.11
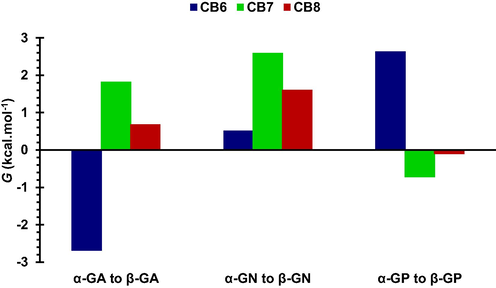
Relative binding free energies for CB6, CB7 and CB8 complexes.
We further performed MD simulations to investigate the formation of 2:1 complexes of glucosamines with CB8, which is known to form ternary host–guest complexes, using two initial relative orientations of the two guests within the cavity of CB8 (parallel and anti-parallel). The MD results revealed that only α-GA ternary complex was stable (for both orientations), while the rest of the complexes dissociated to 1:1 complexes and free guests. The average structure with the anti-parallel orientation revealed both guests were encapsulated and interacted via HBs (Fig. 9). For the parallel orientation, the average structure exhibited full encapsulation and partial for the other. MM-PSA results indicated that free energies of binding were − 32.0 and − 37.1 kcal mol−1 for the parallel and anti-parallel orientations, respectively.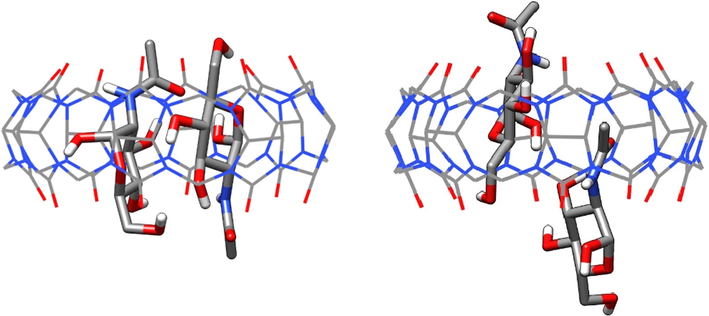
Average structures for 2:1 α-GA/CB8 complexes; anti-parallel (left) and parallel (right) orientations.
4 Conclusion
We used MD and TI to investigate the encapsulation of the α- and β- anomers of neutral, protonated, and acetylated forms of glucosamine with CB6 and CB8, extending our previous work with CB7. MD simulations revealed the formation by all forms of glucosamine of stable 1:1 complexes with CB6 and CB8 in water, and the formation of 2:1 complex with CB8 only for the α-anomer of the acetylated form of glucosamine. MM-PBSA estimates of the electrostatic and van der Waals contributions to the binding free energies were favourable, with the former making the largest contribution in the case of protonated-glucosamine. Furthermore, MM-PBSA revealed that CB6 and CB8 had lower affinities for glucosamine than CB7. Finally, TI calculations were used to compare the selective recognition by the CBs toward the α- and β- anomers for each form of studied glucosamine.
Acknowledgment
The authors wish to acknowledge financial support from the Hashemite University.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Binding sugars: from natural lectins to synthetic receptors and engineered neolectins. Chem. Soc. Rev.. 2013;42(11):4798-4813.
- [CrossRef] [Google Scholar]
- HYDROPHOBE challenge: a joint experimental and computational study on the host–guest binding of hydrocarbons to cucurbiturils, allowing explicit evaluation of guest hydration free-energy contributions. J. Phys. Chem. B. 2017;121(49):11144-11162.
- [CrossRef] [Google Scholar]
- Cucurbiturils: from synthesis to high-affinity binding and catalysis. Chem. Soc. Rev.. 2015;44(2):394-418.
- [CrossRef] [Google Scholar]
- Cucurbituril-based molecular recognition. Chem. Rev.. 2015;115(22):12320-12406.
- [CrossRef] [Google Scholar]
- A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem.. 1993;97(40):10269-10280.
- [CrossRef] [Google Scholar]
- Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett.. 1994;222(6):529-539.
- [CrossRef] [Google Scholar]
- Cucurbit[7]uril recognition of glucosamine anomers in water. J. Mol. Liq.. 2022;358:119178
- [CrossRef] [Google Scholar]
- Case, D. A., Betz, R. M., Cerutti, D. S., Cheatham III, T. E., Darden, T. A., Duke, R. E., Giese, T. J., Gohlke, H., Goetz, A. W., Homeyer, N., Izadi, S., Janowski, P., Kaus, J., Kovalenko, A., Lee, T. S., LeGrand, S., Li, P., Luo, R., Madej, B., Mertz, K. M., Monard, G., Needham, P., Nguyen, H., Nguyen, H. T., Omelyan, I., Onufriev, A., Roe, D., Roitberg, A., Salomon-Ferrer, R, Simmerling, C. L., Smith, W., Swails, J., Walker, R. C., Wang, J., Wolf, R. M., Wu, X., York, D. M., Luchko, T., Kollman, P. A., 2016. AMBER 2016. San Francisco: University of California.
- Elucidation of the controlled-release behavior of metoprolol succinate from directly compressed xanthan gum/chitosan polymers: computational and experimental studies. ACS Biomater. Sci. Eng.. 2020;6(1):21-37.
- [CrossRef] [Google Scholar]
- Biomimetic carbohydrate recognition. Chem. Soc. Rev.. 2020;49(9):2531-2545.
- [CrossRef] [Google Scholar]
- Molecular dynamics simulation study of the structural features and inclusion capacities of cucurbit[6]uril derivatives in aqueous solutions. Supramol. Chem.. 2015;27(1–2):80-89.
- [CrossRef] [Google Scholar]
- Molecular dynamics of nor-seco-cucurbit[10]uril complexes. J. Inclusion Phenom. Macrocyclic Chem.. 2015;82(3):323-333.
- [CrossRef] [Google Scholar]
- A synthetic lectin for O-linked β-N-acetylglucosamine. Angew. Chem. Int. Ed.. 2009;48(10):1775-1779.
- [CrossRef] [Google Scholar]
- Strong binding of hydrocarbons to cucurbituril probed by fluorescent dye displacement: a supramolecular gas-sensing ensemble. Angew. Chem. Int. Ed.. 2011;50(40):9338-9342.
- [CrossRef] [Google Scholar]
- Francesconi, O., Gentili, M., & Roelens, S., 2012. Synthetic tripodal receptors for carbohydrates. pyrrole, a hydrogen bonding partner for saccharidic hydroxyls. J. Org. Chem., 77(17), 7548-7554. doi: 10.1021/jo301341c.
- Free energy calculations by the molecular mechanics Poisson−Boltzmann surface area method. Mol. Inform.. 2012;31(2):114-122.
- [CrossRef] [Google Scholar]
- Cucurbit[7]uril: a high-affinity host for encapsulation of amino saccharides and supramolecular stabilization of their α-anomers in water. Angew. Chem. Int. Ed.. 2014;53(4):1003-1007.
- [CrossRef] [Google Scholar]
- Comparison of simple potential functions for simulating liquid water. J. Chem. Phys.. 1983;79(2):926-935.
- [CrossRef] [Google Scholar]
- New cucurbituril homologues: syntheses, isolation, characterization, and X-ray crystal structures of cucurbit[n]uril (n = 5, 7, and 8) J. Am. Chem. Soc.. 2000;122(3):540-541.
- [CrossRef] [Google Scholar]
- Kirschner, K. N., Yongye, A. B., Tschampel, S. M., González-Outeiriño, J., Daniels, C. R., Foley, B. L., & Woods, R. J., 2008. GLYCAM06: A generalizable biomolecular force field. Carbohydrates. J. Comput. Chem., 29(4), 622-655. doi: https://doi.org/10.1002/jcc.20820
- Selective disaccharide binding by a macrotetracyclic receptor. Chem. Commun.. 2007;23:2390-2392.
- [CrossRef] [Google Scholar]
- Supramolecular analysis of monosaccharide derivatives using cucurbit[7]uril and electrospray ionization tandem mass spectrometry. Isr. J. Chem.. 2018;58(3–4):472-478.
- [CrossRef] [Google Scholar]
- Manifesting subtle differences of neutral hydrophilic guest isomers in a molecular container by phase transfer. Angew. Chem. Int. Ed.. 2016;55(29):8249-8253.
- [CrossRef] [Google Scholar]
- Chapter 13 - Chitosan as biomaterial in drug delivery and tissue engineering. In: Gopi S., Thomas S., Pius A., eds. Handbook of Chitin and Chitosan. Elsevier; 2020. p. :407-431.
- [Google Scholar]
- Molecular dynamics simulation of a cucurbituril based molecular switch triggered by pH changes. Comput. Theor. Chem.. 2015;1066:104-112.
- [CrossRef] [Google Scholar]
- Cucurbituril chemistry: a tale of supramolecular success. RSC Adv.. 2012;2(4):1213-1247.
- [CrossRef] [Google Scholar]
- Recent developments in the molecular recognition of carbohydrates by artificial receptors. RSC Adv.. 2012;2(7):2630-2642.
- [CrossRef] [Google Scholar]
- Molecular recognition of carbohydrates with artificial receptors: mimicking the binding motifs found in the crystal structures of protein−carbohydrate complexes. J. Am. Chem. Soc.. 2005;127(25):9045-9052.
- [CrossRef] [Google Scholar]
- Miller, B. R., III, McGee, T. D., Jr., Swails, J. M., Homeyer, N., Gohlke, H., & Roitberg, A. E., 2012. MMPBSA.py: An efficient program for end-state free energy calculations. J. Chem. Theory Comput., 8(9), 3314-3321. doi: 10.1021/ct300418h.
- Binding studies on a library of induced-fit synthetic carbohydrate receptors with mannoside selectivity. Chem. Eur. J.. 2018;24(52):13971-13982.
- [CrossRef] [Google Scholar]
- Selective carbohydrate recognition by synthetic receptors in aqueous solution. Curr. Org. Chem.. 2003;7(1):81-102.
- [CrossRef] [Google Scholar]
- A hydrogen-bonding receptor that binds cationic monosaccharides with high affinity in methanol. Chem. Eur. J.. 2001;7(24):5270-5276.
- [CrossRef] [Google Scholar]
- Development and testing of a general amber force field. J. Comput. Chem.. 2004;25(9):1157-1174.
- [CrossRef] [Google Scholar]
- How does solvation affect the binding of hydrophilic amino saccharides to cucurbit[7]uril with exceptional anomeric selectivity? Chem. Eur. J.. 2016;22(44):15791-15799.
- [CrossRef] [Google Scholar]
- Molecular boronic acid-based saccharide sensors. ACS Sensors. 2021;6(4):1508-1528.
- [CrossRef] [Google Scholar]
- Applications of cucurbit[n]urils (n=7 or 8) in pharmaceutical sciences and complexation of biomolecules. Isr. J. Chem.. 2018;58(3–4):188-198.
- [CrossRef] [Google Scholar]
Appendix A
Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.arabjc.2023.104779.
Appendix A
Supplementary material
The following are the Supplementary data to this article:Supplementary data 1
Supplementary data 1







