Corrosion test and three-dimensional cellular machine simulation of Q235 steel by ion diffusion in different soil environments

2.1 Soil

The corrosion behavior of buried steel pipelines in the soil is affected by the environment and various physical and chemical factors of soil (Wang Xuankai, et al., 2022), including sulfate ions, bicarbonate ions, chloride ions, water content, -pH, conductivity, etc. Considering the difference between actual soil and simulated soil solution on the growth of pipeline corrosion pit (Liu Menglei, et al., 2022). In order to better explore the pipeline corrosion, the experiment adopts actual soil to simulate the external environment of metal, and appropriately changes the concentration of corrosive ions in natural soil, so as to form a better external environment for the pipeline. The soil was taken from Guiyang, Guizhou Province, and its surrounding areas, and the main soil composition was Guizhou's special red clay. The preparation process of the experiment is divided into three steps:

• The soil is fully dried, then ground into smaller particles, and then sifted with a 2 mm sieve.

• Take the soil after screening and extract the soil extract, and determine the content of ions in the soil according to the Experimental Method of Soil Chemistry.

• According to the requirements of the experimental scheme, combined with the final results of the determination of the soil ratio.

By changing the concentration of typical ions, it is known that different soil components will have a great influence on the corrosion behavior of metal pipes. n this study, three soil matching methods are used to compare the metal corrosion under the action of high concentration Cl- alone ([40]), the action of Cl^- with SO₄^2-, and the synergic action of Cl^-, HCO₃^– with SO₄^2- (Li Xiaohan, et al, 2021). The ratio scheme of soil ion concentration is shown in Table 1. And soil blending map is shown in Fig. 1.

Close

Fig. 1

Soil treatment and allocation.

Export to PPT

2.2 Materials

Because Q235 steel is homogeneous low-carbon steel, the comprehensive performance is better. It is often used as building steel, usually as the main material for structural buildings, cars, machines, and bridges. The characteristics of carbon steel determine that it has stronger corrosion resistance under harsh external conditions. Especially in red soil, various acid and alkali ions contained in red soil will play a role in the infiltration and erosion of Q235 steel (Safira Fitri, et al., 2018), damage the surface of steel and seriously affect its structural stability (Cai Shuo, 2022).

In addition, considering that the ultimate goal of this study is to study the leakage and diffusion law of natural gas-buried steel pipes, Q235 steel is currently used in large-scale medium-pressure and above-pressure pipe networks in Guizhou. in the interest of corroding the actual working conditions, the sake of providing more valuable experimental data for subsequent research, and better combining the experiment with the actual project, the experimental material to be used in this study is Q235 steel, and its chemical composition is shown in Table 2. The length, diameter, and thickness of the steel tube sample are 5 cm * 1 cm * 1 mm, as shown in Fig. 2. After that, the sample was placed in ethylene glycol, ultrasonically cleaned for 30 min to remove the surface grease, and then the residual impurities were cleared with distilled water, placed in a drying oven to dry the water and put into a sealed bag for use.

Close

Fig. 2

Sample size measurement diagram.

Export to PPT

Take three lengths, widths, and height specifications for a 33 cm*33 cm*5cm laboratory special corrosion prevention tray. According to the above ratio scheme, the experimental soil and Q235 steel are put into the tray and numbered, as shown in Fig. 3. Because the temperature change range of the soil in the real external environment is not large (Changxu Huang, et al., 2021), the temperature is an important environmental invariant that needs to be strictly controlled. Therefore, the equipment used in the experiment is an electrothermal constant temperature test chamber to cultivate the soil. The experimental temperature is set to 30 °C (Qi Gang, et al., 2022). During the test, the selected Q235 metal material is subjected to metal electrochemical measurement (Bianli, 2021); including open circuit potential measurement, potentiodynamic measurement, and electrochemical impedance measurement. The measurement period is 7d, 14d, 21d, and 30d to study the change in metal corrosion rate.

Close

Fig. 3

Soil buried pipe setting.

Export to PPT

2.3 Electrochemical analysis

Corrosion between metals is a common natural phenomenon, which not only causes serious waste of resources in all walks of life, hinders economic growth, but also easily leads to greater safety hazards in the industrial production process (Lan Yujie, et al., 2021). The main methods of corrosion research include surface analysis techniques based on X-ray diffraction, metallographic microscope, and scanning electron microscope analysis. The weight loss method, salt spray test method, and electrochemical analysis technology of corrosion rate were studied (Puspalata, 2022). Electrochemical testing technology is widely used in the study of corrosion science because of its simple operation (Miao, 1334), short measurement time, small damage to materials, accurate measurement results, and comprehensive information on electrode corrosion kinetics (Li, 1985). The electrochemical measurement methods used in this study include:

1. Open circuit potential measurement: In this study, the metal was buried in a tray with soil as the corrosive medium, and the electrochemical measurement circuit was connected. Corrosion and passivation of metals or alloys can be studied by measuring the open circuit potential, which does not cause polarization and is also beneficial to protect materials.

2. Potentiodynamic measurement method: through the polarization curve analysis of metal and alloy corrosion resistance, metal dissolution and passivation process is a widely used electrochemical test method, mainly including polarization curve method and cyclic voltammetry method, by the steady-state polarization curve position and shape characteristics can analyze the electrochemical behavior characteristics of the corrosion process, can calculate some important corrosion behavior parameters, analyze the corrosion process, judge the corrosion resistance.

3. Electrochemical impedance method: Electrochemical impedance technology has developed rapidly in recent years, and its application range has also expanded from the traditional electrochemical field to many fields such as chemical power supply, biofilm performance, conductive materials, and material surface modification. Electrochemical impedance technology also has important applications in the field of corrosion. It can be used to study the changes in electrode surface during corrosion and the damage of corrosive substances to coatings and coatings, as well as metals.

In this study, the metal was electrochemically measured in the electrochemical workstation of the three-electrode system. The metal platinum sheet was used as the auxiliary electrode, the sample in the soil was used as the working electrode, and the saturated copper sulfate electrode was used as the reference electrode. Before measuring the AC impedance, the potential polarization range of the open circuit potential is set to −2.5 V to + 2.5 V, the current range is 2 mA, the power frequency is 50 Hz, and the open circuit potential measurement time is set to 1800 s, until the current is stable, the AC impedance frequency is 1.0 × (10⁵ ∼ 10^-2) Hz.

2.3.1

2.3.1 Curve of polarization

Fig. 4 shows the polarization curves of Q235 steel under actual experimental soil at different concentrations of Cl^-, HCO₃^– and SO₄^2- as well as different -pH. it can be seen that under the condition of slightly changing the concentration of Cl^-, SO₄^2- and -pH value, and controlling the water content unchanged, the cathodic polarization curve in scheme 1 has reached the limiting current density value of O₂ reduction at-0.27 V, and the cathodic polarization curve in scheme 3 has reached the limiting current density value of O₂ reduction at-0.75 V. It can be seen from this that the polarization curves of scheme 1 and scheme 3 have obvious deviation, the corrosion current density increases, the polarization curve has small fluctuation, the changing trend has changed, but there is no obvious activation-passivation zone in both schemes. It can be clearly seen that the self-corrosion potential E_corr of scheme 1 is greater than that of scheme 3, indicating that the former may have a lower corrosion tendency than the latter. However, according to the soil ratio scheme, the -pH of scheme 1 is 3.0, while the -pH of scheme 3 is 4.9. Under strongly acidic conditions, the corrosion of metal has an autocatalytic effect, which may lead to the corrosion rate of scheme 1 being slightly larger than that of scheme 3. For scheme 2, HCO₃^–, which will passivate the metal, is added, and the -pH is set to an alkaline condition. It can be seen from the polarization curve that the E_corr of scheme 2 is larger than that of scheme 3. The reason may be that the added HCO₃^– forms a passivation film on the metal surface during the corrosion reaction, thus reducing the rate of corrosion reaction.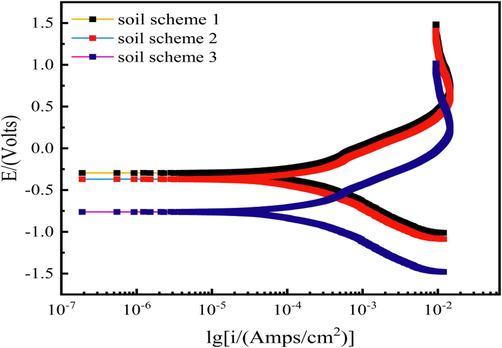

Close

Fig. 4

Polarization curves obtained by electrochemical measurement of three ratio schemes in actual soil.

Export to PPT

Combined with the Tafel formula, the polarization curves of the three schemes are fitted. The fitted data results and corrosion rates are shown in Table 3. In scheme 1, β_c > β_a, indicating that the corrosion reaction rate is controlled by the cathodic reduction reaction. In schemes 2 and 3, β_c < β_a, indicating that the corrosion rate in these two schemes is controlled by the activation dissolution reaction of the anode. According to the corrosion rate of Q235 steel in three different soil environments, it can be seen that schemes 1 and 2 conform to the basic law. However, the soil of scheme 3 contains neither SO₄^2- nor HCO₃^–, which promotes the corrosion of metals. The reason why the slowest rate may be that only a single variable Cl^- is added. In the presence of only one factor, the effect on metal corrosion rate is lower than that of multiple corrosion.

Table 3 Results of the polarization curve fitting data of Taffel slope.

Soil Scheme	βa(mv)	βc(mv)	Jcorr(A·cm2)	Ecorr(V/m)	Corrosion rate(mm/a)
1	196.53	269.23	7.2805 $\times$ 10-5	−0.29433	0.85087
2	558.14	197.32	7.6606 $\times$ 10-5	−0.56230	0.89531
3	572.12	386.53	4.5693 $\times$ 10-5	−0.76346	0.53403

2.3.2

2.3.2 Electrochemical impedance spectroscopy

The soil of the three experimental schemes was electrochemically measured on the 7th, 14th, 21st, and 30th days, respectively, as shown in Fig. 5. According to the Nyquist diagram obtained from the electrochemical measurement on the 7th day, it can be observed that soil scheme 3 represents the addition of high concentration Cl^- alone in the soil corrosive medium. Its Nyquist diagram is composed of an incomplete capacitive arc. The reason may be that there is a very small amount or no SO₄^2- and HCO₃^– in the soil environment with high Cl^- content and as the main influencing variable. In the early stage of the corrosion reaction, the high concentration of Cl^- in the soil reacts with Fe on the surface of Q235 steel to produce Fe^{2 +}, and Fe^{2 +} further hydrolyzes under the action of electrode polarization to form a dense oxide film containing Fe₃O₄. This oxide film protects the metal and prevents the corrosion reaction, resulting in an incomplete capacitive arc curve.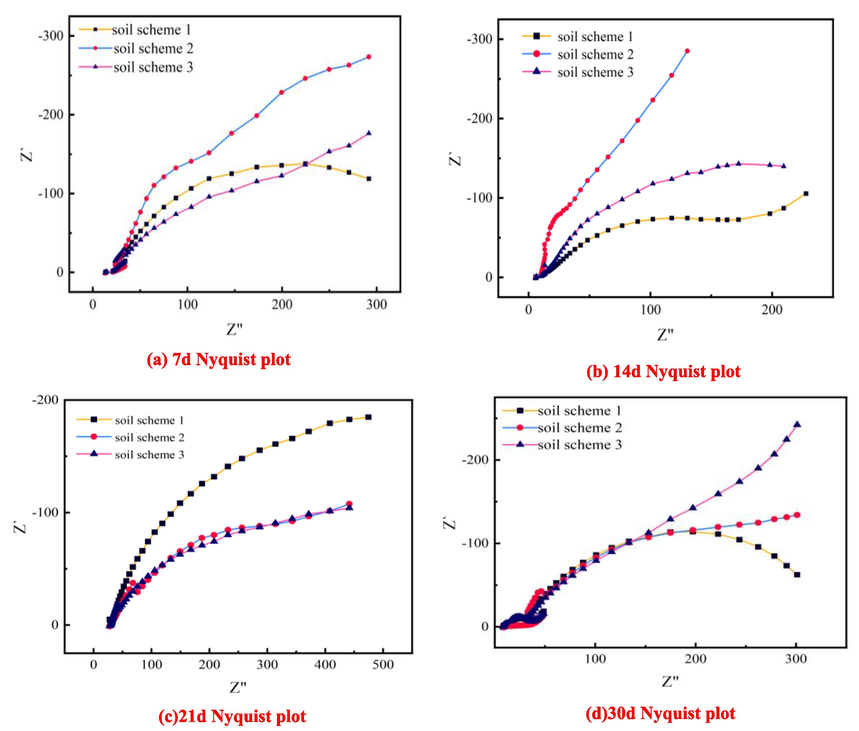

Close

Fig. 5

Nyquist plots of electrochemical measurements of Q235 steel in three soil ratio schemes.

Export to PPT

However, in the data measured on the next 14d, 21d, and 30d, the capacitive reactance arc radius on the Nyquist diagram of the soil ratio scheme 3 shows a gradual increase from the low-frequency region to the high-frequency region at three times. The result may be due to the hydrolysis reaction of Cl^-and Fe in the early stage, resulting in a layer of passivation film attached to the surface, and the size of the capacitive reactance arc is proportional to the corrosion resistance of the metal. With the increase of the capacitive reactance arc, the corrosion resistance of metal increases gradually, and the corrosion reaction rate becomes slower and slower.

For the soil ratio scheme 1, it is controlled by Cl^- and SO₄^2- with higher concentrations. From the Nyquist diagram, it is observed that there is a less obvious Weber impedance phenomenon on the 7th day, and the Weber impedance phenomenon disappears on the 14th day. At the same time, the radius of the capacitive arc gradually increases, and the radius does not appear to continue to increase until the 21st day. During this period, the corrosion rate of the metal showed a decreasing trend. However, on the 30th day, the radius of the capacitive arc on the Nyquist diagram suddenly decreases, which indicates that the corrosion rate of the metal shows an accelerated trend. The reason for this situation may be due to the high concentration of SO₄^2- in the soil ratio scheme. In the later stage of the corrosion reaction, due to the high ion concentration, the oxide film formed on the metal surface is destroyed, resulting in the accelerated corrosion rate of the metal.

In the SO₄^2-, HCO₃^–, and Cl^- three are high concentrations of soil ratio scheme 2, the corrosion rate of the metal is affected by the combined effect of three ions. On the Nyquist diagram, it can be observed that there is a clear Weber impedance line segment phenomenon on the 7th and 14th days, which indicates that there is a large difference between the concentration of corrosive ions on the electrode surface and the concentration of soil reactants in the soil. Due to the concentration difference, there will be a process of reactant diffusion from the soil body to the electrode surface in the soil. This diffusion process is usually shown on the electrochemical impedance spectroscopy (EIS). Similarly, if the electrode reaction rate is too high, the electrode reactant will also diffuse from the solution layer close to the electrode surface to the soil body. The reason may be that the concentration of corrosive ions in the soil is much higher than that of the electrode and the metal surface, which leads to the diffusion of corrosive ions from the soil to the electrode and the metal surface. At the same time, from the data observation results of the 7d, 14d, 21d until the 30d, the radius of the capacitive arc of the ratio 2 shows an increasing trend in the three measurement times until the disappearance of the Weber impedance line segment phenomenon, and the line segment on the graph cannot become a complete capacitive arc. This phenomenon shows that the corrosion rate of the metal in this kind of soil ratio is getting slower and slower.

According to the three schemes of soil ratio, through the results of this experimental study, it can be observed that under the same conditions, in the case of scheme 3, only Cl^- as a single variable to control soil corrosion behavior, the corrosion rate of metal will be due to Cl^- concentration is too high and generate oxide film to inhibit the corrosion rate of the metal. For the soil ratio scheme 1, which is controlled by the high concentration of Cl^- and SO₄^2- as the influencing factors, the high concentration of SO₄^2- exists in the soil and reacts with the passivation film on the metal surface, which destroys the surface structure formed by the reaction with Cl^- in the early stage of metal corrosion, resulting in the corrosion rate of the metal decreasing first and then increasing. At the same time, for the soil ratio scheme 2 controlled by high concentrations of SO₄^2-, HCO₃^–, and Cl^-, the Nyquist diagram shows a more obvious Weber impedance phenomenon, and the metal corrosion rate under the combined action of these three ions also shows a gradually decreasing trend.

2.4 Theoretical model verification

Most researchers focus on the results of ion corrosion of metal pipes. At the same time, the buried environment of metal plays an important role in the corrosion process of metal. Starting from the soil particle size, water content, total salt content and -pH, etc., due to the inhomogeneity between various physical and chemical components in the soil, as well as the electrification of the soil system itself and the different distribution concentrations of ions in the soil, the diffusion of corrosive ions in the soil is affected by the concentration and soil potential gradient. Therefore, in this case, Fick's law cannot be directly used to describe the diffusion process of ions in the soil system. However, based on the thermodynamic point of view and the basic kinetic principle of the material diffusion process, and then based on Fick's first and second laws as the basic theory of formula extension, a hypothesis is made on the influence of corrosive ions in soil on the corrosion of metal pipeline surface.

2.4.2

2.4.2 Diffusion model

Considering that temperature plays an important role in the diffusion coefficient D, the higher the temperature, the faster the ion diffusion, and the greater the diffusion coefficient D. Therefore, when studying the diffusion model of ions in the soil, the temperature is used as a constant invariant, combined with the material length of 5 cm and diameter of 1 mm selected in the experiment, the surface area of the ideal ring cylinder is 100π (1 + h), and the concentration of corrosive ions is c0.Since chloride ion is a single important variable and plays a major role in corrosion in the corrosive environment of soil ratio 3, the chloride ion concentration of scheme 3 of soil ratio is taken as an example, and c₀ = 4.83 mol / kg. At the same time, the electric field is assumed to be independent of the time at the soil interface of the coordinate origin. The number of ions passing through the ring cylinder in unit time is:

(12)

$$\frac{\mathrm{d}\mathrm{N}}{\mathrm{d}\mathrm{t}}=100\pi (1+h)\bullet \mathrm{v}\bullet c(x,t)$$

From (7) and (11), the flux equation at x = 0 is.

(13)

$$\frac{\mathit{dN}}{\mathit{Vdt}}=j=-\frac{D}{h}{\int }_0^h{e}^{\frac{-\theta \left(x,t\right)}{\mathit{RT}}}dx\bullet \frac{\partial \mathrm{\Psi }\left(x,t\right)}{\partial x}\mid x=0$$

According to (6) and the assumed conditions, four definite solution conditions for the boundary of unsteady diffusion are determined:

(14)

$$\frac{\partial \mathrm{\Psi }(x,t)}{\partial t}=D\frac{{\partial }^2\mathrm{\Psi }(x,t)}{\partial x^2}$$

(15)

$$\mathrm{\Psi }\left(0,t\right)={\mathrm{\Psi }}_0=c_0=4.83mol/kg$$

(16)

$$\mathrm{\Psi }(h,t)=0$$

(17)

$$\mathrm{\Psi }(h,t)=f(t)\ne 0$$

Ψ in the definite condition is zero in Ψ value of ×  = 0 interface Ψ (h, t) = f (t) refers to the soil and metal distance as h, diffusion equation and the basic relationship between the change of time. Here, four particular solution conditions are used to obtain:

(18)

$$\mathrm{\Psi }(x,t)=4.83\left\{1-\sum _{n=0}^{\infty }\frac{4}{(2n+1)\pi }{e}^{\left[-\frac{{D\pi }^2}{{4h}^2}{(2n+1)}^{2}t\right]}\bullet \mathit{sin}\left[\frac{x}{h}(2n+1)\frac{\pi }{2}\right]\right\}$$

Where n = 0,1, 2, ….

Substitute (4) into (18):

(19)

$$c(x,t)=4.83e^{\frac{-\theta \left(x,t\right)}{\mathit{RT}}}\left\{1-\sum _{n=0}^{\infty }\frac{8}{(2n+1)\pi }{e}^{\left[-\frac{{D\pi }^2}{{4h}^2}{(2n+1)}^{2}t\right]}\bullet \mathit{sin}\left[\frac{x}{h}(2n+1)\frac{\pi }{2}\right]\right\}$$

In summary, the dynamic distribution equation of chloride ions in soil can be obtained by connecting (18) and (13):

(20)

$$N=4.83\times 100\pi (1+h){\int }_0^h{e}^{\frac{-\theta \left(x,t\right)}{\mathit{RT}}}dx\left[1-\sum _{n=0}^{\infty }\frac{8}{(2n+1){\pi }^2}{e}^{\left[-\frac{{D\pi }^2}{{4h}^2}{(2n+1)}^{2}t\right]}\right]$$

Thus, the total amount of ions diffused into the soil at equilibrium is:

(21)

$$N_{\infty }=4.83\times 100\pi (1+h){\int }_0^h{e}^{\frac{-\mathrm{\theta }\left(\mathrm{x},\mathrm{t}\right)}{\mathit{RT}}}dx$$

Do to (20) and (21) ln (1- $N/N_{\infty }$ ) of time t composing chart shown in Fig. 6.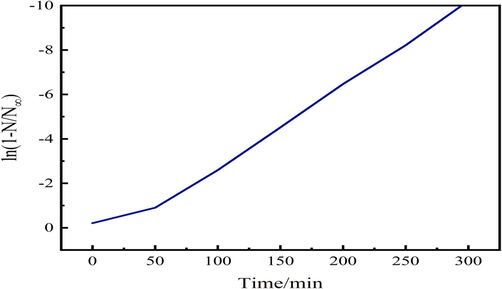

Close

Fig. 6

Fixed temperature ln (1- $N/N_{\infty }$ )-t curve of diffusion theory.

Export to PPT

Taking t = 300 as an example, from equation (20), we can observe the changes of ions with time by referring to the terms of the equation when n = 0. It is concluded that (1- $N/N_{\infty }$ ) in the convergence speed when t > 0. This is consistent with the results obtained by electrochemical measurement in soil proportion-scheme 3.

3.1 Cellular automata

By considering the behavior of imitating the human brain and processing in the framework of complete discretization, and each cell has its own internal state and is composed of a limited amount of information, von Neumann proposed the concept that cellular automata (CA) is a discrete dynamic model in time, space and state (Wang and Han, 2016). Cellular automata (CA) is composed of cellular, cellular space, cellular neighbors, evolution rules (transition function), cellular state, and time. At the same time, in the case of a series of simple rules, the CA model is also a general term for a class of models or a framework of methods (Guiso et al., 2022).

Cells are the most basic components and units (also known as primitives) existing in cellular automata, which are distributed on the lattice points constructed by one-dimensional, two-dimensional, or multi-dimensional Euclidean space, and can constantly update the states at different time points according to the transformation rules (Fatoba et al., 2018). The set of points distributed in space is called cellular space, and two-dimensional cellular space is widely used in research. Theoretical research shows that cellular space can be infinitely extended in all dimensions (Chen et al., 2015), but this ideal condition cannot be achieved in practical research simulation. In order to find the closest method to infinite space, researchers have proposed the concept of periodic boundaries. The so-called periodic boundary refers to the topological torus formed by the upper and lower left and right respectively. The simple top-level periodic boundary conditions are connected as shown in Fig. 7.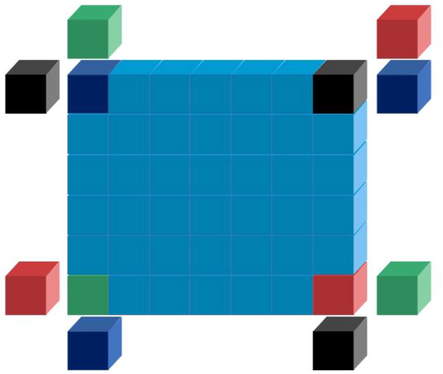

Close

Fig. 7

Schematic diagram of top periodic boundary evolution.

Export to PPT

Cellular and cellular space only belong to the static components of the cellular automata (CA) system. In order to represent the model in a dynamic way, it is necessary to define a neighbor cell that can complete the transformation rules within the spatial range: that is, the cellular state at the next moment determines the state of the cell itself and its neighbor cells (Al-samawi, 2020). Therefore, before defining the transition rule function, it is necessary to define the cellular neighbor rule ^[60]. The widely used neighbor types are von Neumann type, Moore type, and extended Moore type, as shown in Fig. 8. The dynamic function that determines the state of the cell at the next moment through the neighbor state and the current state is called the state evolution rule (transition function), denoted by f: s_i^t + 1 = f(s_i^t,s_N^t),s_N^t is the combination of neighbor states at time t, and f is the local mapping or local rule of cellular automata. Then the dynamic evolution local function determined by the local evolution rule f of each cell is denoted by: F(S_i^t+1) = f (s^t_i-r, …, s^t_i, …s^t_i+r).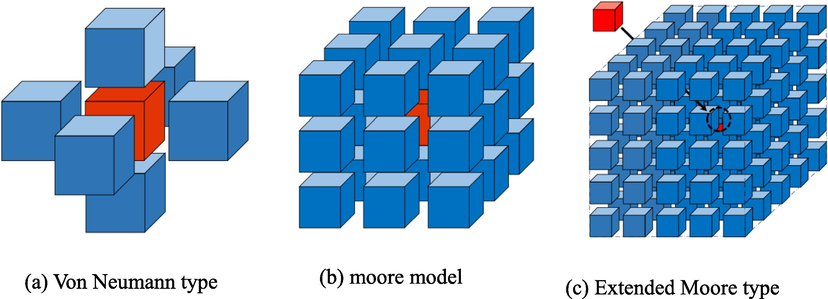

Close

Fig. 8

Cellular neighbor types.

Export to PPT

3.2 Local evolution rules

CA model can be summarized as a mathematical function, expressed as L=（L_a,S,N,φ）, where.

S represents the cellular state;

L_a stands for cellular space;

a is the dimension of space;

N stands for cellular combination;

φ represents the evolution rule of cellular state (transition function);

In this study, the three-dimensional CA model was used to simulate the corrosion pits of steel and metal in the soil corrosion environment. The metal and soil corrosion medium system was defined as a cellular grid, and N_i × N_j × N_k = 100*100*100. In order to simulate the infinity of cellular space, the von Neumann type is considered as the neighbor type, with fixed boundary conditions for upper and lower sides and periodic boundary conditions for front and back. Suppose the cell has four states, expressed as S= (M, C, N, F), Among them, M represents the metal cell that will be corroded, C represents the corrosive cell that is corrosive and can move up and down in six directions. Combined with the soil ratio scheme used in the experimental part, the corrosive cell C that can react with the metal cell M in this study includes the following ions: chloride ion, sulfate ion, bicarbonate ion, N represents the solution water molecule (the position will be occupied by the cell C at any time), F represents the passivation cell (formed by the contact of M and C). Once the passivation cell F is formed in the corrosion reaction, the state of the passivation cell will not change in the next simulation. At the same time, the cell state in the CA model can only be any of the above four. Therefore, the state of the cell at the next moment is determined by the neighbor primitives in the six directions of the cell. In addition, it is assumed that the concentration of the solution is controlled by the numerical results of C / N.

By controlling the time step of the number of iterations and the concentration of the electrolyte solution, the cell C representing the corrosive medium moves randomly in six directions: up, down, left, right, front and back. The corrosive cell C and the metal cell M react with the corrosion probability P_cor. The corrosion reaction between the cells is expressed by the following formula:

the following situations may occur in the corrosion reaction of metal cellular:

① When the dissolution reaction occurs in the contact between metal cellular M and corrosive cellular C, M dissolves with probability Pd, and the position of the original metal cellular M becomes vacant or passivated. If it is vacant, it may be occupied by water molecular cell N in the next time range. If it is a passivation state, the cell position state of the passivation cell F will not change.

② If the neighbor cell of metal cell M is corrosive cell C, and the corrosive cell C does not move in the direction of this cell M, the state of metal cell M remains unchanged.

③If the neighbor cell of metal cell M is passivation cell F or the same type of metal cell M and water molecule N, the cell state remains unchanged.

The bicarbonate ions contained in the corrosive medium in the environment will bring passivation to the metal matrix, resulting in a passivation reaction between metal cells with passivation probability Pp, expressed as:

① If the corrosive cell C moves towards the metal cell M, the metal cell M will be dissolved by the corrosive cell C with a certain dissolution probability of Pd. In the next time step, the position of the cell M will be occupied by cell C, and the original vacancy position of the corrosive cell C will be automatically filled by the water molecule cell N, which is expressed as:

② If the movement direction of the corrosive cell C is toward the same type of corrosive cell C, the original position of the corrosive cell C remains unchanged, and then a target neighbor position is randomly selected in the next time step. If the moving position in the time step of corrosive cell C is a vacant grid position, the cell may abandon the existing grid position and jump to the target position.

3.3 Analysis of effect

Considering the actual situation, and in order to have higher coincidence and consistency with the experimental results. The theoretical model sets the corrosion probability P_cor = 0.89, dissolution probability Pd = 0.8, and passivation probability Pp = 0.02. The single corrosive ion is taken as an important parameter in the CA model to optimize the model with the interaction of HCO3–, SO42- and SO42-, and the influence of the three ions on metals is taken as an important factor to set the evolution rules of the CA model. According to the soil matching scheme of the experiment, Scheme 2, in which the three ions act together, is selected as the main simulation research object of the CA model. Where, C(HCO₃^–) = 0.192 mol/kg, C(SO₄^2-) = 0.08 mol/kg, C(Cl^-) = 4.24 mol/kg, and set the concentration of corrosion solution c = 0.2. The above ion concentration and corrosive medium concentration were substituted into the CA model for simulation. With the continuous diffusion of ions in soil towards the metal surface, the influence of chloride ions on the metal surface gradually expands with the increase of time step. At the same time, corrosion pits can randomly form on the surface of the metal that is not smooth.

Due to the unique properties of the metal itself and the influence of the corrosive medium, when the corrosion reaction occurs to produce pitting pits, the pitting pits are rarely corroded in a single pit, and most of them are accompanied by multi-pit corrosion as a common phenomenon. In this study, the formation process and results of pitting pits were idealized to some extent. The growth process of pitting pits in a certain period of time was selected as the research object, the conditions of pitting pits were limited to some extent, and it was assumed that single-pit corrosion was the main corrosion. For the case of single pit corrosion, the simulation iteration steps of the CA model were set as T = 50, T = 300, T = 500, and T = 700, respectively. According to the simulation results, it can be observed that the morphology of the corrosion pit randomly generated on the metal is an unfixed shape. As shown in Fig. 9, with the larger the time step, the corrosion pits.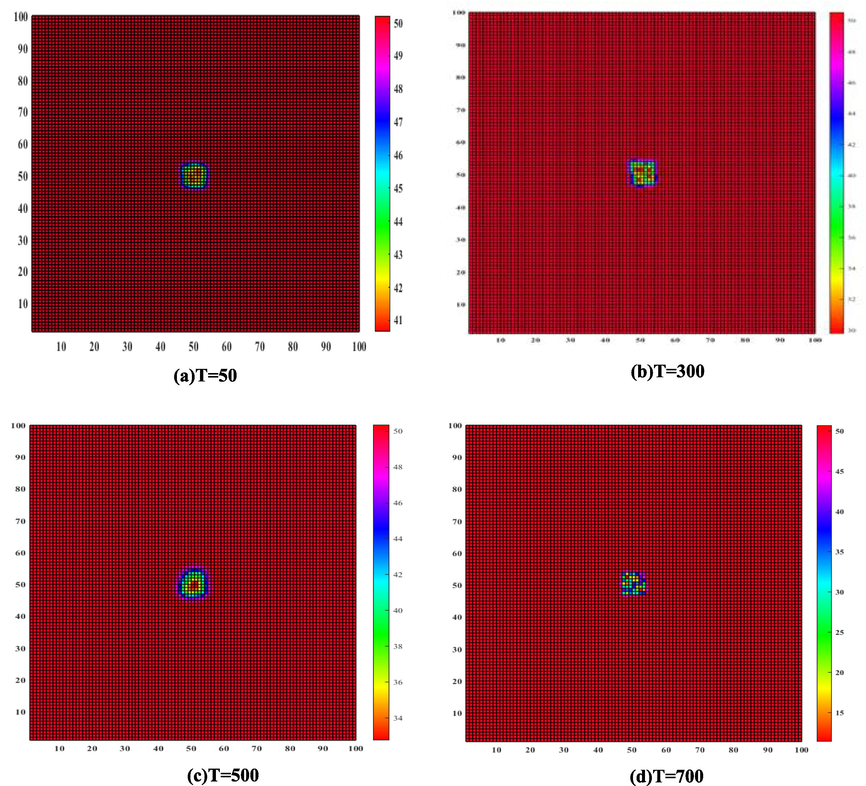

Close

Fig. 9

Growth simulation results of initial single pit with different iteration steps.

Export to PPT

Considering the early stage of corrosion behavior, localized corrosion behavior occurred on the metal surface. According to the value of the fitted corrosion rate, it was combined with the three-dimensional cellular automaton model to study the results of the three-dimensional cellular automaton model under three soil ratio schemes.

Firstly, in the soil ratio scheme 3, which is controlled by a single ion as the main influencing factor, the ion concentration of the soil ratio scheme 3 and the fitted corrosion rate value are substituted into the theoretical model of the soil ratio scheme 1, and the corrosion probability P_cor = 0.53 and the dissolution probability P_d = 0.8 are set. Because there is no HCO₃^– ion in the soil that causes the passivation reaction of the metal, the passivation probability P_p = 0 is considered. The individual corrosive ions are used as important parameters in the CA model. Among them, C (Cl^-) = 4.24 mol / kg, and the concentration of the corrosion solution remains unchanged. As shown in Fig. 10(a), when the iteration step size T = 700, in the case of a single high concentration of Cl^- ions used alone, with the increase of time, the three-dimensional model of the simulated metal matrix is only slightly corroded, and does not show a perforation trend. At the same time, the corrosion shown in the model is basically consistent with the law shown in the electrochemical impedance measurement and polarization curve.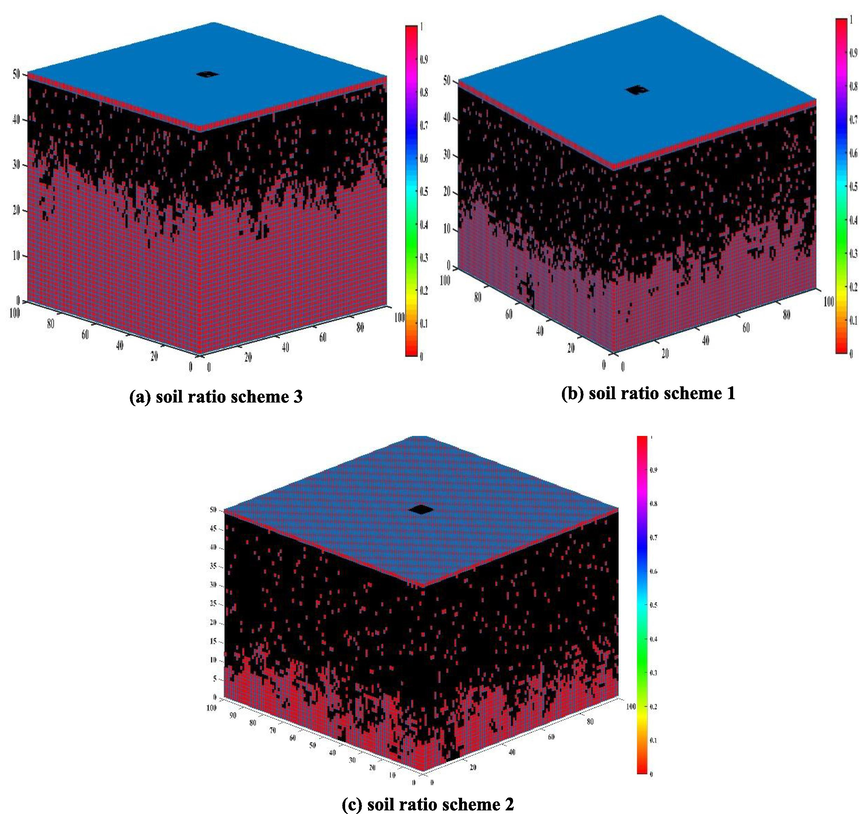

Close

Fig. 10

Three-dimensional cellular machine simulation results of iterative 700-step metal corrosion under three soil ratio schemes.

Export to PPT

Secondly, for the soil ratio scheme 1 with SO₄^2- and Cl^- as the influencing factors, according to the above modeling method, the ion concentration configured in the test and the approximate value of the fitted corrosion rate are substituted into the theoretical model of the soil ratio scheme 1, where the SO₄^2- and Cl^- concentrations are 3.16 mol / kg and 2.54 mol / kg, respectively, and the corrosion probability P_cor = 0.85 and the dissolution probability P_d = 0.8 are set. Similarly, there is no HCO₃^-ion in the soil ratio scheme 1, so the passivation probability P_p = 0 is set. As shown in Fig. 10(b), when the iteration step size T = 700, with the increase of time, the metal matrix model under the combined action of the two influencing factors has been seriously corroded and has shown a slight perforation trend. This is basically consistent with the results of experimental analysis.

Finally, Fig. 10(c) shows that in the soil ratio scheme 2, when the iteration step T = 700, taking the presence of three corrosive ions in the soil medium (where the concentrations of HCO₃^–, SO₄^2-, and Cl^-are 0.192 mol / kg, 0.08 mol/kg, and 4.24 mol/kg, respectively) as an example, under the combined action of the three ions, the model representing the simulated metal matrix has been able to exhibit severe corrosion by the corrosive medium. According to the above-mentioned hypothetical pitting single-pit corrosion phenomenon, it is assumed that the pitting behavior occurs first in the center of the matrix, and the corrosion phenomenon gradually expands from the center of the matrix to the periphery as time increases. When T = 700, according to the simulated model, it can be clearly observed that the metal matrix has shown a trend of being penetrated after being corroded by corrosive ions.

The results of the model study show that among the three soil ratio schemes, the metal matrix in scheme 3 is least affected by the corrosive medium, and the possible perforation trend on the model is also the smallest. Scheme 1 is more affected by corrosive ions than scheme 3, and has shown the possibility of perforation on the simulated metal matrix model. Scheme 3 is most affected by corrosive ions in the soil, and it has shown a penetration on the three-dimensional metal matrix model. In summary, the corrosion behavior of the metal in the three-dimensional cellular machine is basically consistent with the results obtained from the experimental analysis.