Development of advanced computational simulation of two-dimensional plate-like crystals: A comparison with population balance model

1 Introduction

Physical properties of solid particles such as size, porosity, shape, and surface area are included and described basically at the particle level. In the field of crystal engineering, arrangement of the constituting molecules in the crystal lattice defines the molecular-level properties of crystals such as polymorphism, crystal habit, amorphous structure, etc. (Bhoi, 2019). The methods of size reduction are usually employed in different industries such as chemical, pharmaceutical, mineral, etc. to create particles or crystals with the desired properties (Das, 2020). Particle size reduction is an important particle engineering technique that is especially useful to enhance solubility of poorly water-soluble medicines in aqueous media.

Furthermore, there are also several particle size reduction methods, such as milling and grinding. In addition to this, the ultrasound method is used to maintain the quality of drugs in pharmaceuticals (Bari and Pandit, 2014).

Bhoi et al. (Bhoi, 2019) performed several sonofragmentation experiments by changing time and ultrasonic amplitude. They investigated the further simulated breakage using ultrasound. For performing the simulations, Monte Carlo (MC) was used. It was discovered that, in crystal size reduction, both the ultrasonic amplitude and the sonication period play a significant role. Zeiger et al. (Zeiger and Suslick, 2013) presented the modeling and observations on molecular crystals of Sonofragmentation. They discovered that direct particle-shockwave and related particle-turbulent shear interactions are the dominant mechanisms of sonofragmentation (Zeiger and Suslick, 2011). Bari et al. (Bari and Pandit, 2014) investigated the population balance modeling using kinetic parameter estimation for particle breakage assisted with ultrasound. Ultrasound facilitated particle breakage has been shown to be an effective method for size reduction. In gPROMS, the breakage rate for ultrasonic breakage was calculated for various distribution functions by the zeroth moment simulations using different time intervals. It was discovered that the distribution function with uniform binary breakage produces the best PSD results. Thus, it was used to derive the law for energy size reduction law using ultrasonic breakage.

Raman et al. (Raman et al., 2011) studied identification of breakage mechanisms identification and kinetic modeling with high-intensity ultrasound to grind the particles. An ultrasound transducer-like horn-type shape is used to apply HIU to an alumina particle suspension, which causes breakage. They found that the variation of the first Kapur function with particle size is found to have an exponential relationship, which is unique to ultrasound-mediated particle breakage. Zeiger et al. (Zeiger and Suslick, 2011), examined the molecular crystal sonofragmentation. The use of acetylsalicylic acid was used to investigate the mechanisms for breaking of molecular crystals at high-intensity ultrasound medium (Zeiger and Suslick, 2011). Sonofragmentation is independent of slurry concentration, according to particle-loading studies of molecular crystals. This eliminates particle–particle collisions as a significant breakage mechanism. They found that the importance of direct particle-shock wave interactions in the design of sonocrystallization processes cannot be overstated.

Klaue et al. (Klaue, 2019), studied the polymer sonofragmentation for size distribution and controlling the size of the produced particles. Since the activity of Ziegler –Natta catalyst (ZNC) particles, as well as the size and size distribution (SD) of the final polymer particles, can be greatly influenced. For breaking up ZNC particles in the solvent, they used sonofragmentation. Finally, they discovered that the sonofragmentation treated ZNC has a significantly higher catalyst yield than the untreated one.

Kim et al. (Kim and Suslick, 2017) studied the ionic crystal sonofragmentation. The crystal’s fragmentation rate was highly influenced by the materials strength. They discovered that slurry loading, and liquid–vapor pressure do not affect sonofragmentation. Furthermore, it was suppressed by increasing the viscosity of the liquid. Edwin et al. (Edwin and Wilson, 2019), incorporated the Strontium function and investigated the sonofragmentation for hydroxyapatite crystals. Tronium gets attention as strontium-incorporated hydroxyapatite enhances the number of bone-forming sites while also being biocompatible. It was found that strain in the HA lattice correlates with strontium incorporation, resulting in varying degrees of sonofragmentation. Furthermore, the study found that 100% strontium replacement of calcium sites results in a lower strain and, as a result, inadequate fragmentation.

Gopi et al. (Gopi and Nagarajan, 2008) studied the advances in the fabrication of ceramic particle nano alumina using sonofragmentation. They investigated the effects of various parameters on the sonofragmentation process, including frequency, shape, surfactants, particle concentration, applied ultrasonic power, and process time. Raman et al. (Raman and Abbas, 2008) performed experimental investigations of breakage of a mediated particle using ultrasound. They used a 24 kHz horn-type transducer as well as a continuous chord length measurement system.

Jordens et al. (Jordens, 2016), studied the effect of power and frequencies on the breakage of particles. According to Kapur function analysis, stable bubbles are more efficient than transient bubbles at breaking coarse particles larger than 40 µm. Then, it was discovered that stable bubbles produce less abrasion than transient bubbles. Rasche et al. (Rasche, 2018), studied the particle size evolution and carried out mathematical modeling. Further, they studied the aspirin crystals investigated the particle size distribution under ultrasound breakage. They discovered that the breakage rate's dependence on particle mass was small for the binary equal-size breakage model. As a result, a binary equal-size breakage model accurately modelled these crystals. Sato et al. (Sato, 2008) studied the high aspect ratio crystals breakage with a 2D PBM, while two physical assumptions considered in their model.

Alexopoulos et al. (Alexopoulos and Kiparissides, 2007) evaluated the combined effect of breakage and aggregation. Then, developed a bivariate solution for the dynamic population balance equation in batch particulate systems. Saha et al. (Saha, 2019) used the finite volume method for multidimensional fragmentation and developed numerical solutions. They discovered that the scheme accurately estimates several physically considerable moment functions. Furthermore, it has a simple mathematical framework for describing higher dimensions.

Using a variety of tests, the scheme's efficiency was validated. Lee et al. (Lee and Matsoukas, 2000) investigated coagulation and breakup simultaneously using Monte Carlo. Finally, they compared the results with analytical solutions and look at the outcomes of three cases and found them to be validating well with the Monte Carlo method. Das et al. (Das, 2020) used a bivariate model for population balance for rectangular plate crystals. They performed the population balance modeling and compared it with experimental validations. The accuracy of the population balance equations modelling highly depends on the number of cells considered for the discretization of the domain and more cells are required for achieving a certain level of precision, making it computationally expensive. Therefore, in this paper, a predictive tool is developed using the notion of artificial neural networks and validated with experiments. The proposed calculations of empirical relations from ANN were compared with population balance equation (PBE) simulations. Similar to the population balance model, two ANN models based on the length and width of the particles (crystals) are developed using 3 and 4 hidden layers, respectively. Finally, two empirical relations are obtained for number fractions in terms of length and width of the particles.

2 Materials and method

Pyrazinamide (PZA) crystals with 123.12 g/mol molecular weight and 98% purity, toluene and methanol were used in the analysis (Bhoi, 2019). We have taken the data from published sources and developed computational methodology in this work. More detailed description of the experimentation can be found elsewhere (Bhoi, 2019).

The crystals of pyrazinamide are assumed as thin rectangular plate-type particles of uniform thickness that break into two fragments. To begin, the crystal only breaks across the width of the crystal particle, and the fracture can occur at any random point between xl percent and (1-x)l percent of the crystal's length. Finally, crystal particles smaller than 20 µm in length do not further break down into tiny pieces, and crystal particle size is proportionate to the area. The total frequency of stressing loading activities for the entire system remains unchanged for a steady ultrasonic amplitude (Bhoi, 2019; Das, 2020).

3 Overview of artificial neural network

The effectiveness of ANN modeling in identifying the appropriate solution for complicated processes like granulation, crystallization is well known (Velásco-Mejía, 2016). The basic idea of the ANN modeling approach is to use statistical optimization to empirically associate specific inputs to particular outputs (Jin, 2021; Lima, et al., 2022). ANN modeling approach is typically employed when finding a mechanistic model for a process is challenging. A general structure of the ANN model comprises three layers (a) input layer, (b) hidden layer and (c) outer layer. The parameters that affect the system or particulate process are in the input layer, while the hidden layer is made up of multiple layers composed of various numbers of linear and nonlinear neurons that connect the input layer to the output layer (refer to Fig. 1). Moreover, the outer layer is where the output results are obtained from the ANN model. The precision of the ANN model is highly dependent on various factors discussed below:

1. The number of layers and nodes employed,

2. The kind of activation functions chosen for each node,

3. The quantity of data points used in training and validation of the ANN model.

Close

Fig. 1

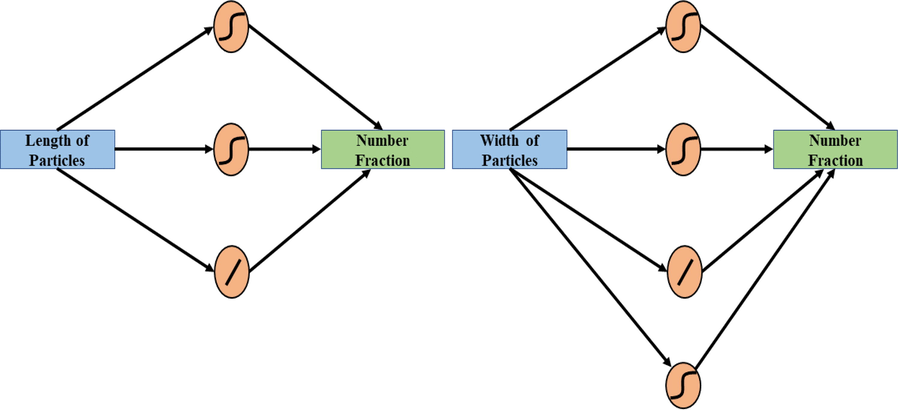
ANN structure for length model (left side), and width model (right side).

Export to PPT

To build accuracy, the number of data points plays a significant role and impacts the solution of ANN model. A coarse data may lead to inaccurate results. In addition, choosing appropriate activation functions is also challenging in developing an accurate ANN model. To make a simple ANN model, linear and nonlinear activation functions are considered. Mathematically these functions can be written as follows:

The coefficient of determination ( $R^2$ ) is used to assess the accuracy of the ANN model in fitting the data:

Here P and E represent the predicted and experimental values, respectively and i is the set of experimental runs (Shirazian, 2017).

4 Results and discussion

This part of the paper is devoted to check the accuracy and robustness of the ANN model against experimental data and population balance model. ANN model is developed for predicting the sonofragmentation of thin rectangular plate-type pyrazinamide crystals via the ultrasound-based technique. Two kinds of models are built in modeling the system: (1) Length-based model and (2) Width-based model (Das, 2020). For the length and width models, three and four hidden layers are used, respectively. The experimental data used for developing the ANN model taken from (Bhoi, 2019) is listed in Table 1. It is important to note that the experimental data considered here is corresponding to ultrasonic amplitude equal to 10%. Among whole data points 32 out of 43 data sets were used in the training the model to determine the unknown parameters, however, 11 data points were used to validate the number fraction results.

One can see from Table 1 that the number fraction calculated using the ANN model the sonofragmentation process of rectangular δ-form pyrazinamide crystals shows highly comparable results compared to the experimental data whereas the PBE shows significant deviation from the experimental values. Table 2 shows that the ANN model provides very good R² values (greater than0.95) for training and validation steps corresponding to both length and width models.

The experimental and training ANN values are compared in terms of number fraction in Fig. 2 for both length and width models. The validation of the ANN model is done in Fig. 3 for both models. Both figures show that the ANN values are matching well with the experimental values, and capable to capture the variations in the process.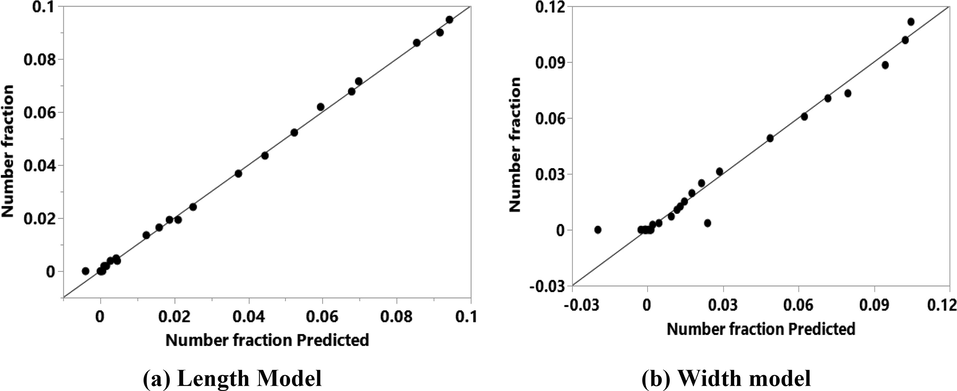

Close

Fig. 2

Comparison of experimental (solid line) Vs. predicted (solid circles) training data for number fraction.

Export to PPT

Close

Fig. 3

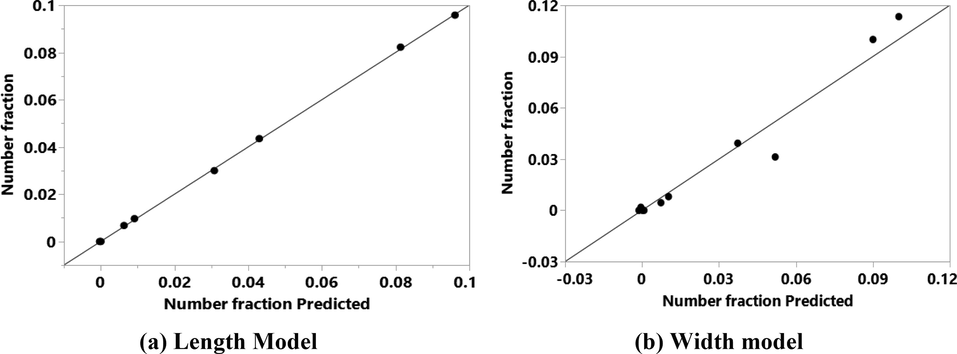
Comparison of experimental (solid line) Vs. predicted (solid circles) validating data for number fraction.

Export to PPT

Furthermore, as shown in Figs. 4 and 5, relatively fewer residual values were produced in both the training and validation tests, respectively. In this case, the SSE values for training and validation are moderate and outstanding, respectively. The constructed neural model is accurate and can be used to estimate the number fraction for both length and width models.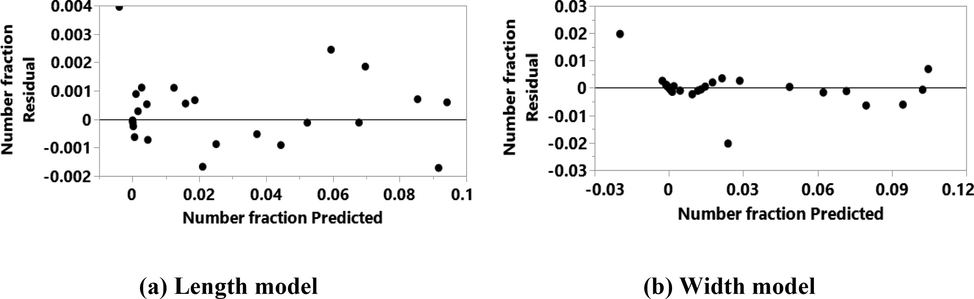

Close

Fig. 4

Residual errors corresponding to training experimental data.

Export to PPT

Close

Fig. 5

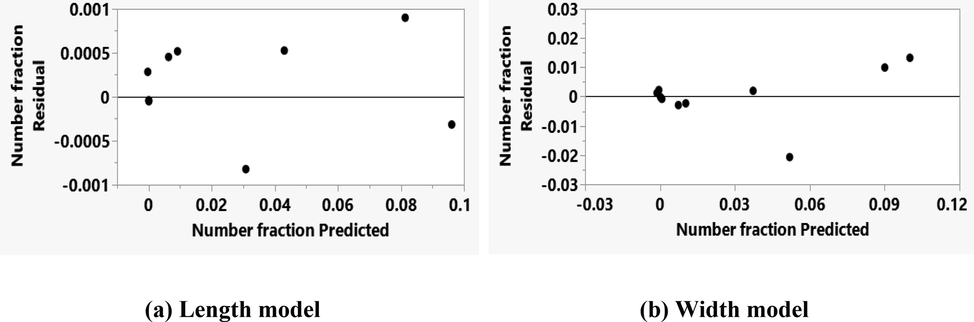
Residual errors corresponding to validating experimental data.

Export to PPT

The following relation of number fraction corresponding to length of particles is obtained:

H1 = tanh(0.5*(0.0207204429309029*Length_of_particles + -1.17799011226555)).

H2 = tanh(0.5*(-0.0637912625023325*Length_of_particles + 8.09956092528305)).

H3 = tanh(0.5*(-0.0657532982458528*Length_of_particles + 3.11428277707588)).

Number fraction = -0.151616499717725*H1 + 0.00402546315007164*H2 + -0.124980283548877*H3 + 0.0303751811701785.

Similarly, using the ANN model the following relation of number fraction corresponding to width of particles is developed:

H1 = tanh(0.5*(-0.04522451367367*Width_of_particles + 4.33200248535175)).

H2 = tanh(0.5*(0.00131127523356585*Width_of_particles + 1.99138412281423)).

H3 = tanh(0.5*(0.0132881291510304*Width_of_particles + -2.23217887065043)).

H4 = tanh(0.5*(0.00232015143889709*Width_of_particles + -0.282504441273059)).

Number fraction = 0.124972843935664*H1 + 44.3111565249285*H2 + -0.237216575217829*H3 + -7.39599653603879*H4 + -35.037207680288.

Here H1, H2, H3 and H4 are the hidden layers used for developing the ANN model. It is important to note that the above equations can be also used to generate more values of fractions corresponding to different lengths and widths of the particles. ANN model helps in reducing the experimental work and allows the researchers to obtain the values of a certain parameter where those are not available. Whereas population balance models fail to do so. Moreover, due to discretization of the continuous domain into discrete cells for the population balance model makes it computationally expensive.

5 Conclusions

This work has been devoted to developing an ANN (Artificial Neural Network) model for tracking the changes in ultrasonic amplitude as well as the sonication time that are properly captured by the proposed ANN model. The ANN model was based on minimizing the RMSE between experimental and predicted number fractions corresponding to lengths and widths of the particles. For length-based model, the training and validation of the ANN model provided R² greater than 0.99, whereas for the width-based model, the ANN model provided R² greater than 0.95. The comparison of results computed using ANN model with the existing population balance model has been done for both length and width models. The outcomes revealed that the ANN model demonstrated better accuracy than the population balance model (PBM). Finally, we can conclude that the ANN model revealed great capability and can be employed as a predictive tool for tracking the sonofragmentation process.