Experimental analysis and thermodynamic modelling of lenalidomide solubility in supercritical carbon dioxide

Seyed Ali Sajadian; Mitra Amani; Nedasadat Saadati Ardestani; Saeed Shirazian

doi:10.1016/j.arabjc.2022.103821

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

06 2022

:15;

103821

doi:

10.1016/j.arabjc.2022.103821

Experimental analysis and thermodynamic modelling of lenalidomide solubility in supercritical carbon dioxide

Seyed Ali Sajadian^{^a,^b}, Mitra Amani^{^c}, Nedasadat Saadati Ardestani^{^d,^e,⁎}, Saeed Shirazian^{^f}

a Department of Chemical Engineering, Faculty of Engineering, University of Kashan, 87317-53153 Kashan, Iran

b South Zagros Oil and Gas Production, National Iranian Oil Company, 7135717991 Shiraz, Iran

c Department of Chemical Engineering, Islamic Azad University, Robat Karim Branch, 37616-16461 Robat Karim, Iran

d Department of Chemical Engineering, Tarbiat Modares University, P.O. Box: 14115-111, Tehran, Iran

e Department of Nanotechnology and Advanced Materials, Materials and Energy Research Center, 14155-4777 Karaj, Iran

f Laboratory of Computational Modeling of Drugs, South Ural State University, 76 Lenin Prospekt, 454080 Chelyabinsk, Russia

⁎Corresponding author at: Department of Chemical Engineering, Tarbiat Modares University, P.O. Box: 14115-111, Tehran, Iran. n.saadati@modares.ac.ir (Nedasadat Saadati Ardestani)

Received: 2021-12-26, Accepted: 2022-2-24,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

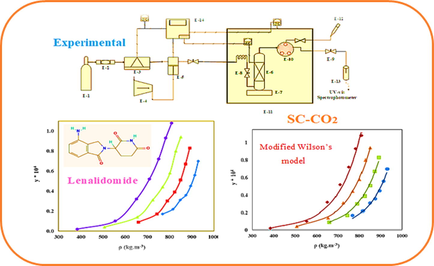
Abstract

Lenalidomide (LND) solubility in supercritical CO₂ (sc-CO₂) was measured for the first time.
Solubility data were correlated by different density-based models.
Experimental data was also correlated by Modeified Wilson and SRK models.
The accuracy of the models was evaluated by statistical criteria (AARD%), (Radj).
Thermodynamic enthalpies of Lenalidomide were estimated.

Abstract

Reduction of the size of pharmaceutical particles to micro/nano scale is an approved strategy to enhance their dissolution rate at decremented side effects. Production of drug micro/nanoparticles via a supercritical carbon dioxide (sc-CO₂)- based process requires accurate data on the drug solubility in sc-CO₂. In this study, the solubility of Lenalidomide (LND), an anti-cancer, was experimentally determined in sc-CO₂ at various temperatures (308–338 K) and pressures (120–300 bar). Furthermore, the obtained solubility data were correlated by different theoretical methods. LND solubility, in terms of mole fraction, was obtained in the range of 0.02 × 10⁻⁴–1.08 × 10⁻⁴ depending on the conditions. The empirical models with different adjustable parameters, Soave–Redlich–Kwong equation of state (SRK-EoS) with two parameters van der Waals (vdW2) mixing rule, and expanded liquid theory (modified Wilson’s model) were applied for experimental data correlation. According to the results, modified Wilson’s model can correlate LND solubility in sc-CO₂ with high accuracy. However, the SRK-EoS did not show acceptable accuracy in the correlation of LND solubility in sc-CO₂. Among the empirical models, Alwi and Garlapati, Sung and Shim, Ch and Madras, Hozhabr et al., Garlapati and Madras, Keshmiri et al., Sparks et al., Reddy and Garlapati, Bian et al. (2011) and Belghait et al. showed R_adj values higher than 0.99 and produced the best correlation with 3,4, 5, 6 and 8 adjustable parameters, respectively. Moreover, the approximate values of total mixing heat ( ${Δ H}_{total}$ ) as well as vaporization ( ${Δ H}_{vap}$ ), and solvation ( ${Δ H}_{sol}$ ) enthalpies were computed.

Keywords

Lenalidomide

Solubility

Supercritical carbon dioxide

Empirical model

Modified Wilson’s model

Soave-Redlich-Kwong (SRK) equation of state

Nomenclature

$a_{0} - a_{10}$: Adjustable parameters of empirical model
AARD%: Average absolute relative deviation
$a (T)$: Energy parameter of the cubic EoS (Nm⁴ mol⁻²)
b: Volume parameter for equations of state (m³ mol⁻¹)
f₂^L: The fugacity of the solid solute in the supercritical phase
f₂^s: The fugacity of the solute in the solid phase
H_f: Molar heat of fusion(kJ.mol⁻¹)
g^E: Excess Gibbs free energy
k_ij: Binary interaction parameters in the mixing rules
l_ij: Binary interaction parameters in the mixing rules
MS_R: Mean square regression
MS_E: Mean square residual
N: Number of data points, dimensionless
P_sub: Sublimation pressure (Pa)
Q: Number of independent variables
R²: Correlation coefficient
R_adj: Adjusted correlation coefficient
S: Equilibrium solubility
SS_E: Error sum of squares
SS_T: Total sum of squares
SS_R: Regression sum of squares
$T_{c}$: Critical temperature
v^s: Solid molar volume
vdW2: Van der Waals mixing rule with two adjustable parameters
y: Mole fraction solubility
Z: Number of adjustable parameters

α(Tr, ω): Temperature-dependent function in the attractive parameter of the EoS
φ: Fugacity coefficient
ω: Acentric factor
α: Regressed parameters of Wilson’s model
β: Regressed parameters of Wilson’s model
Λ′: Regressed parameters of Wilson’s model
Λ: Adjustable parameters
$γ_{2}^{\infty}$: The activity coefficient of the solid solute at infinite dilution

cal: Calculated
exp: Experimental
i, j: Component

1 Introduction

With the commercial name of Revlimid, Lenalidomide (LND) (C13H13N3O3) acts as an angiogenesis inhibitor, an antineoplastic agent as well as an immunomodulatory drug. It is the first FDA-approved oral medication for the treatment of multiple myeloma, since 2004 (Li et al., 2019). In recent years, it was also approved for the treatment of Mantle Cell Lymphoma, Myelodysplastic syndromes (MDS) and deletion 5q Myelodysplastic syndromes (Attal et al., 2012). This drug also exhibited promising therapeutic effects in other hematologic disorders. However, hydrophobicity and poor solubility of LND in water hinder its penetration into tumors; i.e. low bioavailability (less than 33%) (Yang et al., 2019). Therefore, long term usage or high doses of this drug may be accompanied by severe side effects including immune system depletion, metastasis to neighboring organs, cutaneous adverse neutropenia, deep vein thrombosis, infection, and hematological cancer (Patrizi et al., 2014).

Various approaches such as salt formation, co-crystallization, amorphous solid dispersion (ASD), and particle size reduction (micronization/nanonization) have been developed in medicinal chemistry, to enhance aqueous solubility and bioavailability (Liu et al., 2016). Diverse measures have been proposed to improve the aqueous solubility of LND and therapeutic efficacy; including, co-crystallization with various substances such as urea and 3,5-dihydroxybenzoic acid (Song et al., 2014) and gallic acid (GA), formation of different LND salts including methanesulfonate (Rangineni, 2010), sulfate, hydrochloride, and hydrosulphate (Stiegel, 2011), hydrates of benzene sulfonate and p-toluene sulfonate (Eupen, 2011) and acesulfame (Chen et al., 2019), as well as LND conjugation onto polymeric nanoparticles (such as chitosan (Gomathi et al., 2014) and LND complexing with gold ions (Arib and Spadavecchia, 2020).

Among the mentioned methods, micronization/nanonization has attracted a huge deal of attention due to enhancing the surface area of drug particles and incrementing drug solubility, hence lowering drug dosage and side effects. Supercritical fluid (SCF)-based processes are green and clean technologies for micro/nanoparticles formation. Low operational temperature, high quality products with uniform morphology and narrow size distribution, and elimination or significant reduction of used organic solvents are the main advantages of these processes (Ardestani and Amani, 2021). Supercritical carbon dioxide (sc-CO₂) is the most commonly used SFC due to its low price, mild critical pressure and temperature, environmental compatibility, non-exclusivity, non-toxicity and chemical stability (Sodeifian et al., 2016; Sodeifian et al., 2018; Sodeifian et al., 2019 ). The solubility of a drug in sc-CO₂ is the essential parameter in producing fine particles. This parameter determines the feasibility of using the sc-CO₂ process for the considered drug and also the role of sc-CO₂ in the supercritical process (as solvent, anti-solvent or reaction media) (Amani et al., 2021). Generally, RESS-based processes can be utilized for the preparation of nanoparticles and submicron drugs with high solubility in SC–CO₂. In contrast, anti-solvent processes are recommended for the preparation of materials with low solubility in SC–CO₂. To this end, the solubility of solid pharmaceuticals should be estimated in SCFs to select the proper method (Ardestani and Amani, 2021; Saadati Ardestani et al., 2020). Furthermore, solubility should be determined at a wide range of pressures and temperatures for the industrial development of supercritical processes. Given this necessity, the determination of the solubility of different drugs in sc-CO₂ has become one of the most interesting pharmaceutical research topics during the past two decades. In this regard, solubility of various drugs has been assessed since the beginning of 2020, among which; Chloroquine (Pishnamazi, 2021), Capecitabine (Ardestani et al., 2020), Montelukast (Sajadian et al., 2022); Azathioprine (Sodeifian, 2020), Temozolomide (Zabihi, 2021), Lornoxicam (Pelalak, 2021), Aprepitant (Sodeifian et al., 2017); Gliclazide and Captopril (Wang et al., 2021), Glibenclamide (Esfandiari and Sajadian, 2022), Decitabine (Pishnamazi et al., 2021); Tamoxifen (Pishnamazi, 2020), Busulfan (Pishnamazi, 2020), Fenoprofen (Zabihi et al., 2020), Salsalate (Zabihi, 2021), Lornoxicam (Pelalak, 2021), Tolmetin (Pishnamazi et al., 2020), Tenoxicam (Zabihi et al., 2021); Carbamazepine (Kalikin, 2020); Sodium valproate (Sodeifian et al., 2020); Minoxidil (Sodeifian et al., 2020); Loxoprofen (Zabihi et al., 2020), Favipiravir (Sajadian et al., 2022); ipriflavone (Wang and Su, 2020), and Methylsalicylic Acid Isomers (Wang et al., 2021) can be mentioned.

However, experimental measurement of the sc-CO₂ solubility of all the drugs in a wide range of pressure and temperature is costly, time-consuming, and even impossible in some cases. Therefore, several theoretical predictive models such as equation of states (EoSs), expanded liquid models and empirical models have been developed for correlating the sc-CO₂ solubility of various substances at different operational conditions. EoS models (cubic and non-cubic) are one of the most popular theoretical models in which sc-CO₂ is regarded as a condensed gas and the modeling is performed according to solute fugacity coefficient. Cubic EoSs can be rewritten as a cubic function of molar volume (e.g. Peng-Robinson (PR) and Soave- Redlich-Kowang (SRK)), while non-cubic models are based on statistical associating fluid theory (SAFT) (e.g. Perturbed-Chain Polar Statistical Associating Fluid Theory (PCP-SAFT)). In expanded liquid models (e.g. universal quasi-chemical (UNIQUAC) and modified Wilson's models), sc-CO₂ is considered as an expanded liquid and modelling was based on the solute activity coefficient. The necessity of knowledge on the solute physicochemical properties such as acentric factor, critical pressure and temperature, sublimation pressure and its molar volume is the main challenge of EoS and expanded liquid models. These properties are usually unknown, especially for complex pharmaceutical components, and should be computed by various group contribution (GC) methods. In return, the empirical models have been developed according to linear relationship between the logarithm of solute solubility and the sc-CO₂ density. These models only need to know pressure, temperature, and sc-CO₂ density while their correlation accuracy is comparable to the EoSs method (Zabihi, 2021). Noteworthy, the accuracy of the proposed models could be different for each pharmaceutical component, making it impossible to specify the most accurate model for the proper correlation of the sc-CO₂ solubility of all drugs (Zabihi et al., 2020). So, the correct predictive model indicating the best fitting with the experimental results was determined by comparison between the correlation and experimental results.

The sc-CO₂ solubility of many drugs has been measured and correlated as a function of pressure and temperature while no report can be found on LND solubility in sc-CO₂. Thus, this research is aimed to experimentally measure of LND solubility in sc-CO₂ at various temperatures (308–338 K) and pressures (120–300 bar). Afterward, experimental solubility results were correlated by thirty well-known empirical density-based models, EoS model (SRK) and expanded liquid models (modified Wilson's model). The results of these models were validated by computing some statistical criteria including the average absolute relative deviation (AARD%), the adjusted correlation coefficient (R_adj), and F-value.

2 Materials and methods

2.1

2.1 Materials

Lenalidomide (LND) (CAS No. 191732–72-6) was purchased from Abidi pharmaceutical company, with a minimum purity of 99%. Carbon dioxide (CO₂), with a purity of 99.98% was provided from Oxygen Novin Co. (Shiraz, Iran). Analytical-grade methanol was provided by Merck (Darmstadt, Germany). All of these compounds were used with no additional purification.

2.2

2.2 Experimental procedure for solubility determination

The experimental setup for determining the solubility of LND in sc-CO₂ is schematically depicted in Fig. 1. All the equipment, piping and connections were made from stainless steel 316 at 1/8″ in size. As can be seen in Fig. 1, after passing the CO₂ gas from the molecular sieve filter (1 μm in pore size), it enters the refrigerator with an approximate temperature of −15 °C to be liquefied. The liquid CO₂ was guided to the high-pressure reciprocating pump (an air-driven liquid pump, type-M64, Shineeast Co., Shandong, China), at the pressure of 60 bar (the CO₂ tank pressure). Using the pressure gauge (Indumart pressure gauges, Canada), and transmitter, measurements were performed at a precision of ±1 bar. Afterward, liquid CO₂ and LND (3000 mg) were homogenized with a magnetic stirrer (100 rpm) ((E-8, Alfa, D-500 180), in a cell with a capacity of 300 mL to reach an equilibrium phase. To keep the temperature at the desired level, the cell was placed in an oven equipped with a digital display whose temperature was measured with a precision of ±0.1 K. A porous filter (1 μm) was used on both sides of the cell to keep the LND in the cell and prevent its escape. CO₂ was pressurized and transferred to the cell at the appropriate pressure. Based on preliminary experiments, the time required to reach the equilibrium, the static time, was considered as 120 min; after which, saturated sc-CO₂ (600 μL) was introduced into the injection loop using a three-port two-position valve. By redirecting the injection valve, the loop was depressurized into the collection vial containing a certain volume of methanol (solvent). In this part, the micrometer valve was used for controlling the flow. In the final step, 1 mL of solvent was injected by an external needle-valve to wash the loop and the solution was collected in the vial. The final volume of the solution was 5 mL.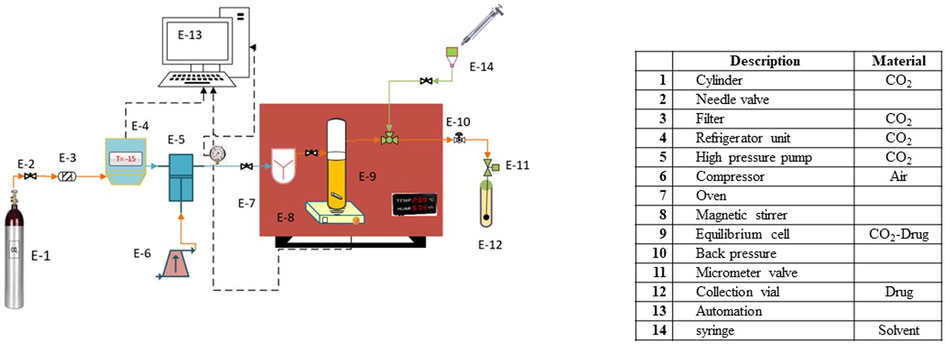

Experimental apparatus for supercritical solubility measurement.

Each experiment was carried out in triplicates and the solubility values were determined by the absorbance assays at λ_max (250 nm) on a Perkin-Elmer UV–Vis spectrophotometer (LAMBDA 365, PerkinElmer-USA) with 1 cm long quartz cell. Finally, LND solubility was calculated from its concentration using the calibration curve (with a regression coefficient of 0.996) and the UV-absorbance. The values of LND solubility in sc-CO₂ in terms of equilibrium mole fraction (y) and solubility (S (g L⁻¹)) were computed at different temperatures and pressures via the equations in the literature (Saadati Ardestani et al., 2020).

The solubility measurement device was validated by evaluating the solubility of naphthalene at 308 K and different pressures and comparing them with the reports by Iwai et al. (Iwai et al., 1991), Yamini et al. (Yamini et al., 1998) and Sodeifian et al. (Sodeifian et al., 2017), as listed in Table 1.

Table 1 Experimental solubility data of naphthalene in sc-CO₂ at 308 K and comparison with the literature data.

Pressure (MPa)^a	Iwai et al.³⁶ (y × 10³)	Yamini et al.³⁷ (y × 10³)	Sodeifian et al.³⁸ (y × 10³)	This work (y × 10³) ^a
10.7	–	11.6	11.4	11.7 ± 0.2
13.8	14.1	15.2	14.3	14.8 ± 0.3
16.8	16.5	16.2	16.6	16.1 ± 0.3
20.4	17.6	17.4	17.7	17.9 ± 0.2
24.0	–	–	–	19.9 ± 0.4

a Standard uncertainty u are u(P) = 0.1 MPa and relative uncertainty (u_r), u (y) = 0.10.

2.3

2.3 Theoretical studies

2.3.1

2.3.1 Empirical models

Numerous empirical models have been proposed for correlating the solubility of a solid solute in sc-CO₂. No need to solute properties (unlike the EoSs), simple application, and acceptable accuracy are the most important benefits, and the requirement of experimental solubility data is the only drawback of these models. Following the model proposed by Stahl et al. (Stahl et al., 1978) in 1978, several models have been developed with various adjustable parameters (in the range of 3 to 10) to enhance the correlation of experimental data.

In this research, thirty traditional empirical models are used to correlate the solubility of LND in sc-CO₂, whose mathematical formulas are presented in Table 2. According to the solubility functions (Table 2), the proposed models can be classified into five groups; (i) solubility as a function of sc-CO₂ density (Stahl et al., 1978), models with solubility dependency to sc-CO₂ density and temperature (Chrastil, 1982; Kumar and Johnston, 1988; Andonova and Chandrasekhar, 2016; Alwi and Garlapati, 2021; Del Valle and Aguilera, 1988; Sung et al., 1999; Adachi and Lu, 1983; Garlapati and Madras, 2010; Bian et al., 2016; Sparks et al., 2008; Si-Moussa et al., 2017; Bian et al., 2011; Belghait et al., 2018; Amooey, 2014 ); (ii) solubility as a function of sc-CO₂ density and pressure (Haghbakhsh et al., 2013); (iii) solubility as a function of pressure and temperature (Mitra and Wilson, 1991; Reddy et al., 2018; Gordillo et al., 1999; Yu et al., 1994; Reddy and Garlapati, 2019 ), and (iv) solubility as a function of sc-CO₂ density, pressure and temperature (Bartle et al., 1991; Méndez-Santiago and Teja, 1999; Jafari Nejad et al., 2010; Ch and Madras, 2010; Hozhabr et al., 2014; Keshmiri et al., 2014; Asgarpour Khansary et al., 2015; Sodeifian et al., 2019; Jouyban et al., 2002 ).

Table 2 Formula of the empirical models used in this work.

Empirical models
Model	Formula	Reference
Stahl et al.	$ln y = a_{0} + a_{1} ln (ρ)$	(Sajadian et al., 2022)
Chrastil	$ln y = a_{0} + a_{1} ln (ρ) + \frac{a_{2}}{T} Δ H_{t} = - a_{2} . R$	(Wang and Su, 2020)
Kumar- Johnston (K-J)	$ln y = a_{0} + a_{1} ρ + \frac{a_{2}}{T} Δ H_{t} = - a_{2} . R$	(Wang et al., 2021)
Bartle et al.	$ln \frac{y . P}{P_{ref}} = a_{0} + a_{1} (ρ - ρ_{ref}) + \frac{a_{2}}{T} Δ H_{vap} = - a_{2} . R$	(Haghbakhsh et al., 2013)
Mendez-Santiago and Teja	$T ln (y . P) = a_{0} + a_{1} ρ + a_{2} T$	(Mitra and Wilson, 1991)
Andonova and Garlapati	$y = a_{0} ρ_{r}^{a_{1}} T_{r}^{a_{2}}$	(Saadati Ardestani et al., 2020)
Alwi and Garlapati	$y = \frac{1}{(ρ_{r} T_{r})} exp (a_{0} + \frac{a_{1}}{T_{r}} + a_{2} ρ_{r})$	(Iwai et al., 1991)
del Valle and Aguilera	$ln y = a_{0} + a_{1} ln (ρ) + \frac{a_{2}}{T} + \frac{a_{3}}{T^{2}}$	(Yamini et al., 1998)
Sung and Shim	$ln y = (a_{0} + \frac{a_{1}}{T}) ln (ρ) + \frac{a_{2}}{T} + a_{3}$	(Stahl et al., 1978)
Jafari Nejad et al.	$ln y = a_{0} + a_{1} P^{2} + a_{3} T^{2} + a_{4} ln (ρ)$	(Reddy and R.S., Chandrasekhar Garlapati, , 2018)
Ch and Madras	$y = {(\frac{P}{P^{ref}})}^{(a_{0} - 1)} exp (\frac{a_{1}}{T} + a_{2} ρ + a_{3})$	(Gordillo et al., 1999)
Hozhabr et al.	$In y = a_{0} + \frac{a_{1}}{T} + \frac{a_{2} ρ}{T} - a_{3} In P$	(Yu et al., 1994)
Mitra and Wilson	$ln S = a_{0} ln (P) + a_{1} T + a_{2} T P + \frac{a_{3} P}{T} + a_{4}$	(Sparks et al., 2008)
Adachi and Lu	$ln y = a_{0} + (a_{1} + a_{2} ρ + a_{3} ρ^{2}) ln ρ + \frac{a_{4}}{T}$	(Chrastil, 1982)
Garlapati and Madras	$ln y = a_{0} + (a_{1} + a_{2} ρ) ln ρ + \frac{a_{3}}{T} + a_{4} ln (ρ T)$	(Kumar and Johnston, 1988)
Keshmiri et al.	$ln y = a_{0} + \frac{a_{1}}{T} + a_{2} P^{2} + (a_{3} + \frac{a_{4}}{T}) ln (ρ)$	(Reddy and Garlapati, 2019)
Khansary et al.	$ln y = \frac{a_{0}}{T} + a_{1} P + \frac{a_{2} P^{2}}{T} + (a_{3} + a_{4} P) ln (ρ)$	(Bartle et al., 1991)
Bian et al. (2016)	$ln y = a_{0} + \frac{a_{1}}{T} + \frac{a_{2} ρ}{T} + (a_{3} + a_{4} ρ) ln ρ$	(Andonova and Chandrasekhar, 2016)
Reddy et al.	$y = (a_{0} + a_{1} P_{r}) T_{r}^{2} + (a_{2} + a_{3} P_{r}) T_{r} + a_{5}$	(Si-Moussa et al., 2017)
Sodeifian et al.	$ln y = a_{0} + a_{1} \frac{P^{2}}{T} + a_{2} ln (ρ T) + a_{3} ρ ln (ρ) + a_{4} P ln (T) + a_{5} \frac{ln (ρ)}{T}$	(Méndez-Santiago and Teja, 1999)
Yu et al.	$y = a_{0} + a_{1} P + a_{2} P^{2} + a_{3} P T (1 - y) + a_{4} T + a_{5} T^{2}$	(Belghait et al., 2018)
Gordillo et al.	$ln y = a_{0} + a_{1} P + a_{2} P^{2} + a_{3} P T + a_{4} T + a_{5} T^{2}$	(Bian et al., 2011)
Jouyban et al.	$ln y = a_{0} + a_{1} P + a_{2} P^{2} + a_{3} P T + a_{4} \frac{T}{P} + a_{5} ln (ρ)$	(Jafari Nejad et al., 2010)
Sparks et al.	$\frac{S}{ρ_{c}} = ρ_{r}^{(a_{0} + a_{1} ρ_{r} + a_{2} ρ_{r}^{2})} exp (a_{3} + \frac{a_{4}}{T_{r}} + \frac{a_{5}}{T_{r}^{2}})$	(Alwi and Garlapati, 2021)
Si-Moussa et al.	$ln y = a_{0} + a_{1} ρ + a_{2} ρ^{2} + a_{3} ρ T + a_{4} \frac{T}{ρ} + a_{5} ln (ρ)$	(Del Valle and Aguilera, 1988)
Reddy and Garlapati	$y = (a_{0} + a_{1} P_{r} + a_{2} P_{r}^{2}) T_{r} + (a_{3} + a_{4} P_{r} + a_{5} P_{r}^{2})$	(Amooey, 2014)
Bian et al. (2011)	$S = ρ^{(a_{0} + a_{1} ρ + \frac{a_{2}}{ln T})} exp (\frac{a_{3} + a_{4} ρ}{T} + a_{5})$	(Sung et al., 1999)
Belghait et al.	$ln y = a_{0} + a_{1} ρ + a_{2} ρ^{2} + a_{3} ρ T + a_{4} T + a_{5} T^{2} + a_{6} ln (ρ) + \frac{a_{7}}{T}$	(Adachi and Lu, 1983)
Amooey	$ln y = (\frac{a_{0} + \frac{a_{1}}{ρ} + \frac{a_{1}}{ρ^{2}} + a_{3} ln (T) + a_{4} {(ln T)}^{2}}{1 + \frac{a_{5}}{ρ} + a_{6} ln T + a_{7} {(ln T)}^{2} + a_{8} ln T})$	(Garlapati and Madras, 2010)
Haghbakhsh et al.	$y = 10^{- 5} (a_{0} + a_{1} P + a_{2} ρ + a_{3} P^{2} + a_{4} ρ^{2} + a_{5} P ρ + a_{6} P^{3} + a_{7} ρ^{3} + a_{8} P ρ^{2} + a_{9} P^{2} ρ$	(Bian et al., 2016)

In these models, y and S represent the equilibrium mole fraction and solubility of the solute (kg m⁻³), ρ, ρ_ref” and ρ_r (=ρ/ρ_c) also denote the sc-CO₂ density, the reference density (700 kg m⁻³) and reduced density in which ρ_c is the sc-CO₂ critical density (467.6 kg m⁻³), respectively. T and T_r (=T/T_c) are temperature (K) and reduced temperature in which T_c is the sc-CO₂ critical temperature (304 K), P, P_ref, and P_r (=P/P_c) are pressure (bar), reference pressure (1 bar), and reduced pressure in which P_c is the sc-CO₂ critical pressure (73.8 bar).

Empirical density-based models rely on simple error minimization and their adjustable parameters can be optimized through the simulated annealing (SA) algorithm in MATLAB software.

2.3.2

2.3.2 Equation of state-based (EOS) model (Soave- Redlich-Kowang (SRK))

Equality of the solute fugacity coefficient in the two phases (solvent (1) - solute (2)) is the vital condition to achieve equilibrium solubility. Equilibrium solute solubility in sc-CO₂ (y₂) can be expressed by Eq. (1), through considering some assumptions such as the insolubility of sc-CO₂ in the solute phase, the purity and incompressibility of the solute, no dependency of the solute molar volume to pressure and very little solute vapor pressure.

(1)

y_{2} = \frac{P_{2}^{sub} (T)}{P} \frac{φ_{2}^{sat, s} (T)}{φ_{2} (T, P, y)} exp [\frac{ν_{2}^{s} (P - P_{2}^{sub} (T))}{R T}]

where P, T, and R are pressure (MPa), temperature (K) and gas constant (8.314 J mol⁻¹ K⁻¹), respectively.

v_{2}^{s}

(m³ mol⁻¹) denotes the solute molar volume and

P_{2}^{sub} (T)

is the solute sublimation pressure, estimated by the Immirzi method (Immirzi and Perini, 1977) and Ambrose-Walton corresponding states method (Poling, 2001), respectively (Table 3).

φ_{2}^{sat, s} (T)

also stands for the solute saturation fugacity coefficient which can be assumed as unity for solutes with very small sublimation pressures.

ϕ_{2} (T, P, y)

is the solute fugacity coefficient in the sc-CO₂ phase was computed by SRK-EoS (Soave, 1972); combined with the van der Waals mixing rule. Using this EoS,

ϕ_{2} (T, P, y)

was calculated by the following equation (Amani and Saadati Ardestani, 2021):

(2)

RT ln φ_{i} = - R T ln Z + \int_{V}^{\infty} [{(\frac{\partial P}{\partial n_{i}})}_{T, V, n_{j} \neq n_{i}} - \frac{RT}{V}] d V

where Z (=PV/RT), n_i, and V are the compressibility factor, the moles number of species i and the sc-CO₂ molar volume, respectively.

The relations of SRK-EoS is as follows:

(3)

P = \frac{RT}{ν - b} - \frac{a (T)}{ν (ν + b)}

Here, a(T) and b, can be defined by the following relations for a single component:

(4)

[\begin{matrix} a (T) = \frac{0.42747 R^{2} T_{c}^{2}}{P_{c}} \times α (T_{r, ω}) & α (T_{r, ω}) = {[1 + m (1 - T_{r}^{0.5})]}^{2} & m = 0.480 + 1.574 ω - 0.176 ω^{2} \\ b = \frac{0.08664 R T_{c}}{P_{c}} \end{matrix}]

In this research, critical pressure (P_c), critical temperature (T_c), boiling point (T_b) and melting point (T_m) of LND were computed using Marrero and Gani contribution method (Marrero and Gani, 2001). Also, LND acentric factor (ω) was estimated by Constantinou - Gani method (Constantinou and Gani, 1994). All the mentioned physical and critical properties of LND are reported in Table 3.

For the binary system (LND/sc-CO₂), a(T) and b can be defined by the van der Waals (vdW) mixing rule considering two parameters (Van der Waals, 1873):

(5)

a_{m} = \sum_{j} y_{i} y_{j} \sqrt{a_{i} a_{j}} (1 - k_{ij})

(6)

b_{m} = \sum_{j} y_{i} y_{j} \frac{(b_{i} + b_{j})}{2} (1 - l_{ij})

where

l_{ij}

and

k_{ij}

are the binary interaction parameters which were optimized by minimizing the AARD% value, using the simulated annealing (SA) algorithm (Sodeifian et al., 2017).

2.3.3

2.3.3 Expanded liquid theory (Wilson’s model)

Due to the relatively high density of supercritical fluids and their proximity to liquids density, they can be considered as an expanded liquid (Higashi et al., 2001). In this case, equality of the fugacity of the solute in the solid phase $(f_{2}^{S})$ with the fugacity of the solute in the SCF (liquid) phase $(f_{2}^{L = S C F})$ was used for the thermo-dynamical description of the equilibrium state between the solute and sc-CO₂. Regarding the negligible solubility of sc-CO₂ in the pure solid phase, the term of $f_{2}^{S}$ can be considered equal to the fugacity of the pure solid solute $(f_{2}^{0 S})$ . The fugacity of the solute in the liquid phase can be expressed based on the solute activity coefficient:

(7)

f_{2}^{L} = γ_{2} y_{2} f_{2}^{0 L}

which can be rewritten as:

(8)

f_{2}^{0 S} = γ_{2} y_{2} f_{2}^{0 L}

where

γ_{2}

y_{2}

and

f_{2}^{0 L}

are the solute activity coefficient, the solute mole fraction (solubility) and the fugacity of the pure solid solute in the expanded liquid phase, respectively. Prausnitz et al. (Prausnitz et al., 1998) defined a relationship between the

f_{2}^{0 L}

and

f_{2}^{0 S}

as:

(9)

ln (\frac{f_{2}^{0 S}}{f_{2}^{0 L}}) = \frac{- Δ H_{2}^{f}}{R} (\frac{1}{T} - \frac{1}{T_{m}}) - \frac{Δ c_{p}}{RT} (\frac{T - T_{m}}{T}) + \frac{Δ c_{p}}{R} l n (\frac{T}{T_{m}})

where

Δ H_{2}^{f}

is the LND heat of fusion which was calculated via the Marrero and Gani group contribution method, as 46.87 kJ mol⁻¹. Also,

T_{m}

and

Δ c_{p}

are the melting point and the variation of heat capacity of the solute, respectively. Ignoring

Δ c_{p}

and considering the condition of infinite dilution due to very poor solubility of the solid solute in sc-CO₂ (Nasri et al., 2013), the solute solubility (

y_{2}

) can be obtained using a combination of Eqs. (8) and (9), in which

γ_{2} ≃ γ_{2}^{\infty}

(10)

y_{2} = \frac{1}{γ_{2}^{\infty}} exp (\frac{- Δ H_{2}^{f}}{R} (\frac{1}{T} - \frac{1}{T_{m}}))

Here, $γ_{2}^{\infty}$ is the activity coefficient of the solid solute at the infinite dilution condition, which in this study was determined using the modified Wilson’s model (Nasri, 2018). This model is somewhat based on Flory’s theory (combinatorial contribution) with the following its usual form according to excess Gibbs energy (G^E):

(11)

\frac{G^{E}}{RT} = - y_{1} ln (y_{1} + y_{2} Λ_{12}) - y_{2} ln (y_{1} Λ_{21} + y_{2})

Here, Λ₁₂ and Λ₂₁ are the adjustable parameters which depend on the molar volume of the pure sc-CO₂ $(υ_{1})$ and the solid solute $(υ_{2})$ and also to characteristic energy differences as:

(12)

Λ_{12} \equiv \frac{υ_{2}}{υ_{1}} exp (- \frac{λ_{12} - λ_{11}}{RT})

(13)

Λ_{21} \equiv \frac{υ_{1}}{υ_{2}} exp (- \frac{λ_{21} - λ_{22}}{RT})

In the above relations, λ is the interaction energy between the specified species in the subscripts (sc-CO₂ (1) and solid solute (2)) (Prausnitz et al., 1998). After differentiation of the excess Gibbs energy function (Eq. (11)) and rearrangement of the equation, the solute activity coefficient ( $γ_{2}$ ) can be expressed by:

(14)

ln γ_{2} = - ln (y_{2} + y_{1} Λ_{21}) - y_{1} [\frac{Λ_{12}}{y_{1} + y_{2} Λ_{12}} - \frac{Λ_{21}}{y_{2} + y_{1} Λ_{21}}]

According to Assael et al. (Assael et al., 1996), for infinite dilution, the above relation can be summarized:

(15)

ln γ_{2}^{\infty} = 1 - Λ_{12} - ln Λ_{21}

Regardless of the terms of λ₁₁ and λ₂₂ at the infinite dilution condition, (Eq. (12)) and (Eq. (13)) can be written in reduced forms as:

(16)

Λ_{12} = υ_{2} ρ_{c 1} ρ_{r} exp (- \frac{λ_{12}^{'}}{T_{r}})

(17)

Λ_{21} = \frac{1}{υ_{2} ρ_{c 1} ρ_{r}} exp (- \frac{λ_{21}^{'}}{T_{r}})

where

ρ_{r} (= \frac{ρ}{ρ_{cr}})

is the reduced density of the sc-CO₂ and

ρ_{cr}

is its critical density. Additionally,

{λ'}_{12} (= \frac{λ_{12}}{R T_{cr}})

and

{λ^{'}}_{21} (= \frac{λ}{R T_{cr}})

are the dimensionless interaction energies. Nasri (Nasri, 2018) applied a simple correlation for expressing the molar volume

(υ_{2}),

as a linear function of the reduced density:

(18)

υ_{2} = α ρ_{r} + β

Accordingly, the Eqs.16 and 17 become:

(19)

Λ_{12} = (α ρ_{r} + β) ρ_{c 1} ρ_{r} exp (- \frac{λ_{12}^{'}}{T_{r}})

(20)

Λ_{21} = \frac{1}{(α ρ_{r} + β) ρ_{c 1} ρ_{r}} exp (- \frac{λ_{21}^{'}}{T_{r}})

where

α

β

{λ'}_{12}

and

{λ'}_{21}

are the model parameters obtained via regression.

The accuracy and precision of the applied models in correlate the sc-CO₂ solubility of solids were assessed by the statistical criteria including the AARD%, R_ad_j and F-value, as follows (Jouyban et al., 2002):

(21)

AARD % = \frac{1}{N - Z} \sum_{i = 1}^{n} (|\frac{y_{i, c a l} - y_{i, exp}}{y_{i, exp}}|) \times 100 %

where y_cal and y_exp stand for computational and experimental solubility values in terms of solute mole fraction and N is the number of data points for each set.

(22)

R_{adj} = \sqrt{|R^{2} - (Q (1 - R^{2}) / (N - Q - 1))|}

Here, Q is the number of independent variables of each model and R² indicates the correlation coefficient which can be calculated by the following equation:

(23)

R^{2} = 1 - \frac{S S_{E}}{S S_{T}}

In this relation, SS_E and SS_T are the error and total sum of squares, respectively.

The parameter of F-value indicates the capability of the model in fitting the experimental data:

(24)

F - v a l u e = \frac{S S_{R} / Q}{S S_{E} / (N - Q - 1)} = \frac{M S_{R}}{M S_{E}}

where SSR stands for the regression sum of squares; MS_R and MS_E represent the mean square regression and the mean square residual, respectively. F-value is distributed as an F statistic function with Q and N-Q-1 degrees of freedom (Montgomery, 2012).

3 Results and discussions

3.1

3.1 Experimental solubility determination

The experimental solubility of LND in sc-CO₂ was determined in terms of equilibrium mole fraction (y) at different temperatures (308, 318, 328, and 338 K) over a pressure range of 120–300 bar. Each experiment was repeated three times and the mean values with a relative standard deviation of less than 3% were reported in Table 4. Sc-CO₂ density was obtained from the NIST chemistry web-book (http://webbook.nist.gov/chemistry). Furthermore, equilibrium solubility, S, of LND in sc-CO₂ was also computed as presented in Table 4.

Table 4 Solubility data of LND in sc-CO₂ at different temperatures (T) and pressures (P).

T (K) ^a	P (bar) ^a	ρ (kg m^—3) ^b	y × 10^4c	Standard deviation of the mean, SD ( $\bar{y}$ ) × (1 0 ⁴)	Expanded uncertainty × 10⁴	S × 10 (g/l) ^d
308	120	768.42	0.17	0.0002	0.011	0.7704
	150	816.06	0.22	0.0042	0.016	1.0596
	180	848.87	0.31	0.0051	0.060	1.5526
	210	874.40	0.36	0.0075	0.052	1.8567
	240	895.54	0.45	0.0067	0.082	2.3765
	270	913.69	0.56	0.0105	0.033	3.0168
	300	929.68	0.70	0.0085	0.079	3.8354
318	120	659.73	0.09	0.0009	0.037	0.3506
	150	743.17	0.17	0.0021	0.064	0.7458
	180	790.18	0.30	0.0048	0.124	1.3987
	210	823.71	0.39	0.0052	0.098	1.8949
	240	850.10	0.51	0.0091	0.148	2.5567
	270	872.04	0.67	0.0086	0.057	3.4449
	300	890.92	0.83	0.0107	0.113	4.3582
328	120	506.85	0.04	0.0008	0.029	0.1201
	150	654.94	0.14	0.0023	0.017	0.5415
	180	724.13	0.31	0.0056	0.123	1.3246
	210	768.74	0.44	0.0090	0.129	1.995
	240	801.92	0.58	0.0103	0.094	2.7426
	270	828.51	0.80	0.0099	0.119	3.9077
	300	850.83	0.94	0.0189	0.079	4.7137
338	120	384.17	0.02	0.0032	0.327	0.0456
	150	555.23	0.10	0.0019	0.109	0.3285
	180	651.18	0.32	0.0063	0.058	1.2302
	210	709.69	0.52	0.0096	0.109	2.1768
	240	751.17	0.72	0.0136	0.049	3.1888
	270	783.29	0.93	0.0153	0.100	4.2939
	300	809.58	1.08	0.0129	0.122	5.1532

a Standard uncertainty u are u(T) = 0.1 K; u(P) = 1 bar; u_r(ρ) = 0.002. Also, standard uncertainties are obtained below 3% for mole fractions and solubilities.

b Values of sc-CO₂ density (ρ) were obtained from NIST web-book (http://webbook.nist.gov/chemistry).

c y is equilibrium mole fraction of LND in sc-CO₂.

d S is equilibrium solubility of LND in sc-CO₂.

Based on Table 4, the maximum solubility of LND in sc-CO₂ is 1.08 × 10⁻⁴ in terms of equilibrium mole fraction, which was achieved at the highest temperature and pressure (338 K and 300 bar). The influence of temperature and pressure on LND solubility in sc-CO₂ can be analyzed in Fig. 2. Increasing the sc-CO₂ pressure/density at a constant temperature enhanced the solubility in sc-CO₂, which was intensified at higher temperatures. Reducing the intermolecular distance of CO₂ molecules and increasing their density at higher pressures led to stronger LND (solute)/sc-CO₂ (solvent) interactions, improving the solvation power of sc-CO₂ (Dong et al., 2010). However, the effect of temperature on solute solubility in sc-CO₂ is more complex, which can be explained according to its inverse effect on two competing parameters of solute vapor pressure (volatility) and sc-CO₂ density (solvency power). Temperature elevation had a positive effect on solute solubility while reducing the second one and limiting the solubility. This opposite trend was usually demonstrated by the presence of a crossover point which is around 18 MPa for the LND/sc-CO₂ binary system (Fig. 2b). At pressures lower than this point, the effect of sc-CO₂ density is dominant and temperature increment declined the solubility. However, at higher pressures, the sensitivity of sc-CO₂ density to temperature got lower, and solute volatility was the determinant parameter. Therefore, temperature increment above the crossover pressure enhanced the solubility ( $y_{338} ≻ y_{328} ≻ y_{318} ≻ y_{308}$ ). The dual influence of temperature on the solubility of different solutes in sc-CO₂ was previously reported as well (Sodeifian et al., 2018; Jin et al., 2014).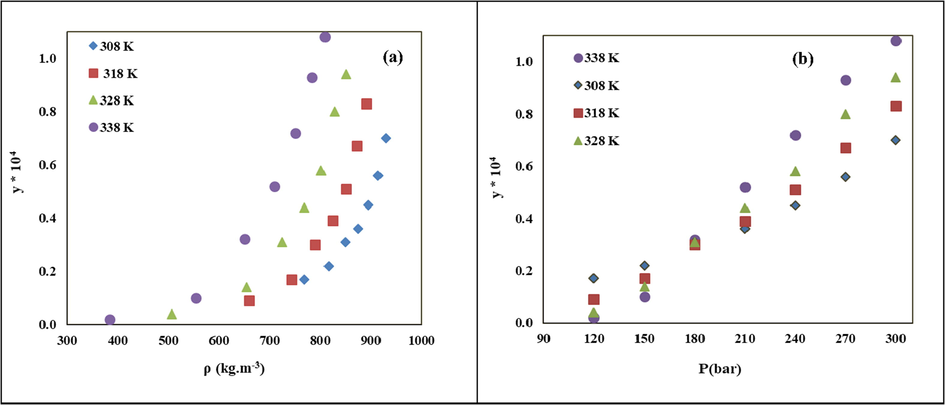

LND solubility at various temperatures vs. (a) sc-CO2 density and (b) pressure.

3.2

3.2 Correlation of solubility data

Due to the high time and cost required for solubility correlation, many theoretical models have been proposed. As previously mentioned, LND solubility in sc-CO₂ was correlated using common empirical models, equation of state (SRK-EoS), and modified Wilson’s model.

3.2.1

3.2.1 Empirical (Density-based) models

In this study, thirty empirical models were applied for correlating the experimental solubility data of LND in sc-CO₂ (Table 2). Obtained solubility values of these models were compared with the experimental data and the results were presented in terms of AARD%, R_adj and F-value. The adjustable parameters along with AARD%, R_adj and F-value of each empirical model are reported in Table 5. These models were compared in terms of R_adj value in the range of 0.90 to 1.0, as shown in Fig. 3. Models proposed by Alwi and Garlapati, Sung and Shim, Ch and Madras, Hozhabr et al., Garlapati and Madras, Keshmiri et al., Sparks et al., Reddy and Garlapati, Bian et al. (2011) and Belghait et al. offered R_adj value above 0.99. Among these, Keshmiri et al. model with the highest R_adj of 0.995 and low AARD% value of 8.535 and the highest F-value of 553.991 showed the smallest deviation from the experimental data. After that, Bian et al. (2011) model (AARD% = 7.781) and Reddy and Garlapati model (AARD% = 10.589) with R_adj values of 0.994 represent high correlation accuracy. Unexpectedly, the Haghbakhsh et al. model with the highest number of adjustable parameters did not represent an acceptable performance (AARD% = 17.47, R_adj = 0.857). Moreover, the solubility values correlated via the best fitting models with different numbers of adjustable parameters were compared with the experimental findings in Fig. 4.

Table 5 Adjustable parameters, AARD%, R_adj and F-value of the (LND/sc-CO₂) binary system achieved various empirical models.

Model	Adjustable parameters										AARD(%)	R_adj	F-value
Model	$a_{0}$	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$	$a_{7}$	$a_{8}$	$a_{9}$	AARD(%)	R_adj	F-value
Stahl et al.	−9.402	4.297	–	–	–	–	–	–	–	–	47.730	0.128	1.224
Chrastil	9.283	6.463	−5.747e + 3	–	–	–	–	–	–	–	15.093	0.983	263.918
Kumar and Johnston	0.594	9.177	−5.801e + 3	–	–	–	–	–	–	–	9.076	0.990	443.568
Bartle et al.	9.631e + 3	13.744	−8.357e + 3	–	–	–	–	–	–	–	16.409	0.982	249.423
Mendez-Santiago and Teja Andonova and Garlapati	−1.158e + 4 1.346e + 13	0.417e + 4 6.480	20.901 17.890	– -	– -	– -	– -	– -	– -	– -	11.867 14.620	0.986 0.98	336.071 263.97
Alwi and Garlapati	−5.555	−20.589	5.025e3	–	–	–	–	–	–	–	8.210	0.991	498.26
del Valle and Aguilera	73.310	6.531	−47149.226	6.683e + 6	–	–	–	–	–	–	12.738	0.979	159.949
Sung and Shim	3.089	−3734.650	–23.748	9921.15	–	–	–	–	–	–	11.268	0.993	515.400
Jafari Nedjad et al.	−16.307	6.968e-7	6.817e-4	5.247	–	–	–	–	–	–	9.886	0.987	269.413
Ch and Madras	1.314	−5.339	8.255	−1.789	–	–	–	–	–	–	8.525	0.992	408.803
Hozhabr et al.	6.460	−7881.083	2822.879	−0.170	–	–	–	–	–	–	7.998	0.993	513.477
Mitra and Wilson	8.660	2.65e-2	7.19e-5	−51.758	–	–	–	–	–	–	36.237	0.968	102.577
Adachi and Lu	9.804	1.934	11.798	−4.692	−5800.866	–	–	–	–	–	7.789	0.988	238.143
Garlapati and Madras Keshmiri et al.	−231.566 1.366	222.734 −3370.615	7.938 5.486e-6	−5228.331 −18.532	2.953 7787.419	– -	– -	– -	– -	– -	8.037 8.535	0.991 0.995	306.508 553.991
Khansary et al.	−3089.229	−7.56e-4	2.585e + 3	6.343	−0.0156	–	–	–	–	–	9.711	0.990	271.296
Bian et al. (2016)	10.248	−5861.46	−36.812	2.975	7.793	–	–	–	–	–	8.108	0.988	239.967
Reddy et al. (2018)	0.00145	0.000202	−0.00364	−0.000186	0.00218	–	–	–	–	–	12.412	0.985	174.016
Sodeifian et al.	−27.75	−0.012	2.414	−3.286	4.57e-3	242.495	–	–	–	–	11.450	0.990	231.4
Yu et al.	1.393e-5	−3.881e-8	2.474e-10	1.14e-9	4.031e-9	−5.11e-10	–	–	–	–	19.413	0.926	28.115
Gordillo et al.	3.484	−0.0748	−6.318e-5	3.546e-4	−0.0397	−6.054e-5	–	–	–	–	19.615	0.961	62.274
Jouyban et al.	0.151	−13.317	−2.37e-5	6.098e-5	−0.0835	11.273	–	–	–	–	11.836	0.990	238.13
Sparks et al.	2.309	10.820	−1.92e5	23.57	–22.35	1.127	–	–	–	–	8.330	0.993	330.33
Si-Moussa et al. Reddy and Garlapati	−15.335 8.766e-5	−8.059 1.16–4	−4.377 6.07e-5	0.0435 6.918e-5	0.0165 1.30e-4	14.814 6.11e-5	– -	– -	– -	– -	10.115 10.589	0.984 0.994	146.014 353.960
Bian et al. (2011)	−20.634	−2.146	116.745	−9.455e3	4.196e3	16.837	–	–	–	–	7.781	0.994	430.118
Belghait et al.	−25.513	0.264	4.248	1.829ee4	0.0196	6.224e5	1.98	26.506	–	–	7.516	0.991	195.48
Amooey	−8.75e15	−1.824e15	8.547e14	1.657e14	−3.96e34	−1.920e14	−1.60e14	4.33e13	7.247e12	–	12.180	0.979	70.317
Haghbakhsh et al.	5.854	−0.238	25.612	7.32e4	−103.85	0.471	6.22e6	15.85	0.694	−5e-3	17.470	0.857	8.48

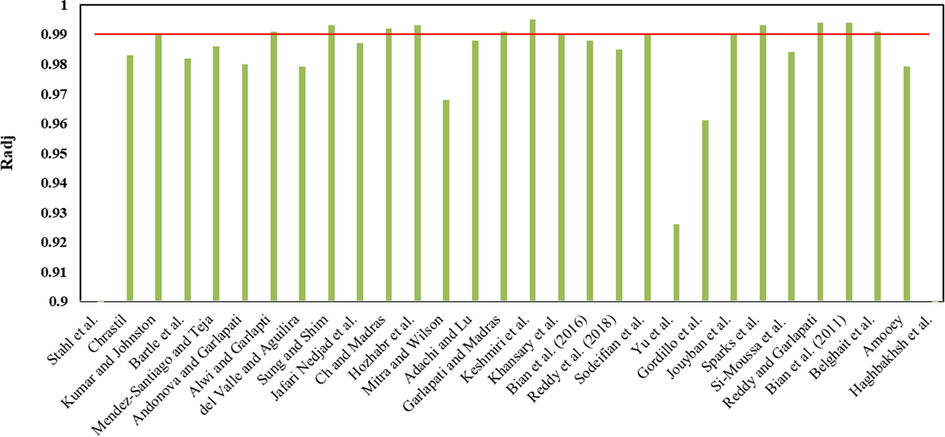
Comparison the empirical models for correlating the solubility of LND in sc-CO2 in terms of Radj.

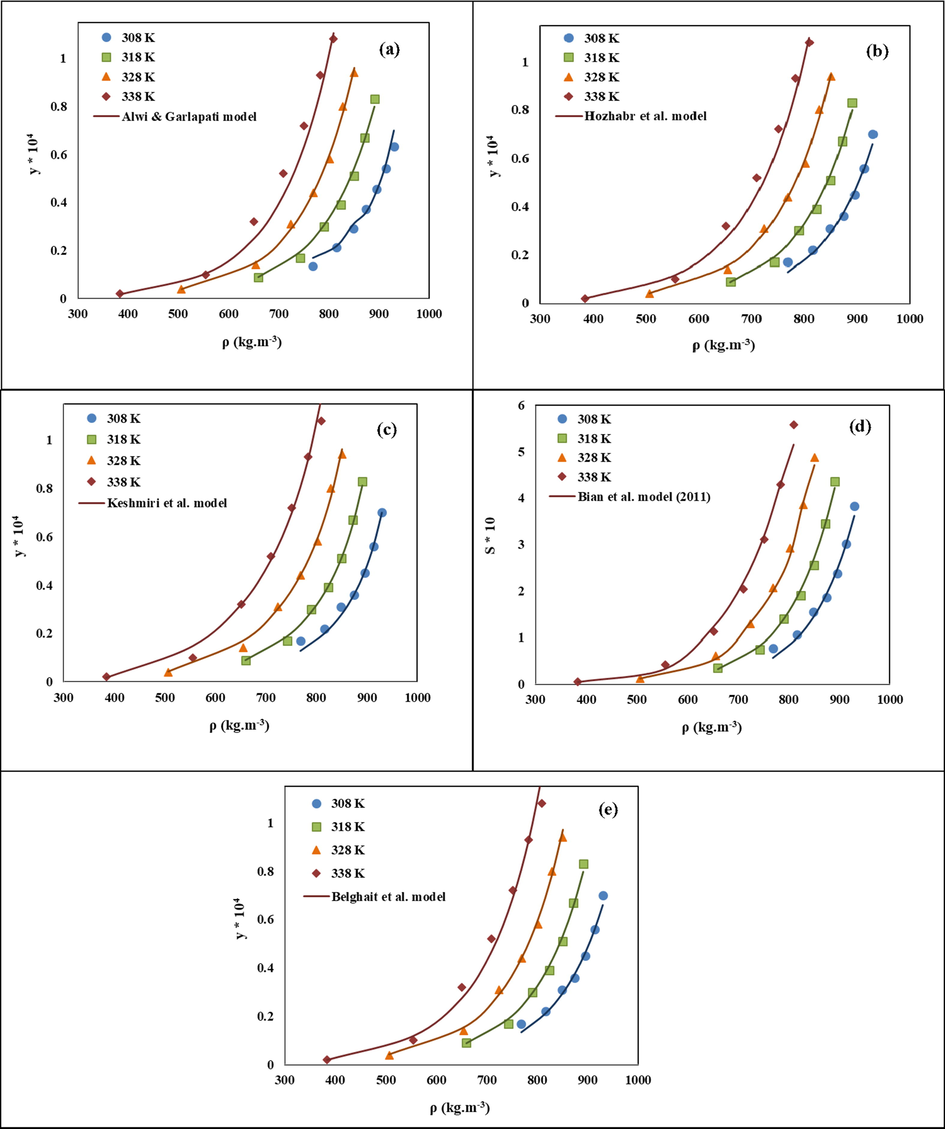
Comparison of experimental (points) and calculated (line) solubility of LND in the sc-CO2: a) Alwi and Garlapati, b) Hozhabr et al., c) Keshmiri et al., d) Bian et al., e) Belghait et al., models at various conditions.

The total mixing heat (ΔH_t) of the LND/sc-CO₂ binary system can be calculated using a₂ adjustable parameter of Chrastil and also Kumar- Johnston models ( $Δ H_{t} = - a_{2} . R$ ). The vaporization enthalpy (ΔH_va_p) of this system can be estimated by utilization of the adjustable parameter of the Bartle model ( $Δ H_{vap} = - a_{2} . R$ ). Furthermore, solvation enthalpy (ΔH_sol) can be obtained by subtraction of vaporization enthalpy from the total reaction heat, based on Hess's rule. The total mixing heat of this binary system is obtained as 47.8 kJ mol⁻¹ and 48.2 kJ mol⁻¹ according to Chrastil and also Kumar- Johnston models, which exhibited good consistency with each other. Similarly, vaporization and solvation enthalpies were computed as 69.5 kJ mol⁻¹ and −21.5 kJ mol⁻¹ (based on the mean value of the obtained ΔH_total (48 kJ mol⁻¹)), respectively. LND evaporation and solvation were endothermic and exothermic processes, respectively. Also, the resulting solvation energy indicates the presence of remarkable intermolecular interactions between the LND and sc-CO₂ molecules in the supercritical fluid phase (Hojjati et al., 2007).

3.2.2

3.2.2 Equation of state (SRK-EoS) based model

Among the available cubic equation of states, SRK-EoS combined with vdW2 mixing rule was selected for correlating of LND solubility in sc-CO₂. The SRK-EoS-correlated solubility data are presented in Fig. 5 at different temperatures (308, 318, 328, and 338 K). As can be seen, correlated solubility values by SRK-EoS did not match the experimental data.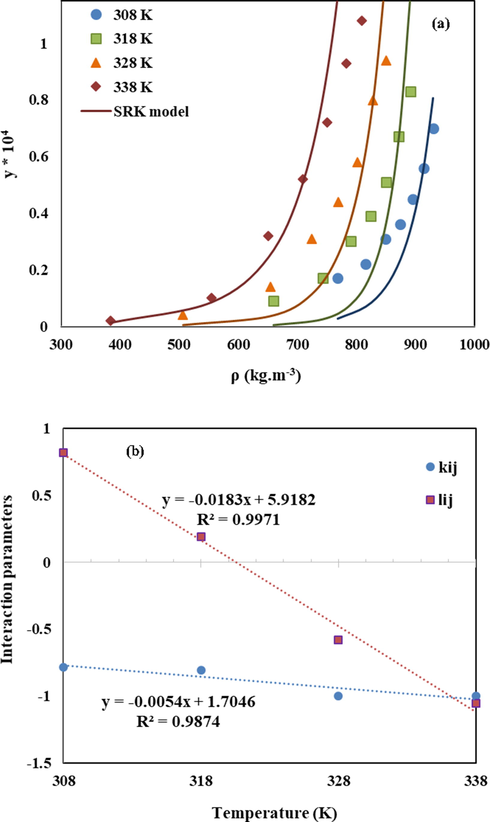

(a) Comparison of experimental (points) and calculated (line) solubility of LND in sc-CO2 based on SRK-EoS model. (b) Linear function of lij and kij versus temperature.

The optimum interaction parameters ( $l_{ij}$ and $k_{ij}$ ) of this model were obtained by minimizing the difference between the experimental LND solubility values and the calculated ones. The optimized values of these binary parameters as well as the statistical parameters (AARD%, R_adj and F-value) of the SRK-EoS are reported in Table 6. Generally, the $l_{ij}$ and $k_{ij}$ interaction parameters are linear functions of temperature, in which the slope and intercept values of these linear functions were estimated by linear regression analysis. Obtained functions for LND/sc-CO₂ binary system were as follows, as also shown in Fig. 5b:

(25)

l_{ij} = - 0.0054 T + 1.7046

(26)

k_{ij} = - 0.0183 T + 5.9182

Table 6 Correlation results for solubility of LND in sc-CO₂ by SRK combined with the vdW2 mixing rule.

Model	Parameter	T = 308 K	T = 318 K	T = 328 K	T = 338 K
SRK- vdW2	$k_{12}$	−0.7859	−0.8057	−0.9995	−1
	$l_{12}$	0.8194	0.1946	−0.5784	−1.0564
	AARD/%	39.17	49.89	45.50	29.27
	F value	798.22	630.14	599.74	688.01
	R_adj	0.983	0.974	0.978	0.990

Accordingly, these equations can be applied for estimating the solubility of LND in sc-CO₂ in the temperature range of 308–338 K. It is clear that both interaction parameters were descending functions of temperature.

3.2.3

3.2.3 Modified Wilson’s model

Optimized adjustable parameters (α, β, Λ^'₁₂ and Λ^'₂₁) and the statistical parameters (AARD%, R_adj, and F-value) of the modified Wilson’s model are reported in Table 7 for the LND/sc-CO₂ binary system. The correlation results are also represented in Fig. 6. According to the statistical parameters of AARD% (5.926), R_adj (0.995) and F-value (1275.581), it can be concluded that Wilson’s model possesses proper accuracy and high precision for correlating the solubility of LND in sc-CO₂. Furthermore, the interaction parameters (Λ₁₂ and Λ₂₁ $)$ were computed (Eqs. (19) and (20)) for each data point of the LND/sc-CO₂ system and the obtained ranges for the Λ₁₂ and Λ₂₁ are 3.906 to 10.985 and 0.025 × 10⁻⁴ to 0.180 × 10⁻⁴, respectively. The parameter of Λ₂₁is significantly smaller than Λ₁₂ which is in accordance with the previously reported data, confirming the higher value of Λ₁₂ $,$ as the interaction parameter of the solvent (1) around the solid solute (2), for complex solute molecules (Sodeifian et al., 2020; Higashi et al., 2001; Nasri, 2018 ).

Table 7 Correlation results for solubility of LND in sc-CO₂ by modified Wilson’s model.

Model	α	β	Λ^'₁₂	Λ^'₂₁	AARD/%	F value	R_adj
Modified Wilson	−7.194	1.788	−1.166	11.803	5.926	1275.581	0.995

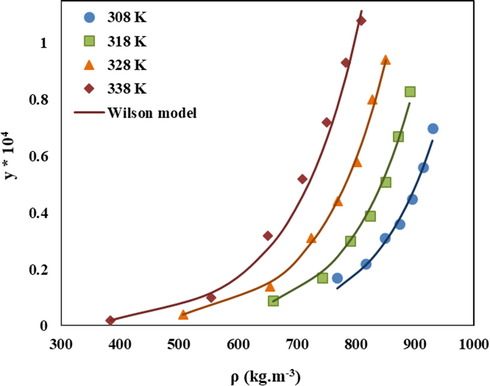
Comparison of experimental (points) and calculated (line) solubility of LND in sc-CO2 based on modified Wilson’s model.

Comparing the statistical criteria of all applied models, it can be concluded that the modified Wilson’s model with the lowest AARD% (5.926) along with the highest R_adj (0.995) and F-value, followed by Keshmiri et al. model with the same R_adj value and low AARD% (8.535) exhibited the lowest deviation from the experimental data and can be reliably used to correlate the solubility of LND in sc-CO₂.

4 Conclusion

In the present research, the solubility of Lenalidomide (LND), as an anti-cancer drug, in supercritical CO₂ (sc-CO₂) was measured at different pressures (120–300 bar) and temperatures (308–338 K) using a statistical method. LND solubility in sc-CO₂ was obtained in the range of 0.02 × 10^-4 to 1.08 × 10^-4 in terms of mole fraction. The maximum solubility was achieved at 338 K and 300 bar.

Furthermore, the experimental data were correlated with well-known empirical density-based models, SRK equation of state (SRK-EoS) with two parameters of van der Waals (vdW2) mixing rule, as well as, expanded liquid theory (modified Wilson’s model). According to the results, modified Wilson’s model exhibited the highest consistency with the experimental data for correlating the solubility of LND in sc-CO₂. However, the SRK-EoS did not show acceptable accuracy in the correlation of LND solubility in sc-CO₂. Among the empirical models, Alwi and Garlapati (AARD% = 8.210), Sung and Shim (AARD% = 11.268), Ch and Madras (AARD% = 8.525), Hozhabr et al. (AARD% = 7.998), Garlapati and Madras (AARD% = 8.037), Keshmiri et al. (AARD% = 8.535), Sparks et al. (AARD% = 8.330), Reddy and Garlapati (AARD% = 10.589), Bian et al. (2011) (AARD% = 7.781), and Belghait et al. (AARD% = 7.516) possessed R_adj value above 0.99 and can be reliably employed to correlate the solubility of LND in sc-CO₂. Various critical properties of LND were calculated by different group contribution methods. Also, the approximate values of total mixing heat ( ${Δ H}_{total} =$ 48 kJ mol⁻¹) as well as vaporization ( ${Δ H}_{vap}$ = 69.5 kJ mol⁻¹), and solvation ( ${Δ H}_{sol}$ = -21.5 kJ mol⁻¹) enthalpies were computed via the obtained adjustable parameters of empirical models.

As mentioned previously, the appropriate supercritical method for producing LND micro/nanoparticles can be selected based on its solubility in sc-CO2. Due to the poor solubility of LND in sc-CO₂, the supercritical gas anti-solvent (GAS) process can be considered a suitable choice. Therefore, producing LND micro/nanoparticles with desired morphology and narrow size distribution via the GAS process can be considered in future investigations.

Acknowledgements

The authors would like to thank the generous financial support provided by the Supercritical fluids development group, Shiraz, Iran.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Adachi Y., Lu B.-Y., . Supercritical fluid extraction with carbon dioxide and ethylene. Fluid Phase Equilib.. 1983;14:147-156.
[Google Scholar]
Alwi R.S., Garlapati C., . A new semi empirical model for the solubility of dyestuffs in supercritical carbon dioxide. Chem. Pap.. 2021;75(6):2585-2595.
[Google Scholar]
Amani M., Saadati Ardestani N., Majd N.Y., . Utilization of supercritical CO2 gas antisolvent (GAS) for production of Capecitabine nanoparticles as anti-cancer drug: Analysis and optimization of the process conditions. J. CO2 Util.. 2021;46:101465
[Google Scholar]
Amani M., Saadati Ardestani N., . Investigation the phase equilibrium behavior in ternary system (CO2, DMSO, Capecitabine as anticancer drug) for precipitation of CPT Nanoparticle via the gas antisolvent supercritical process (GAS) Braz. J. Chem. Eng. 2021:1-12.
[Google Scholar]
Amooey A.A., . A simple correlation to predict drug solubility in supercritical carbon dioxide. Fluid Phase Equilib.. 2014;375:332-339.
[Google Scholar]
Andonova V., Chandrasekhar G., . A New Empirical Model to Correlate the Solubility of Penicillin G and Penicillin V in Supercritical Carbon Dioxide. J. Appl. Sci. Eng. Methodol. 2016:220-223.
[Google Scholar]
Ardestani N.S., Amani M., . Production of Anthraquinone Violet 3RN nanoparticles via the GAS process: Optimization of the process parameters using Box-Behnken design. Dyes Pigm.. 2021;193:109471
[Google Scholar]
Ardestani N.S., Majd N.Y., Amani M., . Experimental Measurement and Thermodynamic Modeling of Capecitabine (an Anticancer Drug) Solubility in Supercritical Carbon Dioxide in a Ternary System: Effect of Different Cosolvents. J. Chem. Eng. Data. 2020;65(10):4762-4779.
[Google Scholar]
Arib C., Spadavecchia J., . Lenalidomide (LENA) Hybrid Gold Complex Nanoparticles: Synthesis, Physicochemical Evaluation, and Perspectives in Nanomedicine. ACS Omega. 2020;5(44):28483-28492.
[Google Scholar]
Asgarpour Khansary M., Amiri F., Hosseini A., Hallaji Sani A., Shahbeig H., . Representing solute solubility in supercritical carbon dioxide: A novel empirical model. Chem. Eng. Res. Des.. 2015;93:355-365.
[Google Scholar]
Assael M.J., Trusler J.M., Tsolakis T.F., . Thermophysical properties of fluids: An introduction to their prediction. Vol vol. 1. World Scientific; 1996.
Attal M., Lauwers-Cances V., Marit G., Caillot D., Moreau P., Facon T., Stoppa A.M., Hulin C., Benboubker L., Garderet L., Decaux O., Leyvraz S., Vekemans M.-C., Voillat L., Michallet M., Pegourie B., Dumontet C., Roussel M., Leleu X., Mathiot C., Payen C., Avet-Loiseau H., Harousseau J.-L., . Lenalidomide maintenance after stem-cell transplantation for multiple myeloma. N. Engl. J. Med.. 2012;366(19):1782-1791.
[Google Scholar]
Bartle K.D., Clifford A.A., Jafar S.A., Shilstone G.F., . Solubilities of Solids and Liquids of Low Volatility in Supercritical Carbon Dioxide. J. Phys. Chem. Ref. Data. 1991;20(4):713-756.
[Google Scholar]
Belghait A., Si-Moussa C., Laidi M., Hanini S., . Semi-empirical correlation of solid solute solubility in supercritical carbon dioxide: Comparative study and proposition of a novel density-based model. C. R. Chim.. 2018;21(5):494-513.
[Google Scholar]
Bian X., Du Z., Tang Y., . An improved density-based model for the solubility of some compounds in supercritical carbon dioxide. Thermochim. Acta. 2011;519(1-2):16-21.
[Google Scholar]
Bian X.-Q., Zhang Q., Du Z.-M., Chen J., Jaubert J.-N., . A five-parameter empirical model for correlating the solubility of solid compounds in supercritical carbon dioxide. Fluid Phase Equilib.. 2016;411:74-80.
[Google Scholar]
Ch R., Madras G., . An association model for the solubilities of pharmaceuticals in supercritical carbon dioxide. Thermochim Acta. 2010;507-508:99-105.
[Google Scholar]
Chen X., Li D., Wang J., Deng Z., Zhang H., . Lenalidomide acesulfamate: Crystal structure, solid state characterization and dissolution performance. J. Mol. Struct.. 2019;1175:852-857.
[Google Scholar]
Chrastil J., . Solubility of solids and liquids in supercritical gases. J. Phys. Chem.. 1982;86(15):3016-3021.
[Google Scholar]
Constantinou L., Gani R., . New group contribution method for estimating properties of pure compounds. AIChE J.. 1994;40(10):1697-1710.
[Google Scholar]
Del Valle J.M., Aguilera J.M., . An improved equation for predicting the solubility of vegetable oils in supercritical carbon dioxide. Ind. Eng. Chem. Res.. 1988;27(8):1551-1553.
[Google Scholar]
Dong P., Xu M., Lu X., Lin C., . Measurement and correlation of solubilities of C.I. Disperse Red 73, C.I. Disperse Yellow 119 and their mixture in supercritical carbon dioxide. Fluid Phase Equilib.. 2010;297(1):46-51.
[Google Scholar]
Esfandiari N., Sajadian S.A., . Experimental and Modeling Investigation of Glibenclamide Solubility in Supercritical Carbon dioxide. Fluid Phase Equilib.. 2022;556:113408.
[CrossRef] [Google Scholar]
Eupen, J.T.H.V., 2011. Lenalidomide salts.
Garlapati C., Madras G., . New empirical expressions to correlate solubilities of solids in supercritical carbon dioxide. Thermochim Acta. 2010;500(1-2):123-127.
[Google Scholar]
Gomathi T., Govindarajan C., Rose M.H., Sudha P.N., Imran P.K.M., Venkatesan J., Kim S.-K., . Studies on drug-polymer interaction, in vitro release and cytotoxicity from chitosan particles excipient. Int. J. Pharm.. 2014;468(1-2):214-222.
[Google Scholar]
Gordillo M.D., Blanco M.A., Molero A., Martinez de la Ossa E., . Solubility of the antibiotic Penicillin G in supercritical carbon dioxide. J. Supercrit. Fluids. 1999;15(3):183-190.
[Google Scholar]
Haghbakhsh R., Hayer H., Saidi M., Keshtkari S., Esmaeilzadeh F., . Density estimation of pure carbon dioxide at supercritical region and estimation solubility of solid compounds in supercritical carbon dioxide: Correlation approach based on sensitivity analysis. Fluid Phase Equilib.. 2013;342:31-41.
[Google Scholar]
Higashi H., Iwai Y., Arai Y., . Solubilities and diffusion coefficients of high boiling compounds in supercritical carbon dioxide. Chem. Eng. Sci.. 2001;56(10):3027-3044.
[Google Scholar]
Hojjati M., Yamini Y., Khajeh M., Vatanara A., . Solubility of some statin drugs in supercritical carbon dioxide and representing the solute solubility data with several density-based correlations. J. Supercrit. Fluids. 2007;41(2):187-194.
[Google Scholar]
Hozhabr S.B., Mazloumi S.H., Sargolzaei J., . Correlation of solute solubility in supercritical carbon dioxide using a new empirical equation. Chem. Eng. Res. Des.. 2014;92(11):2734-2739.
[Google Scholar]
Immirzi A., Perini B., . Prediction of density in organic crystals. Acta Crystall. Sect. A. 1977;33(1):216-218.
[Google Scholar]
Iwai Y., Fukuda T., Koga Y., Arai Y., . Solubilities of myristic acid, palmitic acid, and cetyl alcohol in supercritical carbon dioxide at 35.degree.C. J. Chem. Eng. Data. 1991;36(4):430-432.
[Google Scholar]
Jafari Nejad S.h., Abolghasemi H., Moosavian M.A., Maragheh M.G., . Prediction of solute solubility in supercritical carbon dioxide: A novel semi-empirical model. Chem. Eng. Res. Des.. 2010;88(7):893-898.
[Google Scholar]
Jin J.-s., Wang Y.-W., Zhang H.-F., Fan X., Wu H., . Solubility of 4-Hydroxybenzaldehyde in Supercritical Carbon Dioxide with and without Cosolvents. J. Chem. Eng. Data. 2014;59(5):1521-1527.
[Google Scholar]
Jouyban A., Chan H.-K., Foster N.R., . Mathematical representation of solute solubility in supercritical carbon dioxide using empirical expressions. J. Supercrit. Fluids. 2002;24(1):19-35.
[Google Scholar]
Kalikin N.N., . Carbamazepine solubility in supercritical CO2: A comprehensive study. J. Mol. Liq.. 2020;311:113104
[Google Scholar]
Keshmiri K., Vatanara A., Yamini Y., . Development and evaluation of a new semi-empirical model for correlation of drug solubility in supercritical CO2. Fluid Phase Equilib.. 2014;363:18-26.
[Google Scholar]
Kumar S.K., Johnston K.P., . Modelling the solubility of solids in supercritical fluids with density as the independent variable. J. Supercrit. Fluids. 1988;1(1):15-22.
[Google Scholar]
Li R., Liu L., Khan A., Li C., He Z., Zhao J., Han D., . Effect of Cosolvents on the Solubility of Lenalidomide and Thermodynamic Model Correlation of Data. J. Chem. Eng. Data. 2019;64(10):4272-4279.
[Google Scholar]
Liu C., Chen Z., Chen Y., Lu J., Li Y., Wang S., Wu G., Qian F., . Improving Oral Bioavailability of Sorafenib by Optimizing the “Spring” and “Parachute” Based on Molecular Interaction Mechanisms. Mol. Pharm.. 2016;13(2):599-608.
[Google Scholar]
Marrero J., Gani R., . Group-contribution based estimation of pure component properties. Fluid Phase Equilib.. 2001;183-184:183-208.
[Google Scholar]
Méndez-Santiago J., Teja A.S., . The solubility of solids in supercritical fluids. Fluid Phase Equilib.. 1999;158-160:501-510.
[Google Scholar]
Mitra S., Wilson N.K., . An Empirical Method to Predict Solubility in Supercritical Fluids. J. Chromatogr. Sci.. 1991;29(7):305-309.
[Google Scholar]
Montgomery D.C., . Design and Analysis of Experiments (eighth ed.). John Wiley; 2012.
Nasri L., . Modified Wilson's Model for Correlating Solubilities in Supercritical Fluids of Some Polycyclic Aromatic Solutes. Polycyclic Aromat. Compd.. 2018;38(3):244-256.
[Google Scholar]
Nasri L., Bensaad S., Bensetiti Z., . Correlation and Prediction of the Solubility of Solid Solutes in Chemically Diverse Supercritical Fluids Based on the Expanded Liquid Theory. Adv. Chem. Eng. Sci.. 2013;03(04):255-273.
[Google Scholar]
Patrizi A., Venturi M., Dika E., Maibach H., Tacchetti P., Brandi G., . Cutaneous adverse reactions linked to targeted anticancer therapies bortezomib and lenalidomide for multiple myeloma: new drugs, old side effects. Cutan. Ocul. Toxicol.. 2014;33(1):1-6.
[Google Scholar]
Pelalak R., . Predictive thermodynamic modeling and experimental measurements on solubility of active pharmaceutical ingredient: Lornoxicam case study. J. Mol. Liq.. 2021;326:115285
[Google Scholar]
Pishnamazi M., . Thermodynamic modelling and experimental validation of pharmaceutical solubility in supercritical solvent. J. Mol. Liq.. 2020;319:114120
[Google Scholar]
Pishnamazi M., . Measuring solubility of a chemotherapy-anti cancer drug (busulfan) in supercritical carbon dioxide. J. Mol. Liq.. 2020;317:113954
[Google Scholar]
Pishnamazi M., . Chloroquine (antimalaria medication with anti SARS-CoV activity) solubility in supercritical carbon dioxide. J. Mol. Liq.. 2021;322:114539
[Google Scholar]
Pishnamazi M., Zabihi S., Sarafzadeh P., Borousan F., Marjani A., Pelalak R., Shirazian S., . Using static method to measure tolmetin solubility at different pressures and temperatures in supercritical carbon dioxide. Sci. Rep.. 2020;10(1)
[CrossRef] [Google Scholar]
Pishnamazi M., Zabihi S., Jamshidian S., Borousan F., Hezave A.Z., Marjani A., Shirazian S., . Experimental and thermodynamic modeling decitabine anti cancer drug solubility in supercritical carbon dioxide. Sci. Rep.. 2021;11(1)
[CrossRef] [Google Scholar]
Poling B.E., Prausnitz J.M., O'connell J.P., . Properties of Gases and Liquids (fifth ed.). McGraw-Hill Education; 2001.
Prausnitz J.M., Lichtenthaler R.N., de Azevedo E.G., . Molecular thermodynamics of fluid-phase equilibria. Pearson Education; 1998.
Rangineni, S., N.D., Mudapaka, V.K., Kadaboina, R., Murki, V., Manda, A., Badisa, V.R., Vemula, N., Pulla, R., Seshagiri, R., 2010. Lenalidomide solvates and processes.
Reddy T.A., Garlapati C., . Dimensionless Empirical Model to Correlate Pharmaceutical Compound Solubility in Supercritical Carbon Dioxide. Chem. Eng. Technol.. 2019;42(12):2621-2630.
[Google Scholar]
Saadati Ardestani N., Sodeifian G., Sajadian S.A., . Preparation of phthalocyanine green nano pigment using supercritical CO2 gas antisolvent (GAS): experimental and modeling. Heliyon. 2020;6(9):e04947.
[CrossRef] [Google Scholar]
Saadati Ardestani N., Amani M., Moharrery L., . Determination of Anthraquinone Violet 3RN solubility in supercritical carbon dioxide with/without co-solvent: Experimental data and modeling (empirical and thermodynamic models) Chem. Eng. Res. Des.. 2020;159:529-542.
[Google Scholar]
Sajadian S.A., Ardestani N.S., Esfandiari N., Askarizadeh M., Jouyban A., . Solubility of favipiravir (as an anti-COVID-19) in supercritical carbon dioxide: An experimental analysis and thermodynamic modeling. J. Supercrit. Fluids. 2022;183:105539.
[CrossRef] [Google Scholar]
Sajadian S.A., Ardestani N.S., Jouyban A., . Solubility of montelukast (as a potential treatment of COVID -19) in supercritical carbon dioxide: Experimental data and modelling. J. Mol. Liq.. 2022;349:118219.
[CrossRef] [Google Scholar]
Si-Moussa C., Belghait A., Khaouane L., Hanini S., Halilali A., . Novel density-based model for the correlation of solid drugs solubility in supercritical carbon dioxide. C. R. Chim.. 2017;20(5):559-572.
[Google Scholar]
Soave G., . Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci.. 1972;27(6):1197-1203.
[Google Scholar]
Sodeifian G., . Experimental data and thermodynamic modeling of solubility of Azathioprine, as an immunosuppressive and anti-cancer drug, in supercritical carbon dioxide. J. Mol. Liq.. 2020;299:112179
[Google Scholar]
Sodeifian G., Saadati Ardestani N., Sajadian S.A., Ghorbandoost S., . Application of supercritical carbon dioxide to extract essential oil from Cleome coluteoides Boiss: experimental, response surface and grey wolf optimization methodology. J. Supercrit. Fluids. 2016;114:55-63.
[Google Scholar]
Sodeifian G., Sajadian S.A., Ardestani N.S., . Determination of solubility of Aprepitant (an antiemetic drug for chemotherapy) in supercritical carbon dioxide: empirical and thermodynamic models. J. Supercrit. Fluids. 2017;128:102-111.
[Google Scholar]
Sodeifian G., Sajadian S.A., Saadati Ardestani N., . Experimental optimization and mathematical modeling of the supercritical fluid extraction of essential oil from Eryngium billardieri: Application of simulated annealing (SA) algorithm. J. Supercrit. Fluids. 2017;127:146-157.
[Google Scholar]
Sodeifian G., Ardestani N.S., Sajadian S.A., Moghadamian K., . Properties of Portulaca oleracea seed oil via supercritical fluid extraction: Experimental and optimization. J. Supercrit. Fluids. 2018;135:34-44.
[Google Scholar]
Sodeifian G., Razmimanesh F., Sajadian S.A., . Solubility measurement of a chemotherapeutic agent (Imatinib mesylate) in supercritical carbon dioxide: Assessment of new empirical model. J. Supercrit. Fluids. 2019;146:89-99.
[Google Scholar]
Sodeifian G., Sajadian S.A., Saadati Ardestani N., Razmimanesh F., . Production of Loratadine drug nanoparticles using ultrasonic-assisted Rapid expansion of supercritical solution into aqueous solution (US-RESSAS) J. Supercrit. Fluids. 2019;147:241-253.
[Google Scholar]
Sodeifian G., Saadati Ardestani N., Sajadian S.A., Golmohammadi M.R., Fazlali A., . Prediction of Solubility of Sodium Valproate in Supercritical Carbon Dioxide: Experimental Study and Thermodynamic Modeling. J. Chem. Eng. Data. 2020;65(4):1747-1760.
[Google Scholar]
Sodeifian G., Saadati Ardestani N., Razmimanesh F., Sajadian S.A., . Experimental and thermodynamic analyses of supercritical CO2-Solubility of minoxidil as an antihypertensive drug. Fluid Phase Equilib.. 2020;522:112745.
[CrossRef] [Google Scholar]
Song J.-X., Yan Y., Yao J., Chen J.-M., Lu T.-B., . Improving the Solubility of Lenalidomide via Cocrystals. Cryst. Growth Des.. 2014;14(6):3069-3077.
[Google Scholar]
Sparks D.L., Hernandez R., Estévez L.A., . Evaluation of density-based models for the solubility of solids in supercritical carbon dioxide and formulation of a new model. Chem. Eng. Sci.. 2008;63(17):4292-4301.
[Google Scholar]
Stahl E., Schilz W., Schütz E., Willing E., . A Quick Method for the Microanalytical Evaluation of the Dissolving Power of Supercritical Gases. Angew. Chem.. 1978;17(10):731-738.
[Google Scholar]
Stiegel, H.H., W.A., Brueck, S., Paetz, J., Meergans, D., 2011. Acid addition salts of lenalidomide.
Sung H.-D., Shim J.-J., . Solubility of C. I. Disperse Red 60 and C. I. Disperse Blue 60 in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 1999;44(5):985-989.
[Google Scholar]
Tippana Ashok Reddy R.S., Garlapati Chandrasekhar, . A new empirical model to correlate solubility of pharmaceutical compounds in supercritical carbon dioxide. J. Appl. Sci. Eng. Methodol.. 2018;4(2):575-590.
[Google Scholar]
Van der Waals J.D., . Over de Continuiteit van den Gas-en Vloeistoftoestand (On the Continuity of the Gas and Liquid State). University of Leiden; 1873.
Wang S.-W., Chen J.-Z., Hsieh C.-M., . Measurement and Correlation of Solubility of Methylsalicylic Acid Isomers in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 2021;66(1):280-289.
[Google Scholar]
Wang S.-W., Chang S.-Y., Hsieh C.-M., . Measurement and modeling of solubility of gliclazide (hypoglycemic drug) and captopril (antihypertension drug) in supercritical carbon dioxide. J. Supercrit. Fluids. 2021;174:105244
[Google Scholar]
Wang B.-C., Su C.-S., . Solid solubility measurement of ipriflavone in supercritical carbon dioxide and microparticle production through the rapid expansion of supercritical solutions process. J. CO2 Util.. 2020;37:285-294.
[Google Scholar]
Yamini Y., Fat'hi M.R., Alizadeh N., Shamsipur M., . Solubility of dihydroxybenzene isomers in supercritical carbon dioxide. Fluid Phase Equilib.. 1998;152(2):299-305.
[Google Scholar]
Yang Z., Shao D., Zhou G., . Solubility parameter of lenalidomide for predicting the type of solubility profile and application of thermodynamic model. J. Chem. Thermodyn.. 2019;132:268-275.
[Google Scholar]
Yu Z.-R., Singh B., Rizvi S.S.H., Zollweg J.A., . Solubilities of fatty acids, fatty acid esters, triglycerides, and fats and oils in supercritical carbon dioxide. J. Supercrit. Fluids. 1994;7(1):51-59.
[Google Scholar]
Zabihi S., . Thermodynamic study on solubility of brain tumor drug in supercritical solvent: Temozolomide case study. J. Mol. Liq.. 2021;321:114926
[Google Scholar]
Zabihi S., . Measuring salsalate solubility in supercritical carbon dioxide: Experimental and thermodynamic modelling. J. Chem. Thermodyn.. 2021;152:106271
[Google Scholar]
Zabihi S., Esmaeili-Faraj S.H., Borousan F., Hezave A.Z., Shirazian S., . Loxoprofen Solubility in Supercritical Carbon Dioxide: Experimental and Modeling Approaches. J. Chem. Eng. Data. 2020;65(9):4613-4620.
[Google Scholar]
Zabihi S., Rahnama Y., Sharafi A., Borousan F., Zeinolabedini Hezave A., Shirazian S., . Experimental Solubility Measurements of Fenoprofen in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 2020;65(4):1425-1434.
[Google Scholar]
Zabihi S., Hosseini S., Pishnamazi M., Lashkarbolooki M., Borousan F., Marjani A., Pelalak R., Shirazian S., . Tenoxicam (Mobiflex) Solubility in Carbon Dioxide under Supercritical Conditions. J. Chem. Eng. Data. 2021;66(2):990-998.
[Google Scholar]

Introduction

Materials and methods

Materials
Experimental procedure for solubility determination
Theoretical studies

Results and discussions

Experimental solubility determination
Correlation of solubility data

Conclusion

Fulltext Views
6

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Adachi Y., Lu B.-Y., . Supercritical fluid extraction with carbon dioxide and ethylene. Fluid Phase Equilib.. 1983;14:147-156.
[Google Scholar]

[2] Alwi R.S., Garlapati C., . A new semi empirical model for the solubility of dyestuffs in supercritical carbon dioxide. Chem. Pap.. 2021;75(6):2585-2595.
[Google Scholar]

[3] Amani M., Saadati Ardestani N., Majd N.Y., . Utilization of supercritical CO2 gas antisolvent (GAS) for production of Capecitabine nanoparticles as anti-cancer drug: Analysis and optimization of the process conditions. J. CO2 Util.. 2021;46:101465
[Google Scholar]

[4] Amani M., Saadati Ardestani N., . Investigation the phase equilibrium behavior in ternary system (CO2, DMSO, Capecitabine as anticancer drug) for precipitation of CPT Nanoparticle via the gas antisolvent supercritical process (GAS) Braz. J. Chem. Eng. 2021:1-12.
[Google Scholar]

[5] Amooey A.A., . A simple correlation to predict drug solubility in supercritical carbon dioxide. Fluid Phase Equilib.. 2014;375:332-339.
[Google Scholar]

[6] Andonova V., Chandrasekhar G., . A New Empirical Model to Correlate the Solubility of Penicillin G and Penicillin V in Supercritical Carbon Dioxide. J. Appl. Sci. Eng. Methodol. 2016:220-223.
[Google Scholar]

[7] Ardestani N.S., Amani M., . Production of Anthraquinone Violet 3RN nanoparticles via the GAS process: Optimization of the process parameters using Box-Behnken design. Dyes Pigm.. 2021;193:109471
[Google Scholar]

[8] Ardestani N.S., Majd N.Y., Amani M., . Experimental Measurement and Thermodynamic Modeling of Capecitabine (an Anticancer Drug) Solubility in Supercritical Carbon Dioxide in a Ternary System: Effect of Different Cosolvents. J. Chem. Eng. Data. 2020;65(10):4762-4779.
[Google Scholar]

[9] Arib C., Spadavecchia J., . Lenalidomide (LENA) Hybrid Gold Complex Nanoparticles: Synthesis, Physicochemical Evaluation, and Perspectives in Nanomedicine. ACS Omega. 2020;5(44):28483-28492.
[Google Scholar]

[10] Asgarpour Khansary M., Amiri F., Hosseini A., Hallaji Sani A., Shahbeig H., . Representing solute solubility in supercritical carbon dioxide: A novel empirical model. Chem. Eng. Res. Des.. 2015;93:355-365.
[Google Scholar]

[11] Assael M.J., Trusler J.M., Tsolakis T.F., . Thermophysical properties of fluids: An introduction to their prediction. Vol vol. 1. World Scientific; 1996.

[12] Attal M., Lauwers-Cances V., Marit G., Caillot D., Moreau P., Facon T., Stoppa A.M., Hulin C., Benboubker L., Garderet L., Decaux O., Leyvraz S., Vekemans M.-C., Voillat L., Michallet M., Pegourie B., Dumontet C., Roussel M., Leleu X., Mathiot C., Payen C., Avet-Loiseau H., Harousseau J.-L., . Lenalidomide maintenance after stem-cell transplantation for multiple myeloma. N. Engl. J. Med.. 2012;366(19):1782-1791.
[Google Scholar]

[13] Bartle K.D., Clifford A.A., Jafar S.A., Shilstone G.F., . Solubilities of Solids and Liquids of Low Volatility in Supercritical Carbon Dioxide. J. Phys. Chem. Ref. Data. 1991;20(4):713-756.
[Google Scholar]

[14] Belghait A., Si-Moussa C., Laidi M., Hanini S., . Semi-empirical correlation of solid solute solubility in supercritical carbon dioxide: Comparative study and proposition of a novel density-based model. C. R. Chim.. 2018;21(5):494-513.
[Google Scholar]

[15] Bian X., Du Z., Tang Y., . An improved density-based model for the solubility of some compounds in supercritical carbon dioxide. Thermochim. Acta. 2011;519(1-2):16-21.
[Google Scholar]

[16] Bian X.-Q., Zhang Q., Du Z.-M., Chen J., Jaubert J.-N., . A five-parameter empirical model for correlating the solubility of solid compounds in supercritical carbon dioxide. Fluid Phase Equilib.. 2016;411:74-80.
[Google Scholar]

[17] Ch R., Madras G., . An association model for the solubilities of pharmaceuticals in supercritical carbon dioxide. Thermochim Acta. 2010;507-508:99-105.
[Google Scholar]

[18] Chen X., Li D., Wang J., Deng Z., Zhang H., . Lenalidomide acesulfamate: Crystal structure, solid state characterization and dissolution performance. J. Mol. Struct.. 2019;1175:852-857.
[Google Scholar]

[19] Chrastil J., . Solubility of solids and liquids in supercritical gases. J. Phys. Chem.. 1982;86(15):3016-3021.
[Google Scholar]

[20] Constantinou L., Gani R., . New group contribution method for estimating properties of pure compounds. AIChE J.. 1994;40(10):1697-1710.
[Google Scholar]

[21] Del Valle J.M., Aguilera J.M., . An improved equation for predicting the solubility of vegetable oils in supercritical carbon dioxide. Ind. Eng. Chem. Res.. 1988;27(8):1551-1553.
[Google Scholar]

[22] Dong P., Xu M., Lu X., Lin C., . Measurement and correlation of solubilities of C.I. Disperse Red 73, C.I. Disperse Yellow 119 and their mixture in supercritical carbon dioxide. Fluid Phase Equilib.. 2010;297(1):46-51.
[Google Scholar]

[23] Esfandiari N., Sajadian S.A., . Experimental and Modeling Investigation of Glibenclamide Solubility in Supercritical Carbon dioxide. Fluid Phase Equilib.. 2022;556:113408.
[CrossRef] [Google Scholar]

[24] Eupen, J.T.H.V., 2011. Lenalidomide salts.

[25] Garlapati C., Madras G., . New empirical expressions to correlate solubilities of solids in supercritical carbon dioxide. Thermochim Acta. 2010;500(1-2):123-127.
[Google Scholar]

[26] Gomathi T., Govindarajan C., Rose M.H., Sudha P.N., Imran P.K.M., Venkatesan J., Kim S.-K., . Studies on drug-polymer interaction, in vitro release and cytotoxicity from chitosan particles excipient. Int. J. Pharm.. 2014;468(1-2):214-222.
[Google Scholar]

[27] Gordillo M.D., Blanco M.A., Molero A., Martinez de la Ossa E., . Solubility of the antibiotic Penicillin G in supercritical carbon dioxide. J. Supercrit. Fluids. 1999;15(3):183-190.
[Google Scholar]

[28] Haghbakhsh R., Hayer H., Saidi M., Keshtkari S., Esmaeilzadeh F., . Density estimation of pure carbon dioxide at supercritical region and estimation solubility of solid compounds in supercritical carbon dioxide: Correlation approach based on sensitivity analysis. Fluid Phase Equilib.. 2013;342:31-41.
[Google Scholar]

[29] Higashi H., Iwai Y., Arai Y., . Solubilities and diffusion coefficients of high boiling compounds in supercritical carbon dioxide. Chem. Eng. Sci.. 2001;56(10):3027-3044.
[Google Scholar]

[30] Hojjati M., Yamini Y., Khajeh M., Vatanara A., . Solubility of some statin drugs in supercritical carbon dioxide and representing the solute solubility data with several density-based correlations. J. Supercrit. Fluids. 2007;41(2):187-194.
[Google Scholar]

[31] Hozhabr S.B., Mazloumi S.H., Sargolzaei J., . Correlation of solute solubility in supercritical carbon dioxide using a new empirical equation. Chem. Eng. Res. Des.. 2014;92(11):2734-2739.
[Google Scholar]

[32] Immirzi A., Perini B., . Prediction of density in organic crystals. Acta Crystall. Sect. A. 1977;33(1):216-218.
[Google Scholar]

[33] Iwai Y., Fukuda T., Koga Y., Arai Y., . Solubilities of myristic acid, palmitic acid, and cetyl alcohol in supercritical carbon dioxide at 35.degree.C. J. Chem. Eng. Data. 1991;36(4):430-432.
[Google Scholar]

[34] Jafari Nejad S.h., Abolghasemi H., Moosavian M.A., Maragheh M.G., . Prediction of solute solubility in supercritical carbon dioxide: A novel semi-empirical model. Chem. Eng. Res. Des.. 2010;88(7):893-898.
[Google Scholar]

[35] Jin J.-s., Wang Y.-W., Zhang H.-F., Fan X., Wu H., . Solubility of 4-Hydroxybenzaldehyde in Supercritical Carbon Dioxide with and without Cosolvents. J. Chem. Eng. Data. 2014;59(5):1521-1527.
[Google Scholar]

[36] Jouyban A., Chan H.-K., Foster N.R., . Mathematical representation of solute solubility in supercritical carbon dioxide using empirical expressions. J. Supercrit. Fluids. 2002;24(1):19-35.
[Google Scholar]

[37] Kalikin N.N., . Carbamazepine solubility in supercritical CO2: A comprehensive study. J. Mol. Liq.. 2020;311:113104
[Google Scholar]

[38] Keshmiri K., Vatanara A., Yamini Y., . Development and evaluation of a new semi-empirical model for correlation of drug solubility in supercritical CO2. Fluid Phase Equilib.. 2014;363:18-26.
[Google Scholar]

[39] Kumar S.K., Johnston K.P., . Modelling the solubility of solids in supercritical fluids with density as the independent variable. J. Supercrit. Fluids. 1988;1(1):15-22.
[Google Scholar]

[40] Li R., Liu L., Khan A., Li C., He Z., Zhao J., Han D., . Effect of Cosolvents on the Solubility of Lenalidomide and Thermodynamic Model Correlation of Data. J. Chem. Eng. Data. 2019;64(10):4272-4279.
[Google Scholar]

[41] Liu C., Chen Z., Chen Y., Lu J., Li Y., Wang S., Wu G., Qian F., . Improving Oral Bioavailability of Sorafenib by Optimizing the “Spring” and “Parachute” Based on Molecular Interaction Mechanisms. Mol. Pharm.. 2016;13(2):599-608.
[Google Scholar]

[42] Marrero J., Gani R., . Group-contribution based estimation of pure component properties. Fluid Phase Equilib.. 2001;183-184:183-208.
[Google Scholar]

[43] Méndez-Santiago J., Teja A.S., . The solubility of solids in supercritical fluids. Fluid Phase Equilib.. 1999;158-160:501-510.
[Google Scholar]

[44] Mitra S., Wilson N.K., . An Empirical Method to Predict Solubility in Supercritical Fluids. J. Chromatogr. Sci.. 1991;29(7):305-309.
[Google Scholar]

[45] Montgomery D.C., . Design and Analysis of Experiments (eighth ed.). John Wiley; 2012.

[46] Nasri L., . Modified Wilson's Model for Correlating Solubilities in Supercritical Fluids of Some Polycyclic Aromatic Solutes. Polycyclic Aromat. Compd.. 2018;38(3):244-256.
[Google Scholar]

[47] Nasri L., Bensaad S., Bensetiti Z., . Correlation and Prediction of the Solubility of Solid Solutes in Chemically Diverse Supercritical Fluids Based on the Expanded Liquid Theory. Adv. Chem. Eng. Sci.. 2013;03(04):255-273.
[Google Scholar]

[48] Patrizi A., Venturi M., Dika E., Maibach H., Tacchetti P., Brandi G., . Cutaneous adverse reactions linked to targeted anticancer therapies bortezomib and lenalidomide for multiple myeloma: new drugs, old side effects. Cutan. Ocul. Toxicol.. 2014;33(1):1-6.
[Google Scholar]

[49] Pelalak R., . Predictive thermodynamic modeling and experimental measurements on solubility of active pharmaceutical ingredient: Lornoxicam case study. J. Mol. Liq.. 2021;326:115285
[Google Scholar]

[50] Pishnamazi M., . Thermodynamic modelling and experimental validation of pharmaceutical solubility in supercritical solvent. J. Mol. Liq.. 2020;319:114120
[Google Scholar]

[51] Pishnamazi M., . Measuring solubility of a chemotherapy-anti cancer drug (busulfan) in supercritical carbon dioxide. J. Mol. Liq.. 2020;317:113954
[Google Scholar]

[52] Pishnamazi M., . Chloroquine (antimalaria medication with anti SARS-CoV activity) solubility in supercritical carbon dioxide. J. Mol. Liq.. 2021;322:114539
[Google Scholar]

[53] Pishnamazi M., Zabihi S., Sarafzadeh P., Borousan F., Marjani A., Pelalak R., Shirazian S., . Using static method to measure tolmetin solubility at different pressures and temperatures in supercritical carbon dioxide. Sci. Rep.. 2020;10(1)
[CrossRef] [Google Scholar]

[54] Pishnamazi M., Zabihi S., Jamshidian S., Borousan F., Hezave A.Z., Marjani A., Shirazian S., . Experimental and thermodynamic modeling decitabine anti cancer drug solubility in supercritical carbon dioxide. Sci. Rep.. 2021;11(1)
[CrossRef] [Google Scholar]

[55] Poling B.E., Prausnitz J.M., O'connell J.P., . Properties of Gases and Liquids (fifth ed.). McGraw-Hill Education; 2001.

[56] Prausnitz J.M., Lichtenthaler R.N., de Azevedo E.G., . Molecular thermodynamics of fluid-phase equilibria. Pearson Education; 1998.

[57] Rangineni, S., N.D., Mudapaka, V.K., Kadaboina, R., Murki, V., Manda, A., Badisa, V.R., Vemula, N., Pulla, R., Seshagiri, R., 2010. Lenalidomide solvates and processes.

[58] Reddy T.A., Garlapati C., . Dimensionless Empirical Model to Correlate Pharmaceutical Compound Solubility in Supercritical Carbon Dioxide. Chem. Eng. Technol.. 2019;42(12):2621-2630.
[Google Scholar]

[59] Saadati Ardestani N., Sodeifian G., Sajadian S.A., . Preparation of phthalocyanine green nano pigment using supercritical CO2 gas antisolvent (GAS): experimental and modeling. Heliyon. 2020;6(9):e04947.
[CrossRef] [Google Scholar]

[60] Saadati Ardestani N., Amani M., Moharrery L., . Determination of Anthraquinone Violet 3RN solubility in supercritical carbon dioxide with/without co-solvent: Experimental data and modeling (empirical and thermodynamic models) Chem. Eng. Res. Des.. 2020;159:529-542.
[Google Scholar]

[61] Sajadian S.A., Ardestani N.S., Esfandiari N., Askarizadeh M., Jouyban A., . Solubility of favipiravir (as an anti-COVID-19) in supercritical carbon dioxide: An experimental analysis and thermodynamic modeling. J. Supercrit. Fluids. 2022;183:105539.
[CrossRef] [Google Scholar]

[62] Sajadian S.A., Ardestani N.S., Jouyban A., . Solubility of montelukast (as a potential treatment of COVID -19) in supercritical carbon dioxide: Experimental data and modelling. J. Mol. Liq.. 2022;349:118219.
[CrossRef] [Google Scholar]

[63] Si-Moussa C., Belghait A., Khaouane L., Hanini S., Halilali A., . Novel density-based model for the correlation of solid drugs solubility in supercritical carbon dioxide. C. R. Chim.. 2017;20(5):559-572.
[Google Scholar]

[64] Soave G., . Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci.. 1972;27(6):1197-1203.
[Google Scholar]

[65] Sodeifian G., . Experimental data and thermodynamic modeling of solubility of Azathioprine, as an immunosuppressive and anti-cancer drug, in supercritical carbon dioxide. J. Mol. Liq.. 2020;299:112179
[Google Scholar]

[66] Sodeifian G., Saadati Ardestani N., Sajadian S.A., Ghorbandoost S., . Application of supercritical carbon dioxide to extract essential oil from Cleome coluteoides Boiss: experimental, response surface and grey wolf optimization methodology. J. Supercrit. Fluids. 2016;114:55-63.
[Google Scholar]

[67] Sodeifian G., Sajadian S.A., Ardestani N.S., . Determination of solubility of Aprepitant (an antiemetic drug for chemotherapy) in supercritical carbon dioxide: empirical and thermodynamic models. J. Supercrit. Fluids. 2017;128:102-111.
[Google Scholar]

[68] Sodeifian G., Sajadian S.A., Saadati Ardestani N., . Experimental optimization and mathematical modeling of the supercritical fluid extraction of essential oil from Eryngium billardieri: Application of simulated annealing (SA) algorithm. J. Supercrit. Fluids. 2017;127:146-157.
[Google Scholar]

[69] Sodeifian G., Ardestani N.S., Sajadian S.A., Moghadamian K., . Properties of Portulaca oleracea seed oil via supercritical fluid extraction: Experimental and optimization. J. Supercrit. Fluids. 2018;135:34-44.
[Google Scholar]

[70] Sodeifian G., Razmimanesh F., Sajadian S.A., . Solubility measurement of a chemotherapeutic agent (Imatinib mesylate) in supercritical carbon dioxide: Assessment of new empirical model. J. Supercrit. Fluids. 2019;146:89-99.
[Google Scholar]

[71] Sodeifian G., Sajadian S.A., Saadati Ardestani N., Razmimanesh F., . Production of Loratadine drug nanoparticles using ultrasonic-assisted Rapid expansion of supercritical solution into aqueous solution (US-RESSAS) J. Supercrit. Fluids. 2019;147:241-253.
[Google Scholar]

[72] Sodeifian G., Saadati Ardestani N., Sajadian S.A., Golmohammadi M.R., Fazlali A., . Prediction of Solubility of Sodium Valproate in Supercritical Carbon Dioxide: Experimental Study and Thermodynamic Modeling. J. Chem. Eng. Data. 2020;65(4):1747-1760.
[Google Scholar]

[73] Sodeifian G., Saadati Ardestani N., Razmimanesh F., Sajadian S.A., . Experimental and thermodynamic analyses of supercritical CO2-Solubility of minoxidil as an antihypertensive drug. Fluid Phase Equilib.. 2020;522:112745.
[CrossRef] [Google Scholar]

[74] Song J.-X., Yan Y., Yao J., Chen J.-M., Lu T.-B., . Improving the Solubility of Lenalidomide via Cocrystals. Cryst. Growth Des.. 2014;14(6):3069-3077.
[Google Scholar]

[75] Sparks D.L., Hernandez R., Estévez L.A., . Evaluation of density-based models for the solubility of solids in supercritical carbon dioxide and formulation of a new model. Chem. Eng. Sci.. 2008;63(17):4292-4301.
[Google Scholar]

[76] Stahl E., Schilz W., Schütz E., Willing E., . A Quick Method for the Microanalytical Evaluation of the Dissolving Power of Supercritical Gases. Angew. Chem.. 1978;17(10):731-738.
[Google Scholar]

[77] Stiegel, H.H., W.A., Brueck, S., Paetz, J., Meergans, D., 2011. Acid addition salts of lenalidomide.

[78] Sung H.-D., Shim J.-J., . Solubility of C. I. Disperse Red 60 and C. I. Disperse Blue 60 in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 1999;44(5):985-989.
[Google Scholar]

[79] Tippana Ashok Reddy R.S., Garlapati Chandrasekhar, . A new empirical model to correlate solubility of pharmaceutical compounds in supercritical carbon dioxide. J. Appl. Sci. Eng. Methodol.. 2018;4(2):575-590.
[Google Scholar]

[80] Van der Waals J.D., . Over de Continuiteit van den Gas-en Vloeistoftoestand (On the Continuity of the Gas and Liquid State). University of Leiden; 1873.

[81] Wang S.-W., Chen J.-Z., Hsieh C.-M., . Measurement and Correlation of Solubility of Methylsalicylic Acid Isomers in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 2021;66(1):280-289.
[Google Scholar]

[82] Wang S.-W., Chang S.-Y., Hsieh C.-M., . Measurement and modeling of solubility of gliclazide (hypoglycemic drug) and captopril (antihypertension drug) in supercritical carbon dioxide. J. Supercrit. Fluids. 2021;174:105244
[Google Scholar]

[83] Wang B.-C., Su C.-S., . Solid solubility measurement of ipriflavone in supercritical carbon dioxide and microparticle production through the rapid expansion of supercritical solutions process. J. CO2 Util.. 2020;37:285-294.
[Google Scholar]

[84] Yamini Y., Fat'hi M.R., Alizadeh N., Shamsipur M., . Solubility of dihydroxybenzene isomers in supercritical carbon dioxide. Fluid Phase Equilib.. 1998;152(2):299-305.
[Google Scholar]

[85] Yang Z., Shao D., Zhou G., . Solubility parameter of lenalidomide for predicting the type of solubility profile and application of thermodynamic model. J. Chem. Thermodyn.. 2019;132:268-275.
[Google Scholar]

[86] Yu Z.-R., Singh B., Rizvi S.S.H., Zollweg J.A., . Solubilities of fatty acids, fatty acid esters, triglycerides, and fats and oils in supercritical carbon dioxide. J. Supercrit. Fluids. 1994;7(1):51-59.
[Google Scholar]

[87] Zabihi S., . Thermodynamic study on solubility of brain tumor drug in supercritical solvent: Temozolomide case study. J. Mol. Liq.. 2021;321:114926
[Google Scholar]

[88] Zabihi S., . Measuring salsalate solubility in supercritical carbon dioxide: Experimental and thermodynamic modelling. J. Chem. Thermodyn.. 2021;152:106271
[Google Scholar]

[89] Zabihi S., Esmaeili-Faraj S.H., Borousan F., Hezave A.Z., Shirazian S., . Loxoprofen Solubility in Supercritical Carbon Dioxide: Experimental and Modeling Approaches. J. Chem. Eng. Data. 2020;65(9):4613-4620.
[Google Scholar]

[90] Zabihi S., Rahnama Y., Sharafi A., Borousan F., Zeinolabedini Hezave A., Shirazian S., . Experimental Solubility Measurements of Fenoprofen in Supercritical Carbon Dioxide. J. Chem. Eng. Data. 2020;65(4):1425-1434.
[Google Scholar]

[91] Zabihi S., Hosseini S., Pishnamazi M., Lashkarbolooki M., Borousan F., Marjani A., Pelalak R., Shirazian S., . Tenoxicam (Mobiflex) Solubility in Carbon Dioxide under Supercritical Conditions. J. Chem. Eng. Data. 2021;66(2):990-998.
[Google Scholar]

Component	MW^a (kg kmol⁻¹)	T_b^b (K)	T_m^b (K)	T_c^b (K)	P_c ^b (bar)	ω^c	$v^{s}$ ^d (cm³ mol⁻¹)	T (K)
								308	318	328	338
								P^sub × 10⁶(Pa)^e
LND	259.25	663.20	560.65	1006.12	36.54	0.64	166.40	1.13	4.31	14.98	43.39

Experimental analysis and thermodynamic modelling of lenalidomide solubility in supercritical carbon dioxide

Abstract

Abstract

Abstract

Keywords

Lenalidomide

Solubility

Supercritical carbon dioxide

Empirical model

Modified Wilson’s model

Soave-Redlich-Kwong (SRK) equation of state

Nomenclature

Greek symbols

Superscripts

1 Introduction

2 Materials and methods

2.1 Materials

2.2 Experimental procedure for solubility determination

2.3 Theoretical studies

2.3.1 Empirical models

2.3.2 Equation of state-based (EOS) model (Soave- Redlich-Kowang (SRK))

2.3.3 Expanded liquid theory (Wilson’s model)

3 Results and discussions

3.1 Experimental solubility determination

3.2 Correlation of solubility data

3.2.1 Empirical (Density-based) models

3.2.2 Equation of state (SRK-EoS) based model

3.2.3 Modified Wilson’s model

4 Conclusion

Acknowledgements

Declaration of Competing Interest

References

Suggested read for related articles: