Translate this page into:
Features of hybridized AA7072 and AA7075 alloys nanomaterials with melting heat transfer past a movable cylinder with Thompson and Troian slip effect
⁎Corresponding author. aurangzaib@fuuast.edu.pk (Aurang Zaib)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
A number of scientists have indicated interest in the promising area of research that involves improving heat transmission by utilizing nanoparticles. The dynamic properties of nanofluids reflect several applications in the cooling process, thermal engineering, heat exchangers, magnetic cell separation, energy production, hyperthermia, etc. In light of the appealing implications of nanofluids, the current research aims to explore the melting process of MHD hybrid AA7072 and AA7075 alloy nanoparticles from a movable cylinder. It also incorporates the irregular Thompson and Troian slip effect to simulate the intricate features of the nanofluid flow. The primary nonlinear partial differential equations (NPDEs) are converted into nonlinear ordinary differential equations (NODEs) with the use of the similarity technique. These converted equations are unraveled numerically via applying the built-in program bvp4c in MATLAB. It is visually examined that physical parameters affect the temperature and skin friction. The outcomes suggest that double solutions are found in a certain range of movable cylinder parameter. In addition, the skin friction is decelerated due to the critical shear rate and velocity slip factors while it is enhanced with the influence of suction and nanoparticles volume fraction. Moreover, the temperature is uplifted due to nanoparticles volume fraction and is declined due to Stefan number. In case of quanitative descriptions, the skin friction boosted up by almost 3.64% and 1.18% for the particular upper and lower branch outcomes due to the superior influences of nanoparticle volume fraction. Also, the skin friction decelerated for the branch of upper and lower solutions at about 5.26% and 22.55%, respectively, due to the larger velocity slip parameter.
Keywords
Melting heat transfer
Thompson and Troian slip
Nanofluid
Movable cylinder
Nomenclature
-
Velocity components in the axial and radial direction (m/s)
-
Radius (m)
-
Positive constant speed (m/s)
-
Wall surface velocity of the cylinder (m/s)
-
Heat capacity of the solid surface
-
Tangential velocity (m/s)
-
Mass transfer flux or suction velocity (m/s)
-
Characteristics length (m)
-
Uniform magnetic field strength (Kg/s2 A)
-
Latent heat transfer
-
Magnetic field parameter
-
Melting parameter
-
Temperature (K)
-
Temperature of the melting surface (K)
-
Reference temperature (K)
-
Thermal conductivity (W/m K)
-
Ambient or free-stream temperature (K)
-
Specific heat capacity at constant pressure (J/Kg K)
- Pr
-
Prandtl number
-
Cartesian coordinates in axial and radial directions (m)
-
Dimensionless velocity
-
Curvature parameter
-
Arbitrary constants
-
Mass suction parameter
-
Dimensionless temperature
-
Coefficient of skin friction
-
Local Nusselt number
-
Local Reynolds numbers
-
Velocity slip parameter
-
Navier’s constant slip length
-
Reciprocal of some critical shear rate
-
Dimensionless critical shear rate
-
Thermal diffusivity (m2/s)
-
Dynamic viscosity (N s/m2)
-
Density (Kg/m3)
-
Electrical conductivity (S/m)
-
Stretching/shrinking parameter
-
Solid nanoparticle volume fraction
-
Kinematic viscosity (m2/s)
-
Pseudo-similarity variable
-
Shear stress at the wall surface of the cylinder
-
Stream function
Greek symbols
- 2D
-
Two-Dimensional
- FCF
-
Forced convective flow
- CNT
-
Carbon nanotube
- 3D
-
Three-Dimensional
- GSCE
-
Generalized slip condition effect
- PDEs
-
Partial differential equations
- BLS
-
Boundary layer separation
- LBS
-
Lower branch solution
- ODEs
-
Ordinary differential equations
- BCs
-
Boundary conditions
- MHD
-
Magneto-hydrodynamics
- UBS
-
Upper branch solution
Acronyms
-
Hybrid nanofluid
-
Nanofluid
-
Base fluid
-
Ambient condition
-
Condition at surface
Subscripts
- ′
-
Differentiation with respect to .
Superscript
1 Introduction
The melting process is crucial in the making of semiconductor substances, solidification of molten rock flows, permafrost, and thawing of frozen ground, etc. Problems of the melting heat transfer can be classified based on the ranges of temperature like metal temperature or other melting material temperatures, and ranges of atmospheric temperature in a cold climate. Epstein and Cho (Epstein and Cho, 1976) scrutinized the heat transfer problem in laminar steady forced convective flow (FCF) induced by a melting process, whilst Kazmierczak et al. (Kazmierczak et al., 1986) considered the melting effect on the free CF past horizontal and vertical surfaces in a porous media. Bakier (Bakier, 1997) and Gorla et al. (Gorla et al., 1999) examined the phenomena of melting impact on buoyancy flow immersed in a porous medium past a vertical surafce. The characteristics of the melting process on a steady flow and heat transport towards a stagnation-point through a moving sheet were scrutinized via Bachok et al. (Bachock et al., 2010). Ahmad and Pop (Ahmad and Pop, 2014) discussed the characteristics of the melting impact on the buoyancy steady flow in a porous medium through a vertical plate and presented double solutions. The phenomena of melting heat transport on the buoyancy flow comprising non-Newtonian fluid from a stretchy sheet with heat absorption/generation were anticipated by Hayat et al. (Hayat et al., 2017). Venkateswarlu et al. (Venkateswarlu et al., 2018) inspected the effects of heat source and viscous dissipation on magneto flow through an electrically conducting, warm liquid to melting parallel surface towards a steady free-stream. Ghosh et al. (Ghosh et al., 2019) dissected the unsteady flow from a stretchy sheet with melting heat transfer incorporated by a nanofluid.
Technological progress has resulted in the development of a novel, new class of heat transport fluids known as nanofluids, which are created by diffusing nanosize nanoparticles in regular or conventional heat transport quiescent fluids. Nanoparticles are very translucent particles with diameters ranging from 1 to 100 nm and varying according to size and shape. Nanofluids are extensively utilized in refrigerators, cancer therapies, nuclear reactors, and have numerous electronic and automotive applications. Choi (Choi, 1995) observed that when tiny particles are scattered into regular fluids, the efficiency of thermal conductivity, as well as heat transfer is superior as paralleled to regular fluids. Khan and Pop (Khan and Pop, 2010) inspected the flow incorporated by the nanofluid from a stretchy surface through thermophoresis and the Brownian motion effect. The features of nanofluid flow across an exponentially stretchable sheet were examined by Nadeem and Lee (Nadeem and Lee, 2012) by employing the HAM technique. Das et al. (Das et al., 2014) dissected the unsteady flow incorporated nanofluid from a continuously stretchy surface. The magnetic influence on the radiative flow with melting effect subject to nanofluid over a stretchy sheet incorporated by second-order slip effect was investigated by Mabood and Das (Mabood and Das, 2016). Uddin et al. (Uddin et al., 2018) explored the slip influence on the forced convective radiative flow through a shrinkable and stretchable sheet and applied the Lie group to find the solution. Mishra and Kumar (Mishra and Kumar, 2019; Mishra and Kumar, 2019) examined the significance of nanofluid flow by considering water-based Cu and Ag nanofluids from a stretchable sheet and Riga plate, respectively. Kandwal et al. (Kandwal et al., 2019) inspected the dissipative effect on the magneto flow and heat transport through H2O-based silver nanofluid via a permeable inclined stretchy cylinder with heat generation/absorption. They established that the thermal boundary width expands due to heat absorption/generation and visous dissipation parameters. The impacts of heat absorption (or generation), and magentic on raditive nanofluid flow via a stretched porous sheet embed in a porous media with viscous-Joule heating were discussed by Mishra and Kumar (Mishra and Kumar, 2020). Mishra and Kumar (Mishra and Kumar, 2020) studied the thermal features of magneto slip flow and heat transport of H2O-based silver nanoparticle from a heated stretchable cylinder with viscous dissipative and Joule heating. Endalew and Sarkar (Endalew and Sarkar, 2020) analyzed the 2D flow of Casson nanofluid from wedge with melting effect. They pragmatic that the temperature declines owing to melting effect. The modified Arrhenius impact on the 3D magneto flow persuaded by water-based carbon nanotubes past a bi-directional stretchy sheet with radiation effect respectively with and without porous medium was observed by Upreti et al. (Upreti et al., 2021; Upreti et al., 2021). Endalew et al. (Endalew et al., 2021) analyzed the Navier slip impact on the unsteady magneto flow of Casson nanoliquid via an titled heated plate surrounded in a porous media. The radiative flow near an oblique stagnation point and heat transfer provoked by H2O-based CNT magneto nanofluid from a heated stretchy sheet was investigated by Mandal et al. (Mandal et al., 2012). Mishra and Kumar (Mishra and Kumar, 2021) explored the impacts of heat absorption/generation and magnetic effects on the dissipative flow of nanoliquid through a wedge in a porous media by consuming the Buongiorno model. In their studies, the temperature is shown to rise with greater estimates of viscous dissipation and heat absorption/generation factors. Khan et al. (Khan et al., 2021) dissected the effect of entropy on blood flow including Au particles past a movable curved surface with a magnetic number. Nandi et al. (Nandi et al., 2022) employed the statistical approach and numerical approach to probe the magneto slip flow near a stagnation point incorporated four types of water-based CH3OH/Cu/ Fe3O4/Ag nanofluids along a heated stretchable sheet with activation energy. Mandal et al. (Mandal et al., 2022) evaluated the mechanisms of the heat source/sink and radiative effect on the unsteady flow and heat transport by including the water-based CNT nanoliquid via an elastic sheet. Recently, Upreti et al. (Upreti et al., 2022) inspected the features of heat and mass transfers through 3D flow of a Casson nanofluid incorporating by microorganisms from a Riga plate. They observed that the working liquid is declined due to Casson factor.
An original-fangled class of fluids recognized as hybrid nanoliquids has recently been developed, consisting of a homogenous mixture of composite nanoparticles submerged in conventional fluids. Hybrid nanofluids exchange the discrepancy in rheological and thermal properties of mono nanoparticles, resulting in enhanced thermal conductivity when compared to mono nanofluids. Hybrid nanofluids are extensively utilized in different heat transfer areas like generators coolants, transformers, and electronic systems, biomedicine, drug reduction, refrigeration, etc. Sarkar et al. (Sarkar et al., 2015) discussed the latest developments and potential applications of hybrid nanofluids. The stimulus of entropy generation on the radiative flow of MHD Casson liquid persuaded by hybrid nanofluids from an erratic stretchy sheet was examined by Jamshed and Aziz (Jamshed and Aziz, 2018). Rostami et al. (Rostami et al., 2018) inspected mixed convective heat mechanism flow of water-based hybrid nanofluids from a vertical plate and found double solutions. The MHD steady flow from a stagnation-point through a vertical heated plate induced by hybrid nanofluids and MCF was explored by Zainal et al. (Zainal et al., 2020). They realized that the heat transport can be improved with help of a magnetic effect. Joshi et al. (Joshi et al., 2020) dissected the magneto effect on the mixed convective flow of hybrid nanoliquid from a spongy bidirectional sheet with a higher-order chemical reaction and heat generation. Their results indicate that the rate of mass transfer augments due to chemical reaction and magnetic number. Gangadhar et al. (Gangadhar et al., 2021) studied the slip consequence on the saddle and nodal stagnation point induced by hybrid nanofluids while taking into account the viscous dissipation. The consequence of volumetric heat generation on the magneto flow of water-based SWCNT-Ag hybrid nanofluid through a spongy bidirectional stretchy surface with chemical reaction was examined by Joshi et al. (Joshi et al., 2021). Upreti et al. (Upreti et al., 2021) investigated the entropy generation impact on the fluid radiative flow and heat transmit tempted by hybrid nanofluids past a absorbent stretchy heated surface under the influence of viscous dissipative. The unsteady squeezing flow through parallel plate provoked by magneto hybrid nanofluid with entropy was explored by Upreti et al. (Upreti et al., 2021). Khan et al. (Khan et al., 2021) developed the non-similarity solution of radiative flow past a yawed cylinder in the presence of hybrid nanofluid and mixed convection. Joshi et al. (Joshi et al., 2022) investigated the suction/blowing impact on the radiative magneto flow of hybrid nanofluid through a stretchy sheet in a Darcy-Forchheimer porous medium. They scrutinized that the velocity of hybrid nanofluid decelerates due to increasing values of magnetic, porosity, and Forchheimer parameters in the case of suction. The chemical reactive impact on the radiative flow of H2O-based Ag/MgO hybrid nanofluids through a curved surface was explored by Mishra and Upreti (Mishra and Upreti, 2022). Recently, Pandey et al. (Pandey et al., 2022) studied the natural convection 3D flow of H2O-based MoS2-GO hybrid nanofluid through a porous surface with magnetic, chemical reaction and dual slips.
According to a review of the literature, one of the most important tenets of the Navier–Stokes theory is the no-slip boundary condition. Though, in various cases, this concept does not be appropriate. The slip velocity boundary condition is known as the in-coherence of a liquid to a solid BCs. Fluids with slip-type boundaries are effective in polishing artificial heart faucets and cleaning internal openings. Also, the velocity slip is significant on stretchable surfaces once the liquid is particulate like polymer solutions, foams, and suspensions. Thompson and Troian (Thompson and Troian, 1997) explored the generalized slip condition effect (GSCE), assuming that the length of the slip is a shear stress function. Wang (Wang, 2002) presented an analytic solution of N—S equations including the significant influence of slip condition over a stretchy sheet. The impact of slip condition on a viscous flow via an elastic cylinder was examined by Wang and Chiu (Wang, 2011). They computed asymptotic solutions with high Reynolds numbers and for small slips. Mukhopadhyay (Mukhopadhyay, 2013) investigated the hydro-magnetic flow of a viscous fluid incorporated by a partial slip. She discovered that including higher slip, the velocity declines, whereas the temperature uplifts. The problem of Blasius via a semi-infinite plate along with the generalized slip condition was analysed by Groşan et al. (Groşan et al., 2016). Salahuddin et al. (Salahuddin et al., 2017) dissected the GSCE on magneto flow of Carreau nanofluid past a stretchable cylinder with reactive species.
The liquid flow with heat transfer through a stretchable/shrinkable cylinder is the most significant and relevant research area in mechanical and industrial engineering due to its broad applications. The influence of heat transfer on the product quality can be observed in the fields of polymer processing, chemical engineering, production of glass fibere, metal extrusion, hot rolling, paper production, plastic films and wires drawing. In addition, researchers examined the melting heat transfer and flow characteristics of either Newtonian or shear-thickening fluids over moving geometry with physical features in all of the preceding studies. In view of the forgoing applications, the novelty of the present analysis is to explore numerical solutions of the melting process on the magneto flow induced by the two hybridized AA7072 and AA7075 alloys nanomaterials past a movable cylinder in the attendance of Thompson and Troian irregular slip effect. The multiple solutions for a specific range of the movable parameter are also one of the main objectives of this study. The collocation technique based on the bvp4c solver are used by built-in MATLAB to find the numerical results. In addition, the upper branch solutions of the friction factor with magnetic parameter for the limiting case are analyzed with available outcomes. The outcomes obtained for the various significant parameters are illustrated via graphical images and tabulation. Furthermore, the pertinent research involving heat transfer characteristics comprising alloy nanoparticles has revealed a critical role in a variety of systems, including hip joint replacement operations, surgical implantation, and aerospace technology.
2 Problem formulation
Consider the MHD steady viscous flow of hybrid AA7072 and AA7075 alloy nanomaterials towards a continuous horizontal linearly permeable movable cylinder and radius
kept in an incompressible fluid subject to melting process. The nonlinear Thompson and Troian slip effect is also incorporated in this problem to predict further the complex characteristics of the hybrid nanofluid flow. The schematic flow configurations of the model together with the entrenched hybrid alloys nanoparticles as presented in Fig. 1, where
and
designate the axial and radial directions, respectively. Moreover, the flow is also axisymmetric, meaning the azimuthal axis does not affect on field variables. It is supposed that the linear stretchable/shrinkable velocity is indicated by
, where
is the positive constant speed,
is the corresponding stretchable/shrinkable parameter (
for stretchable and
for shrinkable),
is the coordinate considered along the axial direction of the cylinder, and
is the characteristics length. Note that the liquid is electrically conducted, and the uniform magnetic field strength
is executed perpendicular to the movable cylinder. Since the magneto Reynolds number is nominal, the induced magnetic field can be deemed insignificant. The characteristics of thermophysical of the viscous fluid and the hybrid alloys nanoparticles (AA7072 and AA7075) are taken to remain uniform. Also, it is also presumed that the invariable melting surface temperature is
, while that of the constant free-stream and reference temperatures are signified by
and
, respectively. Also, the terms viscous dissipation and the ohmic or joule heating in the energy equation are supposed to be zero. The leading boundary layer equations with the assumptions mentioned above are (see Ishak (Ishak, 2009) and Bhattacharyya (Bhattacharyya, 2011):
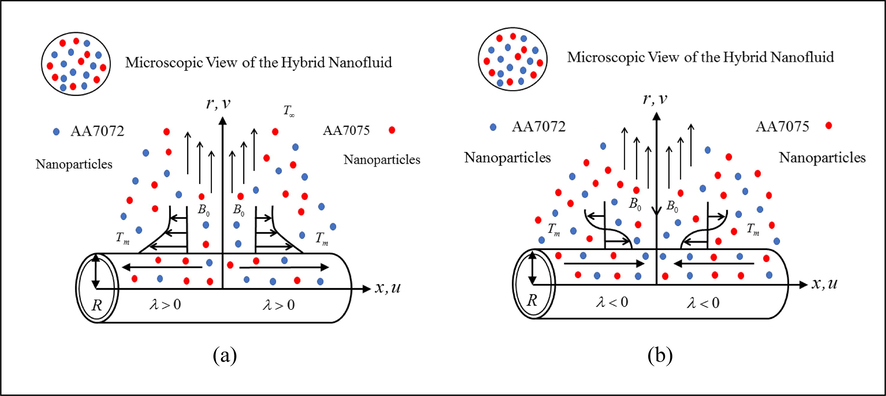
The model of the problem (a) stretchable case (b) shrinkable case.
According to the hybrid AA7072 and AA7075 alloy nanomaterials, the mathematical expression and constraints are distinguished as (Nisar et al., 2020; Khan et al., 2020):
where
,
,
,
and
designate the specific heat capacity, thermal conductivity, the absolute viscosity, the density, and the electrical conductivity, respectively. Also, the subscript AA7072, AA7075, and
communicate to the respective alloys nanoparticles and the regular (viscous) fluid. In addition,
and
are denoted by
and
in the process of numerical simulations, respectively. The physical data of the alloy nanoparticles and the regular (viscous) fluid are decorated in Table 1.
Physical features
Water
AA7072
AA7075
997.1
2720
2810
0.613
222
173
0.05
4179
893
960
6.2
–
–
Thompson and Troian (Thompson and Troian, 1997) employed generalized slip boundary condition which is given by
The relevant GSBCs of the problem are (Mabood and Das, 2016; Uddin et al., 2018; Thompson and Troian, 1997)
By constructing the similarity outcomes of the governing Eqs. (1) to (3), subject to the associated BCs (7), we define the following similarity variables (Uddin et al., 2018; Mukhopadhyay, 2013):
In the above Eq. (8), the symbols like called the stream function and it is signified by the usual way such as and , which satisfies Eq. (1). By describing in this form, the BCs at reduced to the following BCs , which is more suitable for numerical simulations.
Plugging Eq. (8) into above (2) and (3) number of equations, we acquired the following reduced form of the similarity NODEs:
along with boundary conditions (7) which become
The dimensionless parameters include the curvature parameter
, the magnetic field parameter
, the Prandtl number
, the melting parameter
, the mass suction parameter
, the velocity slip parameter
, and the dimensionless critical shear rate
. These influential parameters are mathematically expressed as
2.1 Physical quantity
The single important gradient of practical engineering interest for the considered problem is the shear stress
, which can be merely demarcated as
where
called the wall shear stress and is equal to
. Therefore, implementing Eqs. (6) and (8) into the aforesaid Eq. (13), one obtains the essential compact type of the shear stress as can be effortlessly shown by:
where is the dimensionless Reynolds number.
2.2 Important Note: For this study, the heat transfer rate in the mathematical expression form is simply given by
where
represents the wall heat flux and is equal to
. Plugging the similarity variables (8) into Eq. (15), we get the eased form of the heat transfer:
Now using the similarity BCs (11) into the Eq. (16) which becomes as follows:
According to equation (17), we couldn’t find any dual solutions for varying one selected parameter and fixing the range of the others. The right-hand side of Eq. (17) will be treated just like a constant. Therefore, we have to solve the problem and find multiple solutions only in terms of the shear stress and temperature profile for the selected varying parameters.
3 Procedure of numerical technique
Applying the boundary value solver (bvp4c) in the Matlab, NODEs (9) and (10) with the boundary conditions (11) are numerically solved. Other researchers have frequently employed this well-known solver to resolve the boundary value issue. The solutions are found by starting with an initial guess that is applied at the first mesh point and changing the step size until the accuracy is achieved. Depending on the values of the applied parameters, it is necessary to select the suitable initial guess and the thickness of boundary layer
. First, the equations must be transformed into a system of first-order ordinary differential equations. For the working process, let the factos are
The set of obtained Eqs. (9), (10) and (11) were executed using the new variables (18) to produce the following set of first-order non-linear ODEs, which may be expressed as follows:
along with the boundary conditions
The bvp4c function is then used to code the Eqs. (19) and (20). The function handle @OdeBVP is included in the solver's syntax, sol = bvp4c(@OdeBVP, @OdeBC, solinit, options), and it is used to code the set of acquired equations. The function handle @OdeBC is then coded with the boundary conditions (20). The Optional integration arguments include choices, whereas the initial approximation and initial mesh points of the result are implied in solinit. Furthermore, the solver is launched, and the output, which includes graphs and numerical solutions, is printed. There are multiple solutions exist if the other initial guess value meets the boundary layer requirements. In addition, Shampine et al. (Shampine et al., 2003) describe this procedure in detail.
3.1 Justification of the scheme
This subsection of the work anticipates the authentication, precision, and accuracy of the present computational usual method by the tabular and graphical forms. Table 2 presents the solutions of the shear stress for the upper branch solution (UBS) with varying
(in the absence of
,
,
,
,
, and
) and
. The results obtained are in excellent agreement with Mukhopadhyay (Mukhopadhyay, 2013) and Xu and Lee (Xu and Lee, 2013) as a limiting case which was highlighted in Table 2 and hence gives self-assurance that the computational outcomes are accurate. In addition, the velocity profile of the upper solution branch for numerous values of the magnetic parameter when
,
,
,
,
,
, and
is highlighted in Fig. 2. The outcomes show that the current upper solution branch and the published work or outcome provided by Mukhopadhyay (Mukhopadhyay, 2013) are very well matched/compatible. We may therefore have even more faith that the results generated for the provided model are unique and correct because to this perfect harmony.
Mukhopadhyay (Mukhopadhyay, 2013)
Xu and Lee (Xu and Lee, 2013)
0.0
1.000000
–
1.00000000
0.25
−1.118034
–
−1.11803567
1.0
−1.4142135
−1.41421
−1.41421356
2.25
−1.80277565
–
−1.80277563
5.0
–
−2.4494
−2.44948781
10.0
–
−3.3166
−3.31662435
50.0
–
−7.1414
−7.14142342
100.0
–
−10.0498
−10.04987864
500.0
–22.38302
–22.38302376
1000.0
–
–
−31.63858198
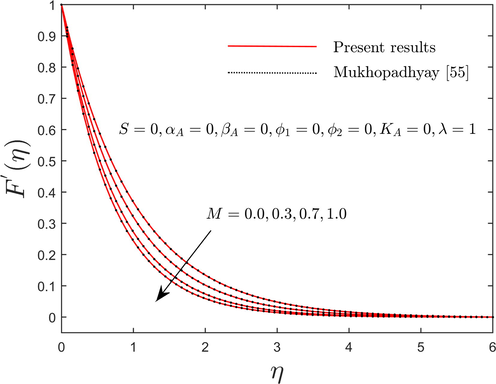
The comparison of velocity profile for numerous values of
.
4 Analysis of results and discussion
The outcomes of the physical parameters such as the dimensionless critical shear rate
, the magnetic field parameter
, the dimensionless velocity slip parameter
, the mass suction parameter
, the curvature parameter
, the nanoparticles volume fraction
and
, the melting parameter
and the stretching/shrinking parameter
on friction factor or shear stress and dimensionless temperature profile of the hybrid AA7072 and AA7075 alloys nanoparticles are discussed in Figs. 3 to 10. The shear stress values determined through computation for UBS and LBS due to the varying parameters are provided in Table 3 when
and
. The table shows that the friction factor upsurges for the upper branch with
,
and
while the impact of the similar parameters are reversed for the lower branch. Moreover, the shear stress was significantly decreased and increased in both outcome branches with the corresponding larger value of
and hybrid alloys nanoparticles, respectively. Alternatively, the curvature parameter
declines the shear stress for the UB while for the LB it is elevated. Additionally, the shear stress escalates for the upper branch solution at about 0.29 %, 5.01 %, 3.64 % and 26.64 % owing to the larger value of
,
,
and
, respectively, but it is declines by almost 5.26 % and 2.16 % for the same branch with superior impact of
and
. However, for the branch of lower solutions, the shear stress shrinkages up to 22.55 %, 1.99 % and 14.8 % due to superior influence of
,
, and
, while the shear stress enhanced via almost 9.71 %, 2.31 % and 1.18 % with
,
, and the hybrid nanoparticles
, respectively. Therefore, the shear stress or the wall drag force highest and lowest augmentation in percentage wise occured with the respective mass suction parameter and the critical shear rate parameter.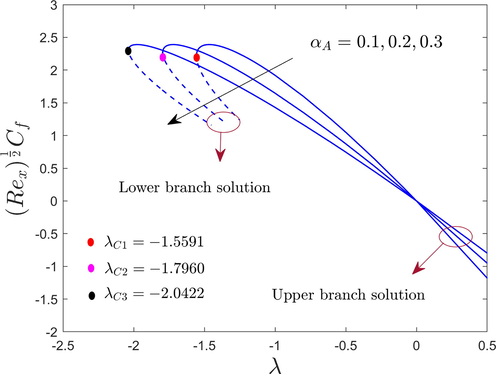
The friction factor with
for numerous values of
.
The friction factor with
for numerous values of
.
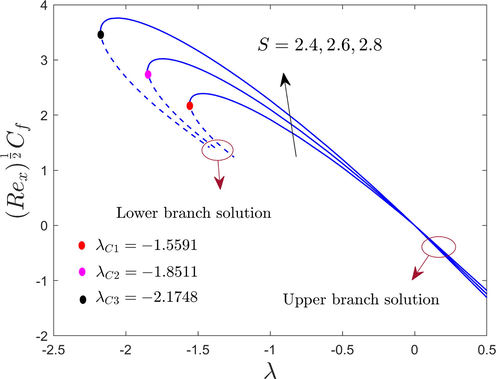
The friction factor with
for numerous values of
.
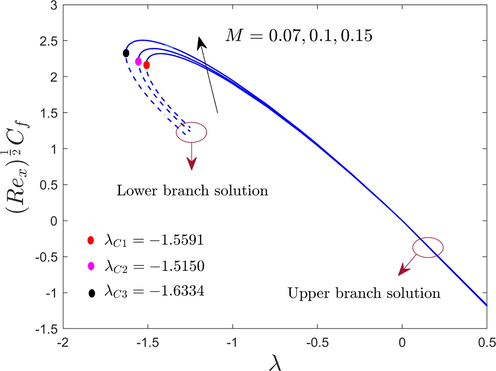
The friction factor with
for numerous values of
.
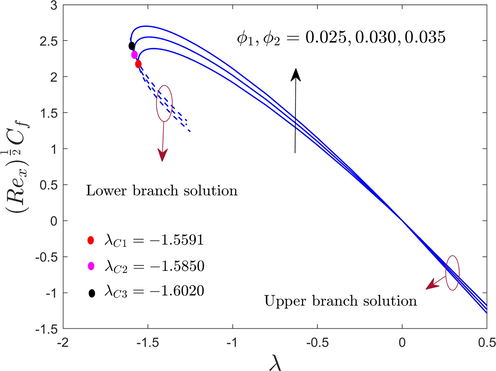
The friction factor with
for numerous values of
and
.
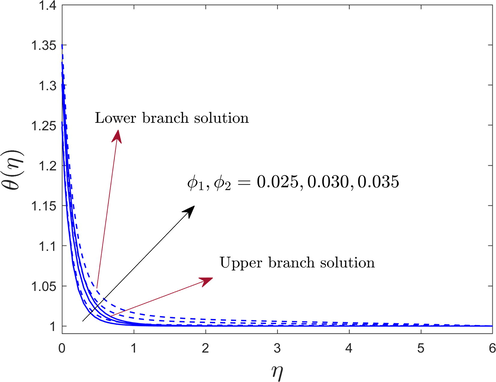
The temperature
profiles for numerous values of
and
.
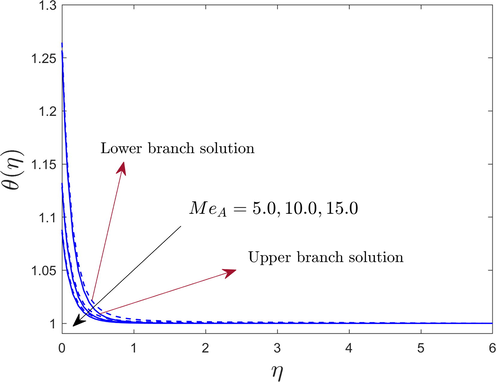
The temperature
profiles for numerous values of
.
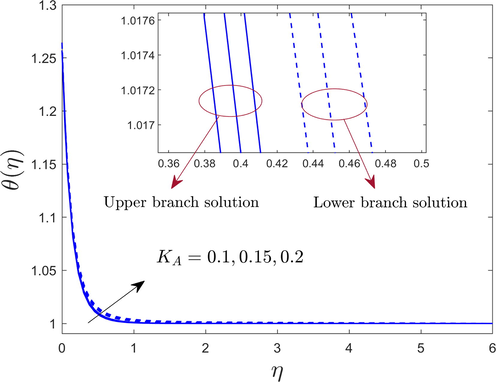
The temperature
profiles for numerous values of
.
Upper branch
Lower branch
0.10
0.05
0.20
0.10
0.025
2.4
2.3817722
1.8767375
0.20
–
–
–
–
–
2.2564981
1.4535673
0.30
–
–
–
–
–
2.0248587
1.2288461
0.10
0.05
0.20
0.10
0.025
2.4
2.3817722
1.8767375
–
0.10
–
–
–
–
2.3887506
1.8393092
–
0.15
–
–
–
–
2.3896475
1.8011476
0.10
0.05
0.10
0.10
0.025
2.4
2.5135616
1.5673113
–
–
0.15
–
–
–
2.4591146
1.7194844
–
–
0.20
–
–
–
2.3817722
1.8767375
0.10
0.05
0.20
0.10
0.025
2.4
2.3817722
1.8767375
–
–
–
0.15
–
–
2.5007951
1.9201470
–
–
–
0.20
–
–
2.5853336
2.5853527
0.10
0.05
0.20
0.10
0.025
2.4
2.3817722
1.8767375
–
–
–
–
0.030
–
2.4686026
1.8989359
–
–
–
–
0.035
–
2.5500159
1.9257284
0.10
0.05
0.20
0.10
0.025
2.4
2.3817722
1.8767375
–
–
–
–
–
2.7
3.0162778
1.5989401
–
–
–
–
–
2.9
3.3028902
1.5393602
Furthermore, the entire simulations of this study were working out for the following fixed selected values of the influencing parameters such as , , , , , , , and . The upper branch and lower branch solutions curves were spontaneously highlighted by the solid blue and dash lines, respectively. These dissimilar branches further meet at a single specific point called a bifurcation point or critical point where it was tainted by the black, pink, and red solid balls throughout the necessary graphs.
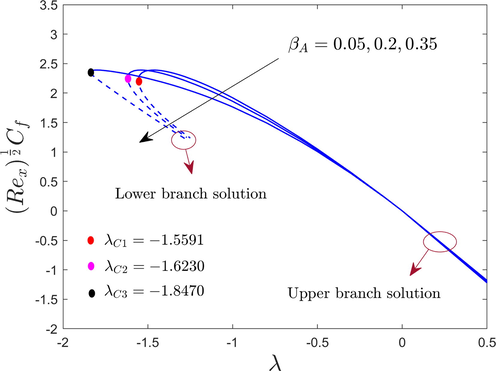
Variations of the wall drag force at the cylinder surface or shear stress, of the hybrid AA7072 and AA7075 alloys nanoparticles with , , , , , and are shown in Figs. 3 to 7 for the upper and lower branch solutions. From the pictures, we can see that there are counties of unique outcomes exists for , no outcomes exist for the range of and multiple outcomes exist for the range of . Therefore, the outcomes are possible up to the bifurcation value ( ). At this critical or bifurcation point , the boundary layer (BL) scaling or approximation breaks down, therefore, we are unable to obtain additional results for the range of . Beyond this value, the BL separates from the cylinder surface and the results based upon the BL approximation are not accessible for each value of the selected influential parameters. The bifurcation value of (say ) is written in each window of the pictures for the selected varying controlling parameters like , , , , and . It is outstandingly noticed from Figs. 3 to 7 that the magnitude of the bifurcation values uplifts with an increase in the aforementioned selected parameters. In this regard or tendency, the BL separation hindered for a cylinder with the augmentation of , , , , and .
The outcomes revealed in Figs. 3 and 4 illustrate that as the and upsurges, the shear stress of the hybrid AA7072 and AA7075 alloys nanoparticles also shrinkages for the upper and lower branch results while their impact is completely changed in the range of for the upper branch solution. According to the general or physical scenario, the velocity curves are inversely proportional to the friction. Therefore, by improving the value of and parameters the velocity elevates, as a result, the shear stress reduces. However, if values of both parameters enhance which ultimately diminish the shear stress.
Figs. 5 and 6 illustrated the outcomes for the lower and upper branches of , and on the shear stress of the hybrid AA7072 and AA7075 alloys nanoparticles, respectively. From the graphs, it is seen that the friction factor stress for the UBS is augmenting due to the superior value of and whilst the performance of the wall drag force reduces for the LBS. Physically, with the continuous improving impacts of , the velocity and momentum boundary layer thicknesses reduces as a result of the hybrid nanoparticles adhering to the cylinder's surface. As a result, the shear stress or wall drag force upsurges (see Fig. 5). Moreover, the drag force improves in the problem due to the larger values of by which the fluid motion ends, as a consequence, the friction factor enriches (see Fig. 6).
The hybrid nanoparticles on the shear stress for the UBS and LBS are detected in Fig. 7. The shear stress or friction factor and nanoparticles volume fraction maintain the rule of direct relations. Results suggest that both solution branches are acting more aggressively due to the greater influence of hybrid nanoparticles. In addition, to test the current picture more genuinely which indicates that the shear stress was initially in the range of declines for the UBS with larger values of hybrid nanoparticles.
The dimensionless temperature profile due to the large influence of and for both branches are depicted in Fig. 8. The temperature and the nanoparticles and maintain the direct law of relation. Results suggest that the larger impact of and is causing both solution branches to behave in an exaggerated way. Physically, the intensification in the thermal boundary layer width as well as the temperature is due to the development in the nanoparticles volume fraction and to improve the thermal conductivity in contrast to the convectional fluid. In addition, the thermal conductivity of hybrid nanofluid is growing due to the increasing and , which results in a faster heat transfer rate in reply to rising temperature profile. Also, the gap between the two dissimilar branch solutions is very small or negligible due to a large Prandtl number .
Figs. 9 and 10 revealed the impact of the melting parameter , and the curvature parameter on the temperature distribution curves of the hybrid AA7072 and AA7075 alloys nanoparticles for both branches, respectively. From the figures, we can see that for a superior values of , the temperature declines abruptly in both solution branches. This occurs because the melting process minimizes the frictional forces and heat flux, preventing boundary layer separation. Therefore, the width of thermal boundary layer shrinks with higher . However, the temperature profile and thickness augment due to the influence of for the LBS and UBS.
5 Final remarks
The idea of this manuscript was to study the MHD steady flow of hybrid AA7072 and AA7075 alloy nanomaterials past a horizontal linearly permeable stretchable/shrinkable cylinder with the significant impacts of the melting process. The nonlinear Thompson and Troian slip effect is also incorporated in this problem to predict further the complex characteristics of the nanoliquid flow. The impact of several physical parameters on the hybrid alloy nanoparticles flow and energy transfer with the magnetic field was analyzed. The numerical outcomes for the upper and lower branch solution were attained by bvp4c in MATLAB. The impression of friction factor at the wall surface of the cylinder was also examined. The result gained is noted as:
-
It was established that even though the solutions for the stretchy case are unique, there are multiple (lower and upper) branch results for the shrinking case for a particular range of the movable parameter.
-
The shear stress shrinkages for the upper branch and lower branch with the higher values of and for the shrinkable case while it is increasing for the stretchable case.
-
The temperature profiles distribution elevates for the UBS and LBS with the higher value of , and hybrid nanoparticles but temperature significantly shrinkages with .
-
The magnitude of the critical or bifurcation value enriches the selected pertinent parameters, which in turn delays the separation of the boundary layer.
-
In the form of quanitative outcomes, the shear stress upsurges at about 5.01 % and 2.31 % for the upper branch and lower branch with higher magnetic parameter while it is declines and accelerates up to 2.16 % and 9.71 % for the upper branch and lower branch, respectively, due to larger impacts of curvature parameter.
-
The lowest and highest percentage wise increment of shear stress developed via almost 0.29 % and 26.64 % for the branch of upper solutions due to the larger impact of critical shear rate and mass suction parameter, respectively.
-
The impact of the hybrid nanoparticles increases the shear stress for both branches of the solution while it is shrinkages for the lower branch and increases for the upper branch with a higher value of and .
Acknowledgment
The authors are very thankful to the support of Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, the authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP.2/154/43).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Melting effect on mixed convection boundary layer flow about a vertical surface embedded in a porous medium: Opposing flows case. Transp. Porous Media. 2014;102:317-323.
- [Google Scholar]
- Melting heat transfer in boundary layer stagnation-point flow towards a stretching/shrinking sheet. Phys. Lett. A. 2010;374:4075-4079.
- [Google Scholar]
- Aiding and opposing mixed convection flow in melting from a vertical flat plate embedded in a porous medium. Transp. Porous Media. 1997;29:127-139.
- [Google Scholar]
- Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Comm. Heat Mass Trans.. 2011;38:917-922.
- [Google Scholar]
- Enhancing thermal conductivity of fluids with nanoparticles. ASME Pub. Fed.. 1995;231:99-106.
- [Google Scholar]
- Nanofluid flow over an unsteady stretching surface in presence of thermal radiation. Alexandria Eng. J.. 2014;53(3):737-745.
- [Google Scholar]
- A numerical study of forced convection Casson nanofluid flow past a wedge with melting process. ASME Int. Mech. Eng. Congress Exposition. 2020;84584:1-7.
- [Google Scholar]
- Convective And dissipative temporal flow of Casson nanofluid past a tilted plate in a porous medium with Navier's slip and slanted magnetic field, Special Topics Reviews Porous Media: Int. J.. 2021;12(6):43-64.
- [Google Scholar]
- Melting heat transfer in steady laminar flow over a flat plate. ASME J. Heat Transf.. 1976;76:531-533.
- [Google Scholar]
- Nodal/Saddle stagnation point slip flow of an aqueous convectional magnesium oxide–gold hybrid nanofluid with viscous dissipation. Arab J. Sci. Eng.. 2021;46:2701-2710.
- [Google Scholar]
- Existence of dual solutions and melting phenomenon in unsteady nanofluid flow and heat transfer over a stretching surface. J. Mech.. 2019;35(5):705-717.
- [Google Scholar]
- Mixed convection effect on melting from a vertical plate in a porous medium. Transp. Porous Media. 1999;36:245-254.
- [Google Scholar]
- Blasius problem with generalized surface slip velocity. J. App. Fluid Mech.. 2016;9(4):1641-1644.
- [Google Scholar]
- Melting heat and thermal radiation effects in stretched flow of an Oldroyd-B fluid. Appl. Math. Mech. -Engl. Ed.. 2017;38(7):957-968.
- [Google Scholar]
- Mixed convection boundary layer flow over a vertical cylinder with prescribed surface heat flux. J. Phys. A: Math. Theor.. 2009;42:195501
- [Google Scholar]
- Cattaneo-Christov based study of TiO2–CuO/EG Casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl. Nanosci.. 2018;8:685-698.
- [Google Scholar]
- Mixed convection flow of magnetic hybrid nanofluid over a bidirectional porous surface with internal heat generation and a higher-order chemical reaction. Heat Transf.. 2020;50(4):3661-3682.
- [Google Scholar]
- Heat and mass transfer assessment of magnetic hybrid nanofluid flow via bidirectional porous surface with volumetric heat generation. Int. J. Appl. Comput. Math.. 2021;7:64.
- [Google Scholar]
- MHD Darcy-Forchheimer Cu-Ag/H2O-C2H6O2 hybrid nanofluid flow via a porous stretching sheet with suction/blowing and viscous dissipation. Int. J. Comput. Meth. Eng. Sci. Mech.. 2022;23(6):527-535.
- [Google Scholar]
- Numerical investigation of nanofluid heat transfer in an inclined strtching cylinder under the influence od suction/injection and viscous dissipation. NanoSci. Technol. Int. J.. 2019;10(1):29-49.
- [Google Scholar]
- Melting from a flat plate embedded in a porous medium in the presence of steady natural convection. Numer. Heat Transf.. 1986;10:571-581.
- [Google Scholar]
- Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf.. 2010;53(11–12):2477-2483.
- [Google Scholar]
- Mixed convective radiative flow through a slender revolution bodies containing molybdenum-disulfide graphene oxide along with generalized hybrid nanoparticles in porous media. Crystals. 2020;10:771.
- [Google Scholar]
- Comparative investigation on MHD nonlinear radiative flow through a moving thin needle comprising two hybridized AA7075 and AA7072 alloys nanomaterials through binary chemical reaction with activation energy. J. Mater. Res. Tech.. 2020;9(3):3817-3828.
- [Google Scholar]
- Non-similarity solutions of radiative stagnation point flow of a hybrid nanofluid through a yawed cylinder with mixed convection. Alexandria Eng. J.. 2021;60:5297-5309.
- [Google Scholar]
- Insight into the dynamics of transient blood conveying gold nanoparticles when entropy generation and Lorentz force are significant. Int. J. Comm. Heat Mass Transf.. 2021;127:105415
- [Google Scholar]
- Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip. Eur. Phys. J. Plus. 2016;131:3.
- [Google Scholar]
- A numerical simulation of mixed convective and arbitrarily oblique radiative stagnation point slip flow of a CNT-water MHD nanofluid. J. Therm. Anal. Calorim.. 2012;143(3):1901-1916.
- [Google Scholar]
- Analysis of unsteady magnetohydrodynamic 3-D rotating flow and transfer of heat in carbon nanotube-water nanofluid: An engineering application. J. Nanofluids. 2022;11(2):204-213.
- [Google Scholar]
- Influence of viscous dissipation and heat generation/absorption on AG-water nanofluid flow over a Riga plate with suction. Int. J. Fluid Mech. Res.. 2019;46(2):113-125.
- [Google Scholar]
- Viscous dissipation and Joule heatings influences past a stretching sheet in a porous medium with thermal radiation saturated by silver-water and copper-water nanofluids. Special Topics Rev. Porous Media. 2019;10(2):171-186.
- [Google Scholar]
- Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl. Sci.. 2020;2:1350.
- [Google Scholar]
- Thermal performance of MHD nanofluid flow over a stretching sheet due to viscous dissipation, Joule heating and thermal radiation. Int. J. Appl. Comput. Math.. 2020;6:123.
- [Google Scholar]
- Numerical analysis of MHD nanofluid flow over a wedge, including effects of viscous dissipation and heat generation/absorption. using Buongiorno model. 2021;50(8):8453-8474.
- [Google Scholar]
- A comparative study of Ag–MgO/water and Fe3O4–CoFe2O4/EG–water hybrid nanofluid flow over a curved surface with chemical reaction using Buongiorno model. Partial Diff. Eq. Appl. Math.. 2022;5:100322
- [Google Scholar]
- MHD boundary layer slip flow along a stretching cylinder. Ain Shams Eng. J.. 2013;4:317-324.
- [Google Scholar]
- MHD boundary layer slip flow along a stretching cylinder. Ain Shams Eng. J.. 2013;4(2):317-324.
- [Google Scholar]
- Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res. Lett.. 2012;7:94-99.
- [Google Scholar]
- MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int. Commun. Heat Mass Transf.. 2022;130:105791
- [Google Scholar]
- Exploration of aluminum and titanium alloys in the stream-wise and secondary flow directions comprising the significant impacts of magnetohydrodynamic and hybrid nanofluid. Crystals. 2020;10:679.
- [Google Scholar]
- Effect of natural convection on 3D MHD flow of MoS2–GO/H2O via porous surface due to multiple slip mechanisms. J. Taibah Univ. Sci.. 2022;16(1):749-762.
- [Google Scholar]
- Dual solutions for mixed convective stagnation-point flow of an aqueous silica–alumina hybrid nanofluid. Chin. J. Phys.. 2018;56:2465-2478.
- [Google Scholar]
- Carreau nanofluid impinging over a stretching cylinder with generalized slip effects: Using finite difference scheme. Results Phys.. 2017;7:3090-3099.
- [Google Scholar]
- A review on hybrid nanofluids: recent research, development and applications. Renewable Sustainable Energy Rev.. 2015;43:164-177.
- [Google Scholar]
- Solving ODEs with Matlab. Cambridge University Press; 2003.
- A general boundary condition for liquid flow at solid surfaces. Nature. 1997;389:360-362.
- [Google Scholar]
- Melting and second order slip effect on convective flow of nanofluid past a radiating stretching/shrinking sheet. Propulsion Power Res.. 2018;7(1):60-71.
- [Google Scholar]
- Assesment of entropy generation and heat transfer in three-dimensional hybrid nanofluids flow due to convective surface and base fluids. J. Porous Media. 2021;24(3):35-50.
- [Google Scholar]
- Modified Arrhenius and thermal radiation effects on three-dimensional magnetohydrodynamic flow of Carbon nanotubes nanofluids over bi-directional stretchable surface. J. Nanofluids. 2021;10(4):538-551.
- [Google Scholar]
- Darcy-Forchheimer flow of CNTs-H2O nanofluid over a porous stretchable surface with Xue model. Int. J. Modern Phys. B 2021
- [CrossRef] [Google Scholar]
- Unsteady squeezing flow of magnetic hybrid nanofluids within parallel plates and entropy generation. Heat Transf.. 2021;50(1):105-125.
- [Google Scholar]
- Thermophoresis and Brownian motion effects on 3D flow of Casson nanofluid consisting microorganisms over a Riga plate using PSO: a numerical study. Chinese J. Phys.. 2022;78:234-270.
- [Google Scholar]
- Melting and viscous dissipation effects on MHD flow over a moving surface with constant heat source. Trans. A. Razmadze Math. Institute. 2018;172:619-630.
- [Google Scholar]
- Flow due to a stretching boundary with partial slip-an exact solution of the Navier-Stokes equations. Chem. Eng. Sci.. 2002;57:3745-3747.
- [Google Scholar]
- Chiu-On Ng, Slip flow due to a stretching cylinder. Int. J. Non-Linear Mech.. 2011;46:1191-1914.
- [Google Scholar]
- Variational iteration method for the magnetohydrodynamic flow over a nonlinear stretching sheet, Abstract. Appl. Anal. 2013573782
- [Google Scholar]
- MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys.. 2020;66:630-644.
- [Google Scholar]







