Translate this page into:
Heterogeneous/homogeneous and inclined magnetic aspect of infinite shear rate viscosity model of Carreau fluid with nanoscale heat transport
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The study of the inclined flow along with the heterogeneous/homogeneous reactions in the fluid has been widely used in many industrial and engineering applications, such as petrochemical, pharmaceutical, materials science, heat exchanger design, fluid flow through porous media, etc. The purpose of this study is to present an infinite shear rate viscosity model using the inclined Carreau fluid with nanoscale heat transport. The model considers the effect of inclined angle on the fluid’s viscosity and the transfer of heat at the nanoscale. The result shows that the viscosity of the fluid decreases by increasing the inclination angle and the coefficient of heat transfer also increases with the inclination. The model can be used to predict the viscosity and heat transfer fluid’s behavior in the inclined systems that is widely used in the industrial and engineering applications. The results provide a better understanding of the inclined flow behavior of fluids and the heat transfer at the nanoscale, which can be useful in heat exchanger design, fluid flow through porous media, etc. Greater Infinite shear rate viscosity parameter gives the higher magnitude of Carreau fluid velocity. Moreover, inclined magnetic field reduces the velocity due to Lorentz force. Two numerical schemes are used to solve the model, BVP4C and Shooting.
Keywords
Infinite shear rate
Carreau model viscosity
Lorentz force
Shooting technique
Non uniform heat sink/source
Thermal radiation
Nomenclature
- Symbol
-
Parameter
-
CF index
-
Density of fluid
- A*
-
Space coefficients
-
Infinite based temperature
-
Cauchy stress tensor
- L
-
Velocity gradient
- , and
-
Heat flux, sink/source and transfer
- C
-
Fluid concentration
- and
-
Local Reynold and Weissenberg number
- M, and Pr
-
Magnetic, Nusselt and Prandtl number
-
Kinematic viscosity
-
Pressure
- and
-
Mean absorption and skin friction coefficient
- and
-
Space and velocity coordinates
-
Rivilin Erickson tenor
-
Radiative heat flux
-
Viscosity ratio
- , and
-
Temperature ratio, unsteadiness and Radiation parameter
-
Stefan Boltzmann constant
-
Specific values of the heat
-
Shear strain tensor rate
- ,
-
Thermal diffusivity and conductivity
- T
-
Fluid’s temperature
-
Thermal Biot number
- B*.
-
Temperature dependent sink/source
-
diffusion coefficient
-
stretching parameter (ε > 0) and shrinking sheet for (ε < 0).
-
coefficient of homogeneous reaction
-
strength coefficient of homogeneous reaction
1 Introduction
In fluid mechanics, viscosity is measured through the fluid’s resistance. It is an important property that determines how a fluid behaves under different flow conditions. Viscosity can be modeled using various constitutive equations, such as the Newtonian, power-law, and Carreau fluid (CF) models. These equations describe the viscosity of fluid under different flow conditions. In this study, CF model is used as a non-Newtonian fluid (NNF) model that can accurately describe the viscosity of fluids under shear rate. This model considers the effect of shear rate on the viscosity and allows to perform the accurate prediction of the viscosity behavior in inclined flow systems. The results represent that the viscosity of the fluid decreases with an increase in the inclination angle, providing a deeper understanding of the inclined flow behavior. There have been many recent studies conducted by the scholars in the field of viscosity in fluids. Spann et al. (Spann et al., 2020) proposed a new viscosity model for the fluids under high pressure and temperature. The model considered the effects of pressure and temperature on the viscosity of the fluid. Bilal et al. (Bilal et al., 2021) presented a numerical analysis of the viscosity behavior on the CF in the laminar flow through a pipe. This study found that the fluid’s viscosity decreases by increasing the power-law index of the fluid. Chen et al. (Chen and Hwang, 2021) investigated the viscosity behavior of a Bingham fluid in a laminar flow through a pipe. This study indicates that the fluid’s viscosity decreases by increasing the shear rate. Khan et al. (Khan et al., 2022) proposed a new viscosity model for fluids with temperature-dependent viscosity. The model considered the effects of temperature on the viscosity of the fluid. Many other articles (Sabir et al., 2020; El Sayed et al., 2022; Ayub et al., 2022; Saleh, 2022; Ayub et al., 2021; Shah et al., 2022; Ayub et al., 2021; Shah et al., 2021) are related to the viscosity models of different fluid associated with different effects, like thermal radiation, buoyancy, heat sink source and Lorentz force.
CF model is widely used in the industrial and engineering applications, such as heat exchanger design and fluid flow through porous media. Additionally, it is used in various biomedical applications where the viscosity of blood and other biological fluids are modeled. CF model is a form of NNF, which is widely used to describe the rheological behavior under shear rate. It is an extension of power-law model along with the shear rate effects based on the fluid’s viscosity. There are various recent studies conducted by the scholars in the field of CF. The model based on the CF model is considered using the temperature effects on the fluid’s viscosity is proposed by Nazir et al. (Nazir et al., 2020). They concluded that the decrement is seen in the fluid’s viscosity by increasing the temperature. Kim et al. (Kim, 2022) presented a numerical analysis of the viscosity behavior of CF in the laminar flow through a pipe. The study found that the viscosity decreases by increasing the fluid’s shear rate. In another study, Bhatti et al. (Bhatti et al., 2021) investigated the heat transfer behavior of CF in a laminar flow through a pipe. The study found that the heat transfer coefficient increases with an increase in the power-law index of the fluid. Salahuddin et al. (Salahuddin et al., 2021) worked on CF model to consider the paraboloid surface and boundary layer region along with variable fluid properties and viscous dissipation. Other related studies can be found in scholarly articles (Shah et al., 2021; Ayub et al., 2022; El Din et al., 2022; Wang et al., 2022; Ayub et al., 2022). The understanding of the heat transfer behavior of CF is important, which has been reported in many industrial and engineering applications, such as heat exchanger design, fluid flow through porous media, and more. Additionally, it is useful in biological and biomedical applications where the heat transfer in biological fluids needs to be modeled.
The transport of energy in the CF has various important aspects to consider the behavior of fluids under different flow conditions. The transport of energy can take place through conduction, convection, and radiation. In this study, the nanoscale heat transport is presented using the heat transfer, which occurs at the nanometer scale. At this scale, the thermal conductivity of the fluid is influenced by the fluid molecules behavior and the size of the fluid particles. There has been a significant amount of research conducted by the scholars in the field of heat transfer using the CFs. Zhang et. al (Zhang et al., 2020) performed the critical analysis on the fluid/ heat transportation and brine-drenching attached with energy generation. Analysis of irreversibility and energy transportation are used to consider the infinite plates is discussed by Khan et. al (Khan et al., 2020). In this study, it is revealed that nanoparticles enhance the transport of fluid. Nayak et al. (Nayak et al., 2020) studied the attitude of entropy optimization using the nanomaterial of the NNF. It is related with intensification of heat transport and solar energy. Chu et. al (Chu et al., 2021) focused on the hybrid nanofluid for solute particles as well as enhancement in the thermal energy. The nanoparticles are engaged with the chemical reaction and activation energy over the geometry of parabolic surface and numerical investigation are performed using the finite element approach. Some recent study related to the energy transport based on the mathematical model of micropolar fluid within MHD environment over cylinder geometry is discussed by Alwawi t. al (Alwawi et al., 2022). The transportation of energy and enhancement of thermal conductivity is available in which scholars found more physical properties of heat transport in these references (Haider et al., 2021; Ayub et al., 2021; Ayub et al.; Shah et al., 2021; Tajik et al., 2022; Botmart et al., 2022).
Nanofluids contain very small particles, typically on the nanometer scale, suspended in a base fluid. These particles can be performed by using the various materials, such as metals, ceramics, and semiconductors, which are used to the base fluid to enhance the thermal conductivity. The enhancement of thermal conductivity is caused by using the increased number of thermal phonons, which are responsible for heat transfer to present the fluid due to the presence of nanoparticles. There has been a significant amount of research conducted by the scholars in the field of nanofluids. Waqas et. al (Waqas, 2020) characterized the impact of nanofluid with different mathematical model using the cross fluid associated with the geometry of expanding-contracting cylinder containing the stagnation region. Haq et. al (Haq et al., 2020) studied the Cross nanofluid attached with the natural bio-convective conditions and gyrotactic microorganisms. The heat flux model based on the Cattaneo–Christov and diffusion analysis based on the CF is discussed by. Nazir et. al (Nazir et al., 2020). Prasannakumara et. al (Prasannakumara, 2021) performed the numerical simulation of Maxwell nanofluid and discussed the heat transport using the geometry of stretching sheet. Some more investigations based on the nanofluid with different effects, buoyancy, magnetics field and chemical process have been presented in these references (Ayub et al., 2022; Ayub et al.; Haider et al.; Darvesh et al.; Darvesh et al., 2022; Sajid et al., 2022).
chemical reactions drive essential processes, such as metabolism and photosynthesis. In the industry, chemical reactions are used to produce a wider range of products, including fuels, medicines, and materials. In addition, chemical reactions are used in daily life applications, such as cooking, cleaning, and manufacturing. Chemical reactions are essential for the functioning of the natural world along with the development of human civilization. They allow us to harness the energy and materials necessary for life, and they provide the foundation of modern technology. A chemical process can be either heterogeneous or homogeneous. In a heterogeneous chemical process, the reactants indicate different phases, such as a solid and a liquid. In a homogeneous chemical process, the reactants have the same phase, such as a gas or a solution. Many scholars (Kuipers and van Swaaij, 1998; Kuipers and van Swaaij, 1997; Toikka et al., 2015; Spalding, 1980) worked on the chemical process with different fluid. Ali et. al (Ali et al., 2021) investigated the Oldroyd-B fluid associated to the chemical reaction, which is dependent to the first-order activation energy based on the paraboloid of revolution. Goud et. al (Goud and Nandeppanavar, 2021) discussed the facts of chemical reaction, MHD and ohmic heating related to the micropolar fluid. Chemical reaction, Lorentz force and injection/suction effects on Jeffrey fluid associated with the geometry of penetrable channel has also been discussed in (Abbas et al., 2021).
1.1 Motivation:
The study of inclined flow behavior of fluids is considered significant due to the variety of applications in the field of engineering and industrial submissions, e.g., heat exchanger design, and fluid flow through porous media. In such systems, the viscosity of the fluid and the heat transfer at the nanoscale play a crucial role. The CF model is a kind of NNF that can accurately describe the viscosity of fluids under shear rate. However, the effect of the inclination angle on the viscosity of the fluid and the heat transfer at the nanoscale has not been fully explored. Therefore, the main motivation behind this research is to develop an infinite shear rate viscosity model for an inclined CF with nanoscale heat transport to better understand the inclined flow behavior of fluids and the heat transfer at the nanoscale in industrial and engineering applications.
1.2 Novelty:
In this study, an infinite shear rate viscosity model for an inclined CF with nanoscale heat transport was developed. The CF can accurately describe the viscosity of fluids under shear rate. The effect of the inclination angle on the viscosity of the fluid, as well as the heat transfer at the nanoscale, was taken into account in the model. The results showed that the viscosity of the fluid decreases with an increase in the inclination angle, and that the heat transfer coefficient also increases with inclination. The model was then applied to analyze the viscosity and heat transfer behavior of fluids in inclined systems. The results provide a better understanding of the inclined flow behavior of fluids and the heat transfer at the nanoscale, which can be useful in various industrial and engineering applications such as heat exchanger design, fluid flow through porous media, and so on.
2 Mathematical formulations
The stretching sheet is considered that arises at y= 0. The confined flow is also assumed in the region at y>0. The magnetic field and thermal radiation dipole movement with non-uniform heat source sink are also considered. Mass transfer phenomenon is studied by isothermal chemical process and assuming autocatalysis. Let E and F are autocatalysts so autocatalysis in case of isothermal reaction is
It is to note that is zero away from the field and it make influence on edge of the stretching sheet. Also, ks, k1, is rate coefficient of heterogeneous/ homogeneous reactions, Ga, Gb is concentration of chemical specie E, F respectively.
Flow is 2-D in -plane, where x shows the axis of horizontal, and y are perpendicular based on the incompressible flow. and are the uniform and ambient fluid’s temperatures, where . Flow is moving in the start using the with nonlinear form of the velocity , indicate the stretching speed.
3 Governing equations
The governing equations in fluid mechanics are important because they provide a mathematical framework for understanding the behavior of fluids and predicting how they will respond to different conditions. These equations describe the fundamental principles of fluid dynamics, such as conservation of mass, momentum, and energy, and they can be used to model a wide range of fluid systems, from simple flows to complex, multiphase systems.
The most common governing equations used in fluid mechanics are the Navier-Stokes equations, which describe the motion of a fluid in terms of its velocity, pressure, and temperature. These equations take into account the effects of viscosity, turbulence, and other forces acting on the fluid, and they are used to model a wide range of fluid flows, from laminar to turbulent.
Other important governing equations include the continuity equation, which states that the mass of a fluid within a fixed volume must remain constant, and the energy equation, which describes how energy is transferred within a fluid (see Table 1).
,
The modeled homologous boundary conditions are given as:
In summary, governing equations in fluid mechanics are important because they provide a mathematical foundation for understanding the behavior of fluids and predicting their response to different conditions, and they are used in a wide range of applications, from engineering and science to industry and medicine. The equations based on mass, momentum and energy are written below as:
The Eqs (4) and (5) are used in Eq (2) with the body force as the Lorentz force. The momentum equation in case of the CF and energy equation take place using the thermal radiation and non-uniform heat sink/source is obtained by utilizing (7) in (3). Hence, mass, momentum and energy equation is given below, respectively as:
The boundary conditions (BCs) are presented as:
Where the tensor based on the CF is
, the viscosity of CF is
that is dependent on the shear rate.
shows the index of Carreau-model that present the shear thinning nature, while n>1 presents the CFs into shear thickening that is known as dilatant fluids. The heat flux is q, gradient of velocity is L, mathematically, given as:
A*, B* present the space and heat source/sink coefficient. The values of A* > 0 and B* > 0 indicate the internal heat absorption, while if A*< 0 and B*< 0, then heat is absorbed internally. Eq (11) gets the form by using Eq (14) and (15) as:
Similarity transformations are
Where is the flow’s locus, which is known as a stream function becomes as:
present the components of velocity. The updated equations are written as:
The corresponding values of the BCs are
When the values of power law index (n) are taken as one and Weissenberg number (We) become zero, then the CF becomes the Newtonian fluid.
Practically, the quantities show the drag force coefficient that normally depicts the coefficient of skin friction as well as heat transfer rate present a significant role.
is the drag force that is used in the Nusselt number
given as:
Putting their requirements in (21, 23)
Here is the Reynolds number, shown as .
4 Methodology
There are several methods (Neirameh and Eslami, 2022; Eslami and Neirameh, 2021; Raheel et al., 2022; Kallel et al., 2021; Rezazadeh et al., 2020) in literature for finding the numerical solution of the equations. In this study, bvp4c along with the shooting method (SM) is presented (see Figs. 1 and 2).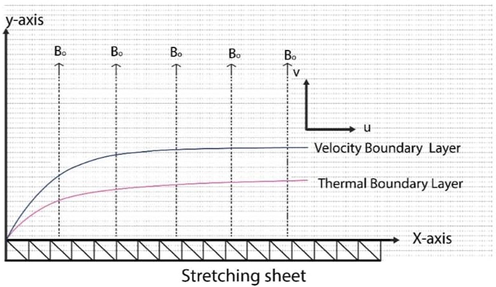
Geometrical interpretation of the model.
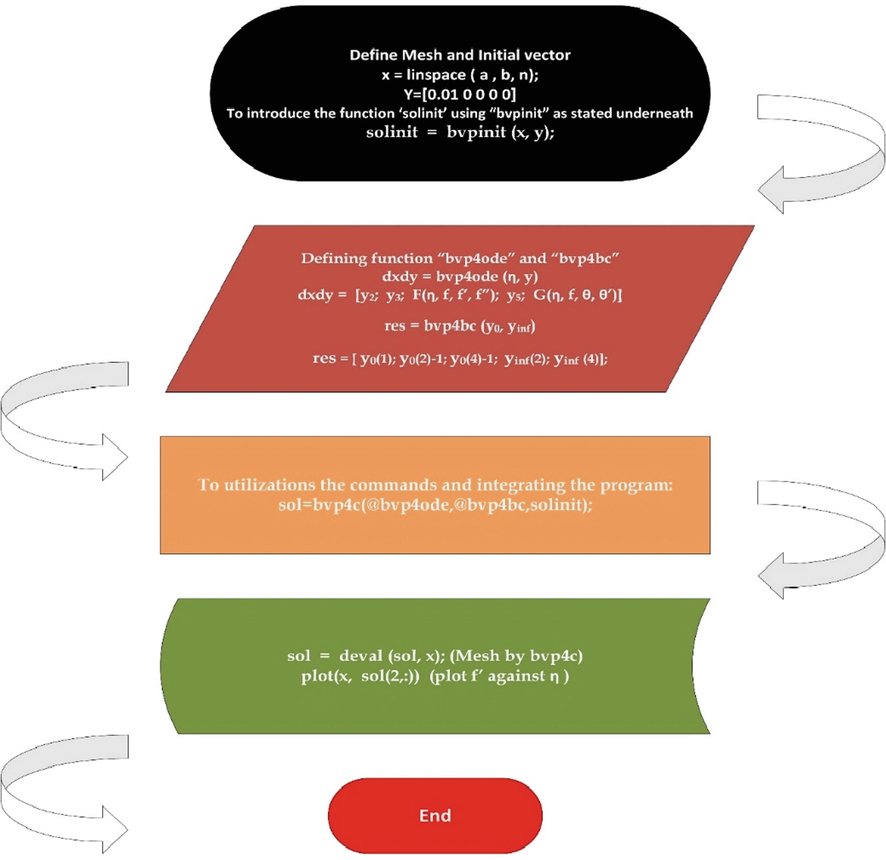
Matlab procedure.
For the accurateness of the solutions, the comparison of achieved results through SM is tabulated in Table 2 and 3 along with literature solutions and the procedures of bvp4c. The validity is approved through the matching of these solutions. Table 2 signifies the
, while Table 3 indicates
.
M
Ref (Ayub et al., 2020)
Ref (Wahab et al., 2021)
Current work
Shooting
Bvp4c
0.2
0.610262
1.607130
1.6078316
1.6078316
0.5
0.595277
1.586759
1.5867361
1.5867361
1.5
0.574537
1.557519
1.5574209
1.5574209
3
0.564472
1.542719
1.5472192
1.5472192
10
0.554960
1.528502
1.5284017
1.5284017
Fixed index
Index
Value
Shooting
Bvp4c
0.5
0.91427578
0.91427577
1.0
1.00006261
1.00006261
1.5
1.18929685
1.18929685
2
1.45421642
1.45421642
2.5
1.53531914
1.51531914
1
0.99113634
0.99113634
2
1.24444955
1.24444955
3
1.46014320
1.46014320
4
1.65747565
1.65747565
5
1.83538918
1.83538918
0.5
1.39001955
1.39001955
1
1.29175377
1.29175377
2
1.10059700
1.10059700
4
0.09904529
0.09904529
5
0.55848101
0.55848101
0.1
1.07399158
1.07399158
0.5
1.28429508
1.28429508
1
1.37421618
1.37421618
1.5
1.43059723
1.43059723
5 Exploration of the results
In this article mathematical model of CF is proposed to describe the behavior of a CF under high shear rate conditions. The model takes into account the effect of heat transport at the nanoscale on the fluid's viscosity. The results of the study indicate that the proposed model can accurately predict the viscosity of the fluid under various conditions of shear rate and temperature. Furthermore, the results show that the presence of nanoscale heat transport has a significant impact on the fluid's viscosity, with an increase in temperature leading to a decrease in viscosity. The authors conclude that the proposed model can be useful for understanding the behavior of CFs in various industrial and engineering applications.
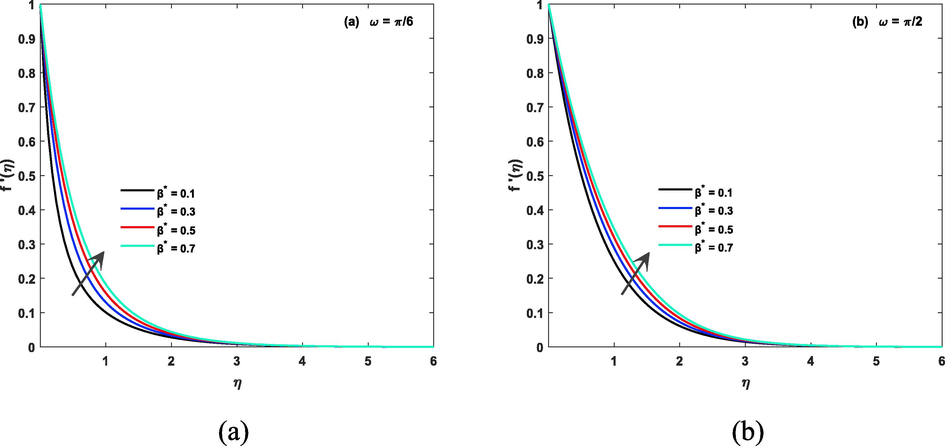
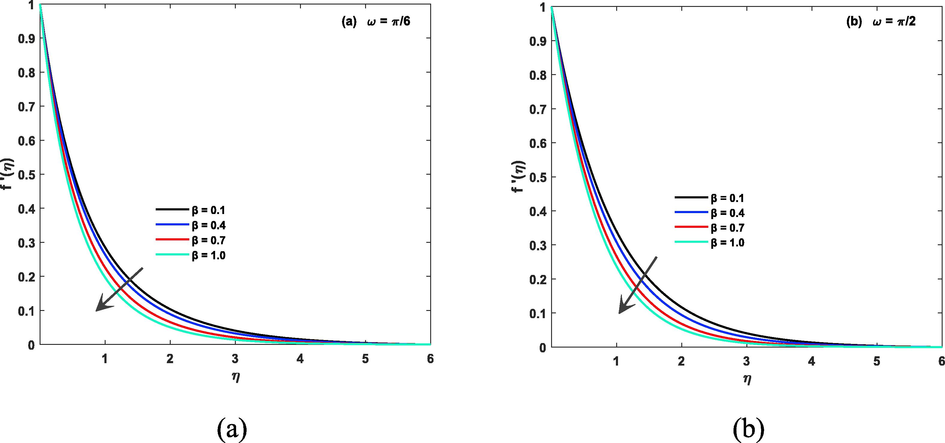
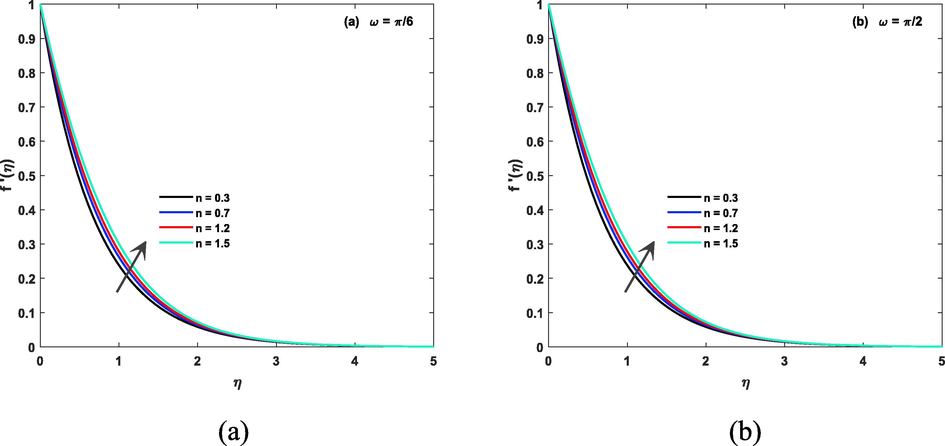
Impact of Weissenberg and magnetic parameters on the velocity of the fluid in both case of inclined and non inclined magnetic field is described by Fig. 3(a, b) and Fig. 4(a, b). Weissenberg number (We), which is a dimensionless parameter that represents the ratio of the fluid's elastic stress to its viscous stress, can have a significant impact on the fluid's velocity. A high Weissenberg number indicates a high degree of elasticity in the fluid, which can lead to an increase in velocity in presence of non inclined magnetic presence, but in inclined magnetic case it is decreasing due to strong Lorentz force. Similarly, the magnetic parameter (M) represents the ratio of magnetic forces to viscous forces in a magnetic fluid, and it can also affect the velocity of the fluid. A high magnetic parameter can lead to decrease in the velocity of a magnetic fluid, as the magnetic forces tend to align the fluid particles due to Lorentz force and hence increase resistance in flow. Impact of infinite shear rate viscosity parameters on the velocity of the fluid in both case of inclined and non inclined magnetic field is described by Fig. 5 (a, b). Greater numerical values of said parameter gives larger velocity. Fig. 6 (a, b) shows impact of stretching parameter on fluid velocity. Power law index can have a significant impact on the velocity of a CF. This parameter determines the degree of NNF behavior, and as it increases, the fluid becomes more shear-thinning, meaning that the viscosity decreases with increasing shear rate. As a result, the velocity of the fluid will increase in both case of inclined/non inclined magnetic field. this fact is shown by Fig. 7(a, b).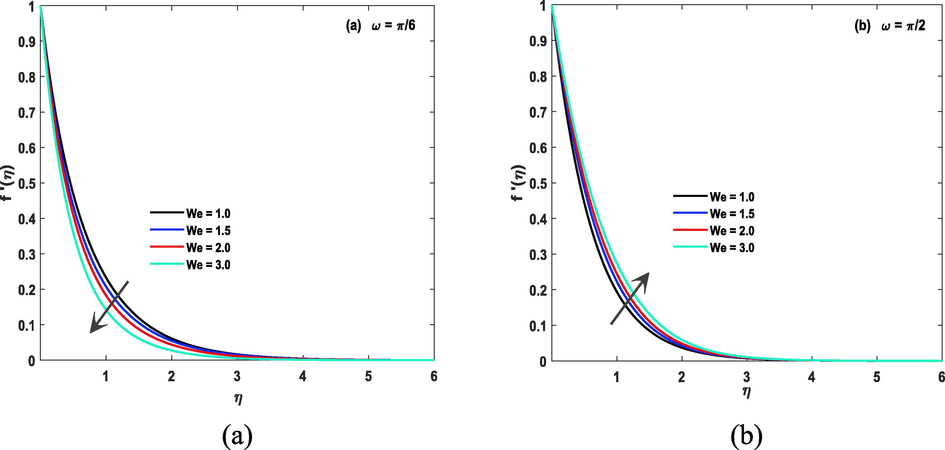
(a): ‘We’ for
.(b):
with
.
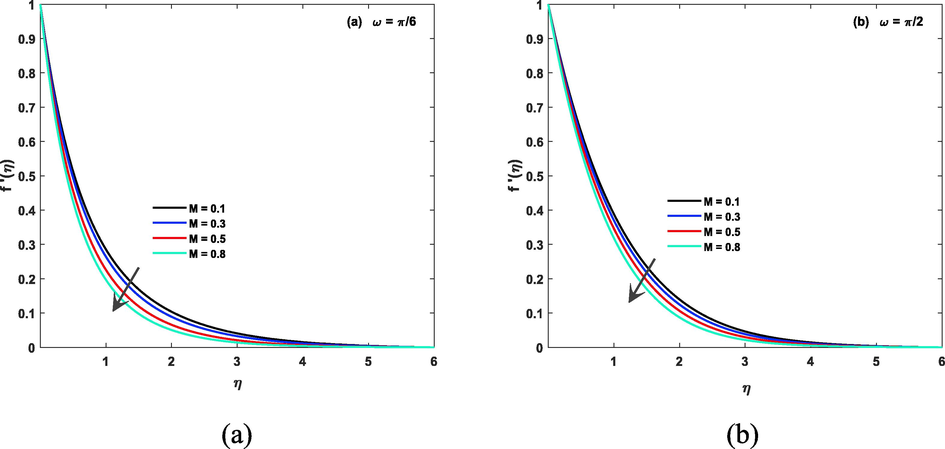
(a):
for
. (b):
for
.
(a):
for
(b):
for
.
(a):
for
(b):
for
.
(a):
for
(b):
for
.
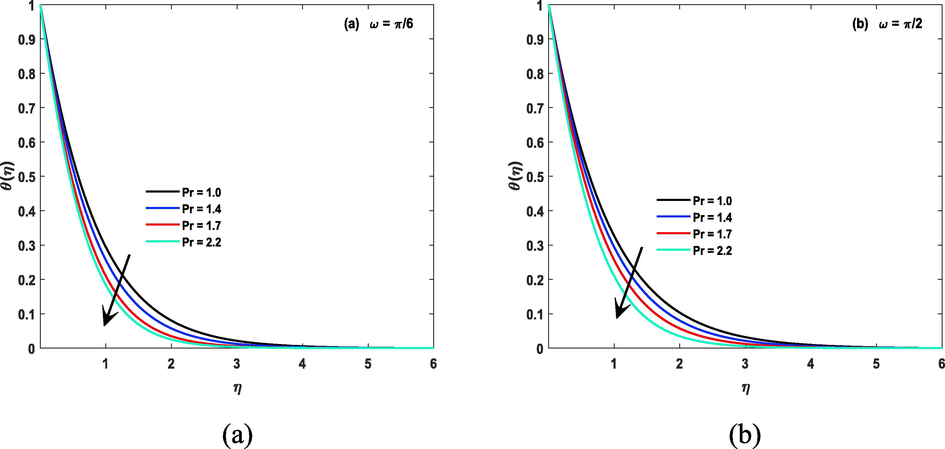
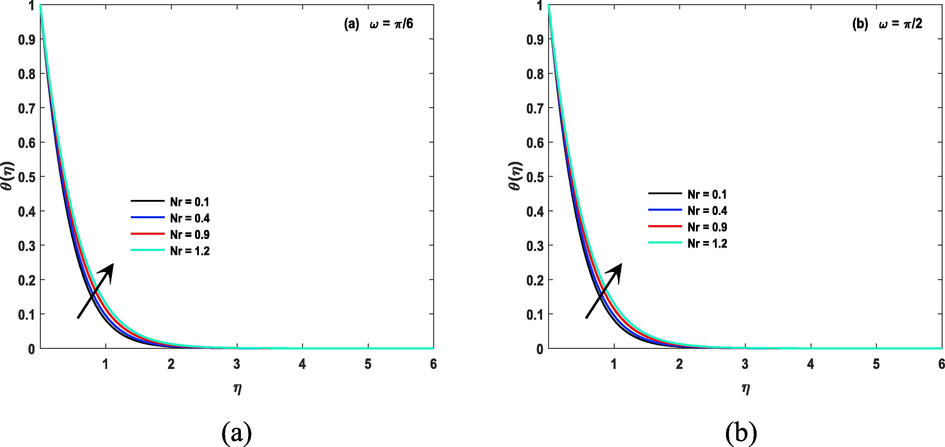
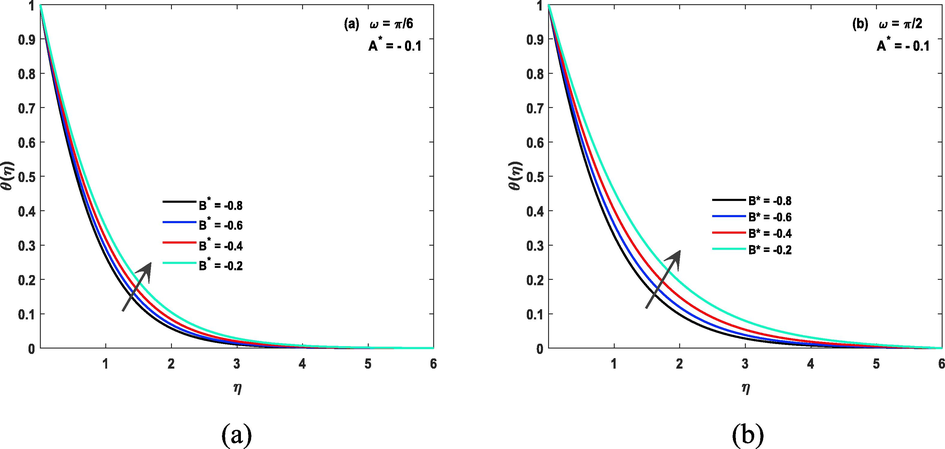
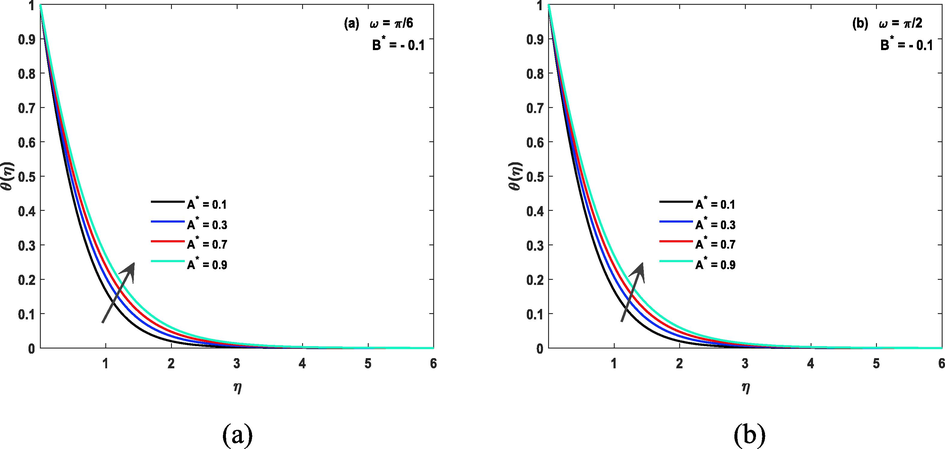
Impact of temperature ratio parameters on the temperature of the fluid in both case of inclined and non inclined magnetic field is described by Fig. 8(a, b) and Fig. 9(a, b) discusses about impact of Prandtl number on temperature file. Prandtl number is a dimensionless number used in fluid dynamics to describe the relative importance of thermal diffusion to momentum diffusion in a fluid. It is defined as the ratio of the momentum diffusivity (viscosity) to the thermal diffusivity (thermal conductivity) of a fluid and is denoted by the symbol “Pr”. A fluid with a high Prandtl number has a relatively low thermal diffusivity, meaning that heat does not diffuse easily through the fluid. This can affect the temperature of the fluid, as heat will not be easily transferred through the fluid and therefore, greater numerical value of this parameter reduces temperature. The thermal radiation parameter, also known as the Stefan-Boltzmann constant, is a physical constant that relates the power emitted by a blackbody to its temperature. It is a fundamental constant of nature and is denoted by the symbol “σ”. The Stefan-Boltzmann constant plays a crucial role in determining the temperature of a fluid that is in thermal equilibrium with its surroundings, and it can affect the temperature of the fluid via thermal radiation. for greater Nr temperature file is also increasing and fact is shown by Fig. 10 (a, b). Fig. 11 (a, b) unwraps the fact of heat sink/ source parameter related to temperature of CF. The heat source/sink parameter has a direct impact on the temperature of a fluid. A heat source increases the temperature of the fluid, while a heat sink decreases the temperature of the fluid. The amount of heat transferred, and therefore the change in temperature, will depend on the heat transfer coefficient, the surface area of the heat exchange, and the difference in temperature between the fluid and the heat source/sink. The coefficients of space parameter refer to the rate at which heat is transferred through a material, the higher the thermal conductivity the more quickly the heat will be transferred and the faster the fluid will heat or cool. The temperature of fluid will be affected by the balance of this coefficients. The fluid will heat up if heat transfer rate is greater than the heat loss rate and will cool down if heat loss rate is greater than the heat transfer rate. This fact is shown by Fig. 12(a, b).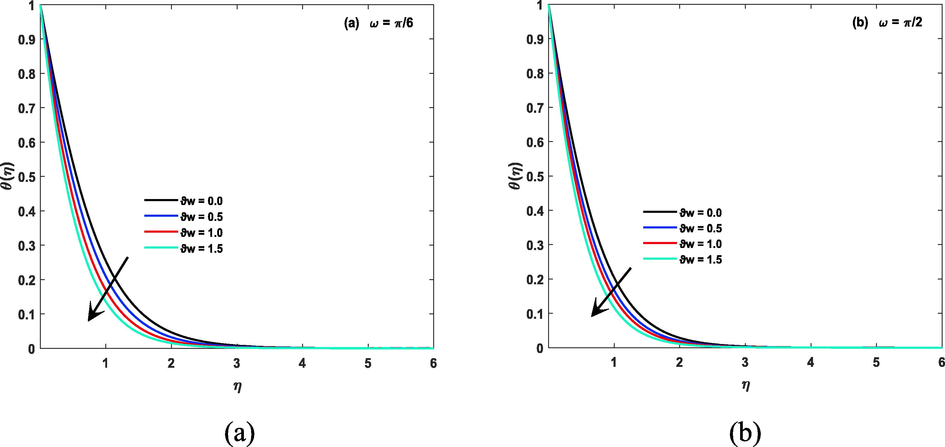
(a):
for
(b):
for
.
(a):
for
(b):
for
.
(a):
for
(b):
for
.
(a):
for
(b):
for
.
(a):
for
(b):
for .
Strength coefficient of homogeneous reaction impact on concentration file is seen by Fig. 13a, b and Fig. 14a, b. The strength coefficient of a homogeneous reaction refers to the rate at which the reaction proceeds. If the strength coefficient is high, the reaction will proceed quickly, and the concentration of reactants will decrease rapidly. If the strength coefficient is low, the reaction will proceed slowly, and the concentration of reactants will change little over time. The diffusion coefficient parameter has a direct impact on the concentration of a substance in a medium, with a higher diffusion coefficient leading to a more uniform concentration and a lower diffusion coefficient leading to a greater concentration gradient. This fact can be noticed by Fig. 15a, b.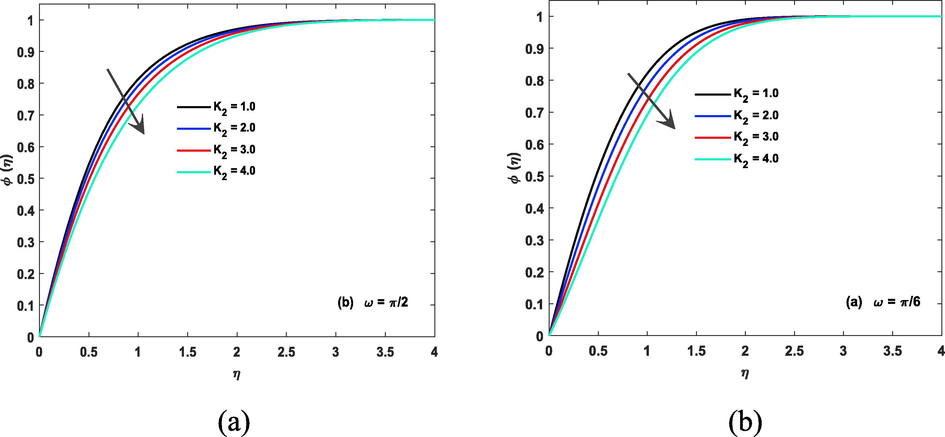
(a):
for
(b):
for
.
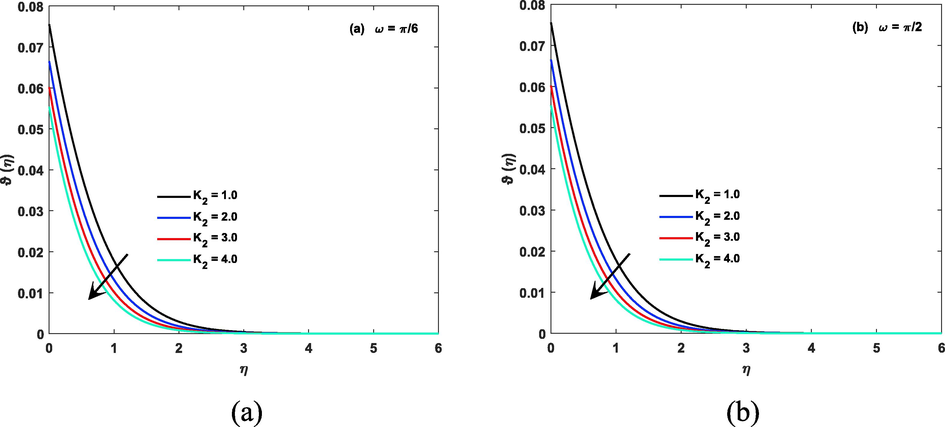
(a):
for
(b):
for
.
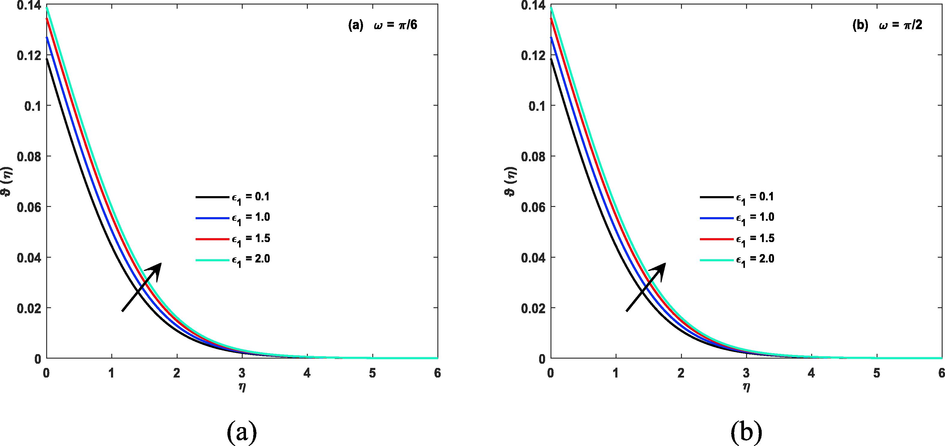
(a):
for
(b):
for
.
5.1 Physical quantities
Skin friction and Nusselt number are two important quantities in fluid dynamics that are used to characterize the heat transfer and fluid flow in a system. They are affected by many factors, such as the properties of the fluid, the velocity of the fluid, the temperature of the fluid, and the surface roughness of the solid boundary. Understanding these quantities and how they are affected by different factors is crucial for designing and optimizing fluid dynamic systems such as heat exchangers, boilers, and pipe flow. Table 3 and Table 4 and Fig. 16 (a, b, c), Fig. 17 (a, b), and Fig. 18. These figures represent impact of n, β and We, M, β*on Skin Friction and Nusselt number. Skin friction is the frictional resistance between a fluid and a solid boundary, and it has a direct impact on the velocity of the fluid. The higher the skin friction, the greater the frictional force acting on the fluid, which results in a lower velocity of the fluid. Conversely, the lower the skin friction, the lesser the frictional force acting on the fluid, resulting in a higher velocity of the fluid. The skin friction coefficient, which is the ratio of the friction force acting on the boundary to the dynamic pressure of the fluid, is used to calculate the frictional head loss, which is a measure of the energy loss due to friction between the fluid and the solid boundary. As the frictional head loss increases, the velocity of the fluid decreases, and as the frictional head loss decreases, the velocity of the fluid increases.
SM
Bvp4c
SM
Bvp4c
0.0
2.0
1.5
0.1
0.1
0.67982984
0.67982989
0.77801139
0.77801134
0.5
–
–
–
–
0.56842585
0.56842588
0.72409385
0.72409382
1.0
–
–
–
–
0.31714632
0.31714637
0.54815852
0.54815856
2.0
–
–
–
–
0.28311652
0.28311656
0.22436803
0.22436803
0.5
1.0
–
–
–
0.66810789
0.66810784
0.64426841
0.64426841
–
2.0
–
–
–
0.56842585
0.56842588
0.70409385
0.70409385
–
3.0
–
–
–
0.48758234
0.48758236
0.75087638
0.75087638
–
5.0
–
–
–
0.37502253
0.37502251
0.81567605
0.81567605
–
2.0
1.0
–
–
0.67875641
0.67875640
0.84858341
0.84858341
–
–
1.5
–
–
0.50817972
0.50817970
0.62347034
0.62347034
–
–
2.0
–
–
0.47003713
0.47003715
0.58153986
0.58153986
–
–
2.5
–
–
0.44365386
0.44365380
0.52511970
0.52511970
–
–
1.5
0.1
–
0.90970382
0.90970387
1.12018678
1.12018678
–
–
–
0.3
–
0.67875641
0.67875640
0.83858341
0.83858341
–
–
–
0.5
–
0.21415754
0.21415752
0.03367694
0.03367694
0.7
0.01287634
0.01287635
0.00987643
0.00987643
–
–
–
0.1
0.1
1.19688843
1.19688846
1.27219245
1.27219245
–
–
–
–
0.3
0.67875641
0.67875640
0.82858341
0.82858341
–
–
–
–
0.5
0.36890945
0.36890945
0.23881123
0.23881123
0.7
0.01248593
0.01248593
0.11957664
0.11957664
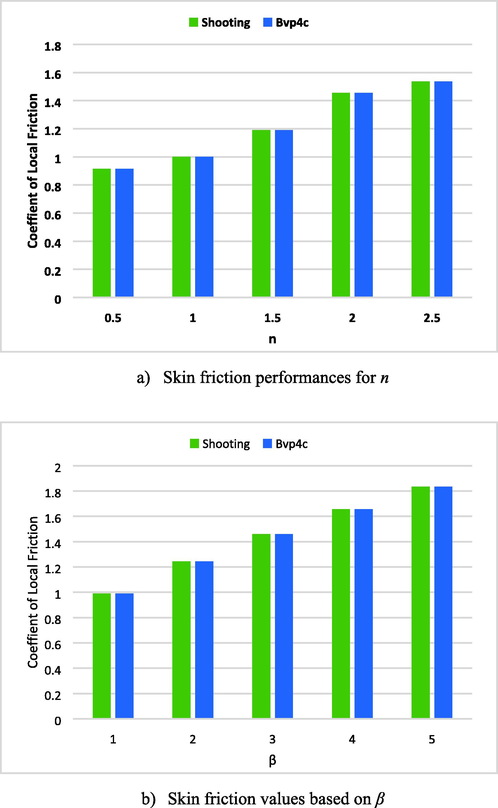
(a, b, c): Skin Friction for n, β and We.
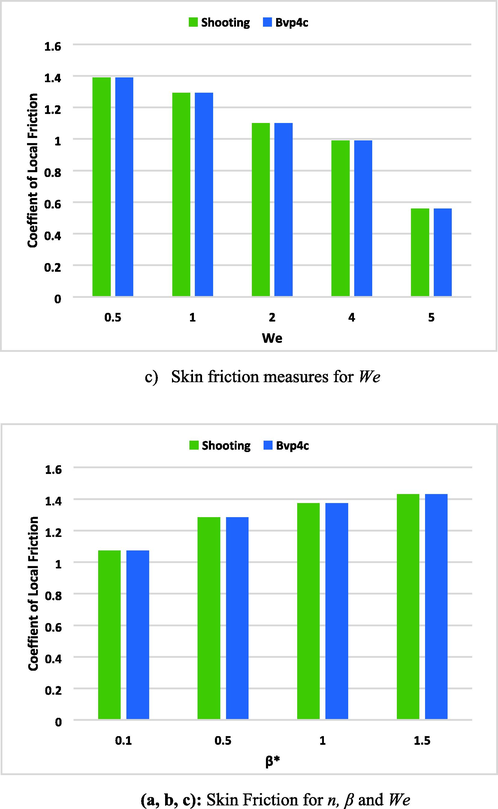
(a, b, c): Skin Friction for n, β and We.
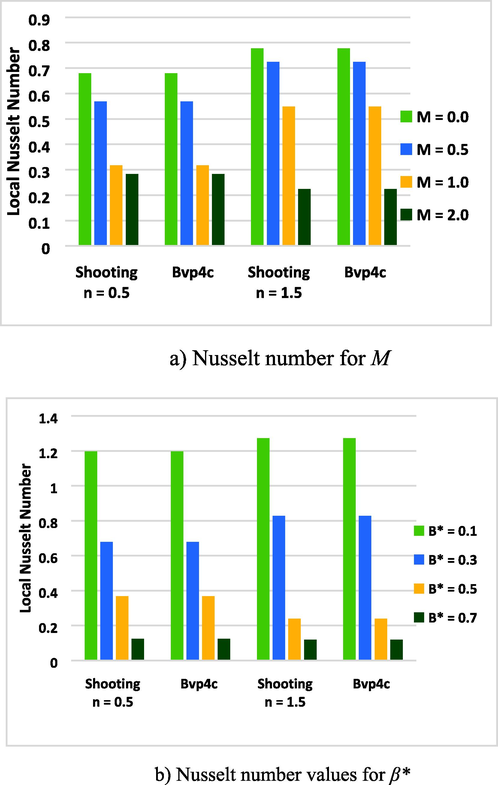
(a, b): Nusselt number graphs for M, β* (n < 1, n > 1).
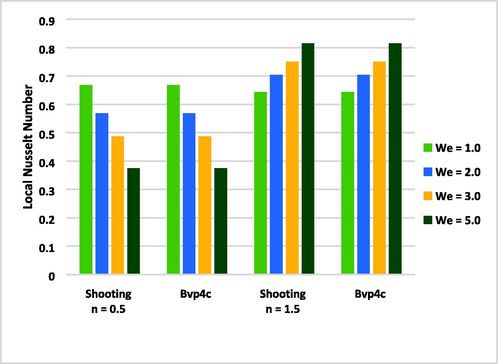
Nusselt Number illustrations for ‘We’ using (n < 1 and n > 1).
In conclusion, skin friction has a direct impact on the velocity of the fluid in a system. The higher the skin friction, the lower the velocity of the fluid, and vice versa. Factors such as the properties of the fluid, the velocity of the fluid, the surface roughness of the solid boundary, and the geometry of the system can affect the skin friction and, subsequently, the velocity of the fluid. Understanding these factors and how they affect skin friction is crucial for designing and optimizing fluid dynamic systems.
6 Concluding remarks
In conclusion, this study investigated the infinite shear rate viscosity model of an inclined CF with nanoscale heat transport. The results of the study showed that the viscosity of the fluid decreased as the inclination angle increased and the heat transport was found to be affected by the size of the nanoparticles in the fluid. The findings of this study have important implications for the design and optimization of industrial processes that involve the use of CFs, particularly those that operate under high shear rate conditions or in inclined geometries. Additionally, the results of this study can also be used to improve the understanding of the behavior of fluids at the nanoscale, which is an area of ongoing research in the field of materials science.
The viscosity of the infinite shear rate using the CF is significant because it affects the fluid's ability to flow and respond to applied stresses. At high shear rates, the viscosity of the fluid decreases, which allows it to flow more easily and respond more quickly to changes in velocity. This can be beneficial in certain industrial applications, such as high-shear mixing, where a low viscosity is desired to achieve efficient mixing.
In the case of shear thinning, the viscosity of the fluid decreases as the shear rate increases. This can lead to an increase in the fluid's velocity, as the fluid is able to flow more easily at high shear rates. This behavior is commonly observed in NNFs such as CFs, and can be beneficial in certain industrial applications, such as high-shear mixing, where a low viscosity is desired to achieve efficient mixing.
On the other hand, shear thickening fluids exhibit an increase in viscosity as the shear rate increases. This can lead to a decrease in the fluid's velocity, as the fluid becomes more resistant to flow at high shear rates. This behavior can be problematic in certain industrial applications, such as pipe flow or in inclined geometries, where a steady flow is desired to prevent fluid separation. Additionally, in some applications such as high-shear mixing, the high viscosity of the fluid may cause the mixer to stall which can lead to mixing inefficiencies.
The impact of the Weissenberg number (We) on the velocity of a CF depends on the specific properties of the fluid and the conditions of the flow. As the Weissenberg number increases, the fluid becomes more non-Newtonian, and its viscosity decreases at high shear rates. This can lead to an increase in the fluid's velocity, as the fluid is able to flow more easily at high shear rates.
The impact of the heat sink/source parameter on the temperature profile of a fluid depends on the specific properties of the fluid and the conditions of the flow. In general, when a heat source is added to the fluid, the temperature of the fluid will increase, and when a heat sink is applied, the temperature will decrease. In the case of a CF, the addition of heat can affect the viscosity of the fluid, leading to changes in the velocity profile and the shear rate. Additionally, the heat sink/source parameter can also affect the heat transport coefficient which in turn can affect the temperature profile.
6.1 Future direction
Future research can focus on the effect of other parameters such as the temperature, concentration of nanoparticles, and the effect of different types of nanoparticles on the viscosity and heat transport of the fluid. The results of these studies can be used to develop more accurate models for the behavior of CFs under various conditions and to improve the performance of industrial processes that involve the use of these fluids.
Conflict of interest
No conflict of interest is claimed.
References
- Impacts of lorentz force and chemical reaction on peristaltic transport of Jeffrey fluid in a penetrable channel with injection/suction at walls. Alex. Eng. J.. 2021;60(1):1113-1122.
- [Google Scholar]
- Insight into the dynamics of Oldroyd-B fluid over an upper horizontal surface of a paraboloid of revolution subject to chemical reaction dependent on the first-order activation energy. Arab. J. Sci. Eng.. 2021;46:6039-6048.
- [Google Scholar]
- Energy transport boosters of magneto micropolar fluid flowing past a cylinder: A case of laminar combined convection. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci.. 2022;236(22):10902-10913.
- [Google Scholar]
- Ayub, A., Wahab, H. A., Hussain Shah, S. Z., Shah, S. L., Sabir, Z., & Bhatti, S. On heated surface transport of heat bearing thermal radiation and MHD Cross flow with effects of nonuniform heat sink/source and buoyancy opposing/assisting flow. Heat Transfer.
- Ayub, A., Darvesh, A., Altamirano, G. C., & Sabir, Z. Nanoscale energy transport of inclined magnetized 3D hybrid nanofluid with Lobatto IIIA scheme. Heat Transfer.
- Ayub, A., Wahab, H. A., Sabir, Z., & Arbi, A. 2020. A note on heat transport with aspect of magnetic dipole and higher order chemical process for steady micropolar fluid. In: Fluid-Structure Interaction. IntechOpen.
- Nanoscale heat and mass transport of magnetized 3-D chemically radiative hybrid nanofluid with orthogonal/inclined magnetic field along rotating sheet. Case Studies in Thermal Engineering 2021:101193.
- [Google Scholar]
- Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller-Box and BVP4C method. Eng. Comput. 2021:1-15.
- [Google Scholar]
- Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat Transfer. 2021;50(5):4192-4232.
- [Google Scholar]
- Aspects of infinite shear rate viscosity and heat transport of magnetized Carreau nanofluid. The European Physical Journal Plus. 2022;137(2):1-17.
- [Google Scholar]
- Spectral relaxation approach and velocity slip stagnation point flow of inclined magnetized cross-nanofluid with a quadratic multiple regression model. Waves Random Complex Media 2022:1-25.
- [Google Scholar]
- Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid. Eng. Comput. 2022:1-20.
- [Google Scholar]
- Activation Energy and Inclination Magnetic Dipole Influences on Carreau Nanofluid Flowing via Cylindrical Channel with an Infinite Shearing Rate. Appl. Sci.. 2022;12(17):8779.
- [Google Scholar]
- Heat transfer effects on electro-magnetohydrodynamic Carreau fluid flow between two micro-parallel plates with Darcy–Brinkman–Forchheimer medium. Arch. Appl. Mech.. 2021;91(4):1683-1695.
- [Google Scholar]
- Thin-film flow of Carreau fluid over a stretching surface including the couple stress and uniform magnetic field. Partial Differential Equations in Applied Mathematics. 2021;4:100162
- [Google Scholar]
- Botmart, T., Ayub, A., Sabir, Z., weera, W., Sadat, R., & Ali, M. R. 2022. Infinite shear rate aspect of the cross-nanofluid over a cylindrical channel with activation energy and inclined magnetic dipole effects. Waves in Random and Complex Media, 1-21.
- Shear rheology of circular particle suspensions in a Bingham fluid using numerical simulations. Korea-Australia Rheology Journal. 2021;33(3):273-282.
- [Google Scholar]
- Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal and Fractional. 2021;5(3):119.
- [Google Scholar]
- Darvesh, A., Altamirano, G. C., Sánchez‐Chero, M., Zamora, W. R., Campos, F. G., Sajid, T., & Ayub, A. Variable chemical process and radiative nonlinear impact on magnetohydrodynamics Cross nanofluid: An approach toward controlling global warming. Heat Transfer.
- Rheology of Variable Viscosity-Based Mixed Convective Inclined Magnetized Cross Nanofluid with Varying Thermal Conductivity. Appl. Sci.. 2022;12(18):9041.
- [Google Scholar]
- Quadratic multiple regression model and spectral relaxation approach for carreau nanofluid inclined magnetized dipole along stagnation point geometry. Sci. Rep.. 2022;12(1):1-18.
- [Google Scholar]
- Cross electromagnetic nanofluid flow examination with infinite shear rate viscosity and melting heat through Skan-Falkner wedge. Open Physics. 2022;20(1):1233-1249.
- [Google Scholar]
- Generalized exponential rational function for distinct types solutions to the conformable resonant Schrödinger’s equation. Int. J. Mod Phys B. 2021;35(30):2150306.
- [Google Scholar]
- Ohmic heating and chemical reaction effect on MHD flow of micropolar fluid past a stretching surface. Partial Differential Equations in Applied Mathematics. 2021;4:100104
- [Google Scholar]
- Energy transference in time-dependent Cattaneo-Christov double diffusion of second-grade fluid with variable thermal conductivity. Heat Transfer. 2021;50(8):8224-8242.
- [Google Scholar]
- Haider, A., Ayub, A., Madassar, N., Ali, R. K., Sabir, Z., Shah, S. Z., & Kazmi, S. H. Energy transference in time‐dependent Cattaneo–Christov double diffusion of second‐grade fluid with variable thermal conductivity. Heat Transfer.
- Investigation of natural bio-convective flow of Cross nanofluid containing gyrotactic microorganisms subject to activation energy and magnetic field. Phys. Scr.. 2020;95(10):105219
- [Google Scholar]
- Optical soliton solutions for the coupled conformable Fokas-Lenells equation with spatio-temporal dispersion. Results Phys.. 2021;26:104388
- [Google Scholar]
- Implication of Arrhenius activation energy and temperature-dependent viscosity on non-Newtonian nanomaterial bio-convective flow with partial slip. Arab. J. Sci. Eng.. 2022;47(6):7559-7570.
- [Google Scholar]
- Irreversibility analysis and heat transport in squeezing nanoliquid flow of non-Newtonian (second-grade) fluid between infinite plates with activation energy. Arab. J. Sci. Eng.. 2020;45:4939-4947.
- [Google Scholar]
- Darcy friction factor and Nusselt number in laminar tube flow of Carreau fluid. Rheol. Acta. 2022;61(3):243-255.
- [Google Scholar]
- Application of computational fluid dynamics to chemical reaction engineering. Rev. Chem. Eng.. 1997;13(3):1-118.
- [Google Scholar]
- Computational fluid dynamics applied to chemical reaction engineering. In: Advances in chemical engineering. Vol Vol. 24. Academic Press; 1998. p. :227-328.
- [Google Scholar]
- Entropy optimized MHD 3D nanomaterial of non-Newtonian fluid: a combined approach to good absorber of solar energy and intensification of heat transport. Comput. Methods Programs Biomed.. 2020;186:105131
- [Google Scholar]
- Study of transport phenomenon in Carreau fluid using Cattaneo-Christov heat flux model with temperature dependent diffusion coefficients. Physica A. 2020;554:123921
- [Google Scholar]
- New solitary wave solutions for fractional Jaulent-Miodek hierarchy equation. Mod. Phys. Lett. B. 2022;36(07):2150612.
- [Google Scholar]
- Numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering magnetic dipole effect. Partial Differential Equations in Applied Mathematics. 2021;4:100064
- [Google Scholar]
- Different soliton solutions to the modified equal-width wave equation with Beta-time fractional derivative via two different methods. Revista Mexicana de Física. 2022;68(1 Jan-Feb):010701.
- [Google Scholar]
- Applications of three methods for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity. Pramana. 2020;94(1):1-11.
- [Google Scholar]
- Sabir, Z., Ayub, A., Guirao, J. L., Bhatti, S., & Shah, S. Z. H. 2020. The effects of activation energy and thermophoretic diffusion of nanoparticles on steady micropolar fluid along with Brownian motion. Advances in Materials Science and Engineering, 2020.
- Trace of chemical reactions accompanied with arrhenius energy on ternary hybridity nanofluid past a wedge. Symmetry. 2022;14(9):1850.
- [Google Scholar]
- A flow study of Carreau fluid near the boundary layer region of paraboloid surface with viscous dissipation and variable fluid properties. J. Mater. Res. Technol.. 2021;14:901-909.
- [Google Scholar]
- Experimental and analytical methods for testing inhibitors and fluids in water-based drilling environments. TrAC Trends Anal. Chem. 2022:116543.
- [Google Scholar]
- Inclined magnetized and energy transportation aspect of infinite shear rate viscosity model of Carreau nanofluid with multiple features over wedge geometry. Heat Transfer. 2021:1-27.
- [CrossRef] [Google Scholar]
- Insight into the dynamics of time-dependent cross nanofluid on a melting surface subject to cubic autocatalysis. Case Studies in Thermal Engineering 2021:101227.
- [Google Scholar]
- Magnetic dipole aspect of binary chemical reactive Cross nanofluid and heat transport over composite cylindrical panels. Waves Random Complex Media 2022:1-24.
- [Google Scholar]
- Higher order chemical process with heat transport of magnetized cross nanofluid over wedge geometry. Heat Transfer. 2021;50(4):3196-3219.
- [Google Scholar]
- Mathematical modeling of fluid-mechanics, heat-transfer and chemical-reaction processes: A lecture course. NASA STI/Recon Technical Report N. 1980;81:30414.
- [Google Scholar]
- Viscosity Model for Liquid Mixtures of Propylene Glycol, Glycerol, and Water. Ind. Eng. Chem. Res.. 2020;60(1):670-677.
- [Google Scholar]
- Simultaneous and selective electrochemical sensing of methotrexate and folic acid in biological fluids and pharmaceutical samples using Fe3O4/ppy/Pd nanocomposite modified screen printed graphite electrode. Chemosphere. 2022;291:132736
- [Google Scholar]
- Phase and chemical equilibria in multicomponent fluid systems with a chemical reaction. Russ. Chem. Rev.. 2015;84(4):378.
- [Google Scholar]
- Multiple characteristics of three-dimensional radiative Cross fluid with velocity slip and inclined magnetic field over a stretching sheet. Heat Transfer. 2021;50(4):3325-3341.
- [Google Scholar]
- Melting and entropy generation of infinite shear rate viscosity Carreau model over Riga plate with erratic thickness: a numerical Keller Box approach. Waves Random Complex Media 2022:1-25.
- [Google Scholar]
- Simulation of revised nanofluid model in the stagnation region of cross fluid by expanding-contracting cylinder. Int. J. Numer. Meth. Heat Fluid Flow. 2020;30(4):2193-2205.
- [Google Scholar]
- Manipulating unidirectional fluid transportation to drive sustainable solar water extraction and brine-drenching induced energy generation. Energ. Environ. Sci.. 2020;13(12):4891-4902.
- [Google Scholar]







