Translate this page into:
Heuristic computing for the novel singular third order perturbed delay differential model arising in thermal explosion theory
⁎Corresponding author. salem.bensaid@uaeu.ac.ae (Salem Ben Said)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this study, a novel singular third order perturbed delay differential model (STO-PDDM) is designed with its two types using the traditional Lane-Emden model. The descriptions of delay/shape perturbed, and singular factors are also presented for both types of STO-PDDM. The artificial neural networks (ANNs) along with the optimization of global/local performances based on genetic algorithm (GA) and interior-point algorithm (IPA) have been used to solve the STO-PDDM. The optimization is performed using the GAIPA based on the activation function through the differential form of STO-PDDM. For solving STO-PDDM, the system's accuracy, substantiation, and authenticity have been performed by using the comparison of obtained and exact solutions. The accessible approximate solutions are used to evaluate the computational approach's robustness, stability, correctness, and convergence. The reliability of the scheme is performed through different statistical measures for solving the STO-PDDM.
Keywords
Perturbed
Delay
Singular differential model
Artificial neural networks
Global scheme
Local approach
1 Introduction
For the community of scientists, the singular form of the differential systems has long been a well-known and attractive subject. The singularity at the origin along with the perturbed factors with the behavior of boundary layers makes these models more fascinating and difficult to manipulate. These projections show quick types of fluctuations near the boundary employing thin layers. Due to the small parameters of the perturbation model, only a few conventional numerical procedures have been verified to identify the singular perturbation systems. Consequently, some trustworthy numerical methods have been developed to address these mathematical problems (Abdelkawy, 2020; Aghilí, 2021; Akkilic, 2022; Amiraliyeva et al., 2010; Azhar et al., 2018; Bahgat, 2020). For such singular perturbed systems, fitting exponential and finite differences methods have been developed (Bahgat, 2021; Bawa, 2007; Beretta and Kuang, 2002). A few investigations using the 2nd order perturbed singular diffusion/convection networks and diffusion reaction semi-linear systems have been reported using the mesh numerical approach (Beretta and Kuang, 2002; Leonid Bogachev et al., 2008; Botmart, 2022; Botmart, 2022).
The mathematical form of the delay differential systems is extremely important for the scientists due to its enormous applications. Recently, the delay systems have been used in abundant submissions, e.g., ship controlling, chemistry, electrodynamics, light absorption based stellar matter, medicine industry, electronics, population dynamics, biology, quantum mechanics, physical systems, number theory, engineering, economics, pharmaceutical kinetics, and infectious viruses (Bukhari, 2020; Bukhari, 2022). Many researchers have shown interest to solve such problems while keeping in mind the importance of such systems, e.g., Perko (Castro, 2000) studies the dynamical structures based on the linear/nonlinear systems, Lasalle (Erdogan et al., 2020) and Kuang (Farrell et al., 2000) proposed the solution schemes using the delay networks, Beretta et al (Forde, 2005) applied the geometric reliability of delay dependent factors and Forde (Gaina et al., 2021) provided the operators using the biological delay systems.
The researchers always faced difficulties to solve such models, which has singularity at the origin. The important types of the singular models are Lane-Emden and Emden-Fowler models, which have enormous applicability in the field of theoretical physics, quantum mechanics, astrophysics, and in the modelling of gas cloud. There have been some existing methods developed to assess the numerical solutions of the singular models (Garg et al., 2022; Garg et al., 2022; Guirao, 2022; Hale and LaSalle, 1963). The literature representations of the Emden-Fowler model is given as (Holevoet et al., 2010; Inapakurthi et al., 2021):
-
The perturbed, singular and delay factors are used to design the mathematical STO-PDDM.
-
The design of novel STO-PDDM is presented with its two types by using the traditional singular model of Lane-Emden and numerical performances have been presented through the procedures of ANNs along with the optimization of GAIPA.
-
The solutions of three problems based on both types of STO-PDDM have been presented by using the ANNs along with the hybrid efficiency of GAIPA.
-
The correctness of the stochastic ANNs along with the hybrid efficiency of GAIPA procedure is accomplished through the comparison performances of obtained and the exact results.
-
The minimal performances of the absolute error (AE) substantiate the precision of the stochastic ANNs along with the hybrid efficiency of GAIPA procedure based on novel STO-PDDM.
-
The constancy, trustworthiness, and convergence of the ANNs along with the hybrid efficiency of GAIPA is performed to solve the novel STO-PDDM using the statistical operators Theil inequality coefficient (TIC), variance account for (VAF), and semi-interquartile range (SIR).
The rest parts of the paper are structured as: Sect 2 shows the design of the novel STO-PDDM. Sect 3 indicates the proposed methodology. Statistical operators are presented in Section 4. The numerical solutions are provided in Sect 5, while the concluding remarks are listed in the last Sect.
2 Construction of novel STO-PDDM
This section shows the novel STO-PDDM design based on the perturbation, delay, and singular factors. The construction of the novel STO-PDDM is presented with its two types using the traditional singular form. Few of the singular models that have been already designed with the help of conventional singular systems have been reported in (Phaneendra et al., 2010; Raja et al., 2018; Reddy et al., 2020; Roos et al., 1996). Keeping the design of these singular models, the authors proposed a construction of the STO-PDDM. The mathematical expression to obtain this model are given as (Sabir, 2020):
Two possibilities to prove the Eq. (3) are presented as:
Form 1 of STO-PDDM.
The updated formulation of Eq. (2) using the Eq. (4) is given as:
The simplified form of
is given as:
Eq. (6) becomes using the above expression
The above expression is known as first kind of STO-PDDM. The multiple singularities arise twice at and , the values of the shape factors are and , while the multiple delays appear three times in the 1st, 2nd and 3rd factor.
Form 2 of STO-PDDM.
An updated form of Eq. (2) by using Eq. (5) is given as:
The simplified form
is presented as:
Eq. (6) takes the form as:
The above expression shows the second form of STO-PDDM. In this model, a single singularity arises, while the delay term appears twice.
3 Methodology
The current section presents the computational performances of ANNs along with the optimization of GAIPA for solving the novel STO-PDDM. The structure of stochastic approach is shown in Fig. 1.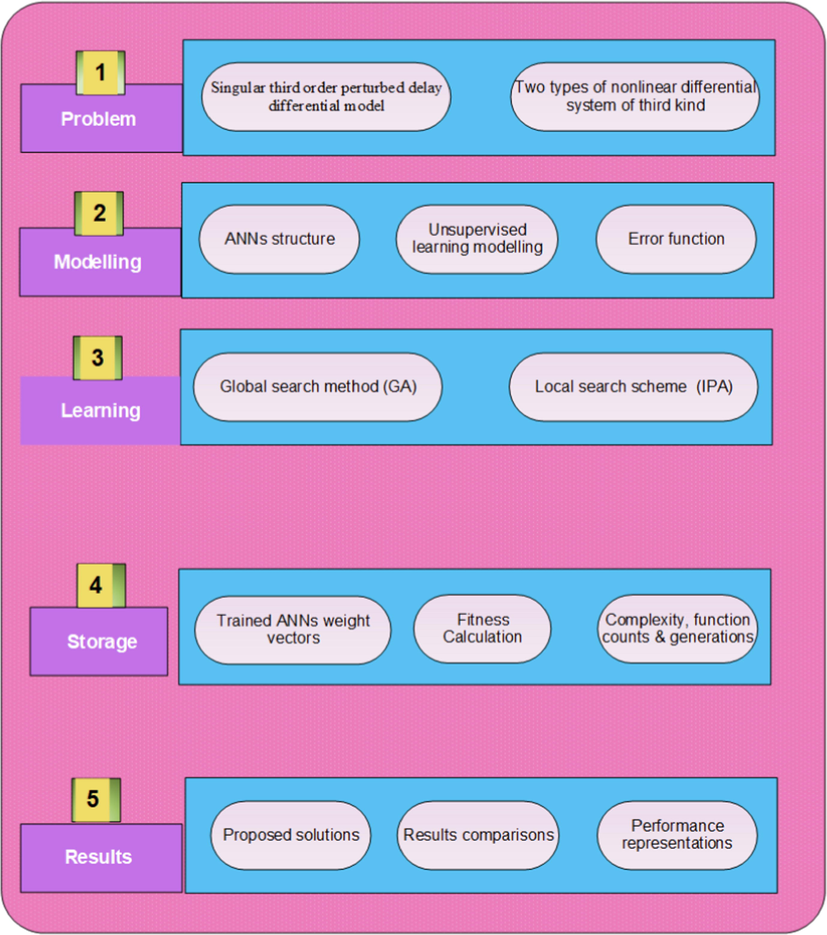
Stochastic procedure of the STO-PDDM.
3.1 Mathematical formulations of ANNs-GAIPA
The mathematical expressions are presented to solve the novel STO-PDDM in this section.
A merit function (
) is presented as:
3.2 Optimization: GAIPA
In this section, the optimization steps using the hybridization of GAIPA have been presented to solve the STO-PDDM.
In the process of population modeling, GA is recognized as a useful optimization solver. It operates using the process of mutation, crossover, and selection. In recent years, GA has been exploited in numerous submissions, e.g., general video game playing (Sabir, 2020), monorail vehicle model (Sabir, 2020), analysis of heart model (Sabir, 2020), piezoelectric multilayer transducer based broadband constructions (Sabir, 2020), astrophysics (Sabir, 2021) and medical image denoising (Sabir, 2021). These extraordinary applications enthused the authors to present the solutions of novel STO-PDDM using the computational proficiency of ANNs along with the hybridization of GAIPA.
GA is used to hybridized with the local search method due to reduce the sluggishness and to get the quick convergences. Therefore, IPA is applied as a local search method to achieve the rapid performances of the results. The optimum GA values is implemented as a primary input in IPA. The local search IPA is applied to present the solutions of the constrained/ unconstrained systems. Some recent IPA applications are nonlinear optimal power flows (Sabir, 2022), dynamic adjustments of step sizes and tolerances (Sabir, 2022), large-scale nonlinear programming (Sabir et al., 2020); multicommodity network flows (Sabir, et al., 2020), branch-price-and-cut method (Sajid, 2021), transmission network synthesis (Sajid et al., 2020) and robust optimal power flow solution (Sánchez et al., 2005).
4 Statistical operators
In this section, the mathematical form of the statistical SIR, MSE and VAF operators have been provided as:
5 Numerical solutions
This section shows the numerical performances of novel STO-PDDM by using ANNs along with GAIPA. The solution of three different problems using the stochastic procedures is presented to solve the novel STO-PDDM. One problem is taken from type 1 and two examples of the novel STO-PDDM have been solved by using the proposed scheme. To verify the convergence and dependability of the method, the essential numerical and graphical depictions are presented.
Suppose 1st type of the novel STO-PDDM by taking , and in Eq. (8), which is mathematically shown as:
is the exact solution of the above equation.
Suppose the novel STO-PDDM of 2nd type by taking , and in Eq. (11), mathematically written as:
represents the exact solution of the Eq. (19).
Suppose the novel STO-PDDM of 2nd type by taking , and in Eq. (11), mathematically written as:
represents the exact solution of the Eq. (20).
The optimization procedures through ANNs-GAIPA for both types of novel STO-PDDM are presented by taking 20 trials along with 10 numbers of hidden neurons. The unidentified weight vectors using the stochastic procedure are presented as:
The obtained ANNs procedures using the GAIPA are presented in Eqs (21–23). The optimum weight vectors, best/mean/ exact result comparisons, AE values and performance indices based on the fitness, EVAF and TIC are plotted in Fig. 2. The overlapping of these results is performed for each example of the novel STO-PDDM, which shows the exactness and accuracy of the stochastic ANNs along with the optimization of GAIPA. The AE is provided in Fig. 2(g), which is measured as 10-04 to 10-06, 10-05 to 10-07 and 10-06 to 10-07 for examples 1 to 3 of the novel STO-PDDM. The convergence performances of the fitness, TIC and EVAF are derived in Fig. 2(h) for the novel STO-PDDM. The optimum fitness performances are calculated 10-10-10-11 for case 1 and 3, while these values are calculated as 10-09-10-10 for the novel STO-PDDM. The optimum TIC operator values are calculated 10-08-10-09, 10-09-10-10, 10-10-10-11 for problems 1 to 3. Similarly, the optimum EVAF are performed as 10-08-10-09, 10-09-10-10, 10-11-10-12 for 1st to 3rd problem of the novel STO-PDDM. These precise performances indicate the accurateness of stochastic ANNs-GAIPA procedure for solving the STO-PDDM.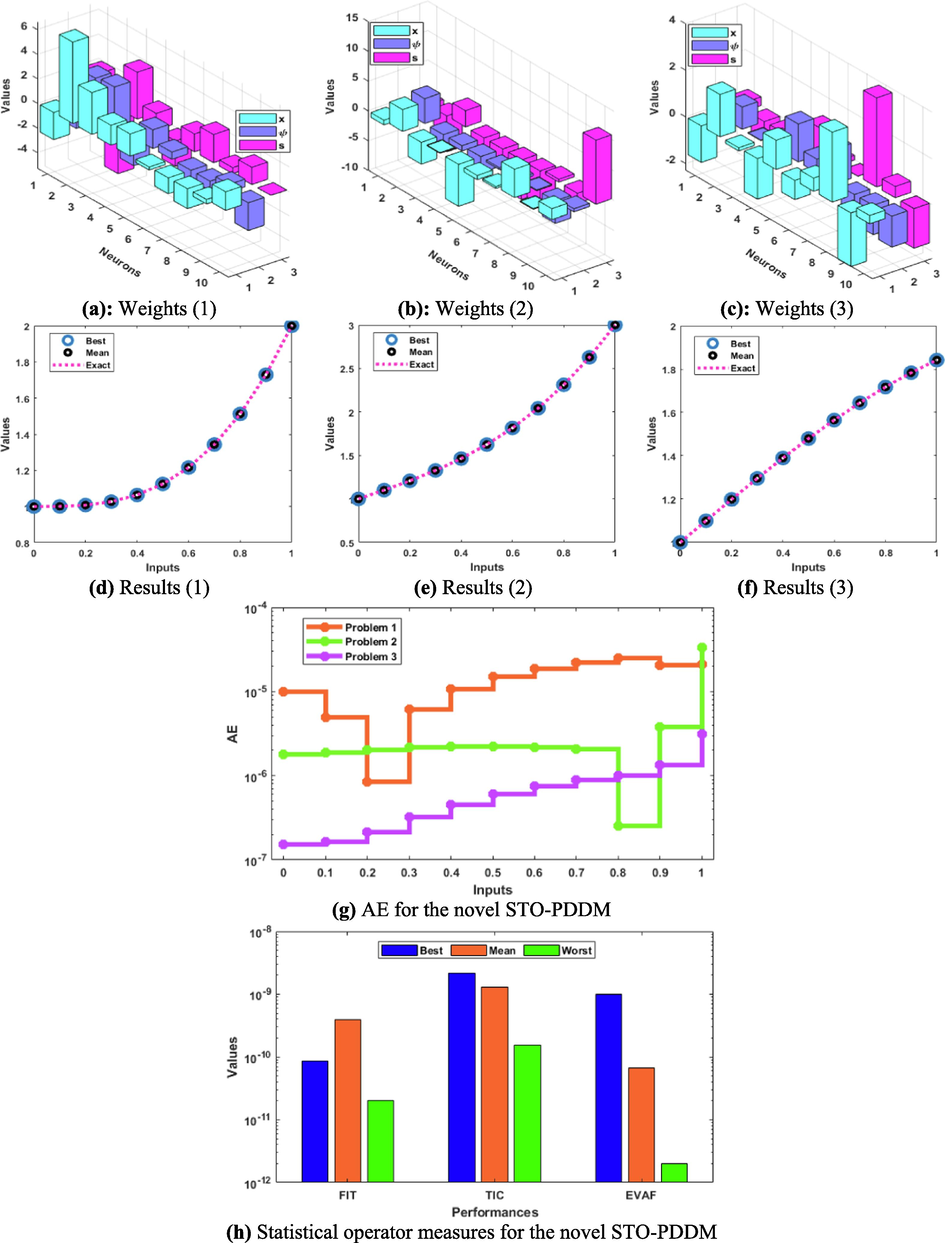
Optimal weights, results, AE, and performances for the novel STO-PDDM.
Figs. 3-5 indicate the convergence plots using the performances of fitness, TIC and EVAF together with the histogram and boxplots to solve the novel STO-PDDM. Twenty numbers of trials have been taken to check the reliability of the proposed scheme based on the performances of these statistical operators. The optimum fitness values are observed in Fig. 3 that are found as 10-06 to 10-10, 10-06 to 10-09 and 10-07 to 10-10 for problem 1 to 3. Fig. 4 shows the TIC measures, which are performed as 10-07 to 10-08, 10-07 to 10-09 and 10-08 to 10-10 for each case of the STO-PDDM. Furthermore, Fig. 5 presents the operator EVAF, which are calculated as 10-06 to 10-08, 10-08 to 10-10 and 10-10 to 10-12 for case 1 to 3. These optimum performances of the statistical operators authenticate the precision and accuracy of ANNs procedure.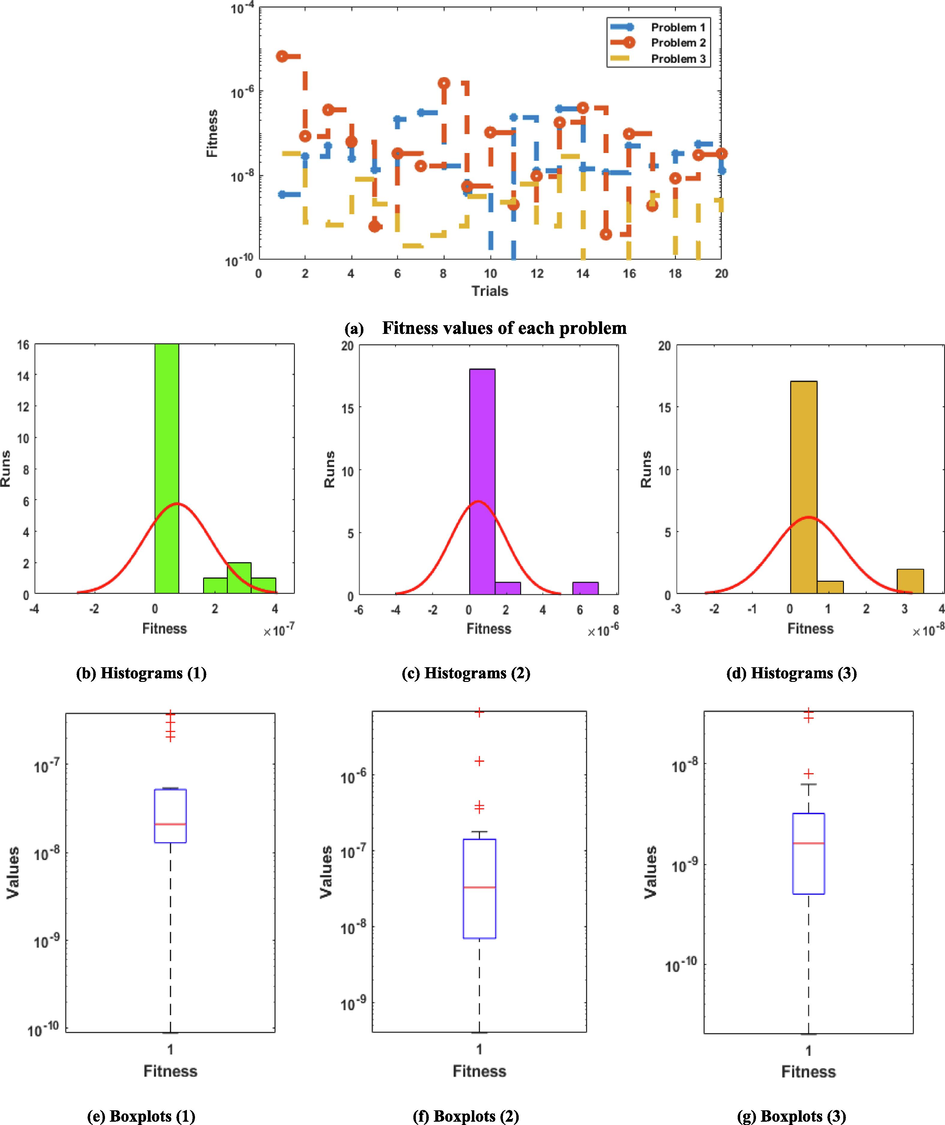
Statistical operator Fitness performances for the novel STO-PDDM.
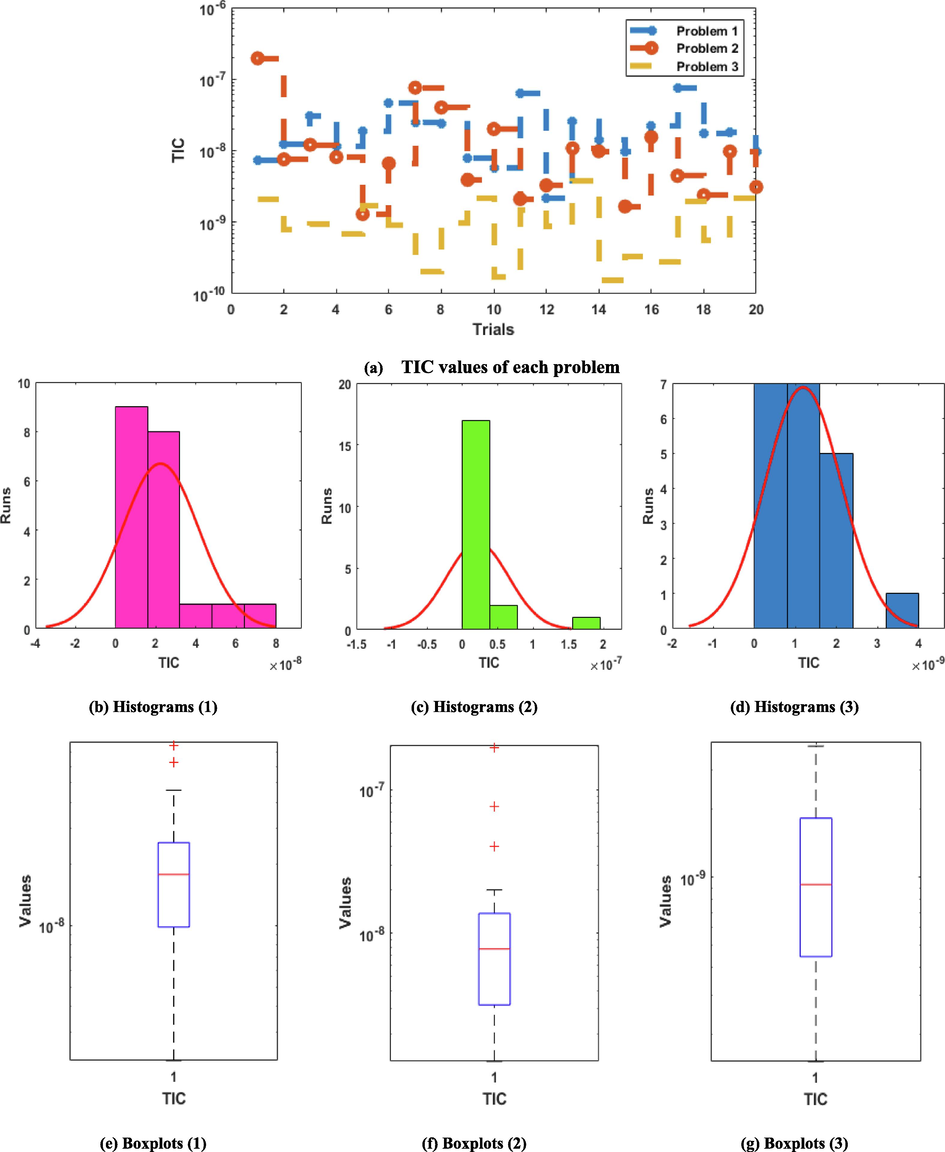
Statistical operator TIC performances for the novel STO-PDDM.
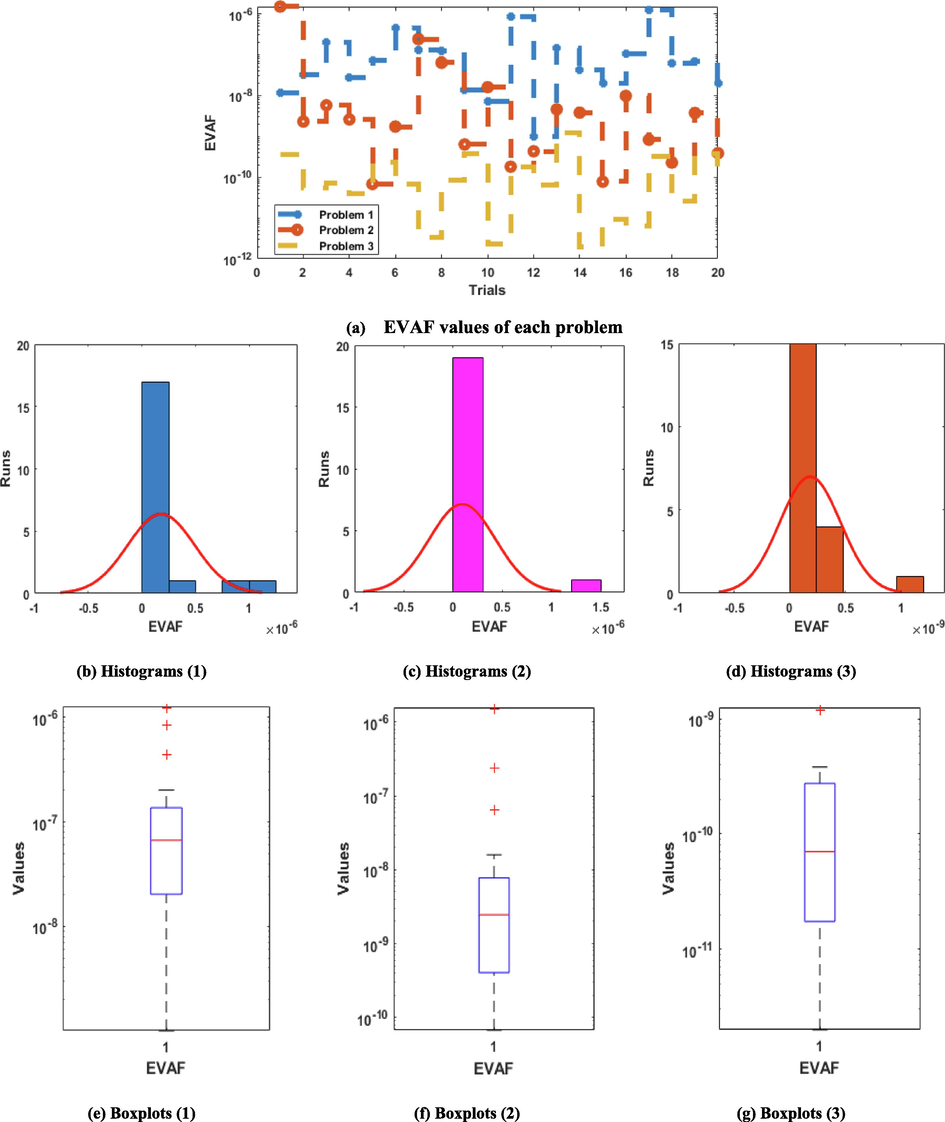
Statistical operator EVAF performances for the novel STO-PDDM.
To find the accuracy of the proposed computational ANNs procedure using the optimization of GAIPA, the statistical performances through the Mean, minimum (Min), Median (Med), SIR and standard deviation (SD) have been presented in Tables 1-3 using twenty independent executions for solving the STO-PDDM. These operator measures using the novel STO-PDDM indicate the accuracy and stability of the procedure using the optimization of GAIPA.
m
Min
Mean
MD
SIR
SD
0
1.22888E-07
2.68799E-06
6.32907E-06
8.19357E-06
3.30382E-06
0.1
1.95999E-07
2.59325E-06
7.03554E-06
1.13119E-05
2.12210E-06
0.2
4.62040E-07
5.86331E-06
1.05120E-05
1.35617E-05
2.57578E-06
0.3
7.29968E-07
1.07992E-05
1.46126E-05
1.49911E-05
3.25204E-06
0.4
9.64055E-07
1.27271E-05
1.78556E-05
1.63665E-05
4.89032E-06
0.5
1.16440E-06
1.53755E-05
2.08731E-05
1.75771E-05
6.81763E-06
0.6
1.33112E-06
1.76506E-05
2.33069E-05
1.87076E-05
8.40900E-06
0.7
1.65137E-06
1.97054E-05
2.58475E-05
1.98576E-05
9.44803E-06
0.8
2.54875E-06
2.30543E-05
2.90338E-05
2.08800E-05
9.59715E-06
0.9
2.50847E-06
2.95573E-05
4.30041E-05
4.01576E-05
2.30042E-05
1
2.12964E-05
4.28659E-04
5.38547E-04
4.65896E-04
1.82360E-04
m
Min
Mean
MD
SIR
SD
0
8.66179E-05
1.28648E-04
1.52817E-04
8.19357E-06
3.83775E-05
0.1
3.11114E-04
3.63273E-04
3.79135E-04
1.13119E-05
3.28319E-05
0.2
6.86823E-04
7.53115E-04
7.53601E-04
1.35617E-05
1.45957E-05
0.3
1.31915E-03
1.37603E-03
1.37773E-03
1.49911E-05
3.23797E-05
0.4
2.20310E-03
2.31167E-03
2.31145E-03
1.63665E-05
4.85365E-05
0.5
3.41518E-03
3.60042E-03
3.58414E-03
1.75771E-05
5.56145E-05
0.6
4.98115E-03
5.22070E-03
5.20365E-03
1.87076E-05
6.17923E-05
0.7
6.88750E-03
7.18340E-03
7.15925E-03
1.98576E-05
6.83255E-05
0.8
9.10418E-03
9.44726E-03
9.41774E-03
2.08800E-05
7.70695E-05
0.9
1.16067E-02
1.19271E-02
1.19105E-02
4.01576E-05
1.17286E-04
1
1.41042E-02
1.44627E-02
1.45126E-02
4.65896E-04
1.68399E-04
m
Min
Mean
MD
SIR
SD
0
4.06035E-07
1.28648E-04
8.37556E-05
8.19357E-06
6.61906E-06
0.1
1.21000E-07
3.63273E-04
8.90470E-05
1.13119E-05
7.30980E-06
0.2
2.62656E-07
7.53115E-04
9.37334E-05
1.35617E-05
8.45516E-06
0.3
1.55746E-06
1.37603E-03
9.67277E-05
1.49911E-05
7.25821E-06
0.4
8.19935E-07
2.31167E-03
9.98779E-05
1.63665E-05
6.45653E-06
0.5
1.18745E-07
3.60042E-03
1.00834E-04
1.75771E-05
7.94238E-06
0.6
1.16108E-06
5.22070E-03
9.86861E-05
1.87076E-05
1.16493E-05
0.7
2.06164E-06
7.18340E-03
9.07995E-05
1.98576E-05
1.48768E-05
0.8
2.51312E-07
9.44726E-03
7.60426E-05
2.08800E-05
1.76821E-05
0.9
1.93482E-07
1.19271E-02
6.73591E-05
4.01576E-05
1.82131E-05
1
3.01573E-05
1.44627E-02
3.18501E-04
4.65896E-04
1.19107E-04
The complexity investigations for the novel STO-PDDM using the computational ANNs procedure along with the GAIPA optimization are presented in Table 4. The computed iterations, executed time along with the function implementations have been presented for each problem of the STO-PDDM. The average values of generations, time instigated, and function computations are performed as 45.20529872, 240.7990046 and 38370.30455, respectively for novel STO-PDDM.
Examples
Generations/Iterations
Time Consumed
Function Computations
Mean
SD
Mean
SD
Mean
SD
1
38.24698362
38.56890412
234.87483481
245.23194756
40920.24567834
4782.8129109
2
68.18456198
98.12986740
267.59370324
298.74960234
34618.87673260
5643.3380271
3
29.18435057
75.12340923
219.92847561
276.29486715
39571.79124726
7792.2485210
6 Concluding remarks
The purpose of this work is to perform the novel design of the singular third order perturbed delay differential model with its two types through the traditional Lane-Emden model. The description of perturbed, shape, singular and delay terms have also been presented for both types of STO-PDDM. The STO-PDDM is numerically presented using the artificial neural networks along with the optimization of global/local genetic algorithm and interior-point scheme. The optimization performances using the GAIPA have been performed based on the activation function through the differential form of the STO-PDDM. The accuracy and authenticity of the designed scheme has been performed through the comparison of the obtained and true results. The negligible values of the absolute error also enhance the correctness of the proposed scheme. The reliability of the scheme has been performed through the statistical EVAF, TIC and SIR performance for solving the STO-PDDM.
In future, the higher order nonlinear models can be numerically solved by using the artificial neural network and deep learning procedures (Sousa et al., 2010; Umar, 2022; Vanani et al., 2011; Wächter and Biegler, 2006; Wang, 2022; Wu et al., 1994; Yan and Quintana, 1999).
Acknowledgement
The authors are thankful to UAEU for the financial support through the UPAR grant number 12S002.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Numerical investigations of a new singular second-order nonlinear coupled functional Lane-Emden model. Open Phys.. 2020;18(1):770-778.
- [Google Scholar]
- Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method. Appl. Math. Nonlinear Sci.. 2021;6(1):9-20.
- [Google Scholar]
- Numerical treatment on the new fractional-order SIDARTHE COVID-19 pandemic differential model via neural networks. Eur. Phys. J. Plus. 2022;137(3):1-14.
- [Google Scholar]
- A uniform numerical method for dealing with a singularly perturbed delay inital value problem. Appl. Math. Lett.. 2010;23:1221-1225.
- [Google Scholar]
- Application of neural network for computing heat performance in axisymmetric viscoelastic transport: Hybrid meta heuristic techniques. Results Phys.. 2018;8:1076-1085.
- [Google Scholar]
- Mohamed S M Bahgat: Approximate analytical solution of the linear and nonlinear multi-pantograph delay differential equations, Phys. Scr. 95 (2020) 055219 (13pp).
- Mohamed S. M. Bahgat and A. M. Sebaq: An Analytical Computational Algorithm for Solving a System of Multipantograph DDEs Using Laplace Variational Iteration Algorithm Advances in Astronomy, Volume 2021, Article ID 7741166, 16 pages, https://doi.org/10.1155/2021/7741166.
- A Paralel aproach for self-adjoint singular perturbation problems using Numerov’s scheme. Int. J. Comput. Math.. 2007;84(3):317-323.
- [Google Scholar]
- Beretta, E. and Kuang, Y., 2002. Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM Journal on Mathematical Analysis, 33(5), pp.1144-1165. pp.447-468.
- Leonid Bogachev, Gregory Derfel, Stanislav Molchanov, and John Ochendon. On bounded solutions of the balanced generalized pantograph equation. In Pao-Liu Chow, George Yin, and Boris Mordukhovich, editors, Topics in Stochastic Analysis and Nonparametric Estimation, volume 145 of The IMA Volumes in Mathematics and its Applications, pages 29–49. Springer New York, 2008.
- A hybrid swarming computing approach to solve the biological nonlinear Leptospirosis system. Biomed. Signal Process. Control. 2022;77:103789
- [Google Scholar]
- A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach. Fract. Fract.. 2022;6(3):139.
- [Google Scholar]
- Design of a hybrid NAR-RBFs neural network for nonlinear dusty plasma system. Alex. Eng. J.. 2020;59(5):3325-3345.
- [Google Scholar]
- Design of intelligent computing networks for nonlinear chaotic fractional Rossler system. Chaos Solitons Fract.. 2022;157:111985
- [Google Scholar]
- A specialized interior-point algorithm for multicommodity network flows. SIAM J. Optim.. 2000;10(3):852-877.
- [Google Scholar]
- A finite difference method on layer-adapted mesh for singularly perturbed delay differential equations. Appl. Math. Nonlinear Sci.. 2020;5(1):425-436.
- [Google Scholar]
- Robust Computational Techniques for Boundary Layers. New York: Chapman-Hall/CRC; 2000.
- Forde, J.E., 2005. Delay differential equation models in mathematical biology (pp. 5436-5436). University of Michigan.
- Rolling horizon evolutionary algorithms for general video game playing. IEEE Trans. Games. 2021;14(2):232-242.
- [Google Scholar]
- Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr.. 2022;30(1):33-42.
- [Google Scholar]
- Predicting elemental stiffness matrix of FG nanoplates using Gaussian process regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem.. 2022;143:779-795.
- [Google Scholar]
- Design of neuro-swarming computational solver for the fractional Bagley-Torvik mathematical model. Eur. Phys. J. Plus. 2022;137(2):245.
- [Google Scholar]
- The optimal exponentially-fitted numerov method for solving two-point boundary value problems. J. Comp. Appl. Math.. 2010;230:260-269.
- [Google Scholar]
- Deep learning based dynamic behavior modelling and prediction of particulate matter in air. Chem. Eng. J.. 2021;426:131221
- [Google Scholar]
- Neural based hybrid metaheuristic technique for computing rotating transport of Falkner-Skan flow. Alex. Eng. J.. 2018;57(3):2123-2132.
- [Google Scholar]
- Design of evolutionary optimized finite difference based numerical computing for dust density model of nonlinear Van-der Pol Mathieu’s oscillatory systems. Math. Comput. Simul.. 2021;181:444-470.
- [Google Scholar]
- Multi-parameter and multi-objective optimisation of articulated monorail vehicle system dynamics using genetic algorithm. Veh. Syst. Dyn.. 2020;58(1):74-91.
- [Google Scholar]
- Numerical simulations of vaccination and Wolbachia on dengue transmission dynamics in the nonlinear model. IEEE Access. 2022;10:31116-31144.
- [Google Scholar]
- Better wind forecasting using evolutionary neural architecture search driven green deep learning. Expert Syst. Appl.. 2023;214:119063
- [Google Scholar]
- Intelligent backpropagation networks with bayesian regularization for mathematical models of environmental economic systems. Sustainability. 2021;13(17):9537.
- [Google Scholar]
- Numerical analysis of a singularly perturbed nonlinear reaction–diffusion problem with multiple solutions. Appl. Numer. Math.. 2004;51(2–3):273-288.
- [Google Scholar]
- Kuang, Y. ed., 1993. Delay differential equations: with applications in population dynamics (Vol. 191). Academic press
- A hybrid difference scheme on a Shishkin mesh for linear convection-diffusion problems. Appl. Numer. Math.. 1999;31:255-270.
- [Google Scholar]
- T. Linss, (2003), Layer-adapted meshes for convection–diffusion problems, Comput. Methods Appl. Mech. Engrg. 192 (9–10) 1061-1105.
- Deep evolutionary networks with expedited genetic algorithms for medical image denoising. Med. Image Anal.. 2019;54:306-315.
- [Google Scholar]
- Fitted Numerical Methods for Singular Perturbation Problems. In: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions. Singapore: World Scientific; 1996.
- [Google Scholar]
- Using the primal-dual interior point algorithm within the branch-price-and-cut method. Comput. Oper. Res.. 2013;40(8):2026-2036.
- [Google Scholar]
- K.C. Patidar (2005), High order fitted operator numerical method for self-adjoint singular perturbation problems, Applied Math. and Comp. 171, 547-566.
- Broadband piezoelectric transducers for under-display ultrasonic fingerprint sensing applications. IEEE Trans. Ind. Electron.. 2020;68(5):4426-4434.
- [Google Scholar]
- Perko, L., 2001. Differential Equations and Dynamical Systems. 3rd edn. Springer, New York, 2001. Numerical Algorithms, 27(4).
- A fitted numerov method for singular perturbation problems exhibiting twin layers. Appl. Math. Information Sci.. 2010;4(3):341-352.
- [Google Scholar]
- A new stochastic computing paradigm for nonlinear Painlevé II systems in applications of random matrix theory. Eur. Phys. J. plus. 2018;133(7):1-21.
- [Google Scholar]
- Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol. Intel.. 2020;13(2):185-196.
- [Google Scholar]
- Numerical Methods for Singularly Perturbed Differential Equations. ConvectionDiffusion and Flow Problems: Springer Verlag, Berlin; 1996.
- Heuristic computing technique for numerical solutions of nonlinear fourth order Emden-Fowler equation. Math. Comput. Simul. 2020;178:534-548.
- [Google Scholar]
- FMNEICS: fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane-Emden system. Comput. Appl. Math.. 2020;39(4):1-18.
- [Google Scholar]
- Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden-Fowler equation. Eur. Phys. J. Plus. 2020;135(5):410.
- [Google Scholar]
- Intelligence computing approach for solving second order system of Emden-Fowler model. J. Intell. Fuzzy Syst. 2020:1-16.
- [Google Scholar]
- Novel design of Morlet wavelet neural network for solving second order Lane-Emden equation. Math. Comput. Simul. 2020;172:1-14.
- [Google Scholar]
- Evolutionary heuristic with Gudermannian neural networks for the nonlinear singular models of third kind. Phys. Scr.. 2021;96(12):125261
- [Google Scholar]
- Solution of novel multi-fractional multi-singular Lane-Emden model using the designed FMNEICS. Neural Comput. Applic.. 2021;33(24):17287-17302.
- [Google Scholar]
- Stochastic numerical investigations for nonlinear three-species food chain system. Int. J. Biomath.. 2022;15(04):2250005.
- [Google Scholar]
- A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model. Fract. Fract.. 2022;6(1):29.
- [Google Scholar]
- Numerical investigations to design a novel model based on the fifth order system of Emden-Fowler equations. Theor. Appl. Mech. Lett.. 2020;10(5):333-342.
- [Google Scholar]
- Sabir, Z. et al., 2020. On a new model based on third-order nonlinear multisingular functional differential equations. Mathematical Examples in Engineering, 2020.
- Impact of oxytactic microorganisms and variable species diffusivity on blood-gold Reiner-Philippoff nanofluid. Appl. Nanosci.. 2021;11(1):321-333.
- [Google Scholar]
- Sajid, T., Tanveer, S., Sabir, Z. and Guirao, J.L.G., 2020. Impact of activation energy and temperature-dependent heat source/sink on maxwell–sutterby fluid. Mathematical Problems in Engineering, 2020.
- Interior point algorithm for linear programming used in transmission network synthesis. Electr. Pow. Syst. Res.. 2005;76(1–3):9-16.
- [Google Scholar]
- Robust optimal power flow solution using trust region and interior-point methods. IEEE Trans. Power Syst.. 2010;26(2):487-499.
- [Google Scholar]
- A computational framework to solve the nonlinear dengue fever SIR system. Comput. Methods Biomech. Biomed. Eng. 2022:1-14.
- [Google Scholar]
- Soleymani Karimi Vanani, Sedighi Hafshejani and Khan. On the numerical solution of generalized pantograph equation. World Applied Sciences Journal, 13(12):2531–2535, 2011
- On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program.. 2006;106(1):25-57.
- [Google Scholar]
- Numerical computing to solve the nonlinear corneal system of eye surgery using the capability of Morlet wavelet artificial neural networks. Fractals 2022
- [Google Scholar]
- A direct nonlinear predictor-corrector primal-dual interior point algorithm for optimal power flows. IEEE Trans. Power Syst.. 1994;9(2):876-883.
- [Google Scholar]
- Improving an interior-point-based OPF by dynamic adjustments of step sizes and tolerances. IEEE Trans. Power Syst.. 1999;14(2):709-717.
- [Google Scholar]







