Translate this page into:
Irregularity molecular descriptors of Cerium oxide based on mathematical model and calculation
⁎Corresponding author. mmunir.math@pu.edu.pk (Muhammad Mobeen Munir),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The irregularities of graphs and their dependencies on the size parameters are recently attracting attention of not only mathematician but also of theoretical chemists. It is found that these irregularities are related with the properties of the substance involved. Cerium oxide is a rare-earth metal having formula and it is light yellow-white powder. In the present article we are concerned with computing the closed forms of irregularity measures of general form of crystal structure of Cerium Oxide based on mathematical model and calculation.
Keywords
Irregularity indices
Cerium oxide
Indices
Imbalance-based irregularity measure
Molecular computing
Mathematical model
1 Introduction
Chemical Graph Theory is recently flourishing because of increasing number of structural dependent functions which exhibit the topological aspects of the chemical substance under consideration. Physio-chemical aspects of the materials are related to these functions in a complex way. Topological degree-based descriptors are numerical estimators which relate these properties. One class of such descriptors is irregularity measure which computes the complexity of the chemical structures. This degree of complexity determines the degree of chemical branching and bonding pattern, enthalpy, stability and strain energy, (Abdo and Dimitrov, 2014; Gutman, 2018; Reti et al., 2018; Hu et al., 2005). The present article computes irregularity measures of Cerium oxide in closed analytic form.
Basic structure of cerium oxide is such that each cerium ion
is surrounded by eight oxide ions
that forms a cubic shape molecule and each oxide ion is enclosed by four
ions which forms a tetrahedron molecule (Sayle et al., 1994). This structure is rich in exceptional physical and chemical properties. Its optical and electrical properties are generally because of the little size and huge thickness of corners. Cerium exists both in
and
in bulk state as demonstrated in Fig. 2. This double oxide nature is because of the electropositive qualities of ceria,
also called the “sesquioxide”, Fig. 3. The magnetic property is profoundly temperature dependent. This property is not present in the large structure as it has only + 4 state (Ribeiro and Ferreira, 2017). Every strange and special property of cerium oxide is because of the oxygen vacancy. In Cerium oxide a stable structure is due to the high oxygen storage capacity. When the size of cerium material is small, these oxygen vacancies tend to increase (Tseng et al., 2019; Wu et al., 2018).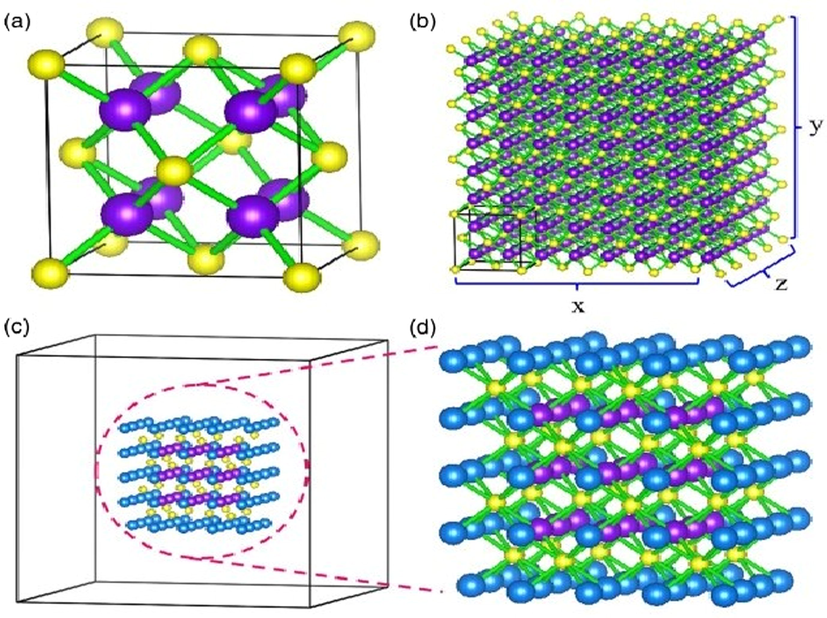
Part (a) shows the unit cell of bulk
, part (b) shows schematic illustration of building the solid atomic assembly of
(cerium) and O (oxygen) atoms by randomly expanding the unit cell of bulk
(enclosed by black solid lines) ×, y, and z times in three orthonormal directions, respectively part (c) the super cell of cubic cerium oxide nanoparticles of 1 nm for relaxation calculation (d) zoom-in picture of the solid atomic assembly in part c.
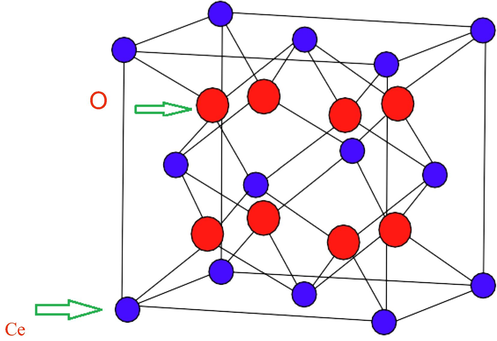
Unit cell of.
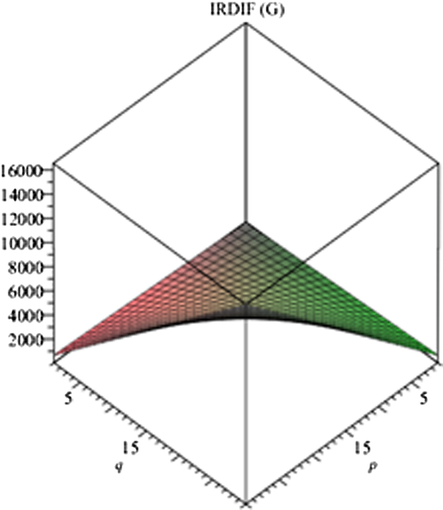
Graph of irregularity index IRDIF.
Topological index is one such rich area of mathematics where it can enter in chemistry and bring revolution in determining properties of the chemical substances (Rucker and Rucker, 1999; Klavžar and Gutman, 1996; Brückler et al., 2011; Deng et al., 2011). The basic branch involved is the Chemical Graph Theory. In order to move on, we need to grasp some rudiments of Graph Theory. Let us denote G to be a simple connected graph having vertex set V and edge set E. Let us fix du and dv for the degrees of vertices u and v respectively. A graph is known to be regular if every vertex of the graph has the same degree. A topological invariant is called an irregularity index if this index vanishes for a regular graph, and remains non-zero for otherwise. Regular graphs are technically nicer than irregular ones and consequently have been extensively investigated, particularly in mathematics. After the discoveries of nanotubes and fullerenes, the regular graphs became more popular especially in Chemical Graph Theory. Today it is well-established that the topology of fullerenes is rich and has potential of many applications in mathematics. However, the irregular graphs remained unnoticed for a long time.
Paul Erdos, the famous Hungarian mathematician, put a lot of emphasis on the study of irregular graphs for the first time in history in (Chartrand et al., 1988). He posed a problem in (1994), that what could be the extreme size of highly irregular graph of a given order, (Majcher and Michael, 1997). This problem in fact opened gates for mathematician to study irregular graphs and the degree of irregularity as well. A particular graph would be highly strange in which in which each vertex has a different degree. Such graphs were termed as perfect graphs. The authors of (Behzad and Chartrand, 1947) demonstrated that no graph is perfect. The graphs lying in between are called quasi-perfect graphs, in which all except two vertices have different degrees (Majcher and Michael, 1997). One way of expressing irregularities of graphs is the computation of irregularity indices. These indices can be based on many pieces of information such as degrees of vertices, eccentricities of vertices etc. Some irregularity indices were studied recently in a novel way (Horoldagva et al., 2016; Liu et al., 2014; Collatz and Sinogowitz, 1957). The first such irregularity index was introduced in (Bell, 1992). Most of these indices which are based on degree of vertices used the concept of the imbalance of an edge defined as ; (Behzad and Chartrand, 1947; Horoldagva et al., 2016; Liu et al., 2014; Collatz and Sinogowitz, 1957; Bell, 1992; Albertson, 1997).
The Albertson index denoted by, AL(G), was initially introduced by Alberston in (Albertson, 1997) as The irregularity index IRL(G) and IRLU(G) were introduced by Vukičević and Gasparov, (Vukičević and Graovac, 2004) as , and where min is used as the minimum of the parameters given. Recently, Abdoo et al. defined the new term “total irregularity measure of a graph G”, as , (Abdo et al., 2014; Abdo and Dimitrov, 2014; Abdo and Dimitrov, 2014). Recently, Gutman et al. introduced the IRF(G) irregularity index of the graph G, which is described as in (Gutman, 2018). Reti et al. discussed the relation of irregularity indices and properties in (Reti et al., 2018). The Randic index itself is directly related to an irregularity measure, which is described as in (Yang et al., 2019). Further irregularity indices of similar nature can be traced in (Gutman, 2018; Reti et al., 2018; Hu et al., 2005) in detail. These indices are given as ; ; , , , and . Further details can be given in (Gutman, 2018; Reti et al., 2018; Hu et al., 2005; Zahid et al., 2019; Gao et al., 2019; Gao et al., 2017; Hussain et al., 2019; Hussain et al., 2020; Yang et al., 2019; Hussain et al., 2019; Estrada, 2010 Sep). These irregularity measures have been put to use in determining an estimate of the properties of octane isomers in (Reti et al., 2018). Reti et al. actually did comparative regression analysis on the eighteen different irregularity indices of five different properties of octane isomers and concluded that these properties such as boiling point, standard enthalapy of vaporization, acentric factor, enthalapy of vaporization and entropy can be estimated with good accuracy of these isomers, (Reti et al., 2018). This side depict the actual applications of these indices. Other side of the story is to consider different matrices based on these irregularity indices and the eigen values of these matrices give us the energies related to these molecular graphs. These energies have deep applications in chemistry and physics such as to determine pi-electron energy. Authors in (Estrada, 2010 Sep) critically analyzed the irregularity of 10 protein–protein interaction networks in different organisms ranging from 50 to 3000 nodes. These indices can play helpful Job in estimating the properties of the molecular substances involved. Recently, Zahid et al. computed the irregularity indices of a nanotube (Zahid et al., 2019). Gao et al. recently computed irregularity measures of some dendrimer structures in (Gao et al., 2019) and molecular structures in (Gao et al., 2017). These structures are used as long infinite chain macromolecules in chemistry and related areas. Hussain et al. computed irregularities of different non-homeomorphic benzenoid structures in (Hussain et al., 2019; Hussain et al., 2020). Yang et al. discussed the imbalance-based irregularities of two types of boron nanotubes in (Yang et al., 2019). Hussain et al. also computed imbalance-based irregularities of nanostar dendrimers in (Hussain et al., 2019). As structures are rich in topology, so more and more investigations of irregular structures are in progress. In this article we focus on the topological structural facts of Cerium Oxide More precisely, we are interested in computing the imbalance-based degree of irregularity measures of general form of Cerium Oxide . Following Fig. 1 shows the topological structure of .
In Cerium Oxide atoms are shown by blue circles and oxygen O atoms are shown by red circles. In the unit cell, each atom located at corner of a cube is coordinated with three atoms, and one oxygen O atom, on other hand each atom located at face of a cube is coordinated with four oxygen O atoms as shown in Fig. 2. Now in the next section we move towards our computational results. We also show some graphical analysis of the irregularities involved. It is worth mentioning that Cerium Oxide doped obsidian glasses are better radiation shielding materials than ordinary obsidian glass, as mass attenuation coefficients of CeO2 doped obsidian glass decrease with increasing photon energy, (Yalcin et al., 2019). In (Yılmaz et al., 2020), authors computed some indices relating to the radiation shielding parameters like linear attenuation coefficients mass attenuation coefficients, effective atomic numbers, effective electron densities, half value of layers and mean free paths for rare earth metal oxides CeO2 doped borosilicate (BS) glasses.
2 Main results
In this section, we present our main theoretical results. Following main result gives closed formulas for as many as twelve irregularity measures of .
Let be the crystal structure of Cerium Oxide. Tthen the irregularity indices of are:
-
-
.
-
.
-
.
-
-
.
-
.
-
.
-
.
-
-
.
-
.
In order to prove the above theorem, we have to consider Figs. 1 and 2 from where some partitions of edge sets and vertex sets can be computed.
Now, using above Table 1 and the above definitions, we have:
-
10.
-
11.
-
12.
| Number of edges ( | Number of indices |
|---|---|
| (4,4) | |
| (4,6) | |
| (4,8) | |
| (6,6) |
Table 2. Shows the values of these irregularity indices for some test values of parameter p, q t.
Irregularity Indices
p = 1, q = 1, t = 1
p = 2, q = 2, t = 2
p = 3, q = 3, t = 3
p = 4, q = 4, t = 4
p = 5, q = 5, t = 5
36.42
171.79
513.74
1160.07
2208.58
88
416
1248
2824
5384
17.837497
83.733197
249.672897
562.894597
1070.636297
22
104
312
706
1342
17.971162
84.364636
251.677097
567.575628
1097.737330
176
872
2720
6296
12,176
17.6757
82.5027
245.7677
553.7707
1052.8917
48.3387
225.5720
669.07533
1503.6286
2854.0120
0.370297
1.367747
5.381157
12.258307
23.470577
8.979147
41.291457
120.872127
269.438337
508.707267
8.88909
43.43484
133.97469
308.14008
553.56245
44
208
624
1412
2692
3 Graphical analysis and discussions
Present part is devoted to the irregularity analysis of above-mentioned Cerium Oxide
. The graphs as indicated in Figs. 4–7 show irregularity behavior of any particular index with respect to the parameters involved in the structure. In the present case, the involved parameters are p, q and t. We obtain almost similar graphs for all irregularity measures which shows that irregularity tends to rise with the increase in the size parameters.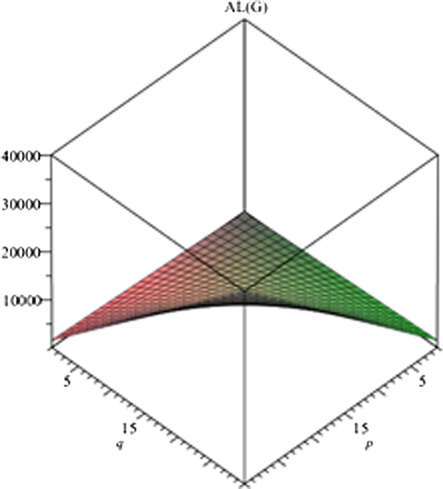
Graph of irregularity index AL.
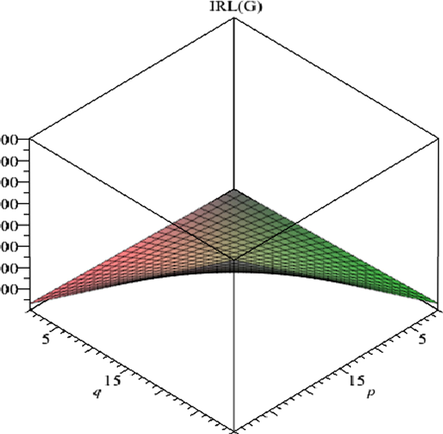
Graph of irregularity index IRL.
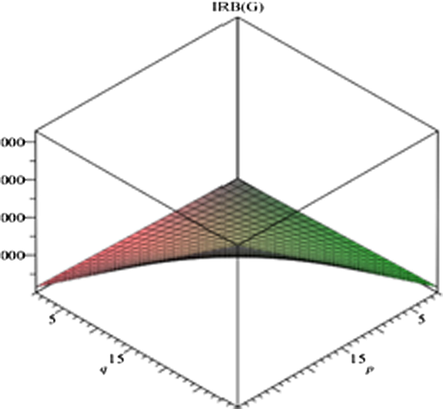
Graph of irregularity index IRB.
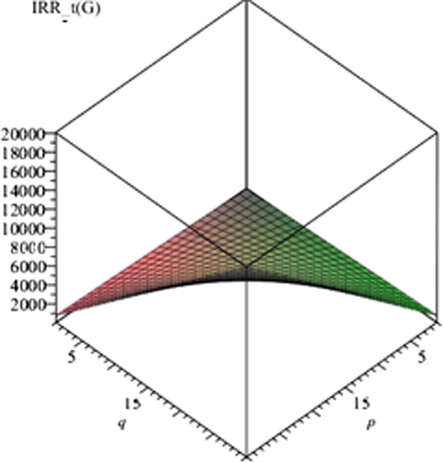
Graph of irregularity index IRRt cerium oxide when p, q are variables and t is fixed (t = 1) as shown in Figs. 4–7.
4 Conclusion
The behaviors and tendencies of topological irregularities can be determined by the graph. All graphs exhibit the similar nature of irregularity indices regardless of the particular irregularity index we prefer to study the irregularity of the cerium oxide. This graphical analysis can be used to model new nanostructures where irregularities can be controlled by controlling involved parameters. Using these graphs and above table of values, the estimate of properties of cerium oxide can be done. Due to the lack of resources regarding wet lab, we pose it as an open problem to give some families of hydrocarbons whose complexity depend on irregularity indices as has been done in (Gutman, 2018; Reti et al., 2018).
Author contributions
M.M. gave the idea, H.A. wrote the article and Jia-Bao Liu and Qi Zhang edited and verified the results.
Data availability statement
No such data has been used for this study.
Acknowledgements
We are thankful to potential reviewers for fruitful suggestions and comments. First author is thankful to the support of Uniersity of the Punjab and HEC of Pakistan.
References
- The total irregularity of graphs under graph operations. Miskolc Math. Notes. 2014;15:3-17.
- [Google Scholar]
- The irregularity of graphs under graph operations. Discuss. Math. Graph. Theory. 2014;34:263-278.
- [Google Scholar]
- The total irregularity of a graph. Discr. Math. Theor. Comput. Sci.. 2014;16:201-206.
- [Google Scholar]
- On a class of distance-based molecular structure descriptors. Chem. Phys. Lett.. 2011;503:336-338.
- [Google Scholar]
- A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Comp. Math. Appl.. 2011;61:3017-3023.
- [Google Scholar]
- Randić index, irregularity and complex biomolecular networks. Acta Chim Slov.. 2010 Sep;57(3):597-603. PMID: 24061806
- [Google Scholar]
- On the irregularity of some molecular structures. Can. J. Chem.. 2017;95:174-183.
- [CrossRef] [Google Scholar]
- Maximum size of maximally irregular graphs. Match Commun. Math. Comput. Chem.. 2016;76:81-98.
- [Google Scholar]
- On molecular graphs with smallest and greatest zeroth-Corder general randic index. MATCH Commun. Math. Comput. Chem.. 2005;54:425-434.
- [Google Scholar]
- Imbalance-Based Irregularity Molecular Descriptors of Nanostar Dendrimers. Processes. 2019;7:517.
- [CrossRef] [Google Scholar]
- Irregularity molecular descriptors of hourglass, jagged-rectangle, and triangular benzenoid systems. Processes.. 2019;7:413.
- [Google Scholar]
- Analysis of irregularity measures of zigzag, rhombic, and honeycomb benzenoid systems. Open Physics. 2020;18(1):1146-1153.
- [CrossRef] [Google Scholar]
- A Comparison of the Schultz molecular topological index with the Wiener index. J. Chem. Inf. Comput. Sci.. 1996;36:1001-1003.
- [Google Scholar]
- The size of maximally irregular graphs and maximally irregular triangle–free graphs. Graphs Comb.. 2014;30:699-705.
- [Google Scholar]
- Highly irregular graphs with extreme numbers of edges. Discr. Math.. 1997;164:237-242.
- [Google Scholar]
- Graph irregularity indices used as molecular discriptors in QSPR studies. MATCH Commun. Math. Comput. Chem.. 2018;79:509-524.
- [Google Scholar]
- Systematic study of the physical origin of ferromagnetism in CeO2_ δ nanoparticles. Physical Review B. 2017;95(14):144-150.
- [Google Scholar]
- On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci.. 1999;39:788-802.
- [Google Scholar]
- The role of oxygen vacancies on ceria surfaces in the oxidation of carbon monoxide. Surface Science. 1994;316(3):329-336.
- [Google Scholar]
- Magnetism and plasmatic performance of macroscopic hollow ceria spheres decorated with silver nanoparticles. Nanoscale. 2019;11(8):3574-3582.
- [Google Scholar]
- Valence connectivities versus Randić, Zagreb and modified Zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat. Chem. Acta. 2004;77:501-508.
- [Google Scholar]
- Co-effects of UV/H2O2 and natural organic matter on the surface chemistry of cerium oxide nanoparticles. Environmental Science: Nano. 2018;5(10):2382-2393.
- [Google Scholar]
- S. Yalcin, B. Aktas, D. Yilmaz, Radiation shielding properties of Cerium oxide and Erbium oxide doped obsidian glass, Radiation Physics and Chemistry, 2019, 160, 83-88, ISSN 0969-806X.
- Computational Analysis of Imbalance-Based Irregularity Indices of Boron Nanotubes. Processes. 2019;7:678.
- [CrossRef] [Google Scholar]
- Erbium oxide and Cerium oxide-doped borosilicate glasses as radiation shielding material. Radiation Effects and Defects in Solids. 2020;175(5–6):458-471.
- [CrossRef] [Google Scholar]
- Characteristic study of irregularity measures of some Nanotubes. Can. J. Phys. 2019
- [CrossRef] [Google Scholar]







