2.1 Sample collection pretreatments and preparation

Plantain peels used in this work were sampled from Genesis Restaurant within Enugu metropolis, Enugu State, Nigeria. Unripped plantain peels was sliced into smaller pieces, cleaned using deionized water, then dried under intense sun for seven days and oven dried at 110 °C for 5 h. It was thereafter reduced to fine powder with grinder and sieved to particle size of 75 µm, and was designated as raw PPF. Stearic acid, sulphuric acid (H₂SO₄), Hydrochloric acid (HCl) and caustic soda (NaOH) used in this work were purchased from major market in Enugu Nigeria. The reagents have a purity of 99.9 % and were applied without any treatment or purification. The crude oil used in this work was sourced from Agip oil field Bayelsa State Nigeria.

2.2 Carbonization of PPF and activation with stearic acid

The approaches of Nick et al. (Ogbodo et al., 2021) and Christian et al. (Asadu et al., 2021) were adopted with little modification. The oven dried sample of raw PPF was subjected to thermal treatment in a muffle furnace (model HCK 15/4 No: 20–40509, Taiwan) at 700 °C for 4 h. PPF after heat treatment was allowed to cool down to room temperature and allowed standing for further 45 mins. Then 15 g of the carbonized samples were added to a Dean Stark apparatus and treated with 0.8 g of stearic acid in 200 ml of 100 % n-hexane which also contain 1 % H₂SO₄ as catalyst. Refluxing of the mixture at 68 ± 1 °C was done for 2.5 h, followed by washing with distilled water followed by n-hexane to remove excess acid. The samples were later dried in oven again at 100 °C for 7 h and stored in a tight polyethylene container. Changes in the weight of the sample were evaluated using equation (1).

2.3 Physical properties and instrumental characterization

The physical properties of the PPF (raw, carbonized and esterified) were determined according to the standard procedures described by Association of Official Analytical Chemists (Didem, 2012; Cadena et al., 2017). The properties include volatile matter, iodine number, ash content, fixed carbon, moisture content, etc. (Table 3). Bulk density was determined via water displacement method. The BET surface area and its properties were determined using nitrogen gas method. The adsorption–desorption isotherms were calculated at 77 K with assumed nitrogen surface area of 0.162 nm² (Ogbodo et al., 2021). The instrumental analysis was done via Scanning Electron Microscope (SEM) (JOEL JSM 6400 model) and Fourier Transform Infrared (FTIR) spectrophotometer (Shimadzu FTIR-8400S). The surface morphology of both the raw PPF and esterified PPF were determined using the SEM while the functional groups present in the samples were identified via FTIR. Elemental composition was determined with an energy dispersive X-ray spectroscopy (EDX, Oxford X-max) coupled to the SEM.

2.4 General experimental procedure for oil layer removal by PPF (raw, carbonized or esterified)

This experiment was conducted following the method described by Nick et al. (Ogbodo et al., 2021) and Banergee et al. (Banerjee et al., 2006). Briefly, 50 ml of 50 mg/l of crude oil–water mixture was produced by mixing known amount of crude oil and water for 10 mins at room temperature, in a 200 ml beaker. With the crude oil floating on surface of water, 0.2 g of the prepared PPF (raw, carbonized or esterified) were added and the mixture agitated for 3 min at 100 rpm. The pH of the mix was adjusted to 7 using 0.1 M NaOH or 0.1 M HCl, and the system incubated at 30 °C for 60 min, before removal of the adsorbent using 50 µm sieving net. The oil-loaded adsorbents (PPF) were dried at 65 °C for 35 min and re-weighed. The experiment was then repeated with oil water concentration of 100 mg/l, 150 mg/l, 200 mg/l and 250 mg/l. Temperature, pH, adsorbent dosage, as well as contact time were also varied to determine their effects. Amount of oil removed was obtained from weight after adsorption and pre-weight of the PPF (raw, carbonized or esterified). Equation (2) (Cheenmatchaya and Kungwakunakorn, 2014) was applied in determining the capacity of adsorption (qe) while the percentage oil removal was determined using equation (3).

Where;

C_o = Initial oil concentration (mg/l).

C_e = Concentration oil in oil–water mixture at equilibrium (mg/l).

V = Volume of the oil–water mixture (ml).

M = Mass of the adsorbent (raw, carbonized or esterified PPF).

2.5 Isotherm modeling of the oil layer removal using esterified PPF

To predict the model that best explains the process of crude oil adsorption onto esterified PPF in experiment 2.5, some of the selected models as listed in Table 1 were examined.

2.6 Thermodynamics and activation energy studies of the process using PPF

Thermodynamics investigation was done to estimate the enthalpy (ΔH), entropy (ΔS), and Gibb’s free energy of activation (ΔG) for the sorption of oil onto the pores. These thermodynamic properties are vital ingredients for interpreting the behavior of adsorption process (Nwabanne et al., 2018; Asadu et al., 2021). To calculate these parameters, activation complex theory established by Eyring was used in evaluating the thermodynamic parameters from temperature-dependent rate constants. Parameters calculated from the Eyring-Polanyi equation (9) are analogous to the Arrhenius equation:

Natural logarithm of equation (9) taken and substituting the value of $\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$ gives equation (10):

K is the rate constant at temperature T, ΔH and ΔS are the changes in enthalpy and entropy of activation for the reaction system, respectively. k_B and h are the Boltzmann (1.38 X 10^-23 J K⁻¹) and Planck (6.63 X 10^-34 Js) constants while R stands for the universal gas constant. Equation (9) is analogous to Van’t Hoff equation explaining the mathematical connection existing between enthalpy and entropy of activation with the rate constant. The plot of $In\left(k/T\right)vs\frac{1}{T}$ gave the slope as $-\mathrm{\Delta }H/R$ and intercept as $[In\left(k_B/h\right)+\mathrm{\Delta }S/R]$ , respectively. Furthermore, the energy of activation is the energy level of the molecules needed to initiate a reaction or diffusion of molecules onto the microporous surface of the PPF. In a second order model, rate constants increase with temperature and is described by the Arrhenius law as shown in equation (11).

Where: K = stands for adsorption rate constant (L g⁻¹ min⁻¹).

A = stands for temperature independent factor (L g^-1min⁻¹).

$E_a$  = stands energy of activation (J mol⁻¹).

R = stands for gas constant (8.314 J mol⁻¹ K⁻¹).

T = stands for absolute suspension temperature (K).

When equation (11) is linearized, equation (12) is obtained. From the plot of Ln (K) verses I/T, the values of the Activation energy ( $E_a$ ) and the temperature independent factor (A) were obtained from the slope and the intercept of the plot, respectively.

2.7 Central composite design (CCD) and optimization

Central composite design of response surface methodology (CCD-RSM) was used in the experimental design. It consists of five coded levels of lower axial, low, medium, high, and upper axial points, denoted by -α, −1, 0, +1, and + α, respectively. An alpha value of 1.633 was used to account for the design orthogonality. An empirical second-order polynomial expressed in equation (13) was appropriate in describing the effect of the input parameters and their interactions on the percentage of crude oil removed.

Where Y is the percentage of crude oil removed, β_o is the second-order model constant, β_i, represent the coefficient of the first-order term, β_ii, is the coefficient of the second-order term, β_ij is the coefficient of the interaction between any two variables; e is the random error (Ogbodo et al., 2021). Fisher’s test (F-test) and Correlation coefficient (R²) were used to evaluate the significance and the ranking of the models. Confidence level of 95 % was used in the analysis. The independent parameters examined were temperature X₁(^oC), oil concentration X₂(mg/l), adsorbent dosage X₃(g), pH X4, and time X₅ (mins). These parameters were the independent factors whereas the percentage of oil adsorbed or removed (%R) was the dependent parameter or response. The ranges of time, temperature, dosage, oil concentration in water and pH of the adsorption reaction mixture were 15 to 75 mins, 20 to 100 °C, 0.3 to 1.5 g, 0.2 to 1.0 mg/l and 2 to 10, respectively were selected. The coded and uncoded levels of these independent variables are shown in Table 2.

2.8 ANN modelling

Artificial neural network (ANN) was used to model the oil removal process. It is usually viewed as a synchronous process which processes information by the neural system with high accuracy (Chijioke Elijah Onu, 2022a; Onu et al., 2022). The neural toolbox of MATLAB version 8.5.0 was utilized in the ANN modeling with Levenberg-Marquardt back propagation as the training algorithm. It functions via a gradient descent optimization technique (Xuedan et al., 2017). The ANN network consists of input layer, hidden layer and output layer. The input layer consists of five neurons depicting the five input variables while the output layer consists of one neuron representing the output variable. The transfer functions used in the input, hidden and output layers were linear, tansigmoid and purelin transfer functions respectively.

To reduce scaling effect, the data points were normalized between 0 and 1 according to equation (13).

Where X_i, X_max, and X_min are the original data, maximum data, and minimum data for each input and output respectively. X^l is the normalized value of X_i. (Rekhate and Shrivastava, 2020).

The number of neurons in the hidden layer directly affects the performance of the neural network. Hence the number of neurons in the hidden layer was used in determining the best network performance by comparing the experimental data with the model’s responses. Iteration method was used to obtain the optimum number of neurons in the hidden layer. The data division was done such that 80 % of the data was used in training, 10 % was used for testing while the remaining 10 % was used for validation of the network.

2.9 ANFIS modeling

Fuzzy Logic toolbox of MATLAB version 8.5.0 was used in the ANFIS modeling as a hybrid of fuzzy and neural networks. The ANFIS architecture is made up of five layers which represent fuzzification, multiplication, normalization, defuzzification, and summation functions sequentially (Onu et al., 2022). Sugeno fuzzy inference system (FIS) was used to convert the process variables into membership values via the membership functions (MF). Each process variables were assigned to five MF from the input layer. The input layer denoted the five process variables (adsorbent dosage, temperature, contact time, oil concentration and pH) while the output layer denoted the output response (percentage of oil removal). The data set was divided into 80 %, 10 % and 10 % for training, testing, and validation/checking respectively.

2.10 Assessment of the model’s performance

Statistical indices were used to assess and rank the performance of the models. The statistical indices used were correlation coefficient (R²), mean relative percent deviation (MRPD), hybrid fractional error (HYBRID), root mean square error (RMSE) and normalized standard deviation (Δq) as shown in equations 15–19. The performance ranking was based on higher values of R² and low values of HYBRID, RMSE, Δq, and MRPD.

Where Y_{exp (i)} is the experimental oil percentage removal, Y_{pred (i)} was the model predicted oil percentage removal, Y_exp,ave was the experimentally determined average oil percentage removal, N was the number of experimental runs while P was the number of parameters.

3.1 Characterization of adsorbent

3.1.1

3.1.1 Instrumental analysis of adsorbent

The appearance of different functional groups on the surface of raw PPF and esterified PPF as depicted by FTIR (Fig. 1a and 1b) is an indication of reaction between the stearic acid and some functional groups on the PPF, leading to the disappearance of old and appearance of new peaks on the spectrum. For the raw PPF, the organic substance with bond OH was observed at 3186.9 cm⁻¹, at the same time C—H was observed at 2374.3 cm⁻¹ (Ogbodo et al., 2021). Bands indicating the presence of alkyne were observed between 1908.4 and 2109.7 cm⁻¹. The absorption bands observed at 1684.8 cm⁻¹, 1028.7 cm⁻¹ and 670.9 cm⁻¹ represents the functional groups C⚌O, C⚌C and C—O respectively [42 (Sud et al., 2008). After the modification of the raw plantain peels fiber to esterified PPF, there was a shift in absorption bands as follow; OH, bands were observed between 3273.6 and 3693 cm⁻¹; 2202.9, 2855.3, 2922.3 and 3008 m⁻¹ bands represent the alkynes, C⚌O bands was observed between 1640 and 1744.4 cm⁻¹ while C—O bands was observed between 853 and 1021.3 cm⁻¹.

Close

Fig. 1

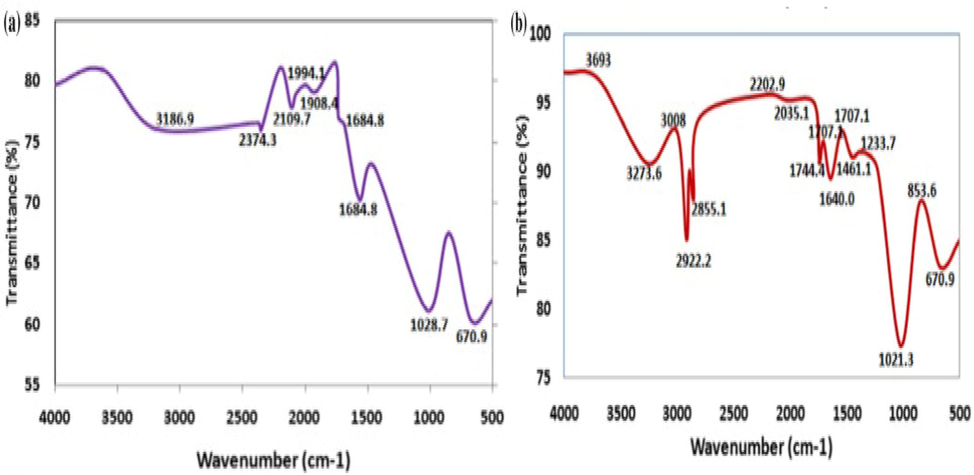
FTIR spectrum of (a) raw plantain peels and (b) Esterified plantain peels.

Export to PPT

The SEM images depicting the surface morphologies of raw PPF and esterified PPF are shown in Fig. 2 (A and B). Compared to the raw PPF, the esterified PPF displayed a higher number of pores, and hence more potentials as an adsorbent.

Close

Fig. 2

(a) SEM image of raw PPF at 1000X (b) SEM image of esterified PPF at 1000X.

Export to PPT

X-ray diffraction is widely used to reveal the characteristics of the crystalline structure of substances (Asadu et al., 2021). Shown in Fig. 3a is the XRD spectra of raw PPF and esterified PPF. The diffraction pattern of the raw PPF showed the presence of compounds associated to carbon C, iron Fe, aluminon Al and silicon Si. This is evident by diffraction peaks at 2θ values of 27.4°, 41.8°, 53.1°, 57.4°, 65.2° and 71.8°, corresponding to the hexagonal pattern of ${\mathit{SiO}}_2$ and ${\mathit{CaCO}}_3$ as dominant compounds at structural plane 201, 220, 221, 401, 421 and 423, respectively. For the esterified PPF, the appearance of new characteristic diffractions at 2θ values of 31.5°, 36.4°, 44.3°, 52.2°, 59.3°, 66.4° and 77.8° were observed, corresponding to the structural planes of 312, 402, 420, 510, 441 and 445, respectively. The changes in the structural planes could be attributed to the disappearance of some compounds after heat treatment and impregnation of the carbonized PPF with organic acid giving rise to the hybrid adsorbent. Similar diffraction peaks in other composites have also been reported by Haldorai et al. (Haldorai et al., 2015) and Nsom et al. (Nsom et al., 2019). Nevertheless, the XRD composition of the adsorbents was also supported by the EDX results, as shown in Fig. 3b and 3c. EDX percentage weight compositions of C (57.15), Fe (11.87), Si (11.65), K (10.17) and Al (9.16) were obtained for raw PPF, while C (93.20), Si (2.07), Ca (3.09), and Mg (1.64) were recorded for esterified PPF.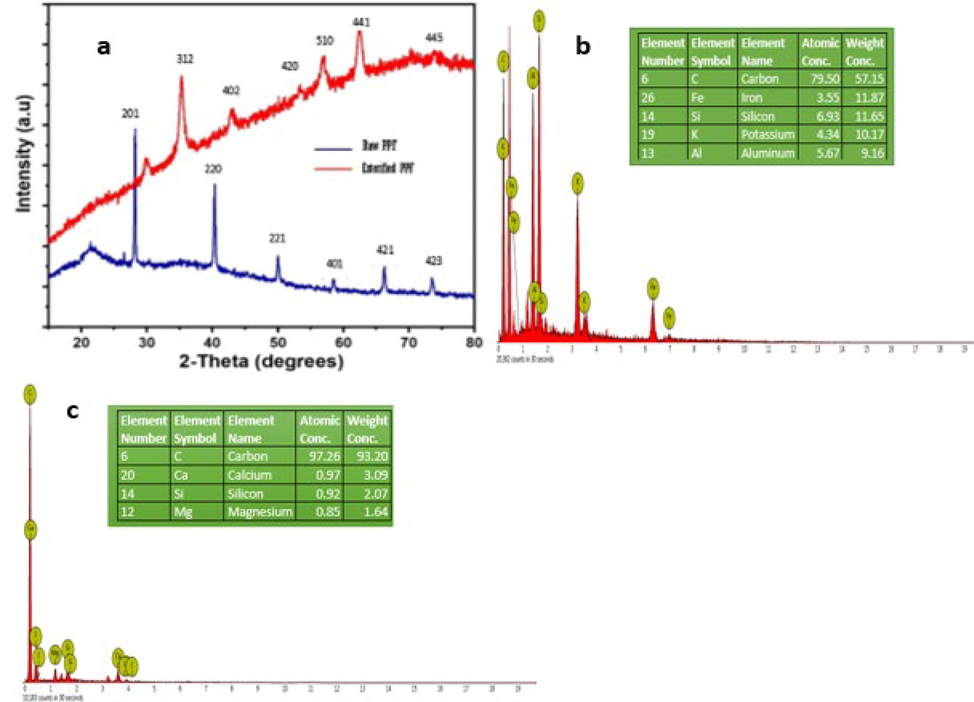

Close

Fig. 3

(a) XRD spectrum of raw PPF and Esterified PPF (a) EDX spectrum of raw PPF (b) EDX spectrum of esterified PPF.

Export to PPT

3.2 Effect of process parameters on crude oil adsorption by PPF

Fig. 4a portrays the impact of pH on oil layer removal by the PPF biomass. It can be stated that optimum oil removal was observed at pH of 5 with esterified PPF recording the most noteworthy percentage as high as 95.3. Interestingly, the rate of oil removal diminished with further increase in pH. This is because of the effect of pH on the net charge on the adsorbent, as well as on the oil surface. In the adsorption reaction mix, a very high pH leads to abstraction of protons from the charged functional groups on the surface of the adsorbent, reducing the net positive charge and the affinity of the adsorbing sites for the negatively charged oil molecules. This explains why increasing the pH beyond 5 led to successive decrease in the quantity of oil removed (Fig. 4a). A very low pH on the other hand (<5 in this study), through proton donation, reduces the net negative charge on the oil molecules, also reducing their affinity for the positively charged adsorbent. Similar preference of mild pH range for optimal adsorption of pollutants have also been observed by other researchers (Muhammed et al., 2016; Naema et al., 2014; Ladhe et al., 2011; Pragnesh et al., 2011).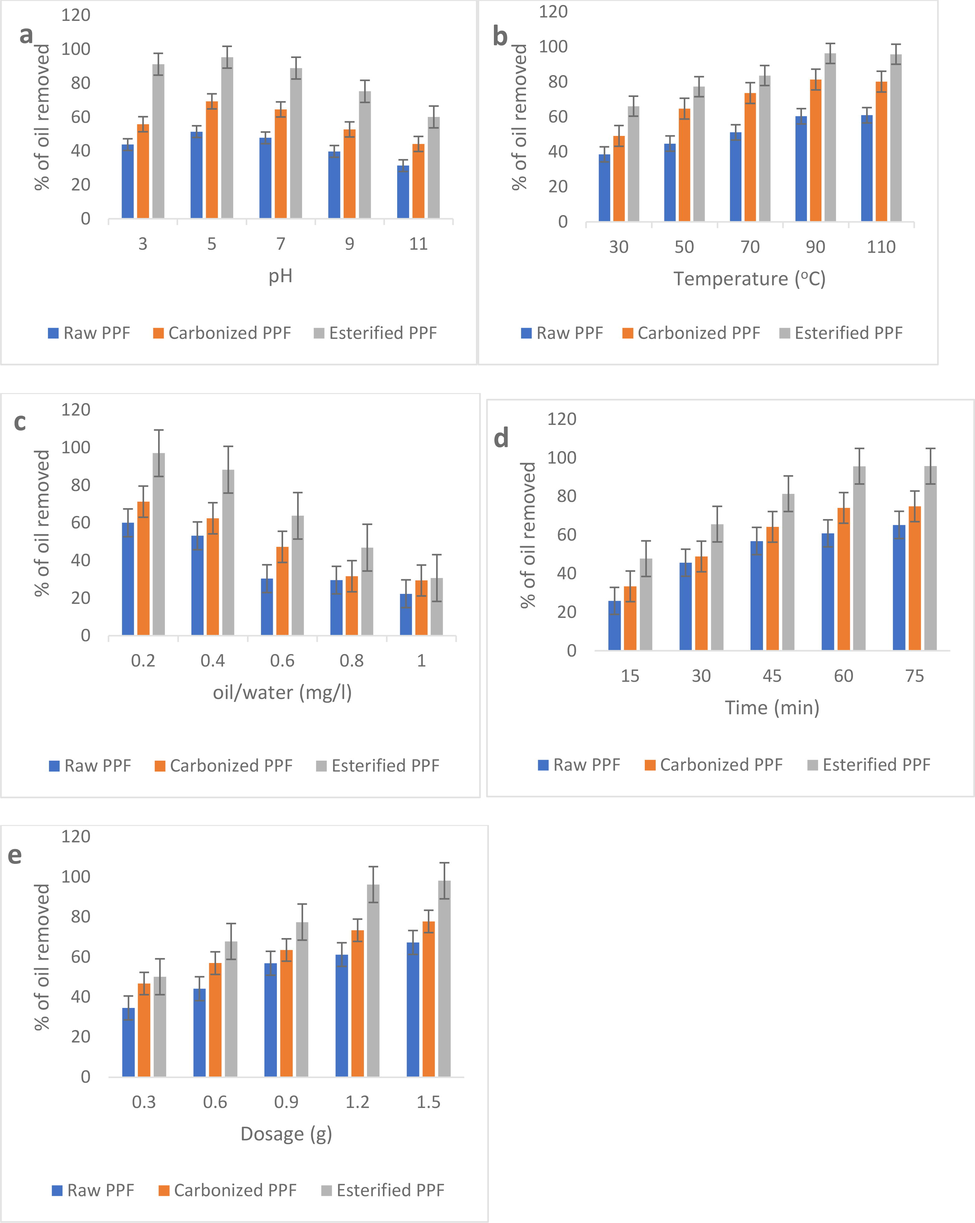

Close

Fig. 4

Effect of pH (a), temperature (b), oil–water ratio (c), time (d), and dosage (e) on crude oil removal by PPF.

Export to PPT

Also, crude oil removal dependency on temperature were evaluated using the developed PPF as depicted in Fig. 4b. It could be seen that crude oil removal by the adsorbents increased with temperature, up until 90 °C. This could be due to improved collision between oil molecules and adsorbents, improved rate of diffusion of oil molecules, or dispersion of oil molecules across the boundary layer and inner pores of the PPF particles. Temperature also changes the interaction of oil molecules, as well as the dissolvability of the oil. Improved rate of pollutants uptake with temperature has also been observed by other researchers (Behnood et al., 2016; Rashmi and Bhattacharya, 2003; Verma and Mishra, 2010; Arivoli et al., 2019).

Moreover, impact of oil–water ratio on oil removal from water surface by PPF was also examined. From Fig. 4c, it is obvious that increasing the ratio, at constant adsorbent dosage, reduces the percentage of oil removed, as the adsorption sites become easily saturated at higher ratio.

Taking from Fig. 4d and Fig. 4e, it can be deduced that increase in contact time and adsorbent dosage increases the amount of oil layers removed which aligns with the general principle of adsorption as stated by Okpe et al. (Chinonye et al., 2018).

Under all the conditions studied, esterified PPF had the best performance, highlighting the efficiency of combined thermal and acid treatments, over thermal treatment alone.

3.3 Thermodynamic modeling of the adsorption process

The values of the activation energy, obtained from the slope of the plot of InK verses 1/T (K⁻¹) [see Eqn (9) and Fig. 5a] for the first order model is presented in Table 4 The energy of activation for the diffusion of molecules onto PPF is 15.82 kJ/mol. This value was lower than those given in literature by Chime et al. (Thompson et al., 2020), (53.99 kJ/mol) for the first order for the diffusion of lead ion onto cassava peels adsorbent, although the energy of activation value of PPF sample was within the range reported by Naena et al. (Naema et al., 2014) for lead adsorption using Petiol and Fiber palm tree.Fig. 6.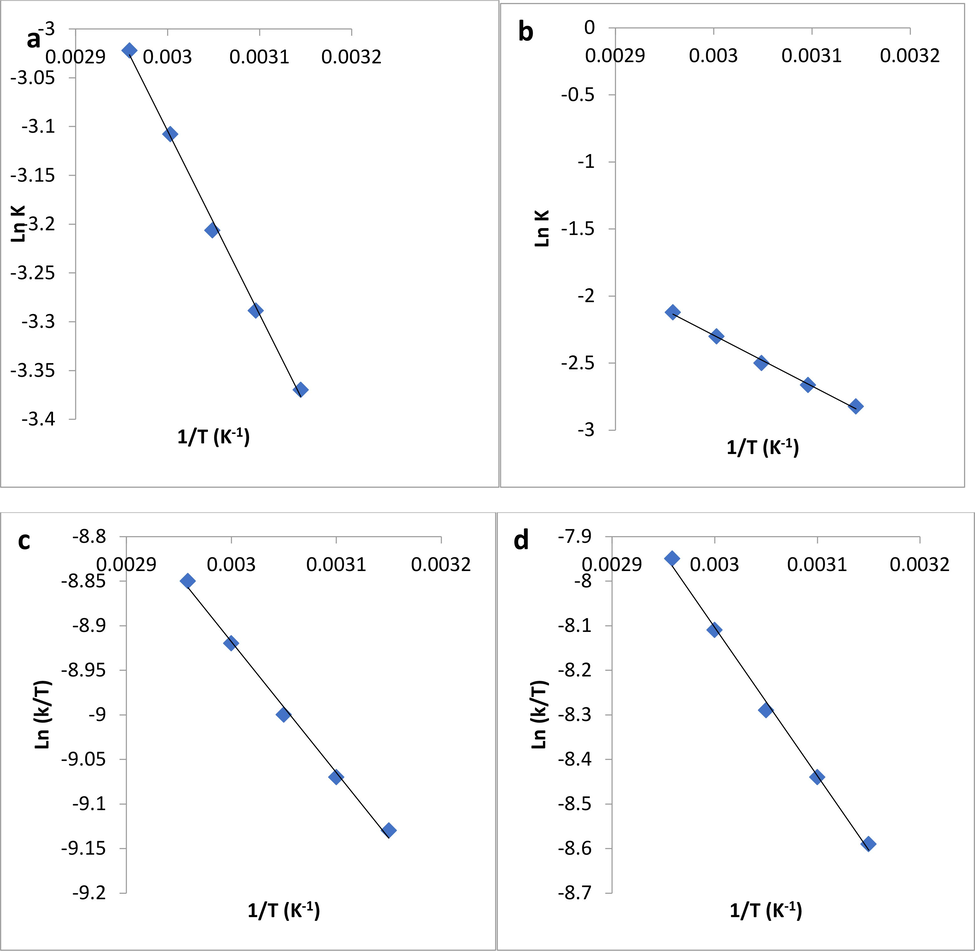

Close

Fig. 5

(a) Plot of In K verses 1/T (K⁻¹) for irreversible pseudo first order model for crude oil sorption by PPF, obtained by using Arrhenius equation. (b) Plot of In K verses 1/T (K⁻¹) for irreversible pseudo second order model for crude oil sorption by PPF, obtained by using Arrhenius equation (c) Plot of Ln (k/T) verses 1/T (K⁻¹) for irreversible pseudo first order model for crude oil sorption by PPF obtained by using Eyring-Polanyi equation (d) Plot of In (k/T) verses 1/T (K⁻¹) for irreversible pseudosecond order model for crude oil sorption onto PPF obtained by using Eyring-Polanyi equation.

Export to PPT

Close

Fig. 6

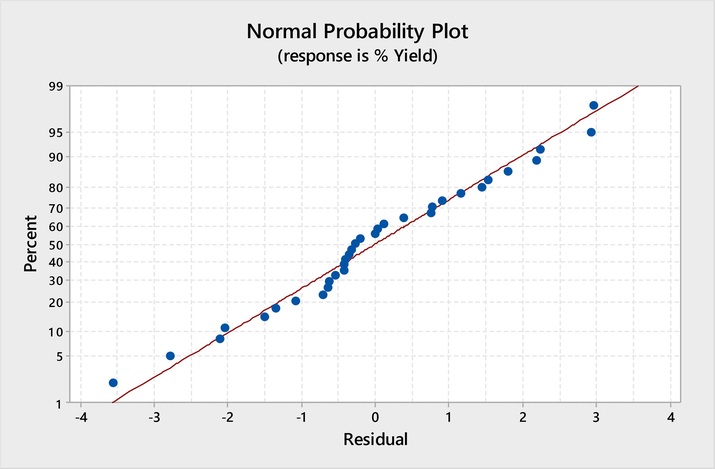
Normal probability plot of residuals for the removal of crude oil by PPF.

Export to PPT

In the same way, the activation energy values obtained from the slope of the plot of InK against 1/T (K⁻¹) [Eqn (9) and Fig. 5b], for the second order model is also shown in Table 4. The activation energy for PPF sample diffusion is 33.21 kJ/mol. This value was within the range of 38.33 kJ/mol, reported by Okpe et al. (Chinonye et al., 2018) for the second order adsorption of orange G onto kola nut shell. It could be noticed that the Ea value for second order kinetic was higher than that of the first order model. This could be attributed to the higher rate constant value of the pseudo-second order model, when compared to the pseudo-first order model. Behnood et al. (Behnood et al., 2016), also reported similar observation in their work.

Also, Fig. 5c and 5d, show the Eyring plot (Equation (10)) for the sorption and diffusion of oil molecules for irreversible pseudo first and second order models. The values of the thermodynamic parameters (ΔH, ΔS and ΔG) gotten from the plots of 1/T vs In(k/T) (Equation (10) and Fig. 5c) for the pseudo-first order of the studied models is presented in Table 4. Likewise, the thermodynamic parameters (ΔH, ΔS and ΔG) values, for the pseudo-second order model (Equation (10) and Fig. 5d) are also presented in Table 4.

As could be seen in Table 4, the values of ΔH for the irreversible pseudo first order for adsorption of oil onto esterified PPF is 24.17 kJ mol⁻¹. This positive value shows that the energy input from external source is needed to raise the energy level for easy diffusion of oil molecules to the transition state. Hence, indicating that the process is endothermic (Asadu et al., 2021; Asadu et al., 2019). This enthalpy value is similar in range to the 16.35 kJ mol⁻¹ obtained for the sorption of oil by spent camellia sinnensis biomass by Falazand and fafique (Fazal and Rafique, 2013). For the entropy change, the value for the irreversible pseudo first order is $-$ 0.614 (Table 4).

The negative value suggests the level of associative mechanism that exist, whereby diffusion.

species have combined together to form a more ordered transition state (Asadu et al., 2019; Muhammed et al., 2013). The value is.

within the range given by Muhammed et al, (Muhammed.RabiulAwual et al., 2013) ( $-$ 0.121 kJ mol⁻¹ K⁻¹) and Nick et al. (Onwu et al., 2019);

( $-$ 0.18 kJ mol⁻¹ K⁻¹) for the sorption of waste cooking and soybean oils, respectively.

The change in Gibb’s free energy ΔG value for the irreversible pseudo first order sorption of oil by PPF was found to be in the range of 13.46 – 20.55 kJ mol⁻¹ (Table 4). The positive value of ΔG shows the non-spontaneous nature of the process (Nwabanne et al., 2018; Asadu et al., 2021). This obtained value is lower than 88.23 kJ mol⁻¹ and 83.30 – 87.69 kJ mol⁻¹, those reported by Ladhe et al. (Ladhe et al., 2011) and Chime et al., (Thompson et al., 2020), for the sorption of waste cooking and lead ion, respectively.

Equally, for the irreversible pseudo second order for adsorption of crude oil onto PPF (Table 4), the ΔH value was 40.31 kJ mol⁻¹. Just like in the pseudo first order model, the positive ΔH shows that there is energy input (heat) from external source necessary to raise the energy level for transformation of reactants to their transition state. Hence, indicating that the process is endothermic (Chinonye et al., 2018). This obtained value of ΔH in the irreversible pseudo second order for adsorption of crude oil onto PPF, was within the range of 28.33 kJ mol⁻¹ obtained by Abert et al. (Albert et al., 2016) for the soybean waste adsorbent.

The change in entropy ΔS for the irreversible pseudo second order for crude oil adsorption onto PPF is $-$ 0.106 kJ mol⁻¹ K⁻¹ (Table 4). As earlier stated, this negative value of ΔS, indicates an existence of associative mechanism, whereby reactant combined together to form a more ordered transition state (Asadu et al., 2018). Like in the first order, the obtained value is also within the $-$ 0.121 kJ mol⁻¹ K⁻¹ range reported by Muhammed et al.. (Muhammed et al., 2016) for palm oil adsorption from water.

Finally, the change in free energy ΔG value for the irreversible pseudo second order for crude oil sorption by PPF was found to be in the range of 42.30 – 55.24 kJ mol⁻¹ (Table 4). The positive values of ΔG indicate the non-spontaneous nature of the reaction (Egbuna et al., 2019). The value was similar in range to 58.23 kJ mol⁻¹ reported by Onwu et al. (Onwu et al., 2019) for crude oil sorption onto groundnut shell.

3.4 Equilibrium or thermodynamic modelling of oil sorption onto PPF

As apparent from the report by (Asadu et al., 2018), adsorption isotherm is the essential prerequisite for planning any sorption framework. It can be said to be a connection between how much a substance eliminated or removed from fluid stage by unit mass of acid treated biomass as sorbent and its amount at constant temperature (Albert et al., 2016; Sheela Tand Arthoba, 2012; Muhammed et al., 2019a). Suitability of the models (see Table 1) was explored and studied. The isotherm boundaries and correlation coefficient (R²) assessed from the plots of the straight fittings are introduced (see Table 5). R² was utilized to anticipate the model with the best fit. The determined dimensionless quantity for the model (see equation 4) called separation factor (R_L) at the four designated temperatures were<1 (0.2014, 0.0235, 0.1902 and 0.03096) showing ideal sorption. This insight can be attributed to the uniform or homogeneity of circulation or dynamic distribution of active site on the outer layer of the esterified PPF (Asadu et al., 2021). K_f as a constant is a proportion of the adsorption limit while constant n is a proportion of the intensity of the sorption process (Sheela Tand Arthoba, 2012). For beneficial adsorption, the value of n lies somewhere in the range of one to ten (Nwabanne et al., 2018; Muhammed et al., 2013). As it stands in Table 5, it very well may be seen that the value of n at four unique temperature falls somewhere in the range of one to ten (2.645, 1.0956, 3.9056 and 1.8042) uncovering a beneficial sorption for oil layer onto esterified PPF. K_f for equation 6 increases with rise in temperature (see Table 5) showing that adsorption limit of oil onto esterified PPF are leaned toward high temperature. Equation 5 explains that assuming the energy required for activation (E) is under 8 kJ/mol, the interaction is physisorption, and however assuming the energy of activation is between 8kj/mol and 16 kJ/mol, the cycle is chemisorption in nature (Sud et al., 2008; Muhammed et al., 2013; Kudaybergenov et al., 2015). Additionally, the average free energy of sorption per mole of the adsorbate (Bd) portrays that adsorption is being constrained by particle diffusion mechanism and E > 16 kJ/mol implies an adsorption is represented by molecule dispersion system (Onu et al., 2021; Nwabanne et al., 2017). From Table 5, it is apparent that the energy of activation was below 8kj/mol at each temperature under study showing that the admission of oil from water surface by the esterified PPF is physisorption. Besides, the values for Bd at the selected temperatures studied were under 16 kJ/mol recommending that the sorption of crude oil onto PPF might not have been controlled by particle diffusion mechanism. In the meantime, the R² at each temperature studied as displayed (see Table 5) proposed that the sorption of oil onto esterified PPF might have inclined toward Langmuir isotherm model since the R² are nearer to unity than other models at each temperature studied.

3.5 Modeling and variables optimization using RSM, ANN and ANFIS

3.5.2

3.5.2 ANN modeling

The analysis of the neural network indicated an optimum of 10 neurons in the hidden layer. This was achieved by varying the neurons in the hidden layer with R² and RMSE as the performance index. It was inferred that 10 neurons in the hidden layer will provide the maximum R² and minimum RMSE. Therefore, the optimum ANN architecture for the oil removal process has a topology of 5–10-1. This topology gave the best prediction accuracy with minimum deviations. The multi-layer perceptron (MLP) model was used because of its ability in approximating nonlinear processes (Chijioke Elijah Onu, 2022a). The ANN plots of training, testing, and validation in Fig. 7 showed R² values of 0.9855, 0.9991 and 0.9995 with RMSE of 2.05 × 10^-3, 5.87 × 10^-4, and 2.03 × 10^-4 respectively. The high R² values and low RMSE values suggested significant model performance. The testing data set adequately guided against model over-fitting while significant training data set implied that there is a correlated relationship between the input variables and the output response. This was confirmed by the R² value of 0.9889 for the overall data.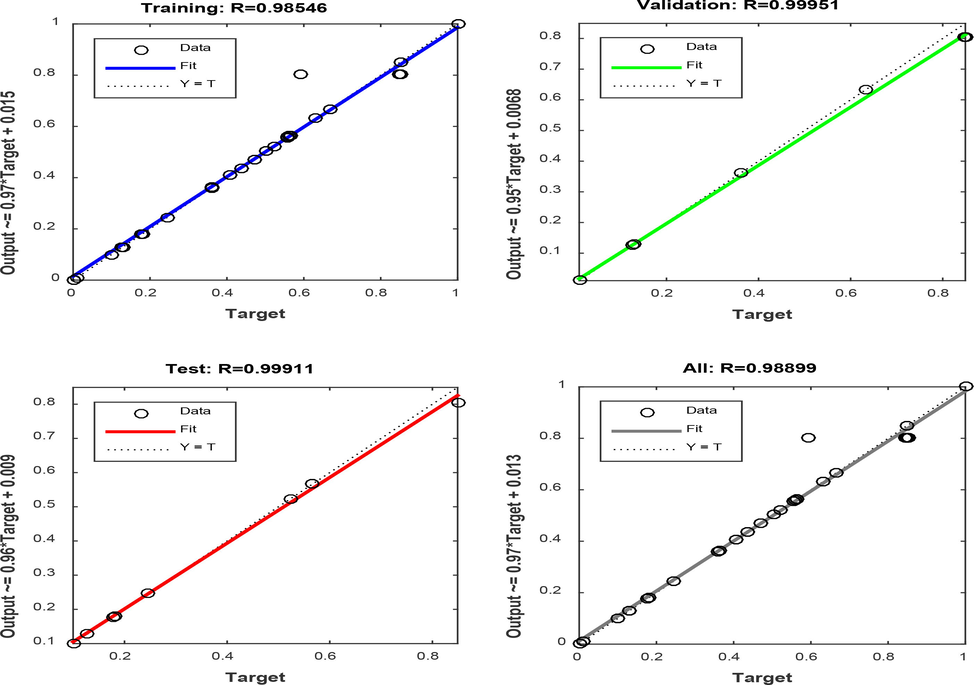

Close

Fig. 7

ANN plots of percentage oil removal using esterified PPF.

Export to PPT

Furthermore, the neural performance plot (Fig. 8) was used to graphically assert the nature of the neural performance. The figure showed that the training, testing and validation curves stabilized at the 8th epoch iteration with RMSE of 5.87 × 10^-4. The curves attained consistency at the 6th epoch iteration. The nature of the curves suggested adequate neural modeling with no over fitting issues.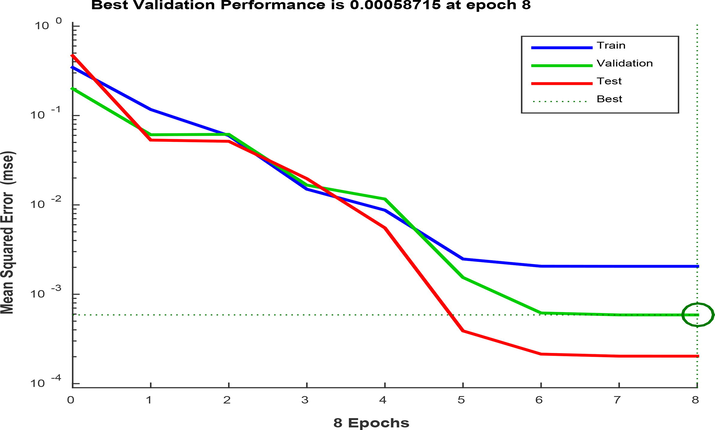

Close

Fig. 8

ANN validation performance plot of the oil removal process.

Export to PPT

3.5.3

3.5.3 ANFIS modeling

The trapezoidal-shaped membership function (trapmf) was used to generate the fuzzy inference system (FIS) in the input membership function. Root mean square errors of 0.0067, 0.0032, and 0.0065 were generated for the training, testing, and validation/checking, respectively. Forty-five nonlinear parameters and 243 training pairs and linear parameters were used for effective ANFIS modeling. Minimum root mean square error of 0.001763 was obtained for the overall data set at 50 epoch iterations with error tolerance of 0.00. Constant membership function was chosen for the output MF while the optimization method used was hybrid. This resulted in ANFIS model with a high R² of 0.9982. Fig. 9 showed that the ANFIS predicted oil removal efficiency perfectly tracked the experimental oil removal efficiency as virtually all the ANFIS data points aligned with the experimental data points.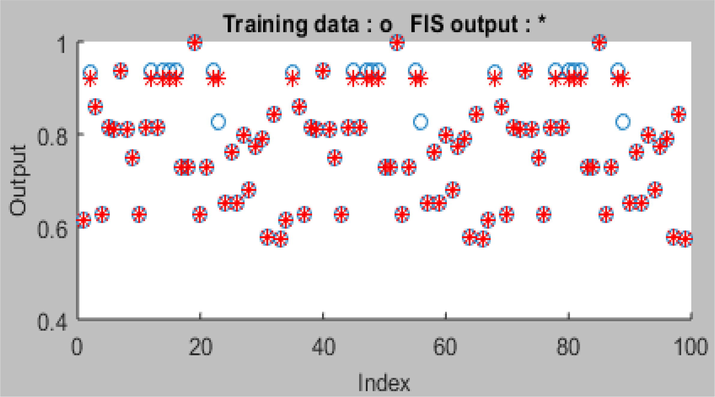

Close

Fig. 9

ANFIS training plot of the percentage oil removal.

Export to PPT

3.6 Kinetics studies

Pseudo first order, pseudo second order, Elovich’s, Lagregan second order models were used to study the time dependency of the crude oil adsorption process. The results of the kinetic analysis, with the correlation coefficients and models’ constant were presented in Table 11. Elovich model and pseudo first order model showed good correlation in the kinetic study, however pseudo first order kinetic model best described the kinetics of the crude oil adsorption with R² of 0.9990 (Table 11). This implied that chemisorption was the rate-limiting step with presence of valence forces between the crude oil molecules and the adsorbent (Ogbodo et al., 2021; Ugwele et al., 2020). Besides, Elovich’s model is usually applied to chemisorption systems with heterogeneous adsorbing surface. The applicability of the pseudo second order inferred a reduction in boundary layer thickness of the PPF at high temperature.

3.7 Comparison between the present studies and prior researches in the similar field

The adsorbent developed from PPF in this work was compared with other adsorbents existing in literature based on performance. The performance was further compared with commercial zeolite adsorbent in the market (see Table 12). The performance index used was the adsorption capacities at a specified period of time. It can be seen that the adsorption capacity of the present study was mostly comparable to the zeolite adsorbent reported by Naena et al., 2014. The most interesting thing about this present study is that we got a relatively high adsorption capacity of 50.34 mg/g at a very short time of 50 mins. The adsorption capacity is far much higher than the ones reported for other agro-wastes (see Table 12). Considering the aforementioned results, we arrived at a conclusion that the PPF used is an efficient low-cost adsorbent for the removal of crude oil from aqueous solution.