Translate this page into:
On physical analysis of synthesis strategies and entropy measures of dendrimers
⁎Corresponding author. imrandhab@gmail.com (Muhammad Imran),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Dendrimers achieved great consideration in gene and drug delivery applications because of having highly administrable architecture. Unambiguous structure of dendrimers might reduce the unpredictability related to the molecule’s shape and size, and also boost the accuracy of drug delivery. Dendrimers have exclusive physical and chemical properties due to which they have extensive range of potential applications like chemical sensors, light harvesting material, enhance the solubility, antitumer therapy, medical diagnostics, drug delivery system, catalysts, and many more. With the total -electron energy, the degree-based topological indices have a lot of iterations.
In this paper, our desideration is to compute the topological aspects of degree based entropy for fractal and cayley tree type dendrimers. More preciously, we explore two tree type dendrimers denoted by ant . Moreover, entropies are estimated of these two structures by generating a correlation between degree based topological indices and their entropies.
Keywords
Entropy
Zagreb type indices
Forgotten index
Balaban index
Dendrimers
Fractal and Cayley type dendrimers
1 Introduction
Dendrimers are a modern type of polymeric substances. They are fabricated three dimensional, maono-disperse structure having tree like branches (Sampathkumar and Yarema, 2007). Dendrimers are also called arborols and cascade. There are different kinds of dendrimers like radially layered poly dendrimers, chiral, liquid crytalline, tacto, hybride, peptide, and frechet type dendrimers (Singh et al., 2017). In 1985, Tomalia familiarized the term dendrimer for the first time. It is acquired from “dendrimer”, that paraphrase to tree, and “meros(part)” (Gardikis et al., 2006).
Dendrimers rose up out of the ocean of polymer sciences in the mid as wonderful period. Stretched atoms in the shape of a star with an extraordinary formation and minimal polydispersity (Beer et al., 1999; Tomalia et al., 1986). In any case, the possibility of planning expanded particles was first imagined by Flory as ahead of schedule as (Flory, 1941). As on account of different revelations that were relatively revolutionary, the engineered and diagnostic techniques at that time were not adequately progressed to tentatively backing such a thought (Lin et al., 2010). In 1978, the principal paper that depicts the blend of purported course atoms, i.e., minimal sub-atomic mass dendritic polyamines, was distributed (Vogtle et al., 1978). Denkewalter, a long time later, used a different approach to protect the synthesis of poly(lysine) dendrimers until the ninth century (Denkewalter et al., 1982). Tomalia (Gardikis et al., 2006) published the combination of poly(amidoamine) (PAMAM) dendrimers up to the ninth century and characterised this type of polymers ”dendrimers”, that straightforwardly interpreted as ”part of a tree”. In the same year, Newkome initiated dispensing a poly(ether) dendrimer blend that was up to the third generation (Kono et al., 2008). Dendrimers are synthesised by two methods, divergent growth method and convergent growth method (Munir et al., 2016).
The synthesis of a dendrimer as indicated by the divergent technique continues step by step beginning from an activated core,
, to whose next dendrimer ages are developed by means of the consecutive connection of components termed as monomers (pattern 1). The monomers utilized are some type of
, in which A and
mean 2 sorts of useful gatherings. The A-useful gathering of the
monomer is a responsive gathering, whereas the
-useful gathering is disabled/secured, allowing for restrained development of the dendrimer. The monomers are joined to a substrate particle (a developing dendrimer) through a synthetic bond arrangement between the monomer’s A-utilitarian gathering and one of the substrate’s activated B-utilitarian gatherings.The linkage of the B-functionalities with a subsequent particle or the evacuation of assuring groupings can guide their actuation. Trifunctional monomers with an
structure are the most commonly used monomers. Following the binding of these monomers to the centre, a unique dendrimer is formed. The two processes that follow, which are dependent on the activation of the B-functionalities on the original dendrimer and their coupling with another arrangement of monomers, result in a second age dendrimer (Sowinska and Urbanczyk-Lipkowska, 2014). The desired greater age dendrimer is attained due to the redundancy of these two steps, see Fig. 1.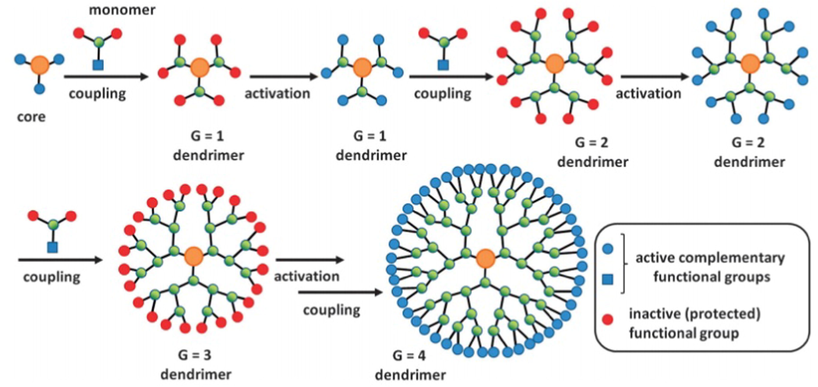
The divergent growth method.
Hawker and Frechet first described the convergent approach in 1989–1990, and it is an optional course for developing dendrimers. particular dendrimer wedges, known as dendrons, are orchestrated first and then connected to an activated core (Scheme 2). The regular
monomer, that has responsive B-functionalities and disabled/ensured A-usefulness, is used to direct the combination of dendrons. The monomer is subjected to a response with a molecule in the first phase, which will eventually establish the dendrimer’s outskirts (outside). The presentation of secure bunches on monomer B-functionalities is frequently the most significant advancement. As a result, it is possible to make an original dendron (G1). The actuation of a dendron point of convergence and its coupling with the
monomers are the next two phases, resulting in a (G2) dendron. Every reiteration of these two steps results in an increase in the dendron age (Sowinska and Urbanczyk-Lipkowska, 2014), see Fig. 2.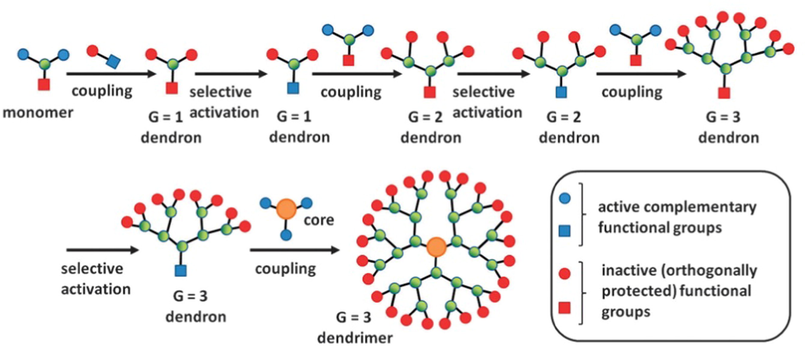
The convergent growth method.
Assume is a graph with for the vertex set and for the edge set. The order and size of the graph in Z are represented by p and q, correspondingly. Any chemical structure with vertices representing atoms and edges representing bonds forms a chemical graph. The number of edges associated with a vertex is called its degree, and it is symbolised by . A topological descriptor is an algorithmic measure accomplished via a projection. diverse sorts of topological indices exist. We shall explore degree-based topological descriptors in this work, which are defined by the degree of a graph’s terminal vertices. (Siddiqui et al., 2016; Siddiqui et al., 2016 and Gao and Farahani, 2015; Gao et al., 2017; Imran et al., 2018) contain more information on topological indices formulas and their employment respectively.
Shannon (1948) was the first to introduce the concept of entropy. It is a measure of a system’s information content’s unpredictability. After this, it’s been employed in chemical networks and graphs. Rashevsky entrenched the entropy of a graph (Rashevsky, 1955). Graph entropy is now employed in a variety of domains, see (Dehmer and Graber, 2013; Mehler et al., 2010; Ulanowicz, 2004).
Intrinsic and extrinsic graph entropy measurements are used to correlate probability distributions with graph invariants (vertices, edges, and so on) (Mowshowitz and Dehmer, 2012). Dehmer (2008, 2012) researched the features of graph entropies, which are established on information functionals. See (Bonchev, 2003; Dehmer and Mowshowitz, 2011; Manzoor et al., 2020; Morowitz, 1953; Quastler, 1954; Rashevsky, 1955; Shannon, 2001; Sol and Valverde, 2004; Trucco, 1956; Tan and Wu, 2004) for more information.
The information entropy (Chen et al., 2014) based on Shannon’s entropy (Shannon, 1948) is described as:
2 Structure of fractal tree dendrimer
A geometrical figure that constitute a smaller curve or pattern that has rigorously the same shape is called Fractal. The way that the stem of a tree break down into shorter and shorter branches and limbs is an approximate fractal pattern. There are many other examples of fractals like Romanesco broccoli, lightning bolt, angelica flowerhead, and Von Koch snowflake, etc.
Dendrimers are macro-molecules with a ramification structure. These are also called fractal polymers. where , stands for the anticipated fractal tree dendrimers in this work, and is the number of iterations. consists of an edge associating two vertices. is made from by taking two steps on each of the ongoing edges in . In the first stage, a three-linked path with the same terminal points is built. In the second stage, each of the two intervening vertices in the path is used to construct l new vertices, join them to the neighboring vertices after that.
The Fig. 3 illustrates the structure for different values of l. In Fig. 4a) and Fig. 4(b),
and
are sketched. Firstly, we calculate above mentioned entropies by using degree-based topological indices for
. Edge partitioning and graph theoretical approaches are employed in this case. There are
pendent vertices in
. The vertices having degree 4 are
and the vertices having degree
are
in numbers. The edge set of
consists of three types of edges based on the degree of end vertices.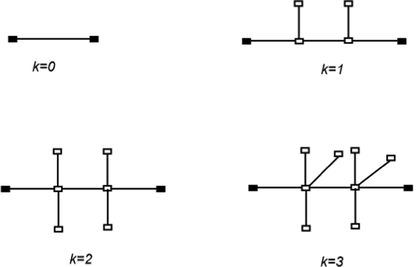
Construction of the fractal trees for
.
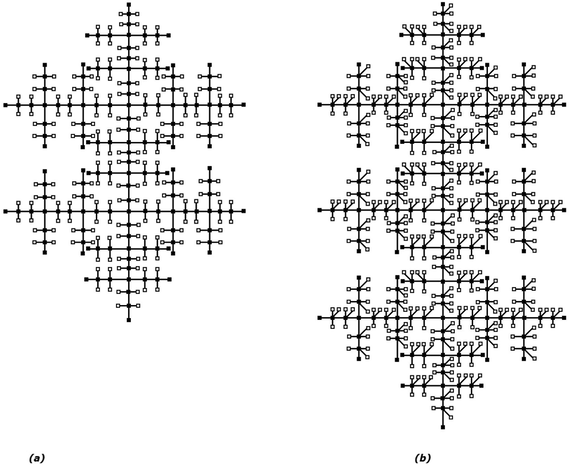
(a) Fractal tree
for
, (b) Fractal tree
for
.
The edge partition of
is illustrated in Table 1.
Number of Repetition
Kind of Edges
2.1 Results for fractal tree dendrimer
The entropies of the structure of the fractal tree dendrimer are listed in this section.
The index is Eq. (1) and Table 1 gives The index is Eq. (1) and Table 1 gives The Hyper Zagreb index is Eq. (1) with Table 1 gives The Forgotten index is Eq. (1), with Table 1 gives The Balaban index is Eq. (1) with Table 1 gives The Redefined first Zagreb index is Eq. (1) with Table 1 gives The Redefined second Zagreb index is Eq. (1) with Table 1 gives The Redefined third Zagreb index is Eq. (1) with Table 1 gives
3 Structure of cayley tree type dendrimer
A cayley tree is one in which each non-leaf graph vertex has a defined number of branches. The star graph is a one-of-a-kind m-cayley tree with
nodes. The cayley tree, also known as Bathelallice, is a type od dendrimers. To construct the cayley tree
where
, we use iterative method.Here m represents the nodes at first iteration.
consists of only a central vertex.
is achieved by creating m nodes and using an edge to connect them to the central vertex.
is obtained from
by generating
nodes and join them to every pendent vertex of
.
Is shown in Fig. 5. The number of pendent vertices is
, while the number of vertices with degree m is
The
edge set has two sorts of edges based on the degree of end vertices. Table 2 shows the edge partition of
.
and
are the total number of vertices and edges in
respectively.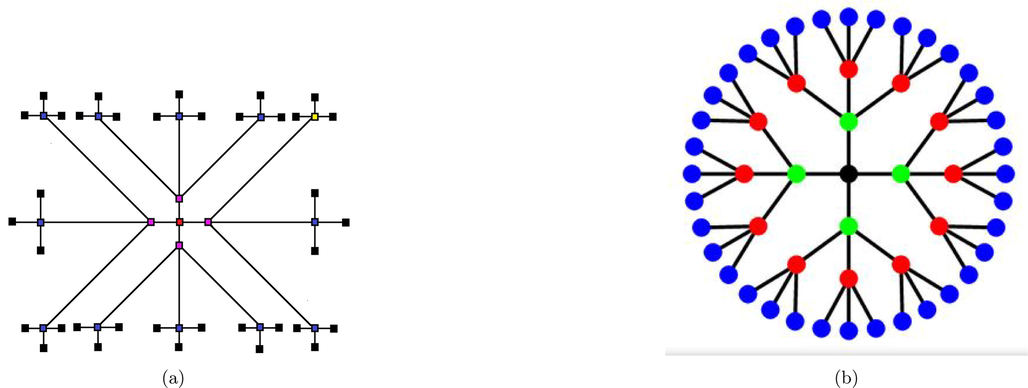
(a) The Molecular graph Cayley tree
, (b) The representation of Cayley tree
.
Number of repetition
Different sorts of edge
3.1 Results for Cayley tree type dendrimer
The entropies of the structure of the Cayley tree dendrimer are listed in this section.
The first Zagreb index is Eq. (1) with Table 2 gives The second Zagreb index is Eq. (1) with Table 2 gives The Hyper Zagreb index is Eq. (1) with Table 2 gives The hyper Zagreb index is Eq. (1) with Table 2gives The Balaban index is The Redefined first Zagreb index is Eq. (1) with Table 2 gives The Redefined second Zagreb index is Eq. (1) with Table 2 gives The Redefined third Zagreb index is Eq. 1 with Table 2 gives
4 Comparisons and Discussion for Fractal tree type dendrimer
Entropy is a structural descriptor that may be used to measure the complexity of chemical structures quickly. In research, degree-based entropy offers a wide range of uses characteristically in software engineering and pharmaceutical. Substantial properties of biological frameworks(strain energy, melting point etc) are confederated with the biological functions of the frameworks via topological indices. Degree-based indices can be used to carry out these assessments because they have a clear decision-making process and are quick. Because molecular structures are so complicated, several molecular descriptors and their entropy metrics are utilised to predict the most structural information. As a result, some degree-based entropies for diverse estimations of
for
have been calculated arithmetically in this articulation. For the assembly of
, we create Tables 3–5 for degree-based entropy to arithmetical correlation. For this, we utilized Maple software and MATLAB software. Diagrammatic illustrations are in Fig. 6, Fig. 7, Fig. 8 and Fig. 9 for distinct considerations of
. The entropy function of a fractal tree type dendrimer grew as the generation size increased. As a system’s entropy rises, so does the uncertainty about its reaction. When the chemical structure
expands, the first Zagreb entropy develops more quickly than other entropy measurements of
, however the redefined third Zagreb entropy grows slowly.
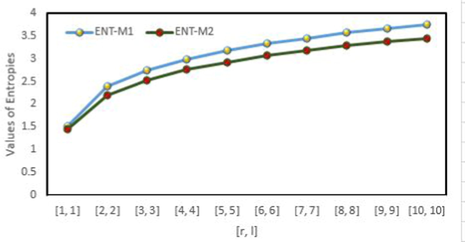
The graphical comparison of the first Zagreb entropy and the second Zagreb entropy for
.
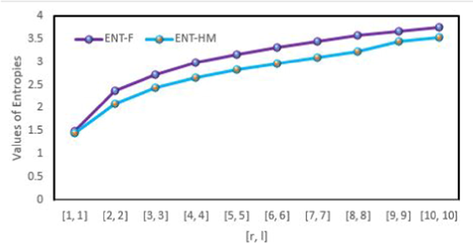
Graphical comparison of the forgotten and the hyper Zagreb entropies for
.
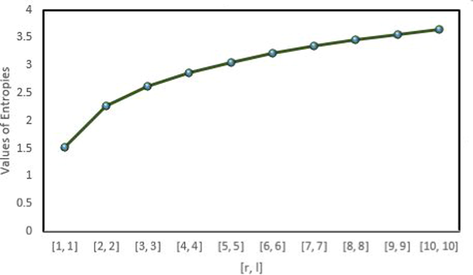
Graphical representation of the Balaban entropy for
.
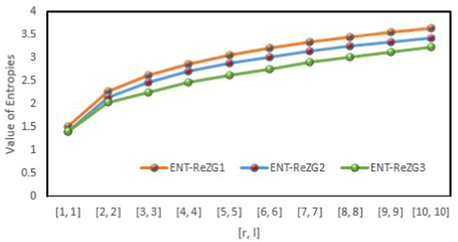
Graphical comparison of redefined Zagreb entropies for
.
5 Comparisons and Discussion for
Computational techniques combined with different scientific fields provide a consistent strategy to better recognize a scientific subject. It is rare to be able to comprehend a problem based solely on one science discipline. As a result, incorporating some computational methodologies into the investigation may produce a clear image that aids in furthering our understanding of the underlying phenomenon. Creating a mathematical model to depict the dynamics of items in a research is a very practical way to approach and examine the problem. In this segment, for distinct considerations, we have quantitatively catalogued all degree-based entropies. This could be a quick technique to comprehend the molecular structure
by looking at its chemical graph structure attributes. Numerically and visually results are shown in Tables 6–8 and Fig. 10–13. We can observe from these calculations that the entropy values grew as the number of unit cells increased. Furthermore, When the chemical structure
expands, the redefined third Zagreb entropy develops more quickly than other entropy measurements of
, however the redefined second Zagreb entropy grows slowly.
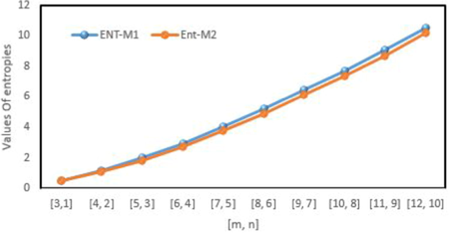
The graphical comparison of first and second Zagreb entropies for
.
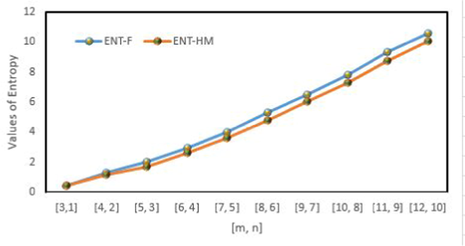
Graphical comparison of the forgotten and the hyper Zagreb entropies for
.
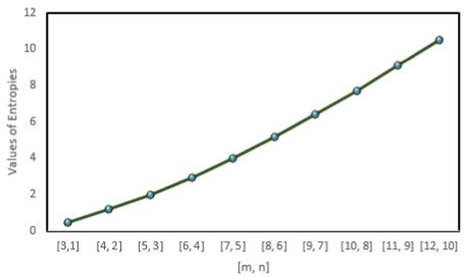
Graphical representation of the Balaban entropy for
.
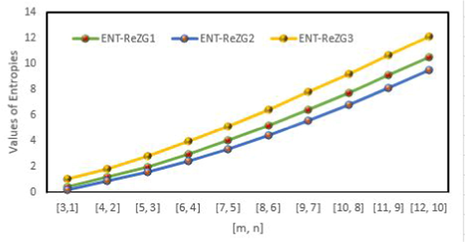
Graphical comparison of redefined Zagreb entropies for
.
6 Conclusion
The physico-chemical features of dendrimer molecules and aggregates are based on chemical structures with regular branching. Theoretically and experimentally, regular dendrimers have been examined. The information entropy technique is used to examine regular dendrimer aggregates in this paper. As demonstrated above, the information entropy of a regular fractal and Cayley tree type dendrimer grows with the number of generations. As a result, the system’s information capacity must be temporarily increased to transfer it from one informational stable condition to another. Information storage with nano patterned materials (Rosen et al., 2009) is one of the potential applications of dendrimers and a material’s information storage is determined by its information entropy (Chawla et al., 2020). The dendrimer’s subsequent frameworks have a greater number of equivalent building blocks. It produces the dendrimer structure more homogeneous with each subsequent generation, and homogeneity is achieved faster with larger generation values, as entropy values indicate. Fascinatingly, in the class of dendrimers, increased information entropy corresponds to structures with minimal branching. The information entropy, of fractal and tree type dendrimer structures, represents the balance between order and disorder, and it may be used to measure this balance numerically in structural design. This could be advantageous if dendrimers are used as energy storage materials (Bar-Haim et al., 1997). In addition, the correlation between the entropy values and other branching parameters must be examined (Bonchev and Trinajstic, 1978). Configuration entropy of glass-forming liquids (Champion and Thurieau, 2020) or thermodynamic entropy of enzyme-substrate complexions (Graf et al., 2013; Putz et al., 2006) are examples of thermodynamic entropy used in molecular dynamics investigations on complex chemical systems. Analogously, a new step in this direction could be to use information entropy as a critical structural criterion.
7 Funding
This research is supported by the UAEU-AUA (Asian Universities Alliance) grants of United Arab Emirates University (UAEU) via Grant No. G00003461.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Dendrimers as controlled artificial energy antennae. J. Am. Chem. Soc.. 1997;119(26):6197-6198.
- [Google Scholar]
- Supramolecular chemistry. Oxford University Press; 1999.
- On topological characterization of molecular branching. Int. J. Quantum Chem.. 1978;14(S12):293-303.
- [Google Scholar]
- Complexity in Chemistry, Introduction and Fundamentals. Boca Raton, FL, USA: Taylor and Francis; 2003.
- The sample size effect in metallic glass deformation. Scientific reports. 2020;10(1):1-7.
- [Google Scholar]
- Optimization and computational studies evaluating molecular dynamics of EDA cored polymeric dendrimer. Scientific Reports. 2020;10(1):1-10.
- [Google Scholar]
- Degree-based indices computation for special chemical molecular structures using edge dividing method. Applied Mathematics and Nonlinear Sciences. 2015;1(1):94-117.
- [Google Scholar]
- Information processing in complex networks: Graph entropy and information functionals. Appl. Math. Comput.. 2008;201:82-94.
- [Google Scholar]
- Uniquely discriminating molecular structures using novel eigenvalue-based descriptors. MATCH Commun. Math. Comput. Chem.. 2012;67:147-172.
- [Google Scholar]
- The discrimination power of molecular identification numbers revisited. MATCH Commun. Math. Comput. Chem.. 2013;69:785-794.
- [Google Scholar]
- Denkewalter, R.G., Kolc, J., Lukasavage, W.J. (1982). U.S. Patent No. 4,360,646. Washington, DC: U.S. Patent and Trademark Office.
- Molecular size distribution in three dimensional polymers. I. Gelation. J. Am. Chem. Soc.. 1941;63(11):3083-3090.
- [Google Scholar]
- Topological Characterization of Carbon Graphite and Crystal Cubic Carbon Structures. Molecules. 2017;22:1496-1507.
- [Google Scholar]
- A DSC and Raman spectroscopy study on the effect of PAMAM dendrimer on DPPC model lipid membranes. International journal of pharmaceutics. 2006;318(1–2):118-123.
- [Google Scholar]
- Molecular dynamics simulations give insight into D-glucose dioxidation at C2 and C3 by Agaricus meleagris pyranose dehydrogenase. Journal of computer-aided molecular design. 2013;27(4):295-304.
- [Google Scholar]
- On Topological Properties of Symmetric Chemical Structures. Symmetry. 2018;10(173):1-21.
- [Google Scholar]
- Preparation and cytotoxic activity of poly (ethylene glycol)-modified poly (amidoamine) dendrimers bearing adriamycin. Biomaterials. 2008;29(11):1664-1675.
- [Google Scholar]
- On entropy measures of molecular graphs using topological indices. Arabian Journal of Chemistry. 2020;13(8):6285-6298.
- [Google Scholar]
- A network model of interpersonal alignment in dialog. Entropy. 2010;12(6):1440-1483.
- [Google Scholar]
- Some order-disorder considerations in living systems. Bulletin of Mathematical Biophysics. 1953;17:81-86.
- [Google Scholar]
- Dendrimers and their applications: a review article. Pakistan Journal of Pharmaceutical Research. 2016;2(1):55-66.
- [Google Scholar]
- Dendrimers in drug-delivery applications. Des. Monomers Polym.. 2010;13(4):301-324.
- [Google Scholar]
- Full analytic progress curves of enzymic reactions in vitro. Int. J. Mol. Sci.. 2006;7(11):469-484.
- [Google Scholar]
- Dendron-mediated self-assembly, disassembly, and self-organization of complex systems. Chemical reviews. 2009;109(11):6275-6540.
- [Google Scholar]
- Sampathkumar, S.G., & Yarema, K.J. (2007). Dendrimers in cancer treatment and diagnosis. Nanotechnologies for the Life Sciences: Online.
- A mathematical theory of communication. ACM SIGMOBILE mobile computing and communications review. 2001;5(1):3-55.
- [Google Scholar]
- On zagreb indices, zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput.. 2016;280:132-139.
- [Google Scholar]
- Computing topological indicesof certain networks. J. Optoelectronics and Advanced Materials. 2016;18(9–10):884-892.
- [Google Scholar]
- Dendrimers: A review on its pharmaceutical applications. World Journal of Pharmacy and Pharmaceutical science. 2017;6(3):1281-1301.
- [Google Scholar]
- Information theory of complex networks: on evolution and architectural constraints. Complex Netw. Lect. Notes Phys.. 2004;650:189-207.
- [Google Scholar]
- Dendritic macromolecules: synthesis of starburst dendrimers. Macromolecules. 1986;19(9):2466-2468.
- [Google Scholar]
- A note on the information content of graphs. Bull. Math. Biol.. 1956;18(2):129-135.
- [Google Scholar]
- Network structure entropy and its application to scale-free networks. Syst. Eng.-Theory Pract.. 2004;6:1-3.
- [Google Scholar]
- Quantitative methods for ecological network analysis. Comput. Biol. Chem.. 2004;28:321-339.
- [Google Scholar]
- Cascade and nonskid-chain-like syntheses of molecular cavity topologies. Synthesis. 1978;2:155-158.
- [Google Scholar]







