Significance of entropy generation and nanoparticle aggregation on stagnation point flow of nanofluid over stretching sheet with inclined Lorentz force

Basim M. Makhdoum; Zafar Mahmood; Bandar M. Fadhl; Musaad S. Aldhabani; Umar Khan; Sayed M Eldin

doi:10.1016/j.arabjc.2023.104787

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

06 2023

:16;

104787

doi:

10.1016/j.arabjc.2023.104787

Significance of entropy generation and nanoparticle aggregation on stagnation point flow of nanofluid over stretching sheet with inclined Lorentz force

Basim M. Makhdoum^{^a}, Zafar Mahmood^{^b}, Bandar M. Fadhl^{^a}, Musaad S. Aldhabani^{^c}, Umar Khan^{^b,⁎}, Sayed M Eldin^{^d}

a Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, P.O. Box 5555, Makkah 21955, Saudi Arabia

b Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan

c Department of Mathematics, Faculty of Science, University of Tabuk, P.O. Box 741, Tabuk 71491, Saudi Arabia

d Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo 11835, Egypt

⁎Corresponding author. umar_jadoon4@yahoo.com (Umar Khan)

Received: 2022-12-15, Accepted: 2023-3-4,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

It is well established that adding a certain number of nanoparticles to a nanofluid improves its thermal conductivity. The cause of this remarkable development is as of yet unidentified. Therefore, knowing the kinematics of nanoparticle aggregation is essential for determining the correct thermal impact of nanoscale particles. There are several potential technical and industrial uses for nanomaterials. From the perspective of these many application aspects, this paper examines the ${Al}_{2} O_{3} - H_{2} O$ nanofluid flow caused by a permeable stretching surface with the influence of an inclined Lorentz force and viscous dissipation. Entropy generation on nanofluid stagnation point flow with the influences of heat generation/absorption, nanoparticles aggregation with suction are also discussed in the current context. With and without nanoparticle aggregation, measurements of velocity, temperature, and entropy production are made. By applying the necessary transformations for heat and motion, ordinary differential equations may be derived from partial differential equations in certain circumstances. For the solution of ordinary differential equations, the Bvp4c technique is used. The effects of several dimensionless limitations on velocity, temperature, and entropy production, skin friction, and Nusselt number profiles are investigated, both when nanoparticle aggregation is present and when it is not. It is concluded that the velocity field is boosted for the velocity ratio and inclined Lorentz force parameters, while the temperature and entropy generation rise for the nanoparticle volume fraction, angle of inclination and Eckert number parameters. The rate of heat transmission improves as a result of the addition of $ϕ$ and $ε$ respectively. When the suction parameter of $(ε = 0.5)$ is used for the aggregation model, it is claimed that there is an increase of roughly 13.2478% in the heat transfer rate. Temperature and entropy generation profiles for all pertinent parameters is higher for nanoparticles that have aggregated together as opposed to nanoparticles that have not aggregated together. This research was compared with previously published results to validate the findings, and great agreement was found.

Keywords

Stagnation point flow

Aggregation effect

Heat generation/absorption

Inclined Lorentz force

Entropy generation

Viscous dissipation

Nomenclature

$a, b, c$: Positive constants $(s^{- 1})$
$f$: Dimensionless stream function (-)
$C_{p}$: Specific heat at constant pressure $(J / k g K)$
$N_{s}$: Entropy generation
$k$: Thermal conductivity $(W / m K)$
$M$: Magnetic parameter (-)
${N u}_{x}$: Local Nusselt number (-)
$Ω$: Temperature difference parameter(-)
$T$: Temperature $(K)$
${\tilde{u}}_{e}$: Inviscid flow velocity $(m / s)$
${\tilde{v}}_{e}$: Mass flow velocity $(m / s)$
$x, y$: “Cartesian coordinates along surface and normal to it $(m) "$
$M$: Magnetic parameter (-)
$θ$: Temperature profile dimensionless
$B e$: Bejan number profile
$ϕ_{a}$: Aggregated nanoparticles volume fraction
$[η]$: Einstein coefficients
$r_{p}, r_{a}$: Radii of aggregated nanoparticles $(m)$
$T_{\infty}$: Ambient temperature $(K)$
$ν$: Kinematic viscosity $(m^{2} / s)$
$τ$: Time variable dimensionless

$f$: Base fluid
$s 1$: Solid components for ${Al}_{2} O_{3}$
$\infty$: Ambient conditions

$'$: Differentiation w.r.t $η$
$C_{f}$: Coefficient of Skin friction
$B$: Velocity ratio parameter (non-dimensional)
$t$: Time (s)
$λ$: Heat generation parameter
$\Pr$: Prandtl number (-)
$Ec$: Eckert number parameter
${Re}_{x}$: Local Reynolds number (-)
$\tilde{u}, \tilde{v}$: Velocity components in $x -$ and $y -$ directions $(m / s)$
${\tilde{u}}_{w}$: Stretching/shrinking velocity $(m / s)$
$σ$: Electrical conductivity $(S / m)$
$ε$: Mass suction (non-dimensionless)
$γ$: Angle of inclination (non-dimensional)
$ϕ$: Nanoparticles volume fraction of ${Al}_{2} O_{3} .$
$η$: Similarity variable (-)
$ϕ_{m}$: “Maximum volume fraction of nanoparticles”
$D$: Fractal index
$k_{a}$: Thermal conductivity of aggregations $(W / m K)$
$μ$: Dynamic viscosity $(N s / m^{2})$
$ρ$: Density $(K g / m^{3})$
$ρ C_{p}$: Heat capacity $(J / k g K)$
$nf$: Nanofluid
$w$: At surface condition’s

1 Introduction

Nanofluids are a type of heat transfer fluid in which nanoparticles, also known as NPs, are suspended in the fluid. Base liquids often include a variety of fundamental liquids, including water, organic fluids, motor oil, bio-liquids, and others. Base liquids themselves are typically composed of these and other fundamental liquids. Nanoparticles that are both much smaller and have a significantly greater surface area have the potential to dramatically improve heat-transfer capabilities as well as fluid stability. To increase the nanofluids' thermal conductivity, Choi (Choi and Eastman, 1995) was the pioneer. Nanofluids find applications in many different fields, including industry and engineering. Analysis of fluid flow using nanoparticles has demonstrated several applications, including energy production, microscale electronics, electrochemical reactions, and more: Nanofluids have unique features that make them very effective in several thermal control activities. When it comes to difficulties with heat transport, thermal conductivity is the most important framework. The thermal conductivity of ethylene glycol is like that of water and oils. To increasing the host fluid's thermal conductivity, nanomaterials such as metal oxides, carbides, and others are incorporated into the fluid. Modeling the thermophysical characteristics in such a manner that they are compatible with the experimental results has always proven to be challenging for the researchers. Experiments have also shown that the aggregation of NPs has a huge influence on the environment and on the rheological and thermal traits of the material. NPs tend to cluster together as a result of the surface charge and the van der Waals force. These NPs may also form linear chains and percolating networks, both of which make it easier for heat to travel through the material. Because heat can travel more rapidly via NP aggregation than it can through nanoparticles, it may move more quickly overall. Motlagh and Kalteh (Motlagh and Kalteh, 2020) examined the movement of heat via a nanochannel by taking the morphology and aggregation of NPs into account in their research. In this study, the researchers concluded that the aggregation and morphology of the NPs had an exaggerated effect on the velocity of nanoliquids. The influence of Joule heating and NP aggregation on the flow of nanoliquid was investigated by Swain and Mahanthesh (Swain and Mahanthesh, 2021). It has been demonstrated that the aggregation of NPs causes a noticeable rise in the temperature of the surrounding area. The kinematics of nanoparticle aggregation in a nanomaterial stream via an inclined flat plate was investigated by Sabu et al. (Sabu et al., 2022). As the tilt of the plate rose, there was a significant decrease in the velocity profile, but there was an increase in the temperature profile. Mahanthesh (Mahanthesh, 2021) scrutinized how the aggregation of NPs affected heat transport via the NPs. In this section, they said that the nanoliquid velocity is inflated due to the aggregation of NPs. Mackolil and Mahanthesh (Mackolil and Mahanthesh, 2021) investigated the impact of nanoparticle aggregation as well as temperature-dependent surface tension on Marangoni convection in $Ti O_{2} - E G$ nanoliquid. They concluded that the aggregation of NPs and the magnetic field both had an effect on the velocity of the nanofluid. Estimating the regulation of the flow of aggregated nanoparticles was accomplished by the use of the fractal modeling approach (Wolthers et al., 1996). The following are some of the most significant studies that have been published about nanoparticle aggregation for example (Madhukesh et al (Madhukesh et al., 2022), Mahmood and Khan (Mahmood and Khan, 2022) and Animasaun and Asogwa (Animasaun and Asogwa, 2021). On the other hand, there haven't been much research done on how nanoparticles aggregate in nanofluid flows yet. (See Fig. 1, Fig. 2.).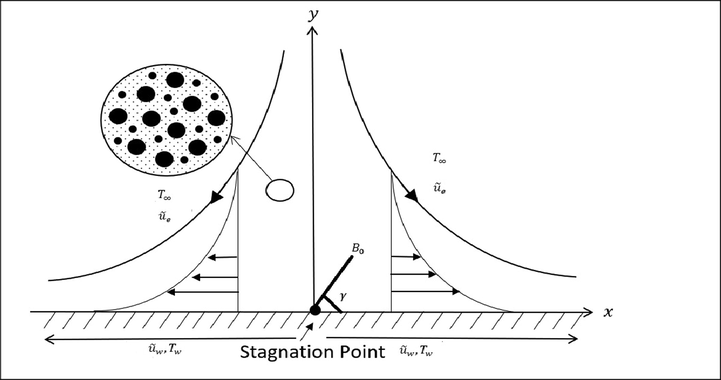

A diagrammatic depiction of the model dilemma.

Nanofluids are defined as liquid substances that are composed of a base fluid and nanoparticles. Because of its low cost and the ease with which it can be obtained, water is often used in industrial settings for the production of nanofluids. Water is a universal solvent that may dissolve a larger percentage of a material or nanoparticles to produce a solution, suspension, or colloidal suspension. Water can also form a colloidal suspension. According to Hassan et al. (Hassan et al., 2015), water has low thermal conductivity. These properties need to be altered if water is to be utilized as a heat exchanger by introducing nanoparticles. The term “base fluid” is often used to refer to water since it has a pH of 7 and can only exist in nature in three separate states (see Syarif (Syarif, 2016) for more information). Because water in particular has such a low surface tension, it is easy for even the smallest particles to move freely over its surface. It is a transport medium that can be identified by spectral analysis and is acceptable for use. When water is used as the base fluid, it is very simple to ascertain the thermo-physical characteristics of nanofluids (Al-Waeli et al. (Al-Waeli et al., 2019). Oke et al. (Oke et al., 2021) investigated the impact of volume fraction, Coriolis force, and heat source/sink on the dynamics of water transporting 47 nm alumina nanoparticles on uniform surfaces. In their research, the authors focused on how these factors influence the dynamics of the water. The comparative examination of the dynamics of water transporting 29 nm $CuO$ and 47 nm ${Al}_{2} O_{3}$ on an upper horizontal surface of a paraboloid of revolution is modelled and given in Hongping et al.'s (Liu et al., 2020) study. Alumina ( ${Al}_{2} O_{3}$ ) has emerged as a topic of interest among the created nanomaterials due to its significant chemical and physical properties (Song et al (Song et al., 2021). In particular, it has been shown that ${Al}_{2} O_{3}$ has higher thermal conductivity, convective heat transfer coefficient, and heat transfer coefficient qualities. This is the case in terms of its thermal properties. As a consequence of this, “ ${Al}_{2} O_{3}$ ” has been put to use in a variety of guises across a wide range of application domains, where its relevance, significance, and efficacy have been shown (Farhana, 2019). Even though it has achieved great achievements in the area of technology and sciences, the influence that it has on human health and the environment has not yet been thoroughly examined. In 2005 alone, about twenty percent of the global market for nanoparticles was accounted for by ${Al}_{2} O_{3}$ nanoparticles (Arul Prakash et al., 2011). “ ${Al}_{2} O_{3}$ ” is a white oxide that consists mostly of sapphire and may be obtained in the forms $γ, α, θ$ $δ - {Al}_{2} O_{3}$ (Mahmood et al (Mahmood et al., 2023). In their research study, Lin et al. (Lin et al., 2011) claimed that ${Al}_{2} O_{3}$ had the lowest precipitation rate and the highest emulsification stability of any other nanoparticle. This was in comparison to all of the other nanoparticles.

Entropy was first defined by Rudolf Clausius in 1850. Unusable for useful purposes, it's the quantity of thermal energy per unit temperature that cannot be obtained. Entropy generation refers to the amount of entropy accumulated in irreversible processes. Take into consideration things like energy transfer, steam turbines, fluid movement, heating systems, hydroelectric dams, air conditioners, and refrigeration to name a few of the more common examples. The thermodynamical system's operation is determined by this. Bejan (Bejan, 1979) began by learning about the creation of entropy. He walked us through the important processes in the depreciation of entropy. Nanofluid entropy formation in a permeable annulus was investigated by Gholam Ali pour et al (Gholamalipour et al., 2019). Disturbance in entropy generation is more apparent with lower Darcy and Rayleigh numbers. It was Dutta and coworkers (Dutta et al., 2019) that looked at the effect of entropy production on a rhombic-shaped closed pattern permeated by $Cu - H_{2} O$ nanofluid. He showed that a rise in the amount of hahnium causes an increment at which entropy is generated to decrease. The results of a research into the effects of corrosive heating on moving Casson fluid were published by Khan et al. (Khan et al., 2020). The Brinkman number increases entropy generation. Ambreen et al. (Ambreen et al., 2020) deliberate the properties of entropy production in Newtonian fluids employing the Darcy model. For his experiment, Cho (Cho, 2020) used a square chamber that had been heated on one or more sides and filled it with $Cu - H_{2} O$ nanofluid. The entropy generation rate was measured by putting a porous media inside the hollow. In the case of a fixed Rayleigh number, the entropy rate is boosted by increasing the Darcy number. Li et al (Li et al., 2020) conducted research on the effect that heat radiation has on a square cavity that is slanted. As a result of this analysis, the entropy generation rate was observed to increase with Rayleigh number. The idea of entropy formation was brought to light in Yu-Ming et al.'s research (Chu et al., 2020). In addition to this, they investigate the two-dimensional MHD boundary layer flow of a non-Newtonian nanofluid (of the second grade) approaching a Riga plate surface that is permeable and stretchy.

Magnetohydrodynamics, known as MHD, is the exploration of the motion of fluids that conduct electricity in relation to the direction of the magnetic field. The MHD idea has been employed by engineers in the design of a broad range of applications in enterprises, such as flow measurement, spacecraft energy, nuclear waste disposal, MHD compressors, boilers, hydrogen fuel, nuclear reactor coolant, and hydroelectric power extractors (Mahmood et al., 2022). Mishra and Kumar (Mishra and Kumar, 2021) use the Buongiorno nanofluid model to do a numerical investigation of the impact that MHD flow has on a wedge. Wei-Mao and colleagues (Qian, 2022) investigated the effect that MHD flow has on the movement of micropolar fluid over an exponentially curved stretching surface. The influence of thermal radiation and Joule heating is taken into consideration while discussing heat transfer studies. Mishra and Kumar (Mishra and Kumar, 2020) investigate the effect that viscous-Joule heating, thermal radiation, and heat production (or absorption) have on the movement of MHD nanofluids via a stretched sheet that is embedded in a porous medium as a result of suction or blowing. The MHD nanofluid flow that is made up of dust particles was explored in Kumar et al.'s paper (Parida, 2021). The influence that dust nanoparticles have on the properties of the flow is quite important. See Mahmood et al (Mahmood et al., 2022), Mudassar et al. (Gulzar et al., 2020) and Hosseinzadeh et al. (Hosseinzadeh, 2023), Mishra and Kumar (Mishra and Kumar, 2020); for some recent work that relates to MHD that may be found here.

Applications in engineering and industry both have considerable preferences for fluid flows that are started by stretching surfaces. For instance, the cooling of stripes, the manufacturing of glass fiber and rubber sheets, the processes of extrusion, the production of paper, the drawing of paper film, the development of crystals, and so on. The stretching and cooling of the sheets both played a significant part in the production of output of an acceptable grade. In the recent past, several experts have looked at the flow that was caused by the stretching and shrinking of surfaces see Salman et al (Ahmad et al., 2021), Hayat et al (Hayat et al., 2017) and Li et al (Li et al., 2021). Upreti and Mishra (Upreti and Mishra, 2022) addresses the problem considering impact of viscous dissipation and convective heating on the flow related to Darcy-Forchheimer past a rotating disk with radial stretching and shrinking.

The transfer of heat is an essential component in the activities that take place in industry, geography, and engineering. They have a wide variety of applications, some of which include insulating material, hydrothermal supply, conditioning of electrical devices, metallic molding, and other uses of a similar kind. The most important aspect in heat production and absorption is the variation in temperature that exists inside a body. When analyzing the impact of heat generation and absorption, Hafeez et al. (Hafeez and Khan, 2021) took into account a spinning disk that was filled with Oldroyd-B fluid. This disk was spinning while the researchers were thinking about the effect. They came to the conclusion that temperature is a function that, when seen in relation to the magnetic number, increases but that, when viewed in relation to the thermal relaxation time parameter, decreases. According to Faghiri et al. (Faghiri et al., 2022), the heat transfer boundary condition on the wall in non-Newtonian fluid flow is a non-uniform heat flux. This was explored in the context of non-Newtonian fluid flow. The research conducted by Najafabadi and colleagues (Fallah Najafabadi et al., 2022) looks at the flow, temperature, and volume fraction of a nanofluid as it moves along a vertical channel while being subjected to natural and forced (mixed) convection heat transfer. The exponential distribution function is used for both the temperature and the volume fraction along the wall of the channel. Because of their remarkable ability to enhance heat transmission, hybrid nanofluids have been garnering an increasing amount of interest in recent years. Zangooee et al. (Zangooee et al., 2022) investigated in this study the impact that the velocity and temperature slip parameters, as well as the volume percentage of nanoparticles, have on a vertical plate when suction is present. Analytical methods were used by Shahin et al. (Akbari et al., 2022) in order to investigate the non-Fourier thermal behavior of a three-dimensional hollow sphere that was exposed to arbitrarily selected space and time-dependent boundary constraints.

According to the findings of the affordable literature study from the section before this one, there has not been any research conducted on the significance of entropy generation with nanoparticle aggregation effects and stagnation point flow across a permeable stretched sheet in the occurrence of heat generation/absorption, viscous dissipation with inclined Lorentz force. To fill the gap in literature, we considered aggregation and non-aggregation model for the said purpose. To the best of the authors' knowledge, the study on the significance of entropy generation on stagnation point flow past a permeable stretching sheet with heat source, viscous dissipation, and inclined Lorentz force in nanofluid using an aggregation model has not been considered. As a result, this endeavor is significant as a future reference for the practitioner, scientist, and engineer, as well as the fluid mechanist, and it will be used as the preliminary study on the real applications. This is the impetus for the work that is currently being done. The focus of this research work on the impact that nanoparticle aggregation, as well as the absence of aggregation, has on a variety of metrics as they pertain to respective profiles. The issues are then solved numerically, but only after the governing equations are first transformed into a system of ODEs. The impact of several different characteristics is investigated in fine detail. The purpose of the present assessment is to collect information that will allow us to answer the ensuing questionnaire:

How does the presence of nanoparticles with or without aggregation affect the value of an inclined magnetic parameter throughout the course of a velocity profile?
In the context of a thermal distribution, what kind of an effect do nanoparticles have, both with and without aggregation?
What are the effects of nanoparticles with and without aggregation on the formation of entropy, and how do these effects differ?
What is the consequence of heat generation parameter, Eckert number, suction, velocity ratio parameter and nanoparticles volume fraction parameter on respective profiles?

2 Description of the problem

Studying an incompressible two-dimensional $H_{2} O$ -based nanofluid as it passes through a stretching sheet while subjected to an inclined magnetic field and viscous dissipation allowed us to construct models that account for both the absence of aggregation and the presence of aggregation. Stagnation points flow and heat source are also examined. The study of thermal transfer also considers the objective of producing and absorbing heat uniformly throughout the system. Frame coordinates with $x$ -and $y$ -axes along the sheet's surface and the normal to the sheet's surface are assumed. $\tilde{u} = {\tilde{u}}_{w} = a x$ , where ‘ $a$ ’ is a constant, is used to calculate the stretched velocity of the object, free stream velocity ${\tilde{u}}_{e} = c x$ and ${\tilde{v}}_{w} = - \sqrt{ν_{f} a} ε$ denoted the mass flux are under considerations. Consideration is also given to a permeable medium. In this case, we'll use $T_{w}$ and $T_{\infty}$ to represent the surface and constant ambient temperatures, respectively. In this article, nanoparticles of alumina ( ${Al}_{2} O_{3}$ ) with water ( $H_{2} O)$ serving as their underlying fluid are investigated. It is also assumed that magnetic field making an angle $γ$ with the stretching sheet.

Table 1 lists the thermophysical features of the nanoparticles and the underlying fluids. In this line of research, the viscosity and thermal conductivity of nanofluids are investigated by using improved versions of the Krieger-Dougarty and Maxwell-Brugman models. After the boundary layer approximation is implemented, the following equations are in effect (see ref (Mackolil and Mahanthesh, 2021; Masood and Farooq, 2021):

(1)

\frac{\partial \tilde{u}}{\partial x} + \frac{\partial \tilde{v}}{\partial y} = 0

(2)

\tilde{u} \frac{\partial \tilde{u}}{\partial x} + \tilde{v} \frac{\partial \tilde{u}}{\partial y} = {\tilde{u}}_{e} \frac{\partial {\tilde{u}}_{e}}{\partial x} + \frac{μ_{nf}}{ρ_{nf}} \frac{\partial^{2} \tilde{u}}{\partial y^{2}} - \frac{σ_{nf}}{ρ_{nf}} B_{0}^{2} \sin^{2} γ (\tilde{u} - {\tilde{u}}_{e})

(3)

\tilde{u} \frac{\partial T}{\partial x} + \tilde{v} \frac{\partial T}{\partial y} = \frac{k_{nf}}{{(ρ C_{p})}_{nf}} \frac{\partial^{2} T}{\partial y^{2}} - \frac{Q_{0}}{{(ρ C_{p})}_{nf}} (T - T_{\infty}) + \frac{μ_{nf}}{{(ρ C_{p})}_{nf}} {(\frac{\partial \tilde{u}}{\partial y})}^{2} .

Table 1 Thermophysical characteristics of the base fluid in the presence of nanoparticles (Mahmood et al (Mahmood et al., 2022).

Properties	${A l}_{2} O_{3}$	$H_{2} O$
$ρ (k g / m^{3})$	$3970$	$997.1$
$Cp (J / k g K)$	$765$	$4179$
$k (W / m K)$	$0.40$	$0.613$
$σ (S m^{- 1})$	$35 \times 10^{6}$	$5.5 \times 10^{- 6}$
$\Pr$		$6.96$

The $x -$ axis component of velocity is represented by $\tilde{u}$ , whereas the $y -$ axis component is represented by $\tilde{v}$ . The following constitute the conditions of the boundary (see Mahmood et al (Mahmood et al., 2022) and Sadaf et al (Masood and Farooq, 2021):

(4)

\tilde{u} = {\tilde{u}}_{w} = a x, \tilde{v} = {\tilde{v}}_{w} = b y, T = T_{w} = T_{\infty} + b x^{2}, a t y = 0,

(5)

\tilde{u} = {\tilde{u}}_{e} = c x, T \to T_{\infty}, a t y \to \infty .

Nanofluid has a temperature of $T$ , a dynamic viscosity of $μ_{nf}$ , a density of $ρ_{nf}$ , a thermal conductivity of $k_{nf}$ , and a heat capacity of ${(ρ C_{p})}_{nf}$ . Applied magnetic field is $B_{0} .$

Table 1 presents several thermophysical parameters associated with aluminum oxide ( ${Al}_{2} O_{3}$ ), with water ( $H_{2} O$ ) serving as the base fluid. The aggregation feature of the NP was used as a criterion in the selection process for the thermophysical qualities. When there is no aggregation present, the Brinkman and Maxwell models are used to determine the effective viscosity and thermal conductivity of the fluid, respectively. The useful qualities of nanoliquids are outlined in Table 2, which may be found here.

Table 2 Efficacious models of nanoliquids with regard to their thermophysical qualities (see Mahmood et al (Mahmood et al., 2022).

Effective Property	Without Aggregation	With Aggregation
Density	$\frac{ρ_{nf}}{ρ_{f}} = (1 - ϕ) + ϕ \frac{ρ_{S}}{ρ_{f}}$	$\frac{ρ_{nf}}{ρ_{f}} = (1 - ϕ_{a}) + ϕ_{a} \frac{ρ_{S}}{ρ_{f}}$
Dynamic Viscosity	$\frac{μ_{nf}}{μ_{f}} = \frac{1}{{(1 - ϕ)}^{2.5}}$	$\frac{μ_{nf}}{μ_{f}} = {(1 - \frac{ϕ_{a}}{ϕ_{m}})}^{- [η] ϕ_{m}}$
Specific Heat Capacity	$\frac{{(ρ C_{p})}_{n f}}{{(ρ C_{p})}_{f}} = (1 - ϕ) + ϕ \frac{{(ρ C_{p})}_{S}}{{(ρ C_{p})}_{f}}$	$\frac{{(ρ C_{p})}_{n f}}{{(ρ C_{p})}_{f}} = (1 - ϕ_{a}) + ϕ_{a} \frac{{(ρ C_{p})}_{S}}{{(ρ C_{p})}_{f}}$
Thermal Conductivity	$\frac{k_{nf}}{k_{f}} = \frac{(k_{S} + 2 k_{f}) - 2 ϕ (k_{f} - k_{S})}{(k_{S} + 2 k_{f}) + ϕ (k_{f} - k_{S})}$	$\frac{k_{nf}}{k_{f}} = \frac{(k_{a} + 2 k_{f}) - 2 ϕ_{a} (k_{f} - k_{a})}{(k_{a} + 2 k_{f}) + ϕ_{a} (k_{f} - k_{a})}$
Electrical Conductivity	$\frac{σ_{nf}}{σ_{f}} = 1 + \frac{3 (\frac{σ_{nf}}{σ_{f}} - 1) ϕ}{(\frac{σ_{nf}}{σ_{f}} + 2) - (\frac{σ_{nf}}{σ_{f}} - 1) ϕ}$	$\frac{σ_{nf}}{σ_{f}} = 1 + \frac{3 (\frac{σ_{nf}}{σ_{f}} - 1) ϕ_{a}}{(\frac{σ_{nf}}{σ_{f}} + 2) - (\frac{σ_{nf}}{σ_{f}} - 1) ϕ_{a}}$

When computing these equations, there are several different variables that need to be considered which discussed above. A solid volume fraction denoted by $ϕ$ may be found in the nanofluid. where $[η]$ denotes the Einstein coefficient and $ϕ_{m}$ denotes the maximum volume fraction that may exist before the flow can take place. The value denoted by $ϕ_{a}$ indicates the aggregates' effective volume fraction. It is determined by comparing the volume fraction to the aggregates' greatest packing fraction and calculating the ratio of the two. A number of adjustments were made to the Krieger-Dougherty model, which are detailed in Table 2 to take into consideration the phenomenon of nanoparticle aggregation. When it comes to the dynamics and the transfer of heat in nanofluid flows, the nanoparticle agglomeration factor is very essential, as shown by Mahmood et al (Mahmood et al., 2022). The findings of the measurements of the nanomaterial corresponded perfectly with one another while taking into account the aggregation part of the process. Calculating the nanoparticle volume fraction when the aggregation kinetic factor is taken into consideration yields the following results (see ref (Mahmood et al., 2022):

(6)

(ϕ_{a} = ϕ {(\frac{r_{a}}{r_{p}})}^{3 - D})

It is compatible with the conclusions of the experiments conducted on nanoliquids when both spherical and dispersion aggregated are taken into consideration. The packing density shifts in accordance with the radial location according to a fixed power law index $D$ . Because it takes into consideration the fractal nature of the aggregates, the letter $D$ is sometimes referred to as the fractal index. $D = 1.8, \frac{r_{a}}{r_{p}} = 3.34, ϕ_{m} = 0.605$ and $[η] = 2.5$ (see ref Mahmood et al (Mahmood et al., 2022). The Bruggeman model and the Maxwell model were both used in the process of developing an aggregation model of thermal conductivity, which was then changed after its initial development. Use the following formula to figure out the thermal conductivity of the aggregate $(k_{a})$ (see ref. (Mahmood et al., 2022):

(7)

\frac{k_{a}}{k_{f}} = \frac{1}{4} \{(3 ϕ_{in} - 1) \frac{k_{S}}{k_{f}} + (3 (1 - ϕ_{in}) - 1) + {[{((3 ϕ_{in} - 1) \frac{k_{S}}{k_{f}} + (3 (1 - ϕ_{in}) - 1))}^{2} + 8 \frac{k_{S}}{k_{f}}]}^{\frac{1}{2}}\} .

Here, $ϕ_{in} = {(\frac{r_{a}}{r_{p}})}^{D - 3} .$

Exploiting the transformations (see (Masood and Farooq, 2021)

(8)

\tilde{u} = a x f^{'} (η), \tilde{v} = - \sqrt{ν_{f} a} f (η), θ (η) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}, η = \sqrt{\frac{a}{ν_{f}}} y .

In this context, prime denotes differentiation with respect to $η$ . The first equation is satisfied in a consistent manner. Even though Eqs. (2)–(5) seem like:

(9)

{\frac{μ_{nf} / μ_{f}}{ρ_{nf} / ρ_{f}} f}^{″'} - f^{' 2} + f f^{″} + B^{2} - M \frac{σ_{nf} / σ_{f}}{ρ_{nf} / ρ_{f}} (f^{'} - 1) {Sin}^{2} γ = 0,

(10)

\frac{k_{nf} / k_{f}}{\Pr {(ρ C_{p})}_{nf} / {(ρ C_{p})}_{f}} θ^{″} + f θ^{'} - 2 θ f^{'} + λ θ + \frac{μ_{nf} / μ_{f}}{{(ρ C_{p})}_{nf} / {(ρ C_{p})}_{f}} E c {(f^{″})}^{2} = 0 .

(11)

f (0) = ε, f^{'} (0) = 1, θ (0) = 1, f^{'} (η) \to B, θ (η) \to 0, a s η \to \infty .

In the above equations $B = b / a$ stands velocity ratio constraint, $\Pr = ν / α$ stands the Prandtl number, $λ = Q_{0} / a {(ρ C_{p})}_{f}$ heat generation/absorption parameter. $M = σ_{f} B_{0}^{2} / a ρ_{f}$ is magnetic parameter. $ε$ is suction/injection factor where $ε > 0$ for suction and $ε < 0$ for injection, $Ec = a / {(ρ C_{p})}_{f}$ is Eckert number. The mathematical version of skin friction, often known as the drag force, is defined as follows:

(12)

C_{f} = \frac{τ_{\tilde{w}}}{ρ u_{w}^{2}},

The expression for the non-dimensional configuration is as:

(13)

{Re}_{x}^{\frac{1}{2}} C_{fx} = \frac{μ_{nf}}{μ_{f}} f^{″} (0),

local Nusselt number is declared as:

(14)

Nu = \frac{x q_{\tilde{w}}}{k_{f} (T_{w} - T_{\infty})},

Its non-dimensional form is as below.

(15)

{Re}_{x}^{- \frac{1}{2}} {Nu}_{x} = - \frac{K_{nf}}{k_{f}} θ^{'} (0),

here local Reynolds number is denoted by ${Re}_{x} = \frac{\tilde{a} x^{2}}{υ_{f}}$ .

3 Entropy generation

In this section, our primary emphasis will be on determining the irreversibility of a system by measuring the creation of entropy. It may be expressed mathematically as (Mishra and Kumar, 2021)

(16)

E_{G} = \frac{k_{nf}}{{(T_{\infty})}^{2}} {(\frac{\partial T}{\partial y})}^{2} + \frac{μ_{nf}}{T_{\infty}} {(\frac{\partial u}{\partial y})}^{2},

The following is a demonstration of how the non - dimensional mathematical expression for the creation of entropy may be proved to be correct (Mishra and Kumar, 2021):

(17)

N_{s} = \frac{{(T_{\infty})}^{2} {(\frac{η}{y})}^{2}}{k_{nf} {(T_{w} - T_{\infty})}^{2}} E_{G},

The design that has been achieved without dimensions is (Mishra and Kumar, 2021).

(18)

N_{s} = θ^{' 2} + \frac{EcPr}{Ω μ_{nf}} \frac{k_{f}}{k_{nf}} f^{″ 2},

The Bejan number is written out as follows (Mishra and Kumar, 2021):

(19)

Be = \frac{E n t r o p y g e n e r a t i o n d u e t o t h e r m a l i r r e v e r s i b i l i t y}{T o t a l e n t r o p y g e n e r a t i o n},

(20

Be = \frac{θ^{' 2}}{θ^{' 2} + \frac{EcPr}{Ω μ_{nf}} \frac{k_{f}}{k_{nf}} f^{″ 2}} .

4 Method of solution and code validation

In the current body of research, the governing equations for a steady flow with heat transfer and entropy generation near a permeable stretching sheet are mathematically modeled. These equations take into account inclined Lorentz force, viscous dissipation, and heat source impacts in occupied with aggregation and without aggregation nanofluid flow model along with subjected free-stream velocity. By including the similarity variables in the modelling process for these sets of PDEs, we were able to convert them into “ordinary” similarity equations. Because the constructed form of the set of differential equations (9)–(10) together with the associated BCs (11) was linked and extremely nonlinear from a mathematical standpoint, it was difficult to locate a solution in the closed explicit form of these ODEs. Because of this, it is able to apply a well-known numerical procedure, which allows us to rapidly resort to its successful techniques for reaching the objectives or targets that have been underlined. In terms of computation, the bvp4c (boundary value problem of fourth-order) finite–difference approach is one of the most suggested built-in codes available in MATLAB sub-routines (Alqahtani et al (Alqahtani et al., 2022). This built-in code is one of the most suggested built-in codes available in MATLAB sub-routines because it can be used successfully to offer fourth-order correct results in this phenomenon. As a result, first-order initial value issues may be solved by using the strategy that has been provided. The following procedures have been carried out in order to include a bvp4c solver into our physical model.

STEP 1: In Eqs. (9)–(10), Higher order nonlinear ODEs are modified to accommodate additional variables that have been introduced to modeled

(22)

f (η) = X_{1}, θ (η) = X_{4}, f^{'} (η) = X_{2}, f^{″} (η) = X_{3}, θ^{'} (η) = X_{5} .

STEP 2: In Eqs. (9), (10) use the additional variables in Eq. (22) to decrease the system of higher-order nonlinear ODEs to a first-order nonlinear ODE system

(23)

\begin{matrix} f^{'} (η) = X_{2}, \\ f^{″} (η) = X_{3}, \\ f^{″'} (η) = {X X}_{1}, θ^{″} (η) = {X X}_{2}, \\ {X X}_{1} = - \frac{ρ_{nf} / ρ_{f}}{μ_{nf} / μ_{f}} [X_{1} X_{3} - {X_{2}}^{2} + B^{2} - \frac{σ_{nf} / σ_{f}}{ρ_{nf} / ρ_{f}} M X_{2} {Sin}^{2} γ], \\ θ^{'} (η) = X_{5}, \\ {X X}_{2} = - [P r \frac{{(ρ C_{p})}_{nf} / {(ρ C_{p})}_{f}}{k_{nf} / k_{f}} (X_{1} X_{5} - 2 X_{4} X_{2} + λ X_{4})] . \end{matrix}

STEP 3: Eq. (11) requires that the boundary conditions be expressed in terms of the additional variables introduced in Eq. (22)

(24)

\begin{matrix} {X_{1}}_{a} = ε, {X_{2}}_{a} = 1, {X_{5}}_{a} = 1, \\ {X_{2}}_{b} = B, {X_{5}}_{b} = 0 . \end{matrix}

The locations indicated by the subscripts ′a′ and ′b′ on the sheet at $η = 0$ and the distance from the sheet for a given value of $η$ are denoted by those values, respectively. In this investigation, the value of $η = 15$ is chosen for his position.

STEP 4: Code the boundary conditions in Eq. (24) and the system of first order nonlinear ODEs in Eq. (23) in the bvp4c solver.

Shear stress $f ″ (0)$ is compared to recent study by Sadaf et al (Masood and Farooq, 2021) and Masood et al (Masood et al., 2019) on stagnation point flow of a viscous fluid in Table 3, which may be found below. The findings of the most recent inquiry are very consistent with those of the many investigations that have come before it. In their study, Sadaf et al (Masood and Farooq, 2021) and Masood et al (Masood et al., 2019) used the homotopy analysis approach, but in our work, we utilized the bvp4c method. The numerical technique was validated by applying it to the “classical situation” of a viscous fluid where no extra effects were taken into account, and the results are shown in Table 3 with complete agreement. As a result, we may reach the conclusion that our numerical technique can be utilized to investigate the topic presented in this work with a high degree of assurance.

Table 3

f^{″} (0), ϕ = ϕ_{a} = γ = ε = M = λ = 0

and

\Pr = 6.2

generates results for certain values of id435

B

$B$	Present Results	Sadaf et al (Masood and Farooq, 2021)	Masood et al (Masood et al.,2019)
$0.1$	$- 0.96948$	$- 0.96939$	$- 0.96939$
$0.2$	$- 0.918106$	$- 0.91811$	$- 0.91811$
$0.5$	$- 0.667263$	$- 0.66726$	$- 0.66726$

5 Analysis and discussion of results

The primary purpose of this part is to conduct an analysis of the variations of a variety of parameters as represented by graphical representations. It is essential to take note of the fact that, even though the Prandtl number $\Pr = 6.96$ (for water) is maintained throughout the entirety of the work (apart from the comparison with the cases that came before it), as can be seen from the tables and figures, the values of the control parameter are changed in a flexible way. We decided on the following values for the physical parameters (see ref. (Mahmood et al., 2022): $0.0 \leq ϕ \leq 0.05$ (nanoparticles volume fraction), $0.0 \leq B \leq 1.0$ (velocity ratio), $2.0 \leq ε \leq 3.0$ (suction), $0^{°} \leq γ \leq 90^{°}$ (inclined angle), $0.0 \leq M \leq 1.0$ (magnetic field), $0.0 \leq E c \leq 1.0$ (Eckert number) and $0.0 \leq λ \leq 1.0$ (heat generation parameter). If the conditions for the far-field boundary (11) are satisfied, then these values will be employed The investigation is carried out in two different ways: (1) with aggregation $ϕ_{a} \neq 1$ , and (2) without aggregation over a permeable stretching sheet with heat generation constraint, inclined Lorentz force, and entropy generation for ${Al}_{2} O_{3} - H_{2} O$ nanofluid. The first method involves the formation of aggregates, while the second method does not.

5.1

5.1 Analysis of results

In this part, we take a look at the behavior of velocity $f^{'} (η),$ temperature $θ (η),$ entropy generation $N_{s},$ skin friction ${Re}_{x}^{1 / 2} C_{fx}$ and Nusselt number ${Re}_{x}^{- 1 / 2} {Nu}_{x}$ profiles in terms of the influence of numerous elements.

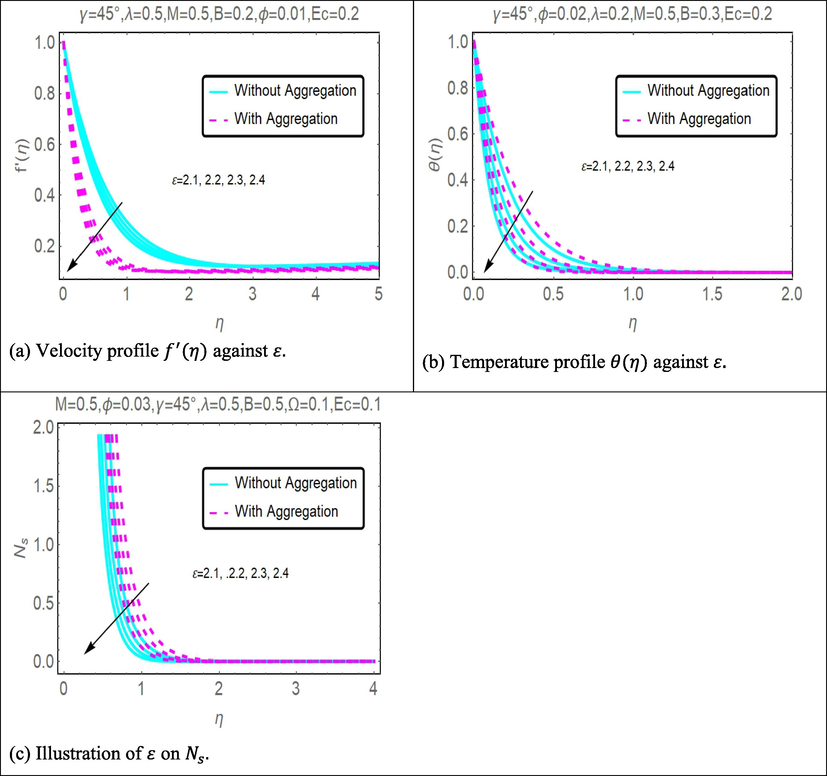
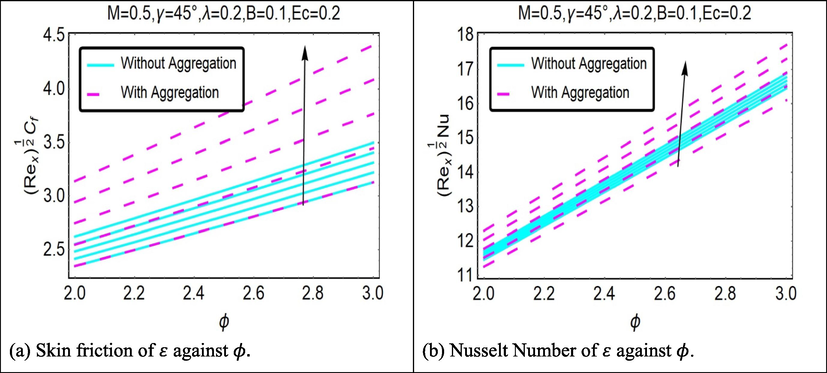
The purpose of drawing Fig. 3 was to illustrate the influence that the volume percent of nanoparticles $ϕ$ had on the corresponding values of velocity, temperature, and entropy production. The graphical representation of the data in Fig. 3(a) shows that the velocity of both situations (without and with aggregation model) slows down as the nanoparticle volume percentage increases. On the other hand, it is determined that temperature and entropy generation profiles in Fig. 3(b) and Fig. 3(c) is found to escalate with enhancement in the values of $ϕ$ respectively. Fig. 4(a), (b) and (c) are drawn for diverse values of velocity ratio parameter $B$ versus velocity $f^{'} (η)$ , temperature $θ (η)$ , and entropy generation $N_{s}$ profiles for without and with aggregation model. Velocity profile enhances for growing values of $B$ while temperature and entropy generation profiles decrease with increases values of $B .$ The illustration of mass suction $ε$ on velocity $f^{'} (η)$ , temperature $θ (η)$ , and entropy generation $N_{s}$ profiles are seen in Fig. 5(a), (b) and (c) respectively. It is observed that by mounting values of $ε,$ velocity, temperature and entropy generation profiles decreases.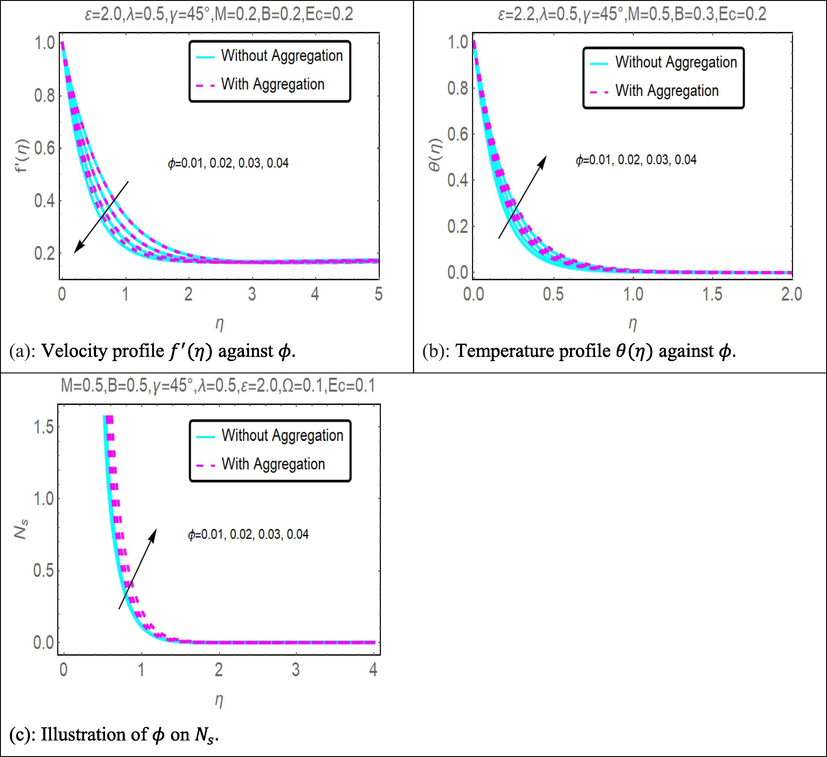

(a, b, c): Impact of ϕ on velocity, temperature, and entropy generation respectively.

(a), (b) and (c): Impact of B on velocity, temperature and entropy generation.

(a), (b) and (c): Impact of ε on velocity, temperature and entropy generation.

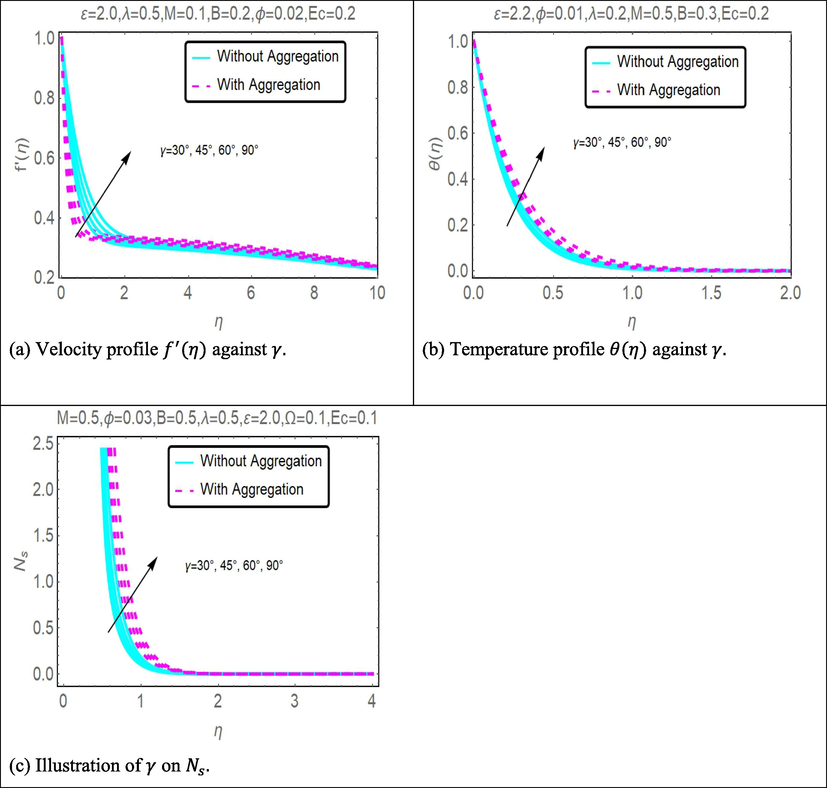
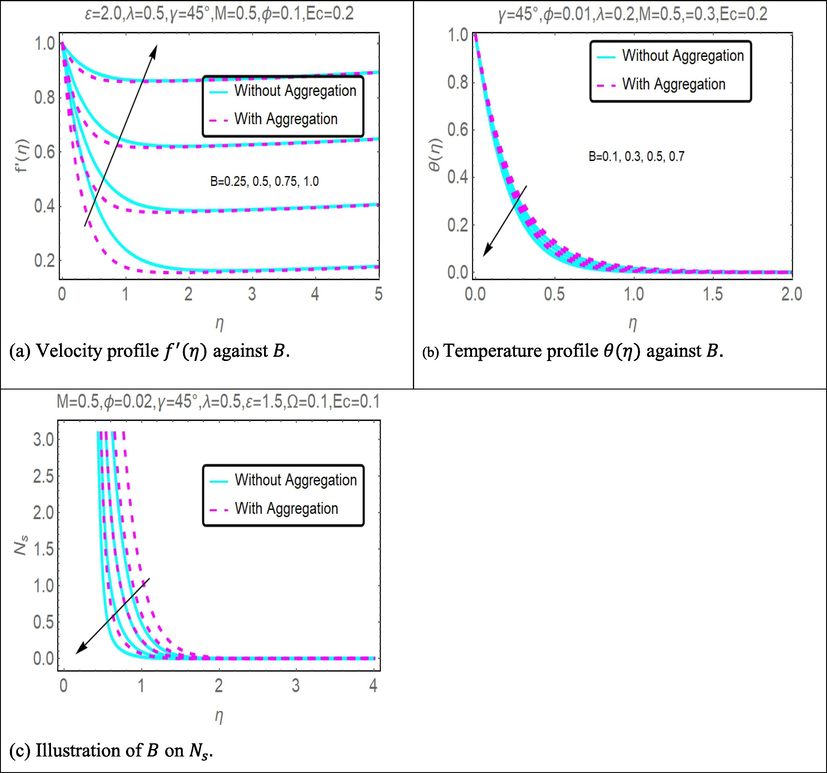
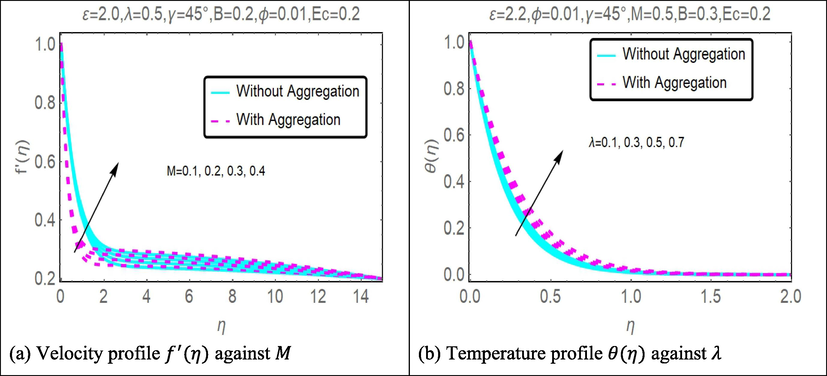
The impact of inclined angle $γ$ on velocity $f^{'} (η)$ , temperature $θ (η)$ , and entropy generation $N_{s}$ profiles are seen in Fig. 6(a), (b) and (c) correspondingly. With increasing degrees of $γ$ , velocity, temperature and entropy generation boost up. Fig. 7(a) present the impact of $M$ on velocity profile. Increasing values of $M$ shows the increases impact. Whereas Fig. 7(b) shows the influence of heat source $λ$ on temperature profile. 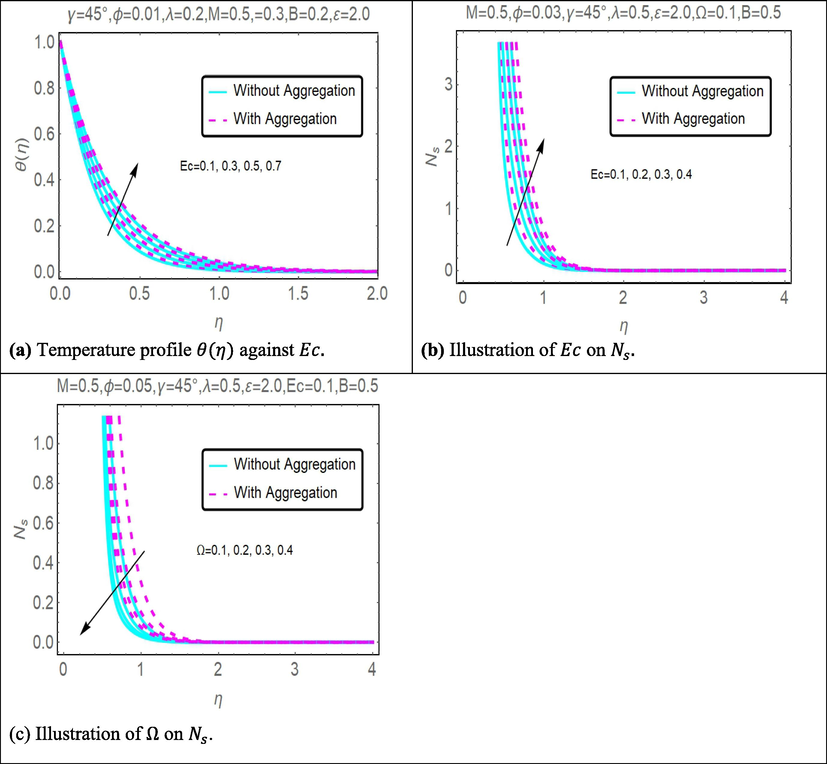The illustration shows that temperature profile enhances with positive values of $λ .$ The impact of Eckert number $Ec$ on velocity and entropy generation is shown in Fig. 8(a) and (b) respectively. With the increasing values of $Ec$ , temperature and entropy generation both profiles increase. On the other hand, impact of temperature ratio parameter $Ω$ on entropy generation is shown in Fig. 8(c) entropy generation profile increases with $Ω .$ The consequence of mass suction $ε$ and $ϕ$ on skin friction and Nusselt number is shown in Fig. 9(a) and (b) respectively. It is observed that skin friction and Nusselt number are enhancing function for both $ε$ and $ϕ .$

(a): Impact of M on f ′ η . (b): Impact of λ on. θ η .

(a) and (b): impact of Ec on θ ( η ) and N s . (c): impact of Ω on N s .

(a) and (b): Impact of ε and ϕ on skin friction and Nusselt number.

The influence of velocity ratio parameter $B$ with $ϕ$ on skin friction and Nusselt number is presented in Fig. 10(a) and (b) respectively. Increasing values of $B$ with $ϕ$ increases the skin friction profile in Fig. 10(a) and diminishes the Nusselt number profile in Fig. 10(b) for without and with aggregation model. The influence of $γ$ with $ϕ$ on skin friction and Nusselt number is shown in Fig. 11(a) and (b) respectively. As the degree of $γ$ increases with $ϕ,$ the skin friction increases and Nusselt number decreases. The impact of $M$ with $ϕ$ towards skin friction is shown in Fig. 12(a) for without and with aggregation model. Increasing values of $M$ increases the skin friction profile. The impact of heat source $λ$ and Eckert number $Ec$ with $ϕ$ on Nusselt number are shown in Fig. 12(b) and (c) respectively. Here increasing values of heat source $λ$ and Eckert number $Ec$ declines the Nusselt number profiles.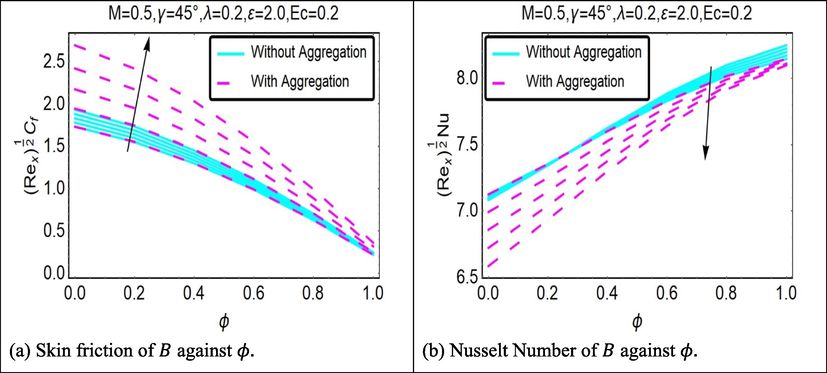

(a) and (b): Impact of B and ϕ on skin friction and Nusselt number.

(a) and (b): Impact of γ and ϕ on skin friction and Nusselt number.

(a): Impact of M and ϕ on skin friction. (b) and (c): Impact of λ and Ec with ϕ on Nusselt number.

5.2

5.2 Discussion of results

All of the previous observations of governing parameters on velocity $f^{'} (η)$ , temperature $θ (η)$ , entropy generation $N_{s}$ , skin friction ${({Re}_{x})}^{1 / 2} C_{f}$ and the local Nusselt number ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ profiles that were reported in Part 5.1 will be validated in this section.

Fig. 3(a), (b), and (c) illustrate how the sensitivity of nanomolecular size is affected by flow velocity, temperature field, and entropy, respectively. Table 2 presents the four nanofluid coefficients that have an effect on the volume fraction $ϕ$ as a result of the development of the without aggregation and with aggregation models. These coefficients are shown to have an influence on the volume fraction. As seen in Fig. 3(a), the fluid's velocity decreases as the volume ratio of nanoparticles increases. These flows are hampered by the rise in magnetic viscosity that happens whenever the flow speed drops below a certain threshold. When seen from a purely physical perspective, increasing the volume fraction results in the formation of viscous forces inside the nanofluid. As a consequence of the friction that is caused by the fluid particles colliding with one another, the velocity of the fluid particles will decrease while the temperature profile will increase. The temperature increases at a quicker rate the greater the volume percentage of nanoparticles that are present. The fluid binding force inside the fluid–solid suspension system is decreased as a result of an improvement in the heat transfer between nanofluid and the conventional nanoparticles found in fluid–solid suspensions. The nanofluid material exhibits a high conductivity coefficient and convectional heat transfer, as shown by the flow distribution. Because of this, nanofluid heat transfer is the primary motivating factor behind the most important industrial and technical breakthroughs of our time. As a result, the thermal improvement seen in Fig. 3(b) is supported. The addition of nanoparticles results in increased thermal boundary expansion caused by ballistic impacts, which in turn enhances heat conduction and the viscosity of the liquid. The effect that changing the nanomaterial term has on the creation of entropy is seen in Fig. 3(c). There was a distinct variation in the behavior of the curves while increasing the volume percentage and approaching the strain wall. The nanofluidic zone exhibited quicker heat transmission and higher entropy formation, both of which contributed to a rise in the total volume fraction parameter. When compared with the non-aggregation model, the with aggregation model has a somewhat greater value.

Fig. 4(a)-4(c) show the impacts of a parameter known as the velocity ratio constraint $B$ on the flow's velocity $f^{'} (η)$ , temperature $θ (η)$ and entropy generation $N_{s}$ trajectories, respectively. This factor is shown to have an influence on the velocity ratio parameter $B$ . This situation demonstrates the exact opposite behavior. It ought to go without saying that elevating the value of $B$ will result in an upsurge in the magnitude of the velocity field. It has a discernible impact in the sense that as time goes on, a rise in the value of $B$ causes the layer of momentum boundary to get thinner and thinner. This is a physical consequence. This is one of the ways it manifests itself in the physical world. Although fluid temperature decreases according to the amount of stretching, the reverse holds true for the pace at which fluid temperature lowers. It is also important to remember that the thickness of the thermal boundary layer increases when a sheet is compressed. The effect that the velocity ratio constraint $B$ has on the generation of entropy is shown graphically in Fig. 4(c), which compares and contrasts both of these counterfactuals. This graphic makes it quite evident that when the estimates of the velocity ratio constraint growth, there is a corresponding drop in the entropy production profile. In addition, the Fig. 4(c) demonstrates that nanoparticles that have not aggregated have an entropy profile that is lower than nanoparticles that have aggregated.

Fig. 5(a) investigates the effect of the mass suction constraint $(ε > 0)$ , on the velocity $f' (η)$ profile of the flow for both of the scenarios. When the suction values are increased, it can be observed that the velocity and thermal boundary layer thickness with the highest boundary velocity are both decreasing. This is the case for both scenarios. In addition, as compared to the case of nanoparticles that do not aggregate, the case of nanoparticles that do aggregate has a higher viscosity, which causes the velocity of the aggregated nanoparticles to be lower. Additionally, the velocity achieves its maximum value when the impermeable sheet is used for both models. This is true for both models. Fig. 5(b) illustrates how the suction affects the temperature distribution around the room. Fluid suction draws the surrounding fluid closer to the stretched sheet, which improves heat transmission and brings the fluid closer together. When there is a greater amount of mass suction, the thermal boundary layer will have a thinner appearance as a result. The impact that suction $ε$ has on the entropy generation number is seen in Fig. 5(c), which applies to both scenarios. With increasing levels of mass suction, it seems that the production of entropy is decreasing both at the surface and in the neighborhood of the sheet. For both scenarios, the formation of the least amount of entropy can be shown in the case of the impermeable sheet. In addition to this, the boundary layer flow of the nanoparticle aggregation model results in the production of a greater amount of entropy.

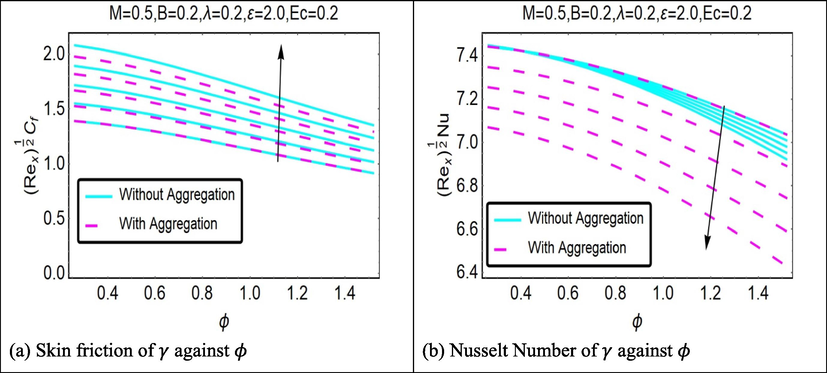
Fig. 6(a)-(c) show the influence that the inclined angle parameter has on $f^{'} (η),$ $θ (η)$ and $N_{s}$ respectively. Because of these statistics, it is feasible to draw the conclusion that an increase in the value of the inclined angle factor would result in a commensurate rise in the velocity of the water-based alumina nanofluid. This is something that can be deduced from the information presented here. As a result of this, a rise in the values of the parameters that characterize the inclined angle is induced by the increasing temperature of the water-based alumina nanofluid, as can be seen in Fig. 6(b). Physically speaking, the existence of the inclined angle, when combined with the properties of the magnetic field, allows the fluid to travel at a quicker pace, while simultaneously creating a sudden rise in the rate at which heat is transferred. The graphic also demonstrates that there is a minor increase in the velocity profile when agglomeration is present as opposed to when there is no agglomeration impact. The effect of the inclined angle $γ$ on the creation of entropy is seen in Fig. 6(c), which applies to both scenarios. When we raised the values of the inclination angle $γ$ , there was an accompanying rise in the amount of entropy generated for both scenarios. On the other hand, nanoparticle aggregation results in a larger creation of entropy than does the absence of aggregation.

Fig. 7(a) illustrates how the magnetic field $M$ influences the velocity curve of the nanofluid by using the situation in which the nanofluid is stretched as an example. Although the Lorentz force may, in principle, slow down motion caused by magnetic parameters, this is not the case in the present scenario; rather, motion is sped up. When there is a magnetic field in the area, a force known as the Lorentz force acts to fight against the flow of fluid. The strength of this force has a one-to-one correlation with $M$ 's overall magnitude. As a direct consequence of this, the Lorentz force will intensify as M increases. As M becomes higher, the increasing resistance causes the momentum of the fluid flow to decrease. This is because of how $M$ affects momentum. This phenomenon is common in the field of magnetohydrodynamics, and it may occur with Newtonian or non-Newtonian fluid under a wide range of different physical situations. In this case, initially with aggregation has lower velocity profile compared to without aggregation but after $η \approx 2$ with aggregation model shows better results. Fig. 7(b) depicts the disparity between the heat production constraint and the heat absorption constraint throughout the course of a temperature profile. This profile is used extensively in engineering applications where heat dispersion is a crucial aspect that must be considered critically. In the system under consideration, an improvement in the generation/absorption factor will lead to a rise in the thermal dispersion of the system. The heat absorption will act in a manner that is functionally analogous to that of a confinement changer, transporting the heat that is produced by the body into the nanoliquid. In the case of a heat production, the thermal propagation is concealed as a result of this, although the exterior of the body is the source of the heat produced in the occurrence of a heat production. When there is heat creation, there is a larger thermal act than when there is no heat absorption. This is the case when compared to the lack of heat absorption. The diagram makes it abundantly evident that the heat dispersion of nanoparticles that have aggregated is much higher than that of nanoparticles that have not aggregated.

Fig. 8(a) is all about the purpose of studying the changes that take place in the parameter $Ec$ and identifying to what extent will variations in thermal distribution $θ (η)$ be affected by those modifications. It has been found that there is an increase in the temperature profile, which is evidence that the temperature gradient around the stretching surface is greater than the temperature of the free stream. This was discovered when it was discovered that there was an increase in the temperature profile. This was discovered as a result of the fact that there is a rising trend in temperature. It was the reflection that there was an increase in the temperature profile that led to the discovery of this. As can be seen in the image, the case in which $Ec$ falls within the range of $0.0 \leq η \leq 1.0$ demonstrates that the model that does not aggregate data yields more accurate results than the model that does. The considerable amount of heat that is released is the direct cause of the temperature increase that occurs inside the nanofluid stretching sheet as a direct consequence of the immediate ramifications of this. Because the dissipation parameter has reached its maximum value, the nanofluid particles have started to collide with one another. When the particles encounter one another, they produce more heat, which is then dispersed over the system. In order to evaluate how much of effect, the Eckert number $Ec$ has on the creation of entropy, Fig. 8(b) is drafted for both scenarios. It has been observed that the rate at which entropy is generated is proportional to a rising Eckert number. Because the Eckert number $Ec$ is increased, supplemental heat will be created, and as a result, the creation of entropy will predominate. In addition, the figure demonstrates that nanoparticles that have not aggregated have an entropy profile that is lower than nanoparticles that have aggregated. On the entropy generation rate for both scenarios, the footprints of the temperature difference parameter $Ω$ is shown in Fig. 8(c). It has been found that the process of heat dissipation accelerates as a consequence of an acceleration in, which results in a reduction in $N_{s} .$ The Eckert number has been seen to exhibit behavior that is opposed to what was expected. When there is a greater temperature differential between the two locations, the entropy creation rate decreases. In addition, the figure demonstrates that nanoparticles that have not aggregated have an entropy profile that is lower than nanoparticles that have aggregated.

Both the skin friction ${({Re}_{x})}^{1 / 2} C_{f}$ and the local Nusselt number ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ are important parameters for industrial application. The local Nusselt number ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ is also often known as the local heat transfer rate. The relevance of these statistics cannot be disputed because of their widespread use in many fields of business. Both the skin friction coefficients, denoted by ${({Re}_{x})}^{1 / 2} C_{f}$ and the local Nusselt number, denoted by ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ react in a manner that is dissimilar to one another when subjected to variations in the parameters.

The influence of $ε$ with $ϕ$ on the skin friction coefficient ${({Re}_{x})}^{1 / 2} C_{f}$ and the local Nusselt number ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ of ${Al}_{2} O_{3} - H_{2} O$ nanofluid is shown in Fig. 9(a) and 9(b), respectively, for the stretching case. For all possible values of equal to $ε = 2.0, 2.25, 2.5, 2.75, 3.0,$ and $\Pr = 6.2$ . In a broad sense, as $ϕ$ grows, the amount of suction that is necessary decreases. In addition, there is no possibility of a solution being found if either an impermeable surface or an injection parameter is taken into account. The rate of heat transfer is accelerated whenever the flow is made more intense by the application of suction. As can be seen in Fig. 9(a) and (b), the suction parameter causes an increase in both the ${({Re}_{x})}^{1 / 2} C_{f}$ and ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ . This occurs regardless of the value of $ϕ$ Suction is required because increasing both the skin friction and the Nusselt number need it. On the other hand, suction may be helpful in increasing both the skin fraction and the local heat transfer rate. This is because it pulls air through the surface of the skin. When hot fluid particles are sucked toward a surface using a vacuum, they move more quickly and effectively, which consequences in an growth in the amount of heat transferred. This is as a result of the increased suction that was used. In the case of a shrinking or stretching surface, on the other hand, the data obtained until this point are definitive since it is essential to determine the location of the separation point. In spite of the possibility that a bigger suction strength will have an effect on the process of heat transfer included in this challenge, nanofluid is anticipated to increase the pace of thermal transfer. On the other hand, this suction force is essential for initiating the flow of the nanofluid. These findings will serve as a standard for other researchers who want to investigate ways to improve the rate of heat transmission in the stretching/shrinking surface instance by altering physical parameters or nanomaterials. These researchers want to find a way to improve the rate of heat transmission without increasing the surface area. These researchers will look at ways to improve the rate of heat transmission by stretching and shrinking the surface.

Fig. 10(a) and (b) show the growing effect of velocity ratio parameter $B$ on the enormous contribution of velocity ratio parameter $B$ on the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ and the ${({Re}_{x})}^{1 / 2} C_{f}$ for both of the aforementioned situations. This is shown by the fact that larger values of $B$ lead to an increase in the ${({Re}_{x})}^{1 / 2} C_{f}$ while at the same time leading to a reduction in the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ , as can be seen in these figures. However, because of the rise in $B$ that occurs when the sheet is shortened, there is a gain in the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ that occurs at the wall. In contrast to this scenario is the condition shown in Fig. 10(b), which demonstrates that the rate of heat transmission reduces as the sheet is expanded.

Fig. 11(a) and (b) illustrate, for both cases respectively, the influence of the angle of inclination $γ$ towards $ϕ$ on the ${({Re}_{x})}^{1 / 2} C_{f}$ and ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ . The angle of the sheet influences the velocity; increasing it results in a reduction in speed. When $γ = 90^{°}$ , the arrangement of the vertical sheet is shown, and it is determined that the greatest velocity occurs under these conditions. In the situation when $γ \to 0$ , $s i n γ \to 0$ , magnetic effects are eliminated (scenario with horizontal sheet in which the magnetic field is perpendicular to the sheet surface and the flow is unaffected by this configuration). The simulation of the sheet alignment is carried out with the assistance of the inclined Lorentz force component, which is derived from the momentum boundary layer equation (2). $s i n γ$ is said to rise in proportion to the value of $γ$ . Because of this, the influence of the Lorentz force will diminish as the angle of inclination of the plate increases. Fig. 11(b) shows that the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ will reduction when the angle of inclination and magnetic parameter are magnified. This is because the Lorentz force will increase as the angle of inclination and magnetic parameter are reduced, as is shown for both cases (with aggregation and without aggregation).

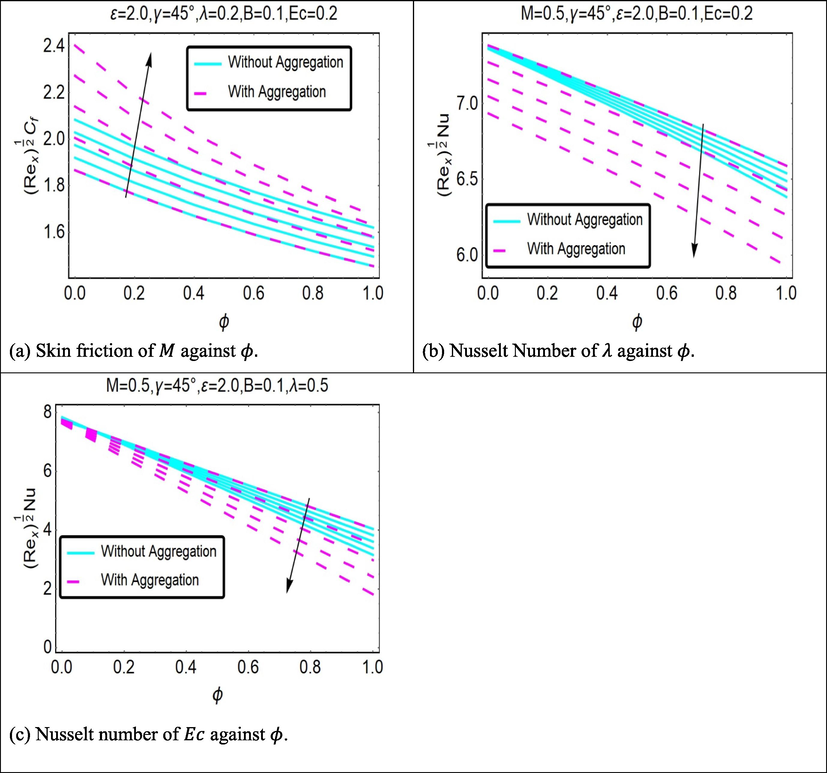
The influence of the magnetic constraint $M$ on ${({Re}_{x})}^{1 / 2} C_{f}$ is shown in Fig. 12(a). The fluid flow in the lowering sheet is significantly altered as a consequence of this effect. Because of the presence of the Lorentz force, which works to slow down the flow of fluid, the lowered skin friction coefficient increases as $M$ increases. This is because of the Lorentz force. The velocity of the fluid is slowed down because the Lorentz force causes a resistance to be formed against the motion of the fluid particles, which in turn causes the velocity of the fluid to decrease. The development of the Lorentz force brought to a synchronism between the magnetic field and the electric field, and this synchronism tends to slow down the velocity of the fluid. Because of the delayed flow, the boundary layer becomes thinner as $M$ gets higher, as seen in Fig. 7(a). This contributes to an upsurge in the amount of skin friction that exists. The impact of the heat generation/absorption constraint $λ$ towards $ϕ$ on the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ is seen in Fig. 12(b) for both cases. It has been detected that the ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ diminishes when the heat generation/absorption constraint increases. The contribution of the heat generation/absorption constraint to the temperature outline is strengthened. As a result, there will be a reduction in the amount of heat transported, and the pace of heat transmission will decrease. In the meantime, an increase in the Eckert number $Ec$ intensity leads to an improvement in the thermal state of the fluid, which, in turn, leads to an elevation in the thermal boundary layer, as shown in Fig. 12(c). This is because an increase in the Eckert number $Ec$ intensity leads to an enhancement in the thermal state of the fluid. Because of this chain of events, the temperature of the fluid as a whole will gradually increase. The Nusselt numbers ${({Re}_{x})}^{- 1 / 2} {Nu}_{x}$ have been found to be lower when there is an expansion in the amount of dissipation that is taking place, and they have been shown to be greater when there is no dissipation taking place at all. This has been shown via a variety of different experiments.

6 Conclusion

The most significant finding of the present study is that heat transmission may be accelerated. On order to locate a two-dimensional stagnation point that exhibits aggregation effects, a nanofluid based in water and containing ( ${Al}_{2} O_{3})$ has been made to flow over a stretched sheet. The thermophysical features were gleaned from the literature and then used into this experiment. To accurately describe basic governance equations, partial differential equations (PDEs) were used. These PDEs were then turned into a set of ordinary differential equations (ODEs), which were then used in the process of transformation and optimization. To identify a solution, the finest possible technique was used. Graphic representations of the disruptive outcomes for the complex parameters are shown below. The primary results are those that convince.

Aggregation of nanoparticles has a considerable impact on temperature, entropy generation, Nusselt number, skin friction and velocity profiles.
The temperature and entropy generation profiles were expanded due to the volume proportion of alumina particles, which also caused the velocity profile to deteriorate.
Increasing the velocity ratio parameter improved the velocity field while also decreasing the temperature and entropy generation profiles.
The heat generation/absorption parameter led to an increase in the temperature profile's overall magnitude.
Temperature and entropy generation profiles increased due to increasing impact of Eckert number.
The entropy production decreases as the temperature difference parameter increases.
The rate of heat transmission increases as a result of the addition of $ϕ$ and $ε$ respectively. When the suction parameter of $(ε = 0.5)$ is used for the aggregation model, it is claimed that there is an increase of roughly 13.2478% in the heat transfer rate.
When $Ec = 0.5$ is applied heat transfer rate is decreased by 3.0162% for aggregation model.
Skin friction increases for increasing values of $ε, B, γ$ and $M$ with $ϕ .$ With aggregation model shows better performance for $ε, B$ and $M$ with $ϕ$ , whereas without aggregation model shows higher results for $γ .$
Nusselt number profiles decreases against $B, γ$ and $λ$ with $ϕ$ for both models.

7 Future suggestions

It's possible that this will be valuable in studies done in the future to improve the efficiency of heat transmission in contemporary industrial settings. In conclusion, it is claimed that this research is authentic and one of a kind. It is generally believed that the contemporaneous analysis will be of great use in terms of modeling better flow obstructions, particularly in the biomedical sector, for the treatment of cancer, the aeronautical industry, power production, nuclear reactors, and solar thermal absorbers.

It is entirely up to the researcher to decide whether or not to apply the slip conditions to the same model.
The current study may be broadened in such a way that it takes into consideration the commercial uses of the diffusive liquids and nanofluids produced by other species.
It is possible that the work that is now being done will be broadened in the future to cover the unstable condition.
The current investigation may be furthered by exchanging the nanofluid with a new and more sophisticated kind of heat transfer fluid known as hybrid and ternary hybrid nanofluid. In addition to this, the scope of the research may be broadened by taking into account the potential for nanoparticles of varying shapes to escape the working fluid at the same time. This might result in flow issues that are both more difficult and more intriguing.

Ethical approval

Not applicable.

Funding

Not available now.

Acknowledgments

“We would like to thank the reviewers for their thoughtful comments and efforts towards improving our paper”.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Ahmad S., Hayat T., Alsaedi A., Ullah H., Shah F., . Computational modeling and analysis for the effect of magnetic field on rotating stretched disk flow with heat transfer. Propuls. Power Res.. 2021;10(1):48-57.
[Google Scholar]
Akbari S., Faghiri S., Poureslami P., Hosseinzadeh K., Shafii M.B., . Analytical solution of non-Fourier heat conduction in a 3-D hollow sphere under time-space varying boundary conditions. Heliyon. 2022;8(12):e12496.
[Google Scholar]
Alqahtani B., Mahmood Z., Alyami M.A., Alotaibi A.M., Khan U., Galal A.M., . Heat and mass transfer analysis of MHD stagnation point flow of carbon nanotubes with convective stretching disk and viscous dissipation. Adv. Mech. Eng.. 2022;14(10) 16878132221128390
[Google Scholar]
Al-Waeli A.H.A., Chaichan M.T., Sopian K., Kazem H.A., . Influence of the base fluid on the thermo-physical properties of PV/T nanofluids with surfactant. Case Stud. Therm. Eng.. 2019;13:100340
[Google Scholar]
Ambreen T., Saleem A., Park C.W., . Analysis of hydro-thermal and entropy generation characteristics of nanofluid in an aluminium foam heat sink by employing Darcy-Forchheimer-Brinkman model coupled with multiphase Eulerian model. Appl. Therm. Eng.. 2020;173:115231
[Google Scholar]
Animasaun I.L., Asogwa K.K., . Significance of suction and dual stretching: Comparative analysis between the dynamics of water-based alumina nanoparticle aggregation with water-based cupric nanoparticle aggregation. J. Niger. Math. Soc.. 2021;40(3):161-181.
[Google Scholar]
Arul Prakash F., Dushendra Babu G.J., Lavanya M., Shenbaga Vidhya K., Devasena T., . Toxicity studies of aluminium oxide nanoparticles in cell lines. Int. J. Nanotechnol. Appl.. 2011;5(2):99-107.
[Google Scholar]
Bejan, A., 1979. A study of entropy generation in fundamental convective heat transfer.
Cho C.-C., . Effects of porous medium and wavy surface on heat transfer and entropy generation of Cu-water nanofluid natural convection in square cavity containing partially-heated surface. Int. Commun. Heat Mass Transf.. 2020;119:104925
[Google Scholar]
Choi S.U.S., Eastman J.A., . Enhancing thermal conductivity of fluids with nanoparticles. IL (United States): Argonne National Lab; 1995.
Chu Y.-M., Shah F., Khan M.I., Kadry S., Abdelmalek Z., Khan W.A., . Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. J. Mater. Res. Technol.. 2020;9(6):13977-13987.
[Google Scholar]
Dutta S., Goswami N., Biswas A.K., Pati S., . Numerical investigation of magnetohydrodynamic natural convection heat transfer and entropy generation in a rhombic enclosure filled with Cu-water nanofluid. Int. J. Heat Mass Transf.. 2019;136:777-798.
[Google Scholar]
Faghiri S., Akbari S., Shafii M.B., Hosseinzadeh K., . Hydrothermal analysis of non-Newtonian fluid flow (blood) through the circular tube under prescribed non-uniform wall heat flux. Theor. Appl. Mech. Lett.. 2022;12(4):100360
[Google Scholar]
Fallah Najafabadi M., Talebi Rostami H., Hosseinzadeh K., Ganji D.D., . Hydrothermal study of nanofluid flow in channel by RBF method with exponential boundary conditions. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022 09544089221133909
[Google Scholar]
Farhana K., . Significance of alumina in nanofluid technology. J. Therm. Anal. Calorim.. 2019;138(2):1107-1126.
[Google Scholar]
Gholamalipour P., Siavashi M., Doranehgard M.H., . Eccentricity effects of heat source inside a porous annulus on the natural convection heat transfer and entropy generation of Cu-water nanofluid. Int. Commun. Heat Mass Transf.. 2019;109:104367
[Google Scholar]
Gulzar M.M., Aslam A., Waqas M., Javed M.A., Hosseinzadeh K., . A nonlinear mathematical analysis for magneto-hyperbolic-tangent liquid featuring simultaneous aspects of magnetic field, heat source and thermal stratification. Appl. Nanosci.. 2020;10:4513-4518.
[Google Scholar]
Hafeez A., Khan M., . Flow of Oldroyd-B fluid caused by a rotating disk featuring the Cattaneo-Christov theory with heat generation/absorption. Int. Commun. Heat Mass Transf.. 2021;123:105179
[Google Scholar]
Hassan M.I., Alzarooni I.A., Shatilla Y., . The effect of water-based nanofluid incorporating Al2O3 nanoparticles on heat pipe performance. Energy Procedia. 2015;75:3201-3206.
[Google Scholar]
Hayat T., Shah F., Khan M.I., Alsaedi A., Yasmeen T., . Modeling MHD stagnation point flow of thixotropic fluid with non-uniform heat absorption/generation. Microgravity Sci. Technol.. 2017;29:459-465.
[Google Scholar]
Hosseinzadeh K., . Investigation of second grade viscoelastic non-Newtonian nanofluid flow on the curve stretching surface in presence of MHD. Results Eng.. 2023;17:100838
[Google Scholar]
Khan A., Shah Z., Alzahrani E., Islam S., . Entropy generation and thermal analysis for rotary motion of hydromagnetic Casson nanofluid past a rotating cylinder with Joule heating effect. Int. Commun. Heat Mass Transf.. 2020;119:104979
[Google Scholar]
Li Z., Hussein A.K., Younis O., Afrand M., Feng S., . Natural convection and entropy generation of a nanofluid around a circular baffle inside an inclined square cavity under thermal radiation and magnetic field effects. Int. Commun. Heat Mass Transf.. 2020;116:104650
[Google Scholar]
Li Y.-X., Shah F., Khan M.I., Chinram R., Elmasry Y., Sun T.-C., . Dynamics of Cattaneo-Christov Double Diffusion (CCDD) and arrhenius activation law on mixed convective flow towards a stretched Riga device. Chaos, Solitons & Fractals. 2021;148:111010
[Google Scholar]
Lin C.-Y., Wang J.-C., Chen T.-C., . Analysis of suspension and heat transfer characteristics of Al2O3 nanofluids prepared through ultrasonic vibration. Appl. Energy. 2011;88(12):4527-4533.
[Google Scholar]
Liu H., Animasaun I.L., Shah N.A., Koriko O.K., Mahanthesh B., . Further discussion on the significance of quartic autocatalysis on the dynamics of water conveying 47 nm alumina and 29 nm cupric nanoparticles. Arab. J. Sci. Eng.. 2020;45(7):5977-6004.
[Google Scholar]
Mackolil J., Mahanthesh B., . Sensitivity analysis of Marangoni convection in TiO2–EG nanoliquid with nanoparticle aggregation and temperature-dependent surface tension. J. Therm. Anal. Calorim.. 2021;143(3):2085-2098.
[Google Scholar]
Mackolil J., Mahanthesh B., . Inclined magnetic field and nanoparticle aggregation effects on thermal Marangoni convection in nanoliquid: a sensitivity analysis. Chinese J. Phys.. 2021;69:24-37.
[Google Scholar]
Madhukesh J.K., Prasannakumara B.C., Khan U., Madireddy S., Raizah Z., Galal A.M., . Time-Dependent stagnation point flow of water conveying titanium dioxide nanoparticle aggregation on rotating sphere object experiencing thermophoresis particle deposition effects. Energies. 2022;15(12):4424.
[Google Scholar]
Mahanthesh B., . Flow and heat transport of nanomaterial with quadratic radiative heat flux and aggregation kinematics of nanoparticles. Int. Commun. Heat Mass Transf.. 2021;127:105521
[Google Scholar]
Mahmood Z., Alhazmi S.E., Alhowaity A., Marzouki R., Al-Ansari N., Khan U., . MHD mixed convective stagnation point flow of nanofluid past a permeable stretching sheet with nanoparticles aggregation and thermal stratification. Sci. Rep.. 2022;12(1):1-26.
[Google Scholar]
Mahmood Z., Khan U., . Nanoparticles aggregation effects on unsteady stagnation point flow of hydrogen oxide-based nanofluids. Eur. Phys. J. Plus. 2022;137(6):1-28.
[Google Scholar]
Mahmood Z., Eldin S.M., Soliman A.F., Assiri T.A., Khan U., Mahmoud S.R., . Impact of an effective Prandtl number model on the flow of nanofluids past an oblique stagnation point on a convective surface. Heliyon 2023
[Google Scholar]
Masood, S., Farooq, M., 2021. Influence of Heat Generation/Absorption and Stagnation point on Polystyrene-TiO₂/H₂O Hybrid Nanofluid.
Masood S., Farooq M., Ahmad S., Anjum A., Mir N.A., . Investigation of viscous dissipation in the nanofluid flow with a Forchheimer porous medium: modern transportation of heat and mass. Eur. Phys. J. Plus. 2019;134(4):178.
[Google Scholar]
Mishra A., Kumar M., . Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl. Sci.. 2020;2(8):1-13.
[Google Scholar]
Mishra A., Kumar M., . Thermal performance of MHD nanofluid flow over a stretching sheet due to viscous dissipation, Joule heating and thermal radiation. Int. J. Appl. Comput. Math.. 2020;6(4):123.
[Google Scholar]
Mishra A., Kumar M., . Numerical analysis of MHD nanofluid flow over a wedge, including effects of viscous dissipation and heat generation/absorption, using Buongiorno model. Heat Transf.. 2021;50(8):8453-8474.
[Google Scholar]
Motlagh M.B., Kalteh M., . Molecular dynamics simulation of nanofluid convective heat transfer in a nanochannel: Effect of nanoparticles shape, aggregation and wall roughness. J. Mol. Liq.. 2020;318:114028
[Google Scholar]
Oke A.S., Animasaun I.L., Mutuku W.N., Kimathi M., Shah N.A., Saleem S., . Significance of Coriolis force, volume fraction, and heat source/sink on the dynamics of water conveying 47 nm alumina nanoparticles over a uniform surface. Chinese J. Phys.. 2021;71:716-727.
[Google Scholar]
Parida S.K., . Dynamics of dust particles in a conducting water-based kerosene nanomaterials: a computational approach. Int. J. Chem. React. Eng.. 2021;19(8):787-797.
[Google Scholar]
Qian W.-M., . Mathematical modeling and MHD flow of micropolar fluid toward an exponential curved surface: heat analysis via ohmic heating and heat source/sink. Arab. J. Sci. Eng.. 2022;47(1):867-878.
[Google Scholar]
Sabu A.S., Mackolil J., Mahanthesh B., Mathew A., . Nanoparticle aggregation kinematics on the quadratic convective magnetohydrodynamic flow of nanomaterial past an inclined flat plate with sensitivity analysis. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng.. 2022;236(3):1056-1066.
[Google Scholar]
Song Y.-Q., Obideyi B.D., Shah N.A., Animasaun I.L., Mahrous Y.M., Chung J.D., . Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Stud. Therm. Eng.. 2021;26:101050
[Google Scholar]
Swain K., Mahanthesh B., . Thermal enhancement of radiating magneto-nanoliquid with nanoparticles aggregation and joule heating: a three-dimensional flow. Arab. J. Sci. Eng.. 2021;46:5865-5873.
[Google Scholar]
Syarif D.G., . Characteristics of ethylene glycol-Al2O3 nanofluids prepared by utilizing Al2O3 nanoparticles synthesized from local bauxite. Journal of Physics: Conference Series. 2016;776(1):12042.
[Google Scholar]
Upreti H., Mishra A., . The performance evolution of hybrid nanofluid flow over a rotating disk using Cattaneo-Christov double diffusion and Yamada-Ota model. Waves in Random and Complex Media 2022:1-21.
[Google Scholar]
Wolthers W., Duits M.H.G., Van Den Ende D., Mellema J., . Shear history dependence of the viscosity of aggregated colloidal dispersions. J. Rheol. (N. Y. N. Y). 1996;40(5):799-811.
[Google Scholar]
Zangooee M.R., Hosseinzadeh K., Ganji D.D., . Hydrothermal analysis of Hybrid nanofluid flow on a vertical plate by considering slip condition. Theor. Appl. Mech. Lett.. 2022;12(5):100357
[Google Scholar]

Introduction

Description of the problem

Entropy generation

Method of solution and code validation

Analysis and discussion of results

Analysis of results
Discussion of results

Conclusion

Future suggestions

Ethical approval

Funding

Fulltext Views
5

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Ahmad S., Hayat T., Alsaedi A., Ullah H., Shah F., . Computational modeling and analysis for the effect of magnetic field on rotating stretched disk flow with heat transfer. Propuls. Power Res.. 2021;10(1):48-57.
[Google Scholar]

[2] Akbari S., Faghiri S., Poureslami P., Hosseinzadeh K., Shafii M.B., . Analytical solution of non-Fourier heat conduction in a 3-D hollow sphere under time-space varying boundary conditions. Heliyon. 2022;8(12):e12496.
[Google Scholar]

[3] Alqahtani B., Mahmood Z., Alyami M.A., Alotaibi A.M., Khan U., Galal A.M., . Heat and mass transfer analysis of MHD stagnation point flow of carbon nanotubes with convective stretching disk and viscous dissipation. Adv. Mech. Eng.. 2022;14(10) 16878132221128390
[Google Scholar]

[4] Al-Waeli A.H.A., Chaichan M.T., Sopian K., Kazem H.A., . Influence of the base fluid on the thermo-physical properties of PV/T nanofluids with surfactant. Case Stud. Therm. Eng.. 2019;13:100340
[Google Scholar]

[5] Ambreen T., Saleem A., Park C.W., . Analysis of hydro-thermal and entropy generation characteristics of nanofluid in an aluminium foam heat sink by employing Darcy-Forchheimer-Brinkman model coupled with multiphase Eulerian model. Appl. Therm. Eng.. 2020;173:115231
[Google Scholar]

[6] Animasaun I.L., Asogwa K.K., . Significance of suction and dual stretching: Comparative analysis between the dynamics of water-based alumina nanoparticle aggregation with water-based cupric nanoparticle aggregation. J. Niger. Math. Soc.. 2021;40(3):161-181.
[Google Scholar]

[7] Arul Prakash F., Dushendra Babu G.J., Lavanya M., Shenbaga Vidhya K., Devasena T., . Toxicity studies of aluminium oxide nanoparticles in cell lines. Int. J. Nanotechnol. Appl.. 2011;5(2):99-107.
[Google Scholar]

[8] Bejan, A., 1979. A study of entropy generation in fundamental convective heat transfer.

[9] Cho C.-C., . Effects of porous medium and wavy surface on heat transfer and entropy generation of Cu-water nanofluid natural convection in square cavity containing partially-heated surface. Int. Commun. Heat Mass Transf.. 2020;119:104925
[Google Scholar]

[10] Choi S.U.S., Eastman J.A., . Enhancing thermal conductivity of fluids with nanoparticles. IL (United States): Argonne National Lab; 1995.

[11] Chu Y.-M., Shah F., Khan M.I., Kadry S., Abdelmalek Z., Khan W.A., . Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. J. Mater. Res. Technol.. 2020;9(6):13977-13987.
[Google Scholar]

[12] Dutta S., Goswami N., Biswas A.K., Pati S., . Numerical investigation of magnetohydrodynamic natural convection heat transfer and entropy generation in a rhombic enclosure filled with Cu-water nanofluid. Int. J. Heat Mass Transf.. 2019;136:777-798.
[Google Scholar]

[13] Faghiri S., Akbari S., Shafii M.B., Hosseinzadeh K., . Hydrothermal analysis of non-Newtonian fluid flow (blood) through the circular tube under prescribed non-uniform wall heat flux. Theor. Appl. Mech. Lett.. 2022;12(4):100360
[Google Scholar]

[14] Fallah Najafabadi M., Talebi Rostami H., Hosseinzadeh K., Ganji D.D., . Hydrothermal study of nanofluid flow in channel by RBF method with exponential boundary conditions. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022 09544089221133909
[Google Scholar]

[15] Farhana K., . Significance of alumina in nanofluid technology. J. Therm. Anal. Calorim.. 2019;138(2):1107-1126.
[Google Scholar]

[16] Gholamalipour P., Siavashi M., Doranehgard M.H., . Eccentricity effects of heat source inside a porous annulus on the natural convection heat transfer and entropy generation of Cu-water nanofluid. Int. Commun. Heat Mass Transf.. 2019;109:104367
[Google Scholar]

[17] Gulzar M.M., Aslam A., Waqas M., Javed M.A., Hosseinzadeh K., . A nonlinear mathematical analysis for magneto-hyperbolic-tangent liquid featuring simultaneous aspects of magnetic field, heat source and thermal stratification. Appl. Nanosci.. 2020;10:4513-4518.
[Google Scholar]

[18] Hafeez A., Khan M., . Flow of Oldroyd-B fluid caused by a rotating disk featuring the Cattaneo-Christov theory with heat generation/absorption. Int. Commun. Heat Mass Transf.. 2021;123:105179
[Google Scholar]

[19] Hassan M.I., Alzarooni I.A., Shatilla Y., . The effect of water-based nanofluid incorporating Al2O3 nanoparticles on heat pipe performance. Energy Procedia. 2015;75:3201-3206.
[Google Scholar]

[20] Hayat T., Shah F., Khan M.I., Alsaedi A., Yasmeen T., . Modeling MHD stagnation point flow of thixotropic fluid with non-uniform heat absorption/generation. Microgravity Sci. Technol.. 2017;29:459-465.
[Google Scholar]

[21] Hosseinzadeh K., . Investigation of second grade viscoelastic non-Newtonian nanofluid flow on the curve stretching surface in presence of MHD. Results Eng.. 2023;17:100838
[Google Scholar]

[22] Khan A., Shah Z., Alzahrani E., Islam S., . Entropy generation and thermal analysis for rotary motion of hydromagnetic Casson nanofluid past a rotating cylinder with Joule heating effect. Int. Commun. Heat Mass Transf.. 2020;119:104979
[Google Scholar]

[23] Li Z., Hussein A.K., Younis O., Afrand M., Feng S., . Natural convection and entropy generation of a nanofluid around a circular baffle inside an inclined square cavity under thermal radiation and magnetic field effects. Int. Commun. Heat Mass Transf.. 2020;116:104650
[Google Scholar]

[24] Li Y.-X., Shah F., Khan M.I., Chinram R., Elmasry Y., Sun T.-C., . Dynamics of Cattaneo-Christov Double Diffusion (CCDD) and arrhenius activation law on mixed convective flow towards a stretched Riga device. Chaos, Solitons & Fractals. 2021;148:111010
[Google Scholar]

[25] Lin C.-Y., Wang J.-C., Chen T.-C., . Analysis of suspension and heat transfer characteristics of Al2O3 nanofluids prepared through ultrasonic vibration. Appl. Energy. 2011;88(12):4527-4533.
[Google Scholar]

[26] Liu H., Animasaun I.L., Shah N.A., Koriko O.K., Mahanthesh B., . Further discussion on the significance of quartic autocatalysis on the dynamics of water conveying 47 nm alumina and 29 nm cupric nanoparticles. Arab. J. Sci. Eng.. 2020;45(7):5977-6004.
[Google Scholar]

[27] Mackolil J., Mahanthesh B., . Sensitivity analysis of Marangoni convection in TiO2–EG nanoliquid with nanoparticle aggregation and temperature-dependent surface tension. J. Therm. Anal. Calorim.. 2021;143(3):2085-2098.
[Google Scholar]

[28] Mackolil J., Mahanthesh B., . Inclined magnetic field and nanoparticle aggregation effects on thermal Marangoni convection in nanoliquid: a sensitivity analysis. Chinese J. Phys.. 2021;69:24-37.
[Google Scholar]

[29] Madhukesh J.K., Prasannakumara B.C., Khan U., Madireddy S., Raizah Z., Galal A.M., . Time-Dependent stagnation point flow of water conveying titanium dioxide nanoparticle aggregation on rotating sphere object experiencing thermophoresis particle deposition effects. Energies. 2022;15(12):4424.
[Google Scholar]

[30] Mahanthesh B., . Flow and heat transport of nanomaterial with quadratic radiative heat flux and aggregation kinematics of nanoparticles. Int. Commun. Heat Mass Transf.. 2021;127:105521
[Google Scholar]

[31] Mahmood Z., Alhazmi S.E., Alhowaity A., Marzouki R., Al-Ansari N., Khan U., . MHD mixed convective stagnation point flow of nanofluid past a permeable stretching sheet with nanoparticles aggregation and thermal stratification. Sci. Rep.. 2022;12(1):1-26.
[Google Scholar]

[32] Mahmood Z., Khan U., . Nanoparticles aggregation effects on unsteady stagnation point flow of hydrogen oxide-based nanofluids. Eur. Phys. J. Plus. 2022;137(6):1-28.
[Google Scholar]

[33] Mahmood Z., Eldin S.M., Soliman A.F., Assiri T.A., Khan U., Mahmoud S.R., . Impact of an effective Prandtl number model on the flow of nanofluids past an oblique stagnation point on a convective surface. Heliyon 2023
[Google Scholar]

[34] Masood, S., Farooq, M., 2021. Influence of Heat Generation/Absorption and Stagnation point on Polystyrene-TiO₂/H₂O Hybrid Nanofluid.

[35] Masood S., Farooq M., Ahmad S., Anjum A., Mir N.A., . Investigation of viscous dissipation in the nanofluid flow with a Forchheimer porous medium: modern transportation of heat and mass. Eur. Phys. J. Plus. 2019;134(4):178.
[Google Scholar]

[36] Mishra A., Kumar M., . Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and Joule heating. SN Appl. Sci.. 2020;2(8):1-13.
[Google Scholar]

[37] Mishra A., Kumar M., . Thermal performance of MHD nanofluid flow over a stretching sheet due to viscous dissipation, Joule heating and thermal radiation. Int. J. Appl. Comput. Math.. 2020;6(4):123.
[Google Scholar]

[38] Mishra A., Kumar M., . Numerical analysis of MHD nanofluid flow over a wedge, including effects of viscous dissipation and heat generation/absorption, using Buongiorno model. Heat Transf.. 2021;50(8):8453-8474.
[Google Scholar]

[39] Motlagh M.B., Kalteh M., . Molecular dynamics simulation of nanofluid convective heat transfer in a nanochannel: Effect of nanoparticles shape, aggregation and wall roughness. J. Mol. Liq.. 2020;318:114028
[Google Scholar]

[40] Oke A.S., Animasaun I.L., Mutuku W.N., Kimathi M., Shah N.A., Saleem S., . Significance of Coriolis force, volume fraction, and heat source/sink on the dynamics of water conveying 47 nm alumina nanoparticles over a uniform surface. Chinese J. Phys.. 2021;71:716-727.
[Google Scholar]

[41] Parida S.K., . Dynamics of dust particles in a conducting water-based kerosene nanomaterials: a computational approach. Int. J. Chem. React. Eng.. 2021;19(8):787-797.
[Google Scholar]

[42] Qian W.-M., . Mathematical modeling and MHD flow of micropolar fluid toward an exponential curved surface: heat analysis via ohmic heating and heat source/sink. Arab. J. Sci. Eng.. 2022;47(1):867-878.
[Google Scholar]

[43] Sabu A.S., Mackolil J., Mahanthesh B., Mathew A., . Nanoparticle aggregation kinematics on the quadratic convective magnetohydrodynamic flow of nanomaterial past an inclined flat plate with sensitivity analysis. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng.. 2022;236(3):1056-1066.
[Google Scholar]

[44] Song Y.-Q., Obideyi B.D., Shah N.A., Animasaun I.L., Mahrous Y.M., Chung J.D., . Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Stud. Therm. Eng.. 2021;26:101050
[Google Scholar]

[45] Swain K., Mahanthesh B., . Thermal enhancement of radiating magneto-nanoliquid with nanoparticles aggregation and joule heating: a three-dimensional flow. Arab. J. Sci. Eng.. 2021;46:5865-5873.
[Google Scholar]

[46] Syarif D.G., . Characteristics of ethylene glycol-Al2O3 nanofluids prepared by utilizing Al2O3 nanoparticles synthesized from local bauxite. Journal of Physics: Conference Series. 2016;776(1):12042.
[Google Scholar]

[47] Upreti H., Mishra A., . The performance evolution of hybrid nanofluid flow over a rotating disk using Cattaneo-Christov double diffusion and Yamada-Ota model. Waves in Random and Complex Media 2022:1-21.
[Google Scholar]

[48] Wolthers W., Duits M.H.G., Van Den Ende D., Mellema J., . Shear history dependence of the viscosity of aggregated colloidal dispersions. J. Rheol. (N. Y. N. Y). 1996;40(5):799-811.
[Google Scholar]

[49] Zangooee M.R., Hosseinzadeh K., Ganji D.D., . Hydrothermal analysis of Hybrid nanofluid flow on a vertical plate by considering slip condition. Theor. Appl. Mech. Lett.. 2022;12(5):100357
[Google Scholar]

Significance of entropy generation and nanoparticle aggregation on stagnation point flow of nanofluid over stretching sheet with inclined Lorentz force

Abstract

Keywords

Stagnation point flow

Aggregation effect

Heat generation/absorption

Inclined Lorentz force

Entropy generation

Viscous dissipation

Nomenclature

Subscripts

Superscripts

1 Introduction

2 Description of the problem

3 Entropy generation

4 Method of solution and code validation

5 Analysis and discussion of results

5.1 Analysis of results

5.2 Discussion of results

6 Conclusion

7 Future suggestions

Ethical approval

Funding

Acknowledgments

Declaration of Competing Interest

References

Suggested read for related articles: