Translate this page into:
Solubility of buprenorphine hydrochloride in supercritical carbon dioxide: Study on experimental measuring and thermodynamic modeling
⁎Corresponding author. sodeifian@kashanu.ac.ir (Gholamhossein Sodeifian)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Abstract
Solubility of buprenorphine hydrochloride in scCO2 was measured for the first time. Equilibrium conditions were selected at T and P of 308–338 K and 120–270 bar. Experimental data were correlated by PR EoS and different semi-empirical models. The ability of the employed models was evaluated. Total and vaporization enthalpies of buprenorphine dissolution in scCO2 were estimated.
Abstract
Nowadays, supercritical fluids (SCFs) technologies present a processing option for obtaining new products with noteworthy characteristics. Access to reliable solubility data of pharmaceutical compounds in SCFs is considered as the first step for recrystallizing, separating, and producing nano particles via processes based on this type of technique. In this study, high-pressure solubility of buprenorphine hydrochloride, a strong pain reliever, in supercritical carbon dioxide (scCO2) was measured at temperature and pressure conditions of 308–338 K and 120–270 bar, for the first time. The minimum and maximum solubility values, in terms of equilibrium mole fractions, were found to be 0.131 × 10-4 (at 338 K and 120 bar) and 4.752 × 10-4 (at 338 K and 270 bar), respectively. Thereafter, the obtained data were correlated using two different approaches, namely Peng-Robinson (PR) equation of state (EoS) and a set of semi-empirical models. Results from applying statistical criteria indicated that Jouyban and Sodeifian models are suitable choices for predicting solubility data. Furthermore, using the obtained correlation results, the total and vaporization enthalpies of buprenorphine hydrochloride dissolution in scCO2 were estimated to be 65.59 and 85.60 kJ/mole, respectively.
Keywords
Supercritical carbon dioxide
Solubility
Buprenorphine hydrochloride
Sodeifian model
Peng-Robinson equation of state
1 Introduction
Buprenorphine hydrochloride is a semi-synthetic opiate and in a class of medications called narcotic analgesics. By exhibiting a unique functionality related to its concurrent agonist and antagonist activities, buprenorphine can block pain signals through binding either to the specific cellular receptors or on the surface of the nerve cells at different organs of the body. Therefore, it is capable of relieving moderate to severe pain from different origins, (e.g., surgical operation, injuries, and cancer (Heel et al., 1979) with an analgesic potency greater than that of morphine. Nowadays, they are commonly applied for the treatment of opioid dependency such as heroin addiction. Buprenorphine carries a complex-structure molecule with a lipophilic nature. The structural formula for buprenorphine is given in Fig. 1 (Johnson et al., 2005).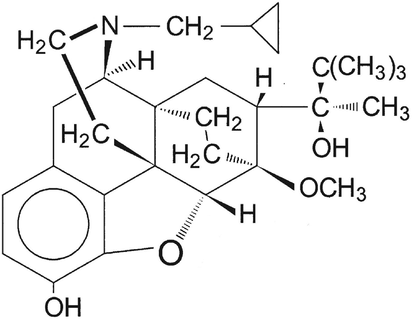
Chemical structure of buprenorphine hydrochloride.
Although different delivery formulations for buprenorphine have been presented, oral bioavailability of this medicine, in the form of both syrup and tablet, was reported to be low (Poliwoda et al., 2022). It means that a high dose of the medicine is required to obtain the planned pharmacological effects, especially for the treatment of opioid dependency for which a much more doses are needed. This associated issue not only with buprenorphine but with a great deal of lipophilic medicines is one of the most important problems facing pharmaceutical industries. However, a number a solutions have been investigated to tackle the problem, one of which is minimizing the size of buprenorphine particles to micro and nano scale (Desai et al., 2012). Reduction of the particle size of the solids through conventional techniques such as recrystallization and spray drying often forces some disadvantages including high energy and organic solvent consumption, environmental pollution and thermal degradation of the products. In recent years, several green and efficient processes based on SCFs technologies such as rapid expansion of supercritical solutions (RESS (Türk, 2022)) and supercritical anti-solvent (SAS (Reverchon et al., 2007)) have attracted attentions due to their beneficial advantages (De Marco, 2022), which cause them to surpass conventional technologies through bringing desirable particle size distribution, reducing the possibly side effects of the drugs, and effectively improving the bioavailability and bioactivity of the medical compounds. To develop and commercialize these pharmaceutical processes, reliable experimental data on the solubility behavior of solid drugs at different conditions of temperature and pressure of the supercritical medium along with phase transitions of the system are of high value. While access to these solubility data through experimental performances are often laborious and time consuming, the use of mathematical approaches such as thermodynamic equations of state (EoSs), empirical and semi-empirical models and other predictive methods on the basis of artificial intelligence (AI) are greatly helpful to researchers. In this regard, selection of a well-established way with an acceptable accuracy is crucial. Frequently used cubic EoSs for CO2 containing systems include Peng-Robinson (Araújo and Meireles, 2000; Lopez-Echeverry et al., 2017; Notej et al., 2023; Sodeifian et al., 2023) and modified Redlich-Kwong (Sako et al., 1988; Valderrama and Silva, 2003; Madras, 2004; Heidaryan and Jarrahian, 2013) EoSs with different mixing rules such as Wong-Sandler (WS), Orbey-Sandler (OS), van der Waals types 1 or 2 (vdW1 and vdW2, respectively), Huron-Vidal (HV), Kwak-Mansoori (KM), and covolume dependent (CVD) (Shimoyama et al., 2008; Esmaeilzadeh et al., 2009; Mansoori and Ely, 1985; Kwak and Mansoori, 1986; Lashkarbolooki et al., 2011; Sodeifian et al., 2023). On the other side, several semi-empirical density based models were proposed in recent decades for solid–fluid equilibrium including Adachi-Lu (Adachi and Lu, 1983); Kumar-Johnston (Kumar and Johnston, 1988); del Valle-Aguilera (Del Valle and Aguilera, 1988); Chrastil (Chrastil, 1982), Bartle (Bartle et al., 1991), Mendez-Santiago-Teja (Méndez-Santiago and Teja, 1999); Keshmiri (Keshmiri et al., 2014); Bian (Bian et al., 2016); Khansary (Khansary et al., 2015), and Alwi-Garlapati (Alwi and Garlapati, 2021). However, correlation process of an EoS with experimental data is more complicated than that of semi-empirical models. Because the former requires many thermodynamic properties of pure solid solute such as critical temperature and pressure as well as Pitzer’s acentric factor, while the latter is independent of these properties and has been developed only by involving equilibrium conditions and density of the system. General form and the number of adjustable parameters are the main differences among semi-empirical models. These adjustable parameters differ from one solute to another and are usually determined by least square curve fitting with experimental data. It seems that density based semi-empirical models with more adjustable parameters show better accuracy for correlating the experimental data. Application of different machine learning-based models such as Kernel Ridge Regression (KRR), Random forest (RF), and Multilayer Perceptron (MLP) are the other subjects of recently published papers that have reported to successfully predict and optimize the solid solutes solubility especially pharmaceutical compounds in the SCFs (Alzhrani et al., 2022; Najmi at el., 2022; Nateghi et al., 2023; Rezaei et al., 2022; Tianhao et al., 2022). Lower sensitivity to incomplete or noisy experimental data, reduced time consumption, and better fitting with solubility points of nonlinear behavior have caused the machine learning- based models to find more popularity among researchers (Cao et al., 2021; Waskita et al., 2023).
Considering the critical constants of the compounds available in the literature (Sapkale et al., 2010) to be employed in the SCFs technologies, ethane and ethylene would be found appropriate at first. But it should be noted that several factors such as flammability and explosive properties can restrict their usage. Being non-flammable, non-toxic, and non-expensive as well as involving other favorable properties (Nikolai et al., 2019), supercritical carbon dioxide (scCO2) has been known as the most applied agent in the different fields of research and development, e.g., material processing (Eckert et al., 1996; Zhang et al., 2014), oil and gas industry (Pavlova et al., 2022), catalyst regeneration (Vradman et al., 2001; Ghadirinejad et al., 2021), extraction from natural substrates (Liza et al., 2010; Sodeifian et al., 2017; Sodeifian and Sajadian, 2017; Tyśkiewicz et al., 2018; Hossein Zadeh et al., 2023), fabrication of polymer foams and hydrogels (Daneshyan and Sodeifian, 2022a,b; Kong at el., 2016; Liang and Wang, 2000; Tsioptsias et al., 2011), nanoparticle formation (Byrappa et al., 2008; Erkey, 2009; Ardestani et al., 2020; Franco and De Marco, 2021; Sodeifian et al., 2022), power generation (Crespi et al., 2017; White et al., 2021), and chromatographic analysis (Bernal et al., 2013; Desfontaine et al., 2015).
The focus of this research is to identify the solubility behavior of buprenorphine hydrochloride in scCO2 and to evaluate the correlating ability of Peng-Robinson (PR) EoS and a set of well-known density based models. For this purpose, the equilibrium solubility of buprenorphine hydrochloride in scCO2 was measured at temperatures of 308–338 K and pressures of 120–270 bar. Thereafter, the obtained experimental data were applied with the following approaches:
1) PR EoS with two different mixing rules, namely van der Waals type 2 (vdW2) and covolume dependent (CVD),
2) Eight semi-empirical models, namely Chrastil, Madras, Bartle, Jouyban, Bian, Wang, Belghait and Sodeifian models.
To determine the capability of each model for describing the solubility of buprenorphine hydrochloride in scCO2, some statistical criteria including average absolute relative deviation ( ), adjusted correlation coefficient ( ), and F-test were applied.
2 Experiment
2.1 Materials
Buprenorphine hydrochloride in the form of crystalline white powder, with the purity exceeding 99% was purchased from Temad CO. (Karaj, Iran). More information on the physicochemical properties of buprenorphine hydrochloride is listed in Table 1. Carbon dioxide (CO2), compressed in the storage cylinder, with a purity of 99% was supplied by Fadak Company (Kashan, Iran). An Analytical reagent grade of methanol with the minimum purity of 99.5%, produced by Merck (Darmstadt, Germany), was selected as the collecting solvent for buprenorphine hydrochloride after the solubility process.
Compound
Expanded formula
CAS Number
Molar mass, M (g/mole)
Peak wavelength at ultraviolet spectrum, λmax (nm)
Purity
Buprenorphine HCl
C29H42ClNO4
53152–21-9
504.10
285.5
≥ 99%
Carbon dioxide
CO2
124–38-9
44.01
–
99%
Methanol
CH3OH
67–56-1
32.04
207
≥ 95%
PR EoS
2.2 Apparatus and experimental procedure
Fig. 2 gives a general view on the experimental process utilized to measure the solubility of buprenorphine hydrochloride in scCO2. As can be seen, CO2 storage cylinder, refrigerator, reciprocating pump, oven, temperature and pressure controlling devices, equilibrium cell, and sample collector make the main parts of the process. Directing from storage cylinder to the refrigerator, after passing a molecular sieve filter with a pore size of 1 µm, gaseous CO2 got liquefied and ready for pumping. Installed after refrigerator, the reciprocating pump (Haskel pump, MSHP-110) provided the desired pressure of supercritical state for CO2. Applying a pressure gauge (WIKA, Germany), the pressure of scCO2 was monitored at an uncertainty of 1 bar. Furthermore, a precise oven (Froilabo AE-60, France) played the role of keeping and controlling the planned temperature of solubility tests at an uncertainty of 0.1 K, through a digital display showing regulated and actual temperature values. Each experiment was started by introducing prepared scCO2 into the solubility cell containing uniformly mixed powder and glass beads. By fixing filter plates on the both ends of the equilibrium cell, undissolved particles were prevented from running out. After passing the equilibration time, set to 60 min, a given volume of saturated fluid was discharged through the sampling loop into a collection vial preloaded with 4 ml methanol. Then, by introducing 1 ml methanol into the rinse tube, precipitated particles in the sampling tube were also discharged.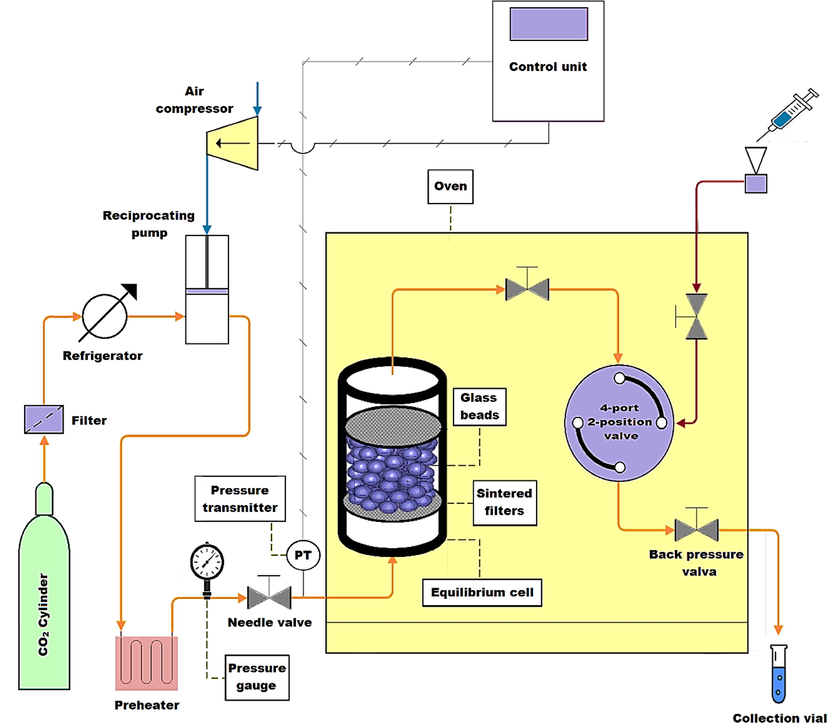
Schematic representation of the experimental setup utilized in this study.
The concentration value of buprenorphine in each collection vial was determined using an established calibration curve obtained from concentration analyzing the solutions on an UV–Vis spectrophotometer (Cintra-101) at the maximum wavelength (λmax) of 285.5 nm (see Table 1). For this purpose, buprenorphine solutions along with a set of standard ones were loaded on the quartz cells of the spectrophotometer setup. Using the obtained absorbance results, the equilibrium mole fraction (
) and solubility (
, in terms of gram per liter) values of buprenorphine in scCO2, corresponding to different operating conditions, were calculated as follows:
Where,
and
are the number of moles and molecular mass of the components (see Table 1), respectively. The system was assumed to be binary, i.e., including carbon dioxide (denoted by subscript 1) and buprenorphine hydrochloride (denoted by subscript 2).
represents density of CO2 at the corresponding temperature and pressure of each test.
and
are the volumes of the collected solution (5 × 10-3 L) and sampling loop (600 × 10-6 L), respectively.
as the concentration of buprenorphine (in terms of gram per liter) corresponding to each test, was obtained from the calibration curve. To define a direct relationship between the equilibrium solubility and mole fraction of buprenorphine hydrochloride in scCO2, Eq. (4) can be rewritten in the following form:
Sodeifian and coworkers have utilized repeatedly this apparatus for different scCO2 based processes associated with medical compounds such as solubility measurements of hydro- and lipophilic drugs (Sodeifian et al., 2018; Sodeifian et al., 2023; Abadian et al., 2023; Sodeifian et al., 2023), impregnation of solid medicines into polymer films (Ameri et al., 2020; Fathi et al., 2022), production of medical nanoparticles via various techniques including gas anti-solvent (GAS (Sodeifian et al., 2022)), rapid expansion of supercritical solution with and without solid co-solvent (RESS-SC (Sodeifian and Sajadian, 2018) and RESS (Sodeifian et al., 2019), respectively), rapid expansion of supercritical solution into aqueous solution (RESSAS (Sodeifian et al., 2019), and ultrasonic assisted rapid expansion of a supercritical solution into a liquid solvent (US-RESOLV (Sodeifian and Sajadian, 2019; Razmimanesh et al., 2021)). Therefore, further details about the apparatus are available in their published papers.
3 Mathematical approaches
3.1 Equations of state (EoSs)
Considering thermodynamics principles (Prausnitz et al., 1998), equilibrium mole fraction of a solid solute in a high pressurized fluid can be calculated by equating the fugacity values of the considered component in two phases, as presented below:
Where
and
are fugacity values of component i in the solid and fluid phases, respectively. Each side of Eq. (6) can be replaced by the following relationships:
Where and represent equilibrium mole fraction and partial pressure of the solute in the mixture at equilibrium conditions. represents universal constant of ideal gas. By involving assumptions below, the final form of Eq. (6) can be simplified to Eq. (9):
1) As mentioned above, the system is composed of two components, i.e., scCO2 (denoted by subscript 1) and buprenorphine hydrochloride (denoted by subscript 2).
2) Solid phase is thoroughly pure, composed of component 2.
3) Carbon dioxide is insoluble in the solid phase.
4) Solid molar volume ( ) is persistently constant, independent of the fluid pressure.
5) Equilibrium pressure of the system ( ) is much higher than solute’s vapor pressure ( ).
6) Fugacity coefficient of the solute at equilibrium (
) equals 1, because of its negligible vapor pressure (
).
As can be seen, equilibrium solubility of buprenorphine, in terms of mole fraction, depends on its physical properties, i.e., vapor pressure, fugacity coefficient in fluid phase (
), and solid molar volume (
) at the equilibrium temperature and pressure of the system. With respect to this fact the required data to solve Eq. (9) for buprenorphine have not yet been reported, the group contribution methods were followed to estimate the values. For this purpose, the methods proposed by Lee-Kesler (Lee and Kesler, 1975) and Fedors (Fedors, 1974) were used in this study to estimate values of
and
, respectively.
was also computed by the relationship below, applying Peng-Robinson (PR) EoS (Peng and Robinson, 1976), with the detailed presentation in Table 2. In Eq. (10),
and
are the volume and compressibility factor of the system.
In PR EoS (Table 2), ν is molar volume of the system and the subscripts
and
indicate the critical and reduced values of temperature and pressure, respectively. ai and bi represent energy (or attractive) and volume (or repulsive) terms of the fluid phase at the thermodynamic equilibrium. In the case of single-component systems, they are calculated from the mentioned relationships, using critical properties (
,
) and the Pitzer’s acentric factor of the considered compound (see Table 2). Whereas, a suitable mixing rule should be inserted for multi-components systems. For the binary system investigated in the present work twin parametric van der Waals (vdW2) and covolume dependent (CVD) mixing rules, presented in Table 3 were applied (Esmaeilzadeh et al., 2009; Mansoori and Ely, 1985).
Mixing rule
Parameter a
Parameter b
vdW2
CVD
In Table 3, and represent the mole fractions of each component in vdW2 and CVD mixing rules, respectively. Subscript denotes mixture for the respective parameters. and are the energy terms of the pure components i and , respectively. The binary interaction parameters in vdW2 (i.e., and ) and CVD (i.e., ) mixing rules are determined by optimization of differences between experimental values and those calculated from the corresponding equation of state, assuming that and (Mukhopadhyay and Rao, 1993).
3.2 Density based models
Empirical and semi-empirical models are other theoretical approaches to predict solid solute solubility in scCO2, with or without co-solvents, over a wide range of temperature and pressure. These models can be divided into density-based, association and complex models. Because of limited information on the thermodynamic properties of different solid solutes, semi-empirical models are always regarded as an acceptable alternative to thermodynamic EoSs. In this study, eight semi-empirical density-based models, presented in Table 4, were used to correlate the experimental solubility of buprenorphine hydrochloride in scCO2.
Name
Relationship
References
Chrastil
(Chrastil, 1982)
Garlapati-Madras
(Garlapati and Madras, 2010)
Bartle
(Bartle et al., 1991)
Bian
(Bian et al., 2016)
Jouyban
(Jouyban et al., 2002)
Wang
(Wang et al., 2016)
Belghait
(Belghait et al., 2018)
Sodeifian
(Sodeifian et al., 2019)
In the above mentioned models (see Table 4), and are the equilibrium solubility and mole fraction of the solid solute in the fluid phase, respectively. and represent temperature and pressure of the system in Kelvin and bar, respectively. The subscript ref in Bartle model indicates the reference values of the corresponding parameters, i.e., and are reference pressure of the system and reference density of scCO2 which were set to 1 bar and 700 kg/m3, respectively. - are also the adjustable parameters for each model.
3.3 Statistical criteria
Among numerous statistical techniques available to assess the correlating ability of the previously mentioned approaches, based on comparing solubility values predicted by each one with those obtained experimentally, average absolute relative deviation percent (
) along with two complementary criteria, including adjusted correlation coefficient (
) and F-test was selected in this study. In order to compare the ability of two models, each one includes different numbers of parameters, the modified form of
as Eq. (11) is often used (Jouyban et al., 2002; Sodeifian et al., 2020).
Where and are the number of data points and adjustable parameters in each model, respectively. and represent calculated and experimental equilibrium mole fraction of buprenorphine hydrochloride in fluid phase, respectively, and subscript i indicates the number of experimental run.
Adjusted correlation coefficient (
) and
are also utilized to assess how well a function can be fitted to the experimental data. These parameters are mathematically defined as below (Jouyban et al., 2002; Sodeifian et al., 2018):
Where, Q (in Eq. (12)) is the number of independent variables in the model. The correlation coefficient (
) was also obtained using the error sum of squares (
) and total sum of squares (
).
Where, is the regressive sum of squares of each investigated model. and are also regressive and error mean of squares, respectively (Montgomery, 2017).
4 Results and discussion
4.1 Experimental data
To ensure that the methodology is reliable and standard, the apparatus and procedure were previously validated by examining the solubility of α-Tocopherol and Naphthalene at different temperatures and pressures and comparing the acquired results with the available ones in the literature (Sodeifian et al., 2018).
Following the above mentioned experimental procedure, solubility of buprenorphine hydrochloride in scCO2 was determined at temperatures ranging from 308 to 338 and pressures within 120–270 bar. To improve the accuracy of the measurements, each run was performed three times. So each reported datum is the average value of three independent experimental data. The obtained results including equilibrium mole fraction and solubility ( and , respectively), calculated using the Eqs. (1–4), are summarized in Table 5. As can be seen, the minimum and maximum values, in terms of equilibrium mole fraction, were both at temperature of 338 K, with the values of 0.131 × 10-4 and 4.752 × 10-4, respectively. Depicted on Fig. 3, are the obtained equilibrium mole factions applied versus CO2 density values, at the corresponding temperature and pressure of the system. For this purpose, the required density (ρ) of scCO2 associated with each point was obtained from National Institute of Science and Technology (NIST) data base (Chemistry WebBook, 2023). As shown, there is an increase in equilibrium mole fraction values when CO2 density increases. Besides, Fig. 4 shows that solubility isotherms have a growing trend along the pressure of the system. In fact, transportation of buprenorphine particles into the fluid phase improves with increasing density followed by increasing solvating power of carbon dioxide under higher pressures (Sodeifian and Usefi, 2023). Furthermore, it can be seen that the isotherms intersect at the pressure region of 150–180 bar, leading to appearance of the crossover pressure point. This phenomenon is often attributed to the situation at which the powers of two competing factors, namely solid’s vapor pressure and carbon dioxide density, are being equal. The effect of temperature on solid solute solubility is contradictory with an isobaric change before and after the crossover point, shown in Fig. 4. In fact, the antagonistic behavior of temperature indicates that the prevailing factor on solubility at 120–150 bar is CO2 density reduction, whereas the progressive behavior of temperature at 180–270 bar shows that enhancement of solute’s vapor pressure prevails (Brunner, 2005). The crossover phenomenon and dualistic effect of temperature have been frequently observed in the literature for the solubility of different compounds in scCO2 (Adenekan and Hutton-Prager, 2020; Araus, 2011; dos Santos, 2019; Sajadian, 2023; Sodeifian et al., 2019a,b; Yang, 2020).
-
CO2 density at different conditions of temperature and pressure were obtained from National Institute of Standards and Technology (NIST) database (Chemistry WebBook, 2023).
-
The equilibrium solubility value can also be calculated directly from equilibrium mole fraction, using Eq. (5).
-
Experimental standard deviation was determined from .
-
Expanded uncertainty was calculated by U = k.ucombined and the relative combined standard uncertainty (ucombined) was obtained from . Standard uncertainty values for temperature u(T) and pressure u(P) were ± 0.1 K and ± 1 bar, respectively. The value of the coverage factor (k) was set to 2 on the basis confidence level of approximately 95 percent.
| Temperature, T (K) | Pressure, P (bar) | Density of scCO21, ρ (kg/lit) | Mole fraction, y2 × 104 | Equilibrium solubility2, S (g/L) | Experimental standard deviation3, S × 104 | Expanded uncertainty of mole fraction4, U × 104 |
|---|---|---|---|---|---|---|
| 308.1 | 120 | 769 | 0.691 | 1.076 | 0.011 | 0.037 |
| 150 | 817 | 0.752 | 1.233 | 0.014 | 0.044 | |
| 180 | 849 | 0.811 | 1.393 | 0.021 | 0.054 | |
| 210 | 875 | 0.972 | 1.720 | 0.041 | 0.092 | |
| 240 | 896 | 1.120 | 2.029 | 0.051 | 0.113 | |
| 270 | 914 | 2.092 | 3.838 | 0.062 | 0.153 | |
| 318.1 | 120 | 661 | 0.513 | 0.680 | 0.012 | 0.032 |
| 150 | 744 | 0.631 | 0.950 | 0.022 | 0.051 | |
| 180 | 791 | 0.970 | 1.546 | 0.041 | 0.093 | |
| 210 | 824 | 1.233 | 2.050 | 0.051 | 0.114 | |
| 240 | 851 | 1.421 | 2.430 | 0.072 | 0.153 | |
| 270 | 872 | 2.440 | 4.279 | 0.063 | 0.181 | |
| 328.1 | 120 | 509 | 0.322 | 0.334 | 0.015 | 0.024 |
| 150 | 656 | 0.451 | 0.597 | 0.011 | 0.030 | |
| 180 | 725 | 1.190 | 1.745 | 0.051 | 0.115 | |
| 210 | 769 | 1.423 | 2.199 | 0.019 | 0.073 | |
| 240 | 802 | 2.431 | 3.918 | 0.121 | 0.264 | |
| 270 | 829 | 3.872 | 6.447 | 0.183 | 0.404 | |
| 338.1 | 120 | 388 | 0.131 | 0.107 | 0.004 | 0.010 |
| 150 | 557 | 0.202 | 0.232 | 0.008 | 0.018 | |
| 180 | 652 | 1.491 | 1.961 | 0.061 | 0.141 | |
| 210 | 710 | 1.724 | 2.454 | 0.058 | 0.139 | |
| 240 | 751 | 2.851 | 4.310 | 0.041 | 0.150 | |
| 270 | 783 | 4.752 | 7.483 | 0.065 | 0.246 |
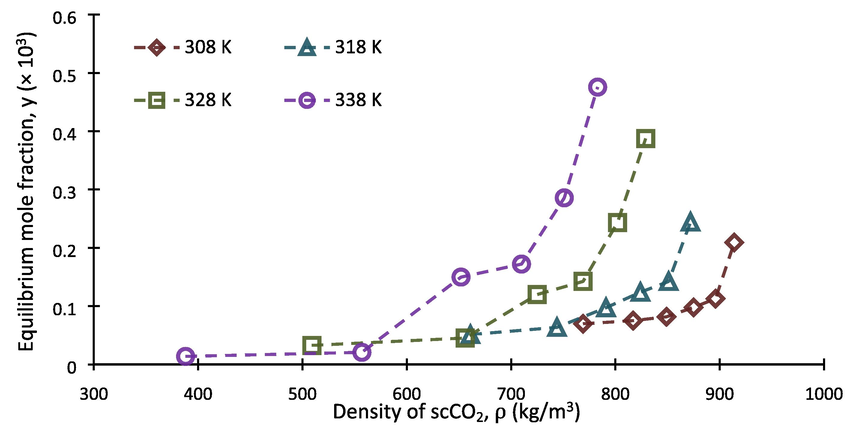
- Solubility of buprenorphine hydrochloride vs. scCO2 density at different temperatures.
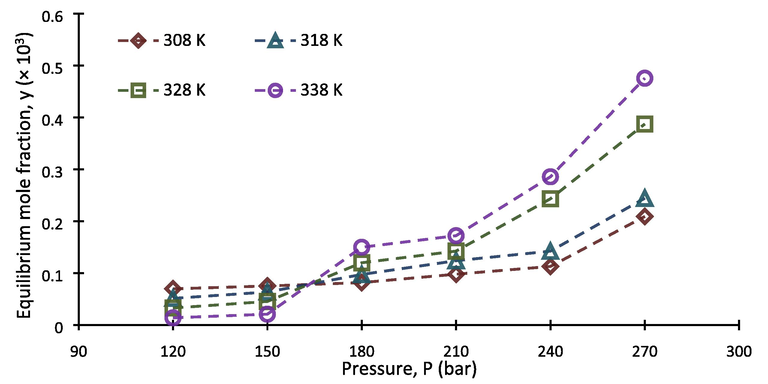
- Solubility of buprenorphine hydrochloride vs. pressure at different temperatures.
| Boiling point, | Critical temperature, | Critical pressure, | Pitzer’s Acentric factor, | Solid molar volume, | Vapor pressure, | |||
|---|---|---|---|---|---|---|---|---|
| 308 K | 318 K | 328 K | 338 K | |||||
| 779 | 947.39 | 10.025 | 1.041 | 370.40 | 0.095 | 0.513 | 2.450 | 10.520 |
4.2 Results from correlation of solubility data
According to what was mentioned above, two approaches were followed to correlate the experimental values as the second step of the recent investigation, including Peng-Robinson (PR) EoS and a set of semi-empirical models. Thereafter, to evaluate prediction capability, not only the correlation results of each one were determined using statistical criteria but their predicted isotherms were also brought on the diagram to be visually compared with the experimental data points.
4.2.1 Correlation results applying Peng-Robinson equation of state
Following theoretical procedure mentioned in section 3.1, fugacity coefficient followed by equilibrium mole fraction of buprenorphine hydrochloride was calculated, applying Peng-Robinson EoS with two different mixing rules (PR + vdW2 and PR + CVD) at the corresponding conditions of each experimental run. The required physicochemical properties of buprenorphine hydrochloride including boiling point (
), critical values (
,
), and Pitzer’s acentric factor (
), presented in Table 6, were estimated using Marrero-Pardillo (Marrero-Morejón and Pardillo-Fontdevila, 1999); Wilson-Japerson atomic contribution and Ambrose-Walton corresponding-state methods (Poling et al., 2001), respectively. Acentric factor and critical values of carbon dioxide were also set to 0.274, 304.2 K, and 73.8 bar.
Temperature
F-value
PR + vdW2
308
—
0.263
0.313
0.285
0.812
16.533
318
—
0.257
0.303
0.654
2.869
15.839
328
—
0.264
0.329
0.921
15.022
22.495
338
—
0.279
0.363
0.961
31.298
24.388
PR + CVD
308
0.705
—
—
0.461
1.673
32.732
318
0.696
—
—
0.754
4.287
38.015
328
0.675
—
—
0.950
24.238
35.329
338
0.657
—
—
0.932
17.540
40.165
Adjustable parameters of the mixing rules, i.e.,
,
in vdW2 and
in CVD were calculated at the optimum level by minimizing the contrast between calculated and experimental solubility data (Haghtalab and Sodeifian, 2002). Results of correlating Peng-Robinson EoS with experimental data are presented both in Table 7 and in Fig. 5. As can be seen in Table 7, deviations between predicted solubility and experimental values grow for both equations when temperature increases. Furthermore, the deviation obtained by PR + CVD at 308 K is observed to be about two times that of PR + vdW2 and even more at 318 K. However, PR + CVD shows more suitable correlation results compared to PR + vdW2 at 308, 318, and 328 K, in terms of F-value and
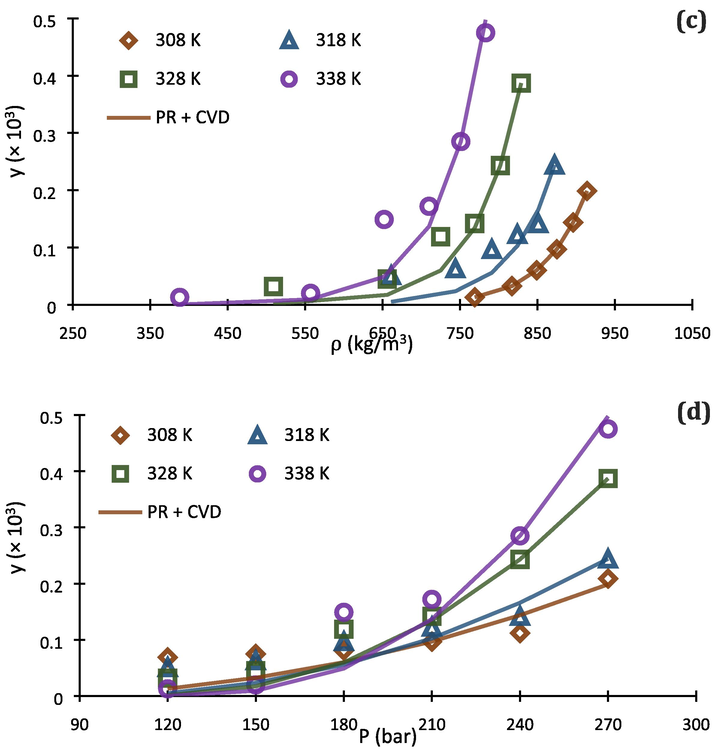
. But at 338 K, it can clearly be concluded that PR + vdW2 is superior to PR + CVD for thermodynamic modeling of the investigated system.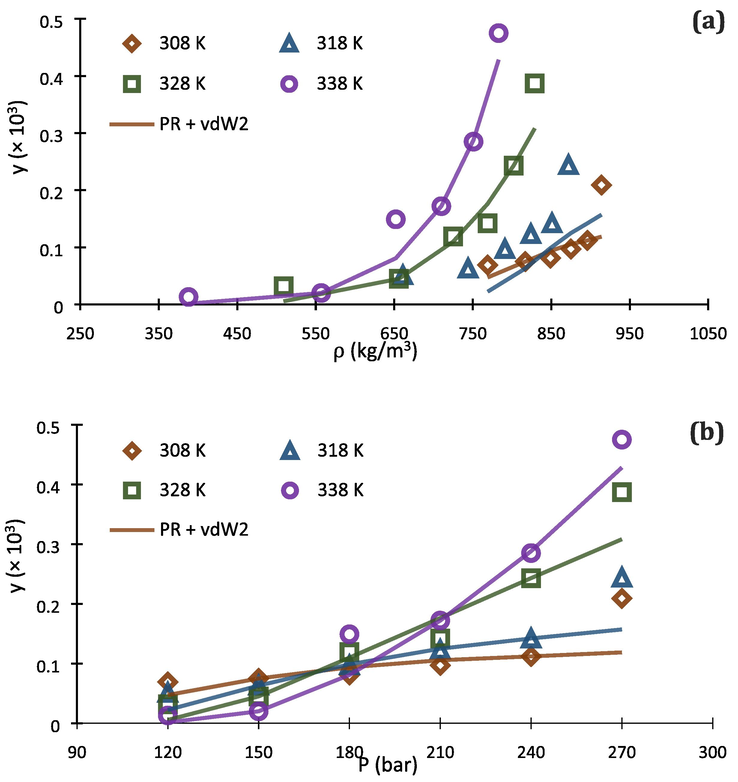
Comparison of experimental data (point) and calculated (line) solubility isotherms for buprenorphine hydrochloride in scCO2 based on PR EoS with vdW2 (a, b) and CVD (c, d) mixing rules.
Comparison of experimental data (point) and calculated (line) solubility isotherms for buprenorphine hydrochloride in scCO2 based on PR EoS with vdW2 (a, b) and CVD (c, d) mixing rules.
Chrastil
Madras
Bartle
Jouyban
Bian
Wang
Belghait
Sodeifian
9.329
56.948
27.035
17.443
−4.474
22.96
−140.046
−79.103
−7.889 × 103
0.417
−1.029 × 104
−34.959
0.019
−4.401 × 104
−0.247
4.399
−37.506
0.002
0.014
−2.20 × 10-5
2.782 × 104
−7.068
5.798 × 10-5
8.889
—
−9.428 × 103
—
9.764 × 10-5
−42.990
−135.203
3.278 × 10-4
0.002
—
−4.024
—
1.610
−62.520
—
−0.528
−0.122
—
—
—
28.779
—
—
5.393 × 10-4
−2.179 × 103
—
—
—
—
—
—
48.156
—
—
—
—
—
—
—
−0.501
—
25.41
21.39
24.85
17.16
19.66
23.41
20.03
18.14
0.952
0.962
0.959
0.989
0.985
0.959
0.972
0.986
F-value
76.58
81.20
77.79
89.21
83.98
78.54
82.91
85.88
Fig. 5 shows the correlated solubility isotherms from PR + vdW2 and PR + CVD, in terms of scCO2 density and pressure of the system. As can be seen in Fig. 5 (a-d), there are considerable lacks of ability for PR + vdW2 and PR + CVD to be correlated with the experimental data at high and low pressures, respectively. In this regard, the existing deviations in Fig. 5 (d) cause PR + CVD to be not good at all for predicting buprenorphine hydrochloride solubility in scCO2 at temperature of 308 K and pressures below 180 bar. On the other hand, PR + vdW2 exhibits good performance at these conditions, based on Fig. 5 (b).
4.2.2 Correlation results applying density-based models
As mentioned previously, eight density-based models, presented in Table 4, were employed to correlate the experimental solubility data. For this purpose, adjustable parameters were optimized through curve fitting and genetic algorithm in MATLAB software (GA; MATLAB Media).
Table 8 includes the results obtained from correlating the models along with , , and F-value corresponding to each one.
Falling into the range of 17.16%-25.41%, values indicated acceptable results for correlating the experimental solubility of buprenorphine hydrochloride in scCO2. With respect to the results, Jouyban and Chrastil models exhibited lowest and highest with the values of 17.16% and 25.41%, respectively. In addition, Jouyban, Bian and Sodeifian models were better fitted to the experimental data points, exhibiting satisfactory ability for prediction of buprenorphine solubility. As a conclusion, Jouyban model with six adjustable parameters, produced the best results for , and F-test with the values of 17.16%, 99%, and 89.21, respectively. As expected, Chrastil, Belghit, and Wang models have poorer ability to be correlated with the experimental data rather than the others. It can be resulted from this fact that the mentioned models have lower numbers of adjustable parameters.
To compare calculated theoretical results with experimental data, the correlated solubility isotherms of eight above mentioned density-based models along with experimental data points is depicted in Fig. 6. As can be seen in Fig. 6 (h), Sodeifian’s model show higher ability for predicting solubility at higher CO2 densities. This ability would be resulted from the more number of adjustable parameters in the model (6 parameters, with respect to Table 4), which make it more flexible to be correlated with experimental data. In addition, it should be mentioned that the companion coefficient of each adjustable parameter (e.g., PlnT and ln(ρT) in Sodeifian model) play important roles in this direction. For example, although Belghait model (Fig. 6 (g)) has been developed on the basis of 8 adjustable parameters, it indicated poorer ability for prediction of solubility in scCO2 compared to Jouyban model (Fig. 6 (e)) that has 6 parameters, because the companion coefficients of Belghait model are not sufficiently correlative for scCO2-buprenorphine system. The graphical results presented in Fig. 6 (a-h) are in agreement with statistical parameters presented in Table 8.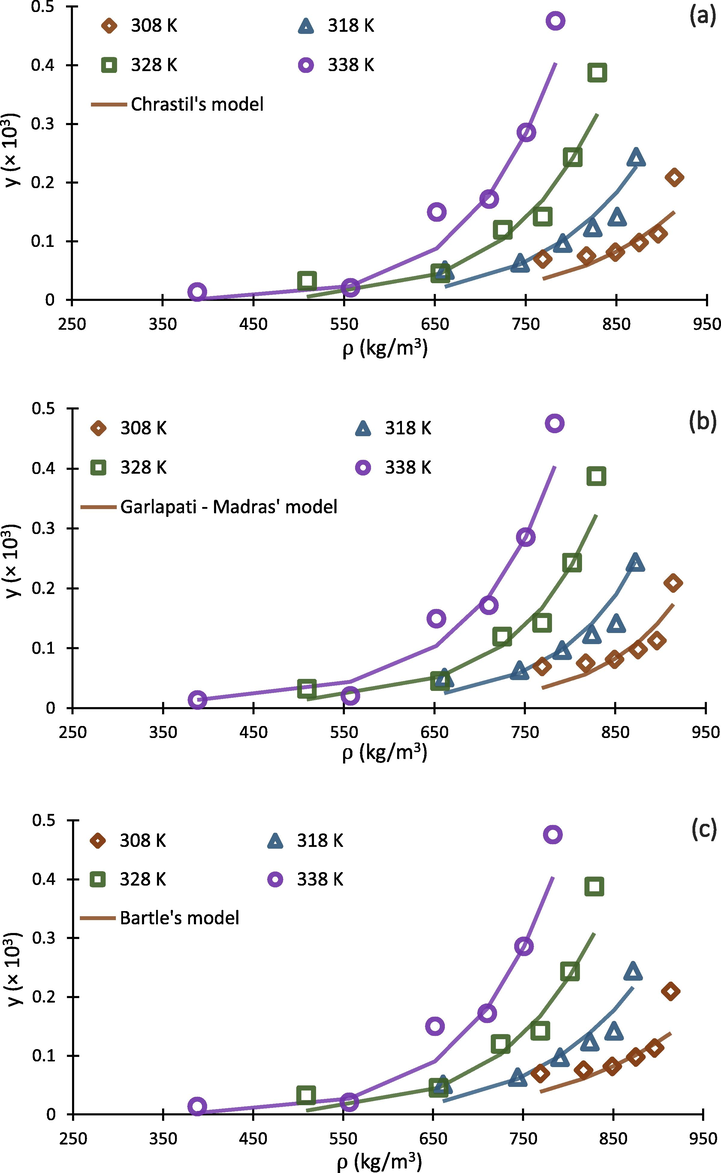
Experimental data (points) and regressed solubility isotherms from investigated density based models (lines) for buprenorphine hydrochloride-scCO2 system.
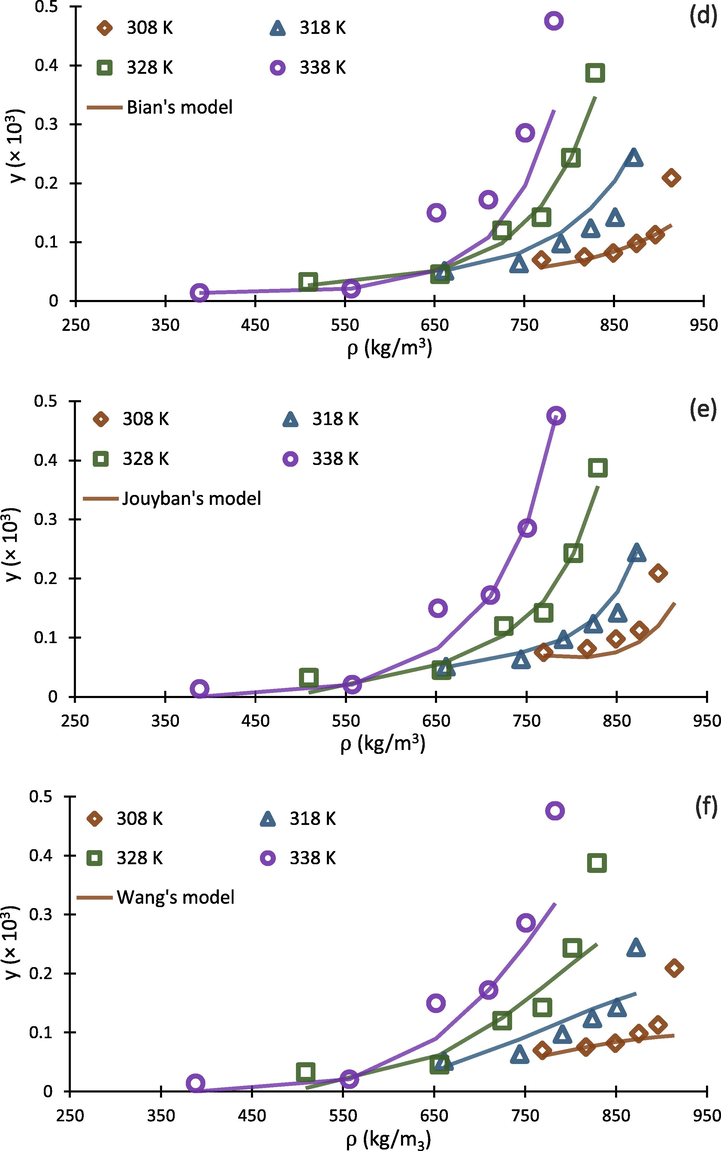
Experimental data (points) and regressed solubility isotherms from investigated density based models (lines) for buprenorphine hydrochloride-scCO2 system.
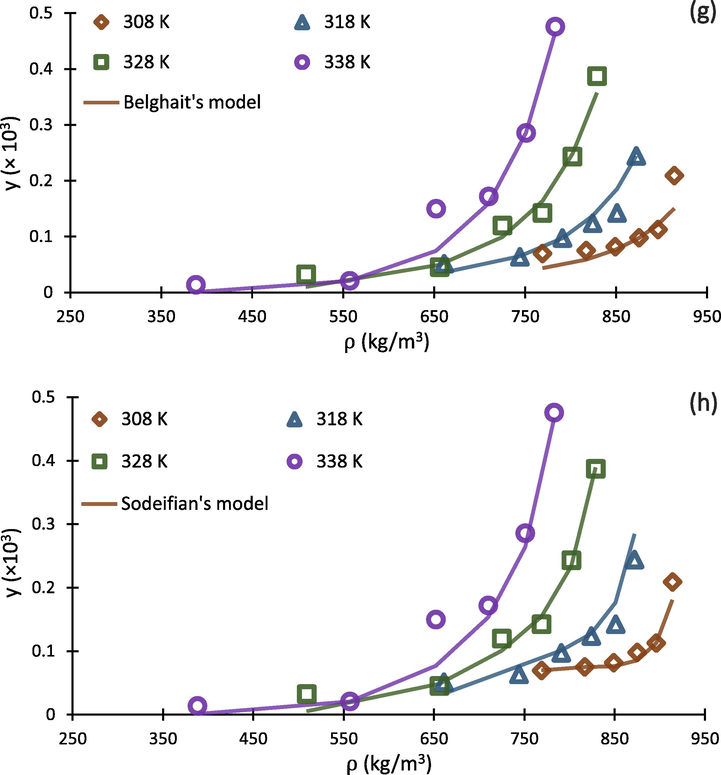
Experimental data (points) and regressed solubility isotherms from investigated density based models (lines) for buprenorphine hydrochloride-scCO2 system.
By applying the correlation results of Chrastil and Bartle models in Eqs. (15) and (16), total (
) and vaporization enthalpies (
) for buprenorphine hydrochloride dissolution in scCO2 can be estimated:
Where
and
are the regressed temperature coefficients of Chrastil and Bartle models, respectively. Considering the difference between the total and vaporization enthalpies, solvation enthalpy of the process (
) was also obtained from Eq. (17). These values are reported in Table 9.
Dissolution of Buprenorphine HCl in scCO2
65.594
85.604
−20.010
These enthalpies are of high value for understanding the type and amount of energy needed for solid particles to dissolve in scCO2. For example, a large value of total enthalpy may indicate that solute particles require more energy to dissolve in scCO2 or release more heat when recrystallizing from scCO2. Similarly, the value of vaporization enthalpy would show how strong the intermolecular forces of solute are against scCO2 particles. However, these values have not been directly measured by experiments but were determined based on the assumptions made for developing the utilized semi-empirical models (Sodeifian et al., 2023).
5 Conclusion
To design the pharmaceutical processes such as synthesis of the pharmaceutical micro- and nano particles, drug crystallization, and selective extraction of medicines from mixtures using the supercritical mediums, solubility data of the proposed compound in the fluid are needed. In this research, solubility behavior of buprenorphine hydrochloride in supercritical carbon dioxide (scCO2) was studied. At the first step, solubility values were measured at different temperatures and pressures over the range of 313–338 K and 120–279 bar, respectively. The highest and lowest equilibrium mole fractions were 4.752 × 10-4 and 0.131 × 10-4, respectively. The crossover pressure point for this binary system was found to be in the middle of the range of 150–180 bar. At the second step, the obtained solubility data were correlated using Peng-Robinson EoS along with two different mixing rules namely van der Waals type 2 (vdW2) and covolume dependent (CVD) mixing rules. The results showed that Peng-Robinson EoS applied with vdW2 at lower pressures and with CVD at higher pressures could exhibit better capability for correlating the experimental data. In addition to Peng-Robinson EoS, eight different semi-empirical density-based models were also examined. Obtaining an of 17.16 and 18.14, Jouyban and Sodeifian models had better agreement with the experimental data, respectively. At last, by applying the correlation results of Chrastil and Bartle models, total and vaporization enthalpies of buprenorphine hydrochloride dissolution in scCO2 were estimated to be 65.59 and 85.60 KJ/mole, respectively.
CRediT authorship contribution statement
Gholamhossein Sodeifian: Conceptualization, Methodology, Validation, Investigation, Supervision, Project administration, Writing – review & editing. Maryam Arbab Nooshabadi: Methodology, Investigation, Software, Resources. Fariba Razmimanesh: Methodology, Validation, Writing – original draft. Amirmuhammad Tabibzadeh: Methodology, Validation, Writing – original draft.
Acknowledgement
The authors appreciate the Research Deputy of University of Kashan for supporting the project financially with the Grant #Pajoohaneh-1401/25. The authors also thank Temad Company for providing the drug required for experimental tests.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Experimental measurement and thermodynamic modeling of solubility of Riluzole drug (neuroprotective agent) in supercritical carbon dioxide. Fluid Phase Equilib.. 2023;567:113711
- [CrossRef] [Google Scholar]
- Adachi, Y. and B.C.-Y. Lu, Supercritical fluid extraction with carbon dioxide and ethylene, in Fluid Phase Equilibria. 1983. p. 147-156.
- Modeling the solubility of Alkyl Ketene Dimer in supercritical carbon dioxide: Peng-Robinson, group contribution methods, and effect of critical density on solubility predictions. Fluid Phase Equilib.. 2020;507:112415
- [CrossRef] [Google Scholar]
- A new semi empirical model for the solubility of dyestuffs in supercritical carbon dioxide. Chem. Pap.. 2021;75:2585-2595.
- [CrossRef] [Google Scholar]
- Novel numerical simulation of drug solubility in supercritical CO2 using machine learning technique: Lenalidomide case study. Arab. J. Chem.. 2022;15(11):104180
- [CrossRef] [Google Scholar]
- Lansoprazole loading of polymers by supercritical carbon dioxide impregnation: Impacts of process parameters. The Journal of Supercritical Fluids. 2020;164:104892.
- [CrossRef] [Google Scholar]
- Improving phase equilibrium calculation with the Peng-Robinson EOS for fats and oils related compounds/supercritical CO2 systems. Fluid Phase Equilib.. 2000;169(1):49-64.
- [CrossRef] [Google Scholar]
- Solubility of β-carotene in ethanol-and triolein-modified CO2. J. Chem. Thermodyn.. 2011;43(12):1991-2001.
- [CrossRef] [Google Scholar]
- Preparation of phthalocyanine green nano pigment using supercritical CO2 gas antisolvent (GAS): experimental and modeling. Heliyon. 2020;6(9):e04947.
- [CrossRef] [Google Scholar]
- Solubilities of solids and liquids of low volatility in supercritical carbon dioxide. J. Phys. Chem. Ref. Data. 1991;20(4):713-756.
- [CrossRef] [Google Scholar]
- Semi-empirical correlation of solid solute solubility in supercritical carbon dioxide: comparative study and proposition of a novel density-based model. Comptes Rendus Chimie. 2018;21(5):494-513.
- [CrossRef] [Google Scholar]
- Supercritical fluid chromatography in food analysis. J. Chromatogr. A. 2013;1313:24-36.
- [CrossRef] [Google Scholar]
- A five-parameter empirical model for correlating the solubility of solid compounds in supercritical carbon dioxide. Fluid Phase Equilib.. 2016;411:74-80.
- [CrossRef] [Google Scholar]
- Supercritical fluids: technology and application to food processing. J. Food Eng.. 2005;67(1–2):21-33.
- [CrossRef] [Google Scholar]
- Nanoparticles synthesis using supercritical fluid technology–towards biomedical applications. Adv. Drug Deliv. Rev.. 2008;60(3):299-327.
- [CrossRef] [Google Scholar]
- Neural simulation and experimental investigation of Chloroquine solubility in supercritical solvent. J. Mol. Liq.. 2021;333:115942
- [CrossRef] [Google Scholar]
- National Institute of Standards and Technology Chemistry WebBook. 2023. https://webbook.nist.gov/chemistry/
- Solubility of solids and liquids in supercritical gases. J. Phys. Chem.. 1982;86(15):3016-3021.
- [CrossRef] [Google Scholar]
- Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy. 2017;195:152-183.
- [CrossRef] [Google Scholar]
- Utilization of CO2 in supercritical conditions for the synthesis of cyclic poly (N-isopropylacrylamide) via emulsion and homogeneous reactions. Scientific Reports. 2022;12(1):17459.
- [CrossRef] [Google Scholar]
- Synthesis of cyclic polystyrene in supercritical carbon dioxide green solvent. The Journal of Supercritical Fluids. 2022;188:105679.
- [CrossRef] [Google Scholar]
- Supercritical fluids and nanoparticles in cancer therapy. Micromachines. 2022;13(9):1449.
- [CrossRef] [Google Scholar]
- An improved equation for predicting the solubility of vegetable oils in supercritical carbon dioxide. Ind. Eng. Chem. Res.. 1988;27(8):1551-1553.
- [CrossRef] [Google Scholar]
- Overcoming poor oral bioavailability using nanoparticle formulations–opportunities and limitations. Drug Discov. Today Technol.. 2012;9(2):e87-e95.
- [CrossRef] [Google Scholar]
- Supercritical fluid chromatography in pharmaceutical analysis. J. Pharm. Biomed. Anal.. 2015;113:56-71.
- [CrossRef] [Google Scholar]
- Solubility of passion fruit (Passiflora edulis Sims) seed oil in supercritical CO2. Fluid Phase Equilib.. 2019;493:174-180.
- [CrossRef] [Google Scholar]
- Supercritical fluids as solvents for chemical and materials processing. Nature. 1996;383(6598):313-318.
- [CrossRef] [Google Scholar]
- Preparation of metallic supported nanoparticles and films using supercritical fluid deposition. J. Supercrit. Fluids. 2009;47(3):517-522.
- [CrossRef] [Google Scholar]
- Calculation of the solid solubilities in supercritical carbon dioxide using a new Gex mixing rule. The Journal of Supercritical Fluids. 2009;51(2):148-158.
- [CrossRef] [Google Scholar]
- Experimental study of ketoconazole impregnation into polyvinyl pyrrolidone and hydroxyl propyl methyl cellulose using supercritical carbon dioxide: Process optimization. The Journal of Supercritical Fluids. 2022;188:105674.
- [CrossRef] [Google Scholar]
- A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci.. 1974;14(2):147-154.
- [CrossRef] [Google Scholar]
- Nanoparticles and nanocrystals by supercritical CO2-assisted techniques for pharmaceutical applications: A review. Appl. Sci.. 2021;11(4):1476.
- [CrossRef] [Google Scholar]
- New empirical expressions to correlate solubilities of solids in supercritical carbon dioxide. Thermochim. Acta. 2010;500(1–2):123-127.
- [CrossRef] [Google Scholar]
- A fuzzy logic model and a neuro-fuzzy system development on supercritical CO2 regeneration of Ni/Al2O3 catalysts. J. CO2 Utiliz.. 2021;54:101706
- [CrossRef] [Google Scholar]
- Buprenorphine: a review of its pharmacological properties and therapeutic efficacy. Drugs. 1979;17:81-110.
- [CrossRef] [Google Scholar]
- Modified Redlich□ Kwong equation of state for supercritical carbon dioxide. J. Supercrit. Fluids. 2013;81:92-98.
- [CrossRef] [Google Scholar]
- A Comparative study on response surface optimization of supercritical fluid extraction parameters to obtain Portulaca Oleracea seed oil with higher bioactive content and antioxidant activity than solvent extraction. Eur. J. Lipid Sci. Technol.. 2023;125(2):2200136.
- [CrossRef] [Google Scholar]
- Buprenorphine: considerations for pain management. J. Pain Symptom Manage.. 2005;29(3):297-326.
- [CrossRef] [Google Scholar]
- Solubility prediction in supercritical CO2 using minimum number of experiments. J. Pharm. Sci.. 2002;91(5):1287-1295.
- [CrossRef] [Google Scholar]
- Mathematical representation of solute solubility in supercritical carbon dioxide using empirical expressions. J. Supercrit. Fluids. 2002;24(1):19-35.
- [CrossRef] [Google Scholar]
- Development and evaluation of a new semi-empirical model for correlation of drug solubility in supercritical CO2. Fluid Phase Equilib.. 2014;363:18-26.
- [CrossRef] [Google Scholar]
- Representing solute solubility in supercritical carbon dioxide: A novel empirical model. Chem. Eng. Res. Des.. 2015;93:355-365.
- [CrossRef] [Google Scholar]
- Preparation of open-cell polymer foams by CO2 assisted foaming of polymer blends. Polymer. 2016;90:331-341.
- [CrossRef] [Google Scholar]
- Modelling the solubility of solids in supercritical fluids with density as the independent variable. J. Supercrit. Fluids. 1988;1(1):15-22.
- [CrossRef] [Google Scholar]
- Van der Waals mixing rules for cubic equations of state. Applications for supercritical fluid extraction modelling. Chem. Eng. Sci.. 1986;41(5):1303-1309.
- [CrossRef] [Google Scholar]
- Comparison the capability of artificial neural network (ANN) and EOS for prediction of solid solubilities in supercritical carbon dioxide. Fluid Phase Equilib.. 2011;308(1–2):35-43.
- [Google Scholar]
- A generalized thermodynamic correlation based on three-parameter corresponding states. AIChE J.. 1975;21(3):510-527.
- [CrossRef] [Google Scholar]
- Production of engineering plastics foams by supercritical CO2. Ind. Eng. Chem. Res.. 2000;39(12):4622-4626.
- [CrossRef] [Google Scholar]
- Supercritical carbon dioxide extraction of bioactive flavonoid from Strobilanthes crispus (Pecah Kaca) Food Bioprod. Process.. 2010;88(2–3):319-326.
- [CrossRef] [Google Scholar]
- Peng-Robinson equation of state: 40 years through cubics. Fluid Phase Equilib.. 2017;447:39-71.
- [CrossRef] [Google Scholar]
- Thermodynamic modeling of the solubilities of fatty acids in supercritical fluids. Fluid Phase Equilib.. 2004;220(2):167-169.
- [Google Scholar]
- Density expansion (DEX) mixing rules: Thermodynamic modeling of supercritical extraction. J. Chem. Phys.. 1985;82(1):406-413.
- [Google Scholar]
- Estimation of pure compound properties using group-interaction contributions. AIChE J.. 1999;45(3):615-621.
- [CrossRef] [Google Scholar]
- The solubility of solids in supercritical fluids. Fluid Phase Equilib.. 1999;158:501-510.
- [CrossRef] [Google Scholar]
- Design and analysis of experiments. John wiley & sons; 2017.
- Thermodynamic modeling for supercritical fluid process design. Ind. Eng. Chem. Res.. 1993;32(5):922-930.
- [CrossRef] [Google Scholar]
- Estimating the dissolution of anticancer drugs in supercritical carbon dioxide with a stacked machine learning model. Pharmaceutics. 2022;14
- [CrossRef] [Google Scholar]
- A machine learning approach for thermodynamic modeling of the statically measured solubility of nilotinib hydrochloride monohydrate (anti-cancer drug) in supercritical CO2. Scientific Reports. 2023;13(1):12906.
- [CrossRef] [Google Scholar]
- Supercritical CO2: Properties and technological applications-a review. J. Therm. Sci.. 2019;28:394-430.
- [CrossRef] [Google Scholar]
- Increasing solubility of phenytoin and raloxifene drugs: Application of supercritical CO2 technology. J. Mol. Liq. 2023121246
- [CrossRef] [Google Scholar]
- Supercritical fluid application in the oil and gas industry: a comprehensive review. Sustainability. 2022;14(2):698.
- [CrossRef] [Google Scholar]
- A new two-constant equation of state. Ind. Eng. Chem. Fundam.. 1976;15(1):59-64.
- [CrossRef] [Google Scholar]
- Properties of gases and liquids. McGraw-Hill Education; 2001.
- Buprenorphine and its formulations: a comprehensive review. Health Psychology Research. 2022;10(3) 10.52965%2F001c.37517
- [Google Scholar]
- Molecular thermodynamics of fluid-phase equilibria. Pearson Education; 1998.
- An investigation into Sunitinib malate nanoparticle production by US-RESOLV method: Effect of type of polymer on dissolution rate and particle size distribution. J. Supercrit. Fluids. 2021;170:105163
- [CrossRef] [Google Scholar]
- Nanoparticles production by supercritical antisolvent precipitation: a general interpretation. J. Supercrit. Fluids. 2007;43(1):126-138.
- [CrossRef] [Google Scholar]
- A universal methodology for reliable predicting the non-steroidal anti-inflammatory drug solubility in supercritical carbon dioxide. Sci. Rep.. 2022;12(1):1043.
- [CrossRef] [Google Scholar]
- Using the supercritical carbon dioxide as the solvent of Nystatin: Studying the effect of co-solvent, experimental and correlating. J. Supercrit. Fluids. 2023;194:105858
- [CrossRef] [Google Scholar]
- Solubilities of naphthalene and indole in supercritical fluids. J. Supercrit. Fluids. 1988;1(1):1-6.
- [CrossRef] [Google Scholar]
- Prediction of vapor–liquid equilibria for supercritical alcohol+ fatty acid ester systems by SRK equation of state with Wong-Sandler mixing rule based on COSMO theory. J. Supercrit. Fluids. 2008;46(1):4-9.
- [CrossRef] [Google Scholar]
- Measurement, correlation and thermodynamic modeling of the solubility of Ketotifen fumarate (KTF) in supercritical carbon dioxide: Evaluation of PCP-SAFT equation of state. Fluid Phase Equilib.. 2018;458:102-114.
- [CrossRef] [Google Scholar]
- Solubility measurement of an antihistamine drug (Loratadine) in supercritical carbon dioxide: Assessment of qCPA and PCP-SAFT equations of state. Fluid Phase Equilib.. 2018;472:147-159.
- [CrossRef] [Google Scholar]
- Experimental measurements and thermodynamic modeling of Coumarin-7 solid solubility in supercritical carbon dioxide: Production of nanoparticles via RESS method. Fluid Phase Equilib.. 2019;483:122-143.
- [CrossRef] [Google Scholar]
- Production of Loratadine drug nanoparticles using ultrasonic-assisted Rapid expansion of supercritical solution into aqueous solution (US-RESSAS) J. Supercrit. Fluids. 2019;147:241-253.
- [CrossRef] [Google Scholar]
- Solubility of palbociclib in supercritical carbon dioxide from experimental measurement and Peng-Robinson equation of state. Sci. Rep.. 2023;13(1):2172.
- [CrossRef] [Google Scholar]
- Solubility measurement and modeling of hydroxychloroquine sulfate (antimalarial medication) in supercritical carbon dioxide. Sci. Rep.. 2023;13(1):8112.
- [CrossRef] [Google Scholar]
- Determination of the solubility of rivaroxaban (anticoagulant drug, for the treatment and prevention of blood clotting) in supercritical carbon dioxide: Experimental data and correlations. Arab. J. Chem.. 2023;16(1):104421
- [CrossRef] [Google Scholar]
- Experimental solubility of fexofenadine hydrochloride (antihistamine) drug in SC-CO2: Evaluation of cubic equations of state. J. Supercrit. Fluids. 2023;200:106000
- [CrossRef] [Google Scholar]
- Solubility measurement and preparation of nanoparticles of an anticancer drug (Letrozole) using rapid expansion of supercritical solutions with solid cosolvent (RESS-SC) J. Supercrit. Fluids. 2018;133:239-252.
- [CrossRef] [Google Scholar]
- Preparation of Aprepitant nanoparticles (efficient drug for coping with the effects of cancer treatment) by rapid expansion of supercritical solution with solid cosolvent (RESS-SC) J. Supercrit. Fluids. 2018;140:72-84.
- [CrossRef] [Google Scholar]
- Solubility measurement of a chemotherapeutic agent (Imatinib mesylate) in supercritical carbon dioxide: Assessment of new empirical model. J. Supercrit. Fluids. 2019;146:89-99.
- [CrossRef] [Google Scholar]
- Solubility measurement of a pigment (Phthalocyanine green) in supercritical carbon dioxide: Experimental correlations and thermodynamic modeling. Fluid Phase Equilibria. 2019;494:61-73.
- [CrossRef] [Google Scholar]
- Investigation of essential oil extraction and antioxidant activity of Echinophora platyloba DC. using supercritical carbon dioxide. J. Supercrit. Fluids. 2017;121:52-62.
- [CrossRef] [Google Scholar]
- Supercritical fluid extraction of omega-3 from Dracocephalum kotschyi seed oil: Process optimization and oil properties. J. Supercrit. Fluids. 2017;119:139-149.
- [CrossRef] [Google Scholar]
- Utilization of ultrasonic-assisted RESOLV (US-RESOLV) with polymeric stabilizers for production of amiodarone hydrochloride nanoparticles: Optimization of the process parameters. Chem. Eng. Res. Des.. 2019;142:268-284.
- [CrossRef] [Google Scholar]
- Experimental measurement and thermodynamic modeling of Lansoprazole solubility in supercritical carbon dioxide: Application of SAFT-VR EoS. Fluid phase equilibria. 2020;507:112422.
- [CrossRef] [Google Scholar]
- CO2 utilization as a supercritical solvent and supercritical antisolvent in production of sertraline hydrochloride nanoparticles. J. CO2 Utiliz.. 2022;55:101799
- [CrossRef] [Google Scholar]
- Solubility, Extraction, and Nanoparticles Production in Supercritical Carbon Dioxide: A Mini-Review. ChemBioEng Reviews. 2023;10(2):133-166.
- [CrossRef] [Google Scholar]
- Prediction of busulfan solubility in supercritical CO2 using tree-based and neural network-based methods. J. Mol. Liq.. 2022;351:118630
- [CrossRef] [Google Scholar]
- Polymeric hydrogels and supercritical fluids: The mechanism of hydrogel foaming. Polymer. 2011;52(13):2819-2826.
- [CrossRef] [Google Scholar]
- Particle synthesis by rapid expansion of supercritical solutions (RESS): Current state, further perspectives and needs. J. Aerosol Sci 2022105950
- [CrossRef] [Google Scholar]
- The application of supercritical fluid extraction in phenolic compounds isolation from natural plant materials. Molecules. 2018;23(10):2625.
- [CrossRef] [Google Scholar]
- Modified Soave-Redlich-Kwong equations of state applied to mixtures containing supercritical carbon dioxide. Korean J. Chem. Eng.. 2003;20:709-715.
- [CrossRef] [Google Scholar]
- Regeneration of poisoned nickel catalyst by supercritical CO2 extraction. Ind. Eng. Chem. Res.. 2001;40(7):1589-1590.
- [CrossRef] [Google Scholar]
- New models for correlating and predicting the solubility of some compounds in supercritical CO2. Fluid Phase Equilib.. 2016;430:135-142.
- [CrossRef] [Google Scholar]
- Development of Novel Machine Learning to Optimize the Solubility of Azathioprine as Anticancer Drug in Supercritical Carbon Dioxide. Jurnal Ilmiah Teknik Elektro Komputer dan Informatika. (JITEKI). 2023;9(1):49-57.
- [Google Scholar]
- Review of supercritical CO2 technologies and systems for power generation. Appl. Therm. Eng.. 2021;185:116447
- [CrossRef] [Google Scholar]
- Measurement and modelling of the solubility of dodecylcyclohexane in supercritical carbon dioxide. Int. J. Global Warming. 2020;21(1):35-49.
- [CrossRef] [Google Scholar]
- Applications of supercritical carbon dioxide in materials processing and synthesis. Rsc Adv.. 2014;4(105):61137-61152.
- [CrossRef] [Google Scholar]
- Determination of the discrete relaxation spectrum for polybutadiene and polystyrene by a non-linear regression method. Iranian Polymer Journal. 2002;11:103-107.
- [Google Scholar]







