Statistical physics modeling of water vapor adsorption isotherm into kernels of dates: Experiments, microscopic interpretation and thermodynamic functions evaluation

1 Introduction

Saudi Arabia is one of the first largely produced of date palm in the world. Fruit of the palm (phoenix dactylifera L.) is rich in mineral salts and vitamins (Assirey, 2015) and excellent material for producing refined sugar, concentrated juice, and fermentation products (Booij et al., 1992). The kernels represent 6–15% of the total weight of the date (AbdulQadir et al., 2011). The date kernels are composed of carbohydrates, dietary fiber, fat, ash and protein. In addition, the antioxidant content in date seed oil (DSO) was found to be similar with olive oil, which can be as a good source of antioxidant in order to fulfill the consumer’s requirements (Golshan Tafti et al., 2017). Date seeds, also called pits, kernels, stones or pipes, are a waste product of dare processing and packing plants (Abdul Afiq et al., 2013).

Beside the nutrition and health, the kernels of date have many features and uses; For examples as animal feed ingredient (Al Sumri et al., 2016) or turned into non caffeinated coffee by the Arabs or used sometimes as a soil organic additive (Elwathig Mirghani, 2012). As proposed in recent researches, the kernels of date have several amazing medicinal properties. Indeed, they help to prevent kidney and liver against toxicity or damage (Al-Farsi et al., 2005) and it is useful in treating problem in blood related to sugar (Ishurd et al., 2004). Because they are rich in antioxidants, they are used to liver diseases, prevent DNA damage and help to fight various viral infections (Vayalil, 2002).

The study of the shelf life and safety of this product is of fundamental interest (Al-Muhtaseb et al., 2002). In fact this is important for predicting the physical and organic procedures which occur during food storage (Al-Muhtaseb et al., 2004). This factor is related to the water content because the water is the principal component of natural food stuffs. It plays a crucial role in the food process and the chemical process and has a major impact on food reactions and quality. The behavior of a food product is often described by the humid air that surrounds it. The investigation of such a phenomenon in this paper is outlined through the water vapor sorption isotherm which establishes the link between the moisture content (total moisture content) and the water activity at different ranges of temperature (Al-Muhtaseb et al., 2004). The water activity a_w represents the dynamic part of water inside the food product and it is often used to justify the food satisfaction. It is defined as the ratio of partial pressure (p) of water vapor in air pressure and water vapor saturation (p_vs) in the same temperature (Aouaini et al., 2018). It also explains the availability of water molecules to contribute in physical, chemical, and microbiological reactions.

Experimental and hypothetical researches of the vapor of water associated with foods have been intensified in an attempt to investigate the water behavior (Al-Muhtaseb et al., 2002). In this way, the interpretation of water vapor sorption into date kernels constitutes the principal motivation, because of its vital importance for predicting the stability of food product (Al-Muhtaseb et al., 2004).

Generally, sorption data are usually presented as isotherms (Aranovich and Donohue, 1998) which attract many researchers due to its interesting applications. Several analytical strategies have been developed in the literature in order to characterize the shape of adsorption isotherms. In this issue the classical density functional theory was used by Monson (2012) to understand adsorption/desorption hysteresis for fluids confined in mesoporous materials. The adsorption of halide ions onto single-crystal electrodes was modeled by Koper (1998) using a lattice-gas approach. Isotherm equation applied to lattice gas with rather general lateral interactions was investigated by Medved et al. (2014). They modeled an adsorption of particles on a solid surface at subcritical temperatures. Centres et al. (2011) provide an improved method for the determination of the energetic topography of the surface from adsorption isotherms. Adsorption on heterogeneous surfaces was also analyzed by following the behavior of surface coverage versus chemical potential (adsorption isotherm) and the differential heat of adsorption as a function of the coverage (Centres et al., 2011). These Previous studies showed that the topography of a given surface can be obtained from the knowledge of the corresponding adsorption isotherm and a reference curve. In this way, the water sorption isotherms can be suitable tools for both predicting shelf life stability and selecting appropriate packaging method. These isotherms give also significant data on the cooperation of portions of date with water vapor. For example, Dural and Hines (1993) developed a theoretical isotherm equation based on multilayer adsorption on heterogeneous surfaces for water vapor food systems. However, this analytical equation and others previous models (Brunauer et al., 1940) are strictly based on empirical or semi-empirical theories. It is difficult to find one equation which gives accurate results throughout the whole range of water activities, and for all types of foods. The novelty of our paper and the progress against recent works is to develop an advanced model expression which provides physico-chemical properties of the date kernels sorption process at the microscopic level.

In this paper, the interpretation of water vapor sorption isotherms of the date kernels at different temperatures is often characterized by the use of the statistical physics formalism (Ben Yahia et al., 2019). This is one of the satisfying ways of describing an activated surface at molecular level (Sellaoui et al., 2018). The use of the statistical physics treatment will allow, firstly, establishing an advanced model expression, and secondly, to better interpret the sorption process at the microscopic state using the physico-chemical parameters (Bouaziz et al., 2019) of the model, which cannot be interpreted by means of empirical methods.

The paper is composed of two parts: The first is dedicated to the measurement of experimental sorption data of water vapor into date kernels using the static gravimetric approach. In the second part, the process of statistical physics is applied to develop the expression of the advanced BET model which leads to a significant characterization of the sorption mechanism.

2 Measurement technique of experimental sorption isotherms

The date kernels used in the experiments of the adsorption isotherms were taken from the date fruit ‘phoenix dactylifera L.’ from the ‘Ajwa’ selection.

The surface morphology of the kernels of dates before adsorption was examined with a Scanning electron microscopy (SEM) (Fig. 1).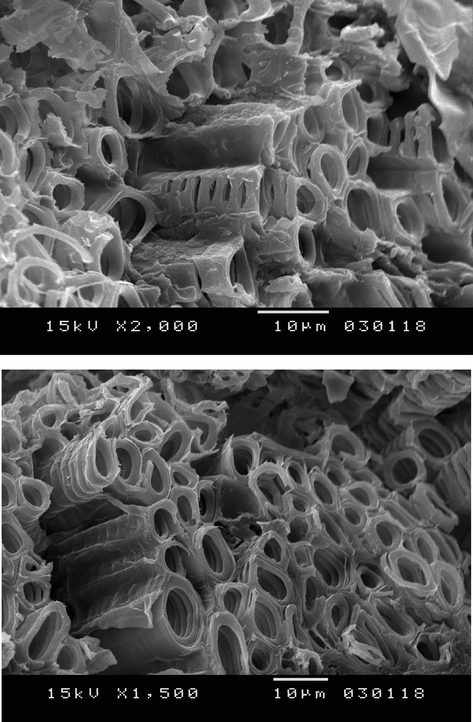

Close

Fig. 1

Scanning electron microscopy (SEM) images of the Surface morphology of kernel of dates.

Export to PPT

Generally, numerous techniques are accessible for determining water sorption isotherms (Gal et al., 1981). These techniques can be arranged into three classes:

• The gravimetric technique (Wolf et al., 1985) which includes the determination of weight changes. Weight changes can be measured continuously and discontinuously in dynamic or static systems. Continuous methods employ the use of electro-balances or quartz micro balances. In the discontinuous systems which is used in our experiments, salt or sulphuric acid solutions are placed in vacuum or atmospheric systems with the food material, to give a measure of the equilibrium relative humidity.

• The manometric method (Gal et al., 1981) which measures the vapor pressure of water in the vapor space surrounding the food. The whole system is maintained at constant temperature and the food sample will lose water to equilibrate with the vapour space. This will be indicated by the difference in height on the manometer.

• The hygrometric method (Gal et al., 1981) which measures the equilibrium relative humidity of air in contact with a food material, at given moisture content. Dew-point hygrometers detect the condensation of cooling water vapor. Electric hygrometers measure the change in conductance or capacitance of hygrosensors. Most hygrosensors are coated with a hygroscopic salt, such as LiCl, which absorbs moisture from the food sample.

The adsorption isotherms of the date kernels are determined at 303 K, 313 K and 323 K for a range of water activity varying from 0.0456 to 0.898, using the most helpful technique in these measurements, which is the static gravimetric technique (Bejar et al., 2012). This technique was developed and standardized in the Water Activity Group of the European COST 90 project (Wolf et al., 1985). We choose to use this experimental technique for its several advantages: (1) Determining the exact dry weight of the sample (Lomauro et al., 1985); (2) Minimizing temperature fluctuation between samples and their surroundings or the source of water vapor (Carbonell et al., 1986); (3) Registering the weight change of the sample in equilibrium with the respective water vapor pressures (Aguerre et al., 1989) and (4) Achieving hygroscopic and thermal equilibrium between samples and water vapor source (Diamante and Murno, 1990).

The experimental setup consists of 11 standard saturated salt solutions which have been used to maintain a regular vapor pressure in a closed space. These salts are LiCl, CaCl₂, MgCl₂, Mg (NO₃)₂, NaBr, KI, NaNO₃, NaCl, KCl, BaCl₂ and K₂SO₄, and the saturated solutions are obtained by dissolving the necessary amount of salt in distilled water up to super-saturation in order to get a_w values ranging from 0.1085 to 0.9661. Eleven glass jars with a protective cover are filled to one quarter depth with a prepared salt solution. Then, the containers are placed in a controlled temperature for one day to be stabilized at the analysis temperature.

After that, a tripod is put in each jar to place the date kernel sample in small crucibles (Bahloul et al., 2008). The date kernel samples are placed in the hermetically sealed jars which are then placed in a controlled oven temperature (303, 313 or 323 ± 27.3 K) for equilibration. The samples are weighted every two days using a Mettler AT 400 balance (Boudhrioua et al., 2008). The physical equilibrium is attained when three consecutive weight estimations showed a difference of less than 0.001 g.

The sorption hygroscopic equilibrium of the date kernels is reached in 18 days. The dry mass of the kernels is determined by the exploitation of the vacuum oven drying technique at 378 K for 24 h.

Finally, the equilibrium moisture content is calculated using the following equation:

With N_a (kg water vapour/kg dry matter) being the moisture content, m_eq (kg) being the equilibrium mass and m_d (kg) being the dried mass.

The experimental isotherms describing the water sorption into the date kernels are illustrated in Fig. 2a.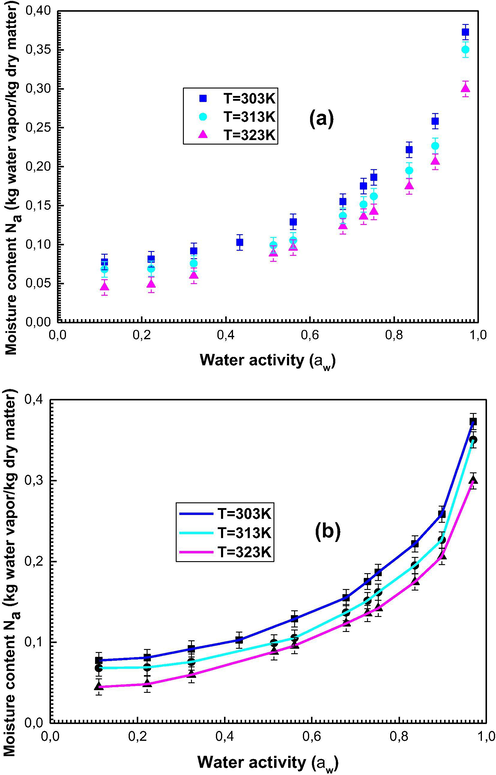

Close

Fig. 2

(a): Experimental isotherms describing the sorption of water onto kernel of dates, (b): Experimental data simulated with the statistical physics model.

Export to PPT

Firstly, it is noted from Fig. 2a that the adsorbed quantity (N_a) decreases by increasing temperature. This fact is explained by the exothermic nature of the adsorption technique which is the normal case of the sorption process. These experimental results need to be interpreted by theoretical explanation.

Moreover, according to the experimental isotherms profiles, the sorption data can be theoretically interpreted by the Guggenheim-Anderson-De Boer (GAB) model (Dural and Hines, 1993); the Brunauer, Emett and Teller (BET) model (Brunauer et al., 1940), and PELEG model (Peleg, 1993). These analytical models provide an interpretation of multi-layer sorption isotherms with empirical manner. In fact, they provide an estimation of the monolayer value of adsorbed moisture on the surface and the adsorption energy. However, all of them do not provide any physical indication about the adsorption mechanism.

The aim of the next section consists to find an advanced statistical physics model that provides a physical description of the experimental isotherms by the intermediate of the physico-chemical parameters included in its expression.

3 Statistical physics modeling

In this theoretical part, we try to develop an analytical expression that gives physical parameters related to the sorption technique. These parameters can facilitate the interpretation of the sorption system at the molecular level.

4 Interpretation of physico-chemical parameters

The parameters of the adjustment of experimental sorption isotherms by numerical simulation using our model are given in Table 2.

For a better interpretation of the adsorption mechanism, the six physicochemical constants are firstly discussed versus the shapes of the adsorption isotherms and secondly, we interpret their variation as a function of temperature.

4.1

4.1 Number of molecules consistent with one site ‘n’

The parameter n is an important factor in the sorption phenomenon due to its steric aspect (Knani et al., 2014).

The influence of this steric parameter on the adsorbed quantity can be understood from Fig. 3a.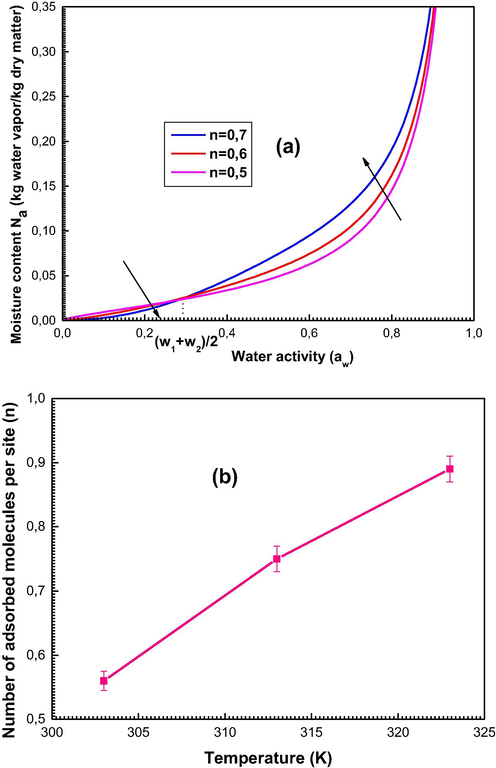

Close

Fig. 3

Interpretation of the steric parameter number of adsorbed molecules per site n: (a) Influence of n on the shapes of sorption isotherms, (b) Evolution of n as function of temperature.

Export to PPT

It is observed that at low water activity, lower values of n correspond to higher quantities of the adsorbed amount. With the exception of the high value of water activity, the inverse observation is noticed. This can be easily understood through the number of empty receptor sites at the beginning of the sorption process. These sites will attract the adsorbed molecules at low water activity range and therefore the aggregation of the adsorbed molecules on one site is difficult. This gives small values for the parameter n. At a high-water pressure and particularly close to the saturation, we note the inverse discover. This is probably attributed to the decrease in the number of empty sites, so the molecules should be aggregated on the receptor sites (highest value of n) in order to increase the moisture content.

Fig. 3b depicts the effect of temperature on the fitted stochiometric constant n.

We noticed that the increase of temperature caused a rise in the number of molecules per site. This can be probably attributed to the thermal agitation factor (Ben Yahia et al., 2013).

It is known that this parameter conveys the anchorage means of the adsorbate onto the adsorbent as proposed by many authors (Knani et al., 2014). It can be larger or smaller than one. In the case of n ≥ 1, this constant describes the number of adsorbed molecules per site so there is formation of a multi-molecular sorption (Knani et al., 2014). Whereas in the case of n ≤ 1, it represents the portion of the molecule anchored on one site and thus it is a multi-anchorage sorption (Knani et al., 2014). Consequently, we note n′ = 1/n which represents the anchorage number of an adsorbed molecule on several adsorbent sites.

In our case, the fitted values of n do not exceed 1 and vary between 0.56 and 0.89 for all temperatures. The fact that n is inferior to 1 shows that no aggregation happens prior to the sorption of water vapor in date kernels and that the adsorption mechanism takes place with a multi-anchorage manner.

4.2

4.2 Receptor site density ‘N_M’

The parameter N_M is a steric constant which represents the number of receptor sites per unit of surface (Wjihi et al., 2019).

We see that an increase in the density of the receptor sites induces an increase in the moisture content (Fig. 4a). It is clear that the rise of the parameter N_M expands the probability of adsorbate molecules to be captured by the surface of the date kernels.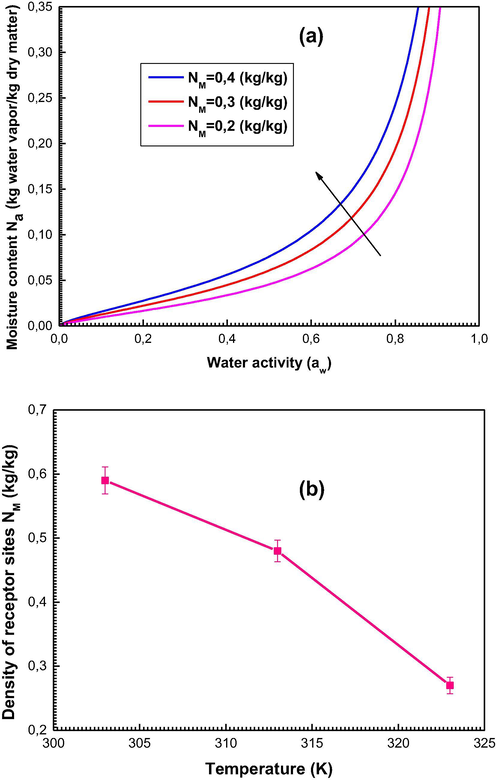

Close

Fig. 4

Interpretation of the steric parameter density of receptor site N_M: (a) Influence of N_M on the shapes of sorption isotherms, (b) Evolution of N_M as function of temperature.

Export to PPT

Fig. 4b depicts the evolution of N_M versus the adsorption temperatures.

Based on Fig. 4b, we notice that N_M decreases with temperature. This behavior is described by means of the energy-releasing nature of the sorption system (Bouzid et al., 2018). This decrease may also be outlined by the steric hindrance during which some sites become hidden by the fact that a set of molecules are adsorbed on one receptor site.

4.3

4.3 Interpretation of Van der Waals parameters a and b

The parameters a and b which are brought in the advanced form of the analytical model using the Van der Waals equation (Ben Yahia et al., 2019), describe the lateral interactions between the adsorbates.

The influence results of the pressure of cohesion a and the covolume b at the wet content are given in Fig. 5a and b respectively.

Close

Fig. 5

Influence of the parameters (a) cohesion pressure a and (b) covolume b on the shapes of the sorption curves generated by the statistical models.

Export to PPT

One can see that the smaller the values of a are, the larger the adsorbed amount is (Fig. 5a). This may be interpreted by the fact that the interaction between the water vapor molecules is weak so the adsorbent-adsorbate interaction becomes excessive.

It should be also noted that the impact of b is opposite to that of a since the expansion of the covolume b causes a growth in the adsorbed amount (Fig. 5b). Indeed, with the increase of the value of b, the adsorbate molecules become more and more distant due to their covolumes, and consequently the attraction between adsorbate molecules becomes weak.

Fig. 6 depicts the evolution of the Van der Waals parameters versus temperatures.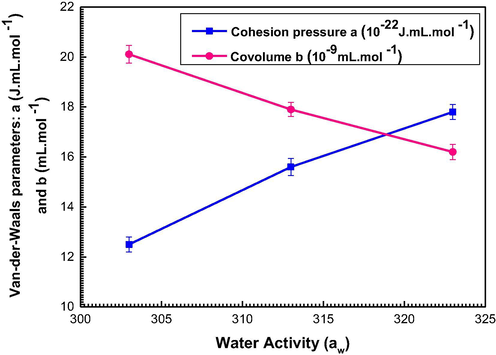

Close

Fig. 6

Variation of the cohesion pressure a and the covolume b versus temperature.

Export to PPT

It is observed from this figure that the parameter a increase by increasing temperature so this parameter acts powerfully at high temperatures. It is also noted that the rise of temperature causes a decrease of the covolume b. Consequently, we deduce that the sorption is more productive at low temperatures. Thus, the introduction of these two parameters in the expression of the multilayer model plays a crucial role in elucidating the exothermic nature of the sorption mechanism.

4.4

4.4 Energetic interpretation: w₁ and w₂ parameters

The energetic aspect of sorption process is managed by the parameters w₁ and w₂ (Nakhli et al., 2014) which are seen in Eqs. (12) and (13).

The effect results of these energetic parameters at the sorption isotherms are illustrated in Fig. 7 which depicts the moisture content as a function of a_w for 3 values of w₁ and w₂.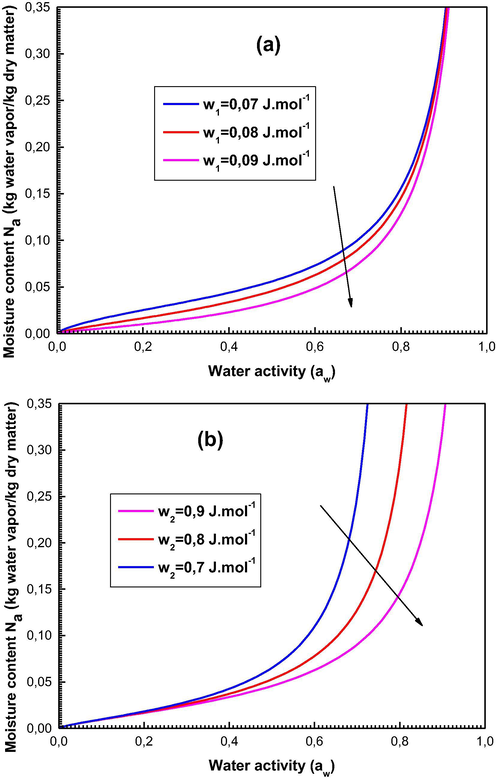

Close

Fig. 7

Effects of the energetic parameters w₁ and w₂ at the sorption isotherms describing the moisture content.

Export to PPT

We observe from Fig. 7 that w₁ acts on the shape of the sorption data at low water activity and that w₂ intervenes at high values of a_w. We also notice that the higher the values of w₁ and w₂ are, the lower the moisture content quantity is. This can be easily understood from Eqs. (12) and (13) where we can note that w₁ and w₂ are explicitly related to the sorption energies (−ΔE^a₁) and (−ΔE^a₂) (kJ·mol⁻¹). The parameters w₁ and w₂ increase as the molar sorption energies decrease in modulus. Therefore, the sorption activity is reduced at high values of w₁ and w₂.

Using the fitting values of w₁ and w₂, we calculate the adsorption energies of the sorption system as follows (Nakhli et al., 2014):

(14)

$$-\mathrm{\Delta }{E}_1^a=-\mathrm{\Delta }{E}_v+RTln\left(w_1\right)$$

(15)

$$-\mathrm{\Delta }{E}_2^a=-\mathrm{\Delta }{E}_v+RTln\left(w_2\right)$$

The values of the molar sorption energies (−ΔE^a₁) and (−ΔE^a₂) calculated at 303 K, 313 K and 323 K are shown in Table 3.

Table 3 Values of the molar sorption energies (−ΔE₁) and (−ΔE₂) estimated at 303 K, 313 K and 323 K.

Temperature (K)	303	313	323
(−ΔEa1) (kJ·mol−1)	−36.15 (±0.5)	−34.28 (±0.52)	−31.44 (±0.59)
(−ΔEa2) (kJ·mol−1)	−25.12 (±0.4)	−20.36 (±0.51)	−19.12 (±0.55)

Fig. 8 depicts the variation of the sorption energies (−ΔE^a₁) and (−ΔE^a₂) versus temperature.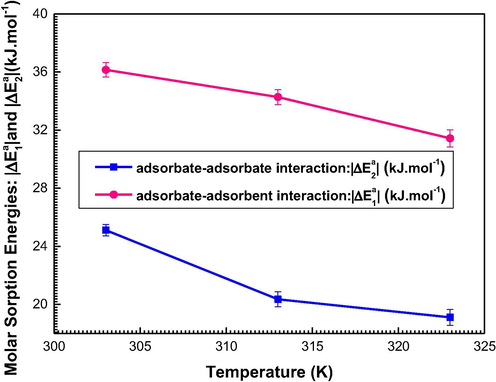

Close

Fig. 8

Temperature dependence of the sorption energies (-ΔE₁) and (-ΔE₂).

Export to PPT

From Table 3 and Fig. 8, one can note three essential results:

• –

  Firstly, the energy (−ΔE^a₁) depicts the cooperation between the water vapor of the primary adsorbed layer and the adsorbent date kernels, i.e. it reflects the adsorbate-adsorbent binding (Ben Yahia et al., 2017). The second energy (-ΔE^a₂) describes the water-water interaction within the multilayer region.

By comparing the results for each temperature, we find that: |−ΔE^a₁| > |−ΔE^a₂|. This is certainly comprehensible because the adsorbate-adsorbent collaboration is larger than the adsorbates interaction.

• –

  Secondly, Table 3 demonstrates that the calculated sorption energies do not exceed 40 kJ/mol. This suggests that the sorption of water vapor in kernels of dates may be a type of physisorption (Diu et al., 1989). Vander Waals or hydrogen bonds are then basically included.

• –

  It may be lastly noticed that an increase of temperature induces a decrease in the sorption energies since the number of receptor sites N_M decrease with respect to temperature (Fig. 8). Thus, this decrease translates the exothermic criterion of the sorption procedure (Knani et al., 2020).

In the next section, the macroscopic physics interpretation of the sorption system is evaluated by a thermodynamic study according to statistical physics treatment.

5 Thermodynamics

Three thermodynamic quantities can be deduced from the advanced BET model, precisely based on the grand canonical partition function.

5.1

5.1 Configurationally entropy

The interpretation of the entropy is fundamental to depict the behavior of the adsorbed particles at the surface. In this case, the entropy taken into account is the configurationally one.

The value of the sorption entropy is calculated based on the grand potential J (Couture and Zitoun, 1992), as follows:

(16)

$$J=-k_{B}Tln{Z}_{\mathit{gc}}=-\frac{\partial ln{Z}_{\mathit{gc}}}{\partial \beta }-T{S}_a$$

(17)

$$T{S}_a=-\frac{\partial ln{Z}_{\mathit{gc}}}{\partial \beta }+k_{B}Tln{Z}_{\mathit{gc}}$$

The entropy is then expressed by:

(18)

$$\frac{S_a}{k_B}=-\beta \frac{\partial ln{Z}_{\mathit{gc}}}{\partial \beta }+ln{Z}_{\mathit{gc}}$$

Subsequently, the sorption entropy S_a can be expressed as:

(19)

$$\frac{S_a}{k_B}=N_M\left[\left(\frac{x_{1}ln(x_1)+x_1{x}_{2}ln(x_2)}{1+x_1-x_2}\right)+ln\left(\frac{1+x_1-x_2}{1-x_2}\right)\right]$$ where x₁ and x₂ are reported in Eqs. (10) and (11).

The profile of the entropy evolution as function of the water activity is given in Fig. 9.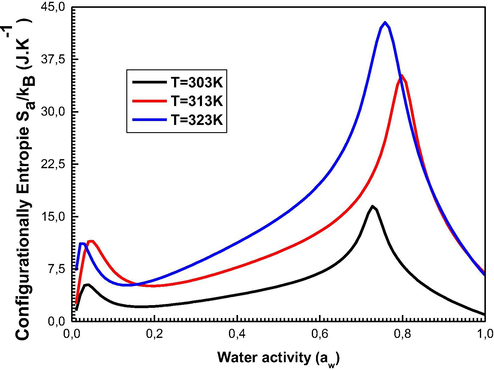

Close

Fig. 9

Development of the Entropy as a feature of water activity at 303, 313, and 323 K.

Export to PPT

Fig. 9 shows that the entropy extends with the increasing value of a_w before w₁ and w₂, and decreases after these particular points. At the beginning, the disorder on the adsorbent surface increases because the adsorbed water vapor has several prospects to find an empty receptor site. After these distinctive points, the adsorbate has an occasional likelihood to choose an adsorbent site due to the surface which tends to the saturation and consequently tends towards being ordered.

One can note that the peak corresponding to w₁ is less than that corresponding to w₂. This can be explained by the fact that w₁ describes the adsorabte-adsorbent interaction and thus the first peak of the entropy reflects a partial disorder at the level of the first layer. However, w₂ is exposed to the adsorbate-adsorbate interaction within the multilayer region (Yahia et al., 2015). At this point, a whole disorder of the sorption system takes place.

5.2

5.2 Free sorption enthalpy

In common, any reaction whose variation in free sorption enthalpy ΔG is negative should be favorable. As a consequence, its investigation is vital to interpret the physical sorption mechanism. It can be expressed by the following expression (Couture and Zitoun, 1992):

(20)

$$G=\mu \ast N_a$$

(21)

$$\frac{G}{k_B.T}=n.N_M\ast \left[ln\left(\frac{N}{z_{\mathit{tr}}}\right)+ln\frac{V}{V-Nb}+\frac{\mathit{Nb}}{V-Nb}-2a\frac{N}{V{k}_{B}T}\right]\ast \left[\frac{x_1+x_1{x}_2+\frac{x_1{x_2}^2}{1-x_2}}{1+x_1-x_2}\right]$$ where μ is the chemical potential given in Eq. (6).

The calculated values of the enthalpy as a function of the temperature are illustrated in Fig. 10.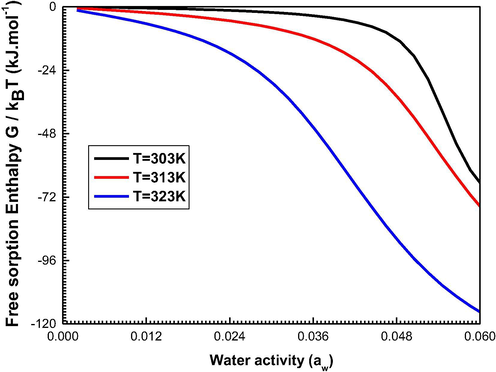

Close

Fig. 10

Evolution of the Gibbs Free Enthalpy at 303, 313, and 323 K.

Export to PPT

We note that the free sorption enthalpy is frequently negative, which suggests that the sorption response is spontaneous (Knani et al., 2020).

5.3

5.3 Internal sorption energy

The investigation of this thermodynamic property specifies the nature of the sorption procedure. Its expression is given in Eq. (22) (Yahia et al., 2015).

(22)

$$E_{int}=-\frac{\partial ln(Z_{\mathit{gc}})}{\partial \beta }+\frac{\mu }{\beta }\left(\frac{\partial ln(Z_{\mathit{gc}})}{\partial \mu }\right)$$

Using the chemical potential and the partition function, the internal energy is reduced to the following expression:

(23)

$$\frac{E_{int}}{k_{B}T}=-N_M\ast \left[\left(\frac{x_{1}ln{x}_1+x_1{x}_{2}ln{x}_2}{1+x_1-x_2}\right)+\left(ln\left(\frac{N}{z_{\mathit{tr}}}\right)+ln\frac{V}{V-Nb}+\frac{\mathit{Nb}}{V-Nb}-2a\frac{N}{V{k}_{B}T}\right)\ast \left(\frac{x_1+x_1{x}_2+\frac{x_1{x}_2^{2}ln{x}_2}{1-x_2}}{1+x_1-x_2}\right)\right]$$

All constants and variables of the internal energy expression are mentioned previously.

We illustrate the evolution of the internal sorption energy at 303 K, 313 K, and 323 K in Fig. 11.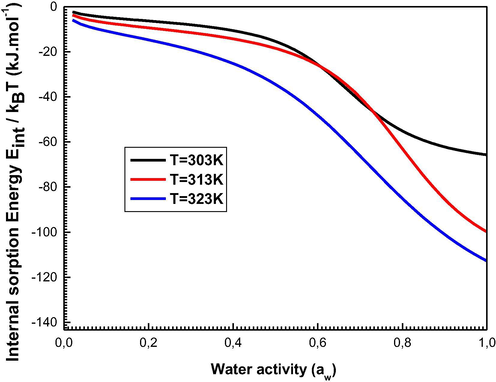

Close

Fig. 11

Evolution of the Internal Energy relative to the sorption system at 303, 313, and 323 K.

Export to PPT

We highlight that the internal sorption energy is usually negative for all adsorption temperatures which shows the energy-releasing nature of the sorption process (exothermic phenomenon).

This thermodynamic magnitude has two states of stability which are clearly seen at 303 K: the first partial stable state returns to the saturation of the first layer and the second is the total state of stability after the formation of all the layers of adsorbed molecules (Knani et al., 2020).

6 Results discussion

The experimental results showed that the sorption capacity of date kernels decreases as a function of temperature (Fig. 2a). The advanced BET model involved physico-chemical parameters that play a significant role on the explanation of the behavior of sorption capacity via temperature. We found that the number of molecules linked per adsorbent site (n) (Fig. 3b) and the cohesion pressure (a) (Fig. 6) increased by increasing temperature. On contrary, the density of receptor sites (N_M) (Fig. 4b), the covolume (b) (Fig. 6) and the sorption energies ((−ΔE^a₁) and (−ΔE^a₂)) (Fig. 8) decreased versus temperature. Based on this finding, it can be established that the number of molecules linked per adsorbent site and the cohesion pressure were not the dominant factor of adsorption process and that the other parameters play a crucial role in elucidating the exothermic nature of the sorption mechanism. It can be also noted that despite the monolayer adsorption capacity is mainly related with the number of molecules linked per adsorbent site and the density of receptor sites (N_mono = nN_M) it is clear that the trends of these two parameters were totally independent.

In view of thermodynamic part, it was highlighted that the study of internal sorption energy (which is specifically due to the sorption energy) confirms the energy-releasing criterion of date kernels adsorption. Correlating this finding with all parameter trends of the statistical physics model, it was possible to understand that the sorption energies ((−ΔE^a₁) and (−ΔE^a₂)) had the most relevant influence on the sorption capacities.

7 Conclusion

The purpose of this paper is to provide an evidence for the behavior of the water vapor in date kernels. The use of the grand canonical ensemble applied to statistical physics allowed the development of an advanced theoretical form of the Brunauer, Emett and Teller (BET) model to describe experimental sorption isotherms. The infinite sorption model seems to be the best way to describe the interaction between the water vapor and the surface of date kernels.

Through the model expression, we determined six physical parameters from the experimental sorption isotherms. The results are mentioned to elucidate the behavior of the parameters versus temperature. We showed that an increase in temperature promotes a rise of the adsorbed molecules per site due to the thermal agitation effect. We found that a rise in temperature caused a decrease of the receptor sites density, which is explained by the exothermic nature of the adsorption process. We also discovered that the sorption is more profitable at low temperature because the cohesion pressure a act powerfully at high temperatures. The calculated sorption energies confirm that the binding between the adsorbates and the surface of date kernels occurs with a physisorption process. Looking at the sorption entropy allows noticing that the disorder reached two maximums when the water activity is equal to w₁ and w₂. An investigation of the free sorption enthalpy and the internal energy demonstrated that the sorption evolves spontaneously and confirmed the exothermic nature of the sorption phenomenon.