Translate this page into:
Statistical physics study of the interaction of the 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP) with magnesium ion: New microscopic interpretations
⁎Corresponding author at: Faculty of Sciences of Monastir, 5000 Monastir, Tunisia. ben_yahia_med@hotmail.fr (Mohamed Ben Yahia)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Adsorption isotherm of Mg(NO3)2 and MgCl2 on H2TPP was achieved using QCM. Advanced model is developed using grand canonical ensemble. Physicochemical parameters in relation with the adsorption mechanism were investigated and interpreted. Steric and energetic interpretations were proposed.
Abstract
In this article, Tetraphenylporphyrin molecules were synthesized and used as biosensor for Magnesium ion. The metallization of porphyrin is a fundamental step which needs to be studied and educated. In fact, adsorption isotherms of magnesium nitrate on porphyrin coated onto Quartz crystal are achieved at four temperatures. Then, statistical physics treatment has been applied to deduce new microscopic interpretations for the experimental data. The main contribution of this analytical treatment is to deduct some physicochemical parameters related to the adsorption process which could not be achieved by means of empirical models. A Layer by Layer adsorption model with two energies was found to be the best model to reproduce the experimental isotherms of magnesium ion on porphyrin. In this model, seven parameters affecting the adsorption process were adjusted, namely the number of ions per site, the density of receptor sites, the two energetic parameters, the cohesion pressure, the covolume and the number of layers. The adsorption mechanisms were characterized by an energetic investigation which demonstrated that the magnesium ion was physisorbed onto porphyrin. Via the exploitation of our advanced model, three classical thermodynamic functions have been investigated and interpreted.
Keywords
Adsorption isotherms
Quartz Crystal Microbalance
Porphyrin complexation
Layer by Layer model
Thermodynamic properties
1 Introduction
Porphyrins and metalloporphyrins are significant in biological systems. Their properties and enzymatic activities have been studied extensively (Buchler, 1975; Pavez et al., 2005; Atsay et al., 2009). A large number of metalloporphyrins and related macrocycles have been investigated due to their electrochemical properties in aqueous and non-aqueous medium. The electrochemistry of metallomacrocycles is known to depend on a variety of factors, some of which are related to the nature of the macrocycle and some to the coordinated metal (Natale et al., 1998).
The synthetic porphyrin studied in this work is the 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP). Metals can be introduced at their peripheral positions (Sayyad et al., 2010). The coordinated metal, peripheral substituents, and macrocyclic skeleton influence the related sensing properties of these compounds (Natale et al., 1998). These characteristics increase the versatility of porphyrin used as sensors (Brunink et al., 1996), showing excellent properties in terms of stability, sensitivity, and reproducibility. The metalloporphyrins with close to 80 different central metal ions has been discussed in a recent review (Pavez et al., 2005) with (TPP)-Co and (TPP)-Fe being perhaps the most studied complexes (Natale et al., 1998; Brunink et al., 1996).
One of the best-known porphyrins is the magnesium - porphyrin complex given in Fig. 1 which constitutes the basic skeleton of chlorophyll, the pigment of life. It is thanks to this molecule that the plant can carry out the photosynthesis phenomenon (Lindsey and Woodford, 1995). So, complexing porphyrin with magnesium is a very important process in biological environment. Consequently, experimental and theoretical studies are considered of interest.
Schematic representation of the chlorophyll nucleus: magnesium – porphyrin complex.
In the same motivation, porphyrin coated electrodes will be used as biosensor to measure the adsorbed mass of magnesium. For this we use the Quartz Crystal Microbalance (QCM) such technique is very active in the biosensor field (Salama et al., 2014; Teresa et al., 2000; Laatikainen and Lindström, 1988; Guiochon et al., 2006; Forssen et al., 2018). The experimental measurements were achieved at equilibrium for different concentration of magnesium in aqueous solution and for four temperatures. Indeed, the crystal holder was immersed in the adsorption cell and the stabilization of the QCM frequency takes the necessary time to ensure the equilibrium. The resonant frequency and the derived adsorbed mass were recorded.
Then, the experimental results are interpreted using the statistical physics formalism. Toward this path, we started by manufacturing a biosensor (Porphyrin (H2TTPP) coated onto Quartz crystal) then controlling the adsorbed mass of Magnesium using the microbalance. The second part will be devoted to the modeling of experimental isotherms based on the grand canonical ensemble in statistical physics. Such treatment allows us to better control the complexation process at solid-liquid interface.
2 Materials and methods
The adsorbate used is the Magnesium nitrate whereas the adsorbent utilized is the porphyrin (H2TTPP) presented in Fig. 2. This compound is a dark purple solid that breaks up in non-polar natural solvents, for example, chloroform and benzene. The general structure of these nitrogenous bases is very inflexible due to pyrrole rings, but it folds to incorporate a small metal or progresses toward becoming dome to accept bigger metal (Qiankun and Xiaoxia, 1997).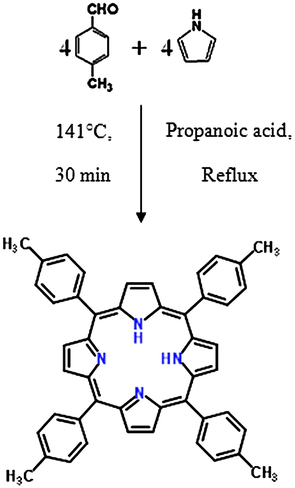
Synthesis of porphyrin H2TTPP.
2.1 Synthesis of the 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP)
All reagents and solvents utilized were industrially accessible and were used as got moving along without any more decontamination. The H2TTPP was incorporated by the standard literature strategy (Adler et al., 1967). All responses and controls for the planning of the H2TTPP were done under aerobic conditions. A UV–Vis spectrum was recorded with a Win ASPECT PLUS spectrometer. A1 H NMR spectrum was gotten at room temperature on a Bruker 300 Ultra shield spectrometer. An IR spectrum was registered on a FT-IR Nexus (Nicolet) spectrometer with a micro-ATR accessory (Pike).
H2TTPP was synthesized by the reaction of pyrrole and 4-tolualdehyde, using the Adler-Longo technique detailed in Fig. 2 (Adler et al., 1967). In a two-necked flask surmounted by a condenser and an expansion channel, we introduced a 12, 5 g of 4-tolualdehyde (106 mmol) and 7 mL of the propanoic acid. This solution is heated under reflux and then is added drop wise 3 mL of distilled pyrrole (43.37 mmol). This reaction was permitted to reflux for 30 min and afterward the heat was turned off and allowed to cool and then made a filtration. After filtration and drying under vacuum, we obtained a mass of 3 g of solid purple.
The synthesized porphyrin (H2TTPP) was spin coated at the crystal surface which was cleaned by Piranha solution before modification. For porphyrin layer deposition, the overlapping gold electrode was covered by coating a volume of 40 µl of H2TTPP at 3000 rpm for 30 s. The coated crystal was then dried at 373 K for at least 1 h. The adsorption cell was effectively prepared, and then we proceed with the experimental measurements of adsorption isotherms.
2.2 Measurement of adsorption isotherms with quartz crystal microbalance apparatus
The use of this method has seen a strong development on wide detection range in the previous decade. Specifically, it has been connected for the investigation of the biochemical reactions since it developed high resolution estimations at solid-liquid interface (Ward and Buttry, 1990).
The experiment setup given in Fig. 3 consisted of the coated electrode, the QCM instrument (model PM 700), the crystal holder, and the adsorption cell.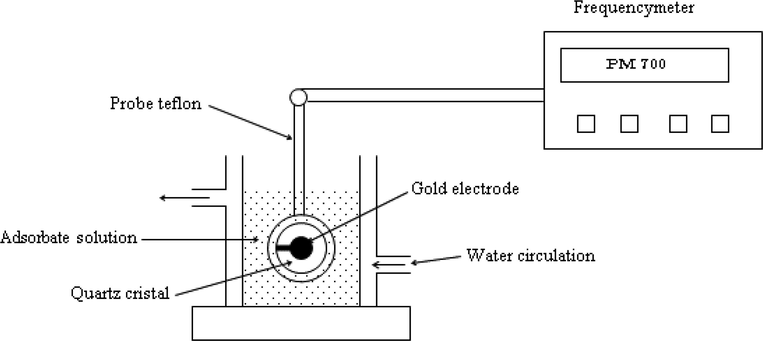
Experimental setup based on Quartz Crystal Microbalance apparatus.
The QCM crystal holder was immersed in the adsorption cell filled with 100 mL of pure water. After stabilization of the QCM frequency change, which usually took around 2 h, 50 μl of the concentrated magnesium nitrate solution (10−3 M) was injected with syringe while the solution was stirred with a magnetic stirrer. The quartz microbalance displays the change in the frequency based on the piezoelectric feature of the quartz crystal (Buttry and Ward, 1985).
The adsorbed amount (Qa) per unit of area is conducted directly from the measured frequency. In the calculation of the adsorbed amount of magnesium, a linear relationship between the change of the areal mass density and the frequency shift was assumed by Sauerbrey relation (Sauerbrey, 1959):
We proceed in the same way to get the adsorbed amounts for the increasing concentrations after each injection.
The experimental setup may be an easy and price effective mass sensing methodology. It additionally offers the likelihood to control the adsorbed amount at the crystal surface while ending the complexation of porphyrin at the same time. That was perhaps a novel feature that could not be achieved by means of other strategies.
The experimental isotherms describing the adsorption of Mg (NO3)2 onto the 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP) are illustrated in Fig. 4.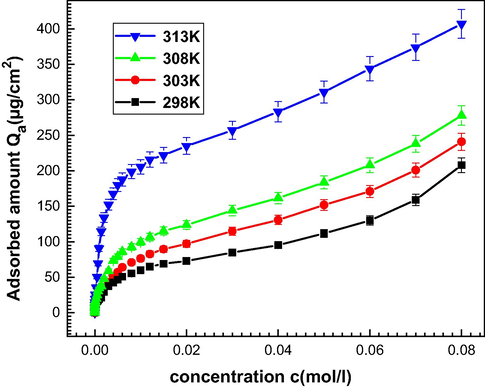
Experimental adsorption isotherms Mg(NO3)2 onto 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP) at 298 K, 303 K, 308 K and 313 K (Stabilization time t = 2 h, volume injected 50 μl).
According to the profiles of the adsorption isotherms, the equilibrium studies can be normally analyzed and interpreted by the Langmuir, Freundlich, and Toth models (Hernández et al., 2013). These models are adequate to obtain the maximum adsorption capacity and the adsorption energy with empirical manner. However, most of them do not provide any indication about the adsorption mechanism.
We note that the research of an adequate model is very useful strategy to interpret the metallization process at the molecular level. In the next part, we will give a detailed treatment of adsorption models based on statistical physics formalism approach. The theoretical models’ expressions will be applied to fit the experimental isotherms.
3 Adsorption models development
Theoretical modeling of adsorption isotherms in liquid phase is a powerful technique used for surface characterization. Thus, the correlation of equilibrium data by either theoretical or empirical equations is essential to the practical design and operation of adsorption systems. Most of the proposed models are empirical or semi-empirical which don’t have any relation with the physicochemical parameters of the adsorption (Meshko et al., 2001; Freundlich, 1906; Liu and Liu, 2008). In contrast to the empirical methods, the use of statistical physics development gives a physical meaning to the model parameters and allows the establishment of significant analytical expressions.
The statistical physics treatment has been successfully studied by Ben Lamine’s group, for solid–liquid and solid–gas adsorption systems. One of the advantages of applying this formula is to give a physicochemical meaning to the parameters involved in the model and then, give new interpretations of the adsorption process at a molecular level (Ben Lamine and Bouazra, 1997; Khalfaoui et al., 2003; Ben Yahia et al., 2017a, 2017b, 2019; Bouzid et al., 2019; Sellaoui et al., 2018; Ben Yahia et al., 2016; Aouaini et al., 2018; Knani et al., 2014; Ben Yahia et al., 2013).
In this work, we try to characterize the adsorbate-adsorbent interaction using adsorption models that contain physicochemical parameters in relation with the adsorption mechanism while having a good correlation with experimental curves.
It is well known that adsorption involves an exchange of particles from the Free State to the adsorbed state. So, during the measurement, it is assumed that equilibrium is reached between the adsorbed phase and the free state. Such equilibrium can be schematized by the subsequent equation (Ben Yahia et al., 2017a):
In this development, we adopt some accompanying suppositions: first, the inner degrees of freedom of the adsorbate are ignored expect the translation level (Ben Yahia et al., 2017a; Azha et al., 2019). Second, to characterize the adsorption procedure we use the grand canonical ensemble knowing that the system, which is maintained at a fixed temperature T, is constituted by all the adsorbed ions and the free phase is considered the reservoir of particles.
Thus, the grand canonical partition function corresponding to an individual porphyrin site is written in the next general expression (Couture and Zitoun, 1992; Diu et al., 1989):
With, (−εi) describes the adsorption energy for a single site, β is the Boltzmann’s constant, Ni is the occupation number which takes the values 0 (site empty) or 1 (site occupied) and µ is the chemical potential of an adsorbed ion.
To take account of the interaction between the adsorbate we use as approach the chemical potential of a real gases (Ben Yahia et al., 2017b). Such chemical potential can be directly deducted from the Van der Waals equation of state and then it has the following expression (Nakhli et al., 2014):
With, µp represents the chemical potential describing an ideal gas, a is the cohesion pressure of the adsorbate, b is the covolume of the magnesium ion and c is the solution concentration. The real gases law was successfully used by Ben Lamine’s research group for describing the complexation of Helicenes molecules with alkali metals (Ben Yahia et al., 2017b, 2019). It was intended firstly to consider the lateral interactions between the adsorbed ions and secondly to introduce new physicochemical parameters (a and b) which leads to supplementary interpretation of the adsorption mechanism.
In the case of a mono-layer formation, the corresponding partition function is given in following expression (Ben Lamine and Bouazra, 1997; Bouzid et al., 2019):
The N complexing sites of porphyrin are supposed identical and independent. Thus, the expression of the average number of occupied sites has the following expression (Ben Lamine and Bouazra, 1997; Ben Yahia et al., 2017b):
Finally, the adsorbed amount of the mono-layer adsorption is expressed as follows (Ben Yahia et al., 2017b, 2019; Bouzid et al., 2019; Sellaoui et al., 2018):
With, c1/2 describes the energetic aspect of the adsorption.
In recent articles, we have demonstrated that the adsorption phenomenon can extend from a mono-layer to a multi-layer formation (Ben Yahia et al., 2016; Aouaini et al., 2018). In particular, the case of ions adsorption, there is multi-layer formation based on layer by layer (LBL) adsorption which implies the presence of complementary ionic charges.
Thus, it is supposed that the first layer of magnesium ions is adsorbed with the energy (–ε1) since it is directly attached to the porphyrin surface and a number L of layers are adsorbed with (–ε2). Then, the grand canonical partition function has the following form (Ben Yahia et al., 2016):
Therefore, the multi-layer adsorption model is written by the subsequent expression:
With, and are the energetic parameters expressed as function of cs which is the solubility of magnesium nitrate in aqueous solution.
In the following section, these adsorption models will be tested to fit the experimental data.
4 Fitting results and interpretation
To choose the proper model that has a good relationship with the experimental adsorption isotherms, we proceed with a fitting computer program. The standard numerical technique used to adjust experimental data with a projected model is based on the Levenberg Marquardt algorithm of iteration employing a multivariate non-linear regression program (Marquardt, 1963).
Three figures of merit were adopted as indicators of the goodness of fit. The first is the accepted coefficient of determination R2 which is a measure of the suitability of the fit, the second is the residual root mean square error RMSE conjointly known as the calculable commonplace error of the regression and the third is the Akaike information criterion (AIC).
A fitting model is correct if the R2 values are near to the unit. The estimated parameters are acceptable if their values should fall within ±2 RMSE of their actual value. So, in comparison between models, the best fitting is obtained if the AIC and RMSE are minimal and R2 is maximal.
Table 1 illustrates the estimated values of R2, RMSE and AIC coefficients deduced from the fitting of the experimental data with the mono-layer and the multi-layer models.
Statistical physics model
Temperature (K)
298
303
308
313
Mono-layer model
R2
0.88
0.89
0.75
0.91
RMSE
4.3
3.6
5.7
2.9
AIC
16.2
13.7
18.9
14
LBL adsorption Model
R2
0.98
0.99
0.97
0.99
RMSE
0.96
1.5
1.7
0.98
AIC
8.98
6.6
9.2
7.3
Based on the errors coefficients values given in Table 1, we conclude that the multi-layer model is the most appropriate model for the description of the complexation process since the coefficients obey to the selection criteria (highest R2 and smallest RMSE and AIC). Using this model, the adsorption of Mg (NO3)2 on porphyrin H2TTPP can be considered with Layer-by-Layer procedure. Thus, the NO3– ions are concerned with the adsorption mechanism and participate to the formation of adsorbed layers as proposed in our previous studies (Ben Yahia et al., 2017b, 2016).
The Fig. 5 depicts the Layer by Layer (LBL) adsorption of magnesium nitrate onto the 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP).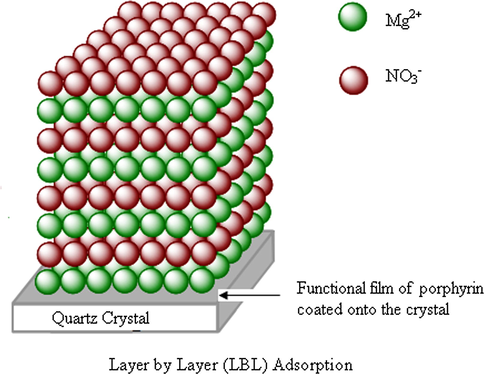
Illustration of the layer by layer (LBL) adsorption of magnesium nitrate onto 5, 10, 15, 20-tetrakis (4-tolylphenyl) porphyrin (H2TTPP).
In the following, the parameters deduced from fitting experimental adsorption isotherms will be discussed and interpreted in order to give a microscopic description of the complexation mechanism.
5 Interpretation of the adsorption formulation by intermediate of the physico-chemical parameters
In the multilayer model expression used for the adjustment of the adsorption system, there are seven parameters. These parameters are classified as steric one such as the number of adsorbed ions per porphyrin site n, the density of receptor sites N and the variety of adsorbed layers L. The second parameters give an energetic aspect such as w1 and w2 parameters. The cohesion pressure a and the covolume b are associated with the lateral interactions between the adsorbate.
Table 2 shows the estimated parameters values concluded from testing the LBL model on the experimental adsorption curves.
Adjusted parameters
298 K
303 K
308 K
313 K
n
0.56 (±0.04)
0.67(±0.07)
0.72(±0.07)
0.84(±0.09)
N
161.2(±4.2)
115.3(±5.3)
97.6(±2.4)
61.4(±1.6)
w1
0.005(±0.0001)
0.009(±0.0003)
0.01(±0.004)
0.007(±0.0006)
w2
0.081(±0.002)
0.093(±0.002)
0.087(±0.003)
0.090(±0.004)
L
87.6(±5.3)
71.3(±6.1)
44.5(±2.4)
23.9(±1.7)
a
31.3(±2.1) 10−20
28.5(±1.3) 10−20
17.9 (±0.5)10−20
11.6 (±0.3)10−20
b
41.7(±2.7) 10−8
38.2 (±2.2)10−8
28. 2 (±1.7)10−8
17.5 (±0.9)10−8
These physicochemical constants are broken down and analyzed in two lines: first, we talk about the impact of every parameter on the experimental adsorption shapes (see Fig. 6) and second, we decipher their evolution as a function of temperature.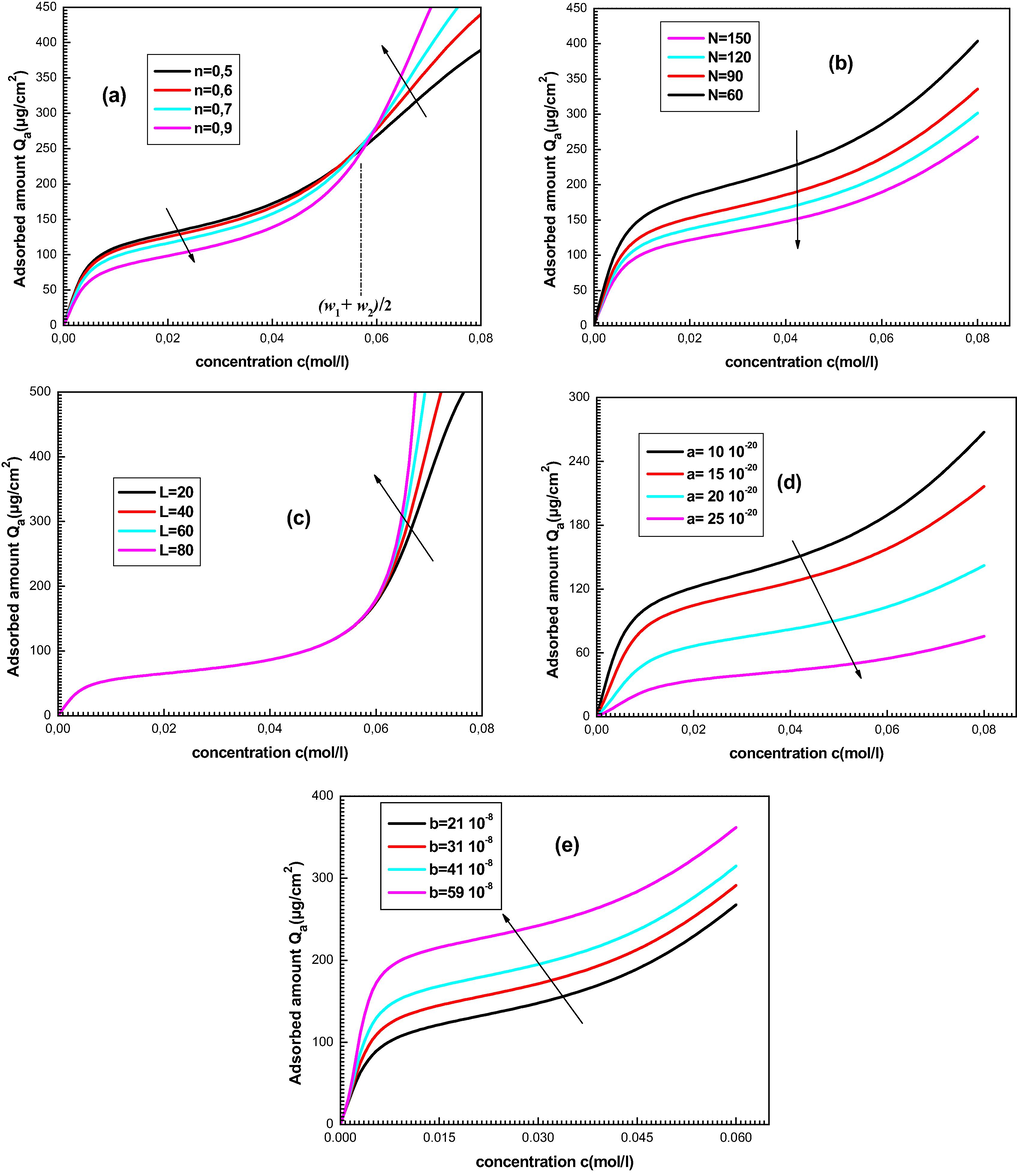
Influence of the physico-chemical parameters on the shapes of experimental isotherms: (a) effect of n, (b) effect of N, (c) effect of L, (d) effect of a and (e) effect of b.
5.1 Interpretation of the parameter n
The parameter n introduced in Eq. (2) is a steric constant which supplies information regarding the number of adsorbates for one receptor site of porphyrin (Ben Yahia et al., 2016). The influence of this physico-chemical constant on the adsorption isotherms is depicted in Fig. 6(a).
The evolution of the parameter n presents two practice behaviors before and above the typical concentration c= (w1 + w2)/2. At low concentrations, an expansion in the quantity of adsorbate particles per site prompts a decrease in the adsorbed quantity while at high concentration the upper the n is the larger the adsorbed amount is, and the saturation is reached quicker. The foremost conceivable and reasonable interpretation is that at low concentration it is tougher to gather adsorbate ions on a unique site: If the worth of n increases, the adsorbed amount becomes smaller whereas at high concentration it is the reverse development which happens: the adsorbate particles are accessible and accordingly it is easier to collect these ions, at that point the adsorption is strengthened and the number of adsorbed layers increases.
Moreover, the porphyrin molecule cannot include more than one adsorbate particle which provides several bonded ions per site n ≤ 1 (Buchler, 1975; Sayyad et al., 2010) as a result of the repulsion interactions between the cationic adsorbates. The fitted values of n estimated by the LBL model in Table 2 vary from 0.56 to 0.84. Therefore, our model confirms that every nucleus of porphyrin is occupied solely by one cationic metal. Note that the adjusted values of this parameter don’t seem to be whole number because n is an average of serial fitting values.
We can likewise take note that for the situation n ≤ 1 the equation (2) can be communicated something else:
In this equation n′ = 1/n shows up as the number of porphyrin (H2TTPP) receptor sites in which an adsorbate is attached (Khalfaoui et al., 2003; Ben Yahia et al., 2017a, 2017b). Thus equation (12) can be expressed as:
Therefore, it looks that the metallic ion Mg2+ admits two simple bonds with the adsorbent pigment (n′ ≈ 1/0.58 ≈ 2) which reflects the complexation of the porphyrin nucleus with the cationic metal conferred in Fig. 1.
As regards the evolution of this parameter as a function of the temperature, one can see from Table 2 that the estimations of n increment by expanding temperature. This reality is likely credited to the thermal agitation.
5.2 Interpretation of the parameter n
This constant is very important since it constitutes a parameter of counting receptor sites available for the adsorbate ions.
In order to investigate the influence of this parameter, we plot the variation of the adsorbed amount versus concentration for various values of N with fixing the other parameters (Fig. 6(b)).
We can note that the adsorbed quantity is higher by decreasing the parameter density of receptor sites N. This is entirely logical since the occupation of the sites by the adsorbed ions (parameter N decreases) causes an increase in the adsorbed quantity.
We can also note from Table 2 that the number of receptors sites N available for adsorbate particles decline by increasing temperature. This result clarified the way that the adsorbed mass of Mg(NO3)2 onto porphyrins increase versus temperature. In fact, a rise in temperature favors the occupation of porphyrin sites by the adsorbates and afterward supports an increase in the adsorbed amount Qa.
5.3 Interpretation of the number of adsorbed layers L
In the case of an LBL adsorption, it is assumed that the first layer of particles is adsorbed with an energy state different from the others since it is directly linked to the porphyrin surface. It is conjointly noted that the number of adsorbed layers L may be a finite value because the succession of layers decreases the influence of the surface on the particles so the adsorption cannot be infinite.
The Fig. 6(c) describes the evolution of the adsorbed amount versus the magnesium nitrate concentration at various values of L.
It is well understood from Fig. 6(c) that the rise of the parameter L favors the adsorption. One can see that this parameter changes the isotherm plot at high concentration because it describes the number of adsorbed layers in the multilayer region.
Another result of this parameter can be interpreted from Table 2 since the fitting values of L decrease as temperature increases.
Generally, the thermal agitation follows up on the cooperation forces between the adsorbed entities in the multilayer local. Accordingly, an increase in temperature forestalls the formation of adsorbed ion layers which prompts a decrease in the parameter L. Such understanding confirms the choice of a limited multi-layer model because the adsorption cannot be interminable since an electrostatic repulsion adsorbate-adsorbate will take place.
5.4 Interpretation of the cohesion pressure a and the covolume b
The parameters a and b which figured in the model expression using the Van Der Waals equation for a real gas (Ben Yahia et al., 2017b; Nakhli et al., 2014) reflect the lateral interactions between the adsorbate particles.
The influence of the cohesion pressure a on the isotherm shape is depicted in Fig. 6(d).
It can be noticed that an increase in the value of the parameter a leads to a decrease in the adsorbed amount. This can be understood by the fact that the rise in the cohesion pressure causes a growth in the adsorbate-adsorbate interaction. So, the attractive interaction of ions by the solution is bigger than the collaboration with the adsorbent. The adsorption of magnesium particles onto porphyrin turns out to be more difficult which leads to a decrease of the quantity Qa.
The impact of the parameter b on the adsorption isotherms is illustrated in Fig. 6(e).
We note that the impact of b is hostile to that of the parameter a since the increase in the values of b results an increase of the adsorbed amount. Without a doubt, when the estimated value of the parameter b increases the particles will be increasingly more far off on account of their covolumes. The repulsive shock between the particles turns out significant which supports adsorption.
It can be noticed from Table 2 that the parameters a and b decrease versus the temperature. Thus, we conclude that the adsorption is increasingly gainful at high temperature since these two parameters act powerfully at low temperature.
5.5 Interpretation of the energetic parameters w1 and w2
The constants w1 and w2 are energetic parameters which govern the complexation process. They also describe the interaction between the complexing adsorbent and the adsorbate ion (Meshko et al., 2001; Ben Yahia et al., 2017a).
5.5.1 Influence of w1 and w2 on the isotherm shape
The physical impact of the energetic parameters on the adsorbed quantity variation is given in Fig. 7(a) and (b).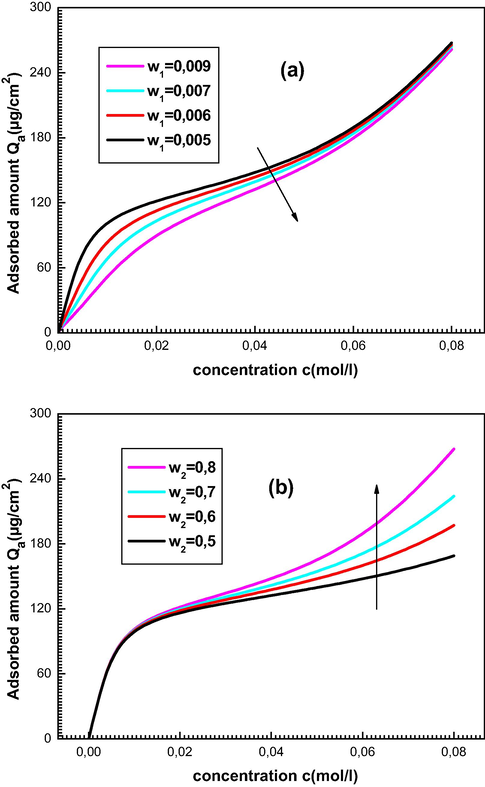
Effect of the energetic parameters w1 (a) and w2 (b) on the adsorption isotherms curves.
Note that this parameter is accountable for the adsorbate-adsorbent association exclusively on the primary layer. Surely, w1 acts on the sorption capability just for the low adsorbate concentrations. We can also see that the rise within the estimations of w1 prompts a decline on the adsorbed amount. As a matter of fact, w1 is identified with the adsorption energy (–ε1); High values of w1 correspond to low values of (–ε1) and then little adsorption energy esteems so that the Mg2 + -porphyrin collaboration is lower and afterward the adsorption of magnesium ions onto the receptor destinations decreases.
It is likewise noticed that an increase of the w2 values which portrays the layers association has no impact on the isotherm’s curves at low concentrations (see Fig. 7(b)). It acts in the multilayer district by increasing the adsorbed quantity at saturation. This is easy to decipher since an increase of w2 leads to limit the adsorbed layers interaction, the influence of the adsorbent surface on these layers turns out to be more significant and accordingly the adsorption is strengthened.
5.5.2 Adsorption energies calculation
The energetic constants referenced above control the complexation system and educate about the bonds nature of the built complexes.
Using the fitting values of w1 and w2 deducted by adjustment of the experimental isotherms with the LBL adsorption model and the magnesium nitrate solubility, we determined the adsorption energies (–ε1) and (–ε2) by the subsequent equation (Ben Yahia et al., 2017b):
Table 3 summarizes the adsorption energies calculated at four temperatures.
Temperature (K)
293
298
303
313
−ε1 (kJ/mol)
−31.5(±3.2)
−35.6(±3.5)
−36.8(±3.7)
−39.6(±4.1)
−ε2 (kJ/mol)
−22.6(±1.1)
−29.3(±1.3)
−30.1(±1.2)
−31.2(±1.4)
It has been mentioned that the energy (−ε1) portrays the cooperation between the metallic Mg2+ adsorbed on the first layer and the adsorbent surface. So, it characterizes the Mg2+-TPP collaboration (Ben Yahia et al., 2017a). Whereas (−ε2) depicts the adsorbate-adsorbate association within the multilayer region. One can see that the |−ε2| values are inferior to |−ε1| values. This is obvious since the adsorbate-adsorbent connection is larger than that between the adsorbed particles. It can be also shown in Table 3 that all adsorption energies estimated do not exceed 40 kJ/mol, which means that the adsorption of Mg (NO3)2 onto porphyrin (H2TTPP) molecules may be a reversible physisorption procedure (Ben Yahia et al., 2015; Hamdaoui and Naffrechoux, 2007). Vander Waals type or hydrogen bonds are then essentially concerned.
It can be additionally observed that an increase in temperature slightly supports a rise within adsorption energies |−ε1,2| since the density of sites N decreases versus temperature. Therefore, a rise in temperature supports the retention of adsorbate particles by the adsorbent sites.
6 Thermodynamics evaluation
Thermodynamic properties (Ben Yahia et al., 2017; Couture and Zitoun, 1992) can be assessed to give macroscopic interpretations about the complexation framework as per of statistical physics formalism.
In this section, the LBL model used to compute potential thermodynamic functions which govern the adsorption mechanism such as entropy, the Gibbs free enthalpy and the internal energy. Using the analytical expression of the grand canonical partition function we give in the corresponding thermodynamic potentials and we decipher their behavior versus temperature.
6.1 Thermodynamic functions calculation
-
The result given by the entropy is extremely vital within the portrayal of the conduct of adsorbed particles since it depicts the arrangement of the adsorbed entities at the surface. In this section, we talk about the configurational aspect of the entropy which describes the disorder of the system. It is proportional to the configurational number needed to accomplish this process (Diu et al., 1989).
The adsorption entropy is determined based on the idea of exploiting the grand potential J and the grand canonical function partition (Couture and Zitoun, 1992; Diu et al., 1989):
The configurational entropy has the accompanying expression (Diu et al., 1989):
The previous expression can be also written as:
With z1 and z2 are defined by the following equations:
-
The examination of the Gibbs free adsorption enthalpy is critical to comprehend the physical adsorption process. Thus, the change in the free enthalpy ΔG must be negative to obtain the reaction of adsorption. Using the grand canonical ensemble, this free enthalpy of Gibbs can be written as (Ben Yahia et al., 2015; Knani et al., 2019):
Thusly, the free enthalpy is given by the following expression:
-
The internal energy concept provides crucial finding for the understanding of the physicochemical adsorption phenomena. Its investigation is important for describing the nature of any reaction.
We calculate internal energy by the intermediate of the following equation (Ben Yahia et al., 2015; Knani et al., 2019):
The internal energy expression is obtained in the following form:
where:
6.2 Macroscopic interpretation
The Fig. 8 depicts the variation of (a) the entropy, (b) the free enthalpy and (c) the internal energy versus adsorbate concentration.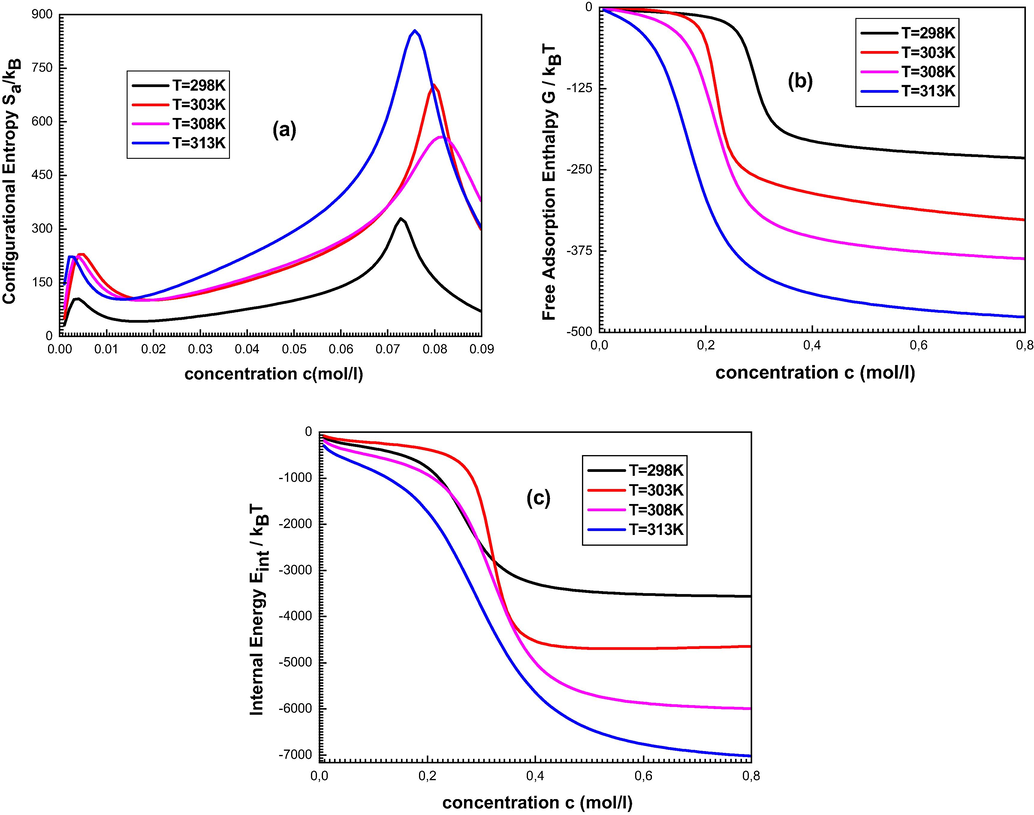
The evolution of the configurationally entropy (a), the Gibbs free enthalpy (b) and the internal energy (c) versus adsorbate concentration.
It is observed from Fig. 8(a) that the entropy has two behaviors before and after w1 and w2. It increases with the adsorbed amount before w1 and w2 and decreases after these specific concentrations. This behavior can be explained by the number of possible arrangements offered to the particles. Once the concentration is lower than the values of w1 or w2, the ions have numerous possibilities to find a receptor site to be adsorbed. So, the disorder increases versus the concentration. After these explicit points, the adsorbate particles have an occasional chance to pick an adsorbent site since the surface tend towards saturation and therefore tend toward the order. We conjointly note that the two peaks don’t seem to be equal since the two energy parameters w1 and w2 portray various sorts of association. Note also that the increase in temperature causes an increase in disorder at a fixed concentration.
It is noticed from Fig. 8(b) that the estimated free enthalpy is perpetually negative, which demonstrated that the adsorption on porphyrins evolves spontaneously. It may also be noted that for low concentrations, this enthalpy begins from zero, and then decrease algebraically with increasing the adsorbate concentration. This is often interpreted by the receptor destinations which are unfilled at the beginning which ends up in high interaction between the adsorbed particles and the adsorbent. Then, by increasing the concentration, the free enthalpy progressively decreases until it reaches the equilibrium state.
From Fig. 8(c), we note that the internal energy is usually negative, which confirms that the system has been spontaneously developed since it releases energy outside. The advancement of this quantity presents two states of stability: the first is a partial stable state returns just to the saturation of the first layer and the second is the absolute state of stability after the formation of all the layers of the adsorbed particles.
7 Conclusion
The coupling of the statistical physics treatment with real gas approach allows the treatment of two advanced models containing physico-chemical parameters associated with the adsorption mechanism. The acceptable model chosen for the adjustment of experimental adsorption isotherms of magnesium nitrate onto H2TTPP pigment is the multi-layer model: it was concluded that an LBL procedure happens since a succession of many adsorbed layers are progressively retained by the adsorbent surface. So, the investigation of the physicochemical parameters promotes deduct the accompanying results:
We found that the estimated values of n are lower than the unity: the LBL adsorption model affirms that every adsorbent site can complex at most one adsorbed entity. We have conjointly shown that an increase in temperature advances a decrease in the density of receptor site N and then, the increasing of temperature supports the porphyrin complexation. The fitted values of the cohesion pressure a and the covolume b decline as a function of temperature. Therefore, it seems that the complexation is progressively favored at high temperature since these two parameters act intensely at low temperature. The energetic calculation demonstrated that the adsorption energy is typical of a physisorption and that the adsorbate-adsorbent interaction is higher than the adsorbate-adsorbate association. The thermodynamic evaluation of the entropy, the free enthalpy of Gibbs and the internal energy show that the disorder is the maximal at the specific concentrations w1 and w2 and that the adsorption process evolves spontaneously, and it is exothermic process.
Acknowledgments
The authors wish to acknowledge the approval and the support of this research study by the grant N° SCI-2018-3-9-F-7620 from the Deanship of the Scientific Research in Northern Border University (N.B.U.), Arar, KSA.
References
- Condensation of pyrrole with benzaldehyde under adler conditions; tetraphenylporphyrins. J. Org. Chem.. 1967;32:476.
- [Google Scholar]
- Study of the CO2 adsorption isotherms on El Hicha clay by statistical physics treatment: microscopic and macroscopic investigation. Sep. Sci. Technol. 2018
- [CrossRef] [Google Scholar]
- Synthesis, electrochemistry and in situ spectroelectrochemistry of water-soluble phthalocyanines. Transit. Met. Chem.. 2009;34:877-890.
- [Google Scholar]
- Iron-modified composite adsorbent coating for azo dye removal and its regeneration by photo-Fenton process: Synthesis, characterization and adsorption mechanism interpretation. Chem. Ing. J.. 2019;361:31-40.
- [Google Scholar]
- Application of statistical thermodynamics to the olfaction mechanism. Chem. Sens.. 1997;22:67-75.
- [Google Scholar]
- Thermodynamic study of krypton adsorbed on graphite using statistical physics treatment. Phys. B. 2013;419:100-104.
- [Google Scholar]
- Energetic and thermodynamic analysis of adsorption isotherm type VI of xenon on graphite nanotubes. J. Thermodyn. Catal.. 2015;6:154.
- [Google Scholar]
- Modeling of adsorption isotherms of zinc nitrate on a thin layer of porphyrin. J. Mol. Liq.. 2016;222:576-585.
- [Google Scholar]
- Statistical studies of adsorption isotherms of iron nitrate and iron chloride on a thin layer of porphyrin. J. Mol. Liq.. 2017;248:235-245.
- [Google Scholar]
- A statistical physics study of the interaction of [7]-helicene with alkali cations (K+ and Cs+): New insights on microscopic adsorption behavior. RSC Adv.. 2017;7:44712-44723.
- [Google Scholar]
- Lamine, adsorption of sodium and lithium ions onto helicenes molecules: experiments and phenomenological modeling. J. Mol. Liq.. 2019;288:110988.
- [Google Scholar]
- Statistical physics modeling of ethanol adsorption onto the phenol resin based adsorbents: Stereographic, energetic and thermodynamic investigations. J. Mol. Liq.. 2019;283:674-687.
- [Google Scholar]
- The application of metalloporphyrins as coating material for quartz microbalance - based chemical sensors. Anal. Chim. Acta. 1996;325:53-64.
- [Google Scholar]
- Buchler, J.W., 1975. In Porphyrins and Metalloporphyrins, ed. by K.M. Smith.
- Measurement of interfacial processes at Electrodes Surfaces with onator in contact with liquid. Ana. Chim. Acta.. 1985;175:99-105.
- [Google Scholar]
- Physique statistique. Paris: Ellipses; 1992.
- Physique Statistique. Paris: Hermann; 1989.
- Reliable strategy for analysis of complex biosensor data. Anal. Chem.. 2018;90:5366-5374.
- [Google Scholar]
- Chapter 3 in: Fundamentals of Preparative and Nonlinear Chromatography (second ed.). Boston: Academic Press; 2006.
- Modeling of adsorption isotherms of phenol and chlorophenols onto granular activated carbon. Part I. Two-parameter models and equations allowing determination of thermodynamic parameters. J. Hazard. Mater.. 2007;147:381-394.
- [Google Scholar]
- Enhanced interpretation of adsorption data generated by liquid chromatography and by modern biosensors. J. Chromatogr. A. 2013;1317:22-31.
- [Google Scholar]
- New theoretical expressions for the five adsorption type isotherms classified by BET based on statistical physics treatment. J. Colloid Interface Sci.. 2003;263:350-356.
- [Google Scholar]
- Lamine, Interpretation of psychophysics response curves using statistical physics. Food Chem.. 2014;151:487-499.
- [Google Scholar]
- Statistical modeling of adsorption isotherm of potassium on aza [7] helicene-coated gold electrode attached to quartz crystal microbalance. Sep. Sci. Technol.. 2019;54:2386-2396.
- [Google Scholar]
- Determination of adsorption isotherms with quartz crystal microbalance in liquid phase. J. Colloid Interface Sci.. 1988;125:610-614.
- [Google Scholar]
- A simple method for preparing magnesium porphyrins. Inorg. Chem.. 1995;34:1063-1069.
- [Google Scholar]
- Biosorption isotherms, kinetics and thermodynamics. Sep. Pur. Tech.. 2008;61:229-242.
- [Google Scholar]
- An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math.. 1963;11:431-441.
- [Google Scholar]
- Adsorption of basic dyes on granular activated carbons ad natural zeolites. Wat. Res.. 2001;35:3357-3366.
- [Google Scholar]
- Modeling of high pressure adsorption isotherm using statistical physics approach: lateral interaction of gases adsorption onto metal–organic framework HKUST-1. Adsorption. 2014;20:987-997.
- [Google Scholar]
- The exploitation of metalloporphyrins as chemically interactive material in chemical sensors. Mater. Sci. Eng., C. 1998;5:209-215.
- [Google Scholar]
- Effect of film thickness on the electro-reduction of molecular oxygen on electropolymerized cobalt tetra-aminophthalocyanine films. J. Solid State Electrochem.. 2005;9:21-29.
- [Google Scholar]
- Electrochemical studies of tetraphenylporphyrin and vanadyl porphyrin. Sci. China Chem.. 1997;40:215-224.
- [Google Scholar]
- Adsorption of benzyldimethyldodecylammonium chloride onto stainless steel using the quartz crystal microbalance and the depletion methods: an optimisation study. Colloids Surf. A: Physicochem. Eng. Aspects. 2014;447:155-165.
- [Google Scholar]
- Use of quartz vibration for weighing thin films of a microbalance. Z. Phys.. 1959;155:206-212.
- [Google Scholar]
- Synthesis of Zn(II) 5,10,15,20 tetrakis(4’-isopropylphenyl) porphyrin and its use as a thin film sensor. Appl. Phys. A 2010:103-109.
- [Google Scholar]
- Insights on the statistical physics modeling of the adsorption of Cd2+ and Pb2+ ions on bentonite-chitosan composite in single and binary systems. Chem. Eng. J.. 2018;354:569-576.
- [Google Scholar]
- The quantification of potassium using a quartz crystal microbalance. Anal.. 2000;125:1983-1986.
- [Google Scholar]
- In situ interfacial mass detection with piezoelectric transducers. Science. 1990;249:1000-1007.
- [Google Scholar]







