1 Introduction

The leather originates from animal skin, generally of the skin of big mammals such as beef or pork, which is tanned that is to say, it becomes by specific technical a dead substance, rot-proof, supple and insoluble in water. It's a natural polymer trained by a cross-linked collagen fiber in a structure of tanning substances. It is a material that is commonly found on our clothes, bags and other accessories of everyday life. Both resistant, flexible and attractive, tanned skin is seen in several ways. Formerly used for its practical aspects, it is now considered a luxury material. The manufacture of leather has become an important industrial development around the world, however, some of the unit operations involved in this industry, in particular the drying process, are still based on the traditional processes, with a very few scientist uses. During recent years, additional constraints regarding quality, pollution, energy cost and security were imposed. To meet these requirements, improve energy efficiency and lower the cost price of the final product, commendable efforts have been made in applied research. From the industrial point of view, the need of leather in the world is huge. Today, what's trending is to have the leather in its interior that requires a lot of research. The leather drying process has been addressed by several researchers, among them we mention: Lionel (2005), Liu et al ( 2010), Roosevelt et al (2000), these authors established the mechanical properties and area retention of leather dried using a combination of biaxial stretching and vacuum. Benmakhlouf et al. (2018) have evaluated the suitability of a set of mathematical equations describing the thin-layer drying behavior of leather. Sander (2006) studied the experimental study of the kinetics of drying of various types of materials made in laboratory scale under different conditions of temperature and pressure, he took samples of wet blue leather bull and dried in a dryer at the microwave. Haghi (2001a-c, 2002, 2003), Haghi and Rondot (2004) proposed a convective drying model for the processing of leather to determine temperature and moisture content distributions. He also determined the drying characteristics of leather during drying by forced convection to predict transient variations in the temperature and moisture content distributions in wet leather. Cabrera et al. (2002, 2004) made an experimental study on samples of tanned leather. The drying process is done in her research by microwave to obtain a distribution of the moisture constant over their entire surface and therefore a better final quality of the material and parallel to a deeper understanding of the process). The sorption isotherms are of a great importance in industries, particularly in storage operations and the preservation of hides. The sorption isotherm is a curve that yields equilibrium moisture content of the studied product as a function of the atmosphere relative humidity that surrounds it. These curves may differ from each other although it is at the same value of the relative humidity at a given temperature Jannot (2003). They provide information on the product stability field after drying and thus provide information on the types of water present in the product (Chkir et al., 2015; Jannot et al., 2006; Kechaou and Maalej, 2000) determined the isosteric heat of sorption for some medicinal and aromatic plants. The authors reported that the differences in isosteric heat values were directly depending on the type of the plant species). They are also useful in a process of convection solar drying. The sorption isotherm could be used for many technological and scientific purposes. In fact, it allows the determination of optimal conditions (temperature and relative humidity) of packaging, storage and/or air drying of the material. The equilibrium moisture content of the product could be compared to the final moisture content of the product dried at the same condition to judge the stability of the processed material. The relationship between water activity (aw) and temperature (T) at constant equilibrium moisture content is described by moisture sorption isosters. Thermodynamic properties such as the isosteric heats of sorption could be deduced from sorption isotherms established at two or more temperatures. The isosteric heats of sorption could be used to analyze, design different material processes and to study moisture–solid interactions (Oswin, 1946). Mathematical models are very useful for describing and predicting sorption isotherms at various experimental conditions and so to calculate all thermodynamic properties that could be deduced. More than 77 equations having two or more parameters have been suggested in the literature for mathematical investigation of experimental data of sorption isotherms Oswin (1946), Bizot et al. (1987) and Dent (1997). These equations are theoretical, semi-theoretical or empirical. Some equations have a dependent temperature term and were used to reflect the temperature dependency of moisture sorption isotherms. Each of the suggested equations has some success in describing sorption isotherms for a given type of product according to the Brunauer classification. This article is a continuation of our old paper (Benmakhlouf et al., 2016) which we have worked on another type of cowhide and it has been suggested that the DENT equation is considered as the most suitable model to be applied to many product types and over a wide range of water activity. The aim of this work is to establish sorption isotherms of leather at four temperatures (30, 40, 50 and 60 °C). Experiments were performed by using the static gravimetric method. Five mathematical equations were chosen from the literature to fit the experimental data. The variations of the isosteric heats of sorption of leather as a function of the equilibrium moisture contents were determined.

2 Experimental analysis

2.1

2.1 Samples preparation and sorption isotherm

There are several experimental methods to determine the sorption isotherms. In this work, we opted for a static method. Thus, we can use either acid solutions or saturated salt solutions. We opted for the latter. Indeed, salt solutions have the advantage of having a narrower range of relative humidity variation and are more stable than the acid solutions. The experimental device consists of a series of nine pots (these salts are: KOH, MgC1₂, K₂CO₃, NaNO₂, KCl, BaCl₂, NaBr, NaCl and LiCl) for each isotherm, we used nine samples cut in square shape with the same initial weight 2(±0.1)g, the same size (2 cm × 2 cm) and thickness (0.2 cm) (Fig. 1). The leather samples are put in nacelles suspended by metal lids and placed in nine jars filled with different salt solutions (Fig. 2). The leather moisture balance is reached after 8 days (Agbaji and Agbaji, 1990), using an electronic scale with digital display, and a precision of 0.01 g. Each sample is weighed regularly by eight days’ time, until obtaining a fixed mass (Me) indicating the end of the exchange between the product and the ambient air. This characterizes the hygroscopic equilibrium position; the dry weights of the samples were determined after drying for 24 h in a vacuum oven at 104± °C. Thus, the mass difference before and after drying in the oven, allowsus to have the equilibrium moisture of the content given in Eq. (1):

(1)

$${\mathrm{X}}_{\mathrm{e}\mathrm{q}}=(M_{\mathit{eq}}-M_d-)/M_d=\frac{{\mathrm{M}}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}}{{\mathrm{M}}_{\mathrm{d}}}$$ where X_eq is the equilibrium moisture of the content, M_eq is the mass reached during the balance, M_d is the dry mass. The water content at equilibrium X_eq, is obtained for four values of temperature (30 °C, 40 °C, 50 °C and 60 °C) shown in the Table 1 which includes the standard values of the air data relative humidity for the new salts according to the temperature.

Close

Fig. 1

Leather samples used in the experiment.

Export to PPT

Close

Fig. 2

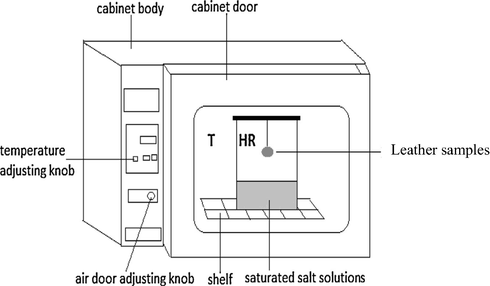
Experimental apparatus for the determination of desorption isotherms.

Export to PPT

Table 1 Selected salt used for preparing saturated salt solutions and their corresponding water activities.

Salt	Water activity
	30 °C	40 °C	50 °C	60 °C
KOH	0.074	0.063	0.057	0.055
LiCl	0.11	0.11	0.11	0.11
MgCl2	0.32	0.31	0.3	0.29
K2CO3	0.43	0.43	0.42	0.42
NaBr	0.56	0.53	0.51	0.49
NaNO3	0.73	0.71	0.58	0.56
NaCl	0.75	0.75	0.71	0.7
KCl	0.84	0.82	0.77	0.75
Agbaji and Agbaji, 1989, 1990; Belghit et al., 2001 BaCl2	0.9	0.89	0.88	0.87

3 Results and discussion

3.1

3.1 Moisture desorption isotherms and desorption model

The experimental desorption isotherms obtained at 30, 40, 50 and 60 °C are shown in Fig. 3. Desorption isotherms of the leather have a sigmoid form and behave like a type II on BET classification. Increasing temperature from 50 to 60 °C sharply affected equilibrium moisture content. The effect of temperature on the desorption isotherms of leather was insignificant between 50 and 60 °C. In fact, for a value of water activity equal to 0.75 equilibrium moisture content of the leather extrapolated from desorption isotherms decreased from 0.195 kg/kg d.b. (at 30 °C) to 0.176 kg/kg d.b. (at 40 °C), to 0.09 kg/kg d.b. (at 50 °C) and to 0.07 kg/kg d.b. (at 60 °C). In general, both temperature and water activity have significant effects on experimental equilibrium moisture content values. Similar trends have been observed in several other studies concerning other polymers produced near to leather (Sander et al., 2003).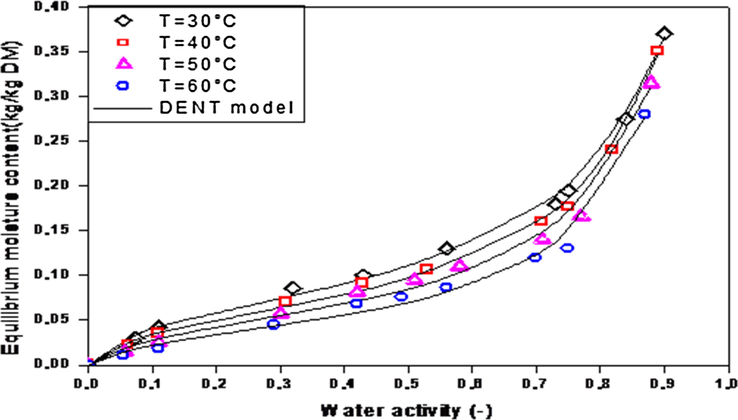

Close

Fig. 3

Desorption isotherms for leather at various temperatures.

Export to PPT

The results of the non-linear regression analysis of desorption isotherms of leather obtained from the tested models and at 30, 40, 50 and 60 °C were presented in Table 3. For all the models tested, it can be observed that all the models have high correlation coefficients r ≥ 0.97 and insignificant standard errors S ≤ 18 × 10⁻³. According to our results, the DENT model, with parameters presents the highest values of the correlation coefficient (0.999) and the lowest values of standard error (0.005), and the best fit for all examined temperatures as depicted in Fig. 3.

Table 3 Parameter values obtained for the five models used to describe desorption isotherms of leather.

Models names	T (°C)	Parameter	r	s
GAB	30	Xm = 0.0554305186 K = 0.9466034844 Cg = −1049397876.23	0.9935	0.01490
	40	Xm = 0.0526631654 K = 0.955116214 Cg = −886090335.129	0.9912	0.0163
	50	Xm = 0.04133915845 K = 0.9851595463 Cg = 450037064457	0.9882	0.0158
	60	Xm = 0.03388809759 K = 1.0089091038 Cg = −8098340904.42	0.9885	0.0140
Dent	30	A = −13.550134 B = 13.61939091 C = 1.166540167	0.9989	0.006120
	40	A = −16.20058217 B = 15.6767011162 C = 1.43826375	0.999	0.0052
	50	A = −18.3376118314 B = 17.1397257 C = 1.94678030	0.9963	0.0089
	60	A = −23.4759771 B = 21.14312331 C = 2.51356392865	0.9958	0.0084
Henderson	30	A = 7.12155757 B = 1.06567659	0.9886	0.01856
	40	A = 6.38868269972 B = 0.94872095966	0.987	0.0185
	50	A = 6.46306579922 B = 0.906628142555	0.9827	0.0181
	60	A = 6.06572262 B = 0.810022395	0.9794	0.0175
OSWIN	30	A = 0.112919466797 B = 0.533367430634	0.9886	0.01856
	40	A = 0.0981941413 B = 0.596414382	0.9976	0.0079
	50	A = 0.0861958500641 B = 0.633308960346	0.9944	0.0103
	60	A = 0.0702718835 B = 0.707593277	0.9919	0.0110
BET	30	A = 0.041518380 B = 3819.310445	0.9721	0.02889
	40	A = 0.04152550932 B = 47.7136463	0.9976	0.0171
	50	A = 0.03949998374 B = 24.5502779736	0.9913	0.0128
	60	A = 0.0368039035 B = 12.27904922	0.9956	0.0080

A comparison of the experimental and predicted equilibrium moisture content values X_eq using the DENT expression, between 30 °C and 60 °C, is illustrated in Fig. 4. From these results, a close approximation by this model estimation can be observed (r = 0.999).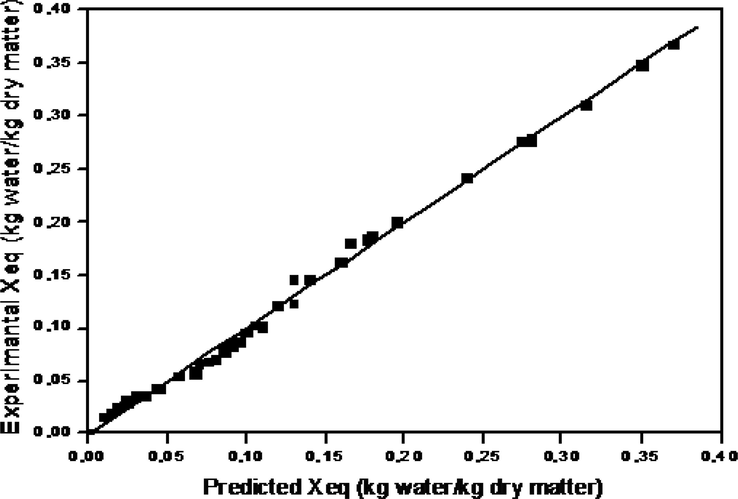

Close

Fig. 4

Comparison of the experimental and predicted equilibrium moisture contents by the DENT equation.

Export to PPT

3.2

3.2 Isosteric heat of desorption

The heat of desorption or sorption at particular moisture contents of the samples was determined by using the Clausius-Clapeyron equation Fig. 5. To describe the relationship between the net isosteric heat of sorption Q_st.n and the moisture content. Tsami (1991) proposed the following empirical exponential correlation:

(6)

$$Q_{\mathit{st},n}=q_{0}exp(\frac{X_{\mathit{eq}}}{X_0})=32.12exp(-\frac{X_{\mathit{eq}}}{0.051})$$ where Q_st,n is the net isosteric heat of desorption, X_eq is the equilibrium moisture of the content and X₀ the initial equilibrium moisture of the content.

Close

Fig. 5

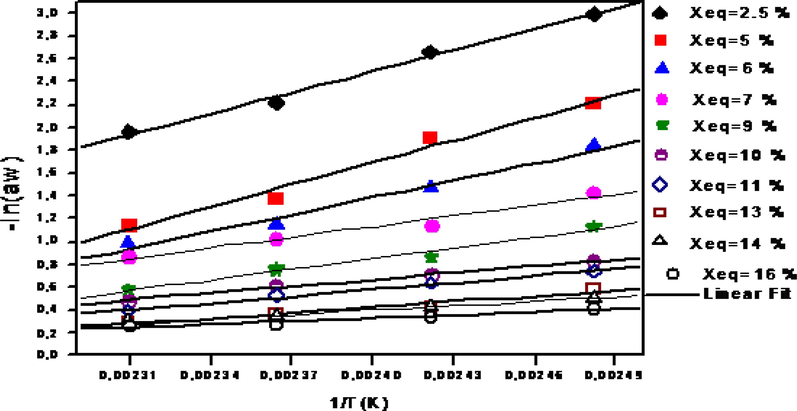
Desorption isosteric curve of leather.

Export to PPT

The net isosteric heat of desorption of leather is a valuable tool in designing the drying process which is important in understanding the mechanism of sorption. The variation of the isosteric heat of desorption versus equilibrium moisture content is shown in Fig. 6. The isosteric heat for desorption decreased rapidly with the increase of moisture content until a moisture content of about 15% was reached. The step increase of qsn at low moisture contents is due to the monomolecular layer formed by highly active polar sites on the surface of the hide material that are covered with water molecules. Furthermore, Fig. 6 shows a comparison between the calculated isosteric heat of desorption and the mathematical correlation describing the isosteric heat of desorption (Eq. (3)). This equation could be used to determine the isosteric heat of desorption for temperatures and equilibrium moisture contents varying respectively from 30 to 60 °C and from 0.02 to 0.17 kg/kg d.b.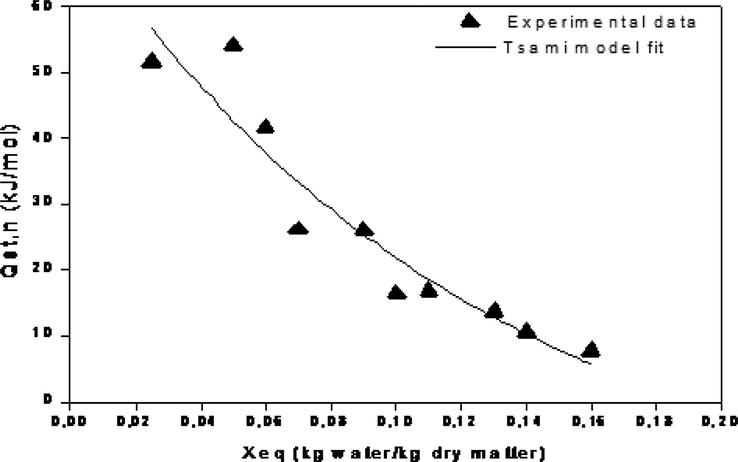

Close

Fig. 6

Isosteric heat of desorption Q_st.n as function of equilibrium moisture content X_eq.

Export to PPT

4 Conclusions

In this study, an experimental investigation is carried out in order to predict desorption isotherms and the isosteric heat of leather at different degrees, namely; 30. 40. 50 and 60 °C. This study determined the bovine leather thermodynamic properties associated with moisture sorption isotherms for temperatures 30, 40, 50, 60 and 70 °C. These thermodynamics parameters can be used to promote the leather use and to improve their drying process with a comprehensive drying model. The experimental desorption isotherms of leather have a sigmoid form and display the type II on BET classification. The equilibrium moisture content is seen to significantly lower by further augmenting the temperature. In the current investigation, five models were tested to describe the experimental leather desorption isotherms. The DENT model was observed to be the most suitable for describing the relationship between the equilibrium moisture content, the water activity as well as the temperature. Besides, the isosteric desorption heat of leather strengthened with decreasing moisture content. Of great interest is the establishment of an empirical equation which describes this variation between 0.02 and 0.17 kg/kg d.b. As perspective of the current experimental investigation, this study can be extended to measure the mechanical properties of these leathers. In this vein, the important mechanical leather behaviors can be predicted before its use. In addition, the results will be used later in the numerical modeling of coupled transfers of heat and mass transfer phenomena during convective drying leather.