Translate this page into:
The effects of rotation on the frequencies and critical speed of CNTs/fiber/polymer/metal laminates cylindrical shell
⁎Corresponding author. lss1214680162@163.com (Shaoshuai Liu), lotfor@ums.edu.my (Md Rahman Lutfor)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This work focuses on the frequencies of rotating carbon nanotubes (CNTs)/fiber/polymer/metal laminates (CNTFPMLs) thin circular cylindrical shell. The cylindrical shell is studied on the basis of Love’s first approximation shell theory with simply supported boundary condition. In this manuscript, Eshelby-Mori-Tanaka is used to define the modulus of carbon nanotubes reinforced composites (CNTRCs) cylindrical shell. In addition, fibers can be reinforced using the obtained matrix by means of extended rule of mixture. The influence of various parameters for example characteristics of fiber phase material, such as circumferential and axial wave numbers, lay-ups, metal volume fraction, composite volume fraction and CNTs mass fraction on the frequencies of rotating CNTFPMLs cylindrical shell have been studied. The outputs illustrated by growing rotational speed, the frequencies of CNTFPMLs cylindrical shell change differently for different fiber volume fractions. Also, the backward and forward frequencies of functionally graded and distributions are more and less than the uniformly distributed ( ) for rotational speed equals to 1, respectively, while this process is reversed for rotational speed equals to 5. In 10 and 20 rotational speeds, while the frequencies of backward and forward modes for distribution are more and less than the , respectively, but this procedure is reversed in distribution.
Keywords
Rotation
Critical speed
Vibration
CNTFPMLs
Circular cylindrical shell
1 Introduction
Bending and vibration analyzes of macro sized structural elements such as beam, panel, plate and shell were widely studied by researchers. Thanks to the developing technology, these structures have designed in micro/nano forms and various higher order theories have been utilized for their analyzes. The technology of nano scaled materials/structures, nanotechnology, has different fields of study in various disciplines such as device physics, chemistry, health, electrical engineering, civil engineering and aerospace engineering. Furthermore, the efficiency of the inhomogeneous macro and micro/nano-sized structures and the diversity of their usage areas have led to an increase in the studies (Akbaş, 2017; Akbaş, 2017) on the behavior of these structures.
During the last years, the composite materials have been predominately used in the most promoted engineering applications and fields namely aerospace and mechanical engineering science. Dynamic and vibration analysis of various structures have attracted some authors (Afsharmanesh et al., 2014; Ghasemi et al., 2016; Mohandes and Ghasemi, 2016; Saidi et al., 2016; Li et al., 2016; Ebrahimi and Dabbagh, 2019; Ghasemi and Mohandes, 2018; Shi et al., 2015; Ye et al., 2014) particularly vibration and dynamic analysis of rotating composite cylindrical shells. Rotating composite cylindrical shells are extremely applied at various engineering fields due to their high strength to weight ratio. They are utilized in rotor systems, high speed centrifugal separators, motors and derive shaft of gas turbines. Free vibration of rotating and non-rotating composite cylindrical shells have been studied by various researchers (Soldatos, 1983; Lam and Loy, 1994; Zhang, 2001; Malekzadeh et al., 2008; Alibeigloo, 2009; Liu and Chu, 2012; Daneshjou and Talebitooti, 2014; Javed et al., 2016; Khayat et al., 2018), while they focused on vibration of fiber-metal laminates (FMLs) cylindrical shells less (Ghasemi and Mohandes, 2019; Khalili et al., 2010; Mohandes et al., 2018). Now a days, study on the behavior of FMLs, which are so-called hybrid structures, has attracted much attention because of benefits of metal such as damage tolerances, impact and ductility as well as good characteristics of composites namely high stiffness to weight ratios, acceptable corrosion and excellent fatigue resistance. Alloys compounds have some disadvantages. Such as low resistance to the temperature, oxygen and electromagnetic radiation (Vinnik et al., 2021; Zdorovets et al., 2021). There are various methods for obtaining metallic alloys compounds which were introduced in some studies (Zubar et al., 2018; Zubar et al., 2019).
Shooshtari and Razavi (Shooshtari and Razavi, 2010) found out nonlinear frequencies of FML rectangular plates according to first order shear deformation using multiple time scale method. Tao et al. (Tao et al., 2016) used von-Karman assumption to investigate nonlinear dynamic of FML Euler-Bernoulli beams under moving loads in thermal environment. The influences of different items such as geometric nonlinearity and temperature on the dynamic responses were investigated for an FML beam. The frequencies of FML perforated annular plate based on three-dimensional elasticity theory were obtained by Rahimi et al. (Rahimi et al., 2014). They determined the natural frequencies of the GLARE plate subjected to various boundary conditions by means of a combination of the DQM, state-apace and Fourier series. The outputs which are compared to the ABAQUS software illustrated excellent agreement.
Recently, composites reinforced by carbon nanotubes (CNTs) have attracted much attention to apply in the advanced industries and different types of carbon nanoforms can be used (Yakovenko et al., 2018; Yakovenko et al., 2020). Thermal, mechanical and electrical behaviors of a matrix can be significantly promoted by adding CNTs. Also, composite properties namely tensile strength and elastic modulus can be improved by substituting the carbon fibers by CNTs. Two reputable categories of CNTs are single-walled and multi-walled structures. Single-walled carbon nanotubes (SWCNTs) are consisting of a rolled single graphene sheet to construct a cylindrical shell with diameter 1 nm and length of order of centimeter (Syah et al., 2021). The multi-walled carbon nanotubes (MWCNTs) are made of an array of these cylinders which are constructed of multi graphene sheets rolled concentrically. The MWCNT is a cylindrical shell, with diameter between 2 and 100 nm and 10 µm length, graphene sheets distance around 0.35 nm. The most researchers studied vibration of various structures reinforced by CNTs (Madani et al., 2016; Nejati et al., 2017; Fantuzzi et al., 2017; Malikan et al., 2018; Civalek and Baltacıoğlu, 2018; Kiani et al., 2018; Zhao et al., 2019) and polymer nanocomposites efficient (Wang et al., 2020; Darwish et al., 2020).
The effects of CNTs on nonlinear vibration of composite cylindrical shells on the bases of higher order shear deformation theory under thermal loading according to von-Karman assumption was considered by Shen and Xiang (Shen and Xiang, 2012). They indicated that as increased the temperature, although the frequencies were declined, the nonlinear to linear frequency ratios were grown. Vibration and damping of functionally graded carbon nanotube-reinforced hybrid composite (FG-CNTRHC) shells were investigated by Thomas and Roy (Thomas and Roy, 2017). They applied Eshelby-Mori-Tanaka to obtain FG-CNTRHC material properties and also Rayleigh damping model employed to consider the impact of CNTs on damping capacity of this hybrid shell. They indicated that the volume fraction of CNTs and carbon fibers influenced all elastic properties of the shell. Ansari et al. (Ansari et al., 2016) analyzed vibration of different FG-CNTRC spherical shells rested on elastic foundation with various boundary conditions. They used variation differential quadrature method (VDQM) to obtain natural frequencies. The results indicated fundamental frequencies of distribution had the most value. Also, as the thickness-to-radius ratio grew, the non-dimensional frequencies declined, considerably. Vibration and buckling of FG-CNTRC conical shells undergoing axial loading using VDQM studied by Ansari and Torabi (Ansari and Torabi, 2016). The results revealed that the more the volume fraction of CNTs, the greater the non-dimensional frequencies and axial buckling loads of the shells. Kamarian et al. (Kamarian et al., 2016) considered free vibration of agglomerated carbon nanotube reinforced composite (CNTRC) conical shells based on first-order shear deformation theory (FSDT) via generalized differential quadrature method (GDQM). Ghasemi and Meskini (Ghasemi and Meskini, 2019; Ghasemi and Meskini, 2019) obtained frequencies of rotating cylindrical porous and FGM shells with respect to porous coefficients, porous type, FGM power laws, length to radius ratio, rotating speed, and axial and circumferential wave numbers. Li et. Al (Li et al., 2020) implemented vibration of FRCCS with partial concentrated layer damping based on Ritz method according to Jones-Nelson theory, energy-based strain energy method, and complex modulus method. Qin e. al (Qin et al., 2020) obtained natural frequencies of laminated functionally graded shallow shells reinforced by graphene platelets (GPLs) subjected to various boundary conditions based on FSDT according to artificial spring technique. Li et al. (Li et al., 2021) investigated vibration of fiber reinforced polymer composite cylindrical shells under thermal loading on the basis of Jones-Nelson nonlinear material theory, complex modulus principle, and polynomial fitting technique. The results showed that with growing the excitation amplitude, the first three natural frequencies were initially declined and then raised. Li et al. (Li et al., 2021) analyzed dynamic of fiber reinforced polymer (FRP) cylindrical shell with functionally graded porous graphene platelets (FGPGP) coating based on FSDT subjected to different boundary conditions using artificial spring method. Theoretical and experimental studies of nonlinear vibration of fiber-reinforced composite cylindrical shells (FRCCS) were done by Li et. Al (Li et al., 2021) for bolted joint boundary conditions according to Love shell and Jones-Nelson theories based on Rayleigh-Ritz method. They fount out that with growing bolt loosing degree and loos bolt number, the natural frequencies and model damping ratios decreased and increased, repectively.
The application of rotating systems reinforced by CNTs has been grown in different industries such as micro/nano motors, nano biomedical devices and nano computers. Study on free vibration of rotating structures with respect to critical speed particularly carbon nanotubes (CNTs)/fiber/polymer/metal laminates (CNTFPMLs) cylindrical shells is one of the most critical problems of advanced technologies. Therefore, in the present research, the influence of rotational speed on the frequency values of CNTFPMLs cylindrical shell subjected to simply supported boundary condition is studied. Some references of vibration of composite cylinders, which are rotating, are available, however none of them are not related to vibration of rotating CNTFPML cylindrical shells. These four phases materials altogether are preferable for cylindrical sells since the benefits of FML cylindrical shell are studied as well as nanocomposite cylindrical shells. Therefore, these four phases materials can improve damage tolerance properties and fatigue resistance as well as modifying mechanical, thermal and electrical behaviors. Four phases of representative volume element are: CNTs, fiber, polymer matrix and metal. To generate CNTFPMLs cylindrical shell, first, the CNTs have been added to the matrix and after that the reinforced matrix has been used to reinforce fiber phase. At the end, the adhesive fiber prepreg has been combined with the thin metal layers. The distributions of CNTs in the thickness direction of isotropic matrix layer are considered either by uniformly distributed (UD) or functionally graded (FG) which are included four types , , and . The frequencies of CNTFPML cylindrical shell are obtained for different material characteristics of fiber, lay-ups, volume fractions of metal and composite sections (Syah et al., 2021).
2 Fundamental equations
The CNTFPMLs circular cylindrical shell is shown in Fig. 1. The FML is consisting of thin aluminum layer with adhesive fiber (Syah et al., 2021).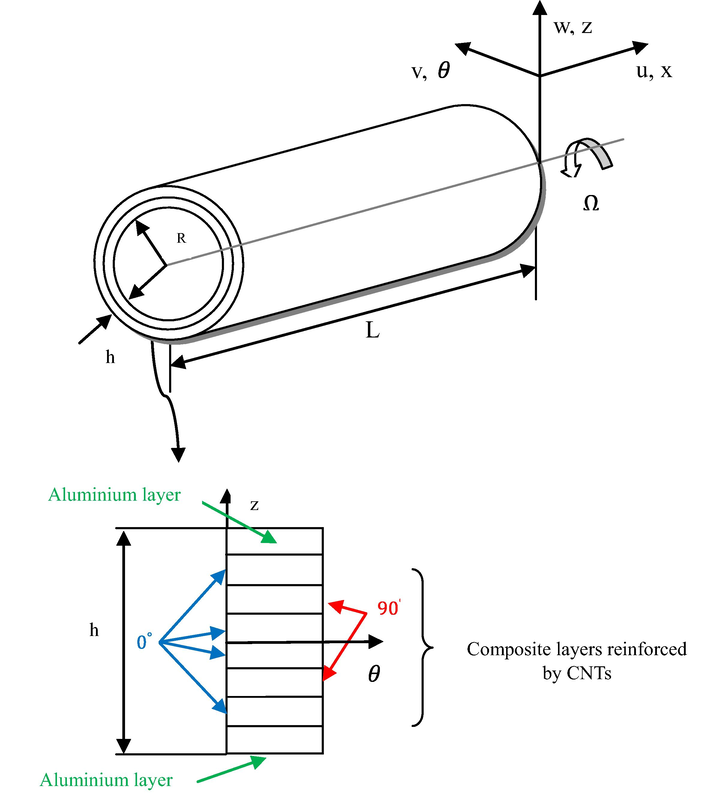
CNTFPMLs rotating circular cylindrical shell.
The equations of motion for thin rotating circular cylindrical shells based on Love's first approximation theory are specified as (Syah et al., 2021; Lam and Loy, 1995):
The elastic modulus of fiber phase are presented by , and in above equation. Also, the Poisson’s ratio and volume fraction of fiber are defined by and . Moreover, the elastic modulus of matrix phase, that has been reinforced by CNTs, are , and and and introduce the Poisson’s ratio and volume fraction of the matrix reinforced by CNTs, as well.
3 Material characteristics of CNTRCs
The effect of CNTs on the characteristics of composite at nanoscale is remarkable. So, some micromechanical models namely Mori-Tanaka and Voigt which are rule of mixture (Esawi and Farag, 2007; Anumandla and Gibson, 2006) were presented to predict the effective material characteristics of CNTRCs. The effective Young's and shear modulus of CNTRCs cylindrical shell can be defined on basis of extended rule of mixture as following (Kiani et al., 2018; Shen, 2009):
The effective density and Poisson's ratio of the CNTRCs shell are considered as follows (Shen, 2009):
The distribution of CNTs in the thickness direction of isotropic matrix layer has a considerable influence on the free vibration of CNTRCs cylindrical shell. The CNTs reinforce the matrix either by uniformly distributed (UD) or functionally graded (FG) continuously and smoothly through the thickness direction of the shell as shown in Fig. 2. In this manuscript, four types of FG-CNTRC shells are studied including
,
,
and
which the mid-plane and both outer and inner surfaces of the shell are CNT-rich (Ghasemi et al., 2019; Syah et al., 2021).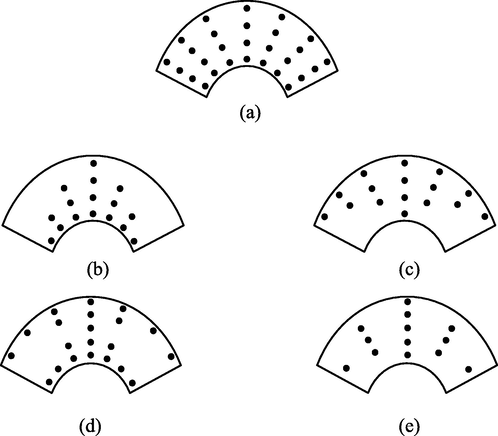
CNTs distributions: a)
; b)
; c)
; d)
; e)
.
The volume fractions of the CNTs for each type of the distributions can be expressed as (Janghorban and Nami, 2016):
The governing equations of motion for thin cylindrical shell can be expressed by introducing stress resultants into equation (1) as following:
4 Analytical solution procedure
In this study, free vibration of FMLs rotating cylindrical shells reinforced by CNTs with simply supported boundary condition is analyzed utilizing analytical method. The simply supported boundary conditions are defined as following:
The displacement terms in closed form to satisfy simply supported boundary conditions at
are provided by following equations (Lam and Loy, 1994; Syah et al., 2021):
By introducing equation (6) into equation (4), a
displacement coefficient matrix
in the non-dimensional form can be expressed as:
where
The determinant of coefficient matrix set to zero to for each values of and for a non-trivial solution of the equations of motion.
5 Numerical results and discussion
Not only are composite materials used in the most cutting-edge engineering applications such as aerospace and mechanical engineering science, but also that is clear that mixture of varies materials can improve their electronic properties (Trukhanov et al., 2020; Kozlovskiy et al., 2021).
The deviation from stoichiometry and appearance of the oxygen anions result in changing the charge state of the cations. It is well known that the complex metal compounds easily allow the oxygen excess (Trukhanov et al., 2011; Kozlovskiy et al., 2020). Moreover, It is necessary to discuss in more details how the average crystallite size distributin of produced samples change by annealing temperature and how they affect their electronic properties. These items were studied in some references (Trukhanov et al., 2008; Kozlovskiy and Zdorovets, 2019).
In this section, free vibration of rotating CNTFPMLs cylindrical shells subjected to simply supported boundary condition is considered.
All characteristics and dimensions to study this circular cylindrical shell are illustrated as follows, except otherwise noted:
Simply supported boundary condition, aluminum and carbon/epoxy are the materials of metal and composite layers, respectively, the lay-ups of the cylindrical shell is considered four-layered and cross-ply
. The metal thickness and one layer of reinforced composite are the same, the distribution of the CNTs is uniformly distributed (UD),
,
. Further, the considered material properties of the circular cylindrical shell are shown in Table 1 (Ghasemi et al., 2019).
Material properties
CNT
Fiber
Matrix
Metal (Aluminum)
Carbon
Glass
5.1 Validation
In order to verify the accuracy of obtained results, the rotating CNTFPMLs circular cylindrical shell is considered without any reinforcement (CNTs). It means that the non-dimensional frequency parameter
of rotating FML cylindrical shell for different rotational speeds is considered. The results calculated for CARALL (carbon reinforced aluminum laminate) subjected to simply supported boundary conditions are compared with the results studied by Ghasemi and Mohandes (Ghasemi and Mohandes, 2019) and they show an excellent agreement to each other as demonstrated in Table 2.
present
(Ghasemi and Mohandes, 2019)
backward
forward
backward
forward
0.1
0.16674
0.16674
0.16674
0.16674
0.2
0.16780
0.16569
0.16780
0.16569
0.3
0.16885
0.16463
0.16885
0.16463
0.4
0.16991
0.16357
0.16991
0.16357
0.5
0.17096
0.16252
0.17096
0.16252
0.6
0.17202
0.16146
0.17202
0.16146
0.7
0.17307
0.16040
0.17307
0.16040
0.8
0.15934
0.17413
0.15934
0.17413
0.9
0.17518
0.15828
0.17518
0.15828
1
0.17623
0.15722
0.17623
0.15722
5.2 Free vibration analysis of CNTFPML rotating cylindrical shell
Hear, the frequencies of rotating CNTFPML cylindrical shell subjected to various parameters namely axial and circumferential modal numbers, the lay-ups of composite section, material properties of fiber, the distribution of CNTs, the CNTs mass fraction, the volume fractions of fiber and metal are obtained for different rotational speeds. It is mentioned that there are two different eigenvalues for rotating cylindrical shells, which leads to bifurcation of natural frequencies, that are backward and forward travelling modes. These two modes are relevant to the rotation direction (Ghasemi et al., 2019; Syah et al., 2021).
The influence of
on the frequencies of CNTFPMLs cylindrical shell for various rotational speeds is shown in Fig. 3. Although the frequencies of the shell decrease as
increases for
because with growing
, the stiffness of cylinder declines, with increasing the rotational speed, this process doesn't remain stable. As depicted in the figure, the slope of backward mode increases remarkably as grow the
, but with increasing the
, the slop of forward mode increases moderately for different circumferential modal numbers. So, as
raises, the difference between forward and backward modes increases because of the fact that the effects of these modes grow. Since with increasing the rotational speed, the impacts of centrifugal and coriolis accelerations grow. As the influences of these two accelerations increase, the difference between the modes will be greater because the effect of rotational speed on the greater
,whih are softer, is larger.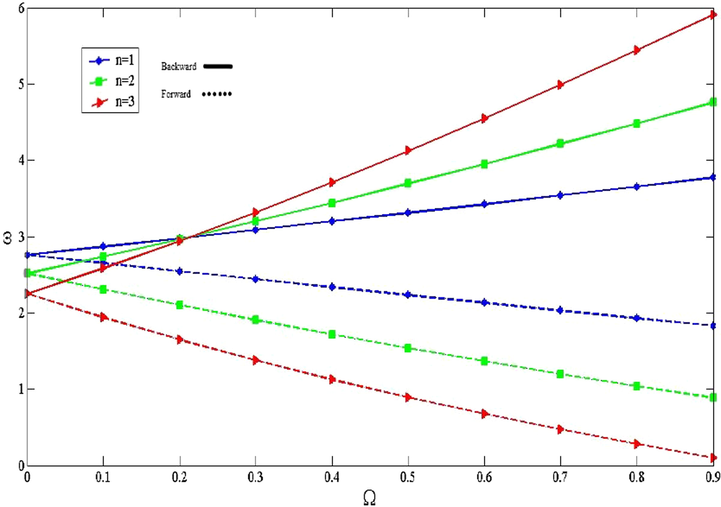
The effect of
on the non-dimensional frequencies for various circumferential wave numbers.
The non-dimensional frequencies with respect to
for various rotational speeds are illustrated in Fig. 4. The figure expresses that not only the non-dimensional frequencies rotating CNTFPMLs cylindrical shell raise with growing the
, but also with growing the
, the difference between backward and forward travelling modes increases.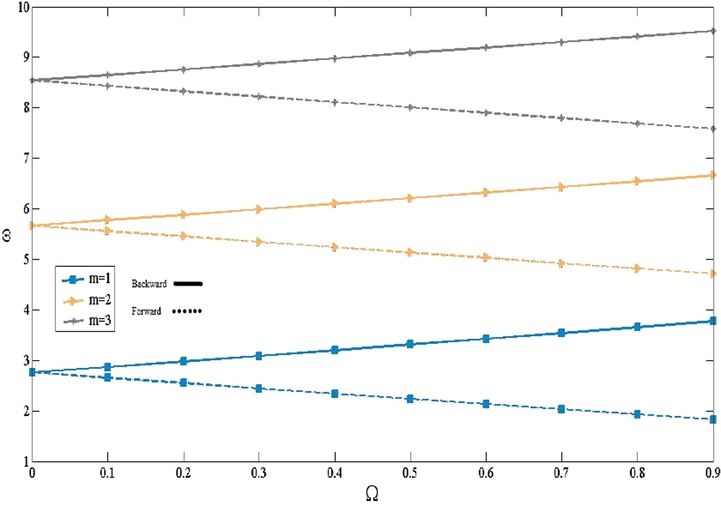
The effect of
on the non-dimensional frequencies for various axial wave numbers.
The influence of volume fraction of fiber on the non-dimensional frequencies of the rotating CNTFPML cylindrical shell is considered in Figs. 5 and 6. It can be seen in Fig. 5 that the non-dimensional frequencies of the shell for
decrease moderately in the first step as increase the
and then they increase considerably. Also, the frequencies of the shell decline with increasing the volume fraction of fiber for both backward and forward modes. Fig. 6 indicates the effect of fiber volume fraction on the vibration of the shell for different
for
. Like CNTFPML cylindrical shell with
, the frequencies of the shell drop with increasing the fiber volume fraction for both backward and forward modes because with increasing the fiber volume fraction, the volume fraction of new matrix decreases (please pay attention to equation (5)) but the drop speed of new matrix is greater than raise speed of fiber. So,
will be increased which leads to the drop of non-dimentional frequencies of the cylindrical shell. In addition, not only is the slop of backward modes more than forward one for different
, but also the difference between backward modes is greater than forward one.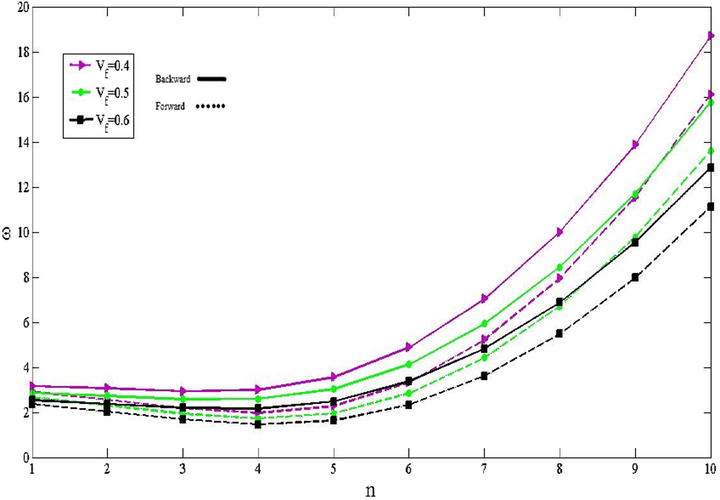
The effect of
on the non-dimensional frequencies for various volume fraction of fiber in
.
The effect of
on the non-dimensional frequencies for various volume fraction of fiber in
.
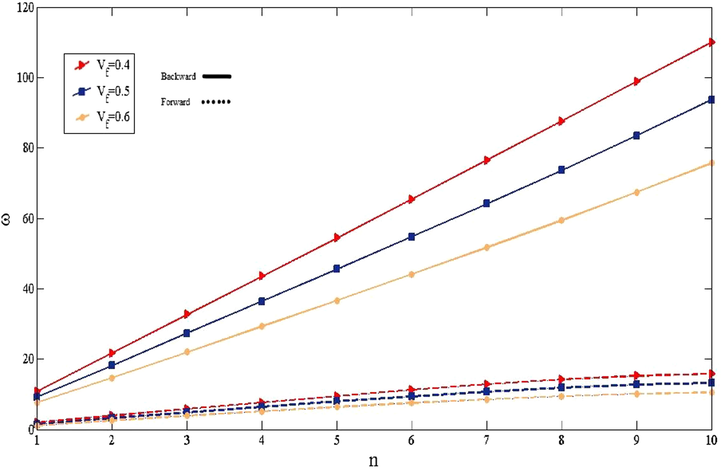
The non-dimensional frequencies of cylindrical shell for different rotational speeds subjected to various volume fraction of metal are shown in Fig. 7. As depicted in the figure, the metal volume fraction has a considerable influence on the frequencies of the shell. Although, with growing
, the non-dimensional frequencies rise, the change slope of backward and forward modes is stable. The reason for rising the non-dimentional frequencies of the shell is the fact that with increasing the volume fraction of metal, the thickness of cylindrical shell will be increases. The greater thickness of cylindrical shell causes more stiffness which leads to the growth of frequencies.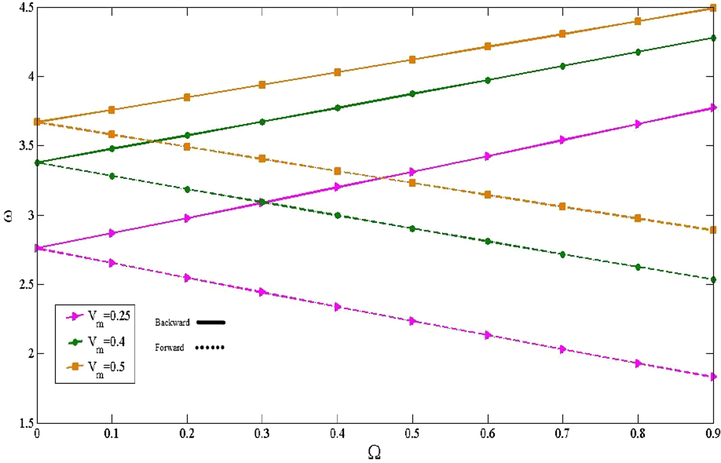
The effect of
on the non-dimensional frequencies for various volume fraction of metal.
Fig. 8 shows the influences of mass fraction of CNTs on free vibration of rotating CNTFPML cylindrical shell subjected to
. As shown, while the distinction between backward and forward modes for various mass fractions is negligible in
, this difference increases with raising the
. Moreover, the difference between the frequencies of different mass fractions of CNTs increase as grow the
. Furthermore, although the more the mass fraction of CNTs raise, the greater the non-dimensional frequencies decrease for
, this process is reversed with growing the
(Syah et al., 2021).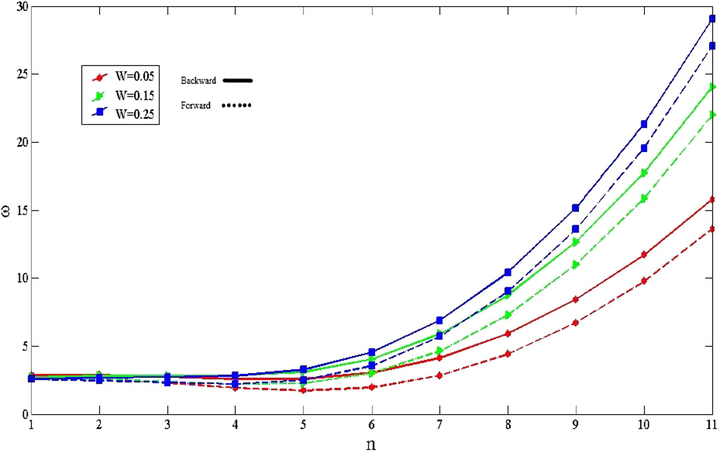
The effect of
on the non-dimensional frequencies for various mass fractions of CNTs in
.
The influence of material properties of fiber on the non-dimensional frequencies of rotating CNTFPML cylindrical shell for
are presented in Fig. 9. As predicted, the frequencies of CNTFPML cylindrical shell constructed by Carbon fiber are more than Glass fiber because the structure made by Carbon fiber is stiffer than Glass one. In addition, with growing the
, the difference between the frequencies of two materials and also backward and forward modes increases.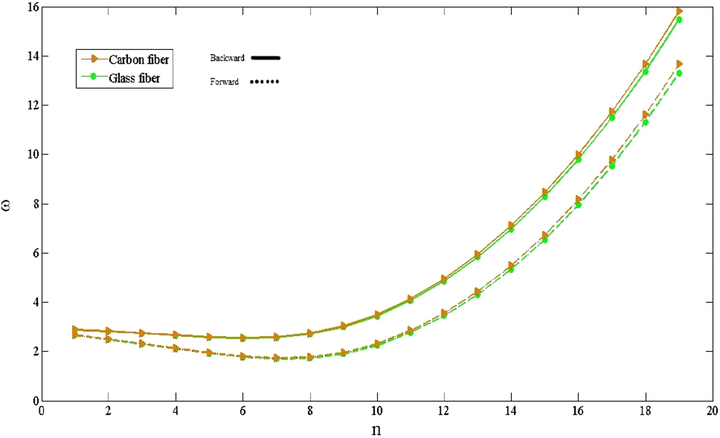
The effect of
on the non-dimensional frequencies for various material properties of fiber.
The lay-ups influence on the non-dimensional frequencies of the shell for differing
are considered in Fig. 10. The figure shows that the frequencies of CNTFPML cylindrical shell with cross-ply lay-up for composite sector are less than unidirectional since the unidirectional lay-up is stiffer than cross-ply. With increasing rotational speed, the frequencies of backward and forward modes raise and drop for both lay-ups with stable slop, respectively.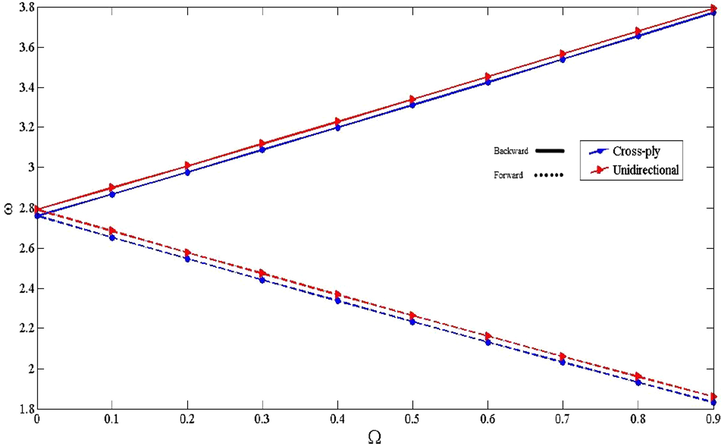
The effect of
on the non-dimensional frequencies for various lay-ups.
The non-dimensional frequencies of CNTFPML cylindrical shells with respect to
for various rotational speeds are shown in Fig. 11. As depicted in the figure, the frequencies of the shell decline with increasing length to radius ratio. In addition, the difference between forward and backward modes grows as raise the rotational speed and the length to radius ratio.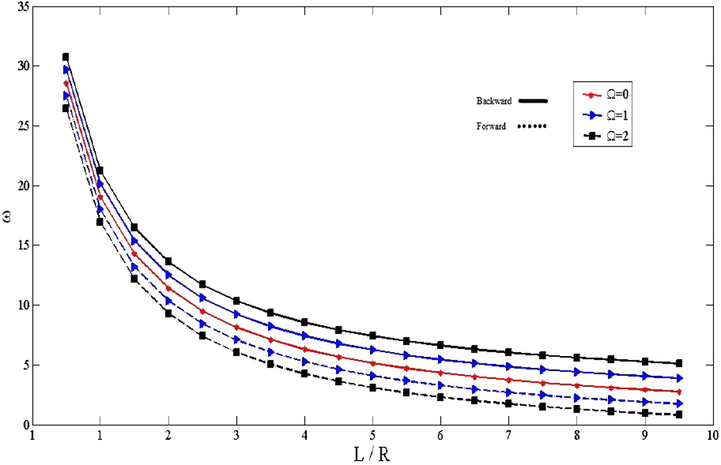
The effect of
on the non-dimensional frequencies for various rotational speeds.
Moreover, Table 3 indicates the influence of CNTs distributions on the non-dimensional frequencies of the non-rotating CNTFPML cylindrical shells for various circumferential wave numbers. As seen in the table, although the frequencies of
,
and
distributions are the same, the frequencies of
and
are less and greater than them, respectively. It means that
and
distributions have the least and most frequencies in a non-rotating CNTFPML cylindrical shells.
Different types
1
2.765857
2.766059
2.765642
2.765857
2.765857
2
2.522489
2.524375
2.520566
2.522489
2.522489
3
2.255084
2.258531
2.251590
2.255084
2.255084
4
2.141174
2.146301
2.135997
2.141174
2.141174
5
2.465258
2.473313
2.457149
2.465258
2.465258
Fig. 12 indicates the natural frequencies of rotating CNTFPML cylindrical shells for various rotational speeds with different ratios of thickness to radius. As illustrated in the figure, the more the ratio of thickness to radius increases, the greater the natural frequencies grow. With increasing the natural frequencies of this cylindrical shell, the critical speed of CNTFPML cylindrical shell is grown so that the cylindrical shell reach the critical speed in the
and forward branch intersect the abscissa at
. In this point, the amplitude of vibration raises sharply and means the cylinder shows an unstable behavior. Further, after this point, the cylindrical shell action changes from forward mode to backward so that the frequencies grow. With increasing the ratio of thickness to radius and in the
and
, the direction of forward mode is changed before reaching the critical speed.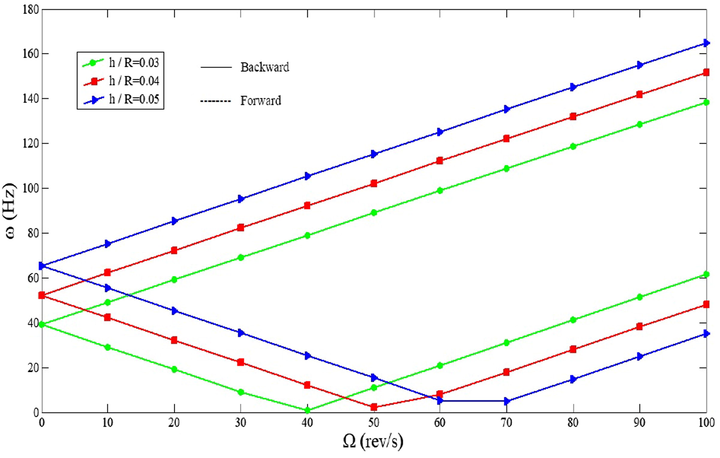
The effect of
on the natural frequencies for various ratios of thickness to radius.
The changes of natural frequencies for differing speeds for volume fraction of metal are shown in Fig. 13. It would be illustrated that with raising the metal volume fraction, the natural frequencies of the shell increase since the thickness of the shell grow. As grown the natural frequency, the critical speed increases. As the natural frequencies of the shell raise, the critical speed of CNTFPML cylindrical shell grows so that the cylindrical shell reach the critical speed in the
and forward branch intersect the abscissa at
.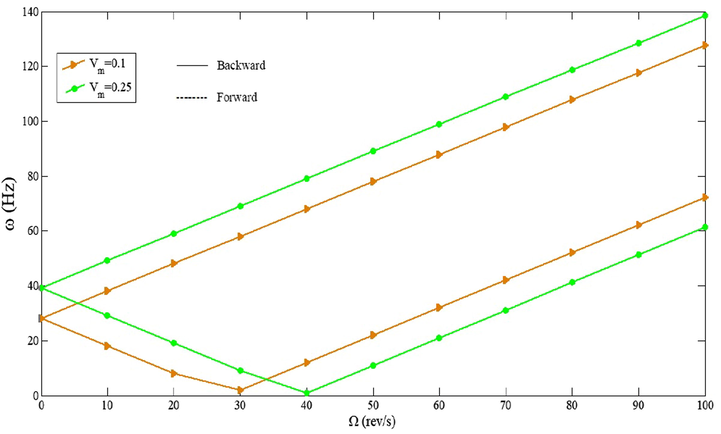
The effect of
on the natural frequencies for various volume fractions of metal.
Also, the effects of different distributions of CNTs for rotating CNTFPML cylindrical shells are studied in Table 4. It can be seen that similar to non-rotating cylindrical shell, the frequencies of
and
distributions are identical. Furthermore, the table indicates that the rotational speed has a great influence on the obtained frequencies of the other distributions. The backward and forward frequencies of
and
distributions are more and less than the
for
= 1, respectively, while this process is reversed for
= 5. It means that the frequencies of both modes for
and
distributions are less and more than the
in
= 5. With increasing the rotational speed the procedure becomes different. In
and
, while the frequencies of backward and forward modes for
distribution are more and less than the
, respectively, but this procedure is reversed in
distribution. a) Backward. b) Forward.
Different types
a
b
a
b
a
b
a
b
1
3.897010
1.737058
3.897021
1.737425
3.896979
1.736678
3.897010
1.737058
5
9.217449
1.549282
9.216819
1.548435
9.218061
1.550140
9.217449
1.549282
10
16.555586
4.772050
16.555846
4.770635
16.555267
4.773476
16.555586
4.772050
20
30.347679
10.574589
30.366683
10.571646
30.328095
10.577551
30.347679
10.574589
6 Conclusion
Present study deals with free vibration of simply supported rotating CNTFPML cylindrical shells according to Love’s first approximation shell theory. In application, nano-scaled rotoating systems have been used in different applications such as micro/nano motors, nano biomedical devices and nano computers. Although free vibration of rotating composite cylindrical shells reinforced by CNTs has been studied in some references, there is not any investigation on free vibration of rotating CNTFPML cylindrical shells. To make CNTFPML cylindrical shell, first thins first, the matrix has been enhanced using CNTs. Since then, the fiber phase has been reinforced by this reinforced matrix. At the end, the adhesive fiber prepreg has been combined with the thin metal layers. Therefore, CNTFPML cylindrical shell includes fiber, CNTs, polymer matrix and metal phases. This cylindrical shell including four phases provides the advantages of nanocomposite as well as FML. The influences of fiber material properties, circumferential and axial wave numbers, metal volume fraction, composite volume fraction, CNTs mass fraction, lay-ups, ratio of length to radius on free vibration of CNTFPML cylindrical shell for different rotational speeds have been considered. The results of this research can be illustrated as:
-
The results represented that circumferential and axial wave numbers had a remarkable effect on free vibration of the rotating shell.
-
Also, it could be found that the frequencies of CNTFPML cylindrical shell changed differently with growing for various volume fraction of fiber. As the volume fraction of fiber increased, the frequencies of the shell declined sine transverse modulus of nanocomposite section raised which caused the reduction of non-dimentional frequencies.
-
In addition, the volume fraction of metal influenced vibration of the rotating CNTFPML cylindrical shell considerably so that the non-dimensional frequencies increased as grows because with growing the volume fraction of metal, the thickness of cylindrical shell increased which leads to the growth of non-dimentional frequencies.
-
Furthermore, the backward and forward frequencies of and distributions were more and less than the for = 1, respectively, while this process was reversed for = 5. In and , while the frequencies of backward and forward modes for distribution were more and less than the , respectively, but this procedure was reversed in O distribution.
-
Moreover, the difference between forward and backward modes grew as raise the rotational speed and the length to radius ratio. 3
-
The difference between backward and forward modes for various mass fractions raised with increasing the .
-
In addition, the frequencies of unidirectional lay-up were greater than cross-ply because of the stiffness.
References
- Vibration and static analysis of functionally graded porous plates. J. Appl. Computat. Mech.. 2017;3(3):199-207.
- [Google Scholar]
- Forced vibration analysis of functionally graded nanobeams. Int. J. Appl. Mech.. 2017;9(07):1750100.
- [Google Scholar]
- Buckling and vibration of laminated composite circular plate on Winkler-type foundation. Steel. Compos. Struct.. 2014;17:1-19.
- [Google Scholar]
- Nonlinear free vibration of an Euler-Bernoulli composite beam undergoing finite strain subjected to different boundary conditions. J. Vib. Control.. 2016;22:799-811.
- [Google Scholar]
- Finite strain analysis of nonlinear vibrations of symmetric laminated composite Timoshenko beams using generalized differential quadrature method. J. Vib. Control.. 2016;22:940-954.
- [Google Scholar]
- A simple hyperbolic shear deformation theory for vibration analysis of thick functionally graded rectangular plates resting on elastic foundations. Geomech. Eng.. 2016;11:289-307.
- [Google Scholar]
- The influence on modal parameters of thin cylindrical shell under bolt looseness boundary. Shock Vib.. 2016;2016:1-15.
- [Google Scholar]
- On thermo-mechanical vibration analysis of multi-scale hybrid composite beams. J. Vib. Control. 2019;25(4):933-945.
- [Google Scholar]
- Free vibration analysis of micro and nano fiber-metal laminates circular cylindrical shells based on modified couple stress theory. Mech. Adv. Mater. Struct. 2018:1-12.
- [Google Scholar]
- A series solution for the in-plane vibration analysis of orthotropic rectangular plates with non-uniform elastic boundary constraints and internal line supports. Arch. Appl. Mech.. 2015;85(1):51-73.
- [Google Scholar]
- A unified Chebyshev-Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions. Arch. Appl. Mech.. 2014;84(4):441-471.
- [Google Scholar]
- On the buckling and vibration of antisymmetric angle-ply laminated circular cylindrical shells. Int. J. Eng. Sci.. 1983;21:217-222.
- [Google Scholar]
- On vibrations of thin rotating laminated composite cylindrical shells. Compos. Eng.. 1994;4:1153-1167.
- [Google Scholar]
- Vibration analysis of cross-ply laminated composite cylindrical shells using the wave propagation approach. Appl. Acoustic.. 2001;62:1221-1228.
- [Google Scholar]
- A three-dimensional layerwise-differential quadrature free vibration analysis of laminated cylindrical shells. Int. J. Pressure. Vessel. Pip.. 2008;85:450-458.
- [Google Scholar]
- Static and vibration analysis of axi-symmetric angle-ply laminated cylindrical shell using state space differential quadrature method. Int. J. Pressure. Vessel. Pip.. 2009;86:738-747.
- [Google Scholar]
- Nonlinear vibrations of rotating thin circular cylindrical shell. Nonlinear. Dynamic.. 2012;67:1467-1479.
- [Google Scholar]
- Free vibration analysis of rotating stiffened composite cylindrical shells by using the layer wise-differential quadrature (LW-DQ) method. Mech. Compos. Mater.. 2014;50:21-38.
- [Google Scholar]
- Free vibration analysis of composite cylindrical shells with non-uniform thickness walls. Steel. Compos. Struct.. 2016;20:1087-1102.
- [Google Scholar]
- Free vibration analysis of functionally graded cylindrical shells with different shell theories using semi-analytical method. Steel. Compos. Struct.. 2018;28:735-748.
- [Google Scholar]
- Free vibration analysis of rotating fiber–metal laminate circular cylindrical shells. J. Sandwich Struct. Mater.. 2019;21(3):1009-1031.
- [Google Scholar]
- Dynamic response of pre-stressed fibre metal laminate (FML) circular cylindrical shells subjected to lateral pressure pulse loads. Compos. Struct.. 2010;92:1308-1317.
- [Google Scholar]
- Development of beam modal function for free vibration analysis of FML circular cylindrical shells. J. Vib. Control. 2018;24(14):3026-3035.
- [Google Scholar]
- Electromagnetic properties of zinc-nickel ferrites in frequency range of 0.05-10 GHz. Mater. Today Chem.. 2021;20:100460
- [Google Scholar]
- “Phase transformations in FeCo - Fe2CoO4/Co3O4-spinel nanostructures as a result of thermal annealing and their practical application. J. Mater. Sci.: Mater Electron.. 2021;32:16694-16705.
- [Google Scholar]
- The Features of the growth processes and magnetic domain structure of NiFe nano-objects. J. Phys. Chem. C. 2019;123(44):26957-26964.
- [Google Scholar]
- A closed form solution for linear and nonlinear free vibrations of composite and fiber metal laminated rectangular plates. Compos. Struct.. 2010;92:2663-2675.
- [Google Scholar]
- Nonlinear dynamic analysis of fiber metal laminated beams subjected to moving loads in thermal environment. Compos. Struct.. 2016;140:410-416.
- [Google Scholar]
- Free vibration analysis of fiber metal laminate annular plate by state-space based differential quadrature method. Adv. Mater. Sci. Eng.. 2014;2014:1-11.
- [Google Scholar]
- Electrophysical properties of epoxy-based composites with graphite nanoplatelets and magnetically aligned magnetite. Mol. Cryst. Liq. Cryst.. 2018;661:68-80.
- [Google Scholar]
- Efect of magnetic fillers and their orientation on the electrodynamic properties of BaFe12 xGaxO19 (x = 0.1-1.2)—epoxy composites with carbon nanotubes within GHz range. Appl. Nanosci.. 2020;10:4747-4752.
- [Google Scholar]
- Differential cubature method for vibration analysis of embedded FG-CNT-reinforced piezoelectric cylindrical shells subjected to uniform and non-uniform temperature distributions. Steel. Compos. Struct.. 2016;22:889-913.
- [Google Scholar]
- Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci.. 2017;130:383-398.
- [Google Scholar]
- Free vibration analysis of arbitrarily shaped functionally graded carbon nanotube-reinforced plates. Compos. Part B: Eng.. 2017;115:384-408.
- [Google Scholar]
- “Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng. Sci. Tech Int J.. 2018;21:778-786.
- [Google Scholar]
- Vibration of carbon nanotube reinforced composite (CNTRC) annular sector plates by discrete singular convolution method. Compos. Struct.. 2018;203:458-465.
- [Google Scholar]
- Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B: Eng.. 2018;147:169-177.
- [Google Scholar]
- Free vibration analysis of functionally graded carbon nanotube reinforced composite truncated conical panels with general boundary conditions. Compos. Part B: Eng.. 2019;160:225-240.
- [Google Scholar]
- Significantly enhanced electrostatic energy storage performance of P(VDF-HFP)/BaTiO3-Bi(Li0.5Nb0.5)O3 nanocomposites. Nano Energy. 2020;78:105247
- [Google Scholar]
- Investigation of AC-measurements of epoxy/ferrite composites. Nanomaterials-Basel. 2020;10(3):492.
- [Google Scholar]
- Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Method. Appl. Mech. Eng.. 2012;213–216:196-205.
- [Google Scholar]
- Vibration and damping analysis of functionally graded carbon nanotubes reinforced hybrid composite shell structures. J. Vib. Control. 2017;23(11):1711-1738.
- [Google Scholar]
- Vibrational analysis of functionally graded carbon nanotube-reinforced composite spherical shells resting on elastic foundation using the variational differential quadrature method. Europ. J. Mech. A/Solid.. 2016;60:166-182.
- [Google Scholar]
- Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Compos. Part B: Eng.. 2016;95:196-208.
- [Google Scholar]
- Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci.. 2016;108–109:157-165.
- [Google Scholar]
- Ghasemi, A.R., Meskini, M., 2019. Free vibration analysis of porous laminated rotating circular cylindrical shells. J. of Vib. Control, 1077546319858227.
- Investigations on dynamic analysis and free vibration of FGMs rotating circular cylindrical shells. SN Appl. Sci.. 2019;1(4):301-306.
- [Google Scholar]
- Nonlinear vibration analysis of fiber reinforced composite cylindrical shells with partial constrained layer damping treatment. Thin-walled Struct.. 2020;157:107000
- [Google Scholar]
- A unified solution for vibration analysis of laminated functionally graded shallow shells reinforced by graphene with general boundary conditions. Int. J. Mech. Sci.. 2020;170(15):105341
- [Google Scholar]
- Nonlinear vibration characteristics of fibre reinforced composite cylindrical shells in thermal environment. Mech. System. Signal. Process.. 2021;156:107665
- [Google Scholar]
- A unified vibration modeling and dynamic analysis of FRP-FGPGP cylindrical shells under arbitrary boundary conditions. Appl. Math. Model.. 2021;97:69-80.
- [Google Scholar]
- Nonlinear vibrations of fiber-reinforced composite cylindrical shells with bolt loosening boundary conditions. J. Sound. Vib.. 2021;496(31):115935
- [Google Scholar]
- Effects of boundary conditions on frequencies of a multilayered cylindrical shell. J. Sound. Vib.. 1995;188:363-384.
- [Google Scholar]
- Analysis of cylindrical shells using generalized differential quadrature. Shock. Vib.. 1997;4:193-198.
- [Google Scholar]
- The nonlinear vibration of orthotropic functionally graded cylindrical shells surrounded by an elastic foundation within first order shear deformation theory. Compos. Part B: Eng.. 2017;116:170-185.
- [Google Scholar]
- Vibration of composite cylindrical shallow shells subjected to hygrothermal loading-experimental and numerical results. Compos. Part B: Eng.. 2016;98:108-119.
- [Google Scholar]
- Carbon nanotube reinforced composites: potential and current challenges. Mater. Des.. 2007;28:2394-2401.
- [Google Scholar]
- A comprehensive closed form micromechanics model for estimating the elastic modulus of nanotube-reinforced composites. Compos. Part A: Appl. Sci. Manufact.. 2006;37:2178-2185.
- [Google Scholar]
- Nonlinear bending of functionally graded carbon nanotubereinforced composite plates in thermal environments. Compos. Struct.. 2009;91:9-19.
- [Google Scholar]
- Wave propagation in functionally graded nanocomposites reinforced with carbon nanotubes based on second-order shear deformation theory. Mech. Adv. Mater. Struct.. 2016;24:458-468.
- [Google Scholar]
- Peculiarities of the microwave properties of hard-soft functional composites SrTb0.01Tm0.01Fe11.98O19-AFe2O4 (A = Co, Ni, Zn, Cu and Mn) RSC Adv.. 2020;10:32638.
- [Google Scholar]
- “Synthesis, structural properties and shielding efficiency of glasses based on TeO2-(1–x)ZnO-xSm2O3”. J. Mater. Sci.: Mater Electron.. 2021;32:12111-12120.
- [Google Scholar]
- Effect of magnetic fields on magnetic phase separation in anion-deficient manganite La0.70Sr0.30MnO2.85. Low Temp. Phys.. 2011;37:465-469.
- [Google Scholar]
- Evaluation of the efficiency of detection and capture of manganese in aqueous solutions of FeCeOx nanocomposites doped with Nb2O5. Sensors. 2020;20:4851.
- [Google Scholar]
- Cation ordering and magnetic properties of neodymium-barium manganites. Tech. Phys.. 2008;53:49-54.
- [Google Scholar]
- Synthesis, structural, strength and corrosion properties of thin films of the type CuX (X = Bi, Mg, Ni) J. Mater. Sci.: Mater Electron.. 2019;30:11819-11832.
- [Google Scholar]
- Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos. B Eng.. 2019;167:700-716.
- [Google Scholar]
- Computational simulation of critical speed and dynamic analysis of agglomerated CNTs/fiber/polymer/metal laminates rotating cylindrical shell. Arabian. J. Chem.. 2021;14:103358
- [Google Scholar]







