2.1 Chemicals

Deionized water was utilized to prepare aqueous solutions (feed and stripping solutions). Both arsenic acid (H₃AsO₄) and mercury(II) chloride (HgCl₂) were used to prepare the synthetic wastewater as feed solution. The initial pH of feed solution was 6 and the initial concentrations of H₃AsO₄ and HgCl₂ were 1 and 4 mg·L^-1, respectively. Such conditions were carried out to simulate the condition of the produced water obtained from the offshore oil and gas production in the Gulf of Thailand (Lothongkum et al., 2011; Pancharoen et al., 2010). Sodium hydroxide (NaOH) and hydrochloric acid (HCl) were employed to adjust the acidity of the feed solution and investigate various types of strippant solutions. Four effective carriers observed from previous studies; namely, Aliquat 336 (Fábrega and Mansur, 2007; Pancharoen et al., 2009), Trioctyl amine (TOA) (Pancharoen et al., 2010), Tributyl phosphate (TBP) (Jantunen et al., 2019), and Trioctylphosphine oxide (Cyanex 921) (Perez et al., 2007)) were chosen to determine the most suitable carrier for the extraction of both arsenic and mercury ions. Toluene was utilized to dilute the organic carriers. All reagents were of AR grade and utilized without additional purification.

2.2 Apparatus

The hollow fiber module comprising 35,000 microporous polypropylene fibers was employed in the removal of arsenic and mercury ions. Table 1 depicts the features of the hollow fiber module utilized. Two gear pumps were implemented for pumping both feed and stripping solutions into the hollow fiber system. Fig. 1 depicts the HFSLM system as well as other equipment used. An atomic absorption spectrometer (AAS) (model AA240FS), which has a detection limit of 0.001 mg·L^-1and a deviation of 0.9995, was utilized to evaluate the concentration of metal ions. The pH meter (model EUTECH pH 700) was utilized to measure the acidity of the feed solution.

Close

Fig. 1

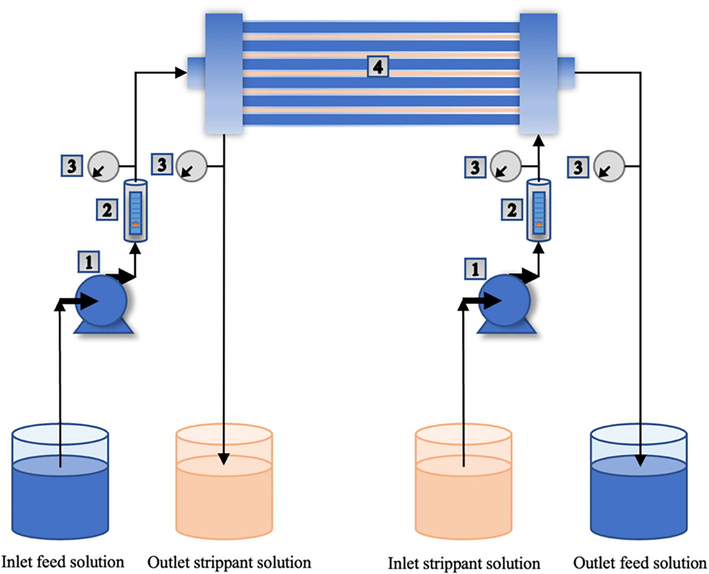
Schema for the removal of arsenic and mercury ions via HFSLM: (1) gear pumps, (2) flow meters, (3) pressure gauges, and (4) hollow fiber module.

Export to PPT

2.3 Procedure

Four effective carriers (Aliquat 336, TOA, TBP, and Cyanex 921) were applied to determine their potential to extract arsenic and mercury ions simultaneously using Liquid-Liquid Extraction (LLE). Such carriers were diluted with toluene and utilized at an excess concentration of 0.68 M. The most potential carrier was applied in the HFSLM process.

In the HFSLM process (see Fig. 1), the chosen carrier diluted with toluene as the liquid membrane was cycled along the tube and shell sides of the hollow fibers concurrently until 0.052 L of the liquid membrane was used. This volume relates to the total volume of hollow-fiber micropores. The excess liquid membrane was then purged by passing deionized water through the tube and shell sides of the hollow fibers. Next, both feed solution (synthetic produced water) and strippant solution were fed counter-currently into the hollow fibers' tube and shell sides. Flow patterns of both feed and strippant solutions were single pass. Finally, 0.02 L for each of the outlet feed and strippant solutions was collected to evaluate the concentration of metal ions using AAS.

The concentration of the chosen carrier, pH of the feed solution, types of strippant solutions used, the concentration of the chosen strippant solution as well as operation time were varied. After each experiment, the liquid membrane was eliminated from the system by allowing the surfactant to flow into the hollow fibers' tube and shell sides. Subsequently, deionized water was pumped into the hollow fibers to remove the surfactant.

The efficiency of extraction and recovery is defined as in Eqs. (1) and (2), respectively:

where ${\mathrm{C}}_{\mathrm{A},\mathrm{F}}\left({\mathrm{x}}_0\right)$ is the concentration of metal ions in the inlet feed solution (mg·L^-1) and ${\mathrm{C}}_{\mathrm{A},\mathrm{S}}\left({\stackrel{Ấ}{\mathrm{x}}}_{\mathrm{i}}\right)$ represents the concentration of metal ions in the outlet stripping solution (mg·L^-1).

3.1 Optimum conditions for the extraction and stripping of arsenic and mercury ions

3.1.1

3.1.1 Types of carriers

The neutral carriers viz. TBP (Jantunen et al., 2019) and Cyanex 921 (Perez et al., 2007) are seen as promising carriers for arsenic ions, whilst basic carriers including Aliquat 336 and TOA are seen as being effective carriers for the extraction of mercury ions (Fábrega and Mansur, 2007; Pancharoen et al., 2010). Hence, such carriers were employed in this study to determine the highest potential carrier for the simultaneous extraction of arsenic and mercury ions. In Fig. 2, results are illustrated. Thus, it is noted that Aliquat 336 had the highest potential for the simultaneous extraction of arsenic and mercury ions, resulting from the utilization of pH 6 of feed solution whereby arsenic(V) occurs mostly as dissociated species (anions) (Wilson et al., 2004). Aliquat 336 is an ionic liquid, which can extract metal ions in a variety of species (neutral and anion), although it interacts considerably better with anions.

Close

Fig. 2

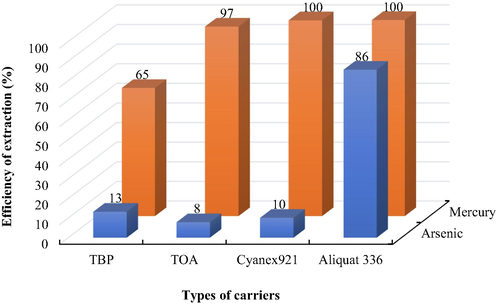
Efficiency of extraction of arsenic and mercury ions using various types of carriers (0.68 M each): pH of feed solution = 6.

Export to PPT

In the case of mercury, Aliquat 336 showed the highest efficiency of mercury extraction as it is a quaternary amine, which reacts with metal ions better than TOA, a ternary amine. Aliquat 336 reacted with Hg(II) via the mechanism of ion exchange. To effectively extract mercury ions using a ternary amine like TOA, the feed solution and/or liquid membrane need(s) the addition of HCl to transform mercury ions into HgCl₄^2- as well as to transform the ternary amine into an anion exchanger (amine salt), which is equivalent to quaternary amines (Chapman, 1997). However, the pH of the initial feed solution in this study was 6 and no HCl was added in the feed or liquid membrane phase. Therefore, TOA revealed its low efficiency in the extraction. For evaluation of other factors, Aliquat 336 diluted in toluene was utilized as the liquid membrane.

3.1.2

3.1.2 Concentration of chosen carrier

In Fig. 3, the impact of concentration of Aliquat 336 on the extraction and recovery of arsenic as well as mercury ions is depicted. It is seen that as the concentration of Aliquat 336 increased, so did the extractability of arsenic ions. Such a result is consistent with Le Chatelier's principle, according to which higher reactant concentration leads to greater reaction. Extractability reached maximum at 0.88 M Aliquat 336. Once Aliquat 336 concentration passed over 0.88 M, no change in the efficiency of extraction was observed. In the case of mercury ions, the percentage of extraction remained constant at ∼ 100 % throughout the range of Aliquat 336 concentration investigated. Therefore, 0.88 M Aliquat 336 was used for further experiments.

Close

Fig. 3

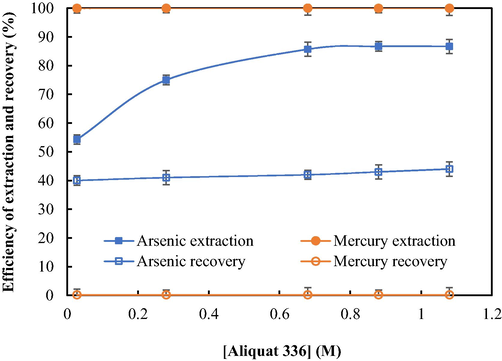
Efficiency of extraction and recovery at various concentrations of Aliquat 336: pH of feed solution = 6, strippant solution = 0.5 M NaOH, flow rate of feed and strippant solutions = 1.67 × 10^-3 L·s⁻¹, and operation time = 600 s.

Export to PPT

3.1.3

3.1.3 pH of feed solution

It is well known that arsenic species in solution varies according to the acidity of the solution. As(V) occurs mostly as undissociated H₃AsO₄ at pH 2 and primarily exists as dissociated H₂AsO₄^–, HAsO₄^2–, and AsO₄^3- in pH ranges of 3 to 6, 8 to 11, and 12 to 14, respectively (Ma et al., 2018). In Fig. 4, results show that extraction of arsenic ions rose as the pH of the feed solution increased; extraction remained unchanged at pH ranging from 11 to 13. This outcome was due to Aliquat 336′s process of extraction, which involved an ion exchange of anion metal ions and Cl^– (Fontàs et al., 2000). When the pH of feed solution increases, undissociated H₃AsO₄ converts to anions and exists mostly as HAsO₄^2– at pH 11 and as AsO₄^3- at pH ranging from 12 to 13 (Wilson et al., 2004), thus contributing to greater arsenic extractability as the pH of the feed solution rises. At pH levels between 11 and 13, the highest extraction of arsenic (99.6 %) was obtained, showing that Aliquat 336 extracted the dissociated species HAsO₄^2– and AsO₄^3-considerably better than H₂AsO₄^–. As for mercury extraction, the acidity of the feed solution did not affect the efficiency of mercury extraction; its efficiency remained constant at around 100 % over pH ranging from 2 to 13. For further investigation, the pH of the feed solution of 11 was employed.

Close

Fig. 4

Efficiency of extraction against pH of feed solution: [Aliquat 336] = 0.88 M, strippant solution = 0.5 M NaOH, flow rate of feed and strippant solutions = 1.67 × 10^-3 L·s⁻¹, and operation time = 600 s.

Export to PPT

3.1.4

3.1.4 Types of strippants

The most potential strippant solutions for recovery of both arsenic and mercury ions were investigated using thiourea, NaOH, and HCl (0.5 M each). NaOH is commonly used as a strippant and has been reported to have the potential for the recovery of arsenic ions (Pancharoen et al., 2009). Thiourea is noted as the favorable strippant for the recovery of target ions from metal-Ailquat 336 complex species (Fábrega and Mansur, 2007). In some cases, the mixture of thiourea and HCl as a synergistic strippant increases the potency of recovery of metal ions. This mixture has been widely used for recovering a variety of metal ions (Mohdee et al., 2021). As shown in Fig. 5, HCl proved to be the most promising strippant for arsenic ions. In contrast, the performance of thiourea and NaOH was quite poor. The low efficiency of recovery of arsenic ions utilizing NaOH and thiourea can be accounted for by the fact that once arsenic ions are stripped into such strippant solutions, they exist as anions, which can subsequently be extracted back by Aliquat 336. The recovery of arsenic and mercury ions using HCl was found to be 71 % and 29 %, respectively. When HCl was mixed with thiourea, the recovery of arsenic and mercury ions reached 82 % and 55 %, respectively. This outcome was expected owing to the synergistic effect (Luo et al., 2004). To verify such an effect, the distribution coefficients (D) of recovery, utilizing each strippant, were determined to calculate the synergistic coefficient R, as defined in Eq. (3):

(3)

$$\mathrm{R}=\frac{{\mathrm{D}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\mathrm{D}}_{\mathrm{A}}+{\mathrm{D}}_{\mathrm{B}}}$$ where D_max represents the optimum distribution coefficient of the synergistic system (utilizing a combination of the reactants A and B) to recover the metal ions. D_A refers to the distribution coefficient of recovery utilizing the single substance A, and D_B is the distribution coefficient of recovery utilizing the single substance B. If R > 1, the synergistic recovery is verified; thus, the higher the synergistic coefficient of the synergistic system, the higher the recovery.

Close

Fig. 5

Efficiency of recovery of arsenic and mercury ions using various types of strippant solutions (0.5 M each): [Aliquat 336] = 0.88 M, pH of feed solution = 11, flow rate of feed and strippant solutions = 1.67 × 10^-3 L·s⁻¹, and operation time = 600 s.

Export to PPT

In Fig. 6, distribution coefficients of recovery of arsenic and mercury ions are presented. Employing Eq. (3), the synergistic coefficients of recovery of arsenic and mercury ions proved to be 1.15 and 1.85, respectively, verifying the synergistic effect of the HCl/thiourea mixture. As a result, this mixture was applied as the strippant solution and their appropriate concentrations were further determined.

Close

Fig. 6

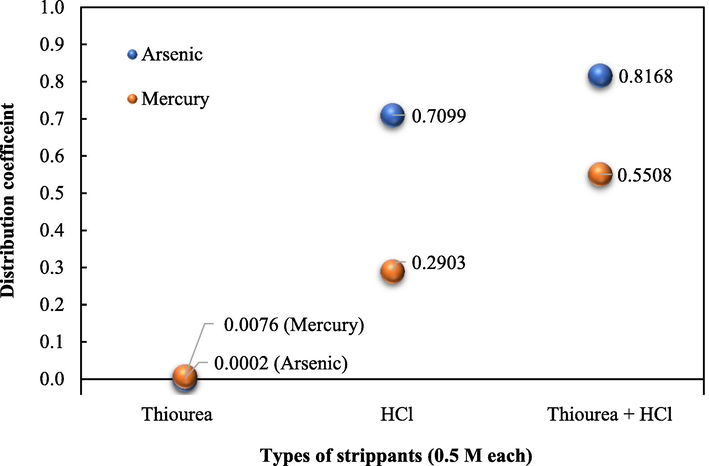
Distribution coefficients of recovery of arsenic and mercury ions utilizing different strippant solutions: extractant = 0.88 M Aliquat 336.

Export to PPT

3.1.5

3.1.5 Concentrations of strippants

Fig. 7(a) and (b) depict the recovery of arsenic and mercury ions against the concentrations of HCl and thiourea. In Fig. 7(a), the recovery of metal ions utilizing 0.5 M thiourea at different concentrations of HCl is shown. Results demonstrate that the recovery of metal ions improved when the concentration of HCl increased, corresponding to chemical kinetics. The recovery of metal ions reached maximum at 0.5 M HCl. After that, the recovery of metal ions decreased due to concentration polarization, obstructing the recovery of the metal ions (Chaturabul et al., 2015; Wannachod et al., 2014).

Close

Fig. 7

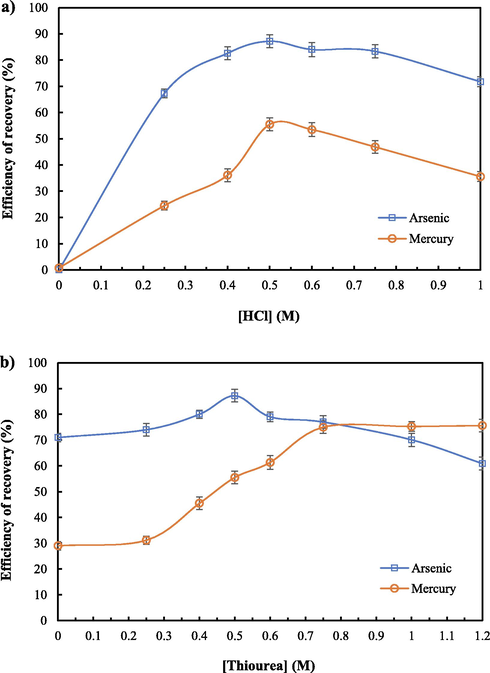
Efficiency of recovery of arsenic and mercury ions utilizing 0.88 M Aliquat 336 as the extractant, pH of feed solution = 11, flow rate of feed and strippant solutions = 1.67 × 10^-3 L·s⁻¹, and operation time = 600 s: a) 0.5 M thiourea mixed with HCl at various concentration, and b) 0.5 M HCl mixed with thiourea at various concentrations.

Export to PPT

In Fig. 7(b), the recovery of metal ions utilizing 0.5 M HCl with different thiourea concentrations is illustrated. Recovery of metal ions increased as the concentration of thiourea rose, in agreement with chemical kinetics. For recovery of arsenic ions, its optimum condition was observed at 0.5 M thiourea. After that, recovery of arsenic ions decreased due to concentration polarization (Chaturabul et al., 2015; Wannachod et al., 2014). In the case of mercury ions, the optimum potential of recovery was attained at 0.75 M thiourea. Hence, 0.5 M HCl and 0.75 M thiourea were applied to study the next parameter.

3.1.6

3.1.6 Flow rates of feed and strippant solutions

Flow rates of feed and strippant solutions ranging from 8.3 × 10^-4 to 6.67 × 10^-3 L·s⁻¹ were evaluated to maximize the removal of arsenic and mercury ions. As seen in Fig. 8, at flow rates ranging from 8.3 × 10^-4 to 1.67 × 10^-3 L·s⁻¹, both extraction and recovery of arsenic and mercury ions remained unchanged at around 100 %. At 1.67 × 10^-3 L·s⁻¹, the concentrations of arsenic and mercury ions in the outlet feed solution proved to be less than 0.02 and 0.001 mg·L^-1, thereby meeting the wastewater discharge standard set by Thailand's Ministry of Industry and Ministry of Natural Resources and Environment. As a result of shorter residence time, extraction and recovery of metal ions declined when the flow rates were higher than 1.67 × 10^-3 L·s⁻¹. Hence, flow rates of feed and strippant solutions of 1.67 × 10^-3 L·s⁻¹ were applied to maximize the recovery of arsenic and mercury ions.

Close

Fig. 8

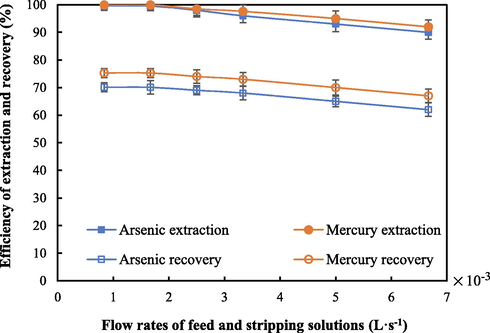
Efficiency of recovery of arsenic and mercury ions at various flow rates of feed and strippant solutions, using 0.88 M Aliquat 336 as the extractant, pH of feed solution = 11, the mixture of 0.5 M HCl and 0.75 M thiourea as the strippant solution, and operation time = 600 s.

Export to PPT

3.1.7

3.1.7 Stability of the HFSLM system

The stability of the HFSLM system for the removal of arsenic and mercury ions was determined by testing the efficiency of extraction and recovery versus time. Thus, stability of the system was tested utilizing the optimum conditions: 0.88 M Aliquat 336 as the extractant, pH of feed solution of 11, the mixture of 0.5 M HCl and 0.75 M thiourea as the strippant solution, and flow rates of feed and stripping solutions of 1.67 × 10^-3 L·s⁻¹. In Fig. 9, results are shown. It is noted that both extraction and recovery of arsenic and mercury ions remained constant at around 100 % during 18 × 10³ s of operation, indicating the stability of the liquid membrane in the HFSLM. Such an outcome also indicated that the system is at a steady state condition. For further studies, using a pilot plant, an investigation into the stability of the HFSLM system undertaking a longer time is recommended.

Close

Fig. 9

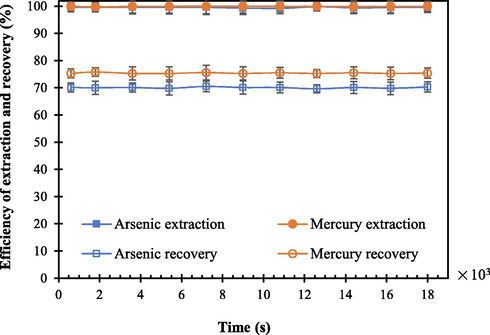
Efficiency of recovery of arsenic and mercury ions versus time, using 0.88 M Aliquat 336 as the extractant, pH of feed solution = 11, the mixture of 0.5 M HCl and 0.75 M thiourea as the strippant solution, and flow rate of feed and strippant solutions = 1.67 × 10^-3 L·s⁻¹.

Export to PPT

3.2 Intermolecular and intramolecular mechanisms of extraction and stripping

3.2.2

3.2.2 Reaction mechanisms as well as intermolecular and intramolecular properties for the separation of arsenic ions

3.2.2.1

3.2.2.1 Extraction of arsenic ions

In this research, H₃AsO₄ was used to prepare the synthetic feed solution. Moreover, the pH of the feed solution was adjusted to 11 whereby H₃AsO₄ was predominantly transformed into ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ (Wilson et al., 2004). Therefore, the extraction reaction of arsenic ions using Aliquat 336 (CH₃R₃N⁺Cl^–) is proposed as in Eq. (4) (Bey et al., 2010):

(4)

$$2\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right){\mathrm{C}\mathrm{l}}^{-}+{\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}\rightleftharpoons \overline{{\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right)}_2\bullet \left({\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}\right)}+{2\mathrm{C}\mathrm{l}}^{-}$$

The overbar in Eq. (4) refers to the arsenic–carrier complex species in the liquid membrane phase.

According to DFT calculations, the mechanism of arsenic extraction can be described as follows. A molecule of ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ reacts with 2 molecules of (C₂₅H₅₄N⁺)Cl^-, resulting in the supramolecular complex (C₂₅H₅₄N)₂·(HAsO₄). The tetrahedral optimized molecular structure of ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ reveals that the lengths of the bond between As and oxygen atoms are 1.72, 1.73, 1.73, 1.88 Å and the O—H bond length is 0.98 Å. The bond angle between O-As-O is approximately 115° and the As—O—H bond angle is around 114°. In Fig. 10, the (C₂₅H₅₄N⁺)Cl^- optimized structure is shown. In the molecular formation, the electrostatic interaction between the opposite charge of C₂₅H₅₄N⁺ and Cl^- is dominant. Thus, when two molecules of (C₂₅H₅₄N⁺)Cl^- react with one molecule of ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ in the extraction process, they lose two chloride anions and form a new supramolecular complex (C₂₅H₅₄N)₂·(HAsO₄) via the coulombic (electrostatic) interaction between the opposite charge of C₂₅H₅₄N⁺ and ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ . Two species of C₂₅H₅₄N⁺ catch ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ on the site opposite by pointing methyl groups to the oxygen atoms with an inter-distance of around 1.7 Å. Results show that the coulombic (electrostatic) interaction plays an important role in the reaction mechanism of ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ extraction. The calculated thermodynamics properties reveal that this reaction is endothermic having a standard enthalpy change of 1.37 × 10⁵ J·mol⁻¹ and Gibbs free energy change of 3.99 × 10⁵ J·mol⁻¹, respectively.

Close

Fig. 10

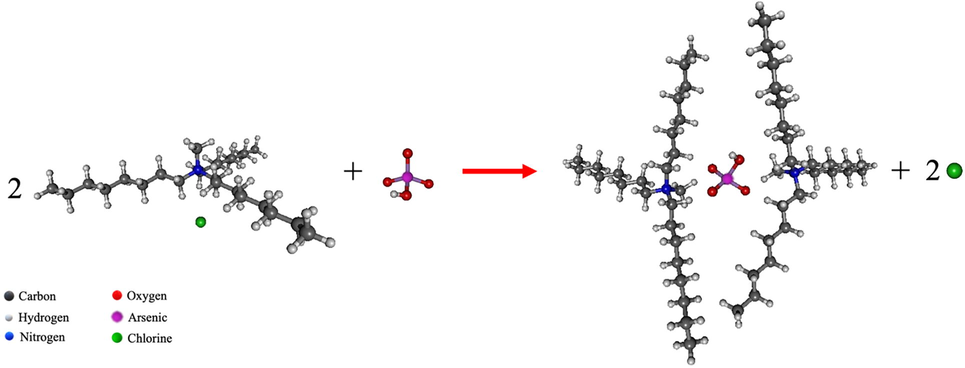
The reaction of (C₂₅H₅₄N⁺)Cl^- and (HAsO₄)^2- at B3LYP/LANL2DZ level of theory.

Export to PPT

3.2.2.2

3.2.2.2 The synergistic stripping of arsenic from the supramolecular complex species

A mixture of thiourea (CS(NH₂)₂) and hydrochloric acid was used as the synergistic strippant solution to enhance the efficiency of recovery of arsenic from the supramolecular complex (C₂₅H₅₄N)₂·(HAsO₄). In Eq. (5) and Fig. 11, the reaction is shown. HCl and thiourea attack ${\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}$ of the supramolecular complex (C₂₅H₅₄N)₂·(HAsO₄). This reaction gives rise to a bond forming between the protons of the HCl and the oxygen atoms, yielding H₃AsO₄ and Cl^- and results in the hydrogen bond between thiourea and H₃AsO₄, yielding the complex H₃AsO₄·CS(NH₂)₂. In the complex H₃AsO₄·CS(NH₂)₂, it is seen that an intramolecular hydrogen bond and chalcogen bond occurred, making the molecules more stable. Besides, the chloride anions, resulting from the breaking of the H-Cl bond, formed a coulombic attraction with two C₂₅H₅₄N⁺, generating two (C₂₅H₅₄N⁺)Cl^- molecules. The synergistic stripping process, using HCl and thiourea, proved to be exothermic with standard enthalpy change of −4.36 × 10⁵ J·mol⁻¹ and Gibbs free energy change of −5.94 × 10⁵ J·mol⁻¹

(5)

$$\overline{{\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right)}_2\bullet \left({\mathrm{H}\mathrm{A}\mathrm{s}\mathrm{O}}_4^{2-}\right)}+2\mathrm{H}\mathrm{C}\mathrm{l}+\mathrm{C}\mathrm{S}{({\mathrm{N}\mathrm{H}}_2)}_2\rightleftharpoons 2\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right){\mathrm{C}\mathrm{l}}^{-}+{\mathrm{H}}_3\mathrm{A}\mathrm{s}{\mathrm{O}}_4\bullet \mathrm{C}\mathrm{S}{({\mathrm{N}\mathrm{H}}_2)}_2$$

Close

Fig. 11

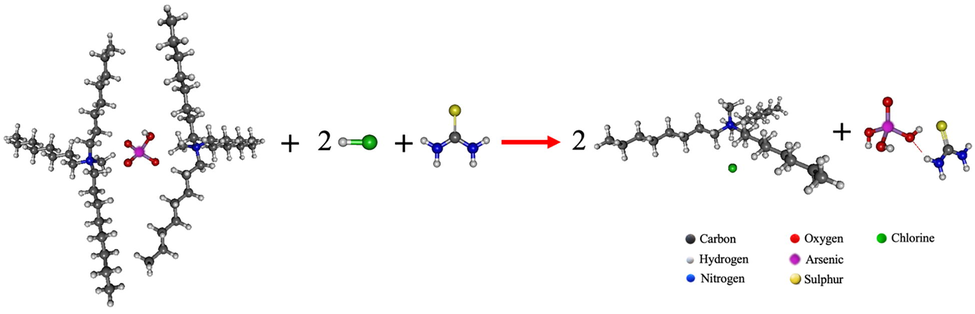
The reaction of arsenic stripping using the mixture of thiourea and hydrochloric acid as the synergistic stripping solution at B3LYP/LANL2DZ level of theory.

Export to PPT

3.2.3

3.2.3 Reaction mechanisms as well as intermolecular and intramolecular properties for the separation of mercury ions

3.2.3.1

3.2.3.1 Extraction of mercury ions

Aliquat 336, (C₂₅H₅₄N⁺)Cl^-, was used to extract mercury ions, which exist in the form of HgCl₂ in the aqueous solution. The extraction reaction of mercury ions using (CH₃R₃N⁺)Cl^– is proposed in this study, as shown in Eq. (6) (Fábrega and Mansur, 2007) and Fig. 12. According to DFT calculations, the lengths of the two bonds between the mercury and chloride anions are 2.60 Å with a bond angle of Cl-Hg-Cl 180.0°. When (C₂₅H₅₄N⁺)Cl^- reacts with HgCl₂, the HgCl₂ molecule forms a covalent bond with a chloride anion establishing a trigonal planar structure of ${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}$ . The coulombic (electrostatic) interaction between the opposite charge of C₂₅H₅₄N⁺ and ${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}$ attracts these two molecules creating a new supramolecular complex (C₂₅H₅₄N⁺)·( ${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}$ ). As shown in Fig. 12, ${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}$ points two chloride anions to the C₂₅H₅₄N⁺. The standard enthalpy change of this reaction is found to be −1.01 × 10⁵ J·mol⁻¹ and the standard Gibb free energy change is 4.62 × 10⁵ J·mol⁻¹.

(6)

$${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_2+\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right){\mathrm{C}\mathrm{l}}^{-}\rightleftharpoons \overline{\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right)\bullet \left({\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}\right)}$$

Close

Fig. 12

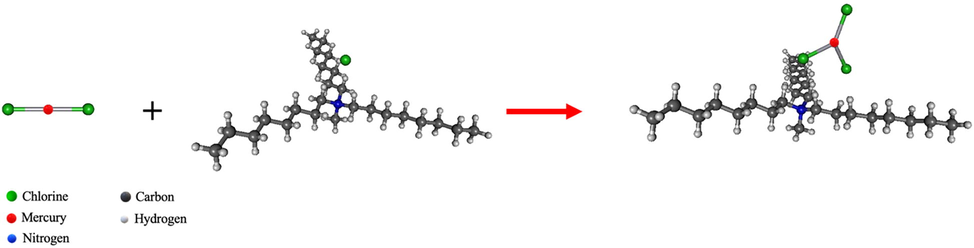
The reaction of HgCl₂ extraction at B3LYP/LANL2DZ level of theory.

Export to PPT

The overbar in Eq. (6) stands for the mercury–carrier complex species in the liquid membrane phase.

3.2.3.2

3.2.3.2 Synergistic stripping of mercury from supramolecular complex species

A mixture of HCl and thiourea, as the synergistic strippant solution, was used to strip the mercury complex species. In Eq. (7) and Fig. 13, the reaction mechanism is presented. The chloride anion of HCl attacks the position of C₂₅H₅₄N⁺ and the proton of HCl forms a covalent bond with one chloride anion in ${\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}$ . This reaction is followed by the attraction of thiourea by the halogen bonding, resulting in the products: (C₂₅H₅₄N⁺)Cl^- and H⁺·(HgCl₃)^-·CS(NH₂)₂. As shown in Fig. 13, it is seen that the intramolecular halogen bonding (2.35 Å) occurred inside the H⁺·(HgCl₃)^-·CS(NH₂)₂ molecule. This synergistic stripping reaction proved to be endothermic, yielding the standard enthalpy change of 2.0 × 10⁵ J·mol⁻¹ and the standard Gibbs free energy change of 2.34 × 10⁵ J·mol⁻¹

(7)

$$\overline{\left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}\right)\bullet \left({\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}\right)}+\mathrm{H}\mathrm{C}\mathrm{l}+\mathrm{C}\mathrm{S}{({\mathrm{N}\mathrm{H}}_2)}_2\rightleftharpoons \left({\mathrm{C}}_{25}{\mathrm{H}}_{54}{\mathrm{N}}^{+}{\mathrm{C}\mathrm{l}}^{-}\right)+{\mathrm{H}}^{+}·{\mathrm{H}\mathrm{g}\mathrm{C}\mathrm{l}}_3^{-}·\mathrm{C}\mathrm{S}{({\mathrm{N}\mathrm{H}}_2)}_2$$

Close

Fig. 13

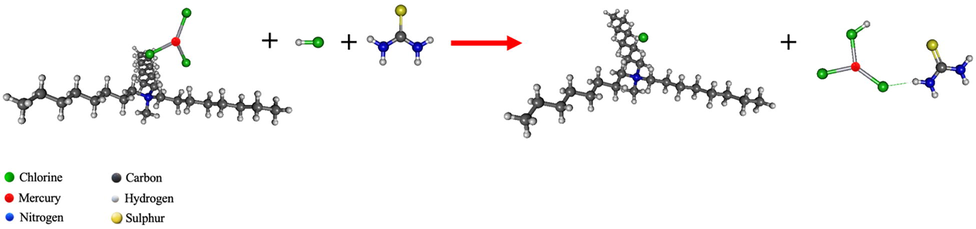
The synergistic stripping reaction of mercury by the mixture of hydrochloric acid and thiourea at B3LYP/LANL2DZ level of theory.

Export to PPT

3.3 Kinetics of extraction and recovery

To determine reaction rate constants and reaction orders of metal extraction and recovery, both integration and graphical approaches plotting the integral concentration of metal ions against time were applied. In Table 2, the results are depicted. In Fig. 14(a)-(d), the best fit is given. As a result of the highest R², reactions for the extraction and recovery of arsenic and mercury ions proved to be of second-order.

Close

Fig. 14

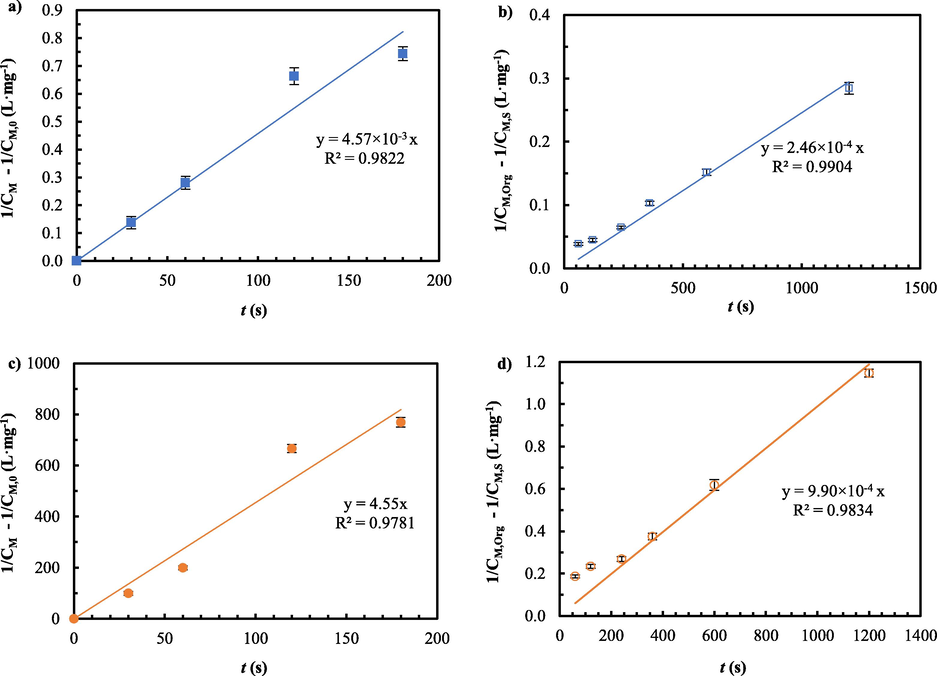
The integral concentration of metal ions versus time: a) extraction of arsenic ions, b) recovery of arsenic ions, c) extraction of mercury ions and d) recovery of mercury ions.

Export to PPT

Consequently, the reaction rate constants of extraction and recovery of arsenic ions were 4.57 × 10^-3 and 2.46 × 10^-4 L·mg⁻¹·s⁻¹, respectively. Those of extraction and recovery of mercury ions proved to be 4.55 and 9.9 × 10^-4 L·mg⁻¹·s⁻¹, respectively. These outcomes suggest that the rates of extraction for both arsenic and mercury ions are faster than those of recovery. In addition, the rate of extraction of mercury ions is seen to be much faster than that of arsenic ions.

3.4 Developing a mathematical model to describe mass transport mechanism and forecast the extractability of arsenic and mercury ions across HFSLM

Fig. 15(a) depicts the schema of transport of arsenic and mercury ions from the feed phase across the liquid membrane to the stripping phase. At the interface of feed and liquid membrane, arsenic and mercury ions in the feed phase combined with the organic carrier molecule(s) to create a supramolecular complex species of metal–carrier. According to the concentration gradient, the supramolecular complex species diffused across the liquid membrane phase to the interface of the liquid membrane and stripping, and then reacted with the strippant in the stripping solution. As a result, target metal ions were released into the stripping phase, whilst the carrier molecule, which was released from the supramolecular complex species, diffused backward to the interface of feed and liquid membrane and reacted with the target metal ions from the feed phase once more. Thus, arsenic and mercury ions can be extracted and recovered in a single-step operation.

Close

Fig. 15

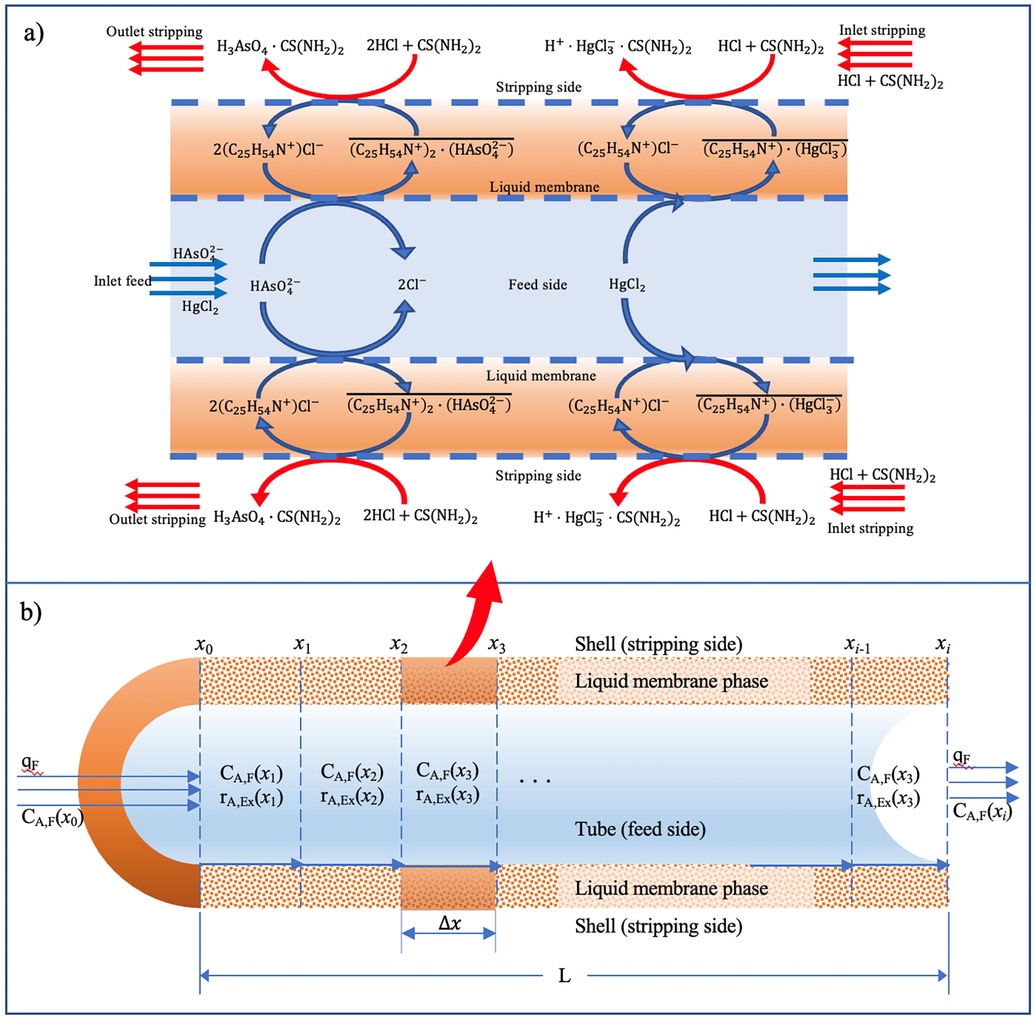
Schema of arsenic and mercury ions transport across HFSLM: (a) mechanism of removal using Aliquat 336 as the carrier and HCl as the strippant, (b) mechanism of removal using Aliquat 336 as the carrier and the HCl/thiourea mixture as the strippant and (c) increment of a hollow fiber.

Export to PPT

The supramolecular complex species of the metal-carrier, occurring at the feed–liquid-membrane interface, diffused to the liquid-membrane–stripping interface and was recovered continuously by the strippant in the stripping phase. The total reactions, therefore, of arsenic and mercury extraction in Eqs. (4) and (6) can be considered as forward reaction. Their reaction rate can be expressed as follows:

where × is the longitudinal axis of the hollow fiber in the feed phase (dm), k_Ex is the reaction rate constant of extraction (L·mg⁻¹·s⁻¹), C_A,F is the concentration of metal ions in the feed phase (mg·L^-1) and m is the reaction order of extraction (-).

The model proposed in this study is considered at a steady state condition and created from the conservation of mass of metal ions in each increment ( $\mathrm{\Delta }$ x) of the hollow fibers (Fig. 15(b)). Factors involved in the model comprise axial convection and extraction reaction at the feed–membrane interface; diffusion is neglected. The hypotheses of the model are:

1. Physical properties of the feed-phase i.e. temperature, pressure, and volume are all constant.

2. The inside diameter of the hollow fiber is extremely small. As a result, the concentration profiles of metal ions in the radial direction are constant, implying that the ion diffusion fluxes in the feed phase occur only in the axial direction.

3. Only the supramolecular complex species of the metal-carrier, produced by the extraction reaction, not metal ions, can transport into the liquid membrane phase.

4. Extraction reaction at the feed–liquid–membrane interface limits the rate of metal ion transport from the feed phase to the liquid membrane phase.

5. The supramolecular complex species of the metal-carrier, occurring at the feed–liquid-membrane interface, diffuses to the liquid-membrane–stripping interface and is recovered continuously by the strippant in the stripping phase. Therefore, the total reaction of metal extraction can be considered as forward reaction.

Conservation of mass of metal ions in each increment of a hollow fiber is given in Eq. (9):

• [Rate of mass transport into the hollow fiber due to convection] –

• [Rate of mass transport out of the hollow fiber due to convection] +

• [Rate of mass extracted due to extraction reaction] =

Eq. (9) can be expressed as:

where q_F refers to the volumetric flow rate of the aqueous feed solution (L·s⁻¹), C_A,F denotes the concentration of metal ions in the feed phase (mg·L^-1), i represents the number of increments, $r_{A,Ex}$ stands for the rate of extraction reaction, and V_F refers to the volume of an increment of the hollow fiber (L): $V_F=\pi r_i^2\mathrm{\Delta }x$ ; $\mathrm{\Delta }x=\frac{L}{i}$ .

At steady state, the rate of mass accumulation is constant where dC_A,F(x_i) / dt = 0. Therefore, Eq. (10) becomes:

Eq. (11) can be solved using the concept of Generating Function (as described in Appendix B) and yields Eq. (12), which is utilized to forecast the concentration of metal ions in the outlet feed solution viz. C_A,F(x_i) measured in mg·L^-1:

The accuracy of the mathematical model for forecasting the extraction of metal ions via HFSLM can be determined by the average relative deviation (ARD):

where $C_{\mathit{Expt}.}$ and $C_{\mathit{Model}}$ are the concentrations of metal ions (mg·L^-1) attained from the experiment and the model, respectively. N is the number of observations.

The mathematical model developed, as in Eq. (12), was validated using the experimental data at various flow rates of feed and strippant solutions. In Fig. 16, the results of validation are depicted. Outcomes demonstrate that the extraction of arsenic and mercury ions estimated using Eq. (12) was in line with the experimental data, attaining average relative deviations of 5 %. These values confirmed that the chemical reaction at the interface of feed and liquid membrane is the predominant factor controlling the rate of arsenic and mercury ions transport from feed to the liquid membrane; diffusion of arsenic and mercury ions is negligible. It can be seen that the percentages of extraction of arsenic and mercury ions obtained from the experiment were slightly lower than those obtained from the prediction. Such an outcome occurred because the model neglected the effect of diffusion at the interface. However, the model developed is still acceptable as the average relative deviation of prediction is as small as 5 %.

Close

Fig. 16

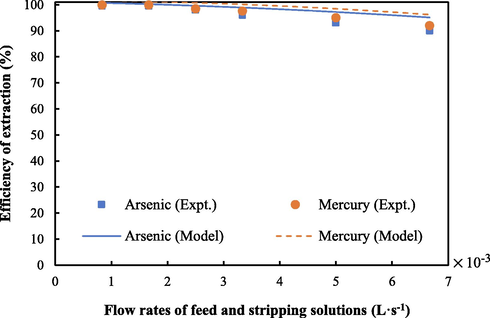
Validation of the mathematical model using the experimental data.

Export to PPT