Theoretical study of the structure and fundamental properties of AZn2N2 (A = Ca, Sr, Ba)

Diwen Liu; Huan Peng; Rongjian Sa

doi:10.1016/j.arabjc.2022.104263

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

11 2022

:15;

104263

doi:

10.1016/j.arabjc.2022.104263

Theoretical study of the structure and fundamental properties of AZn₂N₂ (A = Ca, Sr, Ba)

Diwen Liu^{^a,⁎}, Huan Peng^{^a}, Rongjian Sa^{^b,⁎}

a School of Materials and Chemical Engineering, Pingxiang University, Pingxiang 337055, China

b College of Materials and Chemical Engineering, Fujian Key Laboratory of Functional Marine Sensing Materials, Minjiang University, Fuzhou 350108, China

⁎Corresponding authors. liudiwen1987@163.com (Diwen Liu), rjsa@mju.edu.cn (Rongjian Sa)

Received: 2022-7-6, Accepted: 2022-9-11,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

The structure, stability, elastic, electronic, and optical properties of trigonal AZn₂N₂ (A = Ca, Sr, Ba) are simulated and compared in this work. The stability and physical properties of BaZn₂N₂ are mainly highlighted. According to the calculated results, three compounds are thermodynamically and mechanically stable, and they are brittle materials. The stability of trigonal BaZn₂N₂ is confirmed by using the different theoretical approaches. The direct band gap transition is allowed at the Γ point for each compound. The predicted direct band gaps are 1.733, 1.507, and 1.510 eV for CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂, respectively. The valence band is mostly composed of the N-2p orbitals, while the conduction band is mainly contributed from the Ca-3d/Sr-4d/Ba-5d orbitals. The results show that the electron shows high mobility for carrier transport, and the value of exciton binding energy is less than 80 meV. Furthermore, compared to CaZn₂N₂ and SrZn₂N₂, BaZn₂N₂ shows excellent light absorption capacity in the visible region. This study indicates that BaZn₂N₂ is a desirable material for solar cell applications.

Keywords

AZn2N2

Stability

Elastic constant

Optoelectronic properties

DFT

Show Related Articles from PubMed

1 Introduction

The most representative nitrides are GaN and its alloys such as Ga₁₋_xAl_xN and Ga₁₋_xIn_xN because they are the important materials for optoelectronic devices (Ul Haq et al., 2014; Özdemir et al., 2019). The electronic, optical, and thermoelectric properties of two-dimensional III-nitrides Ga_1–_xAl_xN and Ga_1–_xIn_xN have been been demonstrated through density functional theory (DFT) calculations (Wines et al., 2020). However, these compounds contain the rare or toxic elements, which is difficult to achieve large-scale commercial applications. Therefore, it is of great importance to explore novel nitrides, which are composed of earth-abundant and non-toxic elements. The fundamental physical properties of II–IV–N₂ nitrides and their alloys have been investigated in recent years, such as ZnSiN₂ (Häusler et al., 2017; Mallmann et al., 2019); ZnGeN₂ (Häusler et al., 2017; Mallmann et al., 2019); MgSiN₂ (Mallmann et al., 2019; Häusler et al., 2018), MgGeN₂ (Mallmann et al., 2019; Häusler et al., 2018); ZnSnN₂ (Cao et al., 2017; Laidouci et al., 2020; Tsunoda et al., 2018 ), and Zn₁₋_xMg_xSnN₂ (Yamada et al., 2021).

The computational screening of ternary nitrides is conducted, and some novel compounds are finally identified (Hinuma et al., 2016). For example, CaZn₂N₂ can be synthesized by high-pressure methods, and it is a direct band gap semiconductor with 1.8 eV (Hinuma et al., 2016). The band gap energy of CaZn₂N₂ is narrowed to 1.6 eV by the substitution of Sr for Ca, which is further confirmed by the recent experiment (Kikuchi et al., 2021). In addition, the direct band gap can be widely tuned from ∼ 1.8 to ∼ 3.2 eV between CaZn₂N₂ and CaMg₂N₂ (Tsuji et al., 2019). CaZn₂N₂ is a promising candidate for next-generation semiconductor in the filed of light-emitting diodes and solar cells (Tsuji et al., 2019; Huang et al., 2022). A detailed theoretical study is performed to reveal the impact of pressure on the dynamical, elastic, and thermal properties of CaZn₂N₂ (Zhao et al., 2017). The structure and fundamental physical properties of MgBe₂N₂, CaBe₂N₂, CaMg₂N₂, SrMg₂N₂, CaZn₂N₂, and SrZn₂N₂ are thoroughly studied via first-principles calculations (Khan et al., 2019; Khan et al., 2018; Khan et al., 2018; Murtaza et al., 2018; Murtaza et al., 2018; Murtaza et al., 2018 ). It is revealed from our recent theoretical work that the band gaps of CaZn₂N₂ and SrZn₂N₂ are effectively regulated by the partial substitution of Cd for Zn (Liu et al., 2022).

The structures and physical properties of both CaZn₂N₂ and SrZn₂N₂ have been reported experimentally and theoretically (Hinuma et al., 2016; Kikuchi et al., 2021; Zhao et al., 2017 ). However, no available experimental and theoretical reports are conducted for exploring the fundamental properties of BaZn₂N₂. Therefore, a comprehensive study is required to investigate the structure, stability, elastic, electronic, and optical properties of BaZn₂N₂. Moreover, it is vital to know whether the trigonal phase is stable for BaZn₂N₂. The thermodynamic, dynamic, thermal, and mechanical stability of BaZn₂N₂ is evaluated for the first time. The elastic, electronic, and optical properties of AZn₂N₂ (A = Ca, Sr, Ba) are compared and discussed in detail. The influence of different cations on the various physical properties of AZn₂N₂ is revealed. The results suggest that BaZn₂N₂ is a stable and desirable material for solar cell applications.

2 Computational details

The structure and physical properties of trigonal AZn₂N₂ (A = Ca, Sr, Ba) were simulated in this work by using first-principles calculations as implemented in the Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996). The interaction between icons and valance electrons was dealt by the projector augmented wave (PAW) (Blöchl, 1994) method. The structure was fully relaxed by employing Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) (Perdew et al., 1996). The cut-off energy was set to be 520 eV. The k-point mesh of 8 × 8 × 4 was adopted for all calculations. The convergence criteria of total energy and the forces on each atom were less than 10⁻⁶ eV and 10⁻³ eV/Å, respectively. The electronic and optical properties of AZn₂N₂ (A = Ca, Sr, Ba) were obtained by employing the hybrid functional HSE06 (Heyd et al., 2003). A 3 × 3 × 2 supercell was constructed for trigonal BaZn₂N₂ in order to calculate the phonon dispersion curves based on the Phonon code (Togo and Tanaka, 2015). Furthermore, ab initio molecular dynamics (AIMD) simulations were performed for trigonal BaZn₂N₂ at room temperature (300 K).

3 Results and discussion

3.1

3.1 Structural properties and stability

The compound AZn₂N₂ (A = Ca, Sr) crystallizes in the trigonal structure (space group: P3̅m1) (Hinuma et al., 2016; Kikuchi et al., 2021), while the trigonal crystal structure is not reported experimentally for BaZn₂N₂ so far. Therefore, the trigonal crystal structure of BaZn₂N₂ was constructed by substituting Ba for Ca in CaZn₂N₂. In addition, the physical properties of both CaZn₂N₂ and SrZn₂N₂ are presented in order to explore the effect of different cations on the structure and properties of AZn₂N₂. Fig. 1 depicts the trigonal crystal structure of AZn₂N₂ (A = Ca, Sr, Ba). The obtained structural parameters of three compounds are demonstrated in Table 1. The lattice constants of CaZn₂N₂ and SrZn₂N₂ are consistent with the recent experimental and theoretical data (Hinuma et al., 2016; Kikuchi et al., 2021). The lattice constant and bond length are increased from CaZn₂N₂ to BaZn₂N₂. The computed lattice constants of BaZn₂N₂ are a = b = 3.66 Å and c = 6.60 Å, respectively. The atomic coordinates in the trigonal structure of BaZn₂N₂ are listed in Table 2.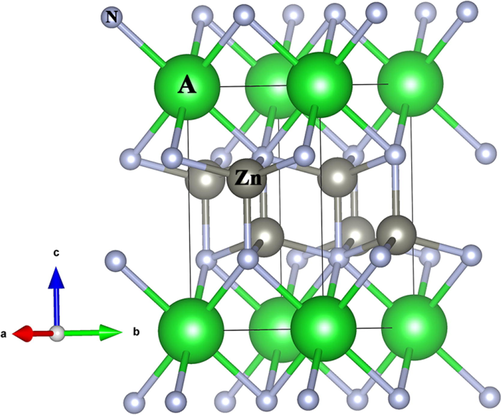

The trigonal structure of AZn2N2 (A = Ca, Sr, Ba).

Table 1 The various structural parameters for AZn₂N₂ (A = Ca, Sr, Ba).

Compound	a = b (Å)	c (Å)	V (Å³)	α = β (◦)	γ (◦)	A − N (Å)
CaZn₂N₂	3.48	6.04	63.35	90	120	2.54
Exp.^a	3.46	6.01	/	/	/	/
Theor.^a	3.45	5.99	/	/	/	/
SrZn₂N₂	3.57	6.28	69.47	90	120	2.69
Theor.^b	3.48	6.15	/	/	/	/
BaZn₂N₂	3.66	6.60	76.64	90	120	2.86

a Hinuma et al. (2016).

b Kikuchi et al. (2021).

Table 2 The atomic coordinates for BaZn₂N₂.

Atom	x	y	z
Ba	0.00000	0.00000	0.00000
Zn1	0.33333	0.66667	0.62018
Zn2	0.66667	0.33333	0.37982
N1	0.33333	0.66667	0.29112
N2	0.66667	0.33333	0.70888

The thermodynamic stability of three compounds is checked by the following formation energy (E_f) formula:

(1)

E_{f} = E_{{AZn}_{2} N_{2}} - E_{A} - 2 \times E_{Zn} - E_{N_{2}}

The calculated values of E_f are −1.94, −1.37, and −0.64 eV/f.u., respectively. The results indicate that three compounds can be synthesized at proper conditions and also confirm their thermodynamic stability. It is well known that the lower the E_f, the better the stability, thus the thermodynamic stability is reduced from CaZn₂N₂ to BaZn₂N₂. Furthermore, it is vital to assess the dynamical stability of trigonal BaZn₂N₂. The computed phonon dispersion curves are illustrated in Fig. 2. It is dynamically stable for trigonal BaZn₂N₂ because there is no negative frequency. It is observed that three acoustic phonon frequencies are zero at the Γ point, which ensure the dynamical stability of BaZn₂N₂. It is noted for BaZn₂N₂ that although the tetragonal structure has a lower total energy (∼80 meV/f.u.) than that of the trigonal structure, the tetragonal structure is not dynamically stable because there are many negative frequencies according to the calculations of phonon spectrum. The AIMD simulations are conducted to further verify the thermal stability of BaZn₂N₂. As shown in Fig. 3, it is widely fluctuated for the temperature, but the total energy varies little throughout the whole simulation. The trigonal structure is still maintained, thus the thermal stability is proved.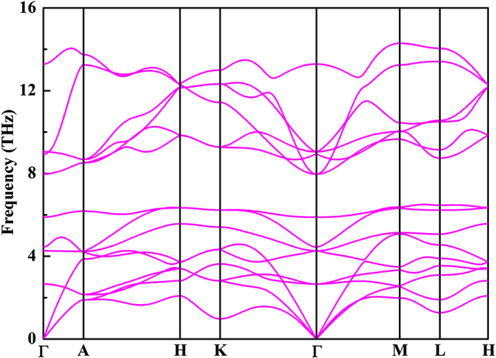

The phonon spectrum curves of trigonal BaZn2N2.

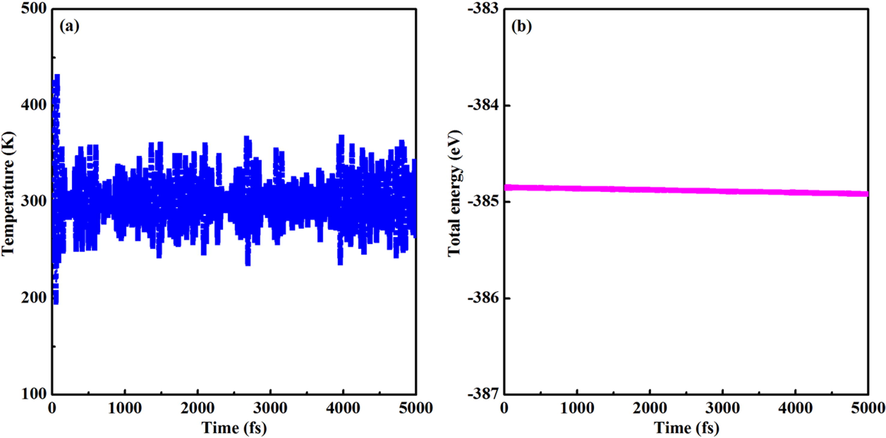
The variations of (a) temperature and (b) total energy for BaZn2N2 at the AIMD simulations.

3.2

3.2 Mechanical properties

The elastic properties of CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂ are calculated for the first time. It is widely known that there are six independent elastic constants for a trigonal crystal system. The complete Born stability criteria for a trigonal system is the following four conditions (Mouhat and Coudert, 2014):

(2)

C_{11} > |C_{12}|, C_{13}^{2} < \frac{1}{2} C_{33} (C_{11} + C_{12}), C_{44} > 0, C_{14}^{2} < \frac{1}{2} C_{44} (C_{11} - C_{12})

The six elastic constants are displayed in Fig. 4. It is verified that three compounds are mechanically stable since all the mentioned conditions are met. It is apparent that five elastic constants (such as C₁₁, C₁₂, C₁₃, C₁₄, and C₄₄) are decreased from CaZn₂N₂ to BaZn₂N₂, while the only elastic constant C₃₃ is increased. The bulk modulus (B) and the shear modulus (G) can be computed by applying the Voigt–Reuss–Hill approximations (Hill, 1952). The Poisson's ratio (ν) is obtained by the formula: ν = (3B − G)/[2(3B + G)] (Wu et al., 2007). Two parameters of B/G and ν can discern the brittleness or ductility feature of a compound. If the values of B/G and ν are less than 1.75 and 0.26, the compound is brittle, otherwise, the ductile behavior is observed (Hadi et al., 2017; Pugh, 1954). The results show that the values of B/G and ν are in the range of 1.41–1.49 and 0.21–0.23, respectively. It can be inferred that three compounds are brittle materials in nature.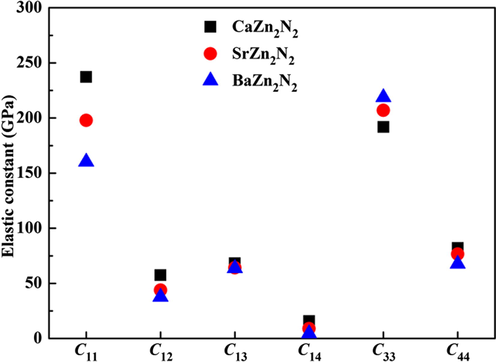

The trend of six independent elastic constants for CaZn2N2, SrZn2N2, and BaZn2N2.

3.3

3.3 Electronic properties

The band structure and transition dipole moment (TDM) in the Brillouin zone of each compound are calculated at the PBE functional. First of all, it can be seen from Fig. 5 that they are direct band gap semiconductors with the valence band maximum (VBM) and conduction band minimum (CBM) at the Γ point. Secondly, the degree of direct electronic transition between the VBM and CBM edges is mainly determined by the value of TDM. According to the previous detailed theoretical study (Meng et al., 2017), there are four types of transitions: (i) all k points forbidden, (ii) partial k points forbidden, (iii) weak transition allowed, and (iv) strong transition allowed. The values of TDM at various k points are illustrated in Fig. 5. It is clear that the allowed and strong transition between the band edges at the Γ point is revealed for the studied three compounds, which is desirable for solar cell applications.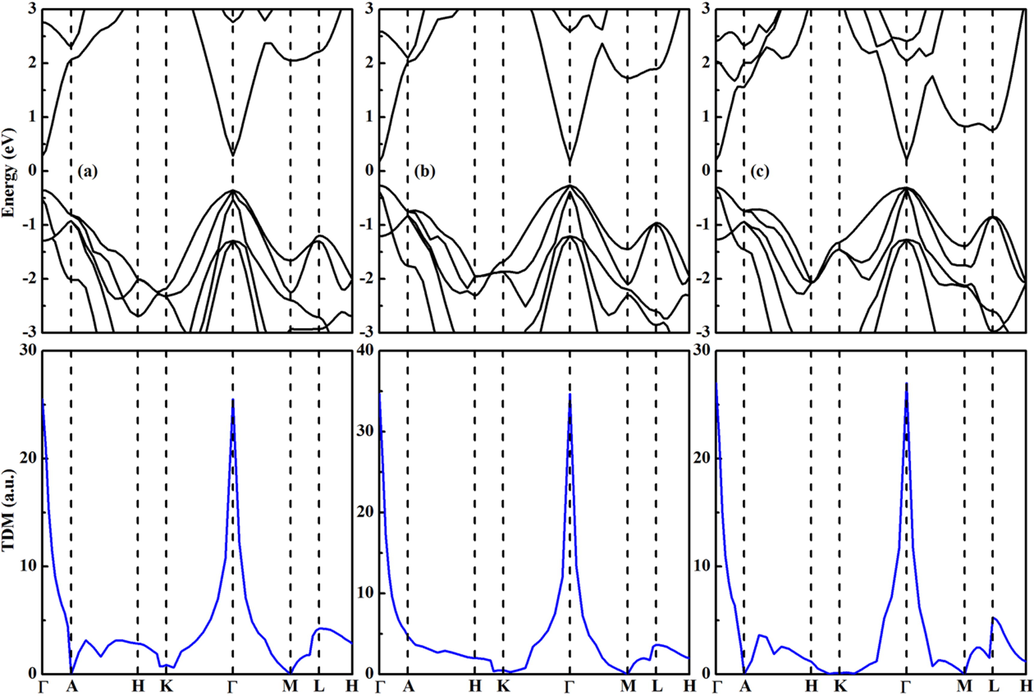

The band structures (upper) and transition dipole moments (lower) of (a) CaZn2N2, (b) SrZn2N2, and (c) BaZn2N2 at the PBE functional.

The calculated band gaps are 0.637 and 0.442 eV for CaZn₂N₂ and SrZn₂N₂ when the standard PBE functional is used. The theoretical band gaps of both compounds are seriously underestimated compared to the experimental values (Kikuchi et al., 2021; Tsuji et al., 2019). The corrected band gaps calculated from the HSE06 functional are 1.733 and 1.507 eV for CaZn₂N₂ and SrZn₂N₂, which are reasonable consistent with the recent experimental data (1.8 eV for CaZn₂N₂ and 1.6 eV for SrZn₂N₂) (Kikuchi et al., 2021; Tsuji et al., 2019). It is concluded that the lower band gap can be realized for AZn₂N₂ by varying the earth-alkali metal element. It is observed from Fig. 6 that BaZn₂N₂ is also a direct band gap compound at the Γ point. It is interesting that the direct band gap is 1.510 eV for BaZn₂N₂. It is noted that the band gap difference between SrZn₂N₂ and BaZn₂N₂ is negligible. By analyzing the density of states of three compounds, it is disclosed that the VBM is largely contributed from the N-2p orbitals, while the CBM is dominated by the contribution from the Ca-3d/Sr-4d/Ba-5d orbitals. The contributions from the Zn-4 s and Zn-4p orbitals are little for the edges of VBM and CBM.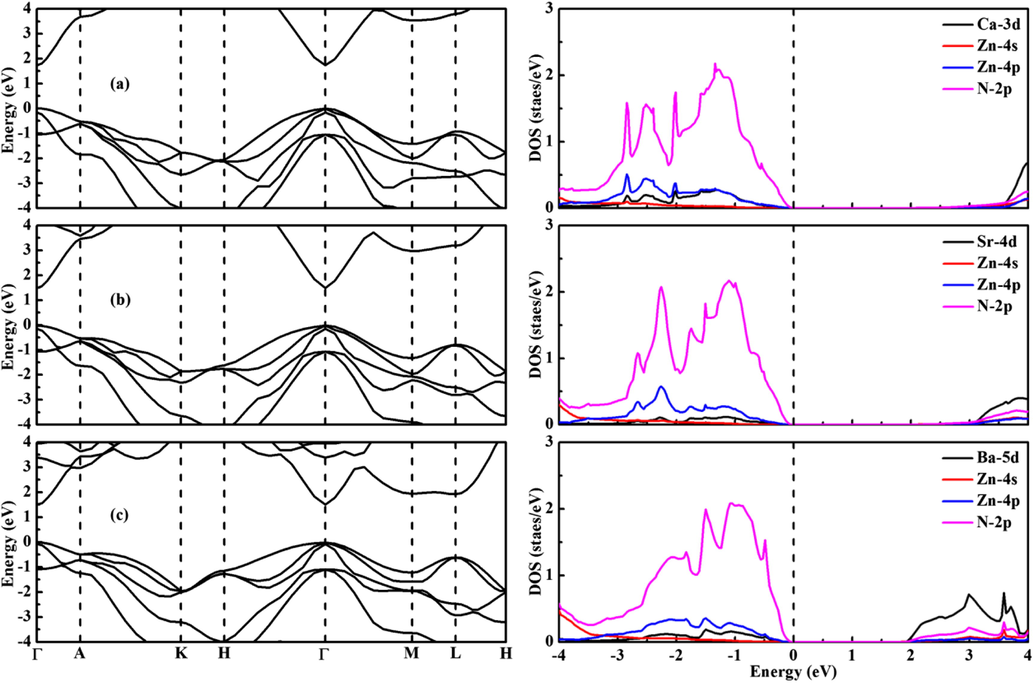

Band structures (left) and density of states (right) of (a) CaZn2N2, (b) SrZn2N2, and (c) BaZn2N2.

The mobility of the carriers is a crucial index for optoelectronic applications. The effective masses of electron (m^∗_e) and hole (m^∗_h) can be derived from the curvatures around the VBM and CBM with the following relation (Green, 1990):

(3)

m^{*} = ħ^{2} {[\frac{\partial^{2} ε (k)}{\partial k^{2}}]}^{- 1}

where ħ and ε(k) are the reduced Planck constant and orbit eigenvalue, respectively. In addition, the exciton binding energy (E_b) can be further obtained by the following equation (Liu et al., 2021):

(4)

E_{b} \approx \frac{13.56 m_{r}^{*}}{m_{0} ε^{2}}

where m^∗_r, m₀, and ε are the reduced effective mass (m^∗_r = m^∗_e × m^∗_h/(m^∗_e + m^∗_h)), static electron mass, and static dielectric constant, respectively. The effective masses of electron (m^∗_e) and hole (m^∗_h) along with the Γ→A direction are computed for AZn₂N₂ (A = Ca, Sr, Ba). It can be seen from Table 3 that the effective masses of electron and hole are in the range of 0.2–0.3 m₀ and 1.3–1.4 m₀, respectively. There is an inverse relationship between the effective mass and conductivity (Khan et al., 2021), so the electron shows better mobility for carrier transport. The value of E_b varies between 60 and 80 meV, which indicates that each compound is suitable for application as an absorption layer in solar cells.

Table 3 The computed values of m^∗_e, m^∗_h, m^∗_r, ε, and E_b for AZn₂N₂ (A = Ca, Sr, Ba).

Compound	m^∗_e (m₀)	m^∗_h (m₀)	m^∗_r	ε	E_b (meV)
CaZn₂N₂	0.209	1.374	0.181	5.705	76
SrZn₂N₂	0.217	1.345	0.187	5.942	72
BaZn₂N₂	0.244	1.317	0.206	6.637	63

3.4

3.4 Optical properties

The light harvesting capacity of a semiconductor material is a crucial index for photovoltaic applications. The various optical properties are directly related to the dielectric function ε(ω), which is given as follows (Tang et al., 2019):

(5)

ε (ω) = ε_{1} (ω) + i ε_{2} (ω)

where ε₁(ω) and ε₂(ω) represent the real part and imaginary part of the dielectric function, respectively. The calculated curves of ε₁(ω) and ε₂(ω) are shown in Fig. 7(a-b). The values of static dielectric constants ε₁(0) are 5.70, 5.94, and 6.64 for CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂, respectively. The ε₂(ω) peak of BaZn₂N₂ is higher than those of CaZn₂N₂ and SrZn₂N₂ in the photon energy range from 2 to 5 eV, indicating that BaZn₂N₂ has better absorption capacity for visible light.

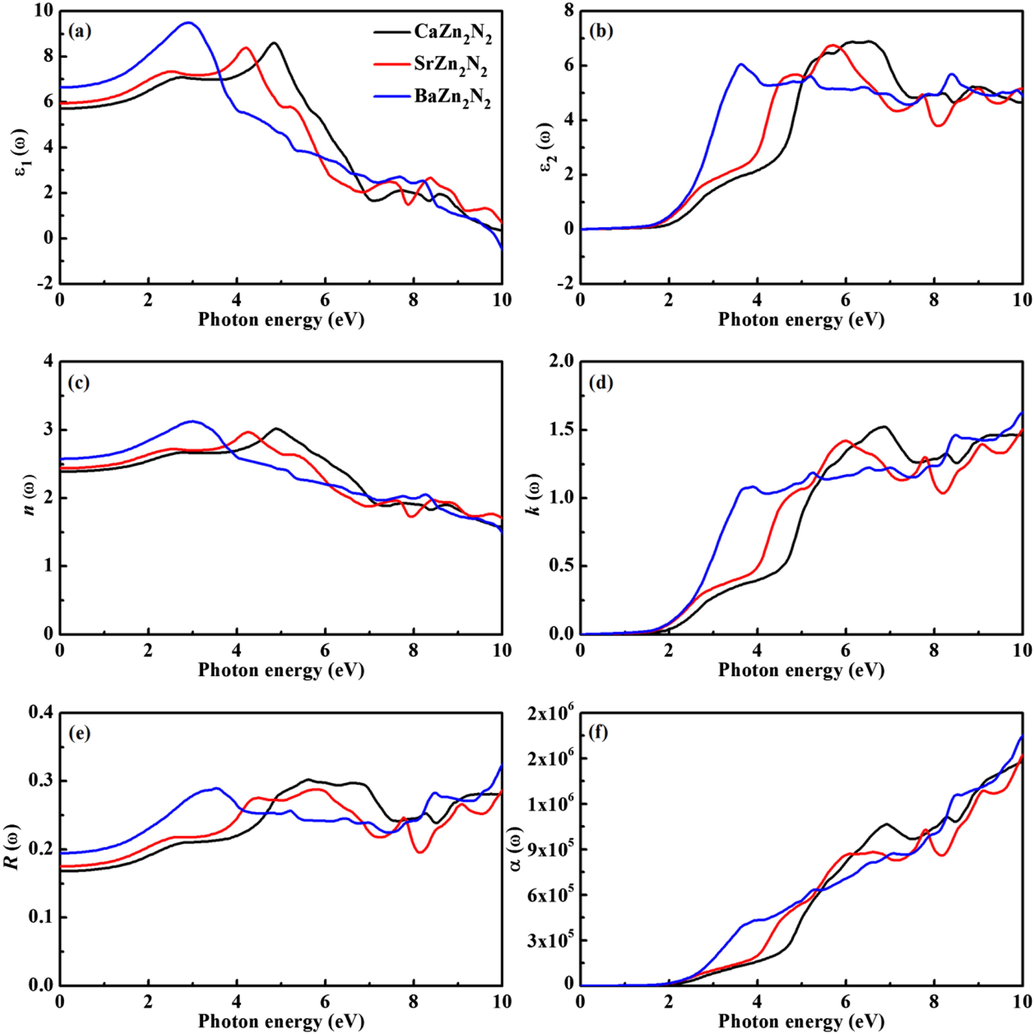
The optical properties of AZn2N2 (A = Ca, Sr, Ba): (a) ε1(ω), (b) ε2(ω), (c) n(ω), (d) k(ω), (e) R(ω), and (f) α(ω).

In addition, the refractive index n(ω), extinction coefficient k(ω), reflectivity R(ω), and absorption coefficient α(ω) of CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂ are computed by the following relations (Zhao et al., 2021):

(6)

n (ω) = {[\frac{ε_{1} (ω)}{2} + \frac{\sqrt{ε_{1}^{2} (ω) + ε_{2}^{2} (ω)}}{2}]}^{\frac{1}{2}}

(7)

k (ω) = {[\frac{- ε_{1} (ω)}{2} + \frac{\sqrt{ε_{1}^{2} (ω) + ε_{2}^{2} (ω)}}{2}]}^{\frac{1}{2}}

(8)

R (ω) = \frac{{[n (ω) - 1]}^{2} + k^{2} (ω)}{{[n (ω) + 1]}^{2} + k^{2} (ω)}

(9)

α (ω) = \sqrt{2} ω {[\sqrt{ε_{1} {(ω)}^{2} + ε_{2} {(ω)}^{2}} - ε_{1} (ω)]}^{1 / 2}

The calculated results are plotted in Fig. 7(c-f). It can be seen that the curves of n(ω) and k(ω) are similar to those of ε₁(ω) and ε₂(ω). The static value of refractive index n(0) can be obtained by the equation $n (0) = \sqrt{ε_{1} (0)}$ (Li et al., 2008). The calculated n(0) values are 2.39, 2.44, and 2.58 for CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂, respectively. The static value of k(0) is close to zero in the low photon energy region (0–2 eV). The static values of R(0) are 0.168 for CaZn₂N₂, 0.175 for SrZn₂N₂, and 0.194 for BaZn₂N₂, respectively. The value of R(ω) always fluctuates between 0.15 and 0.35 in the range of 0–10 eV. It is observed from Fig. 7(f) that the absorption edge is mostly located at about 2 eV, which is linked with the band gap calculated by the direct electronic transition from the top of the valence band to the bottom of the conduction band. In the low photon energy range (0–2 eV), the absorption is negligible. Three compounds show the high light absorption properties. Especially, the efficiency of light absorption is greatly enhanced for BaZn₂N₂ in the visible and ultraviolet regions (2–5 eV), which is very conducive to improve the optical performance.

4 Conclusions

In summary, the structure, stability, elastic, electronic, and optical properties of trigonal AZn₂N₂ (A = Ca, Sr, Ba) are revealed for the first time in the current work. The stability and optoelectronic properties of BaZn₂N₂ are highlighted. The results show that three compounds are thermodynamically and mechanically stable, and they are brittle materials. Moreover, the stability of BaZn₂N₂ is further verified by applying different theoretical approaches. The direct band gap transition at the Γ point is allowed for each compound. The calculated direct band gaps are 1.733, 1.507, and 1.510 eV for CaZn₂N₂, SrZn₂N₂, and BaZn₂N₂, respectively. For three compounds, the electron exhibits high mobility for carrier transport, and the value of E_b is less than 80 meV. Detailed analysis of optical properties displays that BaZn₂N₂ has excellent light absorption capacity in the visible region. This findings reveal that BaZn₂N₂ is a good candidate for optoelectronic applications.

CRediT authorship contribution statement

Diwen Liu: Conceptualization, Supervision, Validation, Writing – original draft. Huan Peng: Formal analysis. Rongjian Sa: Resources, Writing – review & editing.

Acknowledgments

This work was supported by the Science and Technology Research Program of the Education Department of Jiangxi Province (No. GJJ212705).

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Blöchl P.E., . Projector augmented-wave method. Phys. Rev. B. 1994;50:17953-17979.
[Google Scholar]
Cao X., Kawamura F., Ninomiya Y., Taniguchi T., Yamada N., . Conduction-band effective mass and bandgap of ZnSnN₂ earth-abundant solar absorber. Sci. Rep.. 2017;7:14987.
[Google Scholar]
Green M.A., . Intrinsic concentration, effective densities of states, and effective mass in silicon. J. Appl. Phys.. 1990;67:2944-2954.
[Google Scholar]
Hadi M.A., Roknuzzaman M., Chroneos A., Naqib S.H., Islam A.K.M.A., Vovk R.V., Ostrikov K., . Elastic and thermodynamic properties of new (Zr_3-_xTi_x)AlC₂ MAX-phase solid solutions. Comput. Mater. Sci.. 2017;137:318-326.
[Google Scholar]
Häusler J., Schimmel S., Wellmann P., Schnick W., . Ammonothermal Synthesis of Earth-Abundant Nitride Semiconductors ZnSiN₂ and ZnGeN₂ and Dissolution Monitoring by In Situ X-ray Imaging. Chem. Eur. J.. 2017;23:12275-12282.
[Google Scholar]
Häusler J., Niklaus R., Minár J., Schnick W., . Ammonothermal Synthesis and Optical Properties of Ternary Nitride Semiconductors Mg-IV-N₂, Mn-IV-N₂ and Li-IV₂-N₃ (IV=Si, Ge) Chem. Eur. J.. 2018;24:1686-1693.
[Google Scholar]
Heyd J., Scuseria G.E., Ernzerhof M., . Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys.. 2003;118:8207-8215.
[Google Scholar]
Hill R., . The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A. 1952;65:349-354.
[Google Scholar]
Hinuma Y., Hatakeyama T., Kumagai Y., Burton L.A., Sato H., Muraba Y., Iimura S., Hiramatsu H., Tanaka I., Hosono H., Oba F., . Discovery of earth-abundant nitride semiconductors by computational screening and high-pressure synthesis. Nat. Commun.. 2016;7:11962.
[Google Scholar]
Huang M., Wang S., Zhang T., Chen S., . Searching for Band-Dispersive and Defect-Tolerant Semiconductors from Element Substitution in Topological Materials. J. Am. Chem. Soc.. 2022;144:4685-4694.
[Google Scholar]
Khan A.A., Rehman A.U., Laref A., Yousaf M., Murtaza G., . Structural, Optoelectronic and Thermoelectric Properties of Ternary CaBe₂X₂ (X = N, P, As, Sb, Bi) Compounds. Z. Naturforsch. A. 2018;73:965-973.
[Google Scholar]
Khan A.A., Yaseen M., Laref A., Murtaza G., . Impact of anion replacement on the optoelectronic and thermoelectric properties of CaMg₂X₂, X = (N, P, As, Sb, Bi) compounds. Phys. B Condens. Matter. 2018;541:24-31.
[Google Scholar]
Khan A.A., Hasil R., Laref A., Ullah N., Sajjad M., Zeb A., Murtaza G., . DFT prediction of the structural, electronic, thermoelectric and optical properties of ternary pnictides MgBe₂X₂ (X = N, P, As, Sb, Bi): A novel analysis of beryllium with 2A- and 5B-Elements of the structure type CaAl₂Si₂. Solid State Commun.. 2019;300:113667.
[Google Scholar]
Khan I., Shahab I.U., Haq A., Ali Z., Ali I., . Ahmad, Elastic and Optoelectronic Properties of Cs₂NaMCl₆ (M = In, Tl, Sb, Bi) J. Electron. Mater.. 2021;50:456-466.
[Google Scholar]
Kikuchi R., Ueno K., Nakamura T., Kurabuchi T., Kaneko Y., Kumagai Y., Oba F., . SrZn₂N₂ as a Solar Absorber: Theoretical Defect Chemistry and Synthesis by Metal Alloy Nitridation. Chem. Mater.. 2021;33:2864-2870.
[Google Scholar]
Kresse G., Furthmüller J., . Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci.. 1996;6:15-50.
[Google Scholar]
Laidouci A., Aissat A., Vilcot J.P., . Numerical study of solar cells based on ZnSnN₂ structure. Sol. Energy. 2020;211:237-243.
[Google Scholar]
Li C., Lu X., Ding W., Feng L., Gao Y., Guo Z., . Formability of ABX₃ (X = F, Cl, Br, I) halide perovskites. Acta Cryst. B. 2008;64:702-707.
[Google Scholar]
Liu D., Peng H., Huang J., Sa R., . Revealing the stability and optoelectronic properties of novel nitride and phosphide semiconductors: A DFT prediction. Surf. Interfaces. 2022;29:101740.
[Google Scholar]
Liu Y., Wang W., Xiao F., Xiong L., Ming X., . Stability and optoelectronic property of lead-free halide double perovskite Cs₂B'BiI₆ (B' = Li, Na and K) Chin. Phys. B. 2021;30:108102.
[Google Scholar]
Mallmann M., Niklaus R., Rackl T., Benz M., Chau T.G., Johrendt D., Minár J., Schnick W., . Solid Solutions of Grimm-Sommerfeld Analogous Nitride Semiconductors II-IV-N₂ (II=Mg, Mn, Zn; IV=Si, Ge): Ammonothermal Synthesis and DFT Calculations. Chem. Eur. J.. 2019;25:15887-15895.
[Google Scholar]
Meng W., Wang X., Xiao Z., Wang J., Mitzi D.B., Yan Y., . Parity-Forbidden Transitions and Their Impact on the Optical Absorption Properties of Lead-Free Metal Halide Perovskites and Double Perovskites. J. Phys. Chem. Lett.. 2017;8:2999-3007.
[Google Scholar]
Mouhat F., Coudert F.-X., . Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B. 2014;90:224104.
[Google Scholar]
Murtaza G., Ahad Khan A., Yaseen M., Laref A., Ullah N., Ur Rahman I., . The effect of replacing pnictogen elements on the physical properties SrMg₂X₂ (X = N, P, As, Sb, Bi) Zintl compounds. Chin. Phys. B. 2018;27
[Google Scholar]
Murtaza G., Yousaf N., Laref A., Yaseen M., . Effect of Varying Pnictogen Elements (Pn = N, P, As, Sb, Bi) on the Optoelectronic Properties of SrZn₂Pn₂. Z. Naturforsch. A. 2018;73:285-293.
[Google Scholar]
Murtaza G., Yousaf N., Yaseen M., Laref A., Azam S., . Systematic studies of the structural and optoelectronic characteristics of CaZn₂X₂ (X = N, P, As, Sb, Bi) Mater. Res. Express. 2018;5:016304.
[Google Scholar]
Özdemir U., Korcak S., Gültekin A., Öztürk M.K., . Investigation of structural, electronic, elastic, optical and dynamical properties of Ga_1−xAl_xN alloys. Mater. Res. Express. 2019;6:096318.
[Google Scholar]
Perdew J.P., Burke K., Ernzerhof M., . Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.. 1996;77:3865-3868.
[Google Scholar]
Pugh S.F., . XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinburgh Dublin Philos. Magaz. J. Sci.. 1954;45:823-843.
[Google Scholar]
Tang Y., Zhang J., Zhong X., Wang Q., Zhang H., Ren C., Wang J., . Revealing the structural, electronic and optical properties of lead-free perovskite derivatives of Rb₂SnX₆(X = Cl, Br and I): A theory calculation. Sol. Energy. 2019;190:272-277.
[Google Scholar]
Togo A., Tanaka I., . First principles phonon calculations in materials science. Scr. Mater.. 2015;108:1-5.
[Google Scholar]
Tsuji M., Hanzawa K., Kinjo H., Hiramatsu H., Hosono H., . Heteroepitaxial Thin-Film Growth of a Ternary Nitride Semiconductor CaZn₂N₂. ACS Appl. Electron. Mater.. 2019;1:1433-1438.
[Google Scholar]
Tsuji M., Hiramatsu H., Hosono H., . Tunable Light Emission through the Range 1.8–3.2 eV and p-Type Conductivity at Room Temperature for Nitride Semiconductors, Ca(Mg_1–_xZn_x)₂N₂ (x = 0–1) Inorg. Chem.. 2019;58:12311-12316.
[Google Scholar]
Tsunoda N., Kumagai Y., Takahashi A., Oba F., . Electrically Benign Defect Behavior in Zinc Tin Nitride Revealed from First Principles. Phys. Rev. Appl.. 2018;10:011001.
[Google Scholar]
Ul Haq B., Ahmed R., Shaari A., El Haj Hassan F., Kanoun M.B., Goumri-Said S., . Study of wurtzite and zincblende GaN/InN based solar cells alloys: First-principles investigation within the improved modified Becke-Johnson potential. Sol. Energy. 2014;107:543-552.
[Google Scholar]
Wines D., Ersan F., Ataca C., . Engineering the Electronic, Thermoelectric, and Excitonic Properties of Two-Dimensional Group-III Nitrides through Alloying for Optoelectronic Devices (B_1–_xAl_xN, Al_1–_xGa_xN, and Ga_1–_xIn_xN) ACS Appl. Mater. Interfaces. 2020;12:46416-46428.
[Google Scholar]
Wu Z.-J., Zhao E.-J., Xiang H.-P., Hao X.-F., Liu X.-J., Meng J., . Crystal structures and elastic properties of superhard Ir₂ and IrN₃ from first principles. Phys. Rev. B. 2007;76:054115.
[Google Scholar]
Yamada N., Mizutani M., Matsuura K., Imura M., Murata H., Jia J., Kawamura F., . Band Gap-Tunable (Mg, Zn)SnN₂ Earth-Abundant Alloys with a Wurtzite Structure. ACS Appl. Electron. Mater.. 2021;3:4934-4942.
[Google Scholar]
Zhao Y.-Q., Hu C.-E., Liu L., Cheng Y., Cai L.-C., . First-Principles Investigations on Structural, Elastic, Dynamical, and Thermal Properties of Earth-Abundant Nitride Semiconductor CaZn₂N₂ under Pressure. Z. Naturforsch. A. 2017;72:39-49.
[Google Scholar]
Zhao X.-H., Wei X.-N., Tang T.-Y., Gao L.-K., Xie Q., Lu L.-M., Tang Y.-L., . First-principles study on the structural, electronic and optical properties of vacancy-ordered double perovskites Cs₂PtI₆ and Rb₂PtI₆. Opt. Mater.. 2021;114:110952.
[Google Scholar]

Introduction

Computational details

Results and discussion

Structural properties and stability
Mechanical properties
Electronic properties
Optical properties

Conclusions

CRediT authorship contribution statement

Fulltext Views
4

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Blöchl P.E., . Projector augmented-wave method. Phys. Rev. B. 1994;50:17953-17979.
[Google Scholar]

[2] Cao X., Kawamura F., Ninomiya Y., Taniguchi T., Yamada N., . Conduction-band effective mass and bandgap of ZnSnN₂ earth-abundant solar absorber. Sci. Rep.. 2017;7:14987.
[Google Scholar]

[3] Green M.A., . Intrinsic concentration, effective densities of states, and effective mass in silicon. J. Appl. Phys.. 1990;67:2944-2954.
[Google Scholar]

[4] Hadi M.A., Roknuzzaman M., Chroneos A., Naqib S.H., Islam A.K.M.A., Vovk R.V., Ostrikov K., . Elastic and thermodynamic properties of new (Zr_3-_xTi_x)AlC₂ MAX-phase solid solutions. Comput. Mater. Sci.. 2017;137:318-326.
[Google Scholar]

[5] Häusler J., Schimmel S., Wellmann P., Schnick W., . Ammonothermal Synthesis of Earth-Abundant Nitride Semiconductors ZnSiN₂ and ZnGeN₂ and Dissolution Monitoring by In Situ X-ray Imaging. Chem. Eur. J.. 2017;23:12275-12282.
[Google Scholar]

[6] Häusler J., Niklaus R., Minár J., Schnick W., . Ammonothermal Synthesis and Optical Properties of Ternary Nitride Semiconductors Mg-IV-N₂, Mn-IV-N₂ and Li-IV₂-N₃ (IV=Si, Ge) Chem. Eur. J.. 2018;24:1686-1693.
[Google Scholar]

[7] Heyd J., Scuseria G.E., Ernzerhof M., . Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys.. 2003;118:8207-8215.
[Google Scholar]

[8] Hill R., . The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A. 1952;65:349-354.
[Google Scholar]

[9] Hinuma Y., Hatakeyama T., Kumagai Y., Burton L.A., Sato H., Muraba Y., Iimura S., Hiramatsu H., Tanaka I., Hosono H., Oba F., . Discovery of earth-abundant nitride semiconductors by computational screening and high-pressure synthesis. Nat. Commun.. 2016;7:11962.
[Google Scholar]

[10] Huang M., Wang S., Zhang T., Chen S., . Searching for Band-Dispersive and Defect-Tolerant Semiconductors from Element Substitution in Topological Materials. J. Am. Chem. Soc.. 2022;144:4685-4694.
[Google Scholar]

[11] Khan A.A., Rehman A.U., Laref A., Yousaf M., Murtaza G., . Structural, Optoelectronic and Thermoelectric Properties of Ternary CaBe₂X₂ (X = N, P, As, Sb, Bi) Compounds. Z. Naturforsch. A. 2018;73:965-973.
[Google Scholar]

[12] Khan A.A., Yaseen M., Laref A., Murtaza G., . Impact of anion replacement on the optoelectronic and thermoelectric properties of CaMg₂X₂, X = (N, P, As, Sb, Bi) compounds. Phys. B Condens. Matter. 2018;541:24-31.
[Google Scholar]

[13] Khan A.A., Hasil R., Laref A., Ullah N., Sajjad M., Zeb A., Murtaza G., . DFT prediction of the structural, electronic, thermoelectric and optical properties of ternary pnictides MgBe₂X₂ (X = N, P, As, Sb, Bi): A novel analysis of beryllium with 2A- and 5B-Elements of the structure type CaAl₂Si₂. Solid State Commun.. 2019;300:113667.
[Google Scholar]

[14] Khan I., Shahab I.U., Haq A., Ali Z., Ali I., . Ahmad, Elastic and Optoelectronic Properties of Cs₂NaMCl₆ (M = In, Tl, Sb, Bi) J. Electron. Mater.. 2021;50:456-466.
[Google Scholar]

[15] Kikuchi R., Ueno K., Nakamura T., Kurabuchi T., Kaneko Y., Kumagai Y., Oba F., . SrZn₂N₂ as a Solar Absorber: Theoretical Defect Chemistry and Synthesis by Metal Alloy Nitridation. Chem. Mater.. 2021;33:2864-2870.
[Google Scholar]

[16] Kresse G., Furthmüller J., . Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci.. 1996;6:15-50.
[Google Scholar]

[17] Laidouci A., Aissat A., Vilcot J.P., . Numerical study of solar cells based on ZnSnN₂ structure. Sol. Energy. 2020;211:237-243.
[Google Scholar]

[18] Li C., Lu X., Ding W., Feng L., Gao Y., Guo Z., . Formability of ABX₃ (X = F, Cl, Br, I) halide perovskites. Acta Cryst. B. 2008;64:702-707.
[Google Scholar]

[19] Liu D., Peng H., Huang J., Sa R., . Revealing the stability and optoelectronic properties of novel nitride and phosphide semiconductors: A DFT prediction. Surf. Interfaces. 2022;29:101740.
[Google Scholar]

[20] Liu Y., Wang W., Xiao F., Xiong L., Ming X., . Stability and optoelectronic property of lead-free halide double perovskite Cs₂B'BiI₆ (B' = Li, Na and K) Chin. Phys. B. 2021;30:108102.
[Google Scholar]

[21] Mallmann M., Niklaus R., Rackl T., Benz M., Chau T.G., Johrendt D., Minár J., Schnick W., . Solid Solutions of Grimm-Sommerfeld Analogous Nitride Semiconductors II-IV-N₂ (II=Mg, Mn, Zn; IV=Si, Ge): Ammonothermal Synthesis and DFT Calculations. Chem. Eur. J.. 2019;25:15887-15895.
[Google Scholar]

[22] Meng W., Wang X., Xiao Z., Wang J., Mitzi D.B., Yan Y., . Parity-Forbidden Transitions and Their Impact on the Optical Absorption Properties of Lead-Free Metal Halide Perovskites and Double Perovskites. J. Phys. Chem. Lett.. 2017;8:2999-3007.
[Google Scholar]

[23] Mouhat F., Coudert F.-X., . Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B. 2014;90:224104.
[Google Scholar]

[24] Murtaza G., Ahad Khan A., Yaseen M., Laref A., Ullah N., Ur Rahman I., . The effect of replacing pnictogen elements on the physical properties SrMg₂X₂ (X = N, P, As, Sb, Bi) Zintl compounds. Chin. Phys. B. 2018;27
[Google Scholar]

[25] Murtaza G., Yousaf N., Laref A., Yaseen M., . Effect of Varying Pnictogen Elements (Pn = N, P, As, Sb, Bi) on the Optoelectronic Properties of SrZn₂Pn₂. Z. Naturforsch. A. 2018;73:285-293.
[Google Scholar]

[26] Murtaza G., Yousaf N., Yaseen M., Laref A., Azam S., . Systematic studies of the structural and optoelectronic characteristics of CaZn₂X₂ (X = N, P, As, Sb, Bi) Mater. Res. Express. 2018;5:016304.
[Google Scholar]

[27] Özdemir U., Korcak S., Gültekin A., Öztürk M.K., . Investigation of structural, electronic, elastic, optical and dynamical properties of Ga_1−xAl_xN alloys. Mater. Res. Express. 2019;6:096318.
[Google Scholar]

[28] Perdew J.P., Burke K., Ernzerhof M., . Generalized Gradient Approximation Made Simple. Phys. Rev. Lett.. 1996;77:3865-3868.
[Google Scholar]

[29] Pugh S.F., . XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinburgh Dublin Philos. Magaz. J. Sci.. 1954;45:823-843.
[Google Scholar]

[30] Tang Y., Zhang J., Zhong X., Wang Q., Zhang H., Ren C., Wang J., . Revealing the structural, electronic and optical properties of lead-free perovskite derivatives of Rb₂SnX₆(X = Cl, Br and I): A theory calculation. Sol. Energy. 2019;190:272-277.
[Google Scholar]

[31] Togo A., Tanaka I., . First principles phonon calculations in materials science. Scr. Mater.. 2015;108:1-5.
[Google Scholar]

[32] Tsuji M., Hanzawa K., Kinjo H., Hiramatsu H., Hosono H., . Heteroepitaxial Thin-Film Growth of a Ternary Nitride Semiconductor CaZn₂N₂. ACS Appl. Electron. Mater.. 2019;1:1433-1438.
[Google Scholar]

[33] Tsuji M., Hiramatsu H., Hosono H., . Tunable Light Emission through the Range 1.8–3.2 eV and p-Type Conductivity at Room Temperature for Nitride Semiconductors, Ca(Mg_1–_xZn_x)₂N₂ (x = 0–1) Inorg. Chem.. 2019;58:12311-12316.
[Google Scholar]

[34] Tsunoda N., Kumagai Y., Takahashi A., Oba F., . Electrically Benign Defect Behavior in Zinc Tin Nitride Revealed from First Principles. Phys. Rev. Appl.. 2018;10:011001.
[Google Scholar]

[35] Ul Haq B., Ahmed R., Shaari A., El Haj Hassan F., Kanoun M.B., Goumri-Said S., . Study of wurtzite and zincblende GaN/InN based solar cells alloys: First-principles investigation within the improved modified Becke-Johnson potential. Sol. Energy. 2014;107:543-552.
[Google Scholar]

[36] Wines D., Ersan F., Ataca C., . Engineering the Electronic, Thermoelectric, and Excitonic Properties of Two-Dimensional Group-III Nitrides through Alloying for Optoelectronic Devices (B_1–_xAl_xN, Al_1–_xGa_xN, and Ga_1–_xIn_xN) ACS Appl. Mater. Interfaces. 2020;12:46416-46428.
[Google Scholar]

[37] Wu Z.-J., Zhao E.-J., Xiang H.-P., Hao X.-F., Liu X.-J., Meng J., . Crystal structures and elastic properties of superhard Ir₂ and IrN₃ from first principles. Phys. Rev. B. 2007;76:054115.
[Google Scholar]

[38] Yamada N., Mizutani M., Matsuura K., Imura M., Murata H., Jia J., Kawamura F., . Band Gap-Tunable (Mg, Zn)SnN₂ Earth-Abundant Alloys with a Wurtzite Structure. ACS Appl. Electron. Mater.. 2021;3:4934-4942.
[Google Scholar]

[39] Zhao Y.-Q., Hu C.-E., Liu L., Cheng Y., Cai L.-C., . First-Principles Investigations on Structural, Elastic, Dynamical, and Thermal Properties of Earth-Abundant Nitride Semiconductor CaZn₂N₂ under Pressure. Z. Naturforsch. A. 2017;72:39-49.
[Google Scholar]

[40] Zhao X.-H., Wei X.-N., Tang T.-Y., Gao L.-K., Xie Q., Lu L.-M., Tang Y.-L., . First-principles study on the structural, electronic and optical properties of vacancy-ordered double perovskites Cs₂PtI₆ and Rb₂PtI₆. Opt. Mater.. 2021;114:110952.
[Google Scholar]

Theoretical study of the structure and fundamental properties of AZn2N2 (A = Ca, Sr, Ba)