Thermodynamic study for the (butyl, hexyl and octyl) acetoacetate under high pressure CO₂

1 Introduction

An environmentally friendly chemical industrial technology that consumes lesser energy and produces fewer toxic residues is highly sought after (Tsoka et al., 2004; Bolm et al., 1999). One promising approach to achieving this is the use of high-pressure processing in combination with supercritical fluids (SCFs). The use of SCFs in chemical industries has been increasing since the early 1980 s due to their sustainability and environmental friendliness (Khalil, 2019; Ramsey et al., 2009; Wagare et al., 2021; Knez et al., 2014). SCFs are becoming increasingly popular as green solvents because they are potentially more affordable, non-toxic, non-flammable, and sustainable than conventional organic solvents that are harmful to the environment (Manjare and Dhingra, 2019; Calvo-Flores et al., 2018). Supercritical fluid technology has a broad scope of applications, such as separation techniques, reaction mediums, synthesis of new materials, powder formation, processing of oils and fats, thin film deposition, and more (Braga et al., 2023; Preetam et al., 2023; Liu et al., 2022; Liang et al., 2023; Agregán et al., 2023; Senyay-Oncel et al., 2023; Tran and Park, 2021; López-Hortas et al., 2022; Li and Xu, 2019; Tsai and Wang, 2019). Butyl, hexyl, and octyl acetoacetates considered in present study are versatile compounds with industrial applications such as flavorings agents and fragrances (Braunschmid et al., 2021; PubChem, n.d.; butyl acetoacetate, n.d.). Hexyl and octyl acetoacetates are used as fuel lubricity additives (Anastopoulos et al., 2001). Hexyl acetoacetate is a chemical with potential uses in polymer formation and antibacterial applications. It can cross-link in polymers, react with other compounds, and exhibits antibacterial activity against E. coli and S. aureus (FH60066, 2023). It is used in the synthesis of various compounds, such as pharmaceuticals, fragrances, and food additives. Hexyl acetoacetates is also used as a solvent in the manufacture of paints, varnishes, and adhesives (Buy Hexyl acetoacetate, 2023). Octyl acetoacetate is a versatile chemical that can serve as a solvent in organic synthesis, a reactant for the synthesis of various compounds, and a reagent in laboratory experiments. Its applications extend to the synthesis of pharmaceuticals, food additives, and fragrances. Furthermore, it can be used as a starting material for polymer synthesis and in the study of the effects of different compounds on biochemical and physiological processes in organisms (Buy Octyl acetoacetate, 2023).

Supercritical fluids (SCFs) have the unique ability to solubilized a diverse array of chemicals, making them valuable solvents in various industrial processes. Among the different SCFs, supercritical carbon dioxide (sc-CO₂) is widely used and studied (Yang et al., 2022; Tabernero et al., 2022). Byun's group, has processed several polymers/monomers in sc-CO₂ and analyzed the resulting solubility data (Lee et al., 2023; Ghoderao et al., 2023; Ghoderao et al., 2023; Np Ghoderao et al., 2023). Additionally, another groups have provided experimental phase equilibrium data for various hydrocarbons and sc-CO₂ mixtures (Gao et al., 2021; Gao et al., 2020; Li et al., 2019). Moreover, sc-CO2 has several other applications such as materials processing and synthesis (Zhang et al., 2014), precision cleaning technique (Kohli et al., 2019), microelectronics processing (Giles et al., 1998), hydrotreating, extraction, biomass pretreatment, conversion of waste heat into power, and sterilization of medical equipment (Okolie et al., 2022). High-pressure sc-CO₂ has gained significant attention and importance in separation processes due to its unique properties and several advantages over traditional solvents. Here are some key points highlighting the importance of sc-CO₂ in separation processes and its advantages: 1) Tunable Properties: The density and solvation power of sc-CO₂ can be easily tuned by adjusting temperature and pressure, allowing it to be tailored for specific separation tasks. This tunability makes it versatile for a wide range of applications. 2) Environmentally Friendly: sc-CO₂ is considered an environmentally friendly solvent because it is non-toxic, non-flammable, and readily available. It does not contribute to environmental pollution, making it a sustainable choice compared to many traditional organic solvents (Dhamodharan et al., 2023). 3) Low Critical Temperature: Sc-CO₂ has a relatively low critical temperature and critical pressure, making it suitable for processing temperature-sensitive compounds that may degrade at higher temperatures (Girardi et al., 2023). 4) Reduced Energy Consumption: Operating near or above the critical point reduces the energy required for solvent recovery because sc-CO₂ can be easily depressurized and recycled. This can lead to cost savings and improved process efficiency. 5) Minimized Environmental Impact: By reducing the use of hazardous organic solvents, sc-CO₂ contributes to reducing the environmental footprint of separation processes, aligning with sustainability and regulatory goals. 6) Application Diversity: Sc-CO₂ finds applications in various industries, including pharmaceuticals, food and beverage, cosmetics, petrochemicals, and more. Its versatility and compatibility with different compounds make it a valuable tool for separation processes across different sectors (Balbinot Filho et al., 2023; Sodeifian et al., 2023).

This study has explored the phase behavior of binary mixtures of butyl acetoacetate, hexyl acetoacetate, and octyl acetoacetate with sc-CO₂ using high pressure apparatus. The experimental isotherms for all systems are presented in (P-x) space. For the butyl acetoacetate + sc-CO2 system, experimental isotherms (313.2 K ≤ T ≤ 393.2 K) were obtained in a pressure range of 3.04 MPa ≤ P ≤ 20.43 MPa, while the pressure and temperature range for hexyl acetoacetate + sc-CO₂ and octyl acetoacetate + sc-CO₂ systems were 2.69 MPa ≤ P ≤ 22.18 MPa and 2.39 MPa ≤ P ≤ 23.83 MPa. The critical mixture lines in (P-T) space confirm the type-I behavior exhibited by all binary mixes, meaning that a continuous critical line exists between the sc-CO₂ critical point and the critical point of the other component (butyl acetoacetate or hexyl acetoacetate or octyl acetoacetate) and no liquid–liquid critical line exists.

Another part of this work is to correlate the obtained experimental isotherms with theoretical models. The cubic equations of state are widely used tools to estimate vapor–liquid equilibria and thermodynamic properties (Ghoderao et al., 2018; Ghoderao et al., 2019; Ghoderao et al., 2019; Kristanto et al., 2023). The Peng-Robinson (P-R) equation is a simple cubic equation of state that is accepted and used extensively for various applications (Bhawangirkar et al., 2018; Anil et al., 2022; Avula et al., 2015, 2016, 2017; Joshi et al., 2012). In this study, we have employed the P-R equation utilizing the van der Waals (vdW) mixing rule to predict experimental isotherms. The properties of indiviual pure component such as molecular weight, critical properties, boiling temperature, and acentric factor of carbon dioxide, butyl acetoacetate, hexyl acetoacetate, and octyl acetoacetate are given in Table 1. The pure component properties such as critical temperature, critical pressure, and acentric factor are obtained by Joback–Lyderson group contribution method (Reid et al., 1987). The chemical structures of butyl acetoacetate, hexyl acetoacetate, and octyl acetoacetate are depicted in Fig. 1.

Close

Fig. 1

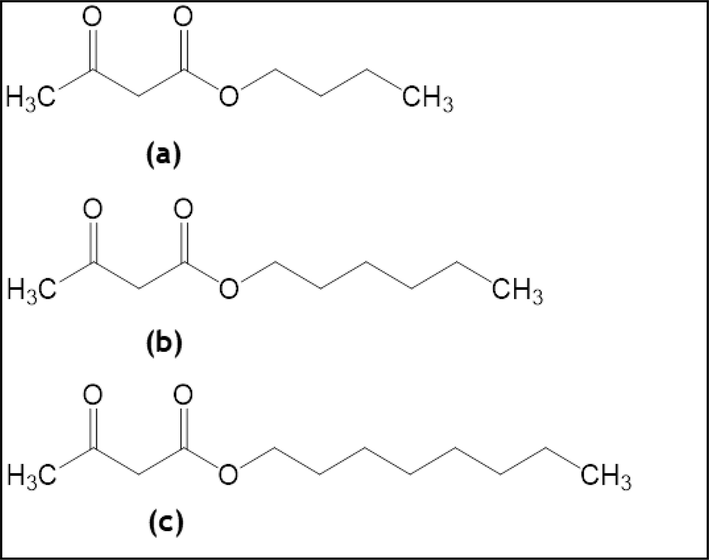
Chemical structure of (a) butyl acetoacetate (b) hexyl acetoacetate and (c) octyl acetoacetate.

Export to PPT

2 Experimental section

3 Experimental apparatus and procedure

High-pressure instruments were utilized to measure the phase behavior, as discussed in previous studies (Baek and Byun, 2016). The detailed information regarding the procedures used to obtain the solubility curves in the described experiment as follows:

Equipment: The equipment used for obtaining solubility curves in this study includes:

High-Pressure Equipment (Fig. 2): The primary instrument used to measure phase behavior under high-pressure conditions is detailed below: (1) Pump Generator: A pump generator, specifically Model 37–5.75–60 (HIP), is employed in the setup. This pump generator is responsible for generating high-pressure conditions within the system. (2) Piston and Heise Gauge: The pump generator is connected to a piston with a diameter of 2.54 cm. The pressure generated by the piston movement is recorded using a Heise gauge, Model CM-53920 (Dresser Ind), with a standard uncertainty of 0.03 MPa. (3) View Cell: A flexible volume view cell is a crucial component of the setup. It has specific characteristics, including a volume capacity of 28 cm³ (inside diameter − 1.59 cm; outside diameter − 6.4 cm). This view cell is designed to withstand pressures up to 70 MPa. (4) Transparent Glass Window: To enable the observation of mixture phase transitions, a transparent glass window is attached to the front portion of the view cell. This window has a thickness of 1.9 cm and a diameter of 1.9 cm. (5) Camera and Monitor: A video monitor is used in conjunction with a camera connected to an Olympus Corp borescope (Model - F100-038–000-50) positioned against the glass window to observe the mixture.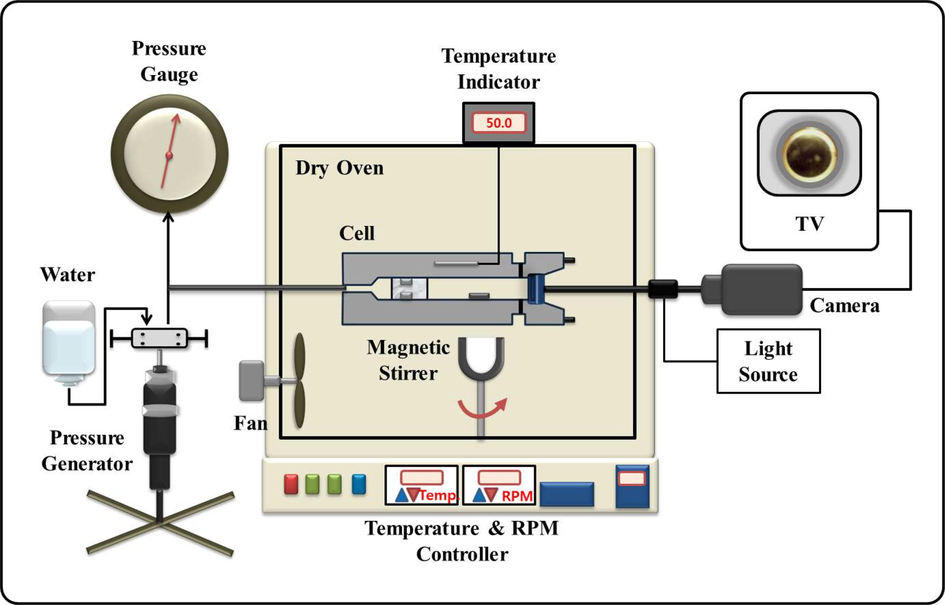

Close

Fig. 2

Schematic diagram of high-pressure apparatus.

Export to PPT

The procedure for obtaining solubility curves involves the following steps: (1) Initial Purging: To eliminate any residual air and organic materials, the view cell is initially purged with nitrogen (N₂) and sc-CO₂. Sc-CO₂ is introduced into the view cell using a pressure bomb with an uncertainty of 0.002 g. (2) Mixture Preparation: A specimen of the binary mixture is prepared and inserted into the view cell using a syringe with an uncertainty of 0.0002 g. The precise composition of this mixture is determined based on the experimental objectives. (3) Pressurization and Equilibration: The binary mixture in the view cell is pressurized and maintained at a constant phase for a duration of thirty minutes. This is achieved by regulating the piston to attain the desired pressure level and temperature, which are then held constant. After thirty minutes, it is assumed that phase equilibrium has been achieved inside the cell. (4) Solubility Measurement: The pressure is gradually decreased to observe different phases. The appearance of small bubbles or a fine mist inside the view cell with varying pressure is recorded as a bubble point (I) or dew point (III), respectively. The critical point (II) of the mixture is noted when opalescence is observed with equal gas and liquid volume. (5) Repetition: Each measurement is repeated at least three times to ensure accuracy and reproducibility.

4 Results and discussion

The article presents an investigation into the binary systems of sc-CO₂ with butyl acetoacetate, hexyl acetoacetate, and octyl acetoacetate. The study reports the isotherms in (P, x) space, where P denotes pressure and × signifies mole fraction. The standard uncertainties (σ) associated with the measurement of pressure, temperature, and mole fraction were found to be σ (P): 0.2 MPa, σ (T): 0.2 K, and σ (x): 0.0008, respectively. The experimental isotherms of the sc-CO₂ + butyl acetoacetate binary system were reported in Table 3 for the pressure range of 3.04 MPa to 20.43 MPa and temperature array of 313.2 K to 393.2 K. The phase equilibrium behaviour of the sc-CO₂ + hexyl acetoacetate solution was shown in Table 4 for the pressure range of 2.69 MPa to 22.18 MPa and temperature array of 313.2 K to 393.2 K. Similarly, the phase characteristics of the sc-CO₂ + octyl acetoacetate system were demonstrated in Table 5 for the pressure range of 2.39 MPa to 23.83 MPa and temperature range of 313.2 K to 393.2 K.

Fig. 3 (a-c) in this study compare experimental isotherms with computed isotherms using the P-R equation for the sc-CO₂ + butyl acetoacetate, sc-CO₂ + hexyl acetoacetate, and Sc-CO₂ + octyl acetoacetate mixtures at a temperature of 353.2 K. T = 353.2 K is an intermediate temperature in the range of temperatures measured. The experimental results indicate that a vapor–liquid equilibrium region is observed beneath each isotherm, while a single-phase region is reported above every isotherm. Furthermore, no three-phase region was detected at any of the five temperatures that were investigated. The fitted interaction two-parameters (ITPs) for the 353.2 K isotherm are shown as a red solid line, with k_ij and η_ij values of 0.015 and −0.055 for butyl acetoacetate + sc-CO₂ (using 14 data points), 0.020 and −0.040 for hexyl acetoacetate + sc-CO₂ (using 14 data points), and 0.050 and −0.025 for octyl acetoacetate + sc-CO₂ (using 14 data points). In contrast, the results with ITPs set to zero (k_ij = 0.0 and η_ij = 0.0) are shown as a solid blue line. The RMSD% (root mean square relative deviation percentage) was calculated at 353.2 K for each system, and the values were 3.24%, 2.09%, and 1.70% for butyl acetoacetate + sc-CO₂, hexyl acetoacetate + sc-CO₂, and octyl acetoacetate + sc-CO₂, respectively. The figures clearly show that the isotherms predicted with zero ITPs significantly deviate from the experimental values. Therefore, the other isotherms were calculated using non-zero ITPs. It is important to note that the ITPs calculated for the 353.2 K isotherms were used to calculate the other isotherms in present case.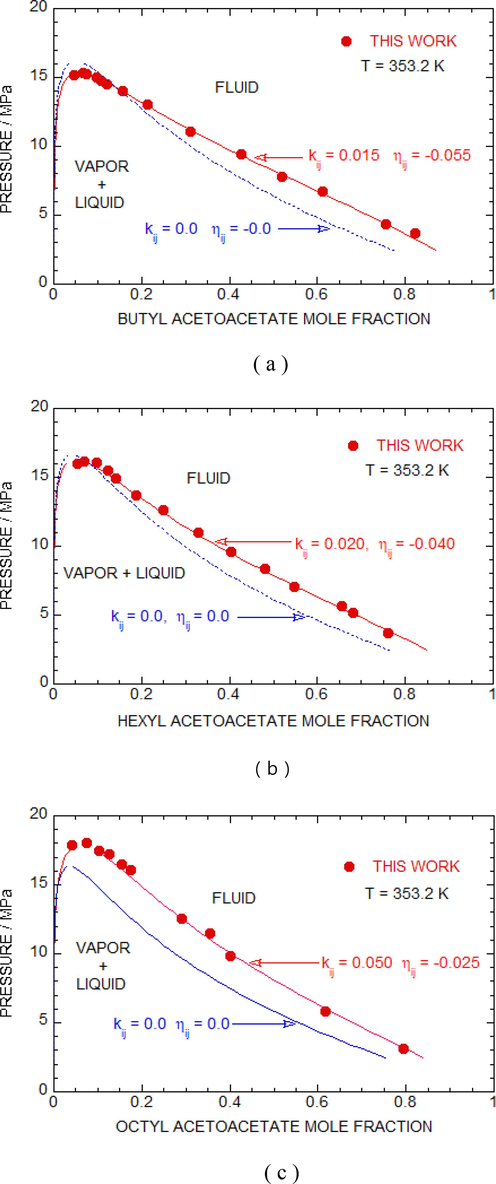

Close

Fig. 3

Pressure vs mole fraction plot (a) butyl acetoacetate + sc-CO₂ (b) hexyl acetoacetate + sc-CO₂ and (c) octyl acetoacetate + sc-CO₂ systems with calculations obtained from PR EOS at 353.2 K. Blue broken and red solid line represent results with zero and non-zero interaction parameters (k_ij and η_ij) respectively.

Export to PPT

The van der Waals mixing rules with ITPs are as given below:

The optimization of the objective function in equation (5) to obtain ITPs was carried out using the least square method in Python programming.

The ITPs obtained in studies of binary mixtures have significant physical significance and are related to the molecular interactions occurring within these mixtures. These parameters are often used to describe and understand the non-ideal behavior of binary systems, where the interactions between molecules are not simply additive. Here's the physical significance of these parameters and their relation to molecular interactions: (1) Deviation from Ideal Behavior: Binary interaction parameters, often denoted as binary interaction coefficients (e.g., k_ij or η_ij), quantify the deviation of a binary mixture from ideal behavior. Ideal behavior assumes that the mixture's properties can be calculated as weighted averages of the pure component properties. When the binary interaction parameter is zero (k_ij = 0), the mixture follows ideal behavior. Positive or negative values of kij indicate deviations from ideality. (2) Attractive and Repulsive Interactions: The sign of the binary interaction parameter indicates the nature of molecular interactions between the components. Positive k_ij: Indicates repulsive interactions between molecules. In such mixtures, the molecules tend to avoid each other, a positive deviation from Raoult's law. Negative k_ij: Suggests attractive interactions between molecules. In these mixtures, molecules tend to be more attracted to each other, which can lead to a negative deviation from Raoult's law.

Fig. 4 (a) presents evaluating agreement between the empirical measurements data and the predicted values using (P, x) data for the sc-CO₂ + butyl acetoacetate solution. To obtain solubility isotherms, the k_ij and η_ij values are optimized for each temperature spanned from 313.2 K to 393.2 K. The vapor + liquid equilibria data determined in this study was in good agreement and fitted well into the P-R equation for the sc-CO₂ + butyl acetoacetate mixture. The RMSD% (Table 6) of the sc-CO₂ + butyl acetoacetate solution was calculated for five different temperatures using the two parameters (k_ij, η_ij) obtained at each temperature.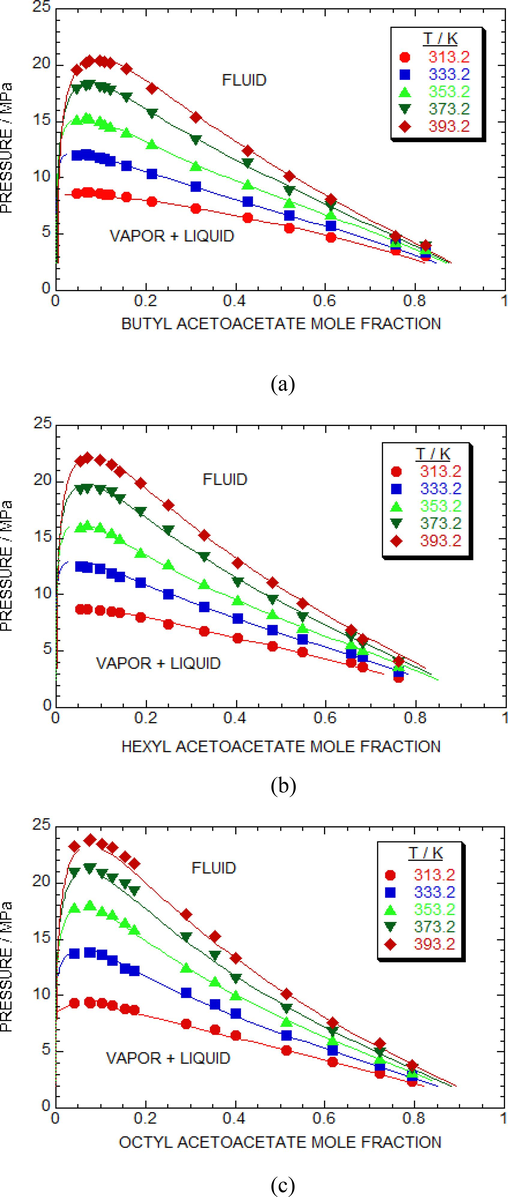

Close

Fig. 4

Experimental and predicted isotherms of (a) butyl acetoacetate + sc-CO₂ (b) hexyl acetoacetate + sc-CO₂ and (c) octyl acetoacetate + sc-CO₂ systems by optimum parameters (k_ij, η_ij) at each temperature. Symbols denotes experimental data points at various temperature. Solid lines are predicted isotherms using PR EOS.

Export to PPT

Fig. 4 (b) shows the experimental and calculated curves obtained from the P-R equation using the optimized two parameters obtained at each temperature for the sc-CO₂ + hexyl acetoacetate solution. In this study, we evaluated the RMSDs at five different temperatures varied between (313.2 K to 393.2 K, interval 20 K) for the sc-CO₂ + hexyl acetoacetate solution using the P-R equation with optimized two parameters (Table 6).

Fig. 4 (c) depicts a comparison between the equilibria data and the estimated results of the (P, x) isotherms at temperatures ranging from 313.2 K to 393.2 K for the sc-CO₂ + octyl acetoacetate system. The adjusted k_ij and η_ij values (Table 6) were obtained at each temperature, which were 0.058 and −0.028 for T = 313.2 K, 0.054 and −0.026 for T = 333.2 K, 0.050 and −0.025 for T = 353.2 K, 0.048 and −0.020 for T = 373.2 K, and 0.046 and −0.018 for T = 393.2 K.

In Fig. 5 (a-c), mixture critical curves of experimental data were compared with the predicted results from the P-R equation for the sc-CO₂ + butyl acetoacetate (a), sc-CO₂ + hexyl acetoacetate (b) and sc-CO₂ + octyl acetoacetate (c) solutions. The projected mixture-critical lines showed a type-I curve, as mentioned before. The red solid lines represented the saturated vapor pressure for individual pure sc-CO₂, butyl acetoacetate, hexyl acetoacetate, and octyl acetoacetate estimated by the Lee-Kesler method (Poling et al., 2001). The red closed circles represented the critical-point for pure sc-CO₂, butyl acetoacetate, hexyl acetoacetate and octyl acetoacetate. Region above the blue dashed curves is in the 1-phase, while below part is in the 2-phase. The dashed curve represented the calculated results determined by the P-R equation, with k_ij and η_ij values of 0.015 and −0.055 (for butyl acetoacetate), 0.020 and −0.040 (for hexyl acetoacetate), and 0.050 and −0.025 (for octyl acetoacetate). The blue closed squares represented the mixture-critical point obtained from the isotherms measured in the experiment.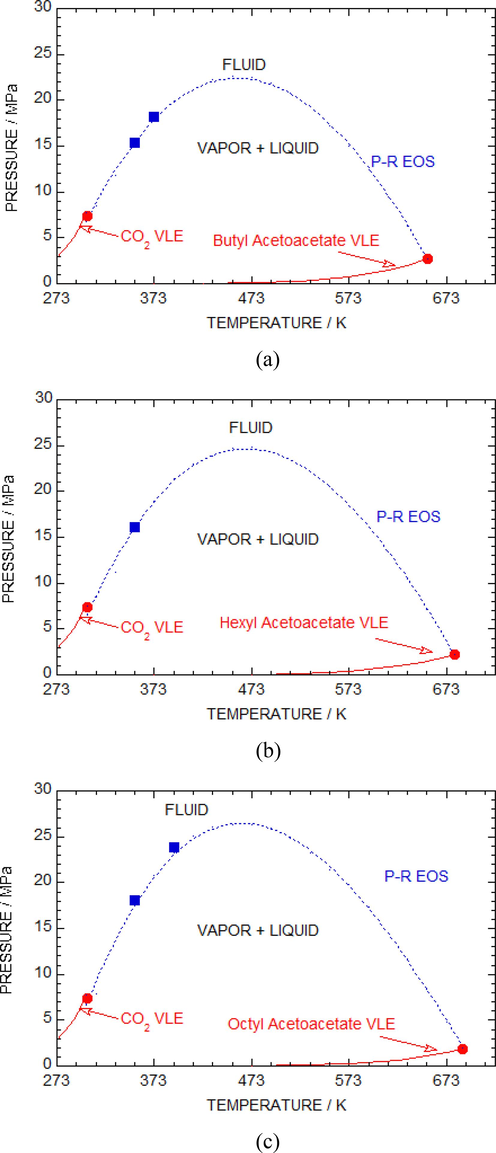

Close

Fig. 5

Diagram in (P vs T) space for the (a) butyl acetoacetate + sc-CO₂ (b) hexyl acetoacetate + sc-CO₂ and (c) octyl acetoacetate + sc-CO₂ systems. The critical-point of pure components (sc-CO₂ or butyl acetoacetate or hexyl acetoacetate or octyl acetoacetate) is represented by red closed circles. Red solid curves are vapor + liquid equilibrium curves. Squares denotes critical points of a mixture taken from experimental isotherms. Black and blue curves show calculations by P-R equation with zero and non-zero interaction parameters.

Export to PPT

5 Conclusion

The equilibrium data of the sc-CO₂ + butyl acetoacetate, sc-CO₂ + hexyl acetoacetate, and sc-CO₂ + octyl acetoacetate systems were obtained at pressures of P ≤ 23.83 MPa and temperatures extending from 313.2 K to 393.2 K. It was observed that the binary mixtures of sc-CO₂ + butyl acetoacetate, sc-CO₂ + hexyl acetoacetate, and sc-CO₂ + octyl acetoacetate exhibited type-I curves and did not display a three-phase region.

To model the experimental equilibria data from the sc-CO₂ + butyl acetoacetate, sc-CO2 + hexyl acetoacetate, and sc-CO₂ + octyl acetoacetate solutions, the P-R equation was used with adjustable temperature dependent two-parameters, k_ij and η_ij. The overall RMSD% values for the sc-CO₂ + butyl acetoacetate, sc-CO₂ + hexyl acetoacetate, and sc-CO₂ + octyl acetoacetate solutions were found to be 4.15 %, 2.7 %, and 2.42 %, respectively. These findings suggest that the P-R equation with adjustable two-parameters (k_ij and η_ij) can effectively model the equilibrium data of the sc-CO₂ + butyl acetoacetate, sc-CO₂ + hexyl acetoacetate, and sc-CO₂ + octyl acetoacetate systems.

The experimental findings and successful application of the Peng-Robinson equation with adjustable parameters (k_ij and η_ij) to model equilibrium data for sc-CO₂ with various acetoacetate compounds have significant practical implications for process design and optimization in separation processes. This research provides valuable insights into the phase behavior of these systems, aiding in the development of selective extraction processes, optimizing temperature and pressure conditions, and potentially reducing the environmental impact through the use of environmentally friendly sc-CO₂ as a solvent. Additionally, the modeling approach's success suggests its applicability to industrial-scale processes, promising more efficient and sustainable separation techniques across industries.

CRediT authorship contribution statement

Hun-Soo Byun: Conceptualization, Validation, Visualization, Supervision, Project administration, Funding acquisition, Writing – original draft. Pradnya NP Ghoderao: Conceptualization, Methodology, Formal analysis, Data curation, Software, Investigation. Hyun-Seok Lee: Methodology, Data curation, Investigation. Min-Soo Park: Methodology, Data curation, Investigation.