Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel

Sohail Rehman; Hashim; Sultan Alqahtani; Siwar Ben Hadj Hassine; Sayed M. Eldin

doi:10.1016/j.arabjc.2022.104475

Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel

Sohail Rehman^{^a,⁎}, Hashim^{^b}, Sultan Alqahtani^{^c}, Siwar Ben Hadj Hassine^{^d}, Sayed M. Eldin^{^e}

a Department Mechanical Engineering, School of Material Sciences and Engineering, Georgia Institute of Technology, Atlanta, GA, 30318 USA

b Department of Mathematics & Statistics, The University of Haripur, Haripur 22620, Pakistan

c Mechanical Engineering Department, College of Engineering, King Khalid University, Abha, Saudi Arabia

d Department of Computer Science, College of Science and Arts at Muhayel, King Khalid University, Saudi Arabia

e Center of Research , Faculty of Engineering, Future University in Egypt, New Cairo 11835, Egypt

⁎Corresponding author. srehman34@gatech.edu (Sohail Rehman)

Received: 2022-8-9, Accepted: 2022-11-26,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Entropy production occurs in all thermohydraulic systems, which results in performance degradation. Entropy production promotes irreversibility in complicated systems, which are commonly found in industrial mechanisms. As a response, this technology is successfully applied in several technological applications involving porous media, propulsion ducts, electronic cooling, turbomachinery, and combustion. In the current computational study, energy transfer and entropy development resulting from pressure-driven flow of a non-Newtonian fluid inside a wedge-shaped expanding channel is evaluated. The direct characterization of the inefficiency mechanisms that cannot be accomplished by the conventional energy analysis. Entropy generation analysis, which precisely quantifies the irreversibility resulting from heat transfer, mass transfer, and viscous heat loss of the Jaffrey-Hamel flow of power-law fluid. The conservation equations are used to develop the governing flow equations for the non-Newtonian Carreau fluid model. For the sake of the current investigation, the equation for entropy generation is modelled using the second law of thermodynamics. The appropriate transformations are implemented in order to convert the governing PDEs into a collection of coupled ODEs. To solve the generated extremely non-linear ODEs, the shooting approach and the fourth, fifth order Runge-Kutta method have been used. The acquired numerical statistics indicate that, while the thermal radiation parameter tends to increase the rate of heat transfer, the Eckert number decreases as it rises. For higher estimation of Weissenberg numbers and power law, the entropy number drops in a divergent channel, but a contrary tendency is revealed for Bejan profile. A growth in the power-law index leads to a significant reduction in several irreversibility. Moreover, entropy generation is lower within divergent channel in comparison to the convergent section. Heat and mass transport are substantially reduced as the power-law index rises.

Keywords

Irreversibility analysis

Wedge-shaped channel

Two-phase model

Power-law fluid

Nanofluid

Bejan profile

Show Related Articles from PubMed

Nomenclature

$(r, θ, z)$: Cylindrical coordinates
$V$: Fluid velocity ( $m s^{- 1}$ )
$α$: Channel apex angle
$V_{\max}$: Fluid maximum velocity ( $m s^{- 1}$ )
$ν_{f}$: Kinematic viscosity ( $m^{2} s^{- 1}$ )
$ρ_{f}$: Fluid’s density ( $kg m^{- 3}$ )
$ρ_{p}$: Nanoparticles density ( $kg m^{- 3}$ )
${(ρ c_{p})}_{f}$: Fluid heat capacity
$c_{p}$: Specific heat ( $j {kg}^{- 1} K^{- 1}$ )
$(T, T_{w})$: Fluid and wall temperature (K)
$(C, C_{w})$: Fluid and wall concentration ( $kg m^{- 3}$ )
$T_{0}$: Reference temperature ( $K$ )
$C_{0}$: Reference concentration ( $kg m^{- 3}$ )
$η (\dot{Y})$: Generalized viscosity $(k g m^{- 1} s^{- 1})$
$\dot{Y}$: Shear rate
$(η_{0}, η_{\infty})$: Zero and infinite shear-rate viscosity
$λ$: Material parameter of Carreau fluid
$n$: Power-law index of Carreau fluid
$τ_{ij}$: Cauchy stress tensor
$p$: Fluid pressure (Pa)
$\nabla p$: Pressure gradient
$τ_{rr}, τ_{r θ}, τ_{θ θ}$: Stress tensor components
$D_{t}$: Thermophoresis diffusion coefficient
$D_{b}$: Brownian diffusion coefficient
$k_{f}$: Thermal conductivity $(W m^{- 1} K^{- 1})$
$k^{*}$: Mean absorption coefficient $(m^{2} {kg}^{- 1})$
$σ^{*}$: Stephan-Boltzmann constant $(W K^{- 4} m^{- 2})$
$η$: Dimensionless angle
$f (η)$: Dimensionless velocity
$Θ (η)$: Dimensionless temperature
$χ (η)$: Dimensionless concentration
$Nt$: Thermophoresis parameter
$\Pr$: Prandtl number
$Re$: Reynold number
$We$: Weissenberg number
$R$: Radiation parameter
$Nb$: Brownian diffusion parameter
$C_{f}$: Skin-friction coefficient
$Nu$: Nusselt number
$Sh$: Sherwood number
$N^{″'}$: Entropy generation rate $(W / m^{3} K)$
$Be$: Dimensionless Bejan number

1 Introduction

Jeffery-Hamel flows have a variety of uses in contemporary physical phenomena, including river and canal exploration, fluid mechanics, aerodynamics, civil, biomechanical, mechanical, and chemical engineering. The flow through rivers, canals, and other biological flows, such as the flow within arteries and venous blood vessels, are the best examples of practical applications for these types of flows. Over the past four decades, non-Newtonian fluid dynamic interactions within surfaces (such as planes, channels, tubes, and wedges) and various kinds of fluid have been studied. (Jeffery, 1915) and (Hamel, 1917) initiated the study of such flows above a century ago by reducing the Naiver–Stokes equations. They inspected heat transference of viscous Newtonian flow in a channel within non-parallel walls, which has subsequently known as Jeffery–Hamel flow. (W, 1931), and (R, 1934) focused on this flow problem following the preliminary analysis of Jeffery and Hamel. A comprehensive set of mathematical solution for this problem was subsequently provided by (Rosenhead and Taylor, 1940). (Fraenkel and Squire, 1962) elaborated on this and established a solution for the 2D Navier-Stokes equations for flow in a channel, their findings revealed that the creation of a boundary layer and a zone of flow reversal. After that, (Mansutti and Ramgopal, 1991) performed numerical analysis to investigate the convergent and divergent flow of a power-law fluid and discovered a solution that allowed boundary layers to exist even in the non-inertial flow between divergent planes. (Nagler, 2017) extend the J-H flow to non-Newtonian fluid considering non-linear viscosity and friction at the channel wall. The analysis of (Mansutti and Ramgopal, 1991) was expanded by (Harley et al., 2018) to include a power-law fluid whose rest viscosity is neither zero nor infinite for any finite value of the power-law exponent. They noted boundary layers for the non-Newtonian fluid even in divergent flow and at approximately zero Reynolds number ( $Re$ ). For greater wedge angles, they also discovered zones where the flow reversed. The literature covering J-H flow problems of non-Newtonian fluid considering several physical phenomena (Garimella et al., 2022), (Asghar et al., 2022), and (Kamran and Azhar, 2022). The Naiver-Stokes equations with entropy production in the Jaffrey-Hamel flow exhibit similarity solutions provided by (Weigand and Birkefeld, 2009). (Makinde and Bég, 2010) considered the inherently irreversible nature of viscous fluid within a non-uniform (convergent/divergent) channel. The essential irreversibility in an intersecting (convergent/divergent) channel was scrutinized by. (Shukla et al., 2020) inspected the hybrid nanofluid in a Jaffrey-Hamel flow with slip mechanism.

Substantial technological developments in electronics and micro devices industries introduce promising elucidations for thermal sink challenges. In the designing process of thermal devices, energy effectiveness is a key concern. This concern can be suitably tackled by the reduction of the entropy generation phenomenon. Energy changes is a natural phenomenon besides an external source is applied. No authentic variation for entropy has ascended if such mechanism is related to the investigation of second law under an irreversible process. This heatline phenomenon is very familiar amongst the recent scientist and researchers due to its potential consequences in heat transport processes. As a result, entropy generation minimization is now extensively monitored throughout in engineering and the manufacturing sectors, for instance, in nuclear power plants, thermal reactors, and petroleum and geothermal reservoirs. The irreversibility of an remote system that experiences fluid friction, thermal and solute transport, molecular vibration, thermal radiation, the Joule Thompson effect, and other non-ideal processes can be estimated via entropy optimization. It is common knowledge that reducing entropy rate is important to increase efficiency of an isolated closed system, especially in power plants, heat exchangers, fuel cells, geothermal energy systems, engineering phenomena, thermal storage, and advanced nanotechnology. (Bejan, 1979), (Bejan and Kestin, 1983) came up with innovative work exploring entropy generation concept. The second law was implemented to the problem of thermal transmission in metallic porous channels was addressed by (Turkyilmazoglu, 2020). (Nayak et al., 2021) reported on the entropy production in electromagnetic nanofluid flow under cubic auto-catalysis reaction. Some important studies about this topic are highlighted in Refs. (Hayat et al., 2017), (Das et al., 2018b), (Das et al., 2018a), (Chu et al., 2020), (Das et al., 2020), (Sarkar et al., 2020), (Shehzad et al., 2021), (Madhu et al., 2021), (Mahanthesh et al., 2021), (Madhu et al., 2022), (Ali et al., 2022), (Xu et al., 2022),.

It is an established fact that the complicated interaction between shear and strain rates prevents Navier Stokes equations from accurately describing the properties of non-Newtonian liquids. Experimental measurements show that non-Newtonian fluids respond differently to the application of shear stress in terms of strain rate. Non-Newtonian liquids are divided into shear thinning and thickening liquids based on this relationship. The importance of non-Newtonian fluids in several engineering, technological, and everyday life activities has increased because of these classifications. A variety of fluid models are offered to better illustrate the physical interpretation of these fluids. These models include the flow characteristics of shear thinning and thickening liquids including Carreau fluid. Carreau model has a wide range of application in the production of polymers, capillary electrophoresis, crystal development, mud drilling, the manufacture of gels and shampoos, powder technology, and biological applications. To understand the rheological behavior of shear thinning fluids, numerous mathematical models have been used in literature. (Ostwald, 1929) model was the first to show the straightforward relationship between shear stress and shear rate. Even so, this version eventually turned to serve as the basis for a variety of viscometers and rheometers that collect rheological data on a variety of fluids that are shear thinning. Technically speaking, the so-called “power law” model is not able to forecast how shear-thinning fluids will behave at extremes of shear rate. Later on, (Cross, 1965) proposed another mathematical formula to assess the rheological behavior of fluids that were shear thinning. When it comes to estimating rheological properties at low and high shear rate values, this model and power-law model are better enough. (Carreau, 1972) offered a concept on the fundamental molecular makeup of a fluid that was shear-thinning. The five factors in this model are used to forecast viscosity behavior. The generalized model is identified as: $\frac{η - η_{\infty}}{η_{0} - η_{\infty}} = {[1 + {(λ |\dot{Y}|)}^{a}]}^{\frac{n - 1}{2}}$ , where $η_{0}$ , $η_{\infty}$ , $λ$ , $n$ , $a$ , and $\dot{Y}$ elucidate zero shear, infinite shear rate viscosity, material time scale constant, power indexed, curvature parameter, the shear rate. In more practical scenario the $η_{0} ≫ η_{\infty}$ , and $λ |\dot{Y}| < 1$ . The Carreau fluid model as referred to shear thickening and shear thinning for $n > 1$ , and $0 < n < 1$ , respectively. Here $n$ the index of Carreau fluid and it contains the values in between [0,1]. Few significant numerical studies considering Carreau model in a recent time are conducted by numerous researchers (Bilal and Shah, 2022), (Ibrahim, 2022), (Rehman et al., 2022), (Hassan et al., 2022).

This investigation work reports the consequences of irreversibility mechanism with second law utilization in Carreau non-Newtonian fluid flow generated within an inclined channel. The innovation of this research is studying the heat transfer, mass transfer, and viscous heating irreversibility of the wedge configuration. The fluid flows in channel have abundant effects in distinctive features like refrigeration, automotive, heat exchangers and aerospace industries. Energy transport mechanism is elucidated by the implications of radiative heat flux and viscous heating phenomenon. System irreversibility are precisely quantified in this work using an entropy generation analysis based on a new multi-scale coupled model. The coupled model includes a two-dimensional (2-D) power-law model, a two-dimensional (2-D) thermal model, and a local entropy generation rate model that account for a comprehensive solution of the flow, mass concentration, heat transfer, and entropy generation rate equations. Entropy creation mechanisms linked to heat transfer, mass transfer, and frictional entropy generation. The study's originality and worth may be determined by the fact that it provides novel and previously unreported treatments of the Carreau nanofluids in intersecting plate with plane walls assuming purely radial flow. The fourth-order R-K technique is used with the shooting strategy to provide the numerical simulation of transformed leading equations. Graphical illustrations are provided of the effects of encoded parameters on the velocity, temperature, nanoparticle concentration, and system irreversibility profiles for the flow models. The outcomes of physically fascinating quantities are explained using the various physical constraint values. According to physical background and characteristics, these outcomes are explored in detail. The study will be helpful and novel for industries and academic institutions researching entropy minimization in channel flows.

2 Modelling framework

2.1

2.1 Problem statement and underlying assumptions

This section addresses a mathematical treatment of the physical problem. The laminar, incompressible flow of non-Newtonian fluid from a source or sink located at the channel apex as displayed in Fig. 1.

The flow is assumed in cylindrical coordinates $(r, φ, z)$ , where $r$ is measured from the wedge's axis, $φ$ from appropriate meridian plane, and $z$ is along the wedge's axis.
Assume that only radial motion affects the flow parameter.
Assuming that the two rigid, non-parallel plane walls are taken at an angle of $2 α$ .
The flow of a non-Newtonian fluid inside a converging divergent wedge originates from a source and driven by a constant pressure gradient.
It is assumed that $T_{w}$ and $C_{w}$ respectively the wall temperature and concentration and $T$ and $C$ are the fluid temperature and concentration.
The walls of the channel are isothermal i.e., no heat exchange occur between fluid and the channel walls.
The conservation of energy equation is constructed using traditional Fourier-law coupled with Buongiorno model and viscous heat mechanism.
The entropy generations equation is derived in term of velocity, heat energy and dissipations.

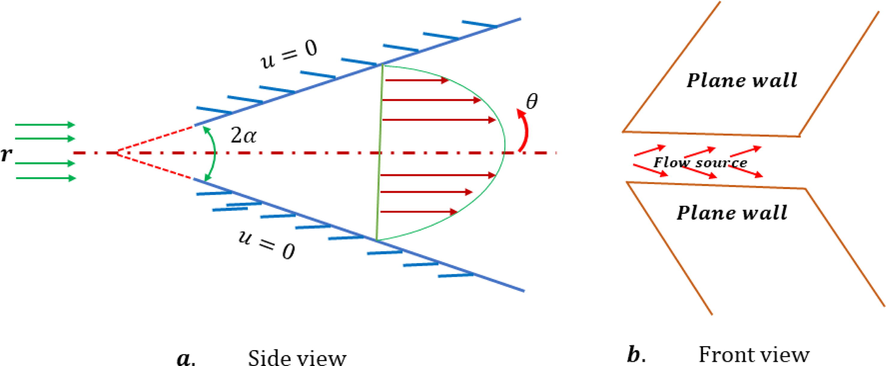
Power-law wedge shape flow model and coordinate system.

In radial coordinates the 2-D the field of velocity, temperature, concentration, and Cauchy stress tensor between intersecting rough plates for Carreau fluid are settled as.

(1)

τ = τ (r, φ), V = V (r, φ), T = T (r, φ), C = C (r, φ) .

2.2

2.2 Mathematical analysis

The conservation of mass, momentum equation for non-Newtonian fluid is written as:

(2)

\nabla ∙ V = 0 .

(3)

ρ_{f} (\frac{DV}{Dt}) = \nabla ∙ τ - \nabla p .

Where $\frac{D}{Dt} (*) = \frac{\partial}{\partial t} (*) + (V ∙ \nabla) (*)$ , is the material time derivative. On the right-hand side of the equation, the first term is the standard Eulerian derivative (i.e., the derivative on a fixed reference frame), and the second term denotes the modifications brought on by the flowing fluid. Advection is the term for this effect. $- \nabla p$ is the pressure gradient, $ρ_{f}$ is the fluid density. For Carreau fluid, we take $a = 2$ and $η_{\infty} = 0$ (practical situation) and the model become:

(4)

η = η_{0} {[1 + {(λ |\dot{Y}|)}^{2}]}^{\frac{n - 1}{2}} .

The shear stress tensor $τ$ is defined as

(5)

τ_{ij} = η {\dot{Y}}_{ij},

where $η$ is the generalized viscosity of the Carreau fluid and ${\dot{Y}}_{ij}$ is the shear strain rate. After invoking Eq. (1), the shear strain rate can be described as follows

(6)

\dot{Y} = \sqrt{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}} .

The stresses components in view of Eq. (2), (5) and (7), we have

(7)

(\begin{matrix} τ_{rr} & τ_{r θ} & 0 \\ τ_{θ r} & τ_{θ θ} & 0 \\ 0 & 0 & 0 \end{matrix}) = (\begin{matrix} η_{0} {[1 + {(λ |\dot{Y}|)}^{2}]}^{\frac{n - 1}{2}} (2 \frac{\partial V}{\partial r}) & η_{0} {[1 + {(λ |\dot{Y}|)}^{2}]}^{\frac{n - 1}{2}} (\frac{1}{r} \frac{\partial V}{\partial θ}) & 0 \\ η_{0} {[1 + {(λ |\dot{Y}|)}^{2}]}^{\frac{n - 1}{2}} (\frac{1}{r} \frac{\partial V}{\partial θ}) & η_{0} {[1 + {(λ |\dot{Y}|)}^{2}]}^{\frac{n - 1}{2}} (\frac{2 V}{r}) & 0 \\ 0 & 0 & 0 \end{matrix}) .

The continuity and Navier-Stokes equations in component form are summarized as follows for the two-dimensional flow (Ahmad et al., 2021), (Garimella et al., 2022), (Ramesh et al., 2022)

(8)

\frac{\partial}{\partial r} (r V) = 0,

(9)

ρ_{f} (V \frac{\partial V}{\partial r}) = - \frac{\partial p}{\partial r} + \frac{1}{r} \frac{\partial}{\partial r} (τ_{rr}) + \frac{1}{r} \frac{\partial}{\partial θ} (τ_{r θ}) + \frac{τ_{rr} - τ_{θ θ}}{r},

(10)

0 = - \frac{1}{ρ_{f} r} \frac{\partial p}{\partial θ} + \frac{1}{ρ_{f} r^{2}} \frac{\partial}{\partial r} (τ_{r θ}) + \frac{2}{ρ_{f} r} τ_{r θ} + \frac{1}{ρ_{f} r} \frac{\partial}{\partial θ} (τ_{θ θ}) .

Applying Eq. (5), into Eqs. (7), and (8), we have

(11)

V \frac{\partial V}{\partial r} = - \frac{1}{ρ_{f}} \frac{\partial p}{\partial r} + v_{f} [\frac{\partial^{2} V}{\partial r^{2}} + \frac{1}{r} \frac{\partial V}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V}{\partial θ^{2}} - \frac{V}{r^{2}}] {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 1}{2}} {+ v_{f} λ}^{2} (n - 1) {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 3}{2}} [4 {(\frac{\partial V}{\partial r})}^{2} \frac{\partial^{2} V}{\partial r^{2}} + \frac{6}{r^{2}} (\frac{\partial V}{\partial r}) (\frac{\partial V}{\partial θ}) (\frac{\partial^{2} V}{\partial r \partial θ}) - \frac{2}{r^{2}} (\frac{\partial V}{\partial r}) {(\frac{\partial V}{\partial θ})}^{2} + \frac{4 V}{r^{2}} {(\frac{\partial V}{\partial r})}^{2} - \frac{4 V^{2}}{r^{3}} \frac{\partial V}{\partial r} + \frac{2}{r^{4}} {(\frac{\partial V}{\partial θ})}^{2} \frac{\partial^{2} V}{\partial θ^{2}} + \frac{4 V}{r^{4}} {(\frac{\partial V}{\partial θ})}^{2}],

(12)

0 = - \frac{1}{ρ_{f} r} \frac{\partial p}{\partial θ} + \frac{2 v_{f}}{r^{2}} {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 1}{2}} \frac{\partial V}{\partial θ} + {v_{f} λ}^{2} {\frac{(n - 1)}{2 r} [1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 3}{2}} [4 (\frac{\partial V}{\partial r}) (\frac{\partial V}{\partial θ}) (\frac{\partial^{2} V}{\partial r^{2}}) + \frac{2}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} (\frac{\partial^{2} V}{\partial r \partial θ}) - \frac{2}{r^{3}} {(\frac{\partial V}{\partial θ})}^{3} + \frac{4 V}{r^{2}} (\frac{\partial V}{\partial θ}) (\frac{\partial V}{\partial r}) - \frac{4 V}{r^{3}} (\frac{\partial V}{\partial θ}) + 8 V (\frac{\partial V}{\partial r}) (\frac{\partial^{2} V}{\partial r \partial θ}) + \frac{4 V}{r^{2}} (\frac{\partial V}{\partial θ}) (\frac{\partial^{2} V}{\partial θ^{2}}) + \frac{8 V^{2}}{r^{2}} \frac{\partial V}{\partial θ}]

2.3

2.3 Thermal analysis

The heat transfer equation for the current problem while taking the combined contributions of the viscous dissipation, thermal radiation effect, and Buongiorno's model (Owhaib and Al-Kouz, 2022), (Chu et al., 2021)

(13)

{(ρ c_{p})}_{f} (V ∙ \nabla T) = \nabla ∙ (k_{f} \nabla T) - \nabla ∙ q_{r} + {(ρ c_{p})}_{s} [D_{b} (\nabla C ∙ \nabla T) + \frac{D_{t}}{T_{0}} (\nabla {T)}^{2}] + τ_{ij} : \nabla V .

In above Eq. (13), $τ_{ij} : \nabla V$ is the viscous dissipation expression, the Rosseland approximation for non-linear radiation, the radiative heat flux $q_{r}$ is simplified as (Shashikumar et al., 2020), (Bhaskar et al., 2022), (Veera Krishna, 2020)

(14)

q_{r} = \{\begin{matrix} q_{r, r a d} = - \frac{4 σ^{*} T^{4}}{3 k^{*}} \frac{\partial T}{\partial r} \\ q_{θ, r a d} = - \frac{4 σ^{*} T^{4}}{3 k^{*}} \frac{\partial T}{\partial θ} \end{matrix}\} .

By invoking Eq. (14) in Eq. (13), the energy conservation equation reduces to (Krishna et al., 2019), (Krishna et al., 2020), (Krishna et al., 2018)

(15)

V \frac{\partial T}{\partial r} = [1 + \frac{16 σ^{*} T_{0}^{3}}{3 k^{*} {(ρ c_{p})}_{f}}] [\frac{1}{r} \frac{\partial T}{\partial r} + \frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} T}{\partial θ^{2}}] + \frac{{(ρ c_{p})}_{s}}{{(ρ c_{p})}_{f}} (D_{b} [\frac{\partial T}{\partial r} \frac{\partial C}{\partial r} + \frac{1}{r^{2}} \frac{\partial T}{\partial θ} \frac{\partial C}{\partial θ}] + \frac{D_{t}}{T_{w}} [{(\frac{\partial T}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial T}{\partial θ})}^{2}]) + \frac{η_{0}}{{(ρ c_{p})}_{f}} {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 1}{2}} [1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}] .

2.4

2.4 Mass concentration equation

The nanoparticles concentration via Buongiorno model is written as:

(16)

V \frac{\partial C}{\partial r} = D_{b} (\frac{1}{r} \frac{\partial C}{\partial r} + \frac{\partial^{2} C}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} C}{\partial θ^{2}}) + \frac{D_{t}}{T_{0}} (\frac{1}{r} \frac{\partial T}{\partial r} + \frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} T}{\partial θ^{2}}) .

2.5

2.5 Boundary conditions

The governing boundary conditions for the flow model are (Khan et al., 2015), (Saif and Jasim, 2019):

At the center of channel:

(17)

V = V_{\max}, \frac{\partial V}{\partial θ} = 0, \frac{\partial T}{\partial θ} = 0, \frac{\partial C}{\partial θ} = 0 .

At the channel walls:

(18)

V = 0, T = T_{w}, C = C_{w} .

2.6

2.6 Normalization mechanism

Introducing similarity variables to normalize the governing equations (Khan et al., 2015), (Al-Saif and Jasim, 2019), (Bhaskar et al., 2022)

(19)

η = \frac{θ}{α}, V (r, θ) = \frac{G (θ)}{r} f (η) = \frac{G (θ)}{f_{\max}}, f_{\max} = r V_{\max}, Θ = \frac{T}{T_{w}}, χ = \frac{C}{C_{w}} .

The converted system of governing ODEs become:

(20)

[\frac{d^{3} f}{d η^{3}} + 4 α^{2} \frac{df}{d η}] {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 1)}{2}} + 2 α R e f \frac{df}{d η} + (n - 1) {We}^{2} {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 3)}{2}} (3 \frac{df}{d η} {(\frac{d^{2} f}{d η^{2}})}^{2} + 32 α^{2} f \frac{df}{d η} \frac{d^{2} f}{d η^{2}} + {(\frac{df}{d η})}^{2} \frac{d^{3} f}{d η^{3}} + 64 α^{4} \frac{df}{d η} f^{2}) + (n - 1) (n - 3) {({We}^{2})}^{2} {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 5)}{2}} ({(\frac{df}{d η})}^{3} {(\frac{d^{2} f}{d η^{2}})}^{2} + 16 α^{2} f {(\frac{d^{2} f}{d η^{2}})}^{3} \frac{d^{2} f}{d η^{2}} + 32 α^{4} f^{3} \frac{df}{d η} \frac{d^{2} f}{d η^{2}} + 16 α^{4} f^{2} {(\frac{df}{d η})}^{3} + 64 α^{6} f^{4} \frac{df}{d η} - 4 α^{2} {(\frac{df}{d η})}^{5}) = 0,

(21)

(1 + R) (\frac{d^{2} Θ}{d η^{2}}) + P r (N_{b} \frac{d Θ}{d η} \frac{d χ}{d η} + N_{t} {(\frac{d Θ}{d η})}^{2}) + P r E c [1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})] {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 1)}{2}} = 0,

(22)

(\frac{d^{2} χ}{d η^{2}}) + \frac{N_{t}}{N_{b}} (\frac{d^{2} Θ}{d η^{2}}) = 0,

with reduced conditions:

(23)

\begin{matrix} f = 1, \frac{df}{d η} = 0, \frac{d Θ}{d η} = 0, \frac{d χ}{d η} = 0, a s η \to 0 \\ f = 0, Θ = 1, χ = 1, a s η \to \pm 1 \end{matrix}\} .

The reduced parameters are:

(24)

Re = \frac{α r V}{v_{f}}, {We}^{2} = \frac{λ^{2} V^{2}}{r^{2} α^{2}}, M^{2} = \frac{σ {B_{0}}^{2}}{ρ_{f} v_{f}}, P r = \frac{μ_{f} C_{p}}{k_{f}}, E c = \frac{V^{2}}{T_{w} c_{p}}, N_{B} = \frac{{(ρ c_{p})}_{s}}{{(ρ c_{p})}_{f}} \frac{D_{b} C_{w}}{v_{f}} a n d N t = \frac{{(ρ c_{p})}_{s}}{{(ρ c_{p})}_{f}} \frac{D_{t} T_{w}}{v_{f} T_{0}} .

2.7

2.7 Entropy mechanism and Bejan analysis

Within the context of the to the second law of thermodynamics the current investigation, for entropy generation which measure the heat sink performance is focused in this communication. Entropy generation in this context is divided into three categories: heat, mass, and frictional entropy generation. The transmitted heat often causes thermal entropy generation (TEG). On the other side, the irreversibility caused by viscous effects during the flow is referred to as frictional entropy formation (FEG). According to these definitions, it is anticipated that TEG and FEG rates will differ greatly depending on the type of fluid used as well as how the morphologies of the nanoparticles in the nanofluid are taken into account. Because these parameters have a significant impact on the flow structure and heat transfer characteristics, which also has an impact on the generated entropy. The totoal rate of entropy generation is obtained by adding the thermal and frictional components of entropy generation. However, energy destruction or created entropy are the main causes of low-efficiency systems. The total entropy generation rate $N^{″'} (W / m^{3} K)$ is constituted of the thermal, mass diffusivity, and frictional entropy generation rates. The total entropy generation rate resulting from the time-averaged steady state, incompressible flow of Carreau fluid within converging diverging wedge is written as (see (Bejan, 1996), (Chen et al., 2018), (Makinde and Bég, 2010), (Shukla et al., 2020), (Weigand and Birkefeld, 2009)), (Abbasi et al., 2022), (Abbasi et al., 2022):

(25)

N^{'''} = \underset{{N^{'''}}_{(Thermal irreversibility)}}{\underset{⏟}{\frac{k_{f}}{{T_{0}}^{2}} {(\nabla T)}^{2}}} + \underset{{N^{'''}}_{\begin{matrix} Viscous dissipition \\ i r r e v e r s i b i l i t y \end{matrix}}}{\underset{⏟}{\frac{η_{0}}{T_{0}} Φ}} + \underset{{N^{'''}}_{(Mass transfer irreversibility)}}{\underset{⏟}{\frac{R D_{b}}{C_{0}} {(\nabla C)}^{2} + \frac{R D_{b}}{T_{0}} (\nabla C \cdot \nabla T)}} .

Where $T_{0} = \frac{T_{w} + T}{2}$ and $C_{0} = \frac{C_{w} + C}{2}$ are referred to the average temperature and concentration of the central line and channel wall. Three primary factors contribute to the rate of entropy generation: the temperature difference-driven heat transfer entropy generation rate, the concentration difference-driven mass transfer entropy generation rate, and the frictional heat loss entropy generation rate. Each term can be determined by integrating over the entire wedge computational domain $[- 1, 1]$ and are given as:

(26)

N_{Therm} = \underset{- 1}{\int^{1}} {N^{″'}}_{(T h e r m a l i r r e v e r s i b i l i t y)} d V

(27)

N_{Diffusivity} = \underset{- 1}{\int^{1}} {N^{″'}}_{(M a s s t r a n s f e r i r r e v e r s i b i l i t y)} d V

(28)

N_{Fritionalheating} = \underset{- 1}{\int^{1}} {N^{″'}}_{(\begin{matrix} Viscousdissipition \\ i r r e v e r s i b i l i t y \end{matrix})} d V

In coordinates system the above equation can be settled as

(29)

N^{'''} = \frac{k_{f}}{{T_{0}}^{2}} [1 + \frac{16 σ^{*} T_{0}^{3}}{3 k^{*} {(ρ c_{p})}_{f}}] [{(\frac{\partial T}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial T}{\partial θ})}^{2}] + \frac{η_{o}}{T_{w}} [1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}] {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 1}{2}} + \frac{R D_{B}}{C_{0}} [{(\frac{\partial C}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial T}{\partial θ})}^{2}] + \frac{{RD}_{B}}{T_{0}} [\frac{\partial T}{\partial r} \frac{\partial C}{\partial r} + \frac{1}{r^{2}} \frac{\partial T}{\partial θ} \frac{\partial C}{\partial θ}],

The normalized entropy generation equation in the context of similarity variables reduces to

(30)

N_{gen} = \frac{r^{2} α^{2} N^{″'}}{κ_{f}} = (1 + R) {(\frac{d Θ}{d η})}^{2} + {P r E c [1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})] {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 1)}{2}} + D}_{f} ({(\frac{d χ}{d η})}^{2} + (\frac{d Θ}{d η}) (\frac{d χ}{d η}))

(31)

N_{gen} = N_{Therm, r a d i a t i o n} + N_{Frictionallosses} + N_{Diffusion},

Here $D_{f}$ denote the diffusion parameter.

(32)

D_{f} = \frac{r D_{B} C_{w}}{k_{f}},

Bejan number $Be$ , which is the ratio of thermal entropy generation rate caused by thermal gradients to the overall entropy generation rate, is used to assess the contribution of thermal generation rates to total entropy generation rates. The confined Bejan number $Be$ measures the ratio of total irreversibility to irreversibility in heat transport. To determine the comparative importance of irreversibility due to heat transmission throughout the entire enclosure, the average Bejan number is utilized.

(33)

Be = \frac{N_{Therm}}{N_{Total}} = \frac{(1 + R) {(\frac{d Θ}{d η})}^{2}}{(1 + R) {(\frac{d Θ}{d η})}^{2} + P r E c [1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})] {[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{(n - 1)}{2}} + D_{f} ({(\frac{d χ}{d η})}^{2} + (\frac{d Θ}{d η}) (\frac{d χ}{d η}))}

The range of the Bejan number is restricted to $0$ to 1. If $Be < 0.5$ indicates that the total entropy generation rate dominates the entropy generation rate and $Be > 0.5$ indicates that the thermal entropy generation rate dominates the total entropy generation rate.

2.8

2.8 Curiosity in engineering parameters

Skin drag force.

The skin drag-force i.e., the skin friction for Carreau fluid is

(34)

C_{f} = \frac{τ_{r θ}}{ρ_{f} {V_{m a x}}^{2}} .

Where $τ_{r θ}$ denote shear stress and is defined as

(35)

τ_{r θ} = {\frac{η_{0}}{r} {[1 + λ^{2} \{2 {(\frac{\partial V}{\partial r})}^{2} + \frac{1}{r^{2}} {(\frac{\partial V}{\partial θ})}^{2} + \frac{2 V^{2}}{r^{2}}\}]}^{\frac{n - 1}{2}} \frac{\partial V}{\partial θ}|}_{θ = \pm α} .

Thus, the dimensionless expression become

(36)

C_{f} = \frac{1}{Re} [{[1 + {We}^{2} ({(\frac{df}{d η})}^{2} + 4 α^{2} f^{2})]}^{\frac{n - 1}{2}} \frac{df}{d η}]

Heat transfer rate

The local Nusselt Number is demarcated as:

(37)

Nu = \frac{r q_{w}}{k_{f} T_{w}} .

Where $q_{w}$ signify surface heat flux and expressed as:

(38)

q_{w} = {- k_{f} (\frac{\partial T}{\partial θ})|}_{θ = \pm α} + q_{r}

Employing the dimensionless variables, we get

(39)

Nu = - \frac{1}{α} (1 + R) (\frac{d Θ}{d η})

Mass transfer rate

The local Sherwood Number is interpreted as:

(40)

Sh = \frac{r j_{w}}{D_{b} C_{w}}

Where $j_{w}$ characterizes surface mass flux and written as:

(41)

j_{w} = - D_{b} (\frac{dC}{d θ})

Thus

(42)

Sh = - \frac{1}{α} \frac{d χ}{d η}

3 Numerical scheme for solution

The shooting method, a well-known numerical methodology, is implemented to numerically solve the governing problem. In order to find the values of $\frac{d f (\pm 1)}{d η}$ , $\frac{d Θ (\pm 1)}{d η},$ and $\frac{d χ (\pm 1)}{d η}$ at the channel wall, a fifth order Rung-Kutta quadrature procedure in conjunction with a Newton iteration approach is used to solve the governing equations (21), (22), and (23) subject to boundary conditions (24). With the help of newly defined variables, the differential equation Eqs. (21), (22), and (23), and (24) is transformed into first-order ordinary differential equations. Now the appropriate guesses of the missing conditions are assumed. The flow domain is taken at $η = - 1$ to $η = 1$ . The stepped used to estimate Eqs. (21), (22), and (23), and (24), employing fifth–fourth-order Runge–Kutta–Fehlberg are listed below (Bég et al., 2020), (Khan et al., 2018):

(43)

\begin{matrix} k_{0} = f (x_{0}, y_{0}) \\ k_{1} = f (x_{0} + \frac{1}{4} h, y_{0} + \frac{1}{4} k_{0} h) \\ k_{2} = f (x_{0} + \frac{3}{8} h, y_{0} + (\frac{3}{32} k_{0} + \frac{9}{32} k_{1})) \\ k_{3} = f (x_{0} + \frac{12}{13} h, y_{0} + (\frac{1932}{2197} k_{0} - \frac{7200}{2197} k_{1} + \frac{7296}{2197} k_{2}) h) \\ k_{4} = f (x_{0} + h, y_{0} + (\frac{439}{216} k_{0} - 8 k_{1} + \frac{3860}{513} k_{2} - \frac{845}{4104} k_{3}) h) \\ k_{5} = f (x_{0} + \frac{1}{2} h, y_{0} + (- \frac{8}{27} k_{0} + 2 k_{1} - \frac{3544}{2565} k_{2} - \frac{1859}{4104} k_{3} - \frac{11}{40} k_{4}) h) \end{matrix}\},

(44)

= y_{i} + (\frac{25}{216} k_{0} + \frac{1408}{2565} k_{2} + \frac{2197}{4104} k_{3} - \frac{1}{5} k_{4}) h

(45)

z_{i + 1} = z_{i} + (\frac{16}{135} k_{0} + \frac{6656}{12825} k_{2} + \frac{28561}{56430} k_{3} - \frac{9}{40} k_{4} + \frac{2}{55} k_{5}) h

The fourth order Runge–Kutta component is denoted by $y_{*}$ , and the fifth order Runge–Kutta stage is denoted by $z_{*}$ . By subtracting the two values obtained, an estimate of the error can be obtained. The findings can be redone with a reduced step size if the deviation reaches a certain threshold. The following is an example of how to determine the new step size:

(46)

h_{new} = h_{old} {[\frac{\in h_{old}}{2 |z_{i + 1} - y_{i + 1}|}]}^{\frac{1}{4}}

The step size is $Δ η =$ 0.01, tolerance is taken $10^{- 5}$ and accuracy of order 4 is supposed.

3.1

3.1 Results validation

We compare the current numerical values for velocity field $f (η)$ when $η$ is taken in the range $[- 1, 1]$ and other parameters are omitted to resemble with earlier work by (Sari et al., 2016) in order to assess the accuracy of our computational system. Table 1 shows a respectable degree of agreement between the current numerical results and the results of earlier studies.

Table 1 The comparative outputs for

f (η)

, when

We = 0

n = 0, M = 0

$η$	$Re = 50$ , ${α = 3}^{0}$		$Re = 50$ , ${α = - 3}^{0}$
$η$	(Sari et al., 2016)	Present results	(Sari et al., 2016)	Present results
−1	0	0	0	0
−0.75	0.346178919	0.34175932	0.956861924	0.95862988
−0.5	0.669320174	0.66929111	0.811457376	0.81146278
-0.25	0.909765342	0.90978112	0.515827995	0.51582911
0.0	1	1	1	1
0.25	0.909765342	0.90980111	0.515827995	0.51579910
0.5	0.669320174	0.66931012	0.811457376	0.81145017
0.75	0.346178916	0.34617239	0.956861924	0.95890181
1.0	0	0	0	0

4 Declaration of result and discussion

This segment focused on examining how various values of the relevant parameter behaved in comparison to the distributions of velocity, temperature, concentration, irreversibility mechanism. All drawings show the effects of various values in two distinct scenarios: the first is a fluid entering a channel that is converging, and the second involves a fluid exiting a channel that is diverging.

4.1

4.1 Flow dynamics within wedge configuration

The fluctuation of velocity profile $f (η)$ for different Reynolds intensities $Re$ is seen in Fig. 2. In a convergent channel, the fluid velocity matching the Reynolds number, producing solid gradients at the medium's center walls and a reduction in the boundary layer thickness momentum. The findings reveal that backflow is completely prevented in convergent channel. A low Reynolds number indicates that the viscous force is dominant, and since the boundary layer region does not extend very deep into the flow region, which consequently accelerate the flow as a result the velocity dominates. Indicative of turbulent flow patterns, such as those seen in turbulent flows, are due to high Reynolds numbers. The results were reversed in the case of a convergent channel and increasing the Reynolds number increased the velocity profiles without causing any apparent reverse flow. Furthermore, the velocity profile along the center line stayed virtually constant at high Reynolds numbers while abruptly dropping to zero at the wall. In a divergent channel, the velocity profile decreases as the Reynolds number increases. Additionally, as the Reynolds number rises, the flow changes and a backflow region may be seen close to the wall. The velocity profile differs between the two channels. The velocity boundary layer thickness falls as the Reynolds number rise. On the other hand, in diverging channels, a rise in the Reynolds number can cause the flow to reverse (see Fig. 3). It's interesting how strong inertial forces influence the flow domain within diverse geometries. That is, in convergent channels, fluid elements near the wall accelerate as the Reynolds number rises, presumably due to an expansion of the beneficial pressure gradient. In diverging-channel flows of Carreau fluids, the inflection point shows that the velocity profiles at high $Re$ may be easily prone to hydrodynamic instability. Since the velocity profile contains detailed information on the flow field, it is particularly significant to us. According to Fig. 4, the velocity in a diverging section is a constantly decreasing function of $We$ , while in a converging section the consequences are conflicting. The dimensionless parameter $We$ distinguish the fluid's viscoelastic characteristics by relating the elastic forces to the viscous forces. In fact, the narrower channel and a higher viscoelasticity, the velocity of the Carreau fluid is suppressed. The most plausible explanation for this is that the shear-thinning property of the fluid is enriched at higher values of the Weissenberg number, which causes a decrease in the apparent viscosity of the fluid. Additionally, fluid radial velocity gradually decreases because of the viscosity drop. The influence of Weissenberg numbers on the normalized radial velocity will undoubtedly be due to main hemodynamic variables, such as shear stress at the wall (WSS), resistive impedance, and volumetric flow rate which exhibit oscillatory behavior. Fig. 4 depict the Weissenberg variation as a function of nanofluid velocity $f (η)$ . It can be perceived that $We$ appears as a mixed derivatives in the momentum conservation equations. In the absence of Weissenberg ( $We = 0$ ), the model is reflected to be a Newtonian fluid, while the model extends to elastic solids model as ( $We \to \infty$ ). However, this rheological fluid model displays the viscoelastic assets of the polymer to adequate values. The velocity of the nanofluid declines with increasing $We$ , while in a convergent channel the influence is conflicting. In diverging case, the elastic force behaves as a dominant effect compared to the viscous force; therefore, the flow resistance is established in the boundary layer. Velocity $f (η)$ decline is therefore considered because of the growing $We$ . Physically, this reduction originates from the direct relationship between Weissenberg and relaxation rate, which led to decreases in fluid movement at higher relaxation rates. Fig. 5 is plotted to scrutinize the change in velocity $f (η)$ for various values of power index $n$ (Shear thickening case). It is perceived that dimensionless radial velocity dwindle with increase of $n (= 1.2, 1.5, 1.8)$ and after attaining its maximum value radial velocity declines to zero in a converging zone. In addition, it is depicted that dimensionless radial velocity profile increases its occurrence in diverging channel. The momentum boundary layer thickness rises with the power-law index and the channel width. Therefore, the velocity of the fluid is improved as a consequence of power indexed. While slight reduction is attained in convergent channel within the narrower zone of the convergent channel. Maximum velocity is seen within the central region of both channel while slight reduction near to the wall of the channel is seen.

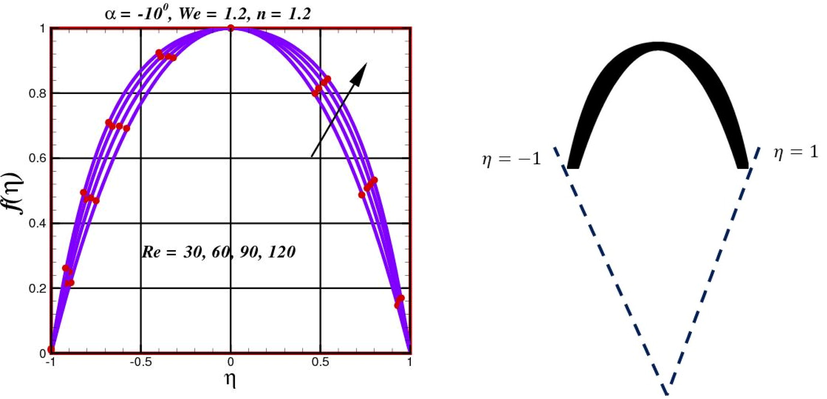
Performance of velocity f η and flux shape in a convergent channel against augmented values of Re .

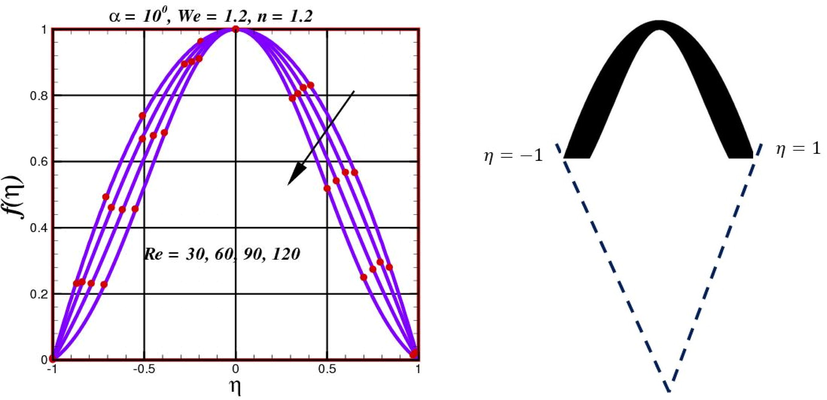
Performance of velocity f η and flux shape in a divergent channel against augmented values of Re .

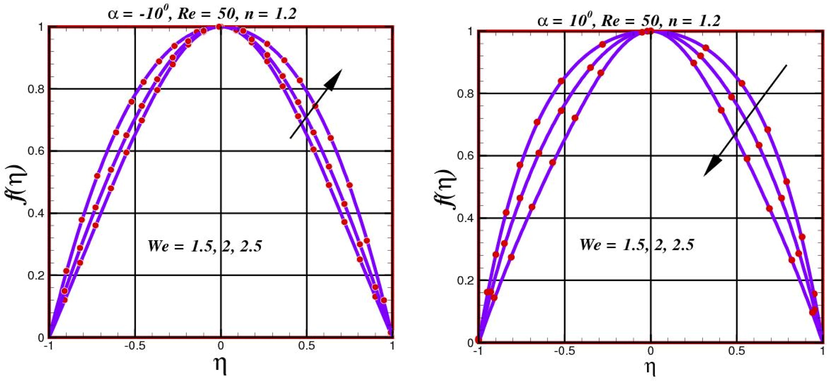
Performance of velocity f η for α = - 10 o and α = 10 o against augmented values of We .

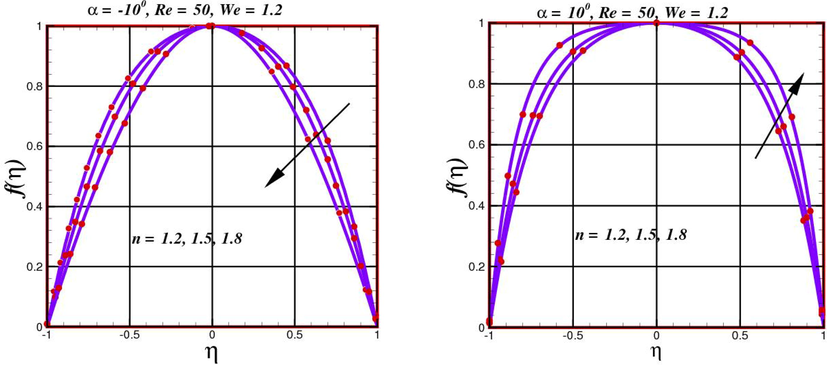
Performance of velocity f η for α = - 10 o and α = 10 o against augmented values of n .

4.2

4.2 Thermal distribution phenomena

The flow and temperature phenomena are combined with each other in the case of viscous heating. Consequently, the flow pattern inside the wedge, debated in the subsection, will significantly influence the corresponding temperature phenomena. In this subsection, we have deliberated the heat transfer features in detail in terms of the non-dimensional temperature distribution. The effect of the Weissenberg number ( $We = 1.2, 1.5, 1.8$ ) on temperature distribution $Θ (η)$ is depicted in Fig. 6. The relationship between the fluid's kinematic viscosity/process time and its relaxation time is acknowledged as the Weissenberg number. Therefore, increasing the Weissenberg number makes it easier for fluid particles to relax over time, which advances friction and fluid thickness and, simultaneously, raises the fluid temperature. The flow and heat transfer features of non-Newtonian fluids are comparable to those of Newtonian fluids at low Weissenberg number values. For instance, at ( $We = 0$ ), like the Newtonian fluid, the Carreau fluid similarly generates a large vortex zone that is virtually in the channel's center, along with two smaller vortex regions that are formed in the channel's up right $η = 1$ and down $η = - 1$ corners. We arrived at the conclusion that the measurement of the fluid's Weissenberg number ( $We > 1$ ) would be severely hampered by polymer breakdown and the relative change in fluid relaxation time. Finally, fluid temperature has a significant impact on all the rheological parameters taken into consideration. The fluid's temperature was sampled at the beginning and end of the channel to determine the magnitude of the temperature shift brought on by the mechanical churning (inlet and outlet of the channel). The modification in temperature distribution as power-index ( $n$ ) becomes higher is demonstrated in Fig. 7. In a convergent channel, a decrease in thermal boundary layer thickness and temperature distribution is perceived versus $n$ . This tendency is demonstrated by the argument that when fluid viscosity increases, the kinetic energy of the fluid molecules reduces, resulting in a narrowing of the temperature distribution. While in diverging geometry scenario, a little degradation is achieved. In fact, large value of $n > 1$ , (shear thickening fluid) the thickness of boundary layer augmented and corresponding the fluid layer thickened, consequently reduced the temperature. The dissipation of heat in the domain is significantly influenced by thermal radiation ( $R$ ). The system is heated by extra heat from a different source. The effective thermophysical characteristics of flow fluids make a strong effort to eliminate these temperatures. Fig. 8 shows that the thermal distribution increases with increasing radiation temperature. Similar trend for radiation parameter is seen in both channels. The higher the radiation parameter $R$ , the more heat is provided to the liquid, raising both temperature and thermal boundary-layer density. This is due to the increased interaction in the thermal boundary layer caused by an increase in the thermal radiation parameter. In fact, significant amount of heat caused by higher radiation parameter values, the nanofluid temperature profile and thermal boundary layer width is also increased.

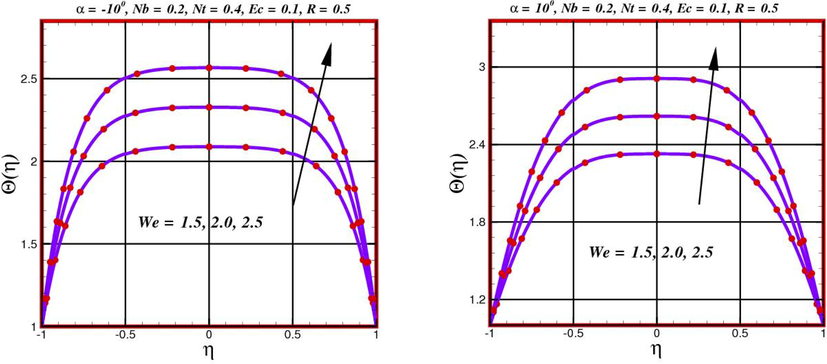
Behavior of temperature Θ η for α = - 10 o and α = 10 o against diverse values of We .

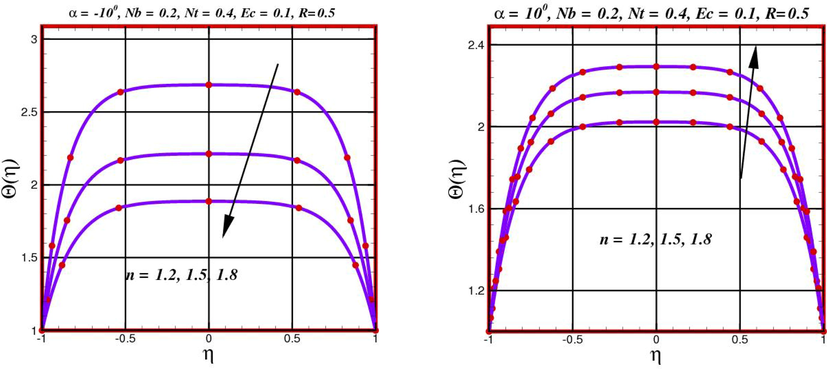
Behavior of temperature Θ η for α = - 10 o and α = 10 o against diverse values of n .

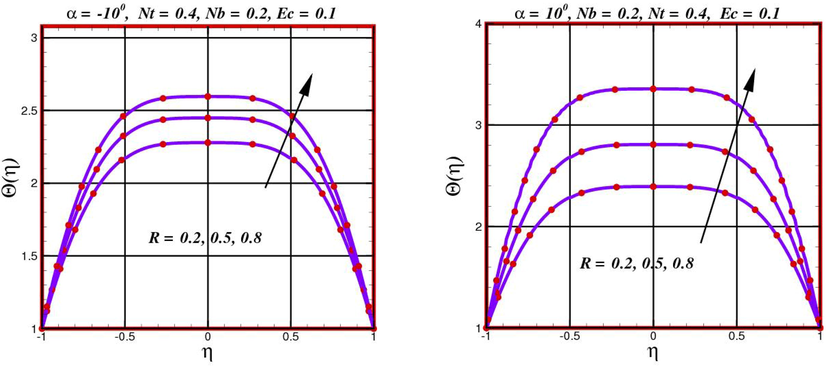
Behavior of temperature Θ η for α = - 10 o and α = 10 o against diverse values of R .

4.3

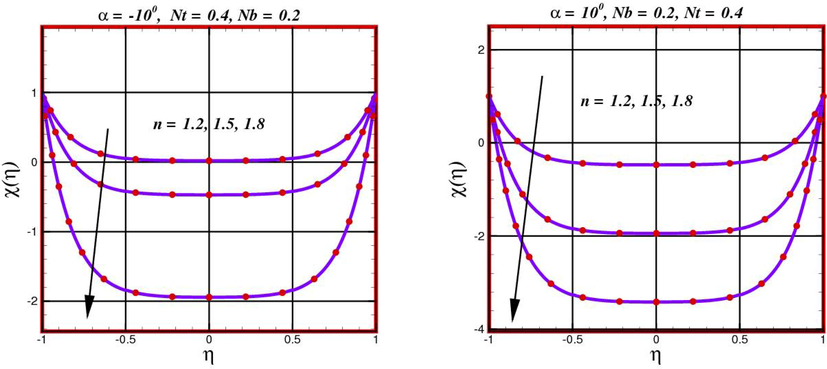
4.3 Concentration profile

The concentration profile inside the wedge shape channel at various Weissenberg values is exposed in Fig. 9. There is no mixing of the fluids with low Weissenberg numbers. The middle of the diverging channel where the fluid mingles the most, as the Weissenberg number rises to $1 < W e < 2$ . This is because the elastic instability is present at this Weissenberg number, increasing chaotic advection and, thus, enhances the mixing phenomenon. The chaotic advection inside the convergent channel becomes weaker as the Weissenberg number rises due to the relaxation period decreasing further, which lessens the mixing phenomenon between the two plates. As the Weissenberg number ( $We$ ) rises, the polymer chain extension and elastic stress increase, which substantially influence the concentration dynamics. It can be observed that as $We$ increases, the concentration profile tends to rise closer to the wedge surface while, in the boundary layer region, it tends to decline far away from the wall. The nanoparticle concentration against power index $n > 1$ is depicted in Fig. 10. Near the solid wedge wall, the concentration profile decreases with higher n values, while the opposite tendency is seen farther out from the wedge wall. The graphic for both converging diverging channel conveys that the nanoparticles concentration diminishes as the power indexed is augmented. Physically, the shear thickening fluid has a low concentration as compared to the shear thinning fluid.

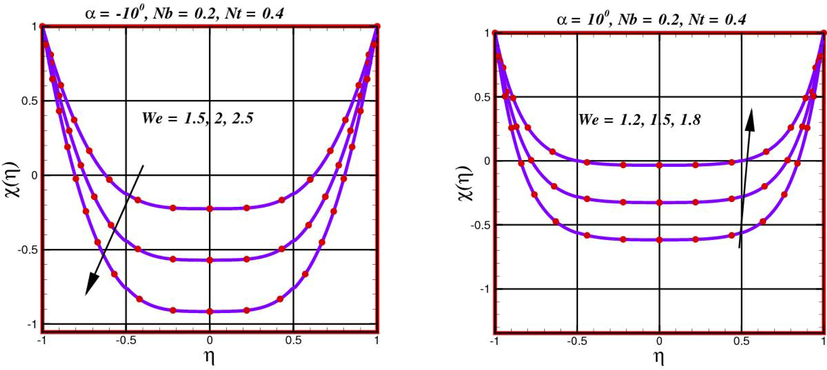
Behavior of concentration χ η for α = - 10 o and α = 10 o against diverse values of We .

Behavior of concentration χ η for α = - 10 o and α = 10 o against diverse values of n .

4.4

4.4 Irreversibility analysis of Power-Law fluid

In this section, entropy-generation rate $N_{gen}$ and Bejan analysis $Be$ is carried out to study the irreversibility of the channel with wedge shape structure. The elastic force in converging system is increased when Weissenberg number ( $We$ ) grows. A dominant nature is also expressed by the elastic force in comparison to the viscous force. $We$ increase entropy $N_{gen}$ and decrease $Be$ because of this behavior. Physically, viscosity difference grows for greater ( $We$ ), which raises resistance and finally causes the system to become more disordered (entropy generation) (Fig. 11). While the effects are conflicting for entropy in divergent channel as clear from the Fig. 12. In the region $η = - 1$ to $0$ , the entropy generation curves are constant, while they change in other parts of the channel (see Figs. 11 and 12). The increased friction towards the walls may be the reason of this. In expanding channel, the entropy generation diminish due to large channel opening against rising trend in $We$ values led to a decline both profiles. Figs. 13 and 14 are plotted for entropy production $N_{gen}$ and Bejan profile $Be$ against power index $n$ in convergent divergent channel respectively. On higher estimates of the power law material constant $n$ , the entropy generation $N_{gen}$ exhibits an uprising tendency and reverse influence for the Bejan profile. The effects of mass and heat transport grow with greater $n$ , but viscous effects significantly rise and entropy decreases (see Figs. 13 and 14). Physically, large estimation of power index $n > 1$ , the shear thickening effects dominates the system discordances in both geometries, consequently entropy distribution is higher, while reduction in Bejan profile is diminished. Entropy generation $N_{gen}$ and Bejan number $Be$ are examined and found to be improved for augmented radiation parameter $(R)$ . Higher intensities of radiation parameter enhance the system's internal energy $.$ This is why systemic disorganization increases (see Fig. 15 and Fig. 16). Higher radiation causes the irreversibility of heat transfer to become more pronounced than the irreversibility of viscous dissipation, raising the value of ( $Be$ ). The non-linear thermal radiation causes an increase in both local and overall entropy generation, which reaches its maximum levels in the areas with the strongest thermal gradients and consequently the greatest energy loss. The analysis of the Bejan number demonstrates that in all sections where conduction is the principal heat transport mechanism, are also with the highest values of entropy generation, the influence of heat transfer irreversibility to total entropy generation is close to 1, whereas it is nearly zero outside these regions.

Fig. 11

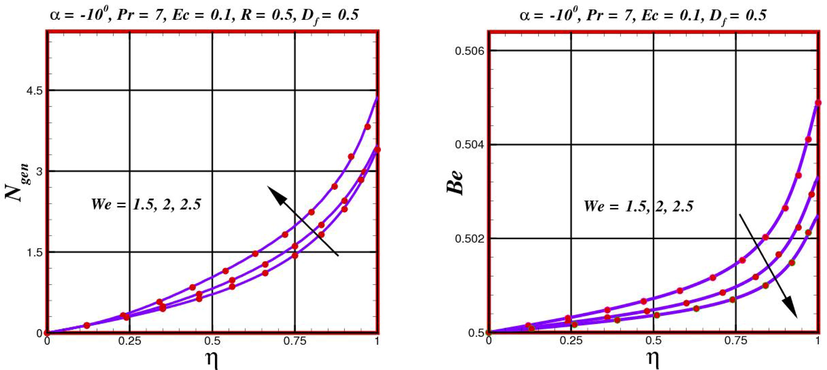
Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a converging channel

α = - 10^{o}

against diverse values of

We

Fig. 12

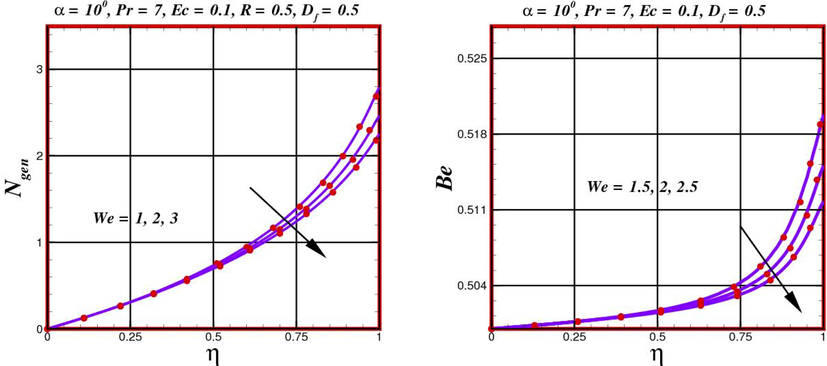
Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a diverging channel

α = 10^{o}

against diverse values of

We

Fig. 13

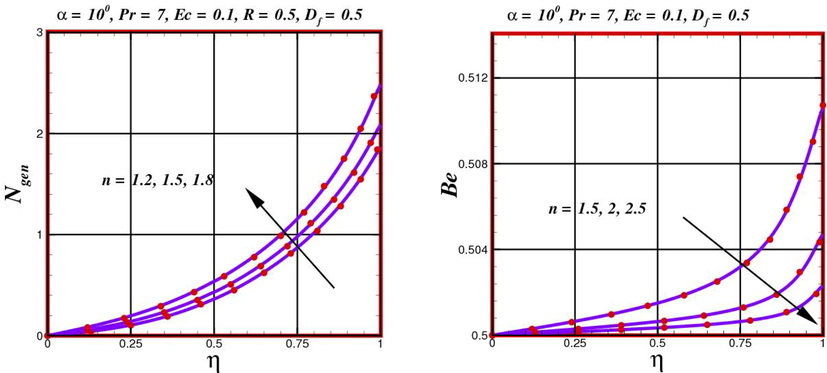
Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a converging channel

α = - 10^{o}

against diverse values of

n

Fig. 14

Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a converging channel

α = 10^{o}

against diverse values of

n

Fig. 15

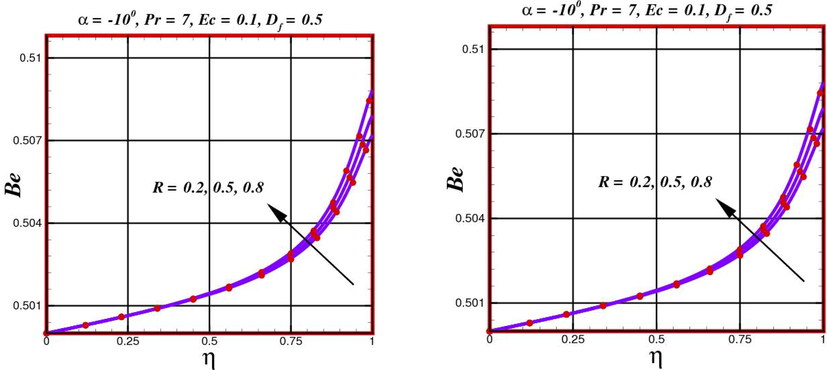
Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a converging channel

α = - 10^{o}

against diverse values of

R

Fig. 16

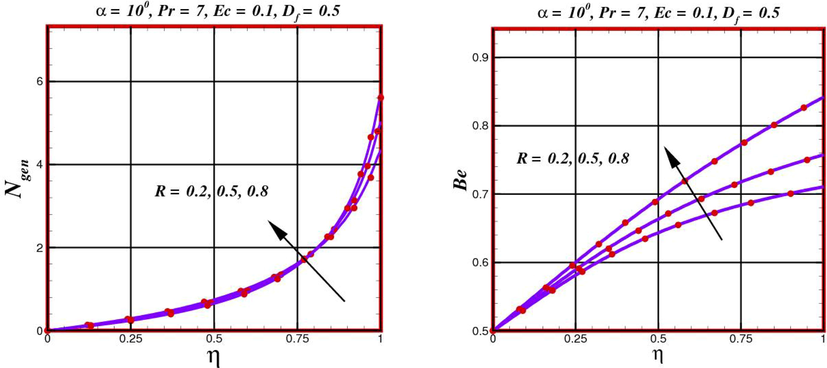
Distribution of entropy generation rate

N_{gen}

and Bejan profile

Be

in a converging channel

α = 10^{o}

against diverse values of

R

4.5

4.5 Quantities of physical interest

Tables 2 and 3 illustrates the effects of physical flow parameter on the rate of mass and heat transmission in the converging and diverging channel. Additionally, a comparison of the outcomes for both geometries are included. From these table, one can infer that as the Eckert number $Ec$ increases, the rate of heat transfer $Nu$ decreases, whereas the rate of heat transfer improves as $Ec$ increases. Consequently, for increasing values of ( $R$ ) and ( $n$ ), the heat transfer rate increases at the convergent channel, but the opposite tendency is observed for ( $We$ ). Physically, it is seen that $Nu$ and $Sh$ increase as $We$ increases, however the relaxation time's declining trend reflects an increasing trend with larger values of $We$ . Tensile stresses in the pseudoplastic nanofluid are accelerated by the lengthening relaxation time. Additionally, heat and mass transfer effects against various parameter are dominate in convergent channel. While significant decrease is seen for Nusselt and Sherwood against various parameter.

Table 2 Numerical result for heat and mass transfer rate for converging case when

{α = - 10}^{0}

$\Pr$	$Nb$	$Nt$	$Ec$	$We$	$n$	$R$	$- \frac{1}{α} (1 + R) (\frac{d Θ}{d η})$	$- \frac{1}{α} \frac{d χ}{d η}$
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.3980	0.2388
	0.6						−0.3980	0.1592
	0.8						−0.3980	0.1194
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.3980	0.2388
		0.6					−0.3924	0.4708
		0.8					−0.3869	0.6965
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.7847	0.9160
			0.2				−1.1608	0.4708
			0.3				−1.5266	0.6965
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.7965	0.4779
				1.2			−0.8195	0.4917
				1.3			−0.8417	0.5050
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.7847	0.4708
					1.2		−0.8816	0.5290
					1.3		−0.9930	0.5958
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.3980	0.9160
						0.2	−0.3974	0.9164
						0.3	−0.3969	0.9160

Table 3 Numerical result for heat and mass transfer rate for diverging case when,

{α = 10}^{0}

$\Pr$	$Nb$	$Nt$	$Ec$	$We$	$n$	$R$	$- \frac{1}{α} (1 + R) (\frac{d Θ}{d η})$	$- \frac{1}{α} \frac{d χ}{d η}$
7	0.4	0.2	0.1	1.0	1.1	0.1	−1.7695	0.8847
	0.6						−1.7695	0.5898
	0.8						−1.7695	0.4424
7	0.4	0.2	0.1	1.0	1.1	0.1	−1.7695	0.9069
		0.6					−1.8137	1.8137
		0.8					−1.8139	2.7209
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.9069	0.4534
			0.2				−1.8137	0.9069
			0.3				−1.8139	1.3603
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.9069	0.4479
				1.2			−1.8137	0.4694
				1.3			−2.7206	0.5050
7	0.4	0.2	0.1	1.0	1.1	0.1	−0.8958	0.4730
					1.2		−0.9177	0.5290
					1.3		−0.9388	0.5931
7	0.4	0.2	0.1	1.0	1.1	0.1	−1.7695	0.9069
						0.2	−1.8690	0.9083
						0.3	−1.9645	0.9097

5 Conclusion

In this theoretical communication, an entropy generation analysis of the Carreau fluid in a Wedge shape convergent divergent channel geometry with different parameter is securitized for the first time to estimate the effects of thermodynamic irreversibility. The Carreau fluid is significant in chemical engineering and polymeric suspensions because it combines the power-law and Newtonian fluid models. The Carreau fluid model can be used to describe the properties of paints, polymer fluids, polyvinyl chloride, and polyethylene. The second law of thermodynamics is used to estimate the local entropy generation rate, which is used to identify irreversibility processes and quantify thermodynamic irreversibility that occur in wedge-shaped channels. In the entropy generation model, the contributions of the power-index $n$ , Weissenberg number ( $We$ ), and non-linear thermal radiation effects are specifically considered. The RK-45 Fehlberg numerical approach was used to address the problem high nonlinear ODEs. Entropy generation and Bejan number patterns for $We$ and $n$ are quite opposite in a divergent channel. The achieved numerical approximation solutions are certified by comparing the results of a limiting case (J-H flow problem) with the solutions determined in the available works. The consequences of the deviation of the embedded parameters on the velocity, temperature, concentration profiles and Entropy generation and Bejan number are presented. From the outcomes we conclude that: The flow is controlled by large estimation of inertial forces $Re$ in a divergent channel, while conflicting trend is seen in a convergent channel. The velocity curve depreciates as the Weissenberg number ( $We$ ) esclates. Whereas the conflicting effect is inspected in the power index number $n$ . The temperature profile is improved by larger estimates of the radiation parameter and neighborhood Wiesenberger number. Concentration of nanoparticles is reduced on increasing either by Wiesenberger number or power index in a convergent portion. We believe the consequences of the current work will contribute to the improved design and optimization of impinging jet, supersonic nozzle design cooling systems. In contrast to how this physical quantity changes when the radiation parameter increases, the rate of heat transfer decreases as the Eckert number rises. Flow through a divergent channel produces reduced entropy compared to the flow through a convergent channel.

6 Future recommendation

The model can be extended to design approach prioritizing heat transmission effectiveness for two-dimensional convergent–divergent rocket nozzle will be more appropriate to reduce exergy destruction for more practical problem. Applying magnetic effects offers extra opportunities for design and heat transfer mechanism optimization. Indeed, magnetic fields and lubricated walls outcome in a very efficient method to condense entropy generation although they degrade heat transfer efficiency. Therefore, combined effect of magnetic field and radiation effects they could offer brilliant equilibrium between heat transfer productivity and exergy destruction.

Acknowledgement

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups Project under grant number (RGP.2/25/43).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Abbasi F.M., Gul M., Shanakhat I., Anjum H.J., Shehzad S.A., . Entropy generation analysis for magnetized peristaltic movement of nanofluid through a non-uniform asymmetric channel with variable thermal conductivity. Chin. J. Phys.. 2022;78:111-131.
[CrossRef] [Google Scholar]
Ahmad S., Hayat T., Alsaedi A., Ullah H., Shah F., . Computational modeling and analysis for the effect of magnetic field on rotating stretched disk flow with heat transfer. Propul. Power Res.. 2021;10:48-57.
[CrossRef] [Google Scholar]
Ali A., Sarkar S., Das S., Jana R.N., . A report on entropy generation and Arrhenius kinetics in magneto-bioconvective flow of Cross nanofluid over a cylinder with wall slip. Int. J. Ambient Energy 2022:1-16.
[CrossRef] [Google Scholar]
Al-Saif A.-S.-J.-A., Jasim A.M., . New analytical study of the effects thermo-diffusion, diffusion-thermo and chemical reaction of viscous fluid on magneto hydrodynamics flow in divergent and convergent channels. Appl. Math.. 2019;10:268-300.
[CrossRef] [Google Scholar]
Asghar Z., Saif R.S., Ghaffari A.Z., . Numerical study of boundary stresses on Jeffery-Hamel flow subject to Soret/Dufour effects. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci.. 2022;09544062221126646
[CrossRef] [Google Scholar]
Bég O.A., Uddin M.J., Bég T.A., Kadir A., Shamshuddin M.D., Babaie M., . Numerical study of self-similar natural convection mass transfer from a rotating cone in anisotropic porous media with Stefan blowing and Navier slip. Indian J Phys. 2020;94:863-877.
[CrossRef] [Google Scholar]
Bejan A., . Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys.. 1996;79:1191-1218.
[CrossRef] [Google Scholar]
Bejan A., . A Study of Entropy Generation in Fundamental Convective Heat Transfer. J. Heat Transfer. 1979;101:718-725.
[CrossRef] [Google Scholar]
Bejan A., Kestin J., . Entropy Generation Through Heat and Fluid Flow. J. Appl. Mech.. 1983;50:475.
[CrossRef] [Google Scholar]
Bhaskar K., Sharma K., Bhaskar K., . Cross-diffusion and chemical reaction effects of a MHD nanofluid flow inside a divergent/convergent channel with heat source/sink. J. Therm. Anal. Calorim. 2022
[CrossRef] [Google Scholar]
Bilal S., Shah I.A., . A comprehensive physical insight about thermo physical aspects of Carreau fluid flow over a rotated disk of variable thickness by implementing finite difference approach. Propul. Power Res.. 2022;11:143-153.
[CrossRef] [Google Scholar]
Carreau P.J., . Rheological equations from molecular network theories. Trans. Soc. Rheol.. 1972;16:99-127.
[CrossRef] [Google Scholar]
Chen L., Zhang L., Xia S., Sun F., . Entropy generation minimization for CO₂ hydrogenation to light olefins. Energy. 2018;147:187-196.
[CrossRef] [Google Scholar]
Chu Y.-M., Al-Khaled K., Khan N., Ijaz Khan M., Ullah Khan S., Sadiq Hashmi M., Azhar Iqbal M., Tlili I., . Study of Buongiorno’s nanofluid model for flow due to stretching disks in presence of gyrotactic microorganisms. Ain Shams Eng. J.. 2021;12:3975-3985.
[CrossRef] [Google Scholar]
Chu Y.-M., Shah F., Khan M.I., Kadry S., Abdelmalek Z., Khan W.A., . Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. J. Mater. Res. Technol.. 2020;9:13977-13987.
[CrossRef] [Google Scholar]
Cross M.M., . Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems. J. Colloid Sci.. 1965;20:417-437.
[CrossRef] [Google Scholar]
Das S., Chakraborty S., Makinde O.D., Jana R.N., . Entropy analysis of MHD variable thermal conductivity fluid flow past a convectively heated stretching cylinder. Defect and Diffusion Forum. 2018;387:244-259.
[CrossRef] [Google Scholar]
Das S., Sarkar S., Jana R.N., . Feature of entropy generation in Cu-Al₂O₃/Ethylene glycol hybrid nanofluid flow through a rotating channel. BioNanoSci.. 2020;10:950-967.
[CrossRef] [Google Scholar]
Das S., Sarkar S., Jana R.N., . Entropy generation analysis of MHD Slip Flow of Non-Newtonian Cu-Casson nanofluid in a porous microchannel filled with saturated porous medium considering thermal radiation. J. Nanofluids. 2018;7:1217-1232.
[CrossRef] [Google Scholar]
Fraenkel L.E., Squire H.B., . Laminar flow in symmetrical channels with slightly curved walls, I. On the Jeffery-Hamel solutions for flow between plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1962;267:119-138.
[CrossRef] [Google Scholar]
Garimella S.M., Anand M., Rajagopal K.R., . Jeffery-Hamel flow of a shear-thinning fluid that mimics the response of viscoplastic materials. Int. J. Non Linear Mech.. 2022;144:104084
[CrossRef] [Google Scholar]
Hamel G., . Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresber. Deutsch. Math.-Verein.. 1917;25:34-60.
[Google Scholar]
Harley C., Momoniat E., Rajagopal K.R., . Reversal of flow of a non-Newtonian fluid in an expanding channel. Int. J. Non Linear Mech.. 2018;101:44-55.
[CrossRef] [Google Scholar]
Hassan M., Mebarek-Oudina F., Faisal A., Ghafar A., Ismail A.I., . Thermal energy and mass transport of shear thinning fluid under effects of low to high shear rate viscosity. Int. J. Thermofluids. 2022;15:100176
[CrossRef] [Google Scholar]
Hayat T., Shah F., Khan M., Alsaedi A., Yasmeen T., . Modeling MHD Stagnation Point Flow of Thixotropic Fluid with Non-uniform Heat Absorption/Generation. Microgravity Sci. Technol.. 2017;29
[CrossRef] [Google Scholar]
Ibrahim M.G., . Adaptive simulations to pressure distribution for creeping motion of Carreau nanofluid with variable fluid density effects: physiological applications. Thermal Sci. Eng. Prog.. 2022;32:101337
[CrossRef] [Google Scholar]
Jeffery G.B., . L. The two-dimensional steady motion of a viscous fluid. The London, Edinburgh, and Dublin Philosophical Magazine J. Sci.. 1915;29:455-465.
[CrossRef] [Google Scholar]
Kamran A., Azhar E., . Numerical outlook of a viscoelastic nanofluid in an inclined channel via Keller box method. Int. Commun. Heat Mass Transfer. 2022;137:106260
[CrossRef] [Google Scholar]
Khan M., Sardar H., Gulzar M.M., Alshomrani A.S., . On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Results Phys.. 2018;8:926-932.
[CrossRef] [Google Scholar]
Khan U., Ahmed N., Mohyud-Din S., . Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels. Chem. Eng. Sci.. 2015;141
[CrossRef] [Google Scholar]
Krishna M.V., Jyothi K., Chamkha A.J., . Heat and mass transfer on mhd flow of second-grade fluid through porous medium over a semi-infinite vertical stretching sheet. JPM. 2020;23
[CrossRef] [Google Scholar]
Krishna M.V., Jyothi K., Chamkha A.J., . HEAT and mass transfer on unsteady, magnetohydrodynamic, oscillatory flow of second-grade fluid through a porous medium between two vertical plates, under the influence of fluctuating heat source/sink and chemical reactioN. FMR. 2018;45
[CrossRef] [Google Scholar]
Krishna M.V., Swarnalathamma B.V., Chamkha A.J., . Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate. J. Ocean. Eng. Sci.. 2019;4:263-275.
[CrossRef] [Google Scholar]
Madhu M., Shashikumar N.S., Gireesha B.J., Kishan N., . Thermal analysis of MHD Powell-Eyring fluid flow through a vertical microchannel. Int. J. Ambient Energy. 2022;43:4454-4462.
[CrossRef] [Google Scholar]
Madhu M., Shashikumar N.S., Gireesha B.J., Kishan N., . Second law analysis of MHD micropolar fluid flow through a porous microchannel with multiple slip and convective boundary conditions. Defect Diffusion Forum. 2021;409:123-141.
[CrossRef] [Google Scholar]
Mahanthesh B., Shehzad S.A., Mackolil J., Shashikumar N.S., . Heat transfer optimization of hybrid nanomaterial using modified Buongiorno model: a sensitivity analysis. Int. J. Heat Mass Transf.. 2021;171:121081
[CrossRef] [Google Scholar]
Makinde O., Bég O., . On inherent irreversibility in a reactive hydromagnetic channel flow. J. Therm. Sci.. 2010;19:72-79.
[CrossRef] [Google Scholar]
Mansutti D., Ramgopal K.R., . Flow of a shear thinning fluid between intersecting planes. Int. J. Non Linear Mech.. 1991;26:769-775.
[CrossRef] [Google Scholar]
Nagler J., . Jeffery-Hamel flow of non-Newtonian fluid with nonlinear viscosity and wall friction. Appl. Math. Mech.-Engl. Ed.. 2017;38:815-830.
[CrossRef] [Google Scholar]
Nayak M.K., Mabood F., Dogonchi A.S., Khan W.A., . Electromagnetic flow of SWCNT/MWCNT suspensions with optimized entropy generation and cubic auto catalysis chemical reaction. Int. Commun. Heat Mass Transfer. 2021;120:104996
[CrossRef] [Google Scholar]
Ostwald W., . Ueber die rechnerische Darstellung des Strukturgebietes der Viskosität. Kolloid-Zeitschrift. 1929;47:176-187.
[CrossRef] [Google Scholar]
Owhaib W., Al-Kouz W., . Three-dimensional numerical analysis of flow and heat transfer of bi-directional stretched nanofluid film exposed to an exponential heat generation using modified Buongiorno model. Sci. Rep.. 2022;12:10060.
[CrossRef] [Google Scholar]
R, D.W., . Note on the divergent flow of fluid. Philos. Mag. 1934;18:759-777.
[Google Scholar]
Ramesh G.K., Madhukesh J.K., Shehzad S.A., Rauf A., . Ternary nanofluid with heat source/sink and porous medium effects in stretchable convergent/divergent channel. Proc. Institution Mech. Engineers, Part E: J. Process Mech. Eng.. 2022;09544089221081344
[CrossRef] [Google Scholar]
Rehman K.U., Shatanawi W., Abodayeh K., . A group theoretic analysis on heat transfer in MHD thermally slip Carreau fluid subject to multiple flow regimes (MFRs) Case Stud. Thermal Eng.. 2022;30:101787
[CrossRef] [Google Scholar]
Rosenhead L., Taylor G.I., . The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. R. Soc. Lond. A. 1940;175:436-467.
[CrossRef] [Google Scholar]
Sari M.R., Kezzar M., Adjabi R., . Heat transfer of copper/water nanofluid flow through converging-diverging channel. J. Cent. South Univ.. 2016;23:484-496.
[CrossRef] [Google Scholar]
Sarkar S., Jana R.N., Das S., . Activation energy impact on radiated magneto-Sisko nanofluid flow over a stretching and slipping cylinder: entropy analysis. Multidiscip. Model. Mater. Struct.. 2020;16:1085-1115.
[CrossRef] [Google Scholar]
Shashikumar N.S., Macha M., Gireesha B.J., Kishan N., . Finite element analysis of micropolar nanofluid flow through an inclined microchannel with thermal radiation. Multidiscip. Model. Mater. Struct.. 2020;16:1521-1538.
[CrossRef] [Google Scholar]
Shehzad S.A., Madhu M., Shashikumar N.S., Gireesha B.J., Mahanthesh B., . Thermal and entropy generation of non-Newtonian magneto-Carreau fluid flow in microchannel. J. Therm Anal. Calorim.. 2021;143:2717-2727.
[CrossRef] [Google Scholar]
Shukla N., Rana P., Pop I., . Second law thermodynamic analysis of thermo-magnetic Jeffery-Hamel dissipative radiative hybrid nanofluid slip flow: existence of multiple solutions. Eur. Phys. J. Plus. 2020;135:849.
[CrossRef] [Google Scholar]
Turkyilmazoglu M., . Velocity Slip and Entropy Generation Phenomena in Thermal Transport Through Metallic Porous Channel. J. Non-Equilib. Thermodyn.. 2020;45:247-256.
[CrossRef] [Google Scholar]
Veera Krishna M., . Hall and ion slip impacts on unsteady MHD free convective rotating flow of Jeffreys fluid with ramped wall temperature. Int. Commun. Heat Mass Transfer. 2020;119:104927
[CrossRef] [Google Scholar]
W, T.,, . Grenzschichttheorie. Handbuch Experimentalphysik. 1931;4:241-287.
[Google Scholar]
Weigand B., Birkefeld A., . Similarity solutions of the entropy transport equation. Int. J. Thermal Sci.. 2009;48:1863-1869.
[CrossRef] [Google Scholar]
Xu Y.-J., Shah F., Khan M.I., Naveen Kumar R., Punith Gowda R.J., Prasannakumara B.C., Malik M.Y., Khan S.U., . New modeling and analytical solution of fourth grade (non-Newtonian) fluid by a stretchable magnetized Riga device. Int. J. Mod. Phys. C. 2022;33:2250013.
[CrossRef] [Google Scholar]

Show Sections

[1] Abbasi F.M., Gul M., Shanakhat I., Anjum H.J., Shehzad S.A., . Entropy generation analysis for magnetized peristaltic movement of nanofluid through a non-uniform asymmetric channel with variable thermal conductivity. Chin. J. Phys.. 2022;78:111-131.
[CrossRef] [Google Scholar]

[2] Ahmad S., Hayat T., Alsaedi A., Ullah H., Shah F., . Computational modeling and analysis for the effect of magnetic field on rotating stretched disk flow with heat transfer. Propul. Power Res.. 2021;10:48-57.
[CrossRef] [Google Scholar]

[3] Ali A., Sarkar S., Das S., Jana R.N., . A report on entropy generation and Arrhenius kinetics in magneto-bioconvective flow of Cross nanofluid over a cylinder with wall slip. Int. J. Ambient Energy 2022:1-16.
[CrossRef] [Google Scholar]

[4] Al-Saif A.-S.-J.-A., Jasim A.M., . New analytical study of the effects thermo-diffusion, diffusion-thermo and chemical reaction of viscous fluid on magneto hydrodynamics flow in divergent and convergent channels. Appl. Math.. 2019;10:268-300.
[CrossRef] [Google Scholar]

[5] Asghar Z., Saif R.S., Ghaffari A.Z., . Numerical study of boundary stresses on Jeffery-Hamel flow subject to Soret/Dufour effects. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci.. 2022;09544062221126646
[CrossRef] [Google Scholar]

[6] Bég O.A., Uddin M.J., Bég T.A., Kadir A., Shamshuddin M.D., Babaie M., . Numerical study of self-similar natural convection mass transfer from a rotating cone in anisotropic porous media with Stefan blowing and Navier slip. Indian J Phys. 2020;94:863-877.
[CrossRef] [Google Scholar]

[7] Bejan A., . Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys.. 1996;79:1191-1218.
[CrossRef] [Google Scholar]

[8] Bejan A., . A Study of Entropy Generation in Fundamental Convective Heat Transfer. J. Heat Transfer. 1979;101:718-725.
[CrossRef] [Google Scholar]

[9] Bejan A., Kestin J., . Entropy Generation Through Heat and Fluid Flow. J. Appl. Mech.. 1983;50:475.
[CrossRef] [Google Scholar]

[10] Bhaskar K., Sharma K., Bhaskar K., . Cross-diffusion and chemical reaction effects of a MHD nanofluid flow inside a divergent/convergent channel with heat source/sink. J. Therm. Anal. Calorim. 2022
[CrossRef] [Google Scholar]

[11] Bilal S., Shah I.A., . A comprehensive physical insight about thermo physical aspects of Carreau fluid flow over a rotated disk of variable thickness by implementing finite difference approach. Propul. Power Res.. 2022;11:143-153.
[CrossRef] [Google Scholar]

[12] Carreau P.J., . Rheological equations from molecular network theories. Trans. Soc. Rheol.. 1972;16:99-127.
[CrossRef] [Google Scholar]

[13] Chen L., Zhang L., Xia S., Sun F., . Entropy generation minimization for CO₂ hydrogenation to light olefins. Energy. 2018;147:187-196.
[CrossRef] [Google Scholar]

[14] Chu Y.-M., Al-Khaled K., Khan N., Ijaz Khan M., Ullah Khan S., Sadiq Hashmi M., Azhar Iqbal M., Tlili I., . Study of Buongiorno’s nanofluid model for flow due to stretching disks in presence of gyrotactic microorganisms. Ain Shams Eng. J.. 2021;12:3975-3985.
[CrossRef] [Google Scholar]

[15] Chu Y.-M., Shah F., Khan M.I., Kadry S., Abdelmalek Z., Khan W.A., . Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. J. Mater. Res. Technol.. 2020;9:13977-13987.
[CrossRef] [Google Scholar]

[16] Cross M.M., . Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems. J. Colloid Sci.. 1965;20:417-437.
[CrossRef] [Google Scholar]

[17] Das S., Chakraborty S., Makinde O.D., Jana R.N., . Entropy analysis of MHD variable thermal conductivity fluid flow past a convectively heated stretching cylinder. Defect and Diffusion Forum. 2018;387:244-259.
[CrossRef] [Google Scholar]

[18] Das S., Sarkar S., Jana R.N., . Feature of entropy generation in Cu-Al₂O₃/Ethylene glycol hybrid nanofluid flow through a rotating channel. BioNanoSci.. 2020;10:950-967.
[CrossRef] [Google Scholar]

[19] Das S., Sarkar S., Jana R.N., . Entropy generation analysis of MHD Slip Flow of Non-Newtonian Cu-Casson nanofluid in a porous microchannel filled with saturated porous medium considering thermal radiation. J. Nanofluids. 2018;7:1217-1232.
[CrossRef] [Google Scholar]

[20] Fraenkel L.E., Squire H.B., . Laminar flow in symmetrical channels with slightly curved walls, I. On the Jeffery-Hamel solutions for flow between plane walls. Proc. Roy. Soc. London. Ser. A. Math. Phys. Sci.. 1962;267:119-138.
[CrossRef] [Google Scholar]

[21] Garimella S.M., Anand M., Rajagopal K.R., . Jeffery-Hamel flow of a shear-thinning fluid that mimics the response of viscoplastic materials. Int. J. Non Linear Mech.. 2022;144:104084
[CrossRef] [Google Scholar]

[22] Hamel G., . Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresber. Deutsch. Math.-Verein.. 1917;25:34-60.
[Google Scholar]

[23] Harley C., Momoniat E., Rajagopal K.R., . Reversal of flow of a non-Newtonian fluid in an expanding channel. Int. J. Non Linear Mech.. 2018;101:44-55.
[CrossRef] [Google Scholar]

[24] Hassan M., Mebarek-Oudina F., Faisal A., Ghafar A., Ismail A.I., . Thermal energy and mass transport of shear thinning fluid under effects of low to high shear rate viscosity. Int. J. Thermofluids. 2022;15:100176
[CrossRef] [Google Scholar]

[25] Hayat T., Shah F., Khan M., Alsaedi A., Yasmeen T., . Modeling MHD Stagnation Point Flow of Thixotropic Fluid with Non-uniform Heat Absorption/Generation. Microgravity Sci. Technol.. 2017;29
[CrossRef] [Google Scholar]

[26] Ibrahim M.G., . Adaptive simulations to pressure distribution for creeping motion of Carreau nanofluid with variable fluid density effects: physiological applications. Thermal Sci. Eng. Prog.. 2022;32:101337
[CrossRef] [Google Scholar]

[27] Jeffery G.B., . L. The two-dimensional steady motion of a viscous fluid. The London, Edinburgh, and Dublin Philosophical Magazine J. Sci.. 1915;29:455-465.
[CrossRef] [Google Scholar]

[28] Kamran A., Azhar E., . Numerical outlook of a viscoelastic nanofluid in an inclined channel via Keller box method. Int. Commun. Heat Mass Transfer. 2022;137:106260
[CrossRef] [Google Scholar]

[29] Khan M., Sardar H., Gulzar M.M., Alshomrani A.S., . On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Results Phys.. 2018;8:926-932.
[CrossRef] [Google Scholar]

[30] Khan U., Ahmed N., Mohyud-Din S., . Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels. Chem. Eng. Sci.. 2015;141
[CrossRef] [Google Scholar]

[31] Krishna M.V., Jyothi K., Chamkha A.J., . Heat and mass transfer on mhd flow of second-grade fluid through porous medium over a semi-infinite vertical stretching sheet. JPM. 2020;23
[CrossRef] [Google Scholar]

[32] Krishna M.V., Jyothi K., Chamkha A.J., . HEAT and mass transfer on unsteady, magnetohydrodynamic, oscillatory flow of second-grade fluid through a porous medium between two vertical plates, under the influence of fluctuating heat source/sink and chemical reactioN. FMR. 2018;45
[CrossRef] [Google Scholar]

[33] Krishna M.V., Swarnalathamma B.V., Chamkha A.J., . Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate. J. Ocean. Eng. Sci.. 2019;4:263-275.
[CrossRef] [Google Scholar]

[34] Madhu M., Shashikumar N.S., Gireesha B.J., Kishan N., . Thermal analysis of MHD Powell-Eyring fluid flow through a vertical microchannel. Int. J. Ambient Energy. 2022;43:4454-4462.
[CrossRef] [Google Scholar]

[35] Madhu M., Shashikumar N.S., Gireesha B.J., Kishan N., . Second law analysis of MHD micropolar fluid flow through a porous microchannel with multiple slip and convective boundary conditions. Defect Diffusion Forum. 2021;409:123-141.
[CrossRef] [Google Scholar]

[36] Mahanthesh B., Shehzad S.A., Mackolil J., Shashikumar N.S., . Heat transfer optimization of hybrid nanomaterial using modified Buongiorno model: a sensitivity analysis. Int. J. Heat Mass Transf.. 2021;171:121081
[CrossRef] [Google Scholar]

[37] Makinde O., Bég O., . On inherent irreversibility in a reactive hydromagnetic channel flow. J. Therm. Sci.. 2010;19:72-79.
[CrossRef] [Google Scholar]

[38] Mansutti D., Ramgopal K.R., . Flow of a shear thinning fluid between intersecting planes. Int. J. Non Linear Mech.. 1991;26:769-775.
[CrossRef] [Google Scholar]

[39] Nagler J., . Jeffery-Hamel flow of non-Newtonian fluid with nonlinear viscosity and wall friction. Appl. Math. Mech.-Engl. Ed.. 2017;38:815-830.
[CrossRef] [Google Scholar]

[40] Nayak M.K., Mabood F., Dogonchi A.S., Khan W.A., . Electromagnetic flow of SWCNT/MWCNT suspensions with optimized entropy generation and cubic auto catalysis chemical reaction. Int. Commun. Heat Mass Transfer. 2021;120:104996
[CrossRef] [Google Scholar]

[41] Ostwald W., . Ueber die rechnerische Darstellung des Strukturgebietes der Viskosität. Kolloid-Zeitschrift. 1929;47:176-187.
[CrossRef] [Google Scholar]

[42] Owhaib W., Al-Kouz W., . Three-dimensional numerical analysis of flow and heat transfer of bi-directional stretched nanofluid film exposed to an exponential heat generation using modified Buongiorno model. Sci. Rep.. 2022;12:10060.
[CrossRef] [Google Scholar]

[43] R, D.W., . Note on the divergent flow of fluid. Philos. Mag. 1934;18:759-777.
[Google Scholar]

[44] Ramesh G.K., Madhukesh J.K., Shehzad S.A., Rauf A., . Ternary nanofluid with heat source/sink and porous medium effects in stretchable convergent/divergent channel. Proc. Institution Mech. Engineers, Part E: J. Process Mech. Eng.. 2022;09544089221081344
[CrossRef] [Google Scholar]

[45] Rehman K.U., Shatanawi W., Abodayeh K., . A group theoretic analysis on heat transfer in MHD thermally slip Carreau fluid subject to multiple flow regimes (MFRs) Case Stud. Thermal Eng.. 2022;30:101787
[CrossRef] [Google Scholar]

[46] Rosenhead L., Taylor G.I., . The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. R. Soc. Lond. A. 1940;175:436-467.
[CrossRef] [Google Scholar]

[47] Sari M.R., Kezzar M., Adjabi R., . Heat transfer of copper/water nanofluid flow through converging-diverging channel. J. Cent. South Univ.. 2016;23:484-496.
[CrossRef] [Google Scholar]

[48] Sarkar S., Jana R.N., Das S., . Activation energy impact on radiated magneto-Sisko nanofluid flow over a stretching and slipping cylinder: entropy analysis. Multidiscip. Model. Mater. Struct.. 2020;16:1085-1115.
[CrossRef] [Google Scholar]

[49] Shashikumar N.S., Macha M., Gireesha B.J., Kishan N., . Finite element analysis of micropolar nanofluid flow through an inclined microchannel with thermal radiation. Multidiscip. Model. Mater. Struct.. 2020;16:1521-1538.
[CrossRef] [Google Scholar]

[50] Shehzad S.A., Madhu M., Shashikumar N.S., Gireesha B.J., Mahanthesh B., . Thermal and entropy generation of non-Newtonian magneto-Carreau fluid flow in microchannel. J. Therm Anal. Calorim.. 2021;143:2717-2727.
[CrossRef] [Google Scholar]

[51] Shukla N., Rana P., Pop I., . Second law thermodynamic analysis of thermo-magnetic Jeffery-Hamel dissipative radiative hybrid nanofluid slip flow: existence of multiple solutions. Eur. Phys. J. Plus. 2020;135:849.
[CrossRef] [Google Scholar]

[52] Turkyilmazoglu M., . Velocity Slip and Entropy Generation Phenomena in Thermal Transport Through Metallic Porous Channel. J. Non-Equilib. Thermodyn.. 2020;45:247-256.
[CrossRef] [Google Scholar]

[53] Veera Krishna M., . Hall and ion slip impacts on unsteady MHD free convective rotating flow of Jeffreys fluid with ramped wall temperature. Int. Commun. Heat Mass Transfer. 2020;119:104927
[CrossRef] [Google Scholar]

[54] W, T.,, . Grenzschichttheorie. Handbuch Experimentalphysik. 1931;4:241-287.
[Google Scholar]

[55] Weigand B., Birkefeld A., . Similarity solutions of the entropy transport equation. Int. J. Thermal Sci.. 2009;48:1863-1869.
[CrossRef] [Google Scholar]

[56] Xu Y.-J., Shah F., Khan M.I., Naveen Kumar R., Punith Gowda R.J., Prasannakumara B.C., Malik M.Y., Khan S.U., . New modeling and analytical solution of fourth grade (non-Newtonian) fluid by a stretchable magnetized Riga device. Int. J. Mod. Phys. C. 2022;33:2250013.
[CrossRef] [Google Scholar]

Thermohydraulic and irreversibility assessment of Power-law fluid flow within wedge shape channel

Abstract

Keywords

Irreversibility analysis

Wedge-shaped channel

Two-phase model

Power-law fluid

Nanofluid

Bejan profile

Nomenclature

1 Introduction

2 Modelling framework

2.1 Problem statement and underlying assumptions

2.2 Mathematical analysis

2.3 Thermal analysis

2.4 Mass concentration equation

2.5 Boundary conditions

2.6 Normalization mechanism

2.7 Entropy mechanism and Bejan analysis

2.8 Curiosity in engineering parameters

3 Numerical scheme for solution

3.1 Results validation

4 Declaration of result and discussion

4.1 Flow dynamics within wedge configuration

4.2 Thermal distribution phenomena

4.3 Concentration profile

4.4 Irreversibility analysis of Power-Law fluid

4.5 Quantities of physical interest

5 Conclusion

6 Future recommendation

Acknowledgement

Declaration of Competing Interest

References

Suggested read for related articles: