Translate this page into:
A significant impact of Carreau Yasuda material near a zero velocity region
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This goal of this study is to examine the incompressible steady 2D flow of MHD Carreau Yasuda model along with the heat generation and chemical reaction near a zero velocity region. The magnetic field and thermally conducting fluid towards a stretching cylinder are very significant due to its usage in the various manufacturing sector. Chemical reactions are widely practice in everyday life as turning nutrition into energy fuel for our body, food change, fireworks expulsions, removing grimes, photosynthesis, etc. The nonlinear flow model equations and their corresponding boundary conditions are changed into non-dimensional shape using similarity variables. The role of vital parameters is discussed with the assistance of MATLAB software by BVP4C method. It is concluded that the momentum increases for rising the curvature and stretching ratio parameter. This is examined that the heat field improves for rising behavior of the magnetic force, curvature coefficient and heat generation. The fluid concentration upsurges due to curvature and magnetic field parameter while reverse results shown due to chemical reaction parameter. We graphically investigate the impression of magnetic effect and chemical force for heat and mass profiles.
Keywords
Carreau Yasuda fluid model
Magnetohydrodynamic
Heat generation
Zero velocity
Chemical reaction
BVP4C
Nomenclature
-
Velocity components ( )
-
Carreau number
-
Cylindrical cordinates ( )
-
Power law index
-
Stretching velocity
-
Dimensionless velocity variable
-
Pressure ( )
-
Free stream velocity
-
Prandtl number
-
Heat Capacity ( )
-
Heat generation parameter
-
Weissenberg number
-
Non-dimensionless temperature (K)
-
Non-dimensionless concentration
-
Reynolds number
-
Temperature at infinity (K)
-
Concentration at infinity
-
Schmidt number
-
Hartmann number
-
Chemical reactive parameter
-
Velocity profile
-
Skin friction Coefficient
-
Mass diffusion parameter
-
Nusselt number
-
Sherwood number
-
Density of fluid ( )
-
Heat conductivity parameter ( )
-
Viscosity ( )
-
Similarity variable
-
Time relaxation parameter
-
Temperature profile
-
Concentration profile
Greek Symbols
1 Introduction
The boundary layer flow analysis across a stretching object has made a lot of interest in industrial engineering e.g. energy production, paper production, system of circulation, crystal growing and food industries. As a result, researchers have suggested a variety of models to examine the nature of non-Newtonian fluids. These models are second grade, Jeffrey model, Maxwell model, Casson model, power law model, third grade and Sisko fluids etc. Among these fluid models, the most suitable non Newtonian fluid is power law model and is the most comprehensive of all the proposed models and it can explains both properties of shear thinning and thickening fluid with two essential fluid parameters. The Carreau Yasuda model is also similar fluid that can explains the shear thinning and thickening properties via five key parameters. Therefore this model is the most effective model then the power law fluid. Mair et al. (Khan et al., 2019) observed the influence of diffusion on the Carreau–Yasuda fluid flow over a spinning channel under the slip effects and resulted that the fluid velocity improved by growing the slip parameter. Waqas et al. (Waqas et al., 2020) inspected the behavior of Carreau Yasuda nanofluid by using the velocity slip condition and effect of thermal radiation passes through the stretched surface. Hayat et al. (Hayat et al., 2014) considered the flow phenomenon of Carreau Yasuda model in a curve surface with slip effects and resulted that the variation in the velocity slip indicates reduction in the peristaltic region. Yesser et al. (Zare et al., 2019) presented the viscosity and shear thinning influence for the Carreau-Yasuda model. Abbasi et al. (Abbasi et al., 2015) examined the Carreau Yasuda model with MHD peristaltic transportation in a curve surface and indicated that the flow velocity in a curved surface was not symmetric around the centerline. Waqas et al. (Alloui and Vasseur, 2015) studied the magnetize Carreau Yasuda nanofluid with slip effect and thermal radiation and presented the importance of bio-convection in fluid flow. Alloui and Vasseur (Premlata et al., 2017) considered the Carreau–Yasuda fluid along with the natural convection in a vertically cavity warmed from the sides. Premlata et al. (Akbar et al., 2014) numerically studied the air bubble in a Carreau-Yasuda fluid and discussed the impact of flow index on fluid flow.
Magnetohydrodynamic has always remained the subject of study due to its significance in engineering applications like, liquid metal, electromagnetic casting and plasma confinement, etc. The magnetic field and thermally conducting fluid towards a stretching cylinder are very significant due to its usage in the various manufacturing sector. Akbar et al. (Bilal et al., 2018) presented the impression of magnetic field on the Eyring-Powell fluid model over a stretched object and revealed the importance of magnetize forces on the flow pattern. Bilal et al. (Ali et al., 2017) considered the theoretical study to observe the flow of Carreau fluid with magnetic field effects and presented that growing magnetic field parameter showed dropping trend in the momentum profile. Farhad et al. (Nourazar et al., 2017) presented numerical study to inspect the magnetic field influence on Casson fluid and resulted that the magnetic force decreases the velocity of magnetic particles. Nourazar et al. (Heidary et al., 2015) examined the heat transformation and nanomaterial fluid flow towards a porous stretched cylinder under magnetic effects and noted that rising magnetic field parameter increased thermal boundary layer and dropped the velocity field. Heidary et al. (Akbar et al., 2015) presented the thermal transformation and magnetic force influence on nanofluid flow in a straightly placed surface. Noreen et al. (Gholinia et al., 2018) scrutinized the flow of 2D Eyring–Powell fluid on a stretched object under magnetic force and demonstrated that the increasing impression of magnetic field indicates the resistance of flow. Gholinia et al. (Mekheimer, 2008) examined the incompressible MHD nanofluid model towards a circular cylinder along with mixed convection near a stationary point. Mekheimer (Akinshilo and Olaye, 2019) considered the impression of magnetic force on a peristaltic flow of couple stress fluid in a slit region.
The heat transformation phenomena are rapidly expanding in the liquid flow area due to their importance in engineering and industrial zone. Energy production, solar collectors, heat conduction in tissues, solar stills, space cooling, oil production, biomedical, thermal exchangers, electromagnetic pumps and energy producing systems are few examples. Akinbowale and Olaye (Malik et al., 2017) considered the impact of heat transformation and heat generation on the Erying Powell fluid model in a pipe and revealed that the thermal field improved for improving the heat generation parameter. Malik et al. (Rehman et al., 2016) investigated the Eyring-Powell fluid model on the cylinder with the heat generation and dual convection. The result shows that the improvement in heat profile was brought out for raising the heat generation parameter. Salahuddin et al. (Adesanya and Makinde, 2015) presented the heat generation impression for the Eyring-Powell flow model towards an incline stretched cylinder and resulted that the improving magnitude of thermal profile was observed by rising the heat generation parameter. Samuel and Makindet (Olanrewaju et al., 2012) considered the third grade flow model towards a vertical surface with influence of heat generation and presented that the heat profile upsurges for improving heat generation coefficient. Olanrewaju et al. (Ahmad et al., 2019) considered the laminar boundary layer flow towards a horizontal plate with thermal generation effect and showed the quick passage of heat from the bottom region to the top region of the plate was slowed by an increase in the internal heat generation.
Chemical reactions are widely practice in everyday life as turning nutrition into energy fuel for our body, food change, fireworks expulsions, removing grimes, photosynthesis, etc. Chemical reaction is primarily used to optimize feed composition, chemical reactors and operating conditions. Ahmad et al. (Mishra et al., 2017) presented analysis of MHD Jeffrey fluid model with chemical heat generation effects, the important parameters were graphically and numerically discussed. Mishra et al. (Arifuzzaman et al., 2019) considered the MHD viscoelastic fluid with the presence of chemical forces on stretching surface and presented the influence of chemical reactive and MHD forces on mass and thermal transformation. Arifuzzaman et al. (Hayat et al., 2008) presented the thermal and concentration characteristics of MHD 4th grade flow model over a porous plate along with the chemical forces and presented that the chemical reaction for large values showed decay in the concentration. Hayat et al. (Khan et al., 2019) observed flow study of a second grade flow model towards an infinite plate with the existence of chemical effect and scrutinized the impact of chemical reactive coefficient on mass transformation rate. Khan et al. (Krishna and Chamkha, 2019) explored the impact of temperature and generalize diffusivity effects on Maxwell nanomaterials with chemical reactive force. Heat generation and chemical reaction are extremely important due to their efficiency in a variety of engineering applications. Some recent published work related to my topic is cited in (Krishna et al., 2021; Krishna et al., 2020; Krishna et al., 2019; Krishna et al., 2019; Krishna and Chamkha, 2020; Krishna et al., 2021; Krishna et al., 2018; Krishna and Chamkha, 2018; Krishna et al., 2018; Haq et al., 2022; Zeeshan et al., 2021; Salahuddin et al., 2022; Song et al., 2022; Khan and Tlili, 2020; Al-Khaled and Khan, 2020; Wang et al., 2022; Venkata Ramudu et al., 2022; Buruju et al., 2021; Salahuddin et al., 2017; Qin et al., 2022; Nadeem et al., 2017; Salahuddin et al., 2021; Wang et al., 2022; Ahmad et al., 2022; Salahuddin et al., 2021; Anantha Kumar et al., 2020; Kumar et al., 2019; Anantha Kumar et al., 2020; Ahmad and Nadeem, 2020).
According to author’s best knowledge, no one has inspected the flow of Carreau Yasuda fluid passing on the stretching cylinder. The main inducement of this work is to examine the mass and heat transfer in incompressible steady 2D flow of MHD Carreau Yasuda model along with thermal generation, stagnation point and chemical reactive force towards a stretching cylinder. The ODEs are construed from the PDEs by similarity transformation. Here the solutions are attained by using BVP4C technique with assistance of Matlab software. The role of parameters is discussed for velocity, mass and heat fields.
2 Mathematical modeling
Consider the steady flow of MHD Carreau Yasuda model along with heat generation, stagnation point and chemical reaction over a stretching cylinder. The fluid is moving across the
direction that is normal to the
- axis of stretching cylindered as presented in Fig. 1.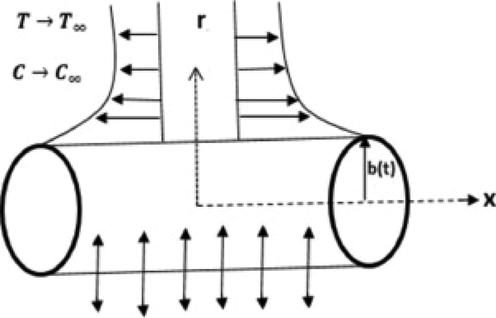
Geometry of the flow problem.
The leading equations (Yang et al., 2021; Kumar et al., 2019) are
near the stagnation region.
with the boundary conditions [58].
Where
are components of velocity along
directions,
is Carreau number,
is the electric charge density,
represents the power law index,
represents time constant,
is the viscosity,
shows stretching velocity and
indicates the free stream velocity. A stream function
can be used to justify the equation of continuity (1), where
and
, we define
and
as (Adesanya and Makinde, 2015).
Hence the momentum equation transforms into.
together with bc’s.
Where represents the stretching ratio parameter, Weissenberg number, Hartman number/magnetic field coefficient and curvature parameter. Where and are constants.
2.1 Heat and concentration equations
The transport analysis of energy and mass is investigated by taking the effects of heat generation coefficient and the chemical reaction parameter. The physical properties of fluid such as thermal conductivity and mass diffusion are assumed to be constant.
together with bc’s.
Where exhibits the specific heat, ( , ) indicates the concentration and temperature at surface, is the heat conductivity, represents density, expresses the concentration and heat away from the surface, indicates the heat generation coefficient and shows the mass diffusion energy.
Describing dimensionless heat and mass by.
so heat and concentration equations become.
together with bc’s.
Where and indicates the Prandtl number, chemical reactive parameter, Schmidt number and source heat generation, respectively.
The expressions of physical quantities are given as
Where is the Reynold number.
3 Numerical analysis
The nonlinear ordinary differential equations for momentum, heat and concentration equations (7), (13) and (14) along with the bc’s (8) and (15) are numerically studied by using BVP4C technique.
Let
hence the leading equations become.
together with bc’s.
The step size is taken to be 0.05, with tolerance 10-6, initial guess [1 0–1 0 0.5] and accuracy of order 4.
4 Discussion and results
The aim of this division is to reveal how the momentum/ velocity, mass and heat fields are affected and graphically displayed by a variety of parameters. Numerical computations are carried out by BVP4C technique.
4.1 Velocity
The velocity behavior is represented versus the curvature parameter
in Fig. 2 and the figure reveals the increasing value of curvature parameter marks rising trend in the velocity profile. As
so the radius of the object drops by improving the curvature parameter which marks the fluid interaction with surface decreases and lowest friction is seen hence speed of fluid improves in the boundary layer. The power law index
impact on the velocity distribution is drawn with the help of Fig. 3. The figure shows both the behavior of shear thinning and thickening due to changing the values of power law
. The enhancement in
for shear thinning and thickening shows drop in the fluid boundary layer thickness and velocity. The power law is the source of increment in the viscosity of fluid and higher viscosity means the reduction in the motion of fluid. It confirms that the upsurge in
reduces the field and prevents the fluid momentum. Fig. 4 reveals the role of Hartmann number
on the momentum. The progressive magnitude of Hartmann number
marks decreasing trend on the velocity field because Hartmann number is the relation of MHD force to viscous force hence, growing magnitude of
improves the magnetic force which decays the velocity distribution. Fig. 5 demonstrates the impression of stretching ratio number on the momentum distribution and it is observed that the rising value of
shows upward behavior in the velocity profile. Fig. 6 shows the impact of the Weissenberg number
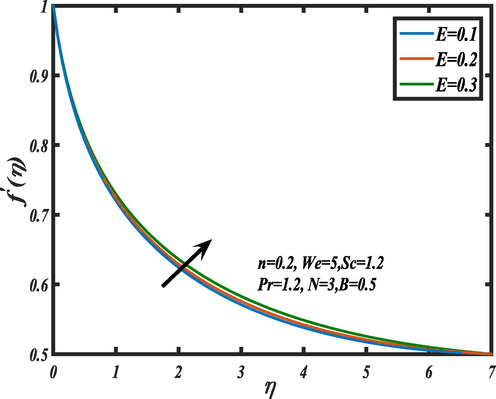
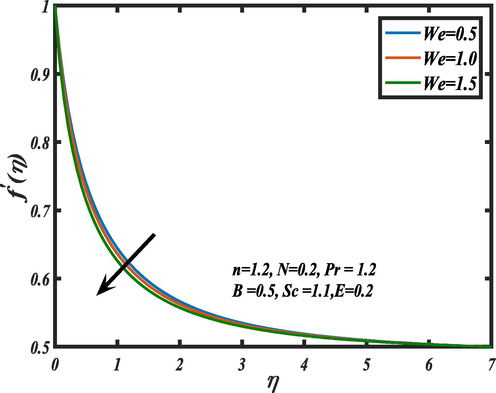
on the momentum distribution. The Weissenberg number is defined as the relation of the fluid's kinematic viscosity/process time to its relaxation time. So, increasing the Weissenberg number enhances the fluid particle's time relaxation hence the friction/fluid thickness progresses which present decay in velocity.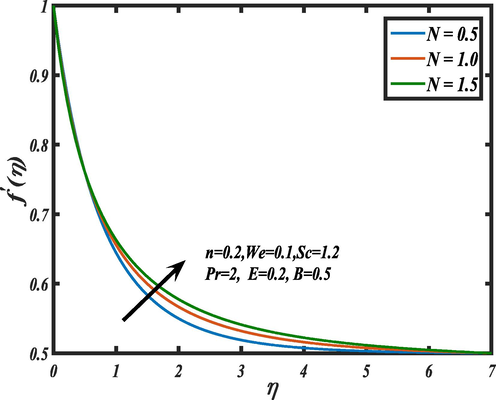
Influence of curvature
on
.
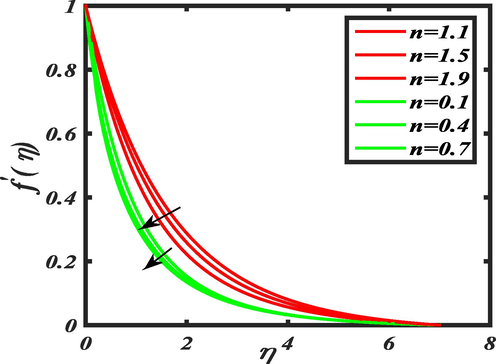
Influence of power index
on
Influence of magnetic field
on
Influence of stretching ratio parameter
on
Influence of Weissenberg number
on
4.2 Temperature
The curvature parameter
influence on a heat distribution is portrayed with the help of Fig. 7. We observe that improving of curvature parameter
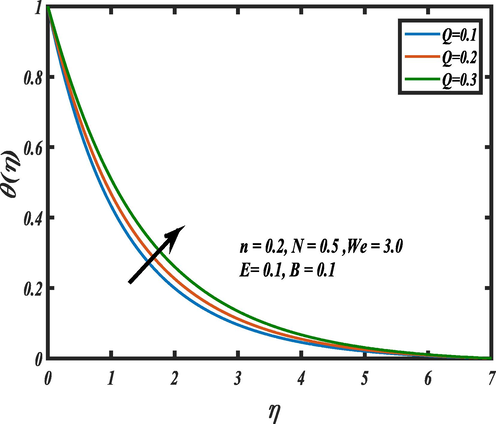
shows increasing trend in the heat profile because of the curvature parameter and radius has inverse relation. Outcome of the heat generation
is revealed in Fig. 8. It is shown that the progressive improvement of
resulted an upward trend in the heat profile. Physically, the coefficient of heat generation is the source to generate more heat in the system. Due to this higher impact of heat generation coefficient increases the temperature profile. Importance of the Prandtl number
on a heat field is presented with the assistance of Fig. 9. As
, so it illustrates the inversely relationship between the Prandtl
and heat conductivity
. Hence, the progressive behavior of the
presents reducing trend in the heat conductivity which results decay in the heat profile of the Carreau Yasuda fluid. The behavior of the magnetic forces
on the heat region is discussed with the assistance of Fig. 10 and it is witnessed that increase in the magnetic force marks rising trend on the heat field.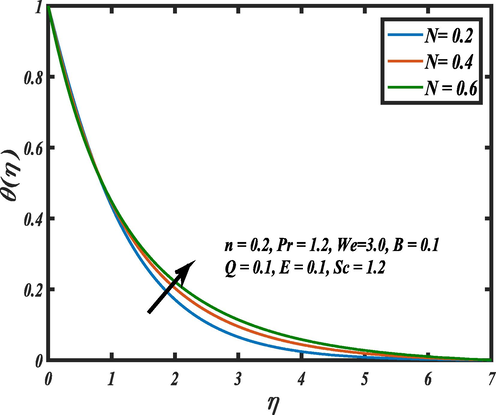
Influence of curvature
on
.
Influence of heat generation
on
.

Influence of Prandtl number
on
.
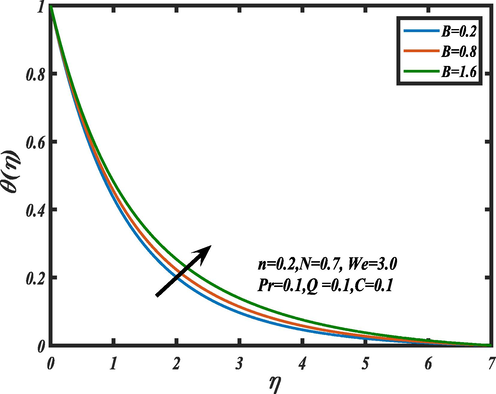
Influence of magnetic field on
.
4.3 Concentration
Fig. 11 reveals the importance of the chemical reaction corfficient
on the mass concentration of Carreau Yasuda fluid. It is noted that the growing magnitude of
presents downward trend in the mass concentration. Significance of the curvature number
is revealed in Fig. 12 and it illustrates that the increase in
marks upward trend in the concentration field and also increases the boundary layer thickness. The magnetic force impression
on the mass concentration of Carreau Yasuda fluid is drawn on Fig. 13. It is well-known that the progressive growth of
results upsurge in the mass concentration field.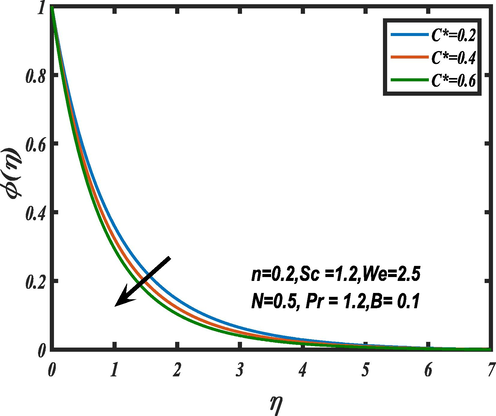
Influence of chemical reaction
on
.
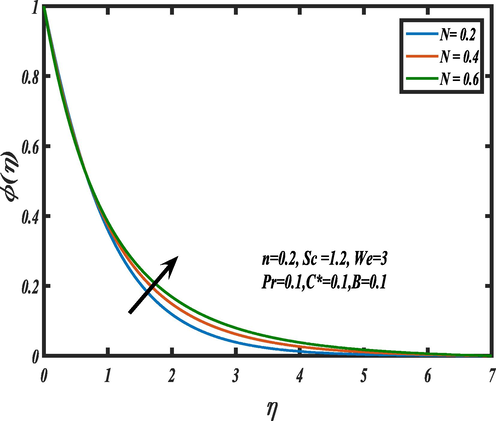
Influence of curvature parameter
on
.
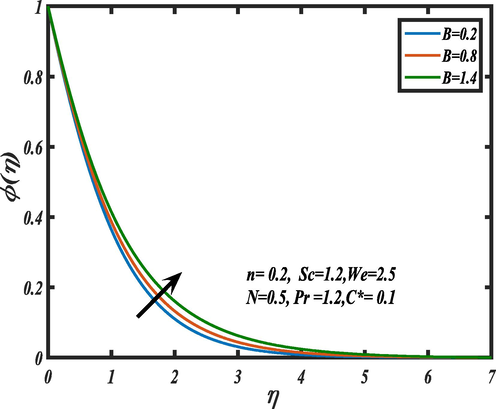
Influence of magnetic field
on
.
Table 1 exhibits the numerical influence of curvature parameter
, heat generation coefficient
and
is investigated here. The decreasing impact noted due to higher values of curvature coefficient and Prandtl number while increment happens due to heat generation coefficient. Table 2 displayed the influence of curvature parameter
, chemical reaction coefficient
and Schmidt number
on Sherwood number. The numerical behavior shows the drop in Sherwood number happens by increasing the values of chemical reaction, curvature coefficient and Schmidt number.
0.1
0.1
0.1
−0.2717
0.2
0.1
0.1
−0.3317
0.3
0.1
0.1
−0.3989
0.2
0.1
−0.2544
0.3
0.1
−0.2365
0.4
0.1
−0.2178
0.2
−0.3186
0.3
−0.3666
0.4
−0.4139
0.1
0.1
0.1
−0.3044
0.2
0.1
0.1
−0.3671
0.3
0.1
0.1
−0.4260
0.2
0.1
−0.3199
0.3
0.1
−0.3350
0.4
0.1
−0.3496
0.2
−0.3763
0.3
−0.4430
0.4
−0.5047
5 Conclusion
The investigation of incompressible steady 2D flow of MHD Carreau Yasuda model along with thermal generation, stagnation point and chemical reactive force through a stretched cylinder. The role of vital parameters is graphically discussed with the assistance of MATLAB software BVP4C.
The conclusion shows that the velocity profile enhances for growing the curvature parameter and stretching ratio parameter Also the velocity profile decays for progressive magnitude of the Weissenberg number , power index and magnetic field On the other hand, heat profile improves for rising behavior of the magnetic field curvature parameter and heat generation , while heat profile decreases for improvement of the Prandtl number The impact of key parameters on concentration field shows that shows upward trend happens for improving the magnetic field and curvature parameter . The chemical reaction coefficient expresses the decay in the concentration field.
The boundary layer flow of non-Newtonian fluid with magnetohydrodynamic across a stretching surface has lots of significance in industrial engineering such as energy production, system of circulation, electromagnetic casting, paper production, plasma confinement, liquid metal, crystal growing and food industries.
Acknowledgements
The author’s work was funded by the Deanship of Scientific Research (Project No.: RGP2/214/43), King Khalid University, Abha, K.S.A. The authors, Basem Al Alwan, therefore, acknowledge with thanks to DSR and the Chemical Engineering Department in the College of Engineering Department (KKU) for financial and technical support.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Reference
- Numerical analysis for MHD peristaltic transport of Carreau-Yasuda fluid in a curved channel with Hall effects. J. Magn. Magn. Mater.. 2015;382:104-110.
- [Google Scholar]
- Thermodynamic analysis for a third grade fluid through a vertical channel with internal heat generation. J. Hydrodyn.. 2015;27(2):264-272.
- [Google Scholar]
- A comparative study and analysis of natural convection flow of MHD non-Newtonian fluid in the presence of heat source and first-order chemical reaction. J. Therm. Anal. Calorim.. 2019;137(5):1783-1796.
- [Google Scholar]
- Hybridized nanofluid with stagnation point past a rotating disk. Phys. Scr.. 2020;96(2):025214
- [Google Scholar]
- Enhanced transport properties and its theoretical analysis in two-phase hybrid nanofluid. Appl. Nanosci.. 2022;12(3):309-316.
- [Google Scholar]
- MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: dual solutions. Ain Shams Eng. J.. 2014;5(4):1233-1239.
- [Google Scholar]
- Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater.. 2015;382:355-358.
- [Google Scholar]
- On the analysis of the Erying Powell model based fluid flow in a pipe with temperature dependent viscosity and internal heat generation. J. King Saud Univ.-Eng. Sci.. 2019;31(3):271-279.
- [Google Scholar]
- Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: a fractional model. J. Magn. Magn. Mater.. 2017;423:327-336.
- [Google Scholar]
- Thermal aspects of casson nanoliquid with gyrotactic microorganisms, temperature-dependent viscosity, and variable thermal conductivity: bio-technology and thermal applications. Inventions. 2020;5(3):39.
- [Google Scholar]
- Natural convection of Carreau-Yasuda non-Newtonian fluids in a vertical cavity heated from the sides. Int. J. Heat Mass Transf.. 2015;84:912-924.
- [Google Scholar]
- Influence of viscous dissipation on MHD flow of micropolar fluid over a slendering stretching surface with modified heat flux model. J. Therm. Anal. Calorim.. 2020;139(6):3661-3674.
- [Google Scholar]
- Effect of thermal radiation on MHD Casson fluid flow over an exponentially stretching curved sheet. J. Therm. Anal. Calorim.. 2020;140(5):2377-2385.
- [Google Scholar]
- Hydrodynamic stability and heat and mass transfer flow analysis of MHD radiative fourth-grade fluid through porous plate with chemical reaction. J. King Saud Univ.-Sci.. 2019;31(4):1388-1398.
- [Google Scholar]
- Analysis of Carreau fluid in the presence of thermal stratification and magnetic field effect. Results Phys.. 2018;10:118-125.
- [Google Scholar]
- Impact of Soret and Dufour on MHD mixed convective flow of non-Newtonian fluid over a coagulated surface. Heat Transf.. 2021;50(8):8243-8258.
- [Google Scholar]
- Investigation on ethylene glycol nano fluid flow over a vertical permeable circular cylinder under effect of magnetic field. Results Phys.. 2018;9:1525-1533.
- [Google Scholar]
- Theoretical investigation of radiative viscous hybrid nanofluid towards a permeable surface of cylinder. Chin. J. Phys.. 2022;77:2761-2772.
- [Google Scholar]
- Peristaltic transport of Carreau-Yasuda fluid in a curved channel with slip effects. PLoS ONE. 2014;9(4):e95070.
- [Google Scholar]
- T. Hayat, Z. Abbas and M. Sajid, Heat and mass transfer analysis on the flow of a second grade fluid in the presence of chemical reaction. Physics letters A, 372(14 (2008) 2400-2408.
- Numerical study of magnetic field effect on nano-fluid forced convection in a channel. J. Magn. Magn. Mater.. 2015;374:11-17.
- [Google Scholar]
- S. U. Khan and I. Tlili, Significance of activation energy and effective Prandtl number in accelerated flow of Jeffrey nanoparticles with gyrotactic microorganisms, Journal of energy resources technology, 142(11), (2020), 112101-1.
- Generalized diffusion effects on Maxwell nanofluid stagnation point flow over a stretchable sheet with slip conditions and chemical reaction. J. Braz. Soc. Mech. Sci. Eng.. 2019;41(3):1-9.
- [Google Scholar]
- Impact of enhancing diffusion on Carreau-Yasuda fluid flow over a rotating disk with slip conditions. J. Braz. Soc. Mech. Sci. Eng.. 2019;41(2):1-8.
- [Google Scholar]
- Hall effects on unsteady MHD flow of second grade fluid through porous medium with ramped wall temperature and ramped surface concentration. Phys. Fluids. 2018;30(5):053101
- [Google Scholar]
- Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int. Commun. Heat Mass Transf.. 2020;113:104494
- [Google Scholar]
- Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates. Phys. Fluids. 2018;30(2):023106
- [Google Scholar]
- Hall effects on MHD peristaltic flow of Jeffrey fluid through porous medium in a vertical stratum. Interf. Phenomena Heat Transf.. 2018;6(3)
- [Google Scholar]
- Heat and mass transfer on MHD free convective flow over an infinite nonconducting vertical flat porous plate. Int. J. Fluid Mech. Res.. 2019;46(1)
- [Google Scholar]
- Heat and mass transfer on free convective flow of amicropolar fluid through a porous surface with inclined magnetic field and hall effects. Special Topics Rev. Porous Media: Int. J.. 2019;10(3)
- [Google Scholar]
- Heat and mass transfer on MHD flow of second-grade fluid through porous medium over a semi-infinite vertical stretching sheet. J. Porous Media. 2020;23(8)
- [Google Scholar]
- Heat and mass transfer on unsteady MHD flow through an infinite oscillating vertical porous surface. J. Porous Media. 2021;24(1)
- [Google Scholar]
- Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng.. 2021;27:101229
- [Google Scholar]
- Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys.. 2019;15:102652
- [Google Scholar]
- Simultaneous solutions for first order and second order slips on micropolar fluid flow across a convective surface in the presence of Lorentz force and variable heat source/sink. Sci. Rep.. 2019;9(1):1-14.
- [Google Scholar]
- MHD stagnation point flow of Willianson and Casson fluids past an extended cylinder: a new heat flux model. SN Appl. Sci.. 2019;1:705.
- [Google Scholar]
- Numerical analysis for MHD thermal and solutal stratified stagnation point flow of Powell-Eyring fluid induced by cylindrical surface with dual convection and heat generation effects. Results Phys.. 2017;7:482-492.
- [Google Scholar]
- Effect of the induced magnetic field on peristaltic flow of a couple stress fluid. Phys. Lett. A. 2008;372(23):4271-4278.
- [Google Scholar]
- Analysis of heat and mass transfer with MHD and chemical reaction effects on viscoelastic fluid over a stretching sheet. Indian J. Phys.. 2017;91(10):1219-1227.
- [Google Scholar]
- Chemically reactive species in the flow of a Maxwell fluid. Results Phys.. 2017;7:2607-2613.
- [Google Scholar]
- Thermal-flow boundary layer analysis of nanofluid over a porous stretching cylinder under the magnetic field effect. Powder Technol.. 2017;317:310-319.
- [Google Scholar]
- Internal heat generation effect on thermal boundary layer with a convective surface boundary condition. Am. J. Fluid Dyn.. 2012;2(1):1-4.
- [Google Scholar]
- Numerical and experimental investigations of an air bubble rising in a Carreau-Yasuda shear-thinning liquid. Phys. Fluids. 2017;29(3):033103
- [Google Scholar]
- Thermal and solutal transport analysis of Blasius–Rayleigh–Stokes flow of hybrid nanofluid with convective boundary conditions. Waves Random Complex Medium. 2022;1–19
- [Google Scholar]
- Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. AIP Adv.. 2016;6(7):075112
- [Google Scholar]
- MHD squeezed flow of Carreau-Yasuda fluid over a sensor surface. Alexand. Eng. J.. 2017;56(1):27-34.
- [Google Scholar]
- Variable thermo-physical characteristics of Carreau fluid flow by means of stretchable paraboloid surface with activation energy and heat generation. Case Stud. Therm. Eng.. 2021;25:100971
- [Google Scholar]
- A flow study of Carreau fluid near the boundary layer region of paraboloid surface with viscous dissipation and variable fluid properties. J. Mater. Res. Technol.. 2021;14:901-909.
- [Google Scholar]
- A noteworthy impact of heat and mass transpiration near the unsteady rare stagnation region. Pramana. 2022;96(1):1-8.
- [Google Scholar]
- Unsteady mixed convection flow of magneto-Williamson nanofluid due to stretched cylinder with significant non-uniform heat source/sink features. Alexand. Eng. J.. 2022;61(1):195-206.
- [Google Scholar]
- Impact of Soret and Dufour on MHD Casson fluid flow past a stretching surface with convective–diffusive conditions. J. Therm. Anal. Calorim.. 2022;147(3):2653-2663.
- [Google Scholar]
- Numerical simulation of hybrid Casson nanofluid flow by the influence of magnetic dipole and gyrotactic microorganism. Waves Random Complex Medium. 2022;1–16
- [Google Scholar]
- Entropy optimized flow of Darcy-Forchheimer viscous fluid with cubic autocatalysis chemical reactions. Int. J. Hydrogen Energy. 2022;47(29):13911-13920.
- [Google Scholar]
- Significance of bioconvection in chemical reactive flow of magnetized Carreau-Yasuda nanofluid with thermal radiation and second-order slip. J. Therm. Anal. Calorim.. 2020;140(3):1293-1306.
- [Google Scholar]
- D. Yang, M. Israr Ur Rehman, A. Hamid and S. Ullah, Multiple solutions for stagnation-point flow of unsteady carreau fluid along a permeable stretching/shrinking sheet with non-uniform heat generation, Coatings, 11(9), (2021), 1012.
- Analysis of complex viscosity and shear thinning behavior in poly (lactic acid)/poly (ethylene oxide)/carbon nanotubes biosensor based on Carreau-Yasuda model. Results Phys.. 2019;13:102245
- [Google Scholar]
- Energy analysis of non-Newtonian nanofluid flow over parabola of revolution on the horizontal surface with catalytic chemical reaction. Heat Transf.. 2021;50(6):6189-6209.
- [Google Scholar]







