Translate this page into:
Experimental analysis and thermodynamic modelling of Nitroxynil solubility in pure solvent and binary solvent
⁎Corresponding author. fuhl2005@sohu.com (Hualin Fu)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
Nitroxynil(NIT) is a commonly used anti-liver fluke drug for cattle and sheep, Its solubility is closely related to its preparation. In this work, the molar solubility of NIT in nine pure solvents (methanol, ethanol, 1,2-propanediolethyl, isopropanol, ethyl acetate, acetonitrile, n-butanol, phemethylol) and two kinds of binary mixtures with different ratio(ethanol + phemethylol; ethanol + acetonitrile) was determined by shake flask method over the temperature from 278.15 ∼ 323.15 K at atmosphere pressure. Results show that the solubility of NIT in all tested solvents was increased with raised temperature. In mono-solvents, the mole fraction solubility of NIT was highest in phemethylol and the solubility order is: phemethylol > acetonitrile > ethyl acetate > methanol > n-butanol > ethanol > 1,2-propanediolethyl > isopropanol > water. In binary solvents, the mole fraction solubility increased with increasing ratio of phemethylol/acetonitrile. In mono-solvents, the modified Apelblat equation, λh equation, Van't Hoff model were applied to correlate the solubility data. In binary solvents, the modified Apelblat equation, λh equation, GSM model and Jouyban-Acree model were to correlate the solubility data. Solubility order of NIT in nine pure solvent and two binary solvent systems were analysed by using the Hansen solubility parameter (HSP). Activity coefficient was to access the solute–solvent molecular interactions. In addition, the dissolution of NIT is an endothermic and entropy-friendly process, since thermodynamic parameters such as enthalpy, entropy, and apparent standard Gibbs free energy are all greater than zero. The results will supply some essential data on recrystallization process, purification and formulation development of NIT in pharmaceutical applications.
Keywords
Nitroxynil
Solubility
Hansen solubility parameters (HSPs)
Activity coefficient
Dissolution thermodynamics

1 Introduction
Solubility is a physical property that shows the thermodynamic balance of active pharmaceutical ingredients in solid–liquid mixtures. Among all the parameters during crystallization process, solid–liquid equilibrium data is of great importance to contribute to the design and optimization of purification processes(Akay et al., 2021). It should be noted that according to FDA, solubility and permeability are the sole critical factors in determining generic bioequivalence(Rezaei et al., 2021). Thus, the determination of solubility of drugs in different cosolvent media is significant, which can supply some reference for future developments.
Nitroxynil (NIT) is an anthelmintic veterinary drug; Its chemical name is 4-hydroxy-3-iodo-5-nitrobenzonitrile(molecular formula: C7H3IN2O3; molar mass: 290.01 g•mol−1 and CASRN:1689–89-0;Figure. S1), which has been found as a yellow crystalline powder, almost odorless, slightly soluble in water, soluble in ethanol, ether and other organic solvents(Soliman et al., 2021). Corbett et al.(Corbett and Goose, 1971) studied the effect of NIT on mitochondrial function of mice liver cells, and proved that it is a kind of uncoupling agent for oxidative phosphorylation, it leads to death by blocking oxidative phosphorylation, reducing ATP concentration and reducing the energy required for cell division. A drug can only perform its pharmacological effects if it binds to a specific receptor, so it must exist in dissolved form before it can cross the gut barrier. This means that only soluble drugs can be used in the absorption process(Azarmi et al., 2007). Therefore, the solubility of drugs is closely related to the absorption of drugs in living organisms. To some extent, only understanding the solubility of a drug in a solvent can make it more effective. So far, the experimental solubility data of NIT in various kinds of solvent have not been systematically researched. Therefore, it is necessary to systematically measure the solubility of NIT in different solvent systems and predict solubility behavior using thermodynamic models. Besides, The single solvent we selected is a common solvent in pharmaceutical process, and the choice of binary solvent also provides a theoretical basis for the recrystalization and purification of NIT.
The main objectives of the study are to determine the solubility of NIT in nine pure solvents (methanol, ethanol, 1,2-propanediolethyl, isopropanol, ethyl acetate, acetonitrile, n-butanol, phemethylol) and two kinds of binary mixtures with different ratio (ethanol + phemethylol; ethanol + acetonitrile) at temperatures ranging from 278.15 K to 323.15 K under atmospheric pressure (p = 0.1 MPa). Afterwards, experimetal solubility results were correlated by different solubility models, the modified Apelblat model, the λh model, Van't Hoff model, GSM equation and Jouyban-Acree model(Li et al., 2017). Based on the concept of linear solvation energy relationship, Hansen solubility parameters (HSPs) were calculated to investigate the effect of solvents on the solid–liquid equilibrium process of NIT. Furthermore, the thermodynamic properties in dissolution, that is, the change of enthalpy (ΔH0sol), entropy (ΔS0sol) and Gibbs free energy (ΔG0sol), were calculated(Shekaari et al., 2018). The solubility data, solubility parameters and other physicochemical parameters of NIT obtained in this research could be useful in purification, recrystallization, drug discovery, pre-formulation studies and formulation on development of NIT, especially in liquid dosage forms.(Alshehri and Shakeel, 2020).
2 Materials and methods
2.1 Materials
Nitroxinil was purchased from Huana Chemicals Co., ltd. The more information of the solvents used in this study was presented in Table S1.
2.2 Experimental procedure for solubility determination
The solubility measurement method was similar to our previous literature(Chen et al., 2020). In this paper, the solubility of NIT was determined by gravimetric analysis in mono solvents and binary solvent mixtures. NIT concentrations were determined after appropriate gravimetric dilution with pure acetonitrile by measuring the UV light absorbance at the wavelength of second largest absorbance, 400 nm UV/visible spectrophotometry, followed by interpolation from a previously constructed UV spectrophotometric gravimetriccalibration curve(Osorio et al., 2020). In order to obtain an accurate solubility, the reported solubility data is the averages of at least three measurements. The mole fraction solubility (x) of NIT can be obtained by the Eq. (1).
2.3 Characterization methods
Differential scanning calorimetry (DSC) and powder X-ray diffractometry (PXRD) were used to characterize NIT in solid phases. DSC measurement was carried out by DSC-200F Instrument (NETZSCH Scientific Instruments Trading (Shanghai) ltd., Germany). Sapphire was selected as the reference. 6.05 mg NIT was put into a alumina pan and measured in the range of 293.15 K to 473.15 K at heating rate of 10 K•min−1 under a N2 atmosphere (100 mL•min−1). PXRD analysis of raw and equilibrated NIT was performed using DX-2800 Diffractometer (Haoyuan Instrument Co., ltd., China). The 2θ range for recording these spectra was set at 2-70° with a scan speed of 3.0° min−1(Wei et al., 2021).
2.4 Hansen solubility parameters (HSPs)
Hansen dissolvability coefficient was employed in this study to clarify the dissolution characteristics of solid in the solvents. The overall HSP (δt) is determined as Eq (2)🙁Yang et al., 2019)(Brett, 2007)
Where δd, δp and δh separately denote dispersion, polar and hydrogen bonded coefficients for Hansen dissolvability. The total and partial Hansen solubility parameters for NIT are estimated by way of group contribution method proposed by Hoftyzer and van Krevelen as Eq (3)-(5) (Shen et al., 2021)(Liu et al., 2021) (Mohammad et al., 2011)
The HSPs of commonly used solvents can be found in many published literatures, while the HSPs for selected binary solvents mixture (
) can be calculated by Eq.(6)(Li et al., 2021)
Herein, the superscript of 1 and 2 represent the solvent ethanol and (phemethylol, acetonitrile) respectively, and α represents the volume fraction of positive solvent 1 in the binary solvents mixture.The HSPs (δt, δd, δp and δh) of the selected two binary solvents as listed in Tables S3.
The Bagley diagram with a two-dimensional plot of the volume-dependent solubility parameter δv against δH has been used in the miscibility investigations and predictions the duration of intestinal absorption for various drugs, δv can be described as Eq.(7)
and subsequently the Ra(v) factor was used to determine the miscibility as Eq.(8)
Ra can be employed to show the miscibility/solubility between solvent and solute. If the solute has better solubility, the Ra magnitude should be<5.6 MPa1/2. So one may estimate the solvent property for solute solubility in terms of the Ra value. The higher the Ra value is, the poor solute solubility will be. The case is vice versa. As a result, the magnitude of Ra < 5.6 MPa1/2 is suggested for better solubility of a solute(Huang et al., 2021)(Mohammad et al., 2011).
Recently, the difference of total solubility parameters (Δδt and Δδ) between the solute and solvent has been used as a tool to predict miscibility as Eq.(9)-(10)(Li et al., 2021):
The HSPs (δt, δd, δp and δh) of the selected nine pure solvents can be obtained directly from the literatures(Huang et al., 2021) (Zhang et al., 2021)(Sha et al., 2021a) (Cao et al., 2020), which was listed in Tables S3.
3 Solid-liquid equilibrium models
The solubility data of NIT in different pure solvents and mixture solvents were correlated by various thermodynamic models, such as the modified Apelblat equation, λh equation, Jouyban-Acree equation, GSM equation were employed to correlate the NIT solubility in different solvents.
3.1 Modified Apelblat model
The modified Apelblat model has already been one of the most commonly and widely used models in solubility correlation and prediction, especially in engineering applications.This model can give the variation trend of solubility with temperature in the same proportion of solvent, and the correlation with the three parameters is relatively accurate (Shen et al., 2021) (Liu et al., 2021):
Where a, b and c are the empirical parameters, a and b have the same meaning as in the modified Apelblat model, the value of c represents the effect of temperature on the fusion enthalpy.
3.2 λh model
The λh equation is a semi-empirical model and can be used to correlate the experimental solubility data for the solid–liquid equilibrium systems (Jia et al., 2021),
Where × is the mole fraction of NIT in different solutions, T stands for the absolute temperature and Tm is the standard melting point of Kelvin temperature. λ and h are determined by correlation of solubility data.
3.3 GSM model
GSM equation was used to calculate the solubility in binary solvents which is one of the theoretical models (Chen et al., 2020), The model is presented as Eq. (13)
Where a, b, c, d and e were the model's five parameters, x0j refers to theinitial mole fraction of ethanol under the assumption of solute is not present.
3.4 Jouyban-Acree model
The Jouyban-Acree model is suggested to describe the solubility of a solute with the variation of both temperature and initial composition of binary solvent mixtures(Yang et al., 2021). The model was presented as Eq. (14)
In GSM Eq. (13), (xj)T and (xi)T can be obtained based on Van't Hoff in the above. When n = 2, a new equation (15) which called Van’t-JA model can be obtained.
Introducing constant parameters (V0 to V6) to Eq. (15), it can be further simplified as Eq. (16).
3.5 Evaluation of thermodynamic models
In order to evaluate the applicability of the tested models, the root-mean-square deviations (RMSD) were calculated as follows equation (17)(R. Sun et al., 2021).
Where N refers the number of experimental data points, xexp and xcal denote the experimental data and model predicted data, respectively.
4 Results and discussion
4.1 Characterization of NIT in solid phases
The solid phases of pure and equilibrated NIT were characterized using DSC and PXRD techniques. The representative DSC spectra of pure NIT is presented in Figure S2. It can be seen that there is a sharp exothermic peak at 402.62 K, which indicates the melting temperature of NIT is 402.62 K and the fusionenthalpy (ΔfusH) is calculated to be 42.75 kJ/mol(Alanazi et al., 2020). At present, no literatureshave reported the Tm value and ΔfusH of NIT. The differences of sample sources, measurement methods and environments(such as heating rates), purity and purification method may be the factor resulting in slightdeviations of melting point and fusion enthalpy between experiment value and literature data(Huang et al., 2021).
The crystalline state for raw material and samples gained from the solution of NIT after dissolution equilibrium were tested by the XRPD and were depicted in Figure S3. From Figure S3, it can be found that no new characteristic peaks were observed, which suggested that no crystal form transition occurred during the dissolution process of NIT in all pure solvents studied. Note that the minor differences among PXRD patterns in peak intensity is likely due to the preferred orientation of samples(Asadi et al., 2020)(Jouyban et al., 2020).
4.1.1 In pure solvents
The studied organic solvents consist of a ester solvent, a nitrile compound and six alcohol solvents. It is obvious that the maximum solubility is in phemethylol and the solubility order in pure solvents is: phemethylol > acetonitrile > ethyl acetate > methanol>n-butanol>ethanol>1,2-propanediolethyl>isopropanol>water, whose sequence was not completely consistent with the polar sequence of solvents(water>methanol>ethanol>phemethylol>n-butanol>isopropanol>acetonitrile>ethyl acetate). The experimental data indicates that the “like dissolves like” rule is not the only factor to determine the solubility of NIT. It is known to all that the solubility of solute was not only influenced by polarity of the solvent, but decided by the size of molecular, spatial conformation, solvent–solute interaction and other factors. The solubility is the result of the comprehensive influence of all factors(W. Sun et al., 2021).
The solubility values of NIT in the chosen mono-solvents of at temperature from 278.15 K to 323.15 K are listed in Table 1 and presented graphically in Fig. 1. It can be seen clearly from the trend graph that the solubility of the compound increased with increasing temperature in nine pure solvents, The solubility of NIT in phemethylol, acetonitrile and ethyl acetate increased significantly with the increase of temperature, even a saturation trend was not reached at the test temperature; On the contrary, in methanol, n-butanol, ethanol, 1,2-propanediolethyl, isopropanol and water, the value did not increase significantly with the increase of temperature, but showed a gentle trend. Experimental data indicate that those with similar structures may be mutually soluble, phemethylol and NIT contain benzene rings, therefore, NIT has the highest solubility in phemethylol. Moreover, NIT and acetonitrile are nitrile compounds. The effect of structural similarity on the solubility of NIT was greater than that of polar similarity. xApel, xλh indicate the calculated mole fraction solubility of NIT obtained by the modified Apelblat model, λh model respectively.
T/K
103xexp
103xApel
103xλh
103xexp
103xApel
103xλh
water
methanol
278.15
0.66
0.65
0.66
9.50
8.87
8.99
283.15
0.74
0.71
0.72
10.94
10.13
10.22
288.15
0.77
0.79
0.79
11.16
11.55
11.59
293.15
0.88
0.86
0.86
12.02
13.13
13.13
298.15
0.96
0.95
0.94
14.47
14.91
14.86
303.15
1.02
1.04
1.03
16.61
16.88
16.79
308.15
1.13
1.14
1.13
20.39
19.08
18.97
313.15
1.20
1.25
1.24
20.50
21.52
21.43
318.15
1.39
1.36
1.36
25.07
24.22
24.21
323.15
1.51
1.49
1.50
26.95
27.22
27.37
ethanol
1,2-propanediolethyl
278.15
7.48
7.22
7.38
6.86
6.14
6.64
283.15
8.12
8.1
8.2
7.45
6.96
7.40
288.15
9.46
9.07
9.1
8.60
7.87
8.24
293.15
10.11
10.13
10.1
8.83
8.89
9.17
298.15
10.97
11.29
11.21
10.21
10.01
10.21
303.15
12.19
12.56
12.44
10.96
11.25
11.36
308.15
14.10
13.94
13.82
12.35
12.62
12.64
313.15
14.85
15.44
15.35
14.47
14.13
14.09
318.15
17.22
17.08
17.08
15.55
15.79
15.71
323.15
19.24
18.86
19.04
17.75
17.62
17.54
isopropanol
ethyl acetate
278.15
5.17
5.14
5.24
79.35
79.69
77.55
283.15
6.09
5.78
5.85
85.91
91.48
90.15
288.15
6.83
6.49
6.52
99.12
104.74
104.24
293.15
7.52
7.27
7.26
118.80
119.64
119.90
298.15
7.86
8.13
8.08
142.41
136.35
137.24
303.15
8.48
9.07
9.00
162.33
155.04
156.34
308.15
9.65
10.10
10.02
179.60
175.92
177.31
313.15
11.06
11.23
11.17
196.90
199.19
200.23
318.15
12.93
12.47
12.46
224.39
225.09
225.17
323.15
13.97
13.81
13.93
250.88
253.85
252.23
acetonitrile
n-butanol
278.15
54.72
57.09
52.95
8.02
7.64
7.53
283.15
72.77
69.05
66.15
9.38
8.76
8.66
288.15
85.91
83.23
81.82
9.90
10.04
9.93
293.15
108.17
100.00
100.23
11.37
11.49
11.36
298.15
119.70
119.79
121.59
12.45
13.13
12.98
303.15
136.32
143.06
146.09
14.26
14.98
14.81
308.15
161.89
170.36
173.89
16.46
17.08
16.88
313.15
200.96
202.29
205.04
18.85
19.44
19.23
318.15
244.40
239.57
239.53
22.42
22.11
21.90
323.15
284.23
282.96
277.25
25.29
25.11
24.95
phemethylol
278.15
78.16
75.71
67.12
283.15
84.33
91.77
85.40
288.15
110.90
110.85
107.30
293.15
125.32
133.46
133.12
298.15
160.99
160.16
163.08
303.15
199.27
191.60
197.24
308.15
226.26
228.53
235.52
313.15
285.49
271.79
277.66
318.15
317.43
322.34
323.19
323.15
376.96
381.24
371.52
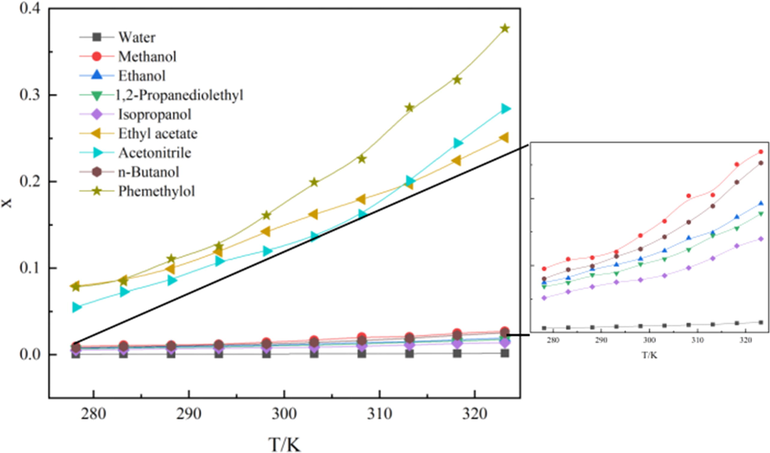
Mole fraction solubility (x) of NIT in nine pure solvents.
4.1.2 In binary solvent mixtures
According to the experimental results of 4.2.1, the solubility of NIT in phemethylol and acetonitrile are greater than that of other organic solvents. As we all known, the solubility is a function of temperature and components of solvent, therefore the solubility of NIT at various binary solvent mixtures (ethanol + phemethylol; ethanol + acetonitrile) increases not only with the rising temperature and also the rise of the ratio phemethylol/acetonitrile content at constant temperature, just as displayed in Tables 2 and 3 and graphically shown in Figs. 2 and 3. According to Figs. 2 and 3, it can be seen that the solubility of NIT increased along with temperature in both investigated binary solvent mixtures, and the solubility was increased as the mole fraction of phemethylol/acetonitrile increases. As long as phemethylol or acetonitrile was added into the binary solvent, the solubility of NIT showed an obvious increasing trend, indicating that phemethylol and acetonitrile can significantly increase the dissolution of NIT, and the greater the proportion of phemethylol and acetonitrile, the more obvious the dissolution ability. a xexp is the experimental mole fraction solubility of NIT. × Apel, xλh, xVan’t-JA and xGSM indicate the calculated mole fraction solubility of NIT obtained by the modified Apelblat model, λh model, Van't-JA model, GSM model respectively. b xj0 represents the initial mole fraction of ethanol in (ethanol + acetonitrile) binary solvent system. c The relative standard deviation of the solubility measurement u(x) = 0.001, u(T) = 0.05 K, u(P) = 2 KPa.
T/K
103xexp
103xApel
103xλh
103xGSM
103xVan’t-JA
xj0 = 0.00
278.15
78.16
75.71
67.12
77.51
70.51
283.15
84.33
91.77
85.40
83.12
87.32
288.15
110.90
110.85
107.30
110.62
107.33
293.15
125.32
133.46
133.12
124.94
131.01
298.15
160.99
160.16
163.08
161.12
158.85
303.15
199.27
191.60
197.24
198.22
191.38
308.15
226.26
228.53
235.52
226.65
229.18
313.15
285.49
271.79
277.66
285.06
272.88
318.15
317.43
322.34
323.19
317.44
323.13
323.15
376.96
381.24
371.52
374.62
380.64
xj0 = 0.10
278.15
64.22
67.27
61.50
64.22
64.72
283.15
77.06
80.90
76.72
80.74
79.31
288.15
105.87
96.97
94.71
106.91
96.49
293.15
110.99
115.86
115.71
112.22
116.62
298.15
132.72
138.01
139.94
131.91
140.05
303.15
161.87
163.91
167.54
165.82
167.18
308.15
197.56
194.12
198.56
195.76
198.41
313.15
229.06
229.27
232.99
231.29
234.20
318.15
289.44
270.05
270.69
290.07
275.01
323.15
302.88
317.27
311.43
313.52
321.33
xj0 = 0.20
278.15
56.69
56.79
52.76
56.58
57.64
283.15
76.05
68.67
65.87
73.23
69.92
288.15
93.36
82.76
81.43
91.54
84.25
293.15
99.00
99.43
99.69
97.32
100.87
298.15
109.27
119.09
120.88
110.71
120.04
303.15
141.83
142.21
145.20
137.47
142.03
308.15
161.14
169.33
172.78
162.92
167.14
313.15
195.20
201.06
203.69
189.30
195.67
318.15
247.20
238.10
237.93
243.19
227.94
323.15
282.20
281.23
275.39
264.33
264.28
xj0 = 0.30
278.15
52.37
50.64
49.05
49.12
50.09
283.15
64.84
59.75
58.78
63.75
60.17
288.15
71.99
70.28
69.99
74.30
71.83
293.15
80.21
82.45
82.80
82.63
85.23
298.15
94.87
96.47
97.37
93.94
100.55
303.15
112.45
112.59
113.84
113.06
117.97
308.15
128.64
131.07
132.36
132.47
137.71
313.15
143.32
152.22
153.08
154.33
159.95
318.15
183.59
176.37
176.13
193.35
184.91
323.15
205.05
203.89
201.66
219.84
212.81
xj0 = 0.40
278.15
41.34
41.06
39.81
43.20
42.59
283.15
49.37
53.86
48.37
54.24
50.69
288.15
58.77
62.21
58.37
59.81
59.97
293.15
69.75
72.15
69.95
69.23
70.55
298.15
82.55
76.83
83.28
79.52
82.53
303.15
97.43
91.05
98.53
92.12
96.06
308.15
114.68
114.25
115.88
106.10
111.25
313.15
134.62
136.50
135.50
124.04
128.25
318.15
157.64
159.20
157.56
149.29
147.18
323.15
184.14
184.47
182.23
177.68
168.19
xj0 = 0.50
278.15
38.70
36.59
36.29
38.16
35.44
283.15
44.12
42.63
42.57
45.48
41.81
288.15
47.98
49.55
49.71
48.89
49.04
293.15
57.95
57.43
57.79
57.30
57.22
298.15
74.10
66.40
66.92
66.29
66.40
303.15
76.94
76.60
77.22
74.10
76.69
308.15
82.78
88.15
88.80
83.94
88.16
313.15
93.89
101.22
101.80
97.50
100.89
318.15
113.20
115.98
116.40
113.20
114.97
323.15
141.75
132.62
132.75
138.29
130.49
xj0 = 0.60
278.15
32.34
33.58
30.49
33.30
28.80
283.15
36.70
36.05
34.48
37.54
33.69
288.15
40.36
39.14
38.89
40.62
39.19
293.15
43.60
42.96
43.79
46.60
45.36
298.15
46.91
47.61
49.24
53.72
52.24
303.15
52.88
53.25
55.28
58.50
59.89
308.15
59.60
60.07
62.02
65.42
68.36
313.15
68.32
68.31
69.52
74.52
77.69
318.15
78.46
78.24
77.91
85.55
87.95
323.15
90.30
90.23
87.31
103.33
99.17
xj0 = 0.70
278.15
26.82
24.22
24.34
28.00
22.72
283.15
30.23
27.86
28.00
30.16
26.37
288.15
32.72
31.98
32.11
33.61
30.44
293.15
35.30
36.63
36.73
36.82
34.98
298.15
41.05
41.86
41.92
41.80
40.00
303.15
46.44
47.75
47.74
44.94
45.54
308.15
52.07
54.35
54.28
49.81
51.63
313.15
59.78
61.75
61.63
55.21
58.30
318.15
69.61
70.03
69.91
63.55
65.58
323.15
82.64
79.28
79.26
74.34
73.50
xj0 = 0.80
278.15
23.79
23.27
23.77
21.95
17.28
283.15
25.11
25.28
25.55
23.10
19.90
288.15
27.34
27.43
27.48
26.51
22.82
293.15
30.71
29.72
29.57
27.74
26.04
298.15
32.41
32.16
31.87
30.86
29.58
303.15
34.22
34.75
34.38
33.24
33.46
308.15
36.73
37.51
37.15
36.56
37.70
313.15
39.34
40.44
40.21
39.59
42.32
318.15
42.58
43.55
43.62
45.93
47.33
323.15
48.81
46.85
47.43
51.95
52.75
xj0 = 0.90
278.15
16.48
15.65
15.91
15.38
12.52
283.15
18.25
17.56
17.73
16.37
14.33
288.15
19.56
19.67
19.74
18.70
16.33
293.15
20.94
21.98
21.95
19.46
18.52
298.15
24.58
24.53
24.40
21.35
20.92
303.15
27.34
27.31
27.13
23.37
23.53
308.15
29.88
30.37
30.16
25.36
26.37
313.15
33.07
33.70
33.54
27.52
29.45
318.15
37.39
37.34
37.34
31.57
32.76
323.15
42.08
41.31
41.61
35.79
36.34
xj0 = 1.00
278.15
7.48
7.22
7.38
9.18
8.53
283.15
8.12
8.10
8.20
10.31
9.72
288.15
9.46
9.07
9.10
10.80
11.01
293.15
10.11
10.13
10.10
12.31
12.43
298.15
10.97
11.29
11.21
13.69
13.97
303.15
12.19
12.56
12.44
15.38
15.64
308.15
14.10
13.94
13.82
16.23
17.45
313.15
14.85
15.44
15.35
18.61
19.40
318.15
17.22
17.08
17.08
19.98
21.50
323.15
19.24
18.86
19.04
24.82
23.74
T/K
103xexp
103xApel
103xλh
103xGSM
103xVan’t-JA
xj0 = 0.00
278.15
78.16
75.71
67.12
77.51
70.51
283.15
84.33
91.77
85.4
83.12
87.32
288.15
110.9
110.85
107.3
110.62
107.33
293.15
125.32
133.46
133.12
124.94
131.01
298.15
160.99
160.16
163.08
161.12
158.85
303.15
199.27
191.6
197.24
198.22
191.38
308.15
226.26
228.53
235.52
226.65
229.18
313.15
285.49
271.79
277.66
285.06
272.88
318.15
317.43
322.34
323.19
317.44
323.13
323.15
376.96
381.24
371.52
374.62
380.64
xj0 = 0.10
278.15
64.22
67.27
61.5
64.22
64.72
283.15
77.06
80.9
76.72
80.74
79.31
288.15
105.87
96.97
94.71
106.91
96.49
293.15
110.99
115.86
115.71
112.22
116.62
298.15
132.72
138.01
139.94
131.91
140.05
303.15
161.87
163.91
167.54
165.82
167.18
308.15
197.56
194.12
198.56
195.76
198.41
313.15
229.06
229.27
232.99
231.29
234.2
318.15
289.44
270.05
270.69
290.07
275.01
323.15
302.88
317.27
311.43
313.52
321.33
xj0 = 0.20
278.15
56.69
56.79
52.76
56.58
57.64
283.15
76.05
68.67
65.87
73.23
69.92
288.15
93.36
82.76
81.43
91.54
84.25
293.15
99
99.43
99.69
97.32
100.87
298.15
109.27
119.09
120.88
110.71
120.04
303.15
141.83
142.21
145.2
137.47
142.03
308.15
161.14
169.33
172.78
162.92
167.14
313.15
195.2
201.06
203.69
189.3
195.67
318.15
247.2
238.1
237.93
243.19
227.94
323.15
282.2
281.23
275.39
264.33
264.28
xj0 = 0.30
278.15
52.37
50.64
49.05
49.12
50.09
283.15
64.84
59.75
58.78
63.75
60.17
288.15
71.99
70.28
69.99
74.3
71.83
293.15
80.21
82.45
82.8
82.63
85.23
298.15
94.87
96.47
97.37
93.94
100.55
303.15
112.45
112.59
113.84
113.06
117.97
308.15
128.64
131.07
132.36
132.47
137.71
313.15
143.32
152.22
153.08
154.33
159.95
318.15
183.59
176.37
176.13
193.35
184.91
323.15
205.05
203.89
201.66
219.84
212.81
xj0 = 0.40
278.15
41.34
41.06
39.81
43.2
42.59
283.15
49.37
53.86
48.37
54.24
50.69
288.15
58.77
62.21
58.37
59.81
59.97
293.15
69.75
72.15
69.95
69.23
70.55
298.15
82.55
76.83
83.28
79.52
82.53
303.15
97.43
91.05
98.53
92.12
96.06
308.15
114.68
114.25
115.88
106.1
111.25
313.15
134.62
136.5
135.5
124.04
128.25
318.15
157.64
159.2
157.56
149.29
147.18
323.15
184.14
184.47
182.23
177.68
168.19
xj0 = 0.50
278.15
38.7
36.59
36.29
38.16
35.44
283.15
44.12
42.63
42.57
45.48
41.81
288.15
47.98
49.55
49.71
48.89
49.04
293.15
57.95
57.43
57.79
57.3
57.22
298.15
74.1
66.4
66.92
66.29
66.4
303.15
76.94
76.6
77.22
74.1
76.69
308.15
82.78
88.15
88.8
83.94
88.16
313.15
93.89
101.22
101.8
97.5
100.89
318.15
113.2
115.98
116.4
113.2
114.97
323.15
141.75
132.62
132.75
138.29
130.49
xj0 = 0.60
278.15
32.34
33.58
30.49
33.3
28.8
283.15
36.7
36.05
34.48
37.54
33.69
288.15
40.36
39.14
38.89
40.62
39.19
293.15
43.6
42.96
43.79
46.6
45.36
298.15
46.91
47.61
49.24
53.72
52.24
303.15
52.88
53.25
55.28
58.5
59.89
308.15
59.6
60.07
62.02
65.42
68.36
313.15
68.32
68.31
69.52
74.52
77.69
318.15
78.46
78.24
77.91
85.55
87.95
323.15
90.3
90.23
87.31
103.33
99.17
xj0 = 0.70
278.15
26.82
24.22
24.34
28
22.72
283.15
30.23
27.86
28
30.16
26.37
288.15
32.72
31.98
32.11
33.61
30.44
293.15
35.3
36.63
36.73
36.82
34.98
298.15
41.05
41.86
41.92
41.8
40
303.15
46.44
47.75
47.74
44.94
45.54
308.15
52.07
54.35
54.28
49.81
51.63
313.15
59.78
61.75
61.63
55.21
58.3
318.15
69.61
70.03
69.91
63.55
65.58
323.15
82.64
79.28
79.26
74.34
73.5
xj0 = 0.80
278.15
23.79
23.27
23.77
21.95
17.28
283.15
25.11
25.28
25.55
23.1
19.9
288.15
27.34
27.43
27.48
26.51
22.82
293.15
30.71
29.72
29.57
27.74
26.04
298.15
32.41
32.16
31.87
30.86
29.58
303.15
34.22
34.75
34.38
33.24
33.46
308.15
36.73
37.51
37.15
36.56
37.7
313.15
39.34
40.44
40.21
39.59
42.32
318.15
42.58
43.55
43.62
45.93
47.33
323.15
48.81
46.85
47.43
51.95
52.75
xj0 = 0.90
278.15
16.48
15.65
15.91
15.38
12.52
283.15
18.25
17.56
17.73
16.37
14.33
288.15
19.56
19.67
19.74
18.7
16.33
293.15
20.94
21.98
21.95
19.46
18.52
298.15
24.58
24.53
24.4
21.35
20.92
303.15
27.34
27.31
27.13
23.37
23.53
308.15
29.88
30.37
30.16
25.36
26.37
313.15
33.07
33.7
33.54
27.52
29.45
318.15
37.39
37.34
37.34
31.57
32.76
323.15
42.08
41.31
41.61
35.79
36.34
xj0 = 1.00
278.15
7.48
7.22
7.38
9.18
8.53
283.15
8.12
8.1
8.2
10.31
9.72
288.15
9.46
9.07
9.1
10.8
11.01
293.15
10.11
10.13
10.1
12.31
12.43
298.15
10.97
11.29
11.21
13.69
13.97
303.15
12.19
12.56
12.44
15.38
15.64
308.15
14.1
13.94
13.82
16.23
17.45
313.15
14.85
15.44
15.35
18.61
19.4
318.15
17.22
17.08
17.08
19.98
21.5
323.15
19.24
18.86
19.04
24.82
23.74
Solvent
ΔH0sol
ΔS0sol
ΔG0sol
ξH
ξS
(KJ·mol−1)
(J·mol−1·K−1)
(KJ·mol−1)
Water
13.56
−12.32
17.25
0.7858
0.2142
Methanol
18.03
25.61
10.35
0.7012
0.2988
Ethanol
15.49
14.75
11.06
0.7778
0.2222
1,2-Propanediolethyl
15.71
14.73
11.29
0.7806
0.2194
Isopropanol
15.78
13.00
11.88
0.8017
0.1983
Ethyl acetate
19.87
50.09
4.84
0.5694
0.4306
Acetonitrile
26.20
70.36
5.09
0.5538
0.4462
n-Butanol
18.87
27.35
10.67
0.6970
0.3030
Phemethylol
27.33
76.49
4.39
0.5436
0.4564
xj0
ΔH0sol
ΔS0sol
ΔG0sol
ξH
ξS
(KJ·mol−1)
(J·mol−1·K−1)
(KJ·mol−1)
0.00
27.33
76.49
4.39
0.5436
0.4564
0.10
26.31
71.82
4.77
0.5498
0.4502
0.20
25.44
67.82
5.09
0.5556
0.4444
0.30
22.25
55.36
5.65
0.5727
0.4273
0.40
24.07
60.14
6.03
0.5716
0.4284
0.50
20.58
46.66
6.59
0.5953
0.4047
0.60
16.47
30.34
7.36
0.6440
0.3560
0.70
18.28
35.12
7.75
0.6344
0.3656
0.80
11.38
9.64
8.49
0.7973
0.2027
0.90
15.60
21.58
9.12
0.7067
0.2933
xj0
ΔH0sol
ΔS0sol
ΔG0sol
ξH
ξS
(KJ·mol−1)
(J·mol−1·K−1)
(KJ·mol−1)
0.00
25.65
68.59
5.07
0.5549
0.4451
0.10
25.34
66.40
5.42
0.5599
0.4401
0.20
25.02
64.09
5.80
0.5655
0.4345
0.30
24.86
62.31
6.16
0.5708
0.4292
0.40
24.43
59.55
6.56
0.5776
0.4224
0.50
24.61
58.69
7.00
0.5830
0.4170
0.60
22.42
49.64
7.53
0.6009
0.3991
0.70
20.57
40.33
8.48
0.6297
0.3703
0.80
21.56
40.85
9.31
0.6377
0.3623
0.90
17.29
23.14
10.35
0.7136
0.2864
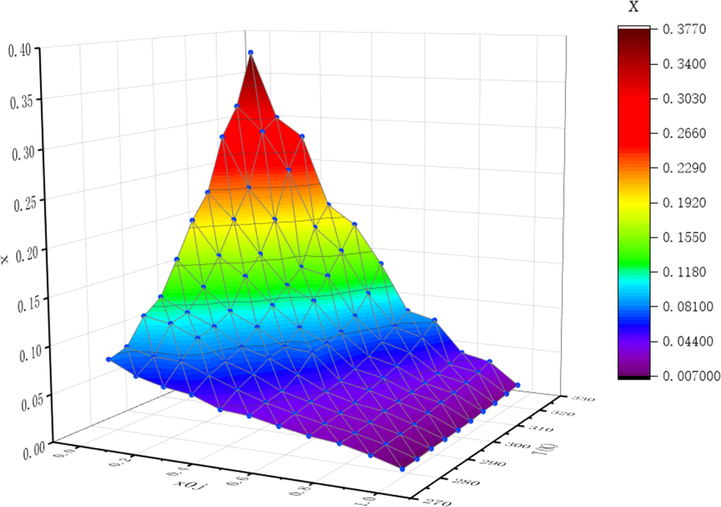
Experimental solubility data of NIT at various temperatures T(K) and different mole fraction compositions of acetone x0j in the binary solvent mixtures of ethanol + phemethylol.
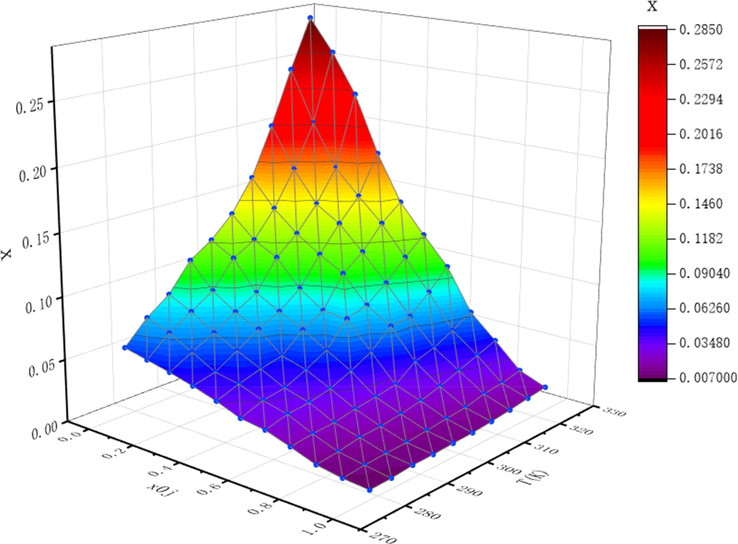
Experimental solubility data of NIT at various temperatures T(K) and different mole fraction compositions of acetone x0jin the binary solvent mixtures of ethanol + acetonitrile.
There are many factors that affect the solubility and its changed trends. In addition to the interaction between the solvents, the interaction between the solute and the solvent, the properties of solvent and solute (such as dielectric constant, polarity, dipole moment, cohesive energy, ionization constant, the surface tension etc.) and so on will also affect the solubility. The influencing factors are numerous and complex, and the specific reasons that affecting the solubility of NIT need to be further studied (Xue et al., 2021).
4.2 Solubility parameters for NIT and various organic solvents
Values of δd, δp, δh, Δδt and δv for NIT and selected mono-solvents are listed in Table S4, and values of Fdi, Fpi and Ehi for group contribution method calculation of NIT are presented in Table S2. Total HSP (δ) for NIT was obtained as 24.94 MPa1/2, indicating that NIT had lower polarity. It has been reported that the solvents having Ra(v) <5.6 MPa0.5 are the most suitable for miscibility/solubility of solutes (Alanazi et al., 2020). From Table S3, values of Ra(v) between NIT and all solvents are greater than 5.6 MPa0.5, which means that NIT may be not soluble in all solvents. It has been reported that the solvents having Δδ̅t<7.0 MPa0.5 are the most suitable for miscibility/solubility of solutes.(Alanazi et al., 2020) Except water and ethyl acetate all the investigated organic solvents had Δδ̅t<7.0 MPa0.5.
In order to have a deeper illustration of the relationship between solubility sequence of NIT and the investigated binary solvents, HSPs of measured solvents and NIT including (δd, δp, δh, Δδt, δt and δv) were summarized in Table S2. As can be seen in Table S2, the δh of selected binary solvent was very close to that of NIT, indicating that hydrogen bond might be the main interaction energy in NIT and selected binary-solvents. With the increment of mass fraction (x0j) of ethanol, the Δδ̅d, Δδ̅p and Δδ̅h of NIT in ethanol + phemethylol increased, the Δδ̅d, and Δδ̅p of NIT in ethanol + acetonitrile decreased, however, the Δδ̅h of NIT in ethanol + acetonitrile system decreased sharply with the rising mass fraction (x0j) of ethanol, achieved the minimum at a mass fraction of ethanol being 0.6000, and then followed by a sharp increase. Furthermore, all values of Δδ̅t in ethanol + phemethylol was lower than 5.0 MPa0.5. the Δδ̅t of NIT in all two selected binary solvents decreased.
4.3 Activity coefficient
The activity coefficient calculation aimed to evaluate the solute–solvent molecular interactions to determine the optimal solvent for the solubilization of NIT. The ideal solubility of NIT is calculated by equation(18)(Liu and Guo, 2021)
Where R denotes the gas constant (8.314 J/K−1·mol−1);Tfus and ΔfusH express fusion/melting temperature and fusion enthalpy of NIT, respectively, as achieved from DSC analysis; ΔCp represents the difference in the molar heat capacity of the solid state from that of the liquid state. The ΔCp was calculatedby equation(19)
The activity coefficient (γi) for NIT in different organic solvents was obtained by equation(20)
Table S5-S7 summarizes the calculated values of γi for NIT in nine pure solvent and two binary solvent systems from T (278.15–323.15 K). γi in nine pure solvents satisfied the sequence of Phemethylol<Acetonitrile<Ethyl acetate<Methanol<n-Butanol<Ethanol<1,2-Propanediolethyl<Isopropanol<Water, which is opposed to the order of decreasing solubility. The values of γi were recorded < 1.0 in organic solvents i.e., phemethylol, acetonitrile and ethyl acetate. Besides, the γi was decreased with the mole fraction of phemethylol/acetonitrile increases in two binary solvent mixtures.
4.4 Comparison of model results
In this paper, the modified Apelblat model, λh model, GSM model and the Van't-JA model were used to fit the solubility of NIT in nine pure solvents and two binary mixed solvents.
As we can see from Tables 7-8, In pure solvent, both the modified Apelblat model and the λh model show a good fitting trend, the correlation coefficients (R2) are above 0.98, the RMSD values are<0.001, the RMSD values of phemethylol, acetonitrile and ethyl acetate with good solubility were significantly higher than those of other solvents with poor solubility. it is worth noting that the modified Apelblat model(ORMSD = 1.9958 × 103) can give better correlation results though other models can also give satisfactory correlation results by used the 103RMSD and 103ORMSD values as appraisal standard in mono-solvents. From the theoretical values by the modified Apelblat model illustrated in Table 1, it can be found that the differences between the experimental and calculated values are very small.
solvent
modified Apelblat model
a
b
c
R2
103RMSD
103ORMSD
water
53.03
−39.85
5.74
0.9918
0.0243
1.9958
methanol
46.73
−47.85
7.63
0.9819
0.8233
ethanol
−280.91
−34.70
5.47
0.9926
0.3172
1,2-propanediolethyl
−261.20
−36.14
5.70
0.9908
0.3316
isopropanol
−93.46
−40.30
6.28
0.9846
0.3428
ethyl acetate
−62.64
−44.61
7.52
0.9943
4.2577
acetonitrile
7.91
−63.12
10.70
0.9954
4.8693
n-butanol
87.64
−52.14
8.34
0.9918
0.4982
phemethylol
−75.71
−61.56
10.53
0.9956
6.4976
solvent
λh model
λ
h
R2
103RMSD
103ORMSD
water
0.01
840250.60
0.9944
0.0200
2.1026
methanol
0.05
32855.55
0.9821
0.7901
ethanol
0.02
56588.44
0.9937
0.2569
1,2-propanediolethyl
0.02
60099.83
0.9937
0.2749
isopropanol
0.02
75751.85
0.9880
0.3029
ethyl acetate
1.12
2141.11
0.9880
3.6055
acetonitrile
3.19
1144.96
0.9911
6.7735
n-butanol
0.06
33297.20
0.9933
0.4531
phemethylol
6.44
629.54
0.9957
6.4464
As Tables 9-12 shown, the 103RMSD and 103ORMSD values of modified Apelblat model, λh model, Van't-JA model and GSM equation were calculated respectively, The correlation coefficients (R2) were all greater than 0.7, and the fitting linearity was good. In modified Apelblat model, λh model and Van't-JA model, the higher the ratio of phemethylol and acetonitrile, the higher the RMSD value, in GSM equation, RMSD value increased with the increase of temperature, which is similar to the result of the single solvent, It can be inferred that the stronger the solubility, the faster the solubility value increases, which will have an impact on the linear fitting. And the value of GSM model(ORMSD = 3.9109 × 103) is lowest in ethanol + phemethylol and Van't-JA model(RMSD = 4.41 × 103) is lowest in ethanol + acetonitrile.The results show that the GSM equation fits ethanol better, and ethanol + acetonitrile can be better fitted by Van't JA equation.
xj0
modified Apelblat model
a
b
c
R2
103RMSD
103ORMSD
ethanol + phemethylol
0.00
−280.91
−34.70
5.47
0.9956
6.4976
3.3570
0.10
−42.43
−59.96
10.20
0.9884
8.6838
0.20
33.57
−63.66
10.78
0.9912
6.6963
0.30
49.31
−56.36
9.45
0.9925
4.2191
0.40
11.90
−59.52
10.00
0.9943
3.4297
0.50
33.62
−52.39
8.70
0.9906
2.9556
0.60
11614.42
−300.49
45.37
0.9985
0.6908
0.70
207.11
−52.86
8.60
0.9876
1.9374
0.80
62.07
−31.41
4.87
0.9855
0.9086
0.90
16.02
−40.95
6.53
0.9948
0.5908
1.00
−280.91
−34.70
5.47
0.9926
0.3172
ethanol + acetonitrile
0.00
7.91
−63.12
10.70
0.9954
4.8693
2.9990
0.10
58.03
−64.71
10.93
0.9896
6.3577
0.20
71.50
−65.54
11.04
0.9843
6.7618
0.30
17.62
−61.49
10.33
0.9970
2.4260
0.40
−3875.64
26.40
−2.83
0.9895
3.7742
0.50
23.39
−58.21
9.70
0.9912
2.8446
0.60
150.83
−59.79
9.86
0.9890
2.4416
0.70
226.65
−59.92
9.77
0.9805
2.1067
0.80
9.45
−55.86
9.13
0.9929
0.5275
0.90
77.79
−47.20
7.50
0.9900
0.5621
1.00
−280.91
−34.70
5.47
0.9926
0.3172
xj0
λh model
λ
h
R2
103RMSD
103ORMSD
ethanol + phemethylol
0.00
6.44
629.54
0.9957
6.4464
3.8761
0.10
3.80
965.82
0.9895
8.2454
0.20
3.14
11161.42
0.9852
8.6500
0.30
1.21
2732.88
0.9898
4.9260
0.40
1.26
2467.75
0.9922
4.0026
0.50
0.52
4660.43
0.9736
5.0275
0.60
0.17
9853.52
0.9883
1.9564
0.70
0.21
9684.66
0.9882
1.8951
0.80
0.02
28673.64
0.9899
0.7588
0.90
0.05
24591.54
0.9966
0.4727
1.00
0.02
56588.44
0.9952
0.2569
ethanol + acetonitrile
0.00
3.19
1144.96
0.9911
6.7735
3.5425
0.10
2.46
1439.67
0.9825
8.2570
0.20
1.94
1790.47
0.9777
8.0578
0.30
1.31
2455.99
0.9953
3.0505
0.40
0.90
3316.02
0.9894
3.7884
0.50
0.64
4384.81
0.9920
2.7070
0.60
0.43
6155.71
0.9883
2.5154
0.70
0.23
10433.87
0.9798
2.1414
0.80
0.16
14744.23
0.9930
0.9137
0.90
0.05
34743.54
0.9919
0.5063
1.00
0.02
56588.44
0.9952
0.2569
T/K
GSM model
a
b
c
d
e
R2
103RMSD
103ORMSD
ethanol + phemethylol
278.15
−4.69
6.16
−10.92
10.32
−3.42
0.9937
1.6240
3.9109
283.15
−4.57
5.37
−8.34
9.09
−4.03
0.9911
1.8154
288.15
−4.53
6.83
−15.34
20.03
−9.20
0.9984
1.3355
293.15
−4.40
5.21
−6.99
6.79
−2.69
0.9968
2.0535
298.15
−4.29
0.86
−4.37
1.84
0.13
0.9939
3.5572
303.15
−4.17
4.57
−4.18
3.14
−0.98
0.9970
3.1666
308.15
−4.12
4.97
−5.53
5.50
−2.29
0.9969
3.8060
313.15
−3.98
4.03
−1.10
−1.16
0.96
0.9944
6.3159
318.15
−3.91
5.12
−6.16
7.69
−3.88
0.9967
5.7776
323.15
−3.70
3.54
1.64
−4.96
2.49
0.9928
9.6574
ethanol + acetonitrile
278.15
−5.00
3.99
−1.81
−0.72
0.63
0.9970
0.8790
4.2904
283.15
−4.99
5.71
−7.36
5.85
−1.82
0.9958
1.3602
288.15
−4.73
4.06
−2.86
1.49
−0.41
0.9991
24.1827
293.15
−4.65
3.47
0.93
−4.84
2.86
0.9979
1.4197
298.15
−4.71
5.38
−4.75
2.25
−0.28
0.9952
2.4877
303.15
−4.59
4.85
−1.03
−3.76
2.54
0.9911
3.8989
308.15
−4.41
4.62
1.02
−7.53
4.49
0.9984
1.9284
313.15
−4.20
3.64
3.71
−10.36
5.61
0.9995
1.3448
318.15
−4.17
4.98
−0.47
−5.48
3.73
0.9992
1.9917
323.15
−4.18
7.67
−12.20
12.64
−5.18
0.9985
3.4107
xj0
Van’t-JA model
V0
V1
V2
V3
V4
V5
V6
R2
103RMSD
ethanol + phemethylol
2.58
−2043.70
6.87
−746.10
−1073.05
810.37
−315.37
0.9920
6.85
ethanol + acetonitrile
4.85
−2855.87
4.25
325.69
−991.31
−138.40
313.98
0.9944
4.41
4.5 Apparent thermodynamics functions of dissolution
Thermodynamic properties are essential to the research of solid–liquid equilibrium systems, which can help us better understand the dissolution behavior of a drug. For the purpose of understand the dissolution process of NIT in the temperature range of 278.15 K–323.15 K, enthalpies of solution (ΔH0sol), Gibb's energy of dissolution (ΔG0sol) and entropy of solutions (ΔS0sol) have also been calculated by Van't Hoff plot from the intercept and slope.(Jia et al., 2021)(Yang et al., 2021).
Where Tmean represents the mean harmonic temperature of the temperature range which is given as Eq.(24).
Where n is the number of experimental temperatures points. In this work, the value of Tmean is 299.96 K.
The resulting data of ΔH0sol,ΔG0sol and ΔS0sol for NIT dissolution are furnished in Table. 4-6. Besides, the contribution of enthalpy and entropy to the standard Gibbs energy also be calculated as Eq.(25), and shown in Table 4-6, too.
From Table. 4-6, In single solvent except water, the values of ΔS0sol were positive, which indicated the entropically driven dissolution process of NIT in the solvent. When NIT was dissolved in water, the degree of the system chaos is decreased, that is, the entropy of the system is decreased, so the ΔS0sol showed negative values. The conclusion can be drawn that ΔH0sol and ΔG0sol for NIT dissolution are positive in the studied mono and binary solvent mixtures, which explains the increasing solubility of NIT as the temperature increases. ΔG0sol>0 indicating that the dissolution process of NIT is apparently not spontaneous. In addition, the higher the mole fraction solubility of NIT shows, the smaller the values of ΔG0sol are. It indicated that forming the force between solute and solvent needed less energy in the solvent system corresponding to the better dissolving performance, ΔH0sol>0, which suggests that the dissolution process is endothermic(Wei et al., 2021). All of the ΔH0sol values are positive and the reason may be that the solute–solvent interaction force is less than other interactions (solute–solute and solvent–solvent interaction) in the dissolution process of NIT. Furthermore, ξH > ξS in both pure and mixed solvent, which suggests ΔH0sol is the main contributor to the standard molar Gibbs energy of solution during the dissolution and the values of ξH are ≥ 54.36 %.
5 Conclusions
In this work, the solubility of NIT in nine pure solvents and two kinds of binary mixtures at tested temperature range (278.15 K ∼ 323.15 K) under atmospheric pressure (p = 0.1 MPa). In all the tested solvent systems, the solubility of NIT increases with the increasing temperature and the ratio of phemethylol/acetonitrile in binary solvents. The overall root mean square deviations(ORMSD) of the Van't Hoff model is lowest in both mono-solvents. The value of GSM model is lowest in ethanol + phemethylol and Van't-JA model is lowest in ethanol + acetonitrile. The results prove that the solubility of NIT in the tested solvent is the result of the combined effect of volume-dependent, solvent polarity and other factors.
Based on the apparent thermodynamic analysis, the thermodynamic properties for the solution process including enthalpy, entropy and Gibbs energy were calculated. According to the results, indicating that the dissolution process of NIT in all solvents is endothermic and not spontaneous. Through the above research will offer an assistance for design and optimization of crystallization and dosage form of NIT.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Solubility and dissolution thermodynamics of 5-fluorouracil in (ethanol + water) mixtures. J. Mol. Liq.. 2021;333:116038
- [CrossRef] [Google Scholar]
- Solubility determination and three dimensional Hansen solubility parameters of gefitinib in different organic solvents: Experimental and computational approaches. J. Mol. Liq.. 2020;299:112211
- [CrossRef] [Google Scholar]
- Solubility determination, various solubility parameters and solution thermodynamics of sunitinib malate in some cosolvents, water and various (Transcutol + water) mixtures. J. Mol. Liq.. 2020;307:112970
- [CrossRef] [Google Scholar]
- Determination and correlation of solubility and solution thermodynamics of 4-aminobenzenesulfonamide in five binary solvent mixtures from 278.15 to 318.15 K. J. Mol. Liq.. 2020;303:112670
- [CrossRef] [Google Scholar]
- Current perspectives in dissolution testing of conventional and novel dosage forms. Int. J. Pharm.. 2007;328:12-21.
- [CrossRef] [Google Scholar]
- Opening the Gateway: St. Louis Union Station. Civ. Eng. Mag.. 2007;77:32-33.
- [CrossRef] [Google Scholar]
- Thermodynamic modelling, Hansen solubility parameter and solvent effect of oxaprozin in thirteen pure solvents at different temperatures. J. Chem. Thermodyn.. 2020;151:106239
- [CrossRef] [Google Scholar]
- Solubility and dissolution thermodynamic properties of Mequindox in binary solvent mixtures. J. Mol. Liq.. 2020;303
- [CrossRef] [Google Scholar]
- A possible biochemical mode of action of the fasciolicides nitroxynil, hexachlorophene and oxyclozanide. Pestic. Sci.. 1971;2:119-121.
- [CrossRef] [Google Scholar]
- Solubility parameters as predictors of miscibility in solid dispersions. J. Pharm. Sci.. 1999;88:1182-1190.
- [CrossRef] [Google Scholar]
- Measurement and correlation of solubility, Hansen solubility parameters and thermodynamic behavior of Clozapine in eleven mono-solvents. J. Mol. Liq.. 2021;333:115894
- [CrossRef] [Google Scholar]
- Solubility measurement and correlation for HNIW·TNT co-crystal in nine pure solvents from T = (283.15 to 318.15) K. J. Mol. Liq.. 2021;323:114592
- [CrossRef] [Google Scholar]
- Jouyban, K., Mazaher Haji Agha, E., Hemmati, S., Martinez, F., Kuentz, M., Jouyban, A., 2020. Solubility of 5-aminosalicylic acid in N-methyl-2-pyrrolidone + water mixtures at various temperatures. J. Mol. Liq. 310, 113143. https://doi.org/https://doi.org/10.1016/j.molliq.2020.113143
- Determination and modelling of solid-liquid phase equilibrium and phase diagram for multicomponent system of nitrobenzaldehyde isomers. (I) Ternary system of 4-nitrobenzaldehyde+3-nitrobenzaldehyde+ethyl acetate. J. Mol. Liq.. 2017;234:164-171.
- [CrossRef] [Google Scholar]
- Solubility measurement, modeling and Hansen solubility parameters of 8-Chloro-11-(4-methyl-1-piperazinyl)-5H-dibenzo[b, e][1,4]diazepine in four binary solvents. J. Mol. Liq.. 2021;339:116733
- [CrossRef] [Google Scholar]
- Solubility determination and crystallization thermodynamics of an intermediate in different organic solvents. J. Mol. Liq.. 2021;339:116821
- [CrossRef] [Google Scholar]
- Systematic thermodynamic study of clorsulon dissolved in ten organic solvents: Mechanism evaluation by modeling and molecular dynamic simulation. J. Mol. Liq.. 2021;341:117217
- [CrossRef] [Google Scholar]
- Hansen solubility parameter as a tool to predict cocrystal formation. Int. J. Pharm.. 2011;407:63-71.
- [CrossRef] [Google Scholar]
- Solubility of sulfacetamide in aqueous propylene glycol mixtures: Measurement, correlation, dissolution thermodynamics, preferential solvation and solute volumetric contribution at saturation. J. Mol. Liq.. 2020;297:111889
- [CrossRef] [Google Scholar]
- Solubility profile of phenytoin in the mixture of 1-propanol and water at different temperatures. J. Mol. Liq.. 2021;334:115936
- [CrossRef] [Google Scholar]
- Solubility determination, model correlation, solvent effect, molecular simulation and thermodynamic properties of flutamide in eleven pure solvents at different temperatures. J. Mol. Liq.. 2021;336
- [CrossRef] [Google Scholar]
- Effect of choline chloride/ethylene glycol or glycerol as deep eutectic solvents on the solubility and thermodynamic properties of acetaminophen. J. Mol. Liq.. 2018;249:1222-1235.
- [CrossRef] [Google Scholar]
- Determination and correlation of solubility of an explosive in different pure solvents. J. Mol. Liq.. 2021;340:117169
- [CrossRef] [Google Scholar]
- A validated RP-HPLC method for determination of nitroxinil and investigation of its intrinsic stability. J. Iran. Chem. Soc.. 2021;18:351-361.
- [CrossRef] [Google Scholar]
- Determination and analysis of flutamide solubility in different solvent systems at different temperatures (T = 278.15–323.15 K) J. Mol. Liq.. 2021;325:114762
- [CrossRef] [Google Scholar]
- Uridine in twelve pure solvents: Equilibrium solubility, thermodynamic analysis and molecular simulation. J. Mol. Liq.. 2021;330:115663
- [CrossRef] [Google Scholar]
- Measurement and correlation of solubility data for atorvastatin calcium in pure and binary solvent systems from 293.15 K to 328.15 K. J. Mol. Liq.. 2021;324
- [CrossRef] [Google Scholar]
- Measurement, correlation of solubility and thermodynamic properties analysis of 2,4,6-trinitroresorcinol hydrate in pure and binary solvents. J. Mol. Liq.. 2021;330:115639
- [CrossRef] [Google Scholar]
- Determination of the solubility and thermodynamic properties of albendazole in a binary solvent of ethanol and water. Phys. Chem. Liq.. 2021;59
- [CrossRef] [Google Scholar]
- Solubility parameter of lenalidomide for predicting the type of solubility profile and application of thermodynamic model. J. Chem. Thermodyn.. 2019;132:268-275.
- [CrossRef] [Google Scholar]
- Equilibrium solubility, Hansen solubility parameter, dissolution thermodynamics, transfer property and preferential solvation of zonisamide in aqueous binary mixtures of ethanol, acetonitrile, isopropanol and N. N-dimethylformamide. J. Mol. Liq.. 2021;326:115219
- [CrossRef] [Google Scholar]
Appendix A
Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.arabjc.2022.104531.
Appendix A
Supplementary material
The following are the Supplementary data to this article:Supplementary data 1
Supplementary data 1






