Effect of number and position of methoxy substituents on fine-tuning the electronic structures and photophysical properties of designed carbazole-based hole-transporting materials for perovskite solar cells: DFT calculations
⁎Corresponding author. nwazzan@kau.edu.sa (Nuha Wazzan)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In perovskite solar cells (PSCs), the state-of-art Spiro-OMeTAD, which used as a hole-transporting material (HTM), suffered from complicated multistep synthesis and difficult purification that make this material cost ineffective, in addition to it being UV-unstable. Thus, new, cost-effective and easy to synthesize small organic molecules is still required. As reported, a carbazole-based compound (R01) was synthesized using a simple two steps method from low-cost commercially available compounds and used as an HTM. R01 exhibited higher conductivity and hole-mobility compared to that of the Spiro-OMeTAD. PSCs fabricated with R01 produced a power conversion efficiency of 12.03%, equivalent to that obtained in devices where Spiro-OMeTAD was the HTM. These findings highlighted R01 as a highly promising HTM with high performance, facile synthesis, and low cost. From a structural perspective, methoxy groups (–OCH3) in the HTM structure are controlling the HOMO level of the compound, apart from the critical role they play in anchoring the material onto the core perovskite layer. In this paper, we report a systematic study of the electronic structures and photophysical properties of twelve designed derivatives of R01. R01 was modified by substituting some hydrogen in the carbazole rings by two, four and six methoxy groups at different positions. The ground and excited state geometries are optimized by applying density functional theory (DFT) and its time-dependent functional (TDDFT), respectively. Detailed investigation of two factors: (i) the number and (ii) position of methoxy groups on the frontier molecular orbitals (FMOs), absorption and emission wavelengths, ionization potential, electron affinity, reorganization energies and charge mobility are examined and discussed. The electro-optical and nonlinear optical (NLO) properties are finely tuned in the R01 derivatives. By incorporating methoxy substituents into this carbazole-based compound, systematic design of potential materials for PSCs can be feasible.
Keywords
Perovskite solar cells
Carbazole-based hole-transporting materials
Methoxy substituents
Nonlinear optical properties
Density functional theory
1 Introduction
Last few years have witnessed an extensive attraction to use the solar cells to convert the sunlight into electricity at low cost (Stranks et al., 2013; Kazim et al., 2014; Liu et al., 2017). Perovskite solar cells (PSCs) as type of solar cells have been emerged as new systems based on renewable sources. To date, perovskite-type solar cells with and without HTMs have been developed. The cells represent a new class of electrochemical solar cells based on sensitized mesoporous TiO2 and a liquid electrolyte in a sandwich-like architecture. These cells are known as the most principal rivals for silicon solar cells because of their unique characteristics and high efficiency (Green et al., 2014). Improving the performance of these systems (as light-driven charge separation in molecular systems) to restore as much as possible of the solar energy into electrical current are very intense. These improvements include the design of new and efficient hole-transport materials (HTMs), one of the major constituent of a PSC devise. These materials are solid-state compounds that play important role in extracting holes from perovskites and transport them to the electrode. HTMs are being deposited in the heart of the cell between the perovskite layer and the evaporated metal electrode. The two folds role of the HTMs in the PSC structure are to (1) prevent the direct contact between the perovskite and the metal contact, which minimizes charge recombination and avoids degradation at the metal-perovskite interface and (2) extract positive charges (holes) from perovskite and transport them to the top-electrode (Calió et al., 2016). Additionally, a good hole-mobility (ideally >10−3 cm2 V−1 s−1), as well as thermal and photochemical stability are required characteristics of an HTM (Yu and Sun, 2015). Furthermore, transparency in the visible spectrum is desirable to avoid the absorption screen effect toward the active materials/absorber. The physical state of these materials is one of its crucial requirements, in order to prevent the perovskite from dissolution in liquid electrolyte. Solid-state HTMs can be categorized into (1) polymeric (2) inorganic and (3) small organic molecule HTMs. The inorganic HTMs, regardless of their good properties, i.e., high hole mobility and cost effective, suffer from the disadvantage that the solvent used for their deposition can partially dissolve the perovskite, reducing the stability of the device. Polymeric materials have the disadvantages of complex purification process, low solubility, complicated characterization because of their approximate molecular weight, and a poor infiltration into the nanostructured material, this led to many endeavors to design small organic molecules as HTMs (Calió et al., 2016). The classical small organic HTM is Spiro-OMeTAD (Shi et al., 2016). However, Spiro-OMeTAD has some deficiencies like its high-cost, multi-steps synthesis and many purification steps. It is essential to find alternatives of Spiro-OMeTAD and work in this direction is growing too fast. In this endeavors, experimentalist and theoretical chemists use their techniques to build and test new efficient HTMs (Cai et al., 2017; Zhang et al., 2017a, 2017b; Ansari et al., 2018; Wazzan et al., 2018). The advantage of the theoretical methods over the experimental methods is its convenient and low-cost tool for molecular design, selection and testing of HTMs with higher efficiency. Wang Wo et al. recently introduced a novel high-performance HTM, R01, with a very simple molecular structure, which was synthesized via a facile route with low cost and high yield. R01 is carbazole-based and bridged by 3,4-ethylenedioxythiophene. Its structure is much simpler than not only Spiro-OMeTAD but also other organic HTMs. The much smaller size of the R01 allows a deeper penetration into the mesoporous TiO2, which facilitates the hole-extraction, thus improving device performance. The perovskite solar cell device using R01 as HTM shows an efficiency (
On the other hand, and from a structural point of view, methoxy groups (–OCH3) in the HTM structure are responsible for adjusting the HOMO level of the material, apart from the important role they play in anchoring the material onto the underlying perovskite layer and improve stability and solubility, thus by doing so result in an efficient hole injection (Calió et al., 2016). Since R01 is a very promising alternative HTM in perovskite solar cells, and its facile synthesis may facilitate driving down the fabrication cost of perovskite-based photovoltaic technology, a number of R01 derivatives will be constructed theoretically using the computer software by introducing methoxy groups at different sites in the carbazole donor. Therefore, it is worth developing low-cost HTMs or developing and improving the performance of HTM-free solar cells. The HTM-free solar cell has a much more straightforward structure that is beneficial for reducing the cost. With efforts on the photoanode and back contact interfacial modification, a PCE in the range of 5–8% has been achieved (Jeon et al., 2013a, 2013b; Laban and Etgar, 2013). To provide a simple method to improve the efficiency and stability of planar perovskite solar cells, A copper salts doped 2,2,7,7-tetrakis(N,N‐di‐p‐methoxyphenylamine)‐9,9‐spirobifluorene (spiro‐OMeTAD) based on a solution processing as the HTM in PSCs was developed (Meng et al., 2016). The incorporation of CuI/CuSCN comprehends a p‐type doping with efficient charge transfer complex that results in improved film conductivity and hole mobility. Consequently, the PCE is improved from 14.82% to 18.02%. A simple route to control perovskite crystallization and to optimize the interfaces in PHJ PSCs simultaneously and obtaining a maximum power conversion efficiency of 17.06% with improved cell stability was achieved by using branch-shaped perylene film as a seed-mediated under layer, crystalline perovskites with fabric morphology (Wang et al., 2016a, 2016b). Perylene played an important role in the energy-level tailoring of poly(3,4-ethylenedioxythiophene): poly(styrenesulphonate) (PEDOT:PSS) and CH3NH3PbIxCl3–x. In addition, perylene and perovskites form a fully crystalline heterojunction, which is beneficial for minimizing the defect and trap densities. In a similar effort, a seed-mediated method by GeO2 nano-particles (NPs) for growing crystal perovskite films was developed (Lou et al., 2016). Higher quality of perovskite films was achieved by tuning the size of the GeO2 NPs, which results in a power conversion efficiency as high as 16.77%. The fabrication and device parameters of inverted planar heterojunction (PHJ) organic–inorganic lead mixed-halide (CH3NH3PbI3−xClx) PSCs using a:CuAlO2 as the hole selective buffer layer between the ITO electrode and PEDOT:PSS were demonstrated (Igbari et al., 2016). A short circuit current density (
Therefore, it is necessary to understand the electronic structures of the existing efficient HTMs, in order to be able to build theoretical novel models of R01 derivatives (Jeon et al., 2013a, 2013b). Hence, this study is undertaken to report two issues: The first one is to study in detail the results of theoretical examination of novel R01 compound new design molecules (see Scheme 1). Of particular interest are the structural, molecular orbitals, absorption and emission properties, and hole transport behavior of the newly designed compounds under probe of the parent (R01). The second issue is to study the nonlinear optical properties (NLO) of the compounds under probe to give insight into the photoelectric conversion performance. These properties will be first predicted and characterized by DFT and TDDFT calculations and will be compared with the available experimental data.
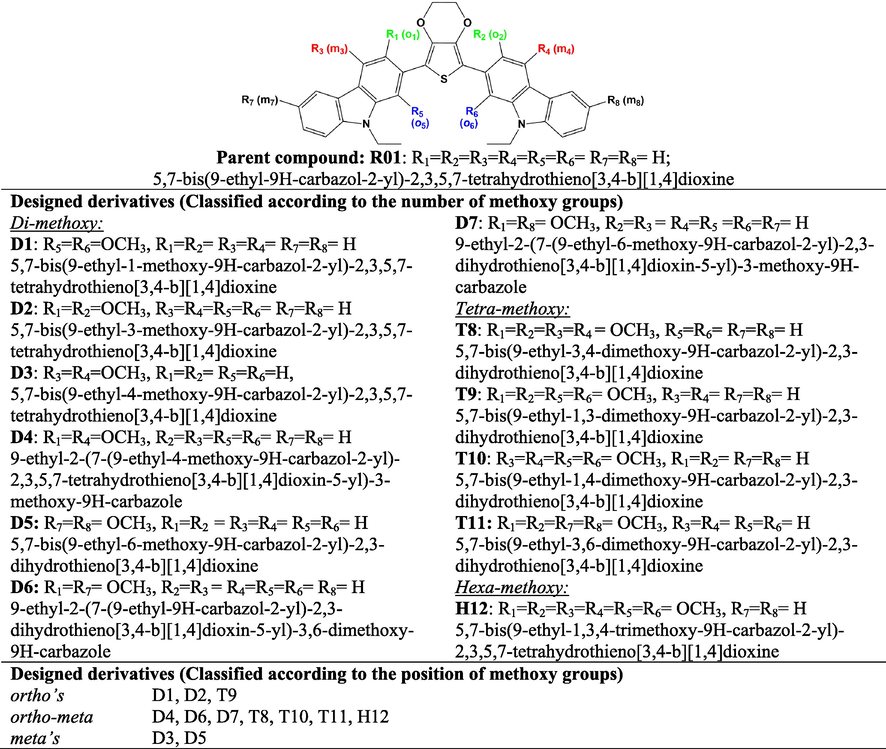
- Chemical structures and IUPAC names of R01 and its designed derivatives designated as D1-to-D7, T8-T11, and H12 investigated by DFT and TDDFT calculations.
2 Calculations details
DFT and TD-DFT methods were used to investigate the structural, electronic and optical properties of the studied compounds. The more computationally efficient B3LYP density functional Becke-three–Lee–Yang–Parr (B3LYP) (Becke, 1988; Lee et al., 1988) was selected for optimization of the ground state (S0) and excited state (S1) geometries of all compounds. The functional has been proved as a suitable method for predicting such geometries/properties (Chen et al., 2014a, 2014b; Bagheri Novir and Hashemianzadeh, 2015; Chi and Li, 2015a, 2015b). The standard 6-31G(d) basis set was used for the optimizations. The use of a 6-31G(d) split-valence double zeta basis set without diffuse functions prevents convergence difficulties in delocalized systems, yet leads to accurate geometries at a reasonable computational cost (Pogantsch et al., 2002; Gao, 2010). The parent hole transporting material (R01) and its twelve designed derivatives (D1 to H12) geometries were optimized with C1 point group. The optimized geometries show no imaginary frequencies, which ensure energetic minima. The absorption and emission spectra were determined on the optimized S0 and S1 geometries, respectively, using TD-B3LYP/6-311++G(d,p) level. The total electronic energies of neutral, cationic, and anionic forms of these compounds were used to compute the reorganization energy (
3 Results and discussion
The principal aim of this study is to design and develop new HTMs which have similar chemical structures but different properties to reveal the underlying principles for the future HTMs design.
3.1 Structural features of designed dyes (D1-D7, T8-T11, and H12)
From the parent molecule 5,7-bis(9-ethyl-9H-carbazol-2-yl)-2,3,5,7-tetrahydrothieno[3,4-b][1,4]dioxine (abbreviated as R01), twelve newly derivatives was designed. The derivatives (abbreviated as D1-to-D7) were designed by introducing methoxy groups at the carbazole rings. In D1-D7 (di-methoxy derivatives), two methoxy groups were introduced at different positions at the carbazole rings. In T8-T11 (tetra-methoxy derivatives), four methoxy groups were present. The maximum number of six methoxy groups was introduced in H12 (hexa-methoxy derivative). The common feature in the designed molecules is the presence of electron-rich methoxy substituents that will improve the contact with the perovskite layer, and by doing so result in an efficient hole-injection (Calió et al., 2016). The chemical structures of the R01 and its designed derivatives along with their IUPAC names are depicted in Scheme 1. On the other hand, the designed molecules could be differentiated according to the positions of the methoxy groups either they are substituted at the ortho or at the ortho and meta position all with respect to the dioxythiophene ring, see Scheme 1. The designed HTMs have a unique general configuration of AD1-D1-D2-D1-AD1, which has the carbazole moieties as the significant electron donors (D1), methoxy groups as an additional electron donor (AD1), dioxythiophene core as a minor electron donor (D2), and a repeated unit of D1, and AD1.
3.2 Optimized geometries
Parent (R01): The inter-ring distances and the torsional angles in the optimized geometries of the parent molecule (R01) in its neutral, cationic, and anionic states at the ground state (So) are collected in Table 1. Fig. 1 represents the HOMOs and LUMOs distribution along with the % contribution to the HOMO and LUMO from different fragments of the HTMs under investigation. Two (R01)/Three (derivatives) main fragments are defined for each molecule. The nature of each fragment as electron-donating/accepting can be demonstrated from its contribution to these orbitals. If the fragment is contributing more to the HOMO than to the LUMO, it is an electron-donating fragment and vice versa. As can be seen from Fig. 1, for R01, the two defined fragments are the dioxythiophene core and two carbazole arms. The two fragments are contributing to the HOMO and LUMO; however, dioxythiophene core is contributing with more significant extent to the HOMO than to the LUMO. Dioxythiophene core is contributing by 42% and 36% to HOMO and LUMO, respectively. In contrast, the carbazole arms are contributing with more significant extent to the LUMO (64%) than to the HOMO (58%). Thus, we could conclude that both groups could be considered as an electron-donating group, however, according to the extent of their contributions to the HOMO and LUMO the carbazole arms are the major ones, and dioxythiophene core is the minor one. In the meantime, no X-ray crystal data is available for this compound, we will focus on the effect of the substituted methoxy groups on these geometrical parameters for the same molecule in its different forms, and we will compare between these geometrical parameters in different derivatives, Table 1. The optimized R01 molecule exhibits a non-planar structure with the C1 symmetry, the non-planarity geometries of R01 regulates the packing of the molecule in the solid state and influences the optoelectrical properties of the carbazole-based materials (Iwan and Sek, 2011).
| R01 |
|
S−C5 | C5−C31 | S−C5–C31–C32 | ||
| neutral | 1.7582 (1.7752) |
1.4637 (1.4215) |
22.800 (2.462) |
|||
| cationic | 1.7622 | 1.4364 | 9.168 | |||
| anionic | 1.7817 | 1.4316 | 2.687 | |||
| D1 |
|
S–C5 | C5–C30 | S–C5–C30–C31 | C31–O66 | C32–O66–C68 |
| neutral | 1.7592 (1.7834) |
1.4702 (1.4272) |
32.699 (17.373) |
1.3866 (1.3800) |
113.856 (114.133) |
|
| cationic | 1.7596 | 1.4456 | 35.082 | 1.3491 | 119.237 | |
| anionic | 1.7847 | 1.4389 | 20.240 | 1.3950 | 112.932 | |
| D2 |
|
S–C5 | C5–C30 | S–C5–C30–C31 | C32–O66 | C31–O66–C68 |
| neutral | 1.7558 (1.7790) |
1.4694 (1.4283) |
47.593 (29.372) |
1.3669 (1.3569) |
118.340 (119.185) |
|
| cationic | 1.7596 | 1.4456 | 35.082 | 1.3491 | 119.237 | |
| anionic | 1.7804 | 1.4420 | 30.897 | 1.3740 | 118.435 | |
| D3 |
|
S–C5 | C5–C30 | S–C5–C30–C31 | C35–O67 | C35–O67–C72 |
| neutral | 1.7574 (1.7757) |
1.4645 (1.4214) |
23.021 (2.357) |
1.3659 (1.3633) |
118.223 (118.490) |
|
| cationic | 1.7601 | 1.4398 | 11.275 | 1.3526 | 118.788 | |
| anionic | 1.7831 | 1.4302 | 2.641 | 1.3794 | 117.610 | |
| D4 |
|
S–C5 | C5–C30 | S–C5–C30–C31 | C35–O71 | C35–O71–C72 |
| neutral | 1.7579 (1.7781) |
1.4652 (1.4213) |
21.994 (1.970) |
1.3663 (1.3614) |
118.199 (118.530) |
|
| cationic | 1.7656 | 1.4385 | 8.384 | 1.3518 | 118.807 | |
| anionic | 1.7782 | 1.4338 | 2.805 | 1.3792 | 117.620 | |
| D5 |
|
S–C5 | C5–C27 | S–C5–C27–C28 | C28–O65 | C28–O69–C66 |
| neutral | 1.7581 (1.7966) |
1.4638 (1.4120) |
23.043 (1.444) |
1.3734 (1.3733) |
118.309 (118.315) |
|
| cationic | 1.7615 | 1.4392 | 9.989 | 1.3590 | 119.263 | |
| anionic | 1.7811 | 1.4319 | 2.900 | 1.3854 | 117.765 | |
| D6 |
|
S–C6 | C6–C12 | S–C6–C12–C13 | C14–O60 | C14–O60–C61 |
| neutral | 1.7566 (1.7978) |
1.4692 (1.4259) |
47.038 (25.717) |
1.3815 (1.3780) |
114.040 (114.539) |
|
| cationic | 1.7587 | 1.4435 | 35.629 | 1.3461 | 119.441 | |
| anionic | 1.7853 | 1.4390 | 27.625 | 1.3876 | 114.280 | |
| D7 |
|
S–C5 | C5–C27 | S–C5–C27–C28 | C29–O60 | C29–O60–C61 |
| neutral | 1.7568 (1.7970) |
1.4691 (1.4268) |
47.074 (26.583) |
1.3811 (1.3777) |
114.089 (114.573) |
|
| cationic | 1.7577 | 1.4431 | 36.334 | 1.3495 | 119.184 | |
| anionic | 1.7847 | 1.4395 | 28.557 | 1.3872 | 114.335 | |
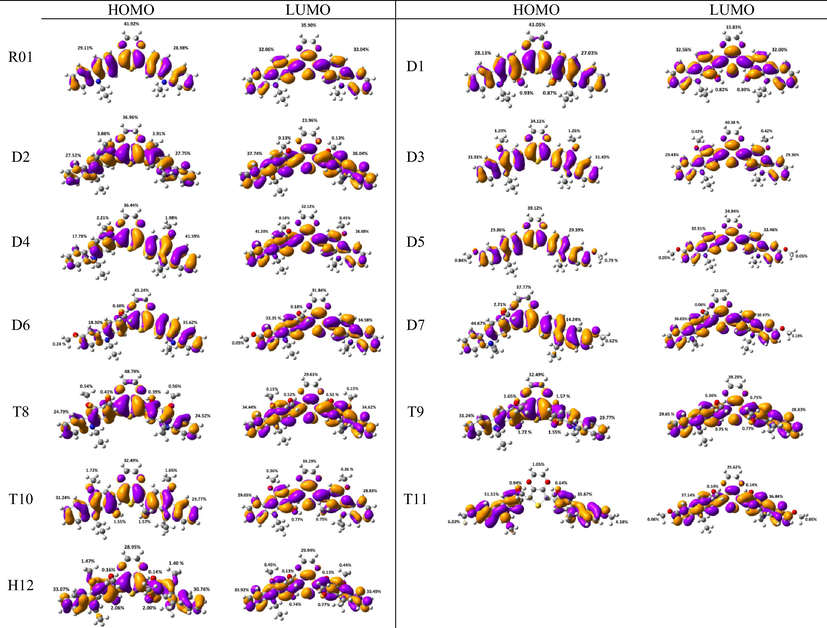
- Electron density isocontours (0.020 au) of HOMO and LUMO orbitals distribution for the ground states of R01 and its methoxy derivatives.
The S–C5 distances are 1.7582, 1.7622, and 1.7817 Å in the neutral, cationic and anionic forms, respectively. These bond distances are elongated in the cationic and anionic forms by 0.004 and 0.024 Å, respectively, compared to that in the neutral form. On the other hand, the C5–C31 distances are shortened in the cationic and anionic forms by 0.027 and 0.032 Å, respectively, compared to that in the neutral form. In the cationic form the electron is removed from the HOMO, and in the anionic form the electron will be added to the LUMO, thus, by visualizing the HOMO and LUMO distribution among the molecule, we can explain the change in the inter-ring distances (Lin et al., 2003), Fig. 1. A large part of the HOMO (−4.793 eV) is delocalized on the dioxythiophene ring, upon removing of an electron from the HOMO in the cationic form leads to elongation of the S–C5 bond distance. Part of the LUMO (−1.346 eV) is distributed over the C5–C31 (and C5–C11), thus adding an electron to the LUMO results in shortening of these bonds. The shortening of the inter-ring distance in the anionic state is due to the bonding interactions between the π-orbitals on the two carbazole rings. The torsional angle S–C5–C31–C32 that simply resemble the extent of the planarity of the molecule shows a significant decrease by 13.6 and 20.1° in the cationic and anionic forms, respectively, compared to that in the neutral form. Thus, the cationic and anionic forms showed more planner geometries compared to the neutral form, and the anionic form is even more planner than the cationic form. In fact, R01 and its derivatives (as will be discussed later) exhibit larger geometric deformation between the neutral and ionic forms, this implies that this type of molecules should be p-channel but not n-channel materials (Zhao et al., 2013).
Di-methoxy derivatives (D1-D7): A general notice is that the investigated geometrical parameters (bond lengths and angles) show somehow significant differences between the parent molecule (R01) and its derivatives. It is then evident that the presence of the methoxy groups makes a significant influence on the geometrical structure and subsequently on the electronic properties. On one hand, due to the steric hindrance effect of the methoxy group/s especially for that/those present in the ortho-position/s, and on the other hand, due to the electron-accepting (by resonance)/donating (inductively) nature of this group. Comparing the torsional angle S–C5–C31–C32 between the parent molecule (R01) and its derivatives those substituted by two methoxy groups (D1-D7), indicated that the planarity of the R01 is distorted with different extent in its derivatives. For instance, for the derivatives D1, D2, D6, and D7, this dihedral angle is in the range ∼33° (D1) to ∼47° (D2, D6, and D7) compared to 22.8° for that of R01. On the other hand, the distortion from planarity for the derivatives D3, D4 and D5 is insignificant, since the dihedral angles for these three molecules are very similar to that of R01, ranges from 22.0° (in D4) to 23.0° (in D3 and D5). Thus, the positions of the methyl groups significantly affect the planarity of geometries of the designed derivatives; the positioning of the methoxy group/s at the ortho-position/s with respect to the dioxythiophene ring will have a more important steric effect than positioning it/them at the meta-position/s (Jeon et al., 2014). For instance, in D3, the two methoxy groups are positioning at the meta-positions corresponding to each other at the two carbazole rings, this molecule shows one of the least deviations from planarity and thus a very similar geometry to that of R01. Another notice is that the significant deviation from planarity shown by D1, D2, D6 and D7 derivatives. The displacement of one/two methoxy groups at the ortho-position (D1 and D2) and the other one at the phenyl ring of the carbazole ring farthest from the dioxythiophene ring (terminal methoxys), either on the same side (D6) or at the opposite side (D7), seems to enhance the steric effect of the methoxy groups.
The change in inter-ring distances, i.e., S–C5 and C5–C32/C30/C28, shows similar trend showed by the parent molecule (R01). The S–C5 distances are elongated in the cationic and anionic forms compared to that of the neutral form, and the other bond distances are shortened. The concept used to explain these changes in the R01 can be applied to the designed derivatives. Since the distribution of the HOMO and LUMO on the thiophene ring and on the C5–C12/17/27/30/31 bond does not show significant differences between that of the R01 and those of its derivatives. Additionally, the geometrical parameters of one of the substituted methoxy groups in the derivatives have been tabulated in Table 1. For instance, for the D2 derivative, the C32–O66 bond distance shortened by 0.018 Å in the cationic form and elongated by 0.007 Å in the anionic forms, the C31–O66–C68 bond angle increases by 0.897 in the cationic form and decreases by 0.095° in the anionic forms. From Fig. 1, it is clear that the HOMOs are delocalized with large extent on the substituted methoxy group over the electronegative oxygen atoms, while the LUMOs are distributed with no/less extent. The total % contributions from the methoxy fragments to the HOMO and LUMO orbitals of the investigated HTMs are collected in Table 2. As appeared from Table 2 and Fig. 1, the methoxy groups are contributing more to the HOMOs (range from 0.84 to 7.77%) than to the LUMOs (0.1–1.62%), indicating that the electron-donating nature by resonance is more predominant. The fact that the C–O distances for these derivatives are shortened in cationic form and elongated in anionic form is consistent with the MO pictures (Lin et al., 2003). The distribution of the HOMOs orbitals on the substituted methoxy groups of the derivatives is not the same, while, LUMOs distribution shows similar observation. In other words, the LUMOs are generally not delocalized on these groups indicating their electron-donating nature (resonance effect). The HOMOs are delocalized on the oxygen atoms of the methoxy groups, but not on all the substituted methoxy groups. The delocalization of the HOMOs on some methoxy groups indicates that the electron-donating nature of the methoxy group is a predominant effect, and the non-delocalization of them indicates that the electron-withdrawing nature is the predominant effect. Due to the high electronegativity of the oxygen atom; this group could become electron-withdrawing in an inductive sense via the σ bonds. Thus, the electron-donating/withdrawing nature of the substituted methoxy group depends on its specific position and interaction with the conjugation system of the phenyl rings. Thus, from MO picture, the methoxy groups that contributed to the HOMO and not contributed to the LUMO, we expected that the C-O bond length would be decreased and increased in the cationic and anionic form, respectively; the expectation is matching the obtained result.
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | T8 | T9 | T10 | T11 | H12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HOMO | 1.80 | 7.77 | 2.55 | 4.19 | 1.63 | 0.84 | 3.33 | 1.90 | 6.49 | 6.49 | 11.79 | 7.23 |
| LUMO | 1.62 | 0.26 | 0.84 | 0.59 | 0.10 | 0.23 | 0.24 | 1.34 | 2.63 | 2.24 | 0.40 | 2.66 |
Tetra-methoxy derivatives (T8-T11): In this kind of designed derivatives, four methoxy groups are substituted either at the two (upper) ortho- and two meta- positions (like in T8), or at the four ortho-positions (like in T9), or at the two meta- and the two other (lower) ortho-positions (like in T10), or finally, at the two ortho-positions and the other two methoxy groups are at the phenyl ring farthest from the dioxythiophene ring (like in T11), see Scheme 1 and Table SD 1. Comparing the planarity of T8-T11 and that of the parent molecule (R01) shows that and similar to the effect of some derivatives substituted with two methoxy groups (D1, D2, D6, and D7), the planarity of all of these derivatives are less than that of R01. The S-C5-C28-C28/29 dihedral angle is ranging from 33° (T10)-to-58° (T9). Since the value of this dihedral angle in R01 is 22.008°. On the other hand, the inter-ring distances included the S–C5, and C5–C27/28/31 bond distances of T8-T11 are slightly shortened and elongated, respectively, compared to those of R01. For instance, the S–C5 bond distances are 1.7582 and 1.7565 Å in R01 and T8, respectively, while their C5–C28/31 bond lengths are 1.4637 and 1.4700 Å, respectively, shortening by 0.002 Å and elongation by 0.006 Å.
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.arabjc.2018.06.014.
Tetra-methoxy derivatives (T8-T11): In this kind of designed derivatives, four methoxy groups are substituted either at the two (upper) ortho- and two meta- positions (like in T8), or at the four ortho-positions (like in T9), or at the two meta- and the two other (lower) ortho-positions (like in T10), or finally, at the two ortho-positions and the other two methoxy groups are at the phenyl ring farthest from the dioxythiophene ring (like in T11), see Scheme 1 and Table SD 1. Comparing the planarity of T8-T11 and that of the parent molecule (R01) shows that and similar to the effect of some derivatives substituted with two methoxy groups (D1, D2, D6, and D7), the planarity of all of these derivatives are less than that of R01. The S-C5-C28-C28/29 dihedral angle is ranging from 33° (T10)-to-58° (T9). Since the value of this dihedral angle in R01 is 22.008°. On the other hand, the inter-ring distances included the S–C5, and C5–C27/28/31 bond distances of T8-T11 are slightly shortened and elongated, respectively, compared to those of R01. For instance, the S–C5 bond distances are 1.7582 and 1.7565 Å in R01 and T8, respectively, while their C5–C28/31 bond lengths are 1.4637 and 1.4700 Å, respectively, shortening by 0.002 Å and elongation by 0.006 Å.
Supplementary data 1
Supplementary data 1The anionic forms of these derivatives show significant changes from the geometries of their counterpart neutral forms, while the cationic forms show slightly different geometries of those of the neutral forms. For instance (for T11), the S-C5 bond lengths are 1.7575, 1.7572, and 1.7829 Å in the neutral, cationic and anionic forms, respectively. Thus, it has been slightly shortened by 0.0004 Å and significantly elongated by 0.025 Å in the cationic and anionic form, respectively. Unlike any other derivative, the HOMO (−4.907 eV) of T11 is not delocalized on the S-C5 bond, and like the other derivatives, part of the LUMO (−1.059 eV) is delocalized on the C5–C27 (Fig. 1) thus removing an electron from the HOMO to form the cationic state should not affect the S-C5 bond length that results in the slight difference that was observed in this bond length in the neutral and cationic form. In contrast, and since the LUMO is delocalized on the C5–C27, adding an electron to the LUMO to form the anionic form would be expected to weaken and thus lengthening this bond as observed.
Hexa-methoxy derivative (H12): The deviation from planarity in this molecule in comparison with R01 is more pronounced, Table SD 2. Since, the S−C5−C28−C29 dihedral angle is 56.2 and 22.8°, for H12 and R01, respectively, a difference of ∼33°. This could be easily attributed to the steric hindrance effect of the six substituted methoxy groups. The inter-ring distances (S–C5) are also elongated by 0.006 and 0.027 Å, while the C5–C28 bond distances are shortened by 0.024 and 0.026 Å in the cationic and anionic forms, respectively. The C–O bond distances of the methoxy group are shortened in the cationic forms and elongated in the anionic forms compared to those of the neutral forms, this combined by reverse trend observed in the C–O–C bond angle. In comparison with the neutral forms, the C–O–C bond angles of the methoxy group increase and decrease in the cationic and anionic forms, respectively. Due to the presence of the six methoxy groups (the maximum number of substitution among all derivatives); the HOMO is showing greater delocalization over more substantial parts of the molecule. Four of the methoxy groups are contributing to the HOMO, except the two methoxy groups at the (upper) ortho-positions.
Hexa-methoxy derivative (H12): The deviation from planarity in this molecule in comparison with R01 is more pronounced, Table SD 2. Since, the S−C5−C28−C29 dihedral angle is 56.2 and 22.8°, for H12 and R01, respectively, a difference of ∼33°. This could be easily attributed to the steric hindrance effect of the six substituted methoxy groups. The inter-ring distances (S–C5) are also elongated by 0.006 and 0.027 Å, while the C5–C28 bond distances are shortened by 0.024 and 0.026 Å in the cationic and anionic forms, respectively. The C–O bond distances of the methoxy group are shortened in the cationic forms and elongated in the anionic forms compared to those of the neutral forms, this combined by reverse trend observed in the C–O–C bond angle. In comparison with the neutral forms, the C–O–C bond angles of the methoxy group increase and decrease in the cationic and anionic forms, respectively. Due to the presence of the six methoxy groups (the maximum number of substitution among all derivatives); the HOMO is showing greater delocalization over more substantial parts of the molecule. Four of the methoxy groups are contributing to the HOMO, except the two methoxy groups at the (upper) ortho-positions.
Optimized S1 geometries of R01 and its designed derivatives: The inter-ring distances and torsional angles in the optimized geometries of the parent molecule R01 and its designed derivatives at the first excited state (S1) calculated with TDB3LYP/6-31G(d) are collected in Table 1, Table SD 1, and Table SD 2. It was found that the excited state structures are different from the ground state structures. The investigated bond angles, bond angles, and dihedral angles are significantly changed upon excitation. The most interesting observation is that the planarity of the molecule is improved due to the transfer from the ground state to the first excited state; this is evident from the significant decrease in the S−C−C−C dihedral angles, more obviously for R01, D3, and D4. Thus, the excited state structure is more planar than the ground state structure. For instance, the values of S−C−C−C dihedral angles in the ground state change from 22.800, 23.021, and 21.994° to 2.462, 2.357, and 1.970° in R01, D3, and D4, respectively. The modifications of the dihedral angle strongly affect the optical properties of the compounds such as the emission properties and radiative lifetimes (discussed later) (Chitpakdee et al., 2014; Wazzan et al., 2017).
Optimized S1 geometries of R01 and its designed derivatives: The inter-ring distances and torsional angles in the optimized geometries of the parent molecule R01 and its designed derivatives at the first excited state (S1) calculated with TDB3LYP/6-31G(d) are collected in Table 1, Table SD 1, and Table SD 2. It was found that the excited state structures are different from the ground state structures. The investigated bond angles, bond angles, and dihedral angles are significantly changed upon excitation. The most interesting observation is that the planarity of the molecule is improved due to the transfer from the ground state to the first excited state; this is evident from the significant decrease in the S−C−C−C dihedral angles, more obviously for R01, D3, and D4. Thus, the excited state structure is more planar than the ground state structure. For instance, the values of S−C−C−C dihedral angles in the ground state change from 22.800, 23.021, and 21.994° to 2.462, 2.357, and 1.970° in R01, D3, and D4, respectively. The modifications of the dihedral angle strongly affect the optical properties of the compounds such as the emission properties and radiative lifetimes (discussed later) (Chitpakdee et al., 2014; Wazzan et al., 2017).
The distribution patterns of HOMOs and LUMOs for R01 and of its derivatives in the first excited states (S1) have been shown in Fig. 2. Unlike R01 and other derivatives, T11 derivative shows the significant difference in the HOMO distribution (and not the LUMO) between the So and S1. In the HOMO of the excited state, the electronic charge is delocalized over a region that was not covered by the HOMO in the ground state geometry, i.e., the dioxythiophene core. Thus, at the S1 the HOMO is distributed over more substantial parts of the molecule. We found general intramolecular charge transfer (ICT) in all investigated HTMs for S0 as well as the S1 state.
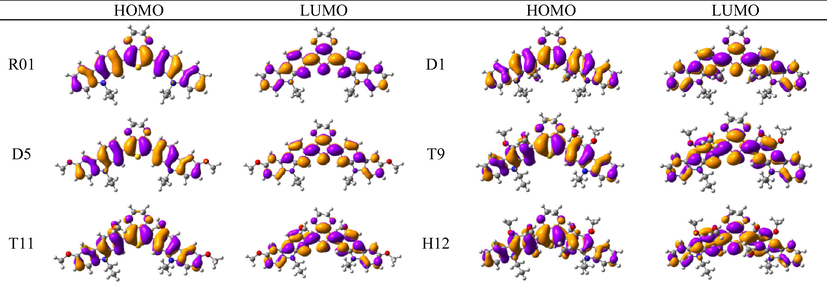
- HOMO and LUMO orbitals distribution for the first excited state (S1) of some investigated HTMs as representative examples.
3.3 Frontier molecular orbital
In the present study, we have carried out a systematic quantum chemical calculations using density functional theory DFT to estimate the electronic and optical properties for 5,7-bis(9-ethyl-9H-carbazol-2-yl)-2,3,5,7-tetrahydrothieno[3,4-b][1,4]dioxin and some of its new designed methoxy derivatives (Scheme 1), which they may be used as an efficient HTMs in the perovskite solar cells. As is known examination of the frontier molecular orbitals (FMOs) is vital to understand the electronic structures of chemical compounds. In addition, FMOs are the backbone factors to illustrate the carrier transport properties of the molecules, which affect the electronic, optical, and conducting properties of materials. By controlling the HOMO and LUMO levels, it is feasible to design materials for PSCs with desirable charge carrier transport properties (Chen et al., 2014a, 2014b). Therefore, examination of HOMOs and LUMOs of the newly designed compounds is highly useful, by which a reasonable qualitative indication of the ability of charge injection and transport can be estimated by knowing the relative ordering of HOMOs and LUMOs. The calculated distribution patterns of the highest occupied molecular orbitals (HOMOs) and lowest unoccupied molecular orbitals (LUMOs) and the energy levels for the ground states of the parent compound and its new design derivatives are plotted in Fig. 3. For the parent compound (R01), as sketched in Fig. 3, the HOMO and LUMO are almost distributed over the whole molecule, indicating that the molecule possesses π-features. A good delocalization of HOMO is favorable to enhancing the hole transfer integral (Zhang et al., 2017a, 2017b). Similarly, other twelve designed molecules exhibit the same results with some exceptions. These exceptions mainly depend on the position and the number of the substituted methoxy groups. For example, new designed compound D4, the HOMO is located on the central and left-hand side of the molecule, and it has a very weak localization on the right-hand side of the molecule, while the LUMO is almost localized on whole the molecule. For D6 and D7 molecules, the indole group on the right-hand side have a week contribution to the HOMOs, while the LUMOs of these molecules are almost localized overall the backbone of the molecule. These results can be attributed to the position of the methoxy groups. In D6 molecule, two methoxy groups are substituted on the carbazole unit, which located on the left-hand side of the molecule. On the other hand, in D7 molecule, the two methoxy groups are substituted on both carbazole units. As is known the methoxy substituent actually impacts the ring electronics via two competing effects. The oxygen's lone pair is well-placed to delocalize and increase electron density within the ring's conjugated system. This allows delocalization to better stabilize positive charges. So the methoxy is electron-donating from a resonance perspective. Additionally, because oxygen is quite electronegative, the methoxy group is electron-withdrawing in an inductive sense via the σ bonds. As can be seen from the distribution of the HOMOs and LUMOs the resonance donation is much stronger than the inductive sense.
- The calculated molecular orbitals for molecule R01 and its newly designed derivatives P1-D7 (blue ones are LUMOs and red ones are HOMOs), using DFT at the B3LYP/6-31G(d) level. HOMO and LUMO energies are in eV. Energy gap values are given in the middle part of the Fig (eV). Value ranges from (−0.2)-to-0.2 eV.
Chi and Li (2015a, 2015b) suggested that the excellent HOMO delocalization is favorable for hole transport and hole transfer integral. As compared with the hole-transport, they have the relative inferior electron transport possibility that is determined by the delocalization of the LUMO. The result of FMO analysis suggests that the parent R01 and most of the designed molecules have good hole-transport properties, and consequently they may be very useful potential candidates as HTMs. Previous studies (Minaev et al., 2012; Baryshnikov et al., 2012) reported that the central principle of HTM in perovskite is similar with that of electron transfer to TiO2 surface in DSSC except that the electron is injected in the latter.
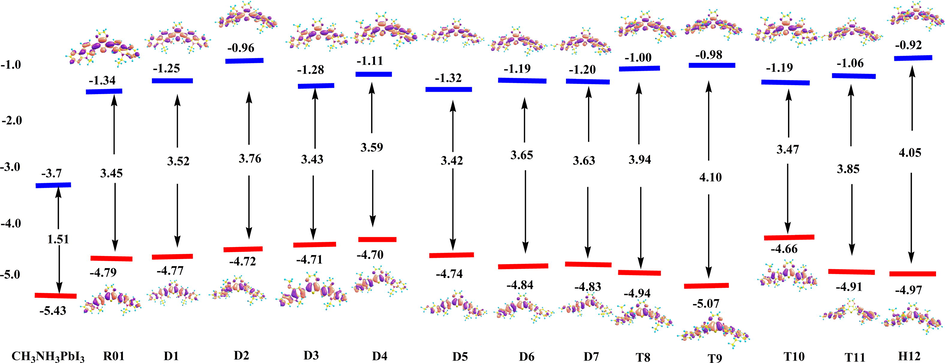
In order to understand the influence of the electronic properties of the R01 compound and the newly designed molecules, the analyzing of the values of HOMO energies (
Table 3 and Fig. 3 summarize the DFT B3LYP/6-31(d) values of
| HTM |
|
Gaussian
|
Gaussian
|
|
Calculated
|
Calculated
|
|
Gaussian
|
Calculated
|
|
|---|---|---|---|---|---|---|---|---|---|---|
| R01 | −4.793 (−5.30) | −1.346 (−2.42) | 3.447 (2.88) | 3.000 | −1.791 | 3.002 | 2.522 | 0.447 | 0.002 | 0.637 (0.86) |
| D1 | −4.771 | −1.252 | 3.519 | 3.060 | −1.709 | 3.062 | 2.560 | 0.459 | 0.002 | 0.659 |
| D2 | −4.724 | −0.962 | 3.763 | 3.200 | −1.528 | 3.196 | 2.606 | 0.563 | −0.004 | 0.706 |
| D3 | −4.706 | −1.279 | 3.427 | 2.990 | −1.711 | 2.995 | 2.490 | 0.437 | 0.005 | 0.724 |
| D4 | −4.703 | −1.111 | 3.592 | 3.090 | −1.610 | 3.092 | 2.535 | 0.502 | 0.002 | 0.727 |
| D5 | −4.741 | −1.316 | 3.424 | 3.067 | −1.671 | 3.069 | 2.460 | 0.357 | 0.002 | 0.689 |
| D6 | −4.844 | −1.195 | 3.649 | 3.247 | −1.598 | 3.246 | 2.532 | 0.402 | −0.001 | 0.586 |
| D7 | −4.828 | −1.199 | 3.629 | 3.220 | −1.607 | 3.221 | 2.532 | 0.409 | 0.000 | 0.602 |
| T8 | −4.939 | −0.995 | 3.944 | 3.482 | −1.456 | 3.483 | 2.651 | 0.462 | 0.001 | 0.491 |
| T9 | −5.075 | −0.979 | 4.096 | 3.599 | −1.470 | 3.605 | 2.732 | 0.497 | 0.006 | 0.355 |
| T10 | −4.662 | −1.189 | 3.473 | 3.091 | −1.570 | 3.092 | 2.467 | 0.382 | 0.001 | 0.768 |
| T11 | −4.907 | −1.059 | 3.848 | 3.403 | −1.500 | 3.407 | 2.567 | 0.445 | 0.004 | 0.523 |
| H12 | −4.970 | −0.923 | 4.047 | 3.476 | −1.497 | 3.473 | 2.697 | 0.571 | −0.003 | 0.460 |
Generally, the open-circuit voltage
The calculated
Wang et al. showed that for a proper HTM material, the LUMO energy level should be higher than the conduction band of perovskite to inhibit the electron in perovskite back to metal electrodes (Liu et al., 2016). The lower LUMO effectively blocks the electron transport from the perovskite to the Au contact, and this causes an increase in the fill factor (FF) value and thus an enhanced PCE (Calió et al., 2016). Almost all of the calculated LUMO energy level values are located between the
According to Table 3 and Fig. 3, the LUMO energy levels of the newly designed molecules are estimated to be destabilized (more positive) than the that of CH3NH3PbI3 perovskite (−3.91 eV). In addition, our results show that the energy difference between the LUMO energy level and the conduction band of CH3NH3PbI3 perovskite is ranged from 2.14 eV to 2.47 eV (Table 3), which is enough to block the charge recombination. Based on the above results, the new designed HTMs are assumed to not only perform as a hole transporting layer but also play as an electron blocking layer in the PSCs, leading to the reduction of an electron from perovskite layer and hole from hole-transporting layer (Liu, Zhu et al.). In order to explore the cause of the HOMO destabilization (energy raised) of most of the di-methoxy derivatives and the cause of its stabilization (energy lowered) for most of the tetra- and hexa-methoxy derivatives, also the cause of LUMO destabilization (energies lowered) in all derivatives, we make an analysis on the molecular orbital population, Fig. 1. Fig. 1 indicates the total % contributions of the substituted methoxy groups
To overcome the electron-injection barrier energy in R01, 3.754 eV (
As is known the magnitude of the HOMO-LUMO gap has significant chemical implications, even if qualitatively evaluated. A large gap implies good thermodynamic stability of the compound, whereas a small gap suggests an easy electronic transition. Inspection of Table 3. indicates that the energy gaps,
3.4 Absorption and emission energy
It is worth mentioning that there are no experimental data for newly designed compounds because they have never been synthesized except for the parent molecule R01, which has been described in reference Wang et al. (2015). In order to adventure the properties of electronically excited states of the studied compounds, electronic transitions, the calculated absorption and emission spectra,
| HTM | Excitation |
|
|
Assignment |
|
|
|
Assignment |
|
|
|---|---|---|---|---|---|---|---|---|---|---|
| R01 | S0 → S1 | 413 (360) | 1.29 | H → L (70%) | 0.949 | 465 (467) | 1.34 | H ← L (70%) | 2.557 | 52 |
| D1 | S0 → S1 | 405 | 1.23 | H → L (70%) | 0.941 | 454 | 1.32 | H ← L (70%) | 2.569 | 49 |
| D2 | S0 → S1 | 388 | 0.83 | H → L (70%) | 0.852 | 476 | 1.17 | H ← L (70%) | 2.897 | 88 |
| D3 | S0 → S1 | 414 | 1.18 | H → L (70%) | 0.934 | 498 | 1.32 | H ← L (70%) | 2.821 | 84 |
| D4 | S0 → S1 | 401 | 0.95 | H → L (70%) | 0.888 | 453 | 1.11 | H ← L (70%) | 2.927 | 52 |
| D5 | S0 → S5 | 404 | 1.19 | H-2 → L (11%) H → L (69%) |
0.935 | 504 | 1.52 | H → L (70%) | 2.509 | 100 |
| D6 | S0 → S5 | 382 | 1.18 | H → L (70%) | 0.934 | 490 | 1.44 | H → L (71%) | 2.502 | 108 |
| D7 | S0 → S5 | 385 | 0.83 | H-1 → L (11%) H → L (69%) |
0.852 | 490 | 1.40 | H → L (70%) | 2.567 | 105 |
| T8 | S0 → S7 | 356 | 1.00 | H → L (70%) | 0.900 | 468 | 1.27 | H ← L (70%) | 2.574 | 112 |
| T9 | S0 → S7 | 344 | 0.83 | H → L (70%) | 0.852 | 454 | 1.13 | H ← L (70%) | 2.724 | 110 |
| T10 | S0 → S5 | 401 | 1.04 | H → L (70%) | 0.909 | 503 | 1.33 | H ← L (70%) | 2.851 | 102 |
| T11 | S0 → S8 | 364 | 0.68 | H-2 → L (55%) H-1 → L (28%) H → L (29%) |
0.791 | 483 | 1.34 | H ← L (71%) | 2.609 | 119 |
| H12 | S0 → S1 | 357 | 0.47 | H → L (68%) | 0.661 | 460 | 1.07 | H ← L (70%) | 2.971 | 103 |
It is apparently evident from Table 4 that all electronic transitions are π-π* type, and no localized electronic transitions are shown among the calculated singlet-singlet transition. In addition the oscillator strength for S0-S1 attributed to HOMOLUMO transition for all compounds leading to maximum absorption was also noted. According to Table 4, the high values of the oscillator strength (
The conclusion can be derived from above that T10 with four-methoxy shows longer (λabs = 401 nm) but stronger maximum absorption wavelength
3.5 Light harvesting efficiency
The ability of the materials and the molecules to capture photons of solar light is called as light harvesting efficiency (LHE). Higher the value of
3.6 Emission properties
In this study TD-DFT//B3LYP/6-31G(d) has been performed for optimized structures on an excited state to simulate the emission spectra of the compounds under study where the first singlet excited states are listed in Table 4. In all cases and similar to the absorption spectra, S1-S0 fluorescence peaks in emission spectra have the largest oscillator strengths in all molecules, and ∼70% arises predominantly from LUMO → HOMO transition. Based on Table 4, the calculated maximum emission wavelength,
3.7 Stokes shift
Stokes shift can reflect the degree of structural deformation between the ground state and excited state geometries. A more substantial Stokes shift is beneficial for pore-filling of HTM (Chi et al., 2016). The computed results of the newly designed molecules yield a stoke shift values (
-
Relatively high λss (from 106 nm to 119 nm) (D6, T8, T9, T8 and T11 compounds): The relatively high
-
Relatively moderate λss (from 84 nm to105 nm) (D3, D2, D5, H12 and D7 compounds). The moderate
-
Relatively small
| HTM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R01 | 0.141 | 0.156 | 0.297 | 0.161 | 0.207 | 0.368 | 0.665 | 5.751 | 5.907 | 0.206 | 0.462 | 0.255 | 0.023 | 2.645 |
| D1 | 0.177 | 0.198 | 0.374 | 0.163 | 0.175 | 0.338 | 0.712 | 5.673 | 5.871 | 0.202 | 0.360 | 0.185 | 0.019 | 2.656 |
| D2 | 0.158 | 0.155 | 0.313 | 0.207 | 0.202 | 0.410 | 0.723 | 5.642 | 5.797 | 0.202 | 0.119 | −0.083 | 0.012 | 2.761 |
| D3 | 0.135 | 0.145 | 0.280 | 0.181 | 0.237 | 0.418 | 0.698 | 5.631 | 5.776 | 0.202 | 0.431 | 0.194 | 0.022 | 2.600 |
| D4 | 0.149 | 0.164 | 0.313 | 0.203 | 0.232 | 0.435 | 0.748 | 5.621 | 5.785 | 0.201 | 0.277 | 0.044 | 0.018 | 2.672 |
| D5 | 0.134 | 0.131 | 0.264 | 0.167 | 0.213 | 0.380 | 0.645 | 5.662 | 5.792 | 0.203 | 0.464 | 0.251 | 0.023 | 2.599 |
| D6 | 0.067 | 0.347 | 0.415 | 0.210 | 0.230 | 0.441 | 0.855 | 5.565 | 5.912 | 0.202 | 0.366 | 0.135 | 0.021 | 2.600 |
| D7 | 0.067 | 0.354 | 0.421 | 0.205 | 0.228 | 0.433 | 0.854 | 5.560 | 5.914 | 0.202 | 0.366 | 0.138 | 0.021 | 2.597 |
| T8 | 0.080 | 0.072 | 0.152 | 0.270 | 0.247 | 0.517 | 0.669 | 6.066 | 6.138 | 0.220 | 0.203 | −0.044 | 0.017 | 2.931 |
| T9 | 0.031 | 0.633 | 0.664 | 0.200 | 0.209 | 0.409 | 1.073 | 5.529 | 6.163 | 0.202 | 0.155 | −0.054 | 0.013 | 2.687 |
| T10 | 0.155 | 0.164 | 0.319 | 0.182 | 0.197 | 0.380 | 0.699 | 5.549 | 5.713 | 0.198 | 0.325 | 0.128 | 0.019 | 2.612 |
| T11 | −0.041 | 0.501 | 0.460 | 0.249 | 0.235 | 0.484 | 0.944 | 5.396 | 5.897 | 0.200 | 0.267 | 0.032 | 0.019 | 2.564 |
| H12 | 0.210 | 0.154 | 0.365 | 0.221 | 0.215 | 0.436 | 0.800 | 5.824 | 5.978 | 0.206 | 0.117 | −0.099 | 0.012 | 2.854 |
Since larger Stokes shift is also typical feature for a good HTM; we could predict that D6, T8, T9, and P9 derivatives as HTMs are better for increasing the performance of PSCs compared with the parent (R01). D6 and T8 combine in the nature of the methoxy position, the two and four methoxy groups in D6 and T8, respectively, are positioning in the ortho- and meta- positions. In D6, the methoxy groups are in o1m7, and in T8 they are in o1o2m3m4, see Scheme 1. While the four methoxy groups in T9 are at the four ortho-positions (o1o2o5o6).
3.8 The radiative lifetimes
The Radiative lifetimes (τ) of the compounds under probe have been computed for a spontaneous emission using the Einstein transition probabilities (Lukeš et al., 2005). This time refers to the average time that molecules stay in their excited state before emitting a photon. If the compounds have a shorter lifetime in the excited state, it means they have more efficiency in the emitting of fluorescence or photons (Zhang et al., 2012a, 2012b), and longer lifetime indicate improved suppression of back reactions of the injected electrons, this results in improvement the
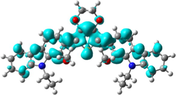
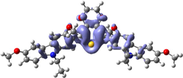
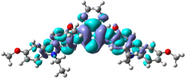
To better explain the contribution of the electron, the charge density differences between ground and excited states of R01 and some of its designed derivatives, D1, D2, T9, T11, and H12 (as representative examples) are plotted in Table 6. In this case, it is assumed to be the difference between HOMO and LUMO since the first transition is mainly from HOMO to LUMO. Electron density moves from the cyan region to the blue region when moving from the ground state to the first excited state. Cyan and blue colors indicate increase and decrease of charge densities, respectively. As evident from Table 6 the R01 and its derivatives demonstrated clearly intramolecular charge transfer (ICT).
| HTM | ED moves from So | ED goes to S1 | Full picture |
|---|---|---|---|
| R01 |
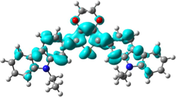
|
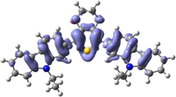
|
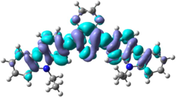
|
| D1 |
|
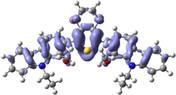
|
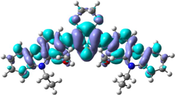
|
| T11 |

|
|
|
| H12 |
|
|
|
3.9 Reorganization energy, electron affinity, and ionization potential
One of the parameters to determine the carrier hopping rate is the reorganization energy (λ
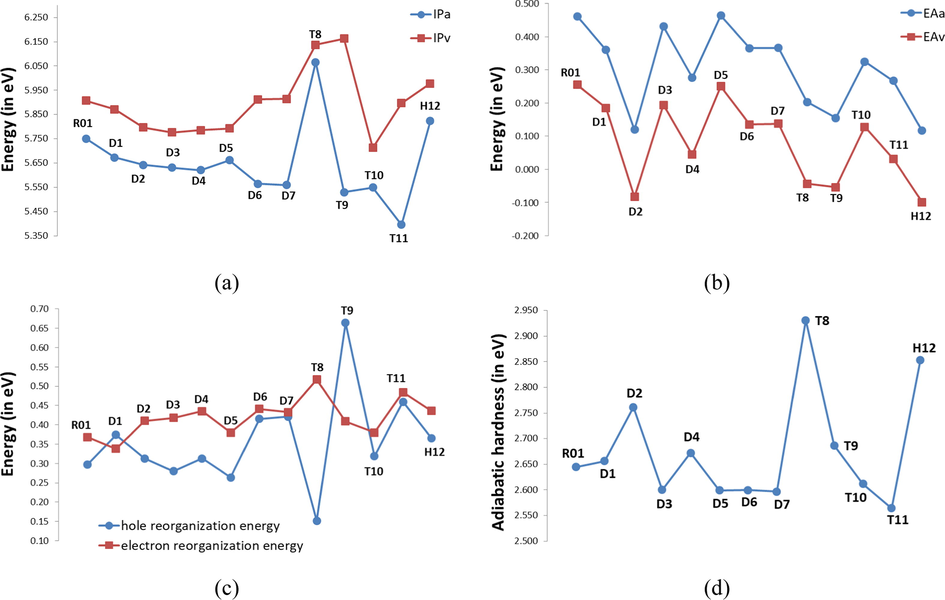
- Adiabatic and vertical ionization potentials (
We find that the
To compare the magnitudes of hole and electron mobilities, we calculate the relative hopping rates of holes versus electrons,
| HTM |
|
|
|
|
|
|---|---|---|---|---|---|
| R01 | 0.246 | 0.391 | 1.86 × 1015 | 4.22 × 1015 | 2 |
| D1 | 0.218 | 0.365 | 1.30 × 1015 | 3.82 × 1015 | 3 |
| D2 | 0.114 | 0.161 | 3.88 × 1014 | 6.79 × 1015 | 18 |
| D3 | 0.205 | 0.451 | 1.34 × 1015 | 5.26 × 1015 | 4 |
| D4 | 0.162 | 0.273 | 7.93 × 1014 | 1.88 × 1015 | 2 |
| D5 | 0.095 | 0.377 | 2.96 × 1014 | 3.86 × 1015 | 13 |
| D6 | 0.047 | 0.262 | 5.79 × 1013 | 1.73 × 1015 | 30 |
| D7 | 0.057 | 0.266 | 8.39 × 1013 | 1.81 × 1015 | 22 |
| T8 | 0.094 | 0.192 | 3.82 × 1014 | 8.55 × 1014 | 2 |
| T9 | 0.033 | 0.113 | 2.22 × 1013 | 3.32 × 1014 | 15 |
| T10 | 0.176 | 0.394 | 9.21 × 1014 | 4.23 × 1015 | 5 |
| T11 | 0.001 | 0.167 | 1.03 × 1014 | 6.69 × 1014 | 6 |
| H12 | 0.028 | 0.139 | 2.24 × 1013 | 4.91 × 1014 | 22 |
As is known the ionization potential and electron affinity are good descriptors to interpret the charge transfer behavior. The energy barrier for the injection of holes and electrons can be predicted by the explicit properties such as adiabatic ionization potential (
The data in Table 5 and Fig. 4 shows that the order of decreasing the adiabatic and vertical
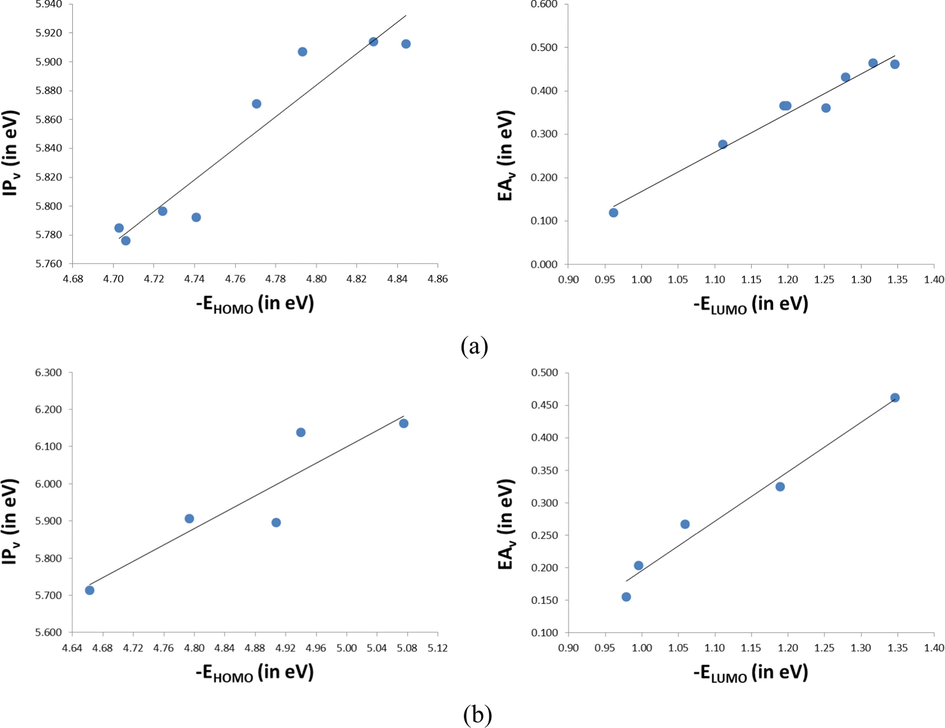
- The correlation between the calculated HOMO and LUMO energies and the vertical
Di-methoxy derivatives (D1, D2, D3, D4, D5, D6, and D7); along with R01
Tetra-methoxy derivatives (T8, T9, T10, and T11); along with R01
Above regression equations may provide a simple formula to predict the vertical
Furthermore, the absolute hardness (η) also has been calculated. As is known, hardness (η) is the resistance of the chemical potential to the change in the number of electrons, and it’s controlled the stability of PSC, since the HTM could play a crucial role in controlling the stability of PSCs; an ideal HTM should be stable, i.e., it should be a hard molecule with large η value (Zhang et al., 2017a, 2017b). The η values of all molecules are also presented in Table 5 and Fig. 4. Inspection of Table 5 and Fig. 4 reveals that the η values of the designed molecules in the range 2.564–2.931 eV with largest deviation of 0.37 eV, indicating that the stabilities of the investigated molecules are almost similar. Indeed, we have found that T8 (η = 2.931 eV) molecule has the highest stability while T11
3.10 First singlet excitation and exciton binding energies
As is known the exciton binding energy (
3.11 NLO properties
It has found that compounds with nonlinear optical properties have good photoelectric conversion performance (Cai-Rong et al., 2009; Kumar et al., 2010; Garza et al., 2014). The polarizabilities and hyperpolarizabilities of the six investigated HTMs were calculated at the B3LYP/6-311++G(d,p), Fig. 6. In addition to the total hyperpolarizabilities, the isotropic polarizability, polarizability anisotropy invariant and hyperpolarizability.
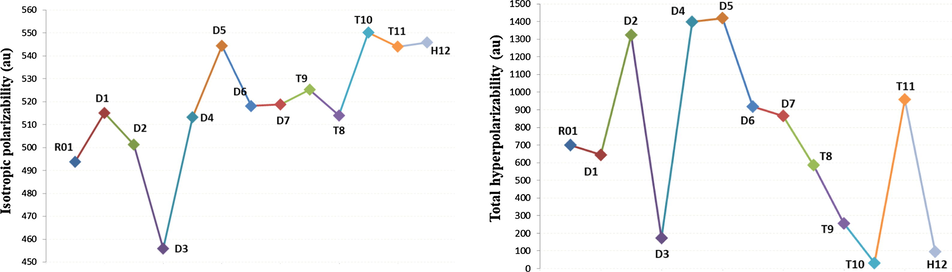
- Isotropic polarizability and total hyperpolarizability values (in au) of investigated HTMs calculated at the B3LYP/6-311++G(d,p).
The calculated isotropic polarizability (
As shown in Fig. 6, the order of decreasing the total hyperpolarizabilities (
4 Conclusion
In this report, an investigation on twelve new designed molecules by means of DFT and TD-DFT methods has been performed. The designed molecules are derivatives of the well experimentally tested R01 used as a hole transporting material for perovskite solar cell applications. R01 is a carbazole-based compound. The designed derivatives differ in number (two, four, and six) and positions of methoxy groups (ortho- and meta-) with respect to the dioxythiophene ring, resulting in the different effect of the substituted methoxy groups with various electronic structures and optoelectronic properties of the designed HTMs. The most important concluded remarks from this report are:
-
In most cases, the number and position of the substituted methoxy groups have a major effect on geometrical parameters of the ground states. The most affected parameter is the S−C−C−C dihedral angles those represent the extent of planarity of the molecule. As expected, the tetra- and hexa-methoxy derivatives showed the most significant changes, due to the steric hindrance of the methoxy groups.
-
Due to methoxy substitution, the HOMO energy levels of most designed HTMs are stabilized and become more close to that of the valence band of perovskite than that of R01, which is beneficial to improving the
-
The investigated HTMs show a dominant ICT that demonstrated by the π-π* that dominated for R01 and most of its derivatives by HOMO-LUMO transition and from the charge density differences between ground and excited states.
-
In comparison to the R01, as the number of substituted methoxy groups increases, the maximum absorption wavelengths would be blue shifted, whereas, the introduction of two methoxy groups keeps the
-
The linear relationships between the vertical
-
The hole reorganization energies of most investigated HTMs including the parent molecule (R01) are smaller than their electron reorganization energies, indicating that these compounds will efficient hole transporting materials, while D1 and T9 derivatives would expect to be effective as electron transporting materials, because their hole reorganization energies are more significant than their electron reorganization energies.
-
The higher Stokes shift values from absorption to emission of D6, T8, T9, and T11 compounds showed that these derivatives would be efficient materials for multipurpose semiconductor applications.
-
NLO parameters calculations showed that
It is not the sole and determined item to affect the overall performance. In view of suitable frontier molecular orbital, larger Stokes shift and high hole mobility and other factors, the designed molecules as HTMs can act as a promising candidate. We believe that this study shed light on the effect of methoxy groups on the electronic and photophysical properties of carbazole-based HTMs, with molecular level insight using the quantum chemical calculations, the methoxy derivatives of R01 may be candidates for optoelectronic materials application and worthy of experimental investigations.
Acknowledgment
This work was supported by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (D-074-130-1438). The authors, therefore, gratefully acknowledge the DSR technical and financial support. Also, Nuha Wazzan acknowledges King Abdulaziz University’s High-Performance Computing Centre (Aziz Supercomputer) (http://hpc.kau.edu.sa) for supporting the computation of the work described in this paper.
References
- Frontiers, opportunities, and challenges in perovskite solar cells: a critical review. J. Photochem. Photobiol., C. 2018;35:1-24.
- [Google Scholar]
- Density functional theory study of new azo dyes with different π-spacers for dye-sensitized solar cells. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc.. 2015;143:20-34.
- [Google Scholar]
- Structure and spectral properties of truxene dye S5. Opt. Spectrosc.. 2012;112(2):168-174.
- [Google Scholar]
- Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38(6):3098-3100.
- [Google Scholar]
- Efficient luminescent solar cells based on tailored mixed-cation perovskites. Science advances. 2016;2(1):e1501170.
- [Google Scholar]
- DFT and TDDFT study on organic dye sensitizers D5, DST and DSS for solar cells. J. Mol. Struct. (Thoechem.). 2009;899(1–3):86-93.
- [Google Scholar]
- Molecular engineering of conjugated polymers for efficient hole transport and defect passivation in perovskite solar cells. Nano Energy 2017
- [Google Scholar]
- Hole-transport materials for perovskite solar cells. Angew. Chem. Int. Ed.. 2016;55(47):14522-14545.
- [Google Scholar]
- Improved quantum efficiency for electroluminescence in semiconducting polymers. Nature. 1999;397(6718):414.
- [Google Scholar]
- Dipole moments, charge-transfer parameters, and ionization potentials of the methyl-substituted benzene–tetracyanoethylene complexes. Can. J. Chem.. 1970;48(2):299-305.
- [Google Scholar]
- Theoretical investigation of charge injection and transport properties of novel organic semiconductor materials—cyclic oligothiophenes. Org. Electron.. 2011;12(7):1198-1210.
- [Google Scholar]
- Theoretical investigation of phenothiazine–triphenylamine-based organic dyes with different π spacers for dye-sensitized solar cells. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc.. 2014;123:282-289.
- [Google Scholar]
- Theoretical study on the electronic structures and properties of diindolocarbazole isomers. J. Phys. Org. Chem.. 2014;27(12):973-980.
- [Google Scholar]
- The theoretical investigation on the 4-(4-phenyl-4-[small alpha]-naphthylbutadieny)-triphenylamine derivatives as hole transporting materials for perovskite-type solar cells. PCCP. 2015;17(8):5991-5998.
- [Google Scholar]
- The theoretical investigation on the 4-(4-phenyl-4-α-naphthylbutadieny)-triphenylamine derivatives as hole transporting materials for perovskite-type solar cells. PCCP. 2015;17(8):5991-5998.
- [Google Scholar]
- A strategy to improve the efficiency of hole transporting materials: introduction of a highly symmetrical core. Nanoscale. 2016;8(41):17752-17756.
- [Google Scholar]
- Theoretical studies on electronic structures and photophysical properties of anthracene derivatives as hole-transporting materials for OLEDs. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc.. 2014;125:36-45.
- [Google Scholar]
- Direct pseudopotential calculation of exciton coulomb and exchange energies in semiconductor quantum dots. Phys. Rev. Lett.. 1997;78(5):915.
- [Google Scholar]
- Theoretical studies of electronic structure and hole drift mobility of host hole transporting material 4,4′-N, N′-dicarbazol-biphenyl. Synth. Met.. 2010;160(19–20):2104-2108.
- [Google Scholar]
- Can Short- and middle-range hybrids describe the hyperpolarizabilities of long-range charge-transfer compounds? J. Phys. Chem. A. 2014;118(50):11787-11796.
- [Google Scholar]
- Gorelsky, S.I., 2015. Program for Molecular Orbital Analysis.
- J. Organomet. Chem.. 2001;635:187-196.
- Well defined carbazole-based hole-transporting amorphous molecular materials. Synthetic Metals. 2006;156(1):46-50.
- [Google Scholar]
- A DFT study of charge-transfer and opto-electronic properties of some new materials involving carbazole units. Comput. Condens. Matter. 2015;3:30-40.
- [Google Scholar]
- A room-temperature CuAlO2 hole interfacial layer for efficient and stable planar perovskite solar cells. J. Mater. Chem. A. 2016;4(4):1326-1335.
- [Google Scholar]
- In-depth quantum chemical investigation of electro-optical and charge-transport properties of trans-3-(3,4-dimethoxyphenyl)-2-(4-nitrophenyl)prop-2-enenitrile. Comptes Rendus Chimie. 2015;18(12):1289-1296.
- [Google Scholar]
- Polymers with triphenylamine units: photonic and electroactive materials. Prog. Polym. Sci.. 2011;36(10):1277-1325.
- [Google Scholar]
- o-Methoxy substituents in spiro-OMeTAD for efficient inorganic-organic hybrid perovskite solar cells. J. Am. Chem. Soc.. 2014;136(22):7837-7840.
- [Google Scholar]
- Efficient inorganic-organic hybrid perovskite solar cells based on pyrene arylamine derivatives as hole-transporting materials. J. Am. Chem. Soc.. 2013;135(51):19087-19090.
- [Google Scholar]
- Efficient inorganic–organic hybrid perovskite solar cells based on pyrene arylamine derivatives as hole-transporting materials. J. Am. Chem. Soc.. 2013;135(51):19087-19090.
- [Google Scholar]
- Novel carbazole-based hole-transporting materials with star-shaped chemical structures for perovskite-sensitized solar cells. ACS Appl. Mater. Interfaces. 2015;7(40):22213-22217.
- [Google Scholar]
- Perovskite as light harvester: a game changer in photovoltaics. Angew. Chem. Int. Ed.. 2014;53(11):2812-2824.
- [Google Scholar]
- The effect of the number, position, and shape of methoxy groups in triphenylamine donors on the performance of dye-sensitized solar cells. Dyes Pigm.. 2015;113:390-401.
- [Google Scholar]
- A swivel-cruciform thiophene based hole-transporting material for efficient perovskite solar cells. J. Mater. Chem. A. 2014;2(18):6305-6309.
- [Google Scholar]
- Quantum chemistry calculations of 3-phenoxyphthalonitrile dye sensitizer for solar cells. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc.. 2010;77(1):45-50.
- [Google Scholar]
- Depleted hole conductor-free lead halide iodide heterojunction solar cells. Energy Environ. Sci.. 2013;6(11):3249-3253.
- [Google Scholar]
- Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37(2):785-789.
- [Google Scholar]
- Reorganization energies in the transports of holes and electrons in organic amines in organic electroluminescence studied by density functional theory. J. Phys. Chem. A. 2003;107(26):5241-5251.
- [Google Scholar]
- Anthracene–arylamine hole transporting materials for perovskite solar cells. Chem. Commun.. 2017;53(69):9558-9561.
- [Google Scholar]
- Energy Technol. 2016
- Seed-mediated superior organometal halide films by GeO2 nano-particles for high performance perovskite solar cells. Appl. Phys. Lett.. 2016;108(5):053301
- [Google Scholar]
- Theoretical study of vibrational and optical spectra of methylene-bridged oligofluorenes. J. Phys. Chem. A. 2005;109(45):10232-10238.
- [Google Scholar]
- Gaussian 09. Wallingford CT: Gaussian, Inc.; 2016.
- Understanding the photo-electrochemistry of metal-free di and tri substituted thiophene-based organic dyes in dye-sensitized solar cells using DFT/TD-DFT studies. Ionics 2017
- [Google Scholar]
- Copper salts doped spiro-OMeTAD for high-performance perovskite solar cells. Adv. Energy Mater.. 2016;6(21):1601156.
- [Google Scholar]
- Electronic structure and spectral properties of the triarylamine-dithienosilole dyes for efficient organic solar cells. Dyes Pigm.. 2012;92(1):531-536.
- [Google Scholar]
- Solvent effects on charge transfer bands of nitrogen-centered intervalence compounds. J. Am. Chem. Soc.. 2001;123(24):5684-5694.
- [Google Scholar]
- Polarization energies in oligoacene semiconductor crystals. J. Am. Chem. Soc.. 2008;130(37):12377-12384.
- [Google Scholar]
- Quantitative prediction of optical excitations in conjugated organic oligomers: a density functional theory study. J. Chem. Phys.. 2002;117(12):5921-5928.
- [Google Scholar]
- Triazatruxene-based hole transporting materials for highly efficient perovskite solar cells. J. Am. Chem. Soc.. 2015;137(51):16172-16178.
- [Google Scholar]
- Roy, Dennington, Keith, T., Millam, J., 2009. GaussView. S. Mission. KS, Semichem Inc.
- Phenothiazine and carbazole substituted pyrene based electroluminescent organic semiconductors for OLED devices. J. Mater. Chem. C. 2016;4(5):1009-1018.
- [Google Scholar]
- Spiro-OMeTAD single crystals: remarkably enhanced charge-carrier transport via mesoscale ordering. Sci. Adv.. 2016;2(4)
- [Google Scholar]
- Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science. 2013;342(6156):341-344.
- [Google Scholar]
- Hole-transporting materials for printable perovskite solar cells. Materials. 2017;10(9):1087.
- [Google Scholar]
- Facile synthesis and high performance of a new carbazole-based hole-transporting material for hybrid perovskite solar cells. ACS Photonics. 2015;2(7):849-855.
- [Google Scholar]
- A new carbazole-based hole-transporting material with low dopant content for perovskite solar cells. Electrochim. Acta. 2016;210:673-680.
- [Google Scholar]
- Induced crystallization of perovskites by a perylene underlayer for high-performance solar cells. ACS Nano. 2016;10(5):5479-5489.
- [Google Scholar]
- DFT and TD–DFT calculations of the electronic structures and photophysical properties of newly designed pyrene-core arylamine derivatives as hole-transporting materials for perovskite solar cells. Theor. Chem. Acc.. 2017;137(1):9.
- [Google Scholar]
- DFT and TD–DFT calculations of the electronic structures and photophysical properties of newly designed pyrene-core arylamine derivatives as hole-transporting materials for perovskite solar cells. Theor. Chem. Acc.. 2018;137(1):9.
- [Google Scholar]
- High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science. 2015;348(6240):1234-1237.
- [Google Scholar]
- Recent progress on hole-transporting materials for emerging organometal halide perovskite solar cells. Adv. Energy Mater.. 2015;5(12)
- [Google Scholar]
- Design new hole transport materials for efficient perovskite solar cells by suitable combination of donor and core groups. Org. Electron.. 2017;49:255-261.
- [Google Scholar]
- Design new hole transport materials for efficient perovskite solar cells by suitable combination of donor and core groups. Org. Electron.. 2017;49(Supplement C):255-261.
- [Google Scholar]
- Theoretical study on the electronic structure and optical properties of carbazole-π-dimesitylborane as bipolar fluorophores for nondoped blue OLEDs. J. Mol. Graph. Model.. 2012;34:46-56.
- [Google Scholar]
- Theoretical investigations on electronic structures and photophysical properties of novel bridged triphenylamine derivatives. Int. J. Quantum Chem.. 2012;112(5):1473-1490.
- [Google Scholar]
- Molecular design toward good hole transport materials based on anthra[2,3-c]thiophene: a theoretical investigation. Comput. Theor. Chem.. 2013;1010:25-31.
- [Google Scholar]
- High-efficiency perovskite solar cells based on new type compounds as hole transport materials: the role of 2, 7-and 3, 6-substituted carbazole derivatives. Chem. – A Eur. J.. 2017;23(18):4373-4379.
- [Google Scholar]
- Zhurko, G., Zhurko, D., 2009. Chemcraft program, Academic version 1.8.







