Calculation method for the dielectric constant of thioglycolic acid grafted modified SBS dielectric elastomer

2.1 Division of repeating units

Many synthetic macromolecular materials have relatively simple structures, and identical structures that recur in the molecular chain are defined as repeating units. If the repeating units are the same, the material is a homopolymer. If there are more than two repeating units, the material is a copolymer. Polymer molecular chains consist of a “backbone” and peripheral atoms or groups. The end groups in finite-size polymer chains are not repeating units and have little effect on the physical properties and are usually not considered.

The polymer molecular chain is divided into repeating units by searching for recurring identical structures along with the polymer' skeleton'. For subsequent analysis, the repeating units containing polar functional groups such as carboxylic acids, alcohols, amides, thiols, and ketones are classified as polar groups. Those containing only nonpolar functional groups such as alkanes and alkenes are classified as nonpolar groups.

The molecular structure of SBS-TGA is shown in Fig. 1a and can be divided into six repeating units, St, Cis-1,4-Bu, Trans-1,4-Bu, 1,2-Bu, 1,4-Bu-TGA, and 1,2-Bu-TGA(Segre et al., 1975; Kussmaul et al., 2011), denoted by G₁,G₂…G₆, respectively, as shown in Fig. 1b. G₁, G₂, G₃, and G₄ are classified as nonpolar sets, and G₅ and G₆ are classified as polar sets.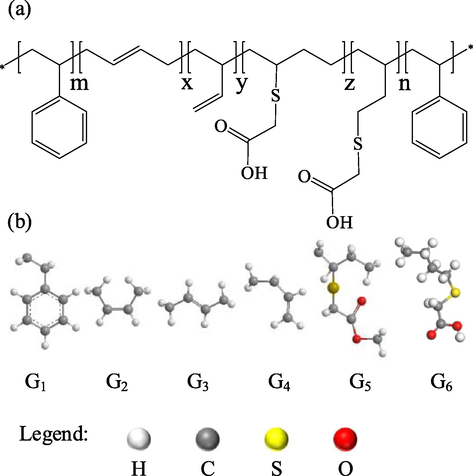

Close

Fig. 1

(a) The molecular structure of SBS-TGA, (b) the repeating units G₁-G₆: St, Cis-1,4-Bu, Trans-1,4-Bu, 1,2-Bu, 1,4-Bu-TGA, 1,2-Bu- TGA.

Export to PPT

2.2 Calculation of dielectric constant of the nonpolar repeating unit

2.2.1

2.2.1 Calculation of connectivity index

For the nonpolar repeating unit G_i, the dielectric constant ε_i is calculated using the CI method. First, the hydrogen-suppressed graph is constructed from the valence bond diagram of the repeating unit, as shown in Fig. 2a and Fig. 2b, taking G₁ as an example.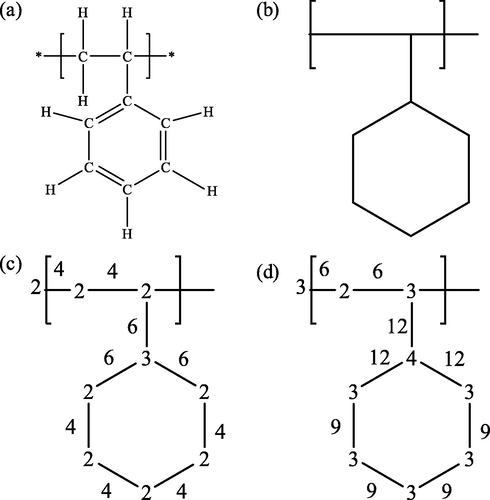

Close

Fig. 2

(a) The valence-bond structure of G₁, (b) The hydrogen-suppressed graph of G₁; (c) The δ value on the vertex and the β value on the edge; (d) The δ^V value on the vertex and the β^V value on the edge.

Export to PPT

The atomic indices δ and δ^V describe the electronic environment and the bond configuration of each non-hydrogen atom in the molecule. δ is the simple connectivity index and is equal to the number of edges emanating from that vertex in the hidden hydrogen diagram. δ^V is the valence connectivity index and is defined by Eq. (7) (Randic, 2015). The calculation results are shown in Fig. 2c and the values at the vertices in Fig. 2d.

(7)

$${\delta }^V=\frac{Z^V-N^H}{Z-Z^V-1}$$ where Z^v is the number of valence electrons of the atom, N_H is the number of hydrogen atoms bonded to it, and Z is its atomic number.

The value corresponding to each bond that does not involve a hydrogen atom is defined as the bond index, and the bond index β and β^V are determined by the product of the atomic indices (δ and δ^V) at the two vertices (i and j) connected by the edges, as shown in Eqs. (8) and (9). Taking G₁ as an example, the calculation results are marked on the edges of the hydrogen-suppressed graph in Fig. 2c and Fig. 2d

(8)

$${\beta }_{\mathit{ij}}={\delta }_i·{\delta }_j$$

(9)

$${\beta }_{\mathit{ij}}^V={\delta }_i^V·{\delta }_j^V$$

The zero-order connectivity index (⁰χ, ⁰χ^V) of the whole molecule and is defined based on the atomic index of all vertices of the hydrogen-suppressed graph, as shown in Eqs. (10) and (11) (Randic, 1975). Taking G₁ as an example, the results are calculated as 5.397 and 4.671, respectively.

(10)

$${}^0\chi =\sum _{\mathit{vertices}}\left(\frac{1}{\sqrt{\delta }}\right)$$

(11)

$${}^0{\chi }^V=\sum _{\mathit{vertices}}\left(\frac{1}{\sqrt{{\delta }^V}}\right)$$

The first-order connectivity index (¹χ, ¹χ^V) of the whole molecule is defined based on the bond index on all edges of the hydrogen-suppressed graph, as shown in Eqs. (12) and (13) (Randic, 1975). Taking G₁ as an example, the results are calculated as 3.966 and 3.015, respectively.

(12)

$${}^1\chi =\sum _{\mathit{edges}}\left(\frac{1}{\sqrt{\beta }}\right)$$

(13)

$${}^1{\chi }^V=\sum _{\mathit{edges}}\left(\frac{1}{\sqrt{{\beta }^V}}\right)$$

The zero-order and first-order connectivity indexes of G₁-G₄ are shown in Table 1. For computational simplicity, this paper does not use higher-order connectivity indexes (Kier and Hall, 1976a,b), and various types of structural parameters are used to supplement the zero- and first-order connectivity indexes.

Table 1 Zero-order and first-order connectivity index.

Repeating units	0χ	0χV	1χ	1χV
G1	5.397	4.671	3.966	3.015
G2	2.828	2.568	2.000	1.649
G3	2.828	2.568	2.000	1.649
G4	2.991	2.568	1.931	1.558

2.3 Calculation of the dielectric constant of the polar repeating unit

The dielectric constants of the polar repeating units (G₅, G₆) cannot be calculated by the structure–property analysis method. Molecular dynamics simulations (MDS) based on first principles can predict them (Bicerano, 2002). In this paper, the MDS of polar repeating units are used to calculate their dielectric constants using the DMF method.

A permanent molecular dipole consisting of two charge ± q at a distance l, giving the dipole moment μ = ql, is shown in Fig. 3. For molecules with complex structures, the dipole moment can be obtained by adding simple dipole moment vectors, as shown in Eq. (21). Similarly, it can be known that the total dipole moment M in a periodic cell is the vector sum of the dipole moments of all molecules in the system.

Close

Fig. 3

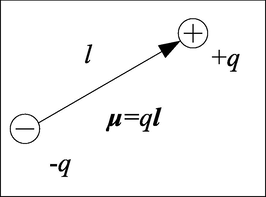
The schematic representation of a permanent molecular dipole.

Export to PPT

An all-atom model of repeating unit is constructed in the Materials Studio software. On this basis, a periodic cell containing N particles is built for MDS (N = 256 (Neumann, 1983)), as shown in Fig. 4. In order to prevent the nesting of molecular structure, we set the initial density to be relatively low, 0.5 g/cm³. The reaction force field is COMPASS. The temperature control method is Andersen’s algorithm. The pressure control method is Berendsen’s, and the calculation of the non-bonded cooperative force is based on the group-based method. The simulation time step is 1 fs, the cutoff distance is 12.5 Å, the spline width is 1 Å, the buffer width is 0.5 Å, and the pressure is 0.1 MPa.

Close

Fig. 4

(a) G₅′s and (b) G₆′s periodic cell model.

Export to PPT

The periodic cells are geometrically optimized with a convergence standard of 0.001 kcal/mol. The geometrically optimized periodic cells are annealed to make their density close to the real value. The annealing process is carried out in the NPT ensemble with a starting temperature of 300 K, an intermediate maximum temperature of 500 K, and a pressure value of 0.1 MPa. The temperature rise step is set to 50 K, and the number of cycles is 5. 100 000 kinetic steps are performed for each temperature, and one frame of output is performed every 500 steps.

On the basis of a stable conformation, 10 frames with a temperature of 298 K are extracted for NVT dynamics simulation with 400 ps, and the output frame is performed every 100 steps. The dielectric constant values of 10 samples are averaged as the final value to reduce the error. The total dipole moment of the system in each frame was statistically calculated using a Perl script. The total dipole moment M, as a vector, has three components M_x, M_y, and M_z in the ×, y, and z directions.

According to molecular theory, the corresponding relationship between dipole moment–time and macroscopic dielectric constant can be constructed (Williams, 1972). For periodic boundary systems, the relationship between total dipole moment–time and macroscopic dielectric constant can be expressed by Eq. (22) (De Leeuw et al., 1980; Heinz et al., 2001).

Each output frame of results during the simulation can be interpreted as a sampling of the dynamics simulation system, and Eqs. (23) and (24) can express the Boltzmann averaging term in Eq. (22).

To investigate the relationship between the dipole moment fluctuation of the repeating unit and the orientation polarization of the material, we calculated the dielectric constant values for different dipole moment fluctuation times, as shown in Fig. 5. Overall, G₆ has a larger dielectric constant than G₅, which is caused by the difference in permanent dipole moment μ₀ due to the structural difference. As time increases, the dielectric constant of both G₅ and G₆ first increase and then decrease. This can be explained by the dielectric orientation polarization process. We assume that the different dipole moment fluctuation times correspond to the time of electric field action, as shown by the blue dashed line in Fig. 5. At the electric field value greater than zero, the dipole inside the material undergoes an oriented arrangement, and the polarization intensity is always intensified. The polarization intensity reaches its highest, and the dielectric constant is maximum when the dipole moment fluctuation time is 300 ps. When the electric field direction is flipped, the dipole arrangement inside the material will reverse with the electric field direction. If the statistical time exceeds 300 ps, the statistical result of Eq. (22) decreases, as shown in the figure for 350 ps, 390 ps, and 400 ps. This phenomenon may correspond to the phenomenon of internal polarization of the material under the action of an alternating electric field. Suppose an alternating electric field of voltage amplitude V acts on the material. When the electric field is positive, the polarization intensity inside the material gradually increases. When the electric field is negative, the dipole arrangement inside the material will turn, and the dielectric constant decreases. We intercepted the total dipole moment fluctuation data of G₆ from 300 ps to 400 ps and calculated the dielectric constant as 6.78 using Eq. (22), which is very close to the result of t = 100 ps, which is consistent with our proposed conjecture.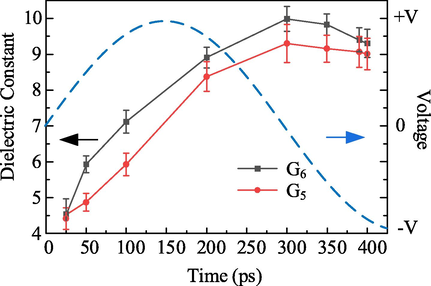

Close

Fig. 5

The dielectric constant of G₅ and G₆ with different simulation times.

Export to PPT

2.4 Calculation of dielectric constant of graft-modified SBS

The molar polarizability of the repeating unit can be calculated using three models, Gladston-Dale, Lorentz-Lorenz, and Vogel, and considering that the molar mass is easier to calculate than the molar volume, the Vogel model is used in this paper. The results calculated according to Eq. (25) are shown in Table 3.

In a semi-empirical approach, the molar properties of non-interacting substances can be calculated by summing the contributions of atoms, groups, or bonds (Zhou et al., 2014). The molar mass, molar polarizability of polymers can be calculated according to Eqs. (26)–(27).

Eqs. (26)–(27) are substituted into Eq. (4) yields Eq. (28) for the calculation of the dielectric constant of the polymer. Dividing the upper and lower parts of this equation simultaneously by ∑n_i the Eq. (29) for calculating the dielectric constant of the polymer expressed in terms of molar content is obtained. The molar content was calculated by equation (30) (Tashiro et al., 1984).

SBS determines the molar content of each repeating unit in SBS-TGA. According to Fig. 1, the molar content of G₁ is equal to that in SBS; G₅ is derived from G₂ and G₃ grafted TGA. The sum of the three is equal to the sum of the molar content of G₂ and G₃ in SBS, and G₆ is derived from G₄ grafted TGA, and the sum of the molar content of the two is equal to the molar content of G₄ in SBS. The C = C located in the side chain is more active and more prone to grafting reactions (Tian et al., 2016; Sun et al., 2016). Therefore, G₄ reacts with TGA first during the grafting process. G₂ and G₃ do not graft TGA until G₄ is completely converted to G₆ and no G₅ is generated. The relationship between c₁-c₆ in SBS-TGA can be written and expressed as Eq. (31).

According to SBS's H Nuclear Magnetic Resonance (HNMR) (Ellingford et al., 2018) and specific area analysis method c_1,SBS = 18%,c_2,SBS + c_3,SBS = 60%,c_4,SBS = 22%.

The variation of G₅ and G₆ molar content in SBS-TGA corresponds to the variation of TGA grafting rate in polybutadiene blocks. Therefore, the equation for the grafting rate of SBS-TGA is shown in Eq. (32), and the variation law of dielectric constant with grafting rate is shown in Fig. 6.

Close

Fig. 6

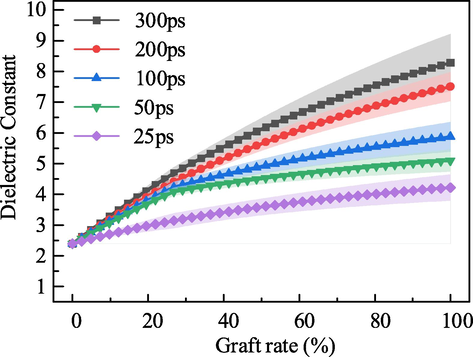
Calculated value of the dielectric constant of SBS-MT with different grafting rate.

Export to PPT

It can be seen from the figure that the constant dielectric increases gradually with the increase of the grafting rate. The dielectric constant of unmodified SBS is 2.4 when the grafting rate is 0. Under the same polarization time, the higher the grafting rate, the greater the dielectric constant, and the maximum value can reach 8.3, which is 3.5 times the initial value. Therefore, for SBS-TGA, increasing its dielectric constant can be achieved by changing the reaction conditions to increase the grafting rate of TGA.

3.1 Materials

SBS (YH-806) is produced by Baling Petrochemical, China, Tetrahydrofuran (THF, AR grade) and Cyclohexane (AR grade) are purchased from Kelon Chemical Co., Ltd., China, 2,2- dimethoxy-2 -phenyl acetophenone (DMPA, 99%) and TGA (AR grade, 96%) were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd., China. All of the above chemicals were not processed before use.

3.2 Synthesis

The reaction principle was mercapto-olefin reaction under UV irradiation, and the catalyst was DMPA. The molar ratio of the sulfhydryl group to the C = C bond was set to 5:1 during the synthesis.

In the first step, SBS and tetrahydrofuran were placed in a beaker at the ratio of 1:9 by weight and stirred magnetically at 30 ℃ until SBS was dissolved entirely, and 50 g of the dissolution solution was used for material preparation. In the second step, 0.1 g of DMPA and 29.9 g of TGA were added to the SBS dissolution solution. Finally, the SBS-TGA was extracted from the solution with cyclohexane, filtered, and dried under vacuum at 60 ℃ for 24 h. The grafting rate of the SBS-TGA was determined by the use of a UV lamp with a wavelength of 365 nm and a power of 50 W. In the third step, the SBS-TGA was extracted from the solution with cyclohexane, filtered, and dried under vacuum for 24 h at 60 ℃.

3.3 Film sample preparation

The samples were prepared using a manual hot press machine model AR1701 from AUPLEX Co., Ltd., China. The raw material was placed in the mold at 150 °C and kept under normal pressure for 15 min to eliminate air bubbles, and the pressure was adjusted to 2.5 MPa and kept for 10 min. The mold was removed, cooled to room temperature, and then the film samples were taken out with a thickness of about 0.5 mm.

3.4 Calculation of grafting rate

The HNMR spectrum was measured using a Bruker AV600MHz high-resolution liquid NMR spectrometer with a solvent of CDCl3 and a chemical shift range of 0–8 ppm. The test results are shown in Fig. 7.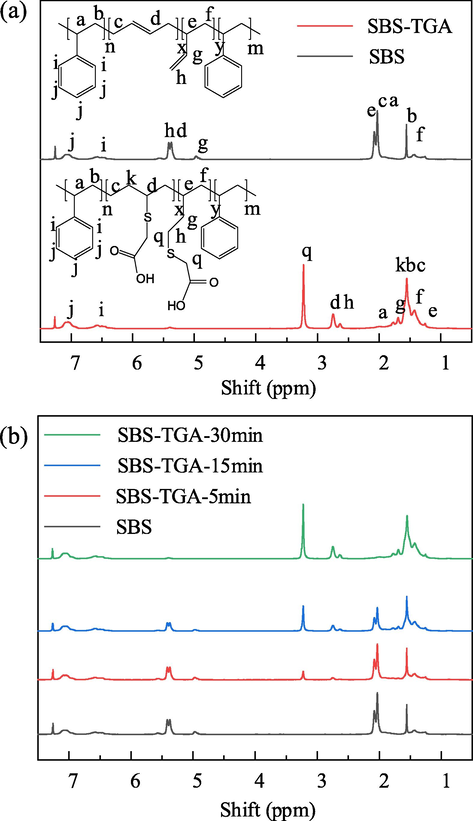

Close

Fig. 7

HNMR of SBS and SBS-TGA, (a) Chemical shifts of hydrogen atoms on the main functional groups, (b) HNMR of SBS-TGA with different grafting rates.

Export to PPT

It can be seen from the figure that the characteristic peaks corresponding to C = C gradually decreased, and the characteristic peaks associated with TGA gradually increased with the increase of reaction time, which indicated that the grafting rate of SBS-TGA gradually increased. The area integrals of the characteristic peaks of the G₁-G₆ repeat units were calculated on the HNMR spectra with the benzene ring H as the reference, and the grafting rate of SBS-TGA could be calculated using the specific area method as shown in Eq. (33). The calculated results showed that the grafting rates of the three SBS-TGA samples were 15.3%, 47.2%, and 89.7%, respectively. The grafting rate gradually increased with the increase of reaction time.

3.5 Dielectric constant test

Measurements were performed using a Concept 80 broadband dielectric test system with an electrode diameter of 20 mm. The polarization ability of the material was enhanced after grafting dipole, and the dipole polarization time range was 10^-10-10^-2 s, corresponding to a frequency range of 10²-10¹⁰ Hz, and considering the measurement range of the equipment, the test frequency range of 10²-10⁶ Hz was chosen in this paper. The variation curve of the real part of the dielectric constant with frequency is shown in Fig. 8.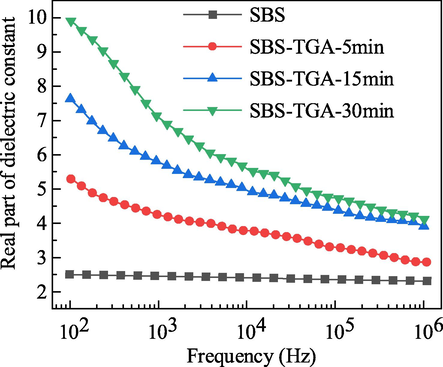

Close

Fig. 8

The real part of the dielectric constant of SBS and SBS-TGA.

Export to PPT

The dielectric constant of SBS is basically not affected by frequency. This is because SBS is nonpolar, and the polarization phenomenon under the action of an electric field is mainly induced polarization, and the molecular polarization rate does not change within the measurement frequency range. The dielectric constant of SBS-TGA will gradually increase as the measurement frequency decreases. According to Eq. (5) and related analysis, the lower the frequency, the longer the electric field action time, the more orderly arrangement of the dipoles, and the greater the polarization intensity, which corresponds to a greater dielectric constant. The dielectric constant of SBS-TGA gradually increases with the increase of grafting rate. This is because the permanent dipole μ₀ inside the material increases after grafting TGA. According to Eq. (5), the higher the grafting rate, the greater the polarization intensity at the same test frequency and the greater the dielectric constant. The difference in the dielectric constant of SBS-TGA with different grafting rates decreases as the frequency increases. This is because higher frequency means shorter dipole turning time and lower molecular polarizability. This leads to a decrease in the difference in the dielectric constant of SBS-TGA materials with different grafting rates.

3.6 Analysis of results

We choose five sets of data for comparison, as shown in Fig. 9. The experimental test values are selected at 0.1 kHz, 1 kHz, 10 kHz, 100 kHz, 1000 kHz, and the dipole moment fluctuation times are selected at 300 ps, 200 ps, 100 ps, 50 ps, and 25 ps, respectively. The difference between the test value at 0.1 kHz and the calculated value of 300 ps is very large for the first set of data, and the reason for this phenomenon is put in the following paragraphs. We can summarize the relationship between the test frequency and the dipole moment fluctuation time by using Eq. (34).

Close

Fig. 9

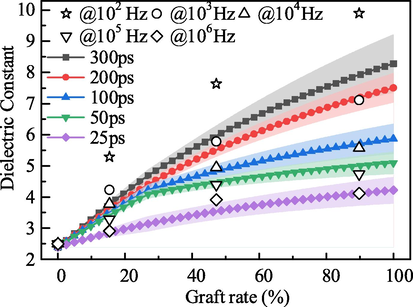
Comparison of experimental value and calculated value for dielectric constant.

Export to PPT

We take the DMF time t₁ = 45 ps, t₂ = 150 ps, and t₃ = 300 ps into Eq. (34) respectively, and calculate the corresponding frequency values f₁ = 141.9 kHz, f₂ = 2.6 kHz, f₃ = 0.26 kHz. The calculated and measured dielectric constant of different samples is shown in Table 4.

Examples 1 and 2 demonstrate that the theoretical calculations match the measured values relatively well in the higher frequency range, 1 kHz-1000 kHz. Example 3 shows that when the frequency is below 1 kHz, there is a significant deviation between the theoretical calculation and the measured value. At below 1 kHz, space charge polarization may occur within the material in addition to dipole shifting polarization, which further increases the overall material polarization intensity and results in larger measured dielectric constant values. The DMF method cannot take into account the space charge polarization process, so the proposed dielectric constant calculation method in this paper cannot perform dielectric constant prediction below 1 kHz. The applicability of the method in the higher frequency range has not been verified due to the measurement error of the experimental equipment and the accuracy of the software calculation. Therefore, the proposed method for calculating the dielectric constant of block copolymers is applicable in the frequency range of 1 kHz to 1000 kHz.