Translate this page into:
Computational simulation of critical speed and dynamic analysis of agglomerated CNTs/fiber/polymer/metal laminates rotating cylindrical shell
⁎Corresponding authors. marischaelveny@usu.ac.id (Marischa Elveny), ahmad.b.albadarin@ul.ie (Ahmad B. Albadarin)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
The main object of this research is to consider the effects of agglomeration on the free vibration and critical speed of rotating carbon nanotubes (CNTs)/fiber/polymer/metal laminates (CNTFPMLs) thin cylindrical shells. The strain–displacement relations are obtained using Love’s first approximation shell theory, and moduli of carbon nanotubes reinforced composites (CNTRCs) cylindrical shells are derived using Eshelby-Mori-Tanaka. Furthermore, fibers are reinforced by means of extended rule of mixture. There are four phases for generating CNTFPMLs cylindrical shell which are fiber, CNTs, polymer matrix and metal. In this work, the effects of several items on vibration of agglomerated CNTFPMLs rotating cylindrical shells are considered, namely, material properties of the fiber phase, lay-ups, volume fractions of metal and composite sections, rotational speed and agglomeration constants. The results demonstrated that the non-dimensional frequencies of symmetric agglomerated CNTs were greater than asymmetric for and , while they were smaller for . In addition, although the cylindrical shell reaches the critical speed for symmetric and asymmetric agglomerated CNTs with glass fiber (at and ), respectively, the non-dimensional frequencies of none of the cylindrical shells reach the critical speed and their forward directions are changed before reaching the critical speed for .
Keywords
Agglomeration
Critical speed
Vibration
CNTFPMLs
Cylindrical shell
1 Introduction
Starting several years ago, composites have been applied increasingly in some modern engineering industries due to their structures with high strength-stiffness ratio compared to structures made by heavy metallic materials. Different fields of mechanical engineering science, namely, vibration, buckling and bending of composite beams, plates and cylindrical shells have been studied in previous years by various researchers (Mohammadimehr et al., 2018; Mohandes and Ghasemi, 2019; Ghasemi and Mohandes, 2019; Mohammadimehr et al., 2016; Ghasemi and Mohandes, 2020; Zhang et al., 2021; Bourada et al., 2020; Bousahla et al., 2020; Al-Furjan et al., 2021) One of the areas where composite materials are widely utilized is rotating cylindrical shells (Lam and Loy, 1994; Liu and Chu, 2012; Daneshjou and Talebitooti, 2014) which are used in different industries such as the drive shaft of gas turbines, rotors and centrifugal separators.
Although composite structures have remarkable benefits, they also have certain deficiency behaviors that can be revised or completely removed by fiber metal laminates (FMLs). The considerable advantages of metals such as ductility, impact and damage tolerances together with the benefits of composites such as high strength and stiffness to weight ratio, excellent fatigue resistance, acceptable corrosion and control of the elastic and structural couplings using fiber orientations and different lay-ups are merged in FMLs (Montazeri et al., 2010). Due to their aforementioned advantages, FMLs are finding increasing use most commonly in industrial applications especially aerospace. A number of companies have shown interest in substituting the traditional aluminium components with FML composites. Both Aramid Reinforced Aluminium Laminate (ARALL) and glass reinforced aluminium laminate (GLARE) are now being used as structural materials in aircrafts. FMLs have been successfully introduced into the Airbus A380. Asundi and Choi (Asundi and Choi, 1997) presented that in comparison with using one thick monolithic sheet, lamination and adhesive bonding of thin sheets in adhesively bonded sheet materials could significantly reduce the likelihood of fatigue cracking. Shooshtari et al. (Shooshtari and Razavi, 2010) studied nonlinear free vibration of FML plates based on first order shear deformation theory (FSDT) applying multiple time scale method. Fu et al. (Fu et al., 2014) studied nonlinear vibration of FML Timoshenko beam subjected to unsteady thermal loading with respect to delamination length, delamination depth and transverse shear deformation. Fu and Tao (Fu and Tao, 2016) proposed nonlinear vibration of FML Timoshenko beams under thermal shock using differential quadrature method (DQM). They investigated dynamic analysis of FML beams with considering the effects of thermal shock, geometric nonlinearity and viscoelasticity circumstances. Rahimi et al. (Rahimi et al., 2014) investigated dynamic analysis of FML annular plate with a central hole in accordance with three-dimensional elasticity theory. The natural frequencies of GLARE plate were determined utilizing a combination of the DQM, state-apace and Fourier series. The out puts of the presented method were compared with the ABAQUS software and had excellent agreement.
One of the composite materials which shows remarkable attention for use in many advanced industrial applications is carbon nanotubes (CNTs). CNTs can be added to matrix, in order to improve its thermal, mechanical and electrical behaviors considerably. The size and morphology of the fibrous carbons are highly significant depending on how they are employed. When the diameter is big, it can be employed in energy systems. As the diameter of the fibrous carbon is decreased, the applications are scaled down in the size. There are a lot of researches which have been done about different structures reinforced by CNTs (Tagrara et al., 2015; Madani et al., 2016; Nejati et al., 2017; Civalek, 2017; Fantuzzi et al., 2017; Arefi et al., 2018; Zerrouki et al., 2021; Arshid et al., 2021; Heidari et al., 2021). Thomas et al. (Thomas and Roy, 2017) applied Eshelby-Mori-Tanaka and Rayleigh damping models to consider the material characteristics of functionally graded carbon nanotube-reinforced hybrid composite (FG-CNTRHC) and the impact of CNTs on damping capacity of FG-CNTRHC shells, respectively. The influences of volume fraction of CNTs and carbon fibers on all elastic properties of the shell were shown in their research. Ansari et al. (Ansari et al., 2016) considered the influences of elastic foundation and boundary conditions on vibration of various functionally graded carbon nanotubes reinforced composites (FG-CNTRC) spherical shells using the variation differential quadrature method (VDQM). They revealed that the most frequencies of this structure were related to distribution. Moreover, one of the items which caused reduction of FG-CNTRC spherical shells frequencies was an increase in the thickness-to-radius ratio. Also, Ansari and Torabi (Ansari and Torabi, 2016) used VDQM to consider vibration and buckling of FG-CNTRC conical shells subjected to axial loading. They showed that the frequencies and axial buckling loads of the FG-CNTRC conical shells increased with a rise in the volume fraction of CNTs. Karamanli and Aydogdu (Karamanli and Aydogdu, 2021) investigated dynamic analysis of two directional FG-CNTRC plates for different boundary conditions. Civalek et al. (Civalek et al., 2020) studied free vibration and buckling of cross-ply laminated composite plates reinforced by CNTs on the basis of first order shear deformation theory (FSDT) using discrete singular convolution. Mahesh and Harursampath (Mahesh and Harursampath, 2020) obtained nonlinear frequencies of magneto-electro-elastic plates reinforced by CNTs based on higher order shear deformation theory using finite element method. Bendenia et al. (Bendenia et al., 2020) studied the effects of elastic foundation on vibration of nanocomposite sandwich plates including with the face sheet reinforced and an homogeneous; core and with an homogeneous face sheet and reinforced core. In a previous article, Al-Furjan et al. investigated the impact of elastic foundation on the frequencies of honeycomb core sandwich disk, which was made of aluminium, with multiscale hybrid nanocomposite face sheets which are imperfect (Al-Furjan et al., 2020c).
The prediction of the mechanical properties of CNTs is one the main aims of performing an extensive study on their behavior. All of the papers mentioned above have assumed the CNTs to be graded in the thickness direction, while agglomeration of CNTs in the matrix phase is a well-known destructive phenomenon. Although all of the above articles which have estimated CNTs through the extended rule of mixture (ROM), it should be noted that this rule is not useful for CNTs oriented randomly in the matrix. The CNTs agglomeration in a polymer matrix occurs due to some mechanical properties (Shaffer and Windle, 1999; Vigolo et al., 2000; Montazeri et al., 2010), namely, a low bending stiffness of CNTs with a small diameter and/or elastic modulus in the radial direction, a high aspect ratio (usually > 1000) and the existence of an adhesive interface between CNTs and their surrounding polymer. Hedayati et al. (Hedayati and Sobhani Aragh, 2012) used an equivalent continuum model to investigate the impact of agglomerated CNTs on natural frequencies of annular sectional plates resting on an elastic foundation. They showed that as the agglomeration parameter grew, the frequencies of asymmetric continuous graded CNTs profile decreased more than the symmetric ones. In 2017, Kamarian et al. (2017) used the generalized differential quadrature method (GDQM) to consider the effect of CNTs agglomeration on free vibration of non-uniform nanocomposite beams bonded by piezoelectric layers subjected to different boundary conditions. In 2017, Kolahchi and Cheraghbak (Kolahchi and Cheraghbak, 2017) studied dynamic buckling of plates in microscale reinforced by agglomerated CNTs using the Kelvin-Voigt model. Natural frequencies of curved Timoshenko microbeam reinforced by agglomerated CNTs, which were rested on elastic foundation, were obtained based on modified couple stress theory using GDQM by Allahkarami and Nikkhah-bahrami (Allahkarami and Nikkhah-Bahrami, 2018). As predicted, CNTs agglomeration caused a decrease in the natural frequencies of the beam. In 2019, Ghasemi et al. (Ghasemi et al., 2019) proposed a novel study on the influences of agglomerated CNTs on CNTs/fiber/polymer/metal laminate (CNTFPML) cylindrical shells. The equations of motion which were presented by Kirchhoff Love’s first approximation shell theory were solved using a beam modal function model which is a semi-analytical model to consider various structures subjected to different boundary conditions. Tornabene et al. (Tornabene et al., 2016) studied agglomeration effects on free vibrations of FG-CNTRC doubly curved shells and panels using GDQM.
In this research, the agglomeration influences on the frequencies and critical speed of CNTFPMLs rotating cylindrical shells are studied for simply supported boundary condition. For CNTFPMLs cylindrical shell generation, firstly, the CNTs were added to the matrix for its reinforcement. Secondly, the reinforced matrix was used to reinforce the fiber phase and finally, the adhesive fiber prepreg was combined with the thin metal layers. It should be mentioned that the effects of agglomeration and critical speed on the vibration of rotating CNTFPML cylindrical shells have not been considered until now. In this study, these effects on the rotating CNTFPML cylindrical shells are studied. The effect of CNTs agglomeration on the elastic properties of CNT-reinforced composites rotating cylindrical shell is determined by the Eshelby-Mori-Tanaka approach based on a similar fiber (Ghasemi et al., 2019).
2 Formulation
Fig. 1 illustrates CNTFPMLs rotating circular cylindrical shell having length L, radius R, thickness h and angular speed of rotation
. The FML is a combination of thin aluminum layer with adhesive fiber. The outer and inner layers are consist of aluminum with uniform thickness and the middle layer is a cross-ply laminated composite reinforced by CNTs with n layers so that each layer has the same thickness (Ghasemi and Mohandes, 2020).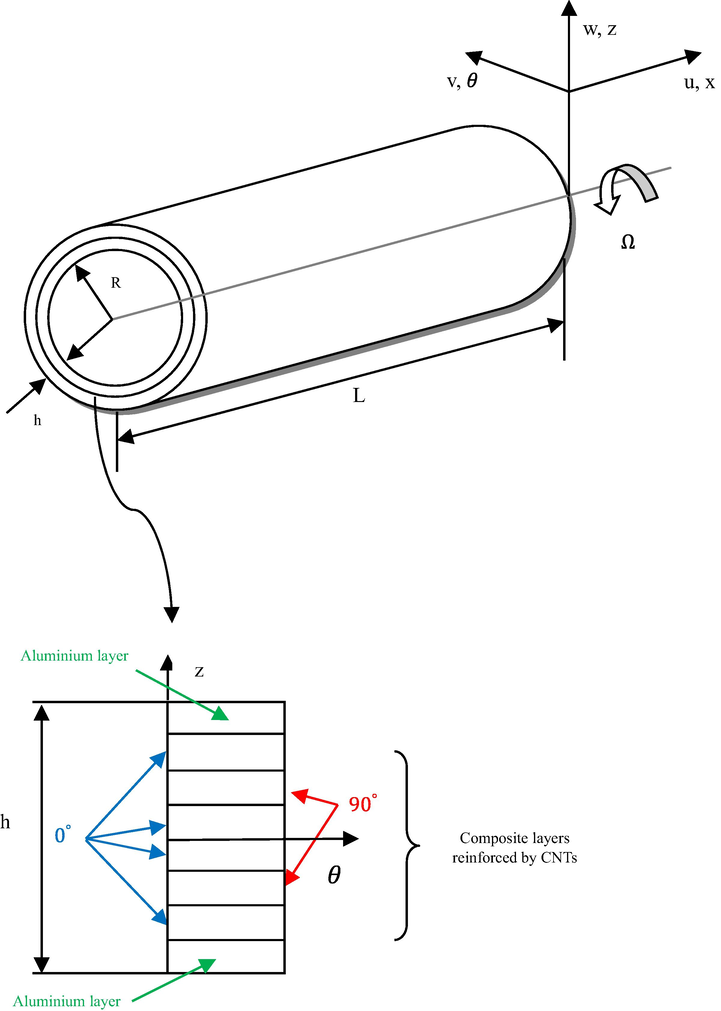
CNTFPMLs rotating circular cylindrical shell (Ghasemi and Mohandes, 2020).
Based on Love's first approximation theory, the equations of motion for this CNTFPMLs rotating circular cylindrical shell according to stress resultants
and
(Loy et al., 1997; Alimirzaei et al., 2019), which are defined using middle surface strains
,
and
, changes in the curvature of the middle surface
,
and
and extensional, coupling and bending stiffnesses
,
and
, are given as (Lam and Loy, 1995):
As mentioned, the stress resultants are including stiffnesses which can be illustrated as following for FML cylindrical shell reinforced by CNTs (Tsai et al., 2003):
where
and
represent the thickness and reduced stiffness of the metal section, respectively,
and
are the distances from the middle surface of the shell to the outer and inner surfaces of the
layer of composite section. Moreover,
shows the transformed reduced stiffness coefficients for the
layer of the composite segment which are given as (Yousefi et al., 2020; Al-Furjan et al., 2020b; Al-Furjan et al., 2020b):
In the above equations, , and are the longitudinal, transverse and shear moduli of the nanocomposite section. Moreover, effective Poisson’s ratios are defined as and . In this work, the composite section is reinforced by CNTs using the following method:
Firstly, the CNTs are added to the matrix and then the reinforced matrix is utilized to reinforce the fiber phase (Mohandes and Ghasemi, 2019). So, the elastic modulus and Poisson’s ratios of composite layers of this cylindrical shell can be predicted for two segments, namely, the fiber and matrix reinforced by CNTs, which can be written as (Ghasemi et al., 2019; Ghasemi and Mohandes, 2019, 2020):
3 Material properties of CNTRCs
3.1 Properties of the equivalent fiber
As illustrated in the previous section, the composite layers are consist of a fiber phase and a reinforced matrix. For the prediction of the mechanical characteristics of the matrix reinforced by CNTs, an equivalent long fiber which is a solid cylinder with a diameter of 2.374 nm (Shokrieh and Rafiee, 2010), depicted schematically in Fig. 2, is considered instead of a straight CNT embedded in a polymer matrix (Ghasemi et al., 2019).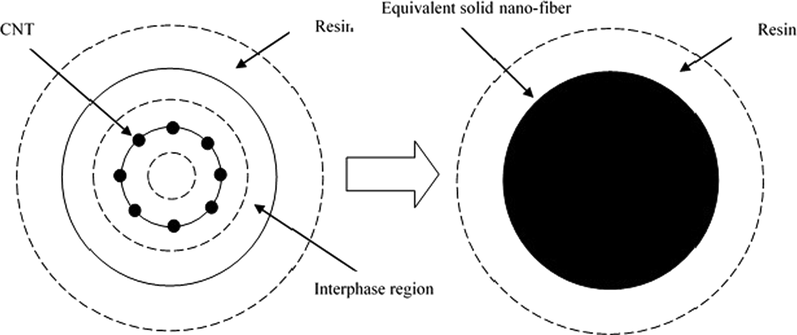
Conversion strategy. Reproduced from (Shokrieh and Rafiee, 2010) with permission from Elsevier.
The ROM is used inversely to obtain the elastic modulus, Poisson’s ratio and volume fraction of equivalent fiber (Shokrieh and Rafiee, 2010)
Mechanical properties
Equivalent fiber
Matrix phase
–
2.1
649.12
–
11.27
–
5.13
Poisson’s ratio
0.284
0.34
Density
1400
1150
3.2 The effect of CNTs agglomeration on material properties of composites
Since the CNTs have some properties such as low bending stiffness (i.e. small diameter and small elastic modulus in the radial direction), large aspect ratio (usually > 1000) and interfacial bonding parameters between CNTs and the polymeric surrounding matrix, they tend to bundle or cluster together (Ghasemi et al., 2019; Ghasemi and Mohandes, 2019, 2020; Shi et al., 2004). The influence of CNTs agglomeration on the elastic attributes of randomly oriented CNTRC has been investigated with a two-parameter micromechanics model developed in (Shi et al., 2004). As shown in Fig. 3, a certain number of CNTs is uniformly distributed (UD) throughout the matrix and the others appear in the cluster form due to which is created because of the different elatic attributes of the CNTs and the surrounding matrix (Ghasemi et al., 2019; Ghasemi and Mohandes, 2019, 2020).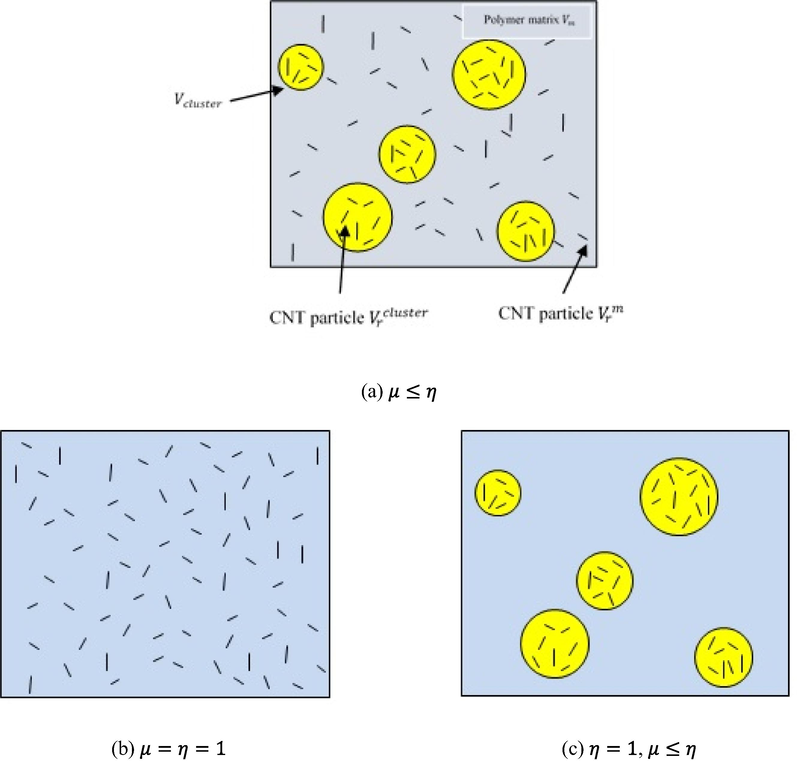
Shell element with a cluster model of CNT agglomeration. Reprinted from (Ghasemi et al., 2019) with permission from Elsevier.
The total volume of representative volume element (RVE), denoted by
, can be expressed as the following two parameters (Kamarian et al., 2013):
Eventually, the useful Young's modulus
and Poisson's ration
of the composite can be illustrated by the following equations (Tornabene et al., 2016)
In addition,
is the volume fraction of equivalent fiber in Eq. (10). For investigation of the influence of different CNTs distributions on the vibration of CG-CNTRC rotating cylindrical shell throughout its thickness direction, symmetric and asymmetric material profiles are considered as follows (Hedayati and Sobhani Aragh, 2012):
4 Analytical solution procedure
In this work, the analytical method is applied to solve the natural frequencies of simply supported agglomerated CNTFPMLs rotating cylindrical shells. The simply supported boundary conditions can be illustrated as:
The displacement fields in closed form to satisfy simply supported boundary conditions at
can be expressed as (Lam and Loy, 1994):
The determinant of coefficient matrix is set to zero for each value of and for a non-trivial solution of the equations of motion.
5 Numerical results and discussion
The outputs of agglomerated CNTFPMLs rotating cylindrical shell are presented for simply supported boundary conditions. The polymer matrix reinforced by agglomerated CNTs is utilized for reinforcing the fiber phase. To generate the CNTFPML cylindrical shells, the composites lay-ups are attached to thin metal layers. All the other properties and dimensions to investigate this agglomerated CNTFPMLs rotating cylindrical shell are illustrated as follows, unless otherwise noted:
Simply supported boundary condition, aluminum and carbon reinforced aluminum laminate (CARALL) reinforced by the agglomerated CNTs for the materials of metal and composite, the lay-up of the cylindrical shell is considered four-layered and cross-ply
. The thickness of metal is equal to the one layer of the composite reinforced by the CNTs, the distribution of the agglomerated CNTs is symmetric,
,
,
. Moreover, the considered material properties of the CNTFPML rotating circular cylindrical shell are shown in Table 2 (Ghasemi et al., 2019).
Material properties
CNT
Fiber
Matrix
Metal (Aluminum)
Carbon
Glass
6 Verification
For verification of the accuracy of the obtained results, the non-dimensional frequencies
of CARALL non-rotating cylindrical shell without any reinforcement (CNTs) for
are compared with the results presented by Mohandes et al. (Mohandes et al., 2018) for a simply supported boundary condition as summarized in Table 3. The excellent agreement of results confirms the feasibility and accuracy of the proposed method. Also, the non-dimensional frequencies of non-rotating cylindrical shell reinforced by CNTs with respect to agglomeration constant are compared to Ghasemi et al. (Ghasemi et al., 2019) with results shown in Fig. 4. The comparison indicates that the present results have excellent agreement with the other research.
n
1
2
3
4
5
present
0.1731
0.0645
0.0329
0.0260
0.0320
(Mohandes et al., 2018)
0.1731
0.0645
0.0329
0.0260
0.0320
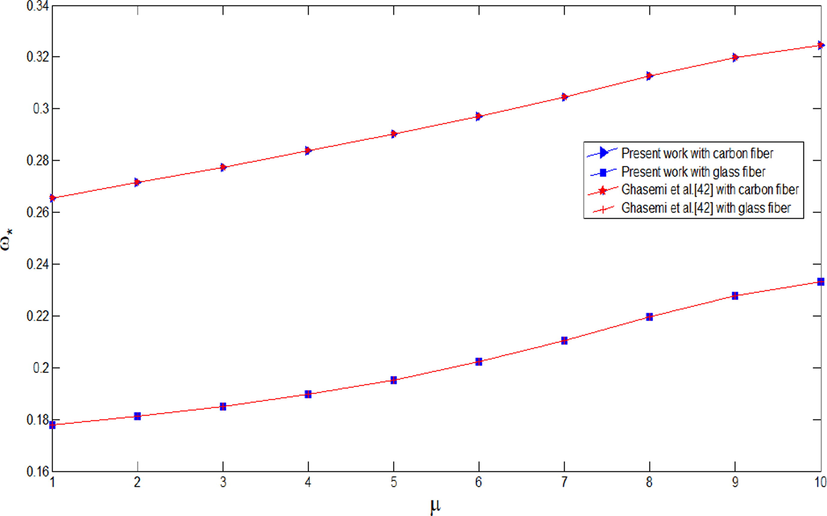
Comparison of the non-dimensional frequencies for a CNTFPMLs non-rotating cylindrical shell subjected to simply supported boundary condition.
7 Parametric investigations
Some investigations on the effect of agglomeration on the free vibration and critical speed of CNTFPMLs rotating circular cylindrical shell are illustrated in this study. Specifically, the following instances show the variation of natural frequency of agglomerated CNTFPMLs cylindrical shells with respect to different parameters such as agglomeration effects, volume fraction of metal, layups, distribution of CNTs, critical speed and rotational speed. The variations of non-dimensional frequencies of CNTFPMLs rotating cylindrical shells with respect to different rotational speed for parameters of
and
are considered.
shows from 0.1 to 0.5 the non-dimensional frequencies of non-rotating cylindrical shell increase (Fig. 5), while the opposite is the case as
grows (Fig. 6). Moreover, with raising rotational speeds, forward and backward frequencies of this cylindrical shell decreases and increases steadily for different parameters of agglomeration constants, respectively.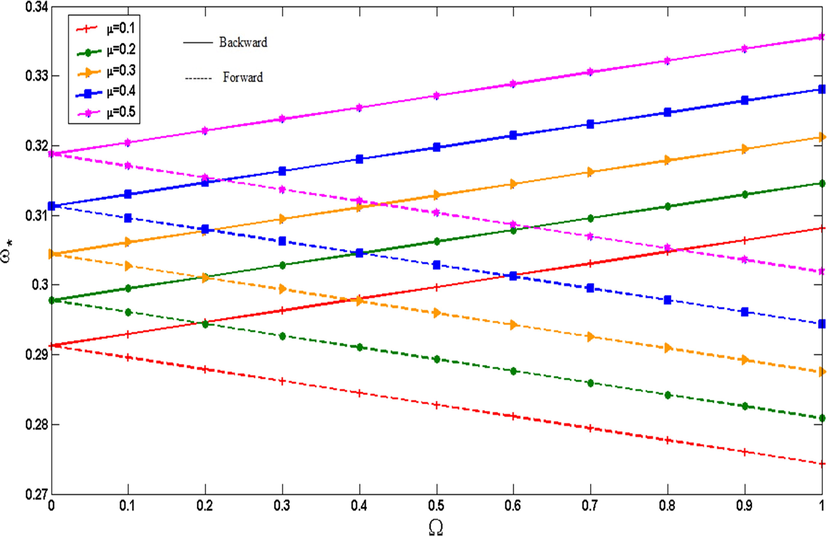
Non-dimensional frequencies of CNTFPML rotating cylindrical shell vs. rotational speed for different
.
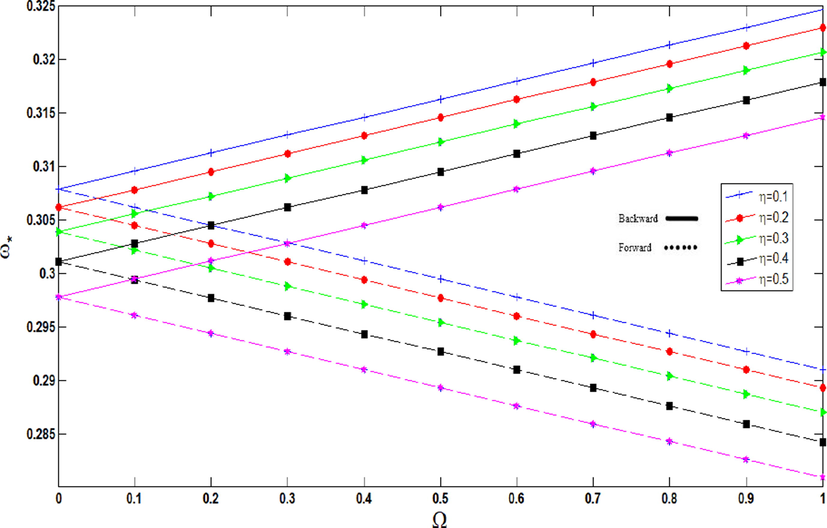
Non-dimensional frequencies of CNTFPML rotating cylindrical shell vs. rotational speed for different
.
The influence of volume fraction of metal on non-dimensional frequencies of agglomerated CNTFPMLs rotating cylindrical shell are indicated in Fig. 7 for different rotational speeds. As seen, enhancing volume fraction of metal, resulted in a reduction of the non-dimensional frequencies because by increasing the volume fraction of metal, the volume fraction of the composite section decreases and the elastic modulus of the whole structure is declined. So, as the elastic modulus of the structure drops, the non-dimensional frequencies of that structure decrease. As seen, by increasing the rotational speed, the frequencies of forward and backward wave modes decrease and increase before reaching the critical speed, respectively. As grown, the non-dimensional frequencies of the shell, critical speed of cylindrical shell is increased, cylindrical shell reaches the critical speed in the
and forward branch intersect the abscissa. At this point, the cylinder demonstrates unstable behavior with a fast increase in amplitude vibration. Also, beyond this point, the behavior of the cylindrical shell changes from forward mode to backward one and the frequencies increase. As the volume fraction of metal increases and with
or
, the direction of forward mode is changed before reaching the critical speed.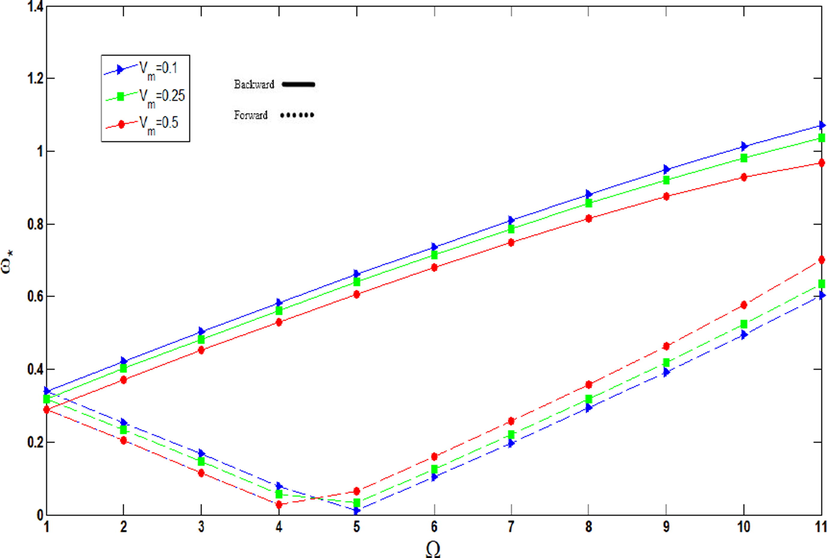
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs. rotational speed for different volume fraction of metal.
The influence of lay-ups of the composite section and fiber material attributes of agglomerated CNTFPML rotating cylindrical shell on the non-dimensional frequencies of the shell for different values of
are considered in Fig. 8. It should be noted that
equals 10 for the results presented in Fig. 8. As mentioned, the non-dimensional frequencies of agglomerated cylindrical shell made by CARALL are greater than GLARE since the elastic modulus of carbon fiber is much greater than that of glass. Further, the frequencies of unidirectional lay-up for the composite section are greater than cross-ply because of the stiffness. In addition, the difference between the frequencies of cross-ply and unidirectional for CARALL is greater than GLARE. Also, with a rise in the agglomeration constant, the non-dimensional frequencies of CNTFPML cylindrical shells comprised by both CARALL and GLARE for cross-ply and unidirectional lay-ups increase. This shows that the increase of the volume fraction of clusters with respect to the total volume of RVE causes the increase of frequencies since with increasing the volume fraction of clusters causes the amount of agglomeration to decrease and this leads to growth in frequencies.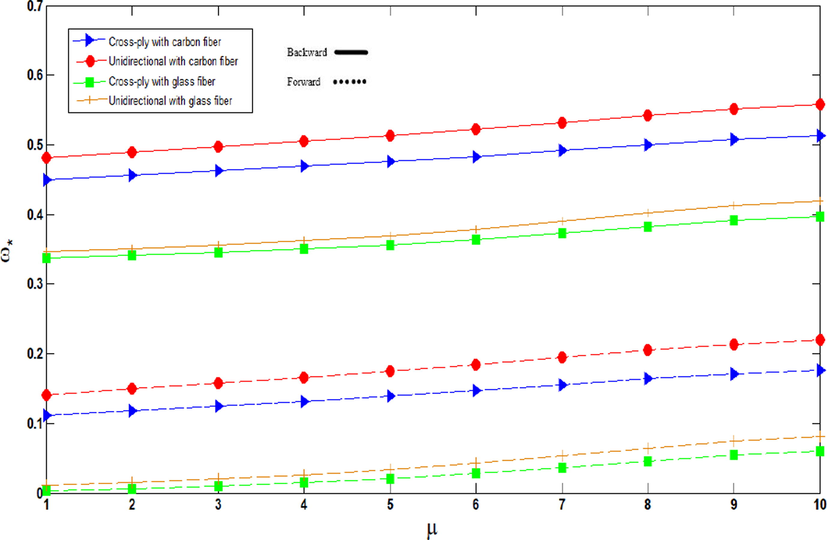
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs.
for different lay-ups and material properties of fiber,
.
The changes of non-dimensional frequencies with respect to different values of rotational speed for various ratios of thickness to radius are indicated in Fig. 9. As seen, by increasing the ratio of thickness to radius the non-dimensional frequencies are decrease while, as the non-dimensional frequencies of the shell, the critical speed of the cylindrical shell is increased, and forward branch direction changes sharply. Beyond this point, the behavior of the cylindrical shell changes from forward mode to backward one before reaching the critical speed and the frequencies increase.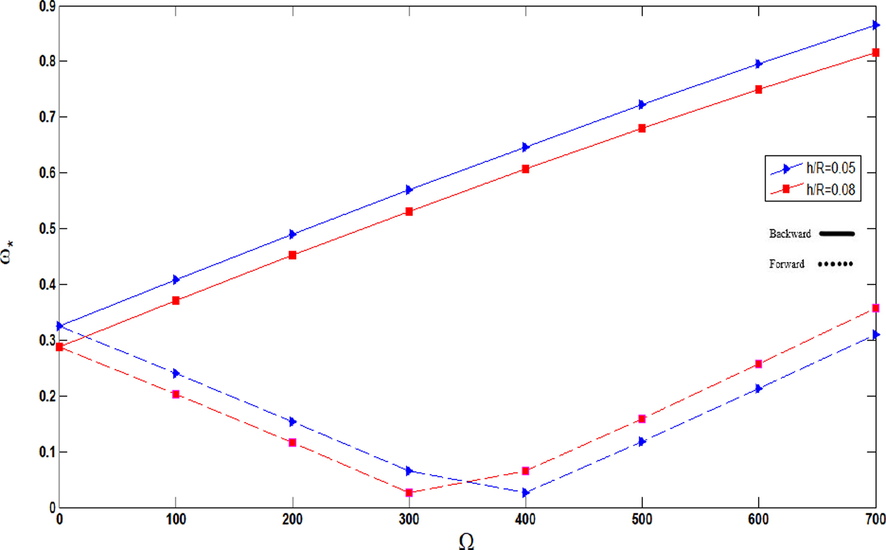
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs. rotational speed for different
.
Fig. 10 shows the influence of material attributes of fiber and distribution of CNTs on non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell for various rotational speeds. As predicted, when the non-dimensional frequencies of the shell grow, the critical speed of the cylindrical shell increases. As depicted in Fig. 10a and Fig. 10b, for
and
, which mean all CNTs dispersed in the matrix and concentrated into the cluster, the non-dimensional frequencies of the CARALL shell are more than GLARE. In addition, the frequencies of symmetric agglomerated CNTs are greater than for asymmetric. Also, the cylindrical shell with reach the critical speed for symmetric and asymmetric agglomerated CNTs with glass fiber (
and
, respectively, and forward branch intersect the abscissa, while the direction of forward mode is changed before reaching the critical speed for the other distributions and material properties of fiber. Fig. 10c indicates the non-dimensional frequencies of shell for
which shows a completely different trend in comparison with the others. It is demonstrated that the non-dimensional frequencies of none of the cylindrical shells reaches the critical speed and their forward directions are changed before reaching the critical speed.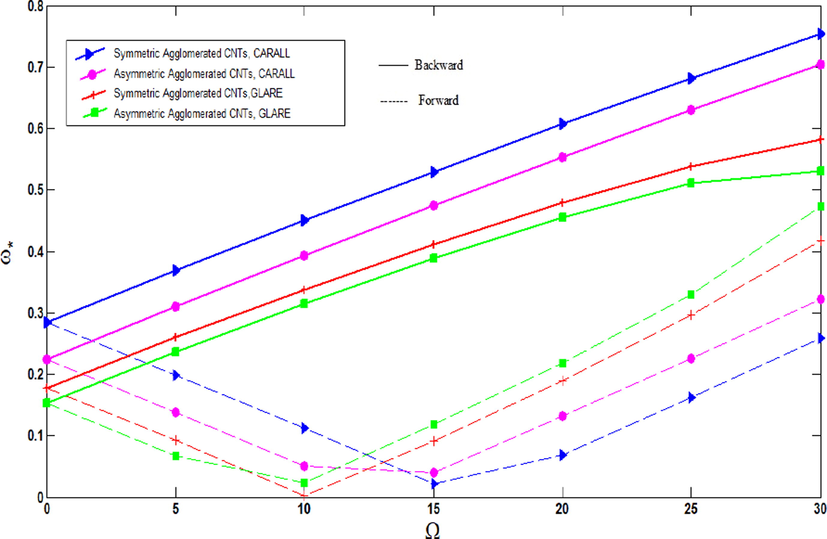
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs. rotational speed for
, different material properties and distributions of CNTs.
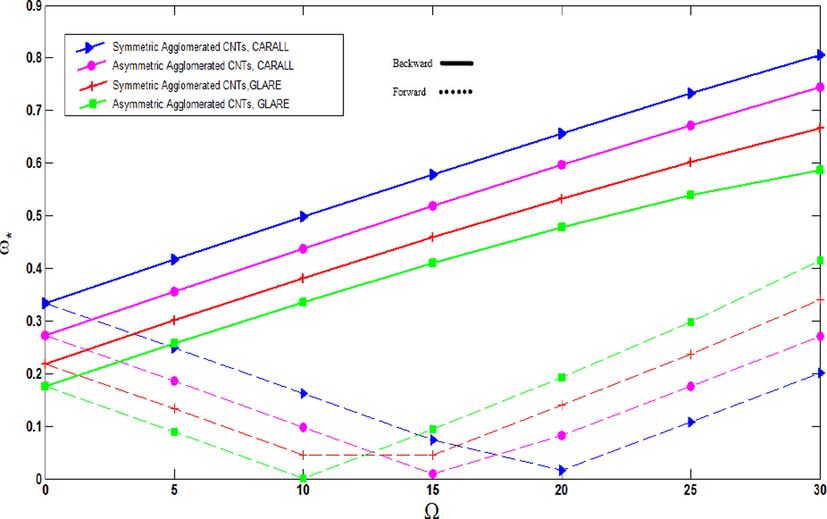
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs. rotational speed for
, different material properties and distributions of CNTs.
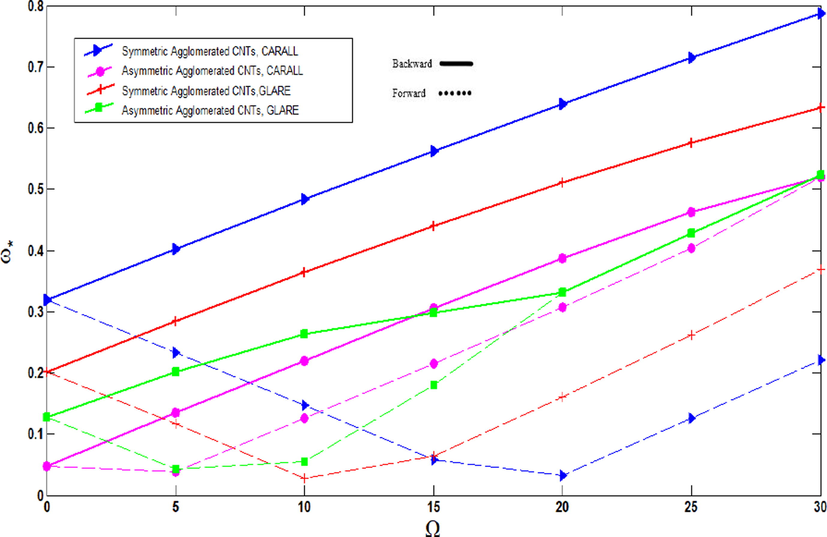
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs. rotational speed for
, different material properties and distributions of CNTs.
The impact of mass fraction of fiber on the non-dimensional frequencies of an agglomerated CNTFPML rotating cylindrical shell for different values of
is considered in Fig. 11. The figure illustrates that as the mass fraction of fiber increases, the non-dimensional frequencies of the shell grow for backward mode. Also, the frequencies of these cylindrical shells are compared between
and
in Fig. 11a and 11b. It is shown that when increasing the agglomeration constant, although the forward and backward modes drop in the rotating cylindrical shell with
, the forward and backward modes rise and fall in rotating cylindrical shell with
. As well as this, the difference between non-dimensional frequencies of the shells for different values of mass fraction of fiber decrease as the rotational speed increases.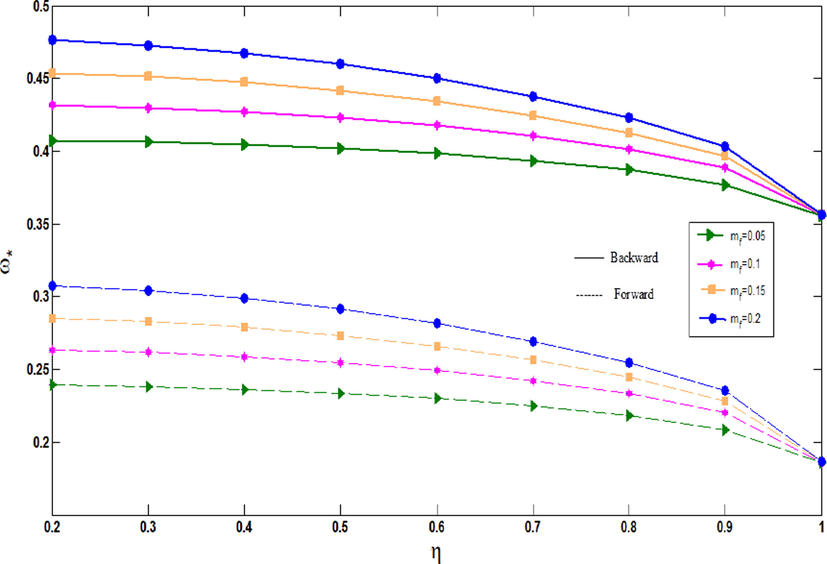
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs.
for Ω
and different mass fractions of fiber.
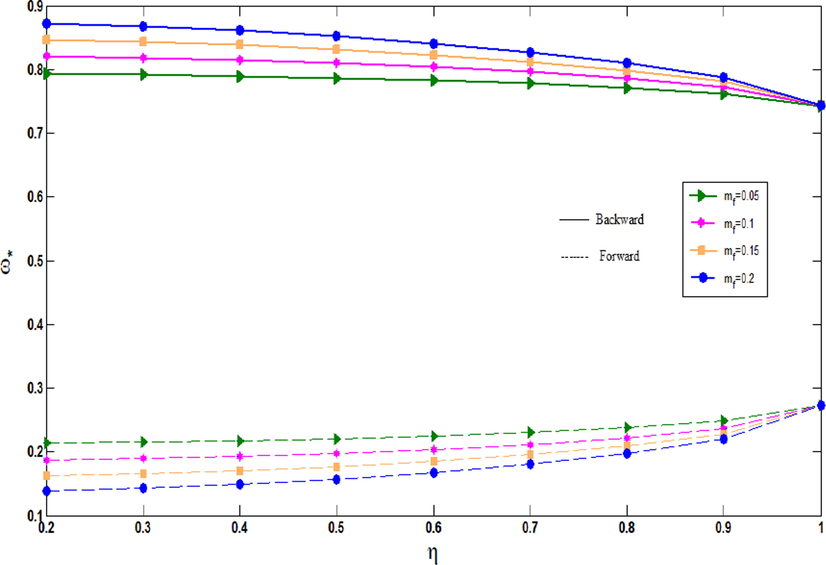
Non-dimensional frequencies of agglomerated CNTFPML rotating cylindrical shell vs.
for Ω
and different mass fractions of fiber.
8 Conclusion
In this research, critical speed and free vibration of agglomerated CNTFPMLs rotating cylindrical shells based on Love’s first approximation shell theory and subjected to simply supported boundary conditions have been studied. The elastic properties of CNTRCs cylindrical shell are determined using Eshelby-Mori-Tanaka, while assuming an equivalent fiber scheme. The CNTFPML cylindrical shell consists of four phases: fiber, CNTs, polymer matrix and metal. To obtain a CNTFPML cylindrical shell, in the first step the CNTs were added to the matrix to reinforce it. In a second step, the reinforced matrix was used to reinforce the fiber phase and, finally, the adhesive fiber prepreg has been combined with the thin metal layers. The influences of rotational speed, agglomeration constants, material properties of the fiber phase, lay-ups, volume fractions of metal and composite sections, mass fraction of CNTs, length to radius ratio on the free vibration of the CNTFPML cylindrical shell with respect to rotational speed were considered. The results represent:
-
Effect of agglomeration on vibration of the rotating cylindrical shell is remarkable. Non-dimensional frequencies of the CNTFPML rotating cylindrical shell grow for to , while these frequencies decline for to .
-
Non-dimensional frequencies of the agglomerated CNTFPML rotating cylindrical shell decrease as the volume fraction of metal increase since a growth in the volume of the metal creats a drop in the volume fraction of the composite leading to a reduction in the elastic modulus of the structure. Also, the cylindrical shell reaches the critical speed in the .
-
Lay-ups affect significantly the non-dimensional frequencies of the shell. Moreover, the frequencies of unidirectional lay-up for the composite section are greater than cross-ply due to the greater stiffness. Furthermore, when increasing the volume fraction of clusters with respect to the total volume of RVE, the frequencies of the CNTFPML rotating cylindrical shell grow because the agglomeration value declines.
-
As the non-dimensional frequencies increase, the critical speed of the cylindrical shell grows. Further, the non-dimensional frequencies of the CARALL shell are greater than GLARE for and , while this trend is completely different for . In addition, although the frequencies of symmetric agglomerated CNTs are greater than asymmetric for and , they show a completely different trend for .
-
As increases, although the forward and backward modes drop in the rotating cylindrical shell with , the forward and backward modes rise and fall in the rotating cylindrical shell with
Acknowledgments
The authors are thankful to the Russian Government and Institute of Engineering and Technology, Department of Hydraulics and Hydraulic and Pneumatic Systems, South Ural State University, Lenin prospect 76, Chelyabinsk, 454080, Russian Federation for their support to this work through Act 211 Government of the Russian Federation, contract No. 02. A03.21.0011.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Reference
- Chaotic simulation of the multi-phase reinforced thermo-elastic disk using GDQM. Eng. Comput. 2020
- [CrossRef] [Google Scholar]
- A computational framework for propagated waves in a sandwich doubly curved nanocomposite panel. Eng. Comput. 2020
- [CrossRef] [Google Scholar]
- Frequency simulation of viscoelastic multi-phase reinforced fully symmetric systems. Eng. Comput. 2020
- [CrossRef] [Google Scholar]
- On the vibrations of the imperfect sandwich higher-order disk with a lactic core using generalize differential quadrature method. Compos. Struct.. 2021;257:113150.
- [Google Scholar]
- Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM: MSGT electro-magneto-elastic bending, buckling and vibration solutions. Struct. Eng. Mech.. 2019;71:485-502.
- [Google Scholar]
- The effects of agglomerated CNTs as reinforcement on the size-dependent vibration of embedded curved microbeams based on modified couple stress theory. Mech. Adv. Mater. Struct.. 2018;25:995-1008.
- [Google Scholar]
- Vibrational analysis of functionally graded carbon nanotube-reinforced composite spherical shells resting on elastic foundation using the variational differential quadrature method. Eur. J. Mech.-A/Solids. 2016;60:166-182.
- [Google Scholar]
- Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Compos. B Eng.. 2016;95:196-208.
- [Google Scholar]
- Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol.. 2018;81:108-117.
- [Google Scholar]
- Porosity-dependent vibration analysis of FG microplates embedded by polymeric nanocomposite patches considering hygrothermal effect via an innovative plate theory. Eng. Comput. 2021
- [CrossRef] [Google Scholar]
- Fiber metal laminates: an advanced material for future aircraft. J. Mater. Process. Technol.. 1997;63:384-394.
- [Google Scholar]
- Deflections, stresses and free vibration studies of FG-CNT reinforced sandwich plates resting on Pasternak elastic foundation. Comput. Concr.. 2020;26:213-226.
- [Google Scholar]
- Stability and dynamic analyses of SW-CNT reinforced concrete beam resting on elastic-foundation. Comput. Concr.. 2020;25:485-495.
- [Google Scholar]
- Buckling and dynamic behavior of the simply supported CNT-RC beams using an integral-first shear deformation theory. Comput. Concr.. 2020;25:155-166.
- [Google Scholar]
- Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Compos. B Eng.. 2017;111:45-49.
- [Google Scholar]
- Buckling and free vibrations of CNT-reinforced cross-ply laminated composite plates. Mech. Based Des. Struct. Mach. 2020
- [CrossRef] [Google Scholar]
- Free vibration analysis of rotating stiffened composite cylindrical shells by using the layer wise-differential quadrature (LW-DQ) method. Mech. Compos. Mater.. 2014;50:21-38.
- [Google Scholar]
- Free vibration analysis of arbitrarily shaped functionally graded carbon nanotube-reinforced plates. Compos. B Eng.. 2017;115:384-408.
- [Google Scholar]
- Analysis of nonlinear dynamic response for delaminated fiber–metal laminated beam under unsteady temperature field. J. Sound Vib.. 2014;333:5803-5816.
- [Google Scholar]
- Nonlinear dynamic responses of viscoelastic fiber–metallaminated beams under the thermal shock. J. Eng. Math.. 2016;98:113-128.
- [Google Scholar]
- Free vibration analysis of micro and nano fiber metal laminates circular cylindrical shells based on modified couple stress theory. Mech. Adv. Mater. Struct.. 2020;27:43-54.
- [Google Scholar]
- Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos. B Eng.. 2019;167:700-716.
- [Google Scholar]
- Free vibration analysis of rotating fiber–metal laminate circular cylindrical shells. J. Sandwich Struct. Mater.. 2019;21:1009-1031.
- [Google Scholar]
- Influence of graded agglomerated CNTs on vibration of CNT-reinforced annular sectorial plates resting on Pasternak foundation. Appl. Math. Comput.. 2012;218(17):8715-8735.
- [Google Scholar]
- On the mechanics of nanocomposites reinforced by wavy/defected/aggregated nanotubes. Steel Compos. Struct.. 2021;38:533-545.
- [Google Scholar]
- A self-consistent mechanics of composite materials. J. Mech. Phys. Solids. 1965;13:213-222.
- [Google Scholar]
- Eshelby-Mori-Tanaka approach for vibrational behavior of functionally graded carbon nanotube-reinforced plate resting on elastic foundation. J. Mech. Sci. Technol.. 2013;27(11):3395-3401.
- [Google Scholar]
- Vibrational behavior of non-uniform piezoelectric sandwich beams made of CNT-reinforced polymer nanocomposite by considering the agglomeration effect of CNTs. Polym. Compos.. 2017;38:E553-E562.
- [Google Scholar]
- Vibration behaviors of two-directional carbon nanotube reinforced functionally graded composite plates. Compos. Struct.. 2021;262:113639
- [Google Scholar]
- Agglomeration effects on the dynamic buckling of viscoelastic microplates reinforced with SWCNTs using Bolotin method. Nonlinear Dyn.. 2017;90:479-492.
- [Google Scholar]
- On vibrations of thin rotating laminated composite cylindrical shells. Compos. Eng.. 1994;4:1153-1167.
- [Google Scholar]
- Effects of boundary conditions on frequencies of a multilayered cylindrical shell. J. Sound Vib.. 1995;188(3):363-384.
- [Google Scholar]
- Nonlinear vibrations of rotating thin circular cylindrical shell. Nonlinear Dyn.. 2012;67:1467-1479.
- [Google Scholar]
- Analysis of cylindrical shells using generalized differential quadrature. Shock Vib.. 1997;4(3):193-198.
- [Google Scholar]
- Differential cubature method for vibration analysis of embedded FG-CNT-reinforced piezoelectric cylindrical shells subjected to uniform and non-uniform temperature distributions. Steel Compos. Struct.. 2016;22:889-913.
- [Google Scholar]
- Nonlinear vibration of functionally graded magneto-electro-elastic higher order plates reinforced by CNTs using FEM. Eng. Comput. 2020
- [CrossRef] [Google Scholar]
- Size dependent effect on the buckling and vibration analysis of double-bonded nanocomposite piezoelectric plate reinforced by boron nitride nanotube based on modified couple stress theory. J. Vib. Control. 2016;22(7):1790-1807.
- [Google Scholar]
- Bending, buckling and vibration analyses of MSGT microcomposite circular-annular sandwich plate under hydro-thermo-magneto-mechanical loadings using DQM. Int. J. Smart Nano Mater.. 2018;9:233-260.
- [Google Scholar]
- Development of beam modal function for free vibration analysis of FML circular cylindrical shells. J. Vib. Control. 2018;24(14):3026-3035.
- [Google Scholar]
- A new approach to reinforce the fiber of nanocomposite reinforced by CNTs to analyze free vibration of hybrid laminated cylindrical shell using beam modal function method. Eur. J. Mech. A. Solids. 2019;73:224-234.
- [Google Scholar]
- Mechanical properties of multi-walled carbon nanotube/epoxy composites. Mater. Des.. 2010;31(9):4202-4208.
- [Google Scholar]
- Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci.. 2017;130:383-398.
- [Google Scholar]
- Free vibration analysis of fiber metal laminate annular plate by state-space based differential quadrature method. Adv. Mater. Sci. Eng.. 2014;2014:1-11.
- [Google Scholar]
- Fabrication and characterization of carbon nanotube/poly (vinyl alcohol) composites. Adv. Mater.. 1999;11:937-941.
- [Google Scholar]
- The effect of nanotube waviness and agglomeration on the elastic property of carbon nanotube-reinforced composites. J. Eng. Mater. Technol.. 2004;126:250-257.
- [Google Scholar]
- Prediction of mechanical properties of an embedded carbon nanotube in polymer matrix based on developing an equivalent long fiber. Mech. Res. Commun.. 2010;37(2):235-240.
- [Google Scholar]
- A closed form solution for linear and nonlinear free vibrations of composite and fiber metal laminated rectangular plates. Compos. Struct.. 2010;92:2663-2675.
- [Google Scholar]
- On bending, buckling and vibration responses of functionally graded carbon nanotube-reinforced composite beams. Steel Compos. Struct.. 2015;19:1259-1277.
- [Google Scholar]
- Vibration and damping analysis of functionally graded carbon nanotubes reinforced hybrid composite shell structures. J. Vib. Control. 2017;23:1711-1738.
- [Google Scholar]
- Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. B Eng.. 2016;89:187-218.
- [Google Scholar]
- Composite Materials, Design and Applications. Boca Raton: CRC Press; 2003.
- Vigolo, B., Penicaud, A.P., Couloun, C., Sauder, S., Pailler, R., Journet, C., Bernier, P., Poulin, P., 2000. Macroscopic fibers and ribbons of oriented carbon nanotubes, 290, 1331–1334.
- Agglomeration effects on free vibration characteristics of three-phase CNT/polymer/fiber laminated truncated conical shells. Thin-Walled Struct.. 2020;157:107077
- [Google Scholar]
- Effect of nonlinear FG-CNT distribution on mechanical properties of functionally graded nano-composite beam. Struct. Eng. Mech.. 2021;78:117-124.
- [Google Scholar]
- A new analytical solution of vibration response of orthotropic composite plates with two adjacent edges rotationally-restrained and the others free. Compos. Struct. 2021
- [CrossRef] [Google Scholar]







