Translate this page into:
Double-proton transfer triggering mechanism of nitromethane caused by intermolecular hydrogen bonding at low temperature
⁎Corresponding authors. pengyajing@126.com (Yajing Peng), yqyang@hit.edu.cn (Yanqiang Yang)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The initial triggering mechanism of nitromethane is investigated by first-principles molecular dynamics simulations and temperature-dependent Raman spectroscopy experiment. The Raman spectra at different temperature are obtained by Car-Parrinello molecular dynamics simulation to explore the activated vibration modes caused by low-temperature heat. The temperature-dependent Raman spectra experiment is constructed to compare with the theoretical data. Each possible initial reaction path caused by the activated vibration mode is analyzed to reveal the triggering mechanism of the initial chemical bond breaking for nitromethane. The results show that the intermolecular double-proton transfer is the first reaction step which is triggered by the intermolecular hydrogen bond reinforced with the active C–H stretching vibration (near 3000 cm−1), which is not reported before. The scanning energy barrier related to the increase of C–H bond lengths is about 60 kcal/mol, which is consistent with the calculated activation barrier (59.8 kcal/mol) of intermolecular proton transfer reaction. This proves the reliability of our conclusions. The results provide a new interpretation for the long-debated initial decomposition mechanism of nitromethane.
Keywords
Energetic materials
Raman spectra
Active vibration modes
Initial triggering mechanism
1 Introduction
Energetic materials (EMs) in weapons come out of slow chemical reactions at relatively low temperature such as storage/transit conditions (Liu et al., 2015; Liu et al., 2012). The heat released by the exothermic slow reaction will gather to cause the initiation to detonation of energetic materials. Therefore, understanding of the initial thermal trigger mechanism is crucial in safety for energetic materials to avoid accidents (Peng et al., 2018a;Wu et al., 2015). Nitromethane (NM), as a typical EMs, is currently extensively applied in many energetic formulations and has already been employed as a prototype for studying Ems (Lu et al., 2019; Zhong et al., 2017). To date, the initial decomposition step of nitromethane has been debated. At first, it was indicated that the C-N bond of gas-phase nitromethane had the lowest dissociation energy (Chen et al., 1999), so the rupture of the C-N bond is speculated to be the initial decomposition step of nitromethane. However, the initial decomposition step of heat- or pressure-induced condensed nitromethane has been shown experimentally and theoretically to involve not only a single molecule but also two molecules (Zhao & Truhlar, 2008; Ouillon et al., 2008; Siavosh-Haghighi et al.,2010a; Siavosh-Haghighi et al., 2010b). Citroni et al. (Citroni et al., 2010) investigated the decomposition mechanism of condensed nitromethane under static pressure (around 30 GPa) and showed that the first step of the decomposition reaction is the intermolecular proton transfer, forming CH2NO2– and CH3NOOH+ ions. Ye et al (Ye et al., 2019) showed that the first step of the high-temperature thermal decomposition for solid-phase nitromethane is the intramolecular proton transfer followed by C-N bond breakage by Car-Parrinello molecular dynamics simulations. However, Han et al. (Han et al., 2011) showed the intermolecular proton transfer is the initial thermal decomposition step of nitromethane at high temperatures (3000 K) by using the reaction force field (ReaxFF) molecular dynamics method. Xu et al. (Xu et al., 2014) showed that the first step of initial decomposition of nitromethane is the intramolecular proton transfer, not the C-N bond crack under gradual heating (2200–4000 K) by using the Car-Parrinello molecular dynamics method. This indicates that the initial decomposition mechanism of nitromethane is related to the external energy loading condition. Importantly, the triggering mechanism of the initial reaction has not been investigated. For storage/transit environments, the temperature is usually relatively low (below 1000 K). Therefore, clarifying the initial thermal trigger mechanism at low temperature is significant for the storage, usage, and further development of energetic materials. This might artificially impede deflagration or detonation by regulating the trigger mechanism. So it is necessary to explore the triggering path from the external heat injection to the initial fracture of the chemical bonds.
Thermally triggered chemical reactions are greatly related to the vibrational properties of molecules. The vibrational motions of a molecule in its equilibrium or during a chemical reaction provide a wealth of information about its structure, stability, and reactivity.(Kühne et al., 2020) This information can be unraveled by utilizing vibrational spectroscopy. In this paper, the dynamic behavior of intramolecular and intermolecular hydrogen bonds of nitromethane are examined under low-temperature heat loading using the radial distribution functions (RDFs). The active vibration modes are obtained by Car–Parrinello molecular dynamics (CPMD) calculations combined with the temperature-dependent Raman spectroscopy experiment. The initial decomposition steps and its triggering mechanism are predicted in view of vibration excitation by DFT calculations. The intermolecular double-proton transfer are determined to be the first reaction step and the triggering mechanism is attributed to the enhancement of intermolecular hydrogen bonding caused by C–H stretching vibration.
2 Material and methods
The nitromethane was commercially available. The excitation laser used in the experiment comes from MSL-FN-532 (Changchun New Industrial Optoelectronic Technology Co., Ltd., China). The Raman emission is collected and collimated at 180° back scattering geometry and then passed through a notch filter (NF01-532U-25, Semrock, NY). The spectrometer (500 IS/SM, Bruker Optics, DE) covers the entire spectrum of the Raman emission. The temperature controller within 2 ℃ is used by Linkam THMS600. The experimental temperature is ranged from 20 to 140 ℃, and each temperature change was controlled within 2℃.
At ambient conditions, NM is liquid with the density of 1.137 g/cm3 (Qin et al., 2020; Liu et al., 2018). For comparing the intra- and intermolecular hydrogen bond dynamic behaviors, the bimolecular system is simulated in a cubic box with an edge length of 4.5 Å (see Fig. 1) using the CPMD code (Hutter et al., 1995–1999). The simultaneous motion of electrons and nuclei is described using the Car–Parrinello equations. All degrees of freedom are taken into account (Damianos & Frank, 2010). The density functional theory in the Kohn–Sham formulation (Hohenberg & Kohn, 1964, Son et al., 2019) was used within the local spin-density (LSD) approximation (spin-unrestricted calculations). A plane wave basis set is used with an energy cutoff of 50 Rydberg to describe the valence electrons. The valence electrons were treated explicitly with the valence-core interactions described by the non-local norm-conserving pseudopotentials (Brańka, 2000). The time step of the simulations is 5a.u. (0.121 fs). After equilibration, the system was quickly heated to the desired temperatures in the range from 300 to 640 K and the simulations were continued at these temperatures for 12 ps (100000 simulation steps). The Nose-Hoover thermostats was employed for ions and electrons to control the temperature in the NVT ensemble (Nose, 1990; Bučko, 2011). The fictitious electrons mass is chosen to be 400 a.u.. The Raman spectrum was calculated using CP2K software package based on the molecular dynamics results (Kühne et al., 2020; Pylaeva et al., 2017). In addition, static calculations were performed with the functional B3LYP (Becke, 1993) using the 6–311++G(d,p) basis set as implemented in the Gaussian 09 program package (Frisch et al.,2009). The trajectory post-processing and the investigation of structural properties have been carried out with the TRAVIS package (Brehm & Kirchner, 2011).
Bimolecular simulation boxes after pre-equilibration via molecular dynamic calculations.
3 Results and discussion
3.1 Low-temperature dynamic properties of hydrogen bonding
To analyze the relaxation dynamic behavior of the intra- and intermolecular hydrogen bonds at low temperature, the radial distribution functions(RDFs) g(r), which is a measure of the probability that an atom will be located at a distance from another atom (Fan et al., 2021), for the intra- and intermolecular O–H separations (as shown in Fig. 2) are calculated at different temperatures using the TRAVIS program based on the CPMD trajectories. Fig. 3(a) shows the intramolecular H1-O1 RDF plot. It can be seen that the H1-O1 RDF peak is mainly distributed at near 2.4 Å at all temperature. The peak height is reduced and the peak position is shift toward a lager distance as the temperature increases, suggesting a weakening of the H1-O1 interaction. Fig. 3(b) shows the RDF peak of intramolecular H1-O2 distance is mainly distributed at near 3.2 Å. As the temperature increases, the peak height is smaller but still the most dominant. Therefore, the H1-O1 peak most likely arises from intramolecular hydrogen bonds, while the H1-O2 peak is probably non-hydrogen bonded interactions because hydrogen bonds usually form in a range lower than 3 Å (Fan et al., 2021; Perkins et al., 2014).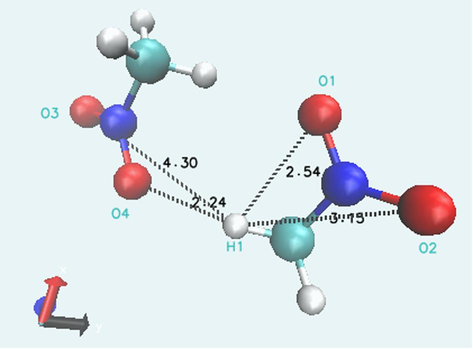
The relaxed bimolecular configurations.
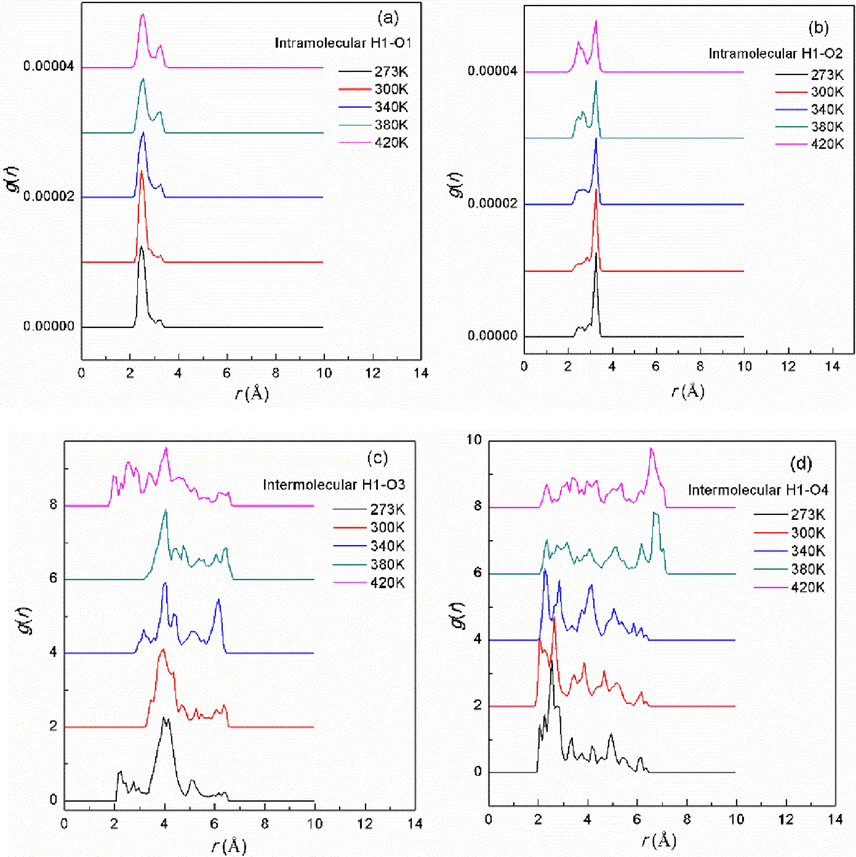
Radial distribution functions of the intramolecular H1-O1(a) and H1-O2 (b) and the intermolecular H1-O3(c) and H1-O4(d) distances for the bimolecular nitromethane system at different temperatures.
Fig. 3(c) shows the RDF peak of intermolecular H1-O3 is mainly located at near 4.1 Å at all temperature. The RDF peaks at distances close to 6 Å are usually attributed to the dispersion of van der Waals forces, which are instantaneous dipole forces between molecules, rather than hydrogen bonding. (Buckingham et al., 1988; Tsuji & Yoshizawa, 2021). The Fig. 3(d) shows the RDF peak position of the intermolecular H1-O4 distance is decreased from about 2.5 Å to 2.1 Å with the increase of temperature, indicating that the distance of H1-O4 becomes small and has a bonding possibility, which is expected to trigger easily the intermolecular proton transfer reactions of nitromethane.
3.2 Active vibration modes
Chemical reactions usually start with a vibrational motion that is forced to adopt larger and larger vibrational amplitudes due to bond loosening or cleavage (Cremer & Kraka, 2010), which is the initial decomposition caused by a specific vibration (Yu et al., 1995). Raman spectroscopy is suited for studying the evolution of the bond character in molecules under thermal loading, which allows an easy interpretation and highly sensitive structural identification of trace amounts of chemicals based on their unique vibrational characteristics (fingerprints) (Rostron et al., 2016; Peng et al., 2021; Zhou et al., 2017).
The Raman spectra of the bimolecular nitromethane calculated using CPMD method at different temperature are shown in Fig. 4. The spectrum at room temperature is compared with that calculated using quantum chemistry method in Gaussian software package in Figure S1 in the Supporting Information. It can be seen that the main peaks are basically consistent except for the difference of several peak sites.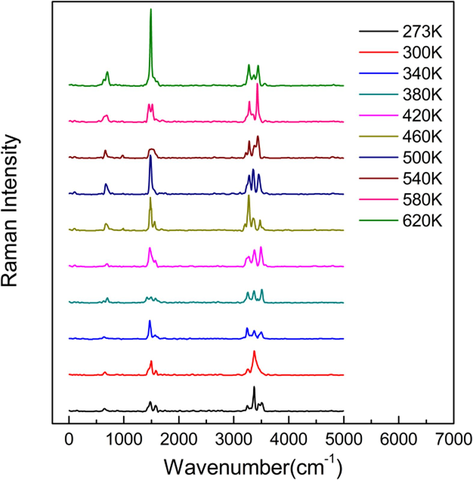
The Raman spectra of nitromethane at different temperature obtained by CPMD method (The curves are shifted upward for clarity).
The (anti-)Stokes intensity of Raman spectra is proportional to the number of phonons (Hayes & Loudon, 1978; Peng et al., 2018a), which is utilized to reflect the energies of different vibrational modes. Without loss of generality, the proportion of the (anti-)Stokes intensity over all modes is chosen to describe the energy proportion of the modes for simplification, which is expressed as
The spectral intensity proportion variations versus temperature for different vibration modes are shown in Fig. 5(a). In order to demonstrate the validity of the calculations, anti-Stokes Raman spectroscopy experiments are performed at low temperature of 273–420 K in the 400–1500 cm−1 wavenumber range. The experimental Raman spectroscopy is shown in Figure S2 and the corresponding variation of Raman intensity proportions versus temperature is shown in Fig. 5(b). The comparison of the theoretical and experimental data are shown in Fig. 6 for the same vibration mode. Usually, the theoretically calculated wavenumber corresponds to the experimentally measured wavenumber by multiplying a factor of 0.9–1 (Merrick et al., 2007)). As can be seen, the CPMD calculations agree well with the experimental results, indicating the rationality of CPMD calculations.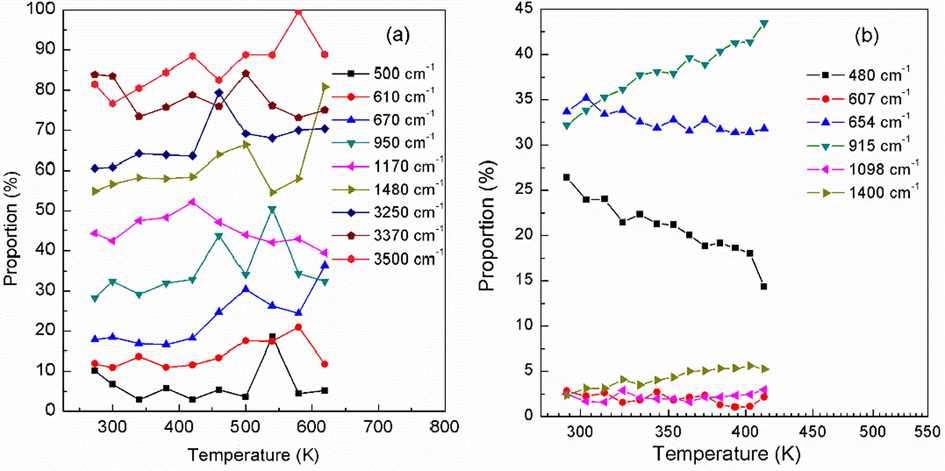
The calculated (a) (the curves are shifted upward for clarity) and experimental (b) Raman intensity proportions versus temperature for different vibration modes.
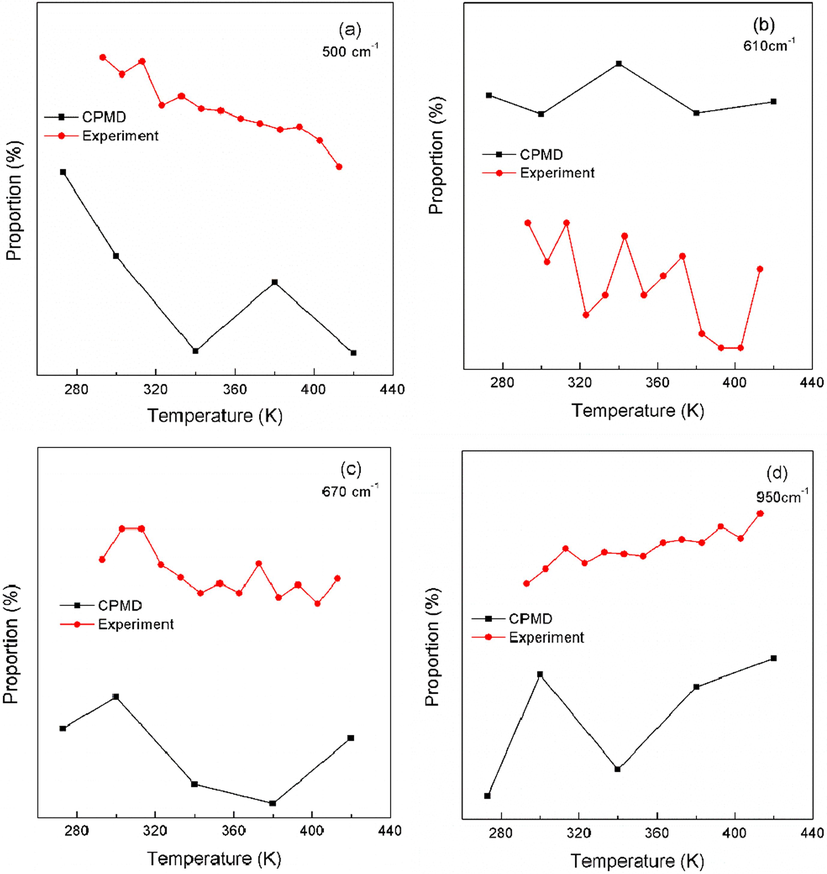
Comparison of experimental and theoretical variation of Raman intensity proportion with temperature for different vibration modes.
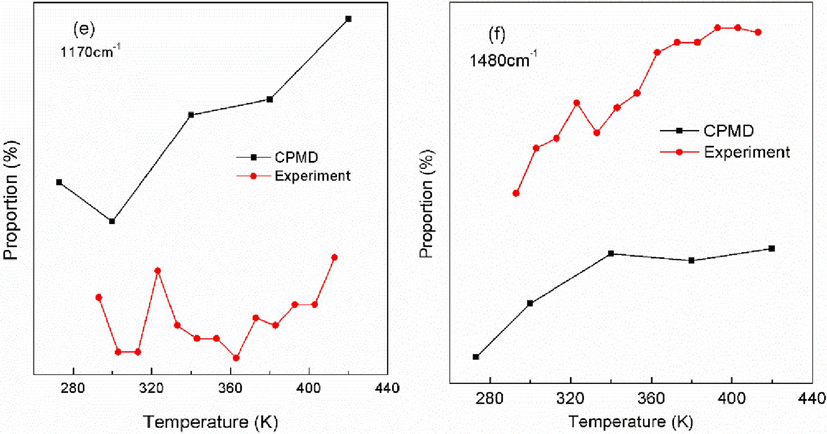
Comparison of experimental and theoretical variation of Raman intensity proportion with temperature for different vibration modes.
Fig. 7 shows the activated vibration modes whose vibration strength increases with increasing temperature. It can be noted that there are five active vibration modes, which are located at 670, 950, 1480, 3250 and 3500 cm−1, respectively. Their vibration characteristics are shown in Fig. 8(a) and are assigned in Table 1 based on our DFT calculation and previous literatures (Ouillon et al., 2008; Peng et al., 2018b), which are the wagging vibration of nitro group (670 cm−1), stretching vibration of C-N bond (950 cm−1), asymmetric deformation (shearing and bending)of C–H bond (1480 cm−1), C–H bond symmetric stretching vibration (3250 cm−1), and C–H bond asymmetric stretching vibration (3500 cm−1), respectively. Their energies are enhanced fastest with rising temperature, and as a result, they are active and have large vibrational amplitudes (Brock & Dunitz, 1982), which would probably trigger the initial chemical reaction due to vibrational excitation (Kim et al., 2002).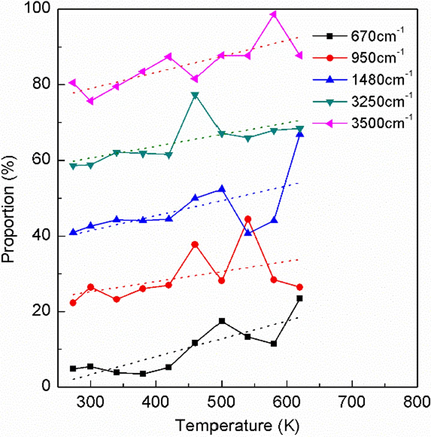
The active vibration modes whose Raman intensity proportion increases with temperature rising.
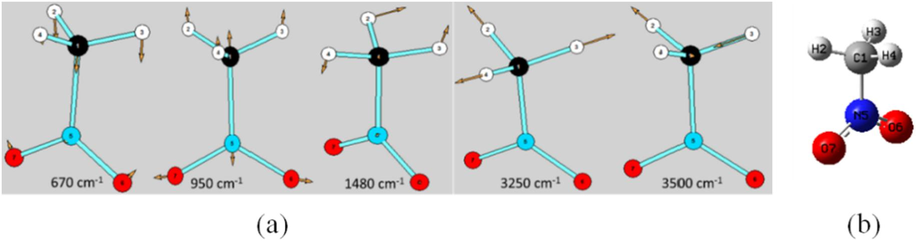
Vibrational schematic diagram of the five active vibration modes (a) and the optimized single nitromethane configuration (b).
Feature peak position(cm−1)
Corresponding vibration conditions
670
wagging vibration of nitro group
950
stretching vibration of C-N bond
1480
asymmetric deformation (shearing and bending)of C–H bond
3250
symmetric stretching vibration C–H bond
3500
asymmetric stretching vibration of C–H bond
3.3 Vibrational triggering path of initial reaction
The changes in bond length or bond angle induced by the five active vibration modes are indicated in Fig. 8(a), which should be analyzed to clear the triggering path leading to the initial reaction. The relaxed scan is performed for each change in bond length or bond angle based on the optimized nitromethane configuration (Fig. 8(b)) to explore the triggering channel of initial chemical bond breakage.
3.3.1 Effect of 670 cm−1 mode vibration
The vibration mode located at 670 cm−1 is mainly assigned to the wagging vibration of nitro group, which leads to a reduction of C-N bond length, an increase of O-N-O angle and a decrease of C-N-O angle. The decrease of C-N-O angle is scanned to explore the potentially triggering path of initial chemical reaction. The scanned result is shown in Fig. 9(a), together with the corresponding evolution of molecular configurations. As can be seen, a reduction of the C-N-O angle might cause a rearrangement reaction, forming the C-O = N from C-N = O, whose barrier height is about 67.9 kcal/mol. The remaining two motions are also examined simultaneously. The scanned results are shown in Fig. 9(b). It can be seen that the increase of O-N-O angle and the decrease of C-N bond do not cause a chemical reaction.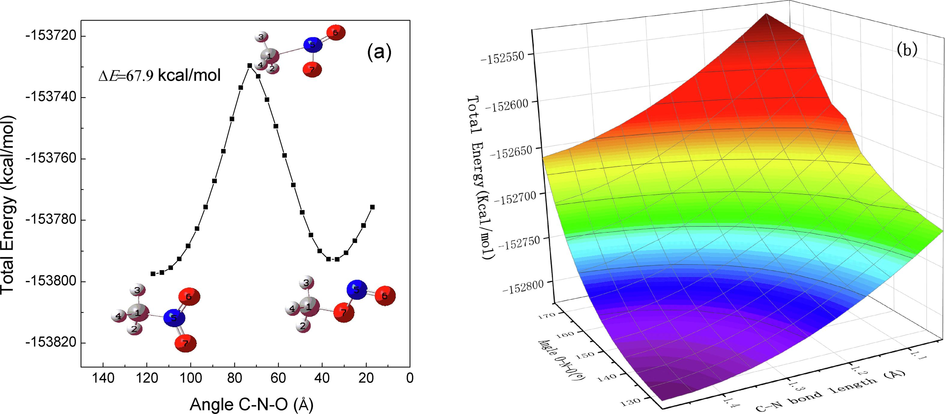
A relaxed scan optimizat1ion algorithm plot is presented along the decrease of one C-N-O angle (a) and the reduce of the C-N bond together with the increase of the O-N-O angle (b).
3.3.2 Effect of 950 cm−1 mode vibration
The C-N stretching vibration located at 950 cm−1 leads to an increase of the C-N bond length. The potential energy scans related to the increase of C-N bond is shown in Fig. 10 and the corresponding structural changes are also given here. It can be seen that no other chemical reactions will occur unless the cleavage of C-N bond with the increase of C-N bond. The dissociation energy of the C-N bond is about 72 kcal/mol (Blanksby & Ellison, 2003).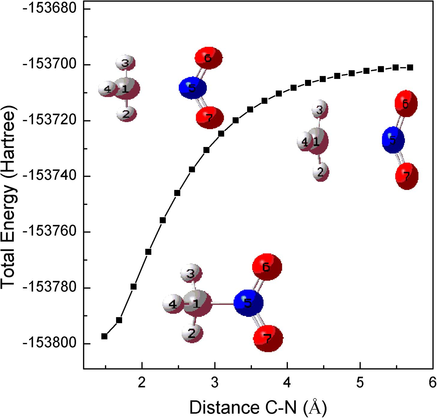
The relaxed scan optimization algorithm plots are presented for the increase of C − N bond length.
3.3.3 Effect of 1480 cm−1 mode vibration
The C–H asymmetric deformation mode located at 1480 cm−1 includes mainly the shearing and bending vibration of C–H bond, which leads a decrease (or increase) of H-C–H angle and a decrease of H-C-N angle accompanying an increase of C-N bond. The potential energy scan plots obtained by reducing H-C-N angle is shown in Fig. 11(a). As can be seen that the decrease of H-C-N angle might cause the intramolecular proton transfer. But it is difficult to happen because of a high energy barrier of about 116 kcal/mol. The C-N bond growth and H-C-N angle reduction are scanned simultaneously and the result is shown in Fig. 11(b). It is clear that the two vibration can trigger an intramolecular proton transfer reaction with the lowest scanned energy barrier of about 78.5 kcal/mol. The decrease (or increase) of H-C–H angle does not cause an initial chemical reaction as shown in Fig. 11 (c) and (d) unless the cleavage of C–H bond which is difficult due to the high dissociation energy of 112.9 kcal/mol Blanksby & Ellison, 2003.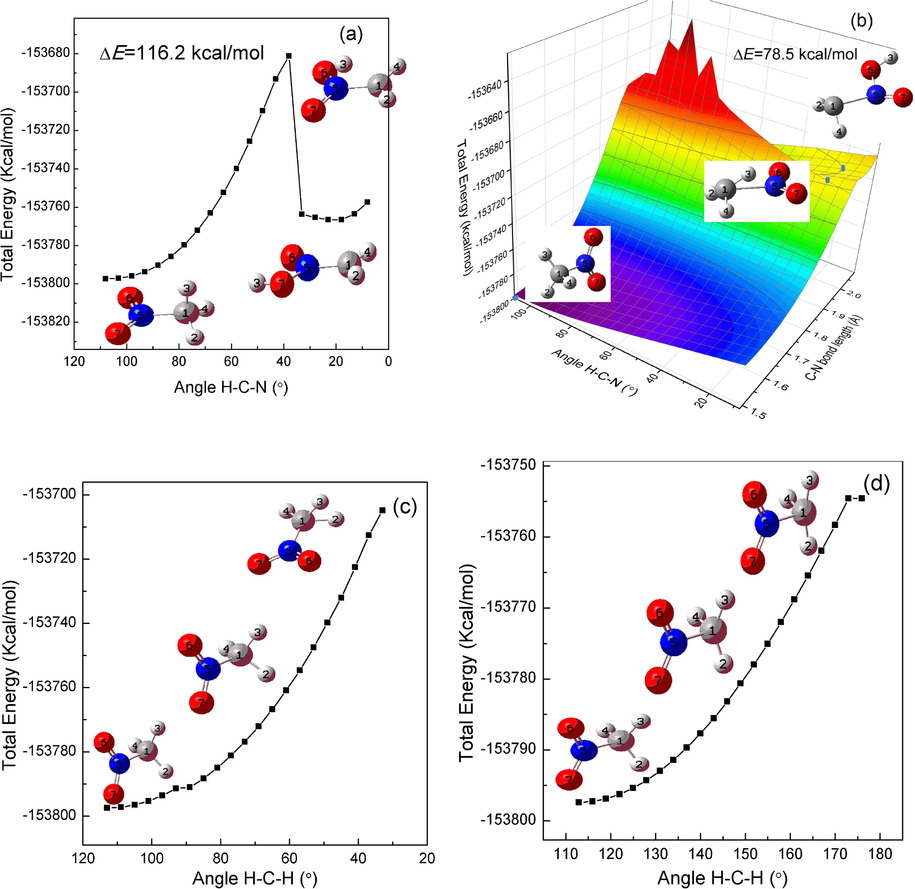
The relaxed scan optimization algorithm plots are presented for the decrease of H-C − N angle (a), the increase of C-N bond together with the reduction of angle H-C-N angle (b), the decrease (c) and the increase (d) of H-C–H angle in nitromethane.
3.3.4 Effect of 3250 cm−1 and 3500 cm−1 mode vibrations
The C–H symmetric (3250 cm−1) and asymmetric (3500 cm−1) stretching vibration do not trigger a single-molecule chemical reaction. However, it is possible to trigger an intermolecular proton transfer reaction in view of the vibration case as shown in Fig. 12(a). The potential energy plots by scanning the increase of C1-H4 and C8-H11 bonds simultaneously based on the optimized bimolecular configuration (Fig. 12(b)) is indicated in Fig. 13(a). It can be noted that the two hydrogen atoms will be transferred to the oxygen atoms in another nitromethane molecule synchronously with the increase of the two C–H bond lengths, that is, the intermolecular double-proton transfer reaction occurs. The lowest scanned energy barrier is about 59.9 kcal/mol and the corresponding stagnation points have been marked by the blue dots. In order reduce the fixed factor, the increase of single C1-H4 bond is relaxedly scanned and the double-proton transfer still occurs with scanned energy barrier of 61.2 kcal/mol as shown in Fig. 13(b). Therefore, the reaction energy barrier of intermolecular double-proton transfer is lower than that of the single-molecular lowest reaction channel (rearrangement reaction of the C-N = O group with barrier height of about 68 kcal/mol). Therefore, it can be concluded that the initial decomposition step of nitromethane is more prone to an intermolecular double-proton transfer rather than an intramolecular reaction such as a C-N bond breakage, a rearrangement reaction or an intramolecular proton transfer. The triggering mechanism of intermolecular double-proton transfer is attributed to the enhance of intermolecular hydrogen bonding cause by the stretching vibration of C–H bond (near 3000 cm−1). The hydrogen bond enhancement is consistent with the results of the previous RDFs analysis of the intermolecular hydrogen bonds.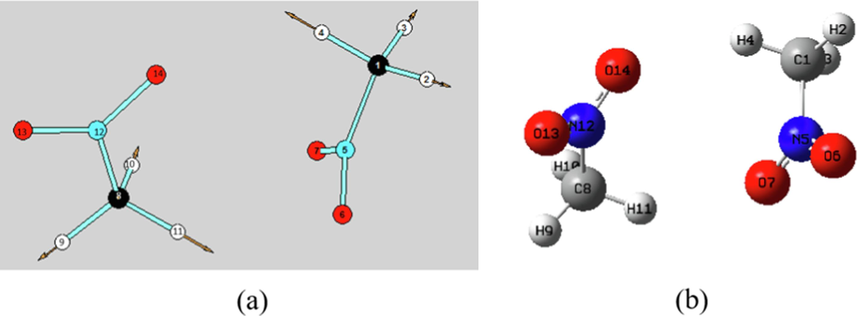
The scheme diagram of C–H systematic streching vibration (a) and the optimized bimolecular nitromethane configuration.
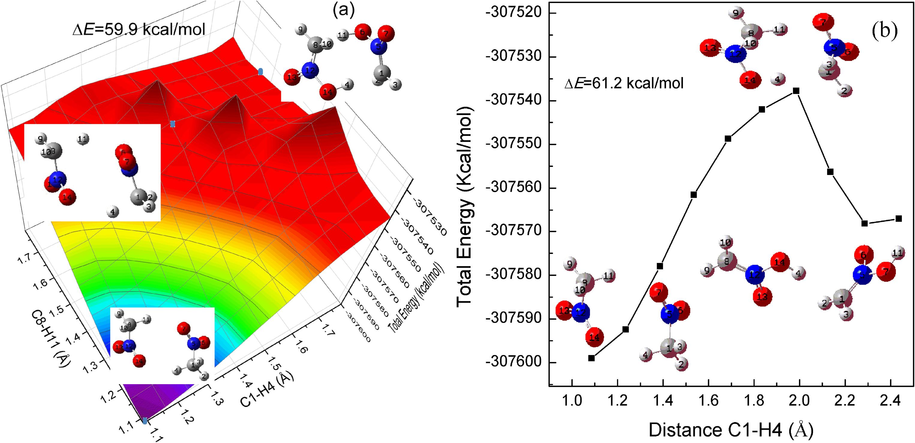
A relaxed scan optimization algorithm plot is presented along the increase of two C–H bonds (a) and that of a single C–H bond (b) in the bimolecular nitromethane. Some molecular structures at the beginning, middle, and end of the scan are shown in the figures.
3.4 Activation barrier of intermolecular double-proton transfer
In order to confirm the rationality of the predicted triggering path, the transition state of intermolecular double-proton transfer reaction is obtained by DFT calculation. The potential energy profile for the reaction path is given in Fig. 14 together with the relative energy and geometries of each stationary point. The IRC path is determined to confirm the accuracy of the transition state (see Supporting Information Figure S3). One can noted that the activation barrier is about 59.8 kcal/mol, which is quite close to the scanned barrier height (59.9 or 61.2 kcal/mol) obtained by increasing the C–H bond lengths. So it proves the rationality of our conclusions. Therefore, the initial thermal decomposition step of nitromethane is the intermolecular double-proton transfer, which is triggered by the intermolecular hydrogen bonding reinforced by stretching vibration of C–H bond located at near 3000 cm−1 wavenumber.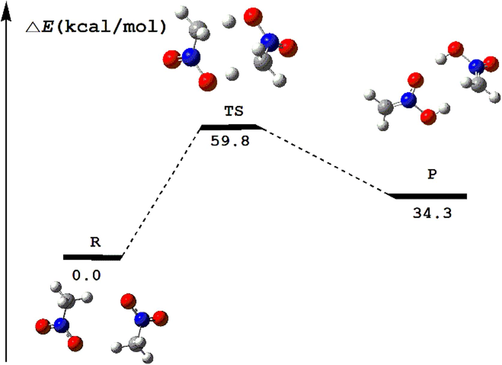
Calculated reaction potential energy profile based on DFT/B3LYP/6–311 ++ G (d,p) level.
4 Conclusions
The initial decomposition step of nitromethane and its triggering mechanism are investigated in detail at low temperatures by the CPMD theoretical calculations and the temperature-dependent Raman spectroscopy experiments. The thermal kinetic behavior of intra- and intermolecular hydrogen bonding are examined by RDFs analysis, indicating that the intermolecular hydrogen bonding is strengthened with increasing temperature.
Five activated vibrational modes are obtained for nitromethane by the calculated and experimental dependent-temperature Raman spectra, which are the wagging vibration of nitro group (670 cm−1), stretching vibration of C-N bond (950 cm−1), asymmetric deformation (shearing and bending)of C–H bond (1480 cm−1), C–H bond symmetric stretching vibration (3250 cm−1), and C–H bond asymmetric stretching vibration (3500 cm−1), respectively. The relaxed scans are performed for each change in bond lengths and bond angles from the five active vibration modes. The results show the increase of C–H bond length from C-H stretching vibration located at near 3000 cm−1 could leads to the intermolecular double-proton transfer, which is predicted to be the optimal reaction path due to the lowest scanned barrier height of ∼ 60 kcal/mol. The scanned barrier is very close to the calculated activation barrier (59.8 kcal/mol), proving the reliability of our calculations.
Therefore, the initial decomposition step of nitromethane is indicated to be the intermolecular double-proton transfer, which is not reported in previous findings. Our study further reveals the triggering path of the intermolecular double-proton transfer, that is, the C–H stretching vibration (near 3000 cm−1) is activated with increasing temperature and leads to the enhance of intermolecular hydrogen bond, which thus triggers the initial intermolecular double-proton transfer reaction. Our results provide a new interpretation for the long-debated initial decomposition mechanism of nitromethane.
Acknowledgement
This work were supported by the Education Department of Liaoning Province (NO.LJKMZ20221495), Natural Science Foundation of Liaoning Province (NO.2022-MS-368), and the Inter-school Cooperation Project of Liaoning Province (NO.XJXM2020005).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys.. 1993;98:5648-5652.
- [CrossRef] [Google Scholar]
- Bond dissociation energies of organic molecules. Acc. Chem. Res.. 2003;36(4):255-263.
- [CrossRef] [Google Scholar]
- Nosé-Hoover chain method for nonequilibrium molecular dynamics simulation. Phys. Rev. E. 2000;61(5):4769.
- [CrossRef] [Google Scholar]
- TRAVIS-a free analyzer and visualizer for Monte Carlo and molecular dynamics trajectories. J. Chem. Inf. Model. 2011
- [CrossRef] [Google Scholar]
- Temperature dependence of thermal motion in crystalline naphthalene. Acta Crystallogr. Sect. B: Struct. Crystallogr. Cryst. Chem.. 1982;38:2218-2228.
- [CrossRef] [Google Scholar]
- Theoretical studies of van der waals molecules and intermolecular forces. Chem. Rev.. 1988;88:963-988.
- [CrossRef] [Google Scholar]
- Monomolecular cracking of propane over acidic chabazite: An ab initio molecular dynamics and transition path sampling study. J. Catal.. 2011;279(1):220-228.
- [CrossRef] [Google Scholar]
- Electron affinity, gas-phase acidity, bond dissociation energy, and negative ion states of nitromethane. Chem. A Eur. J.. 1999;103(45):9072-9079.
- [CrossRef] [Google Scholar]
- Nitromethane decomposition under high static pressure. J. Phys. Chem. B. 2010;114(29):9420-9428.
- [CrossRef] [Google Scholar]
- From molecular vibrations to bonding, chemical reactions, and reaction mechanism. Curr. Org. Chem.. 2010;14(15):1524-1560.
- [CrossRef] [Google Scholar]
- Car-Parrinello molecular dynamics study of the thermal decomposition of sodium fulminate. Chem. Eur. J.. 2010;16(27):8041-8046.
- [CrossRef] [Google Scholar]
- A theoretical study on terpene-based natural deep eutectic solvent: relationship between viscosity and hydrogen-bonding interactions. Global Chall.. 2021;5(3):2000103.
- [CrossRef] [Google Scholar]
- M.J. Frisch et al., 2009.Gaussian 09, Revision E.01.
- Thermal decomposition of condensed-phase nitromethane from molecular dynamics from ReaxFF reactive dynamics. J. Phys. Chem. B. 2011;115(20):6534-6540.
- [CrossRef] [Google Scholar]
- Scattering of light by crystals. New York: Dover; 1978.
- J. Hutter et al., CPMD. MPI fur Festkorperforschungand IBM Zurich Research Laboratories, Stuttgart, 1995-1999.
- Single-molecule reaction and characterization by vibrational excitation. Phys. Rev. Lett.. 2002;89(12):126104
- [CrossRef] [Google Scholar]
- CP2K: an electronic structure and molecular dynamics software package-Quickstep: efficient and accurate electronic structure calculations. J. Chem. Phys.. 2020;152:194103
- [CrossRef] [Google Scholar]
- Dynamic vacuum stability test method and investigation on vacuum thermal decomposition of HMX and CL-20. Thermochim. Acta. 2012;537:13-19.
- [CrossRef] [Google Scholar]
- Thermal kinetic performance and storage life analysis of a series of high-energy and green energetic materials. J. Therm. Anal. Calorim.. 2015;119:659-670.
- [CrossRef] [Google Scholar]
- Structural rearrangement of energetic materials under an external electric field: a case study of nitromethane. J. Phys. Chem. A. 2018;122(8):2129-2134.
- [CrossRef] [Google Scholar]
- Ab initio molecular dynamics simulation of vibrational energy redistribution of selective excitation of C-H stretching vibrations for solid nitromethane. PCCP. 2019;21(37):20822-20828.
- [CrossRef] [Google Scholar]
- An evaluation of harmonic vibrational frequency scale factors. J. Phys. Chem. A. 2007;111(45):11683-11700.
- [CrossRef] [Google Scholar]
- Constant-temperature molecular dynamics. J. Phys. Condens. Matter. 1990;2(S):SA115.
- [CrossRef] [Google Scholar]
- Raman and infrared investigations at room temperature of the internal modes behaviour in solid nitromethane-h3 and-d3 up to 45 GPa. J. Raman Spectrosc.. 2008;39(3):354-362.
- [CrossRef] [Google Scholar]
- Predicting the initial thermal decomposition path of nitrobenzene caused by mode vibration at moderate-low temperatures: Temperature-dependent anti-stokes raman spectra experiments and first-principals calculations. J. Phys. Chem. A. 2018;122:8336-8343.
- [CrossRef] [Google Scholar]
- Coherent anti-Stokes Raman scattering spectrum of vibrational properties of liquid nitromethane molecules. Acta Phys. Sin.. 2018;67(2):024208
- [CrossRef] [Google Scholar]
- Phase transition and trigger mechanism of initial reaction under pressure for benzofuroxan energetic materials: Raman spectroscopy and first-principle calculations. J. Raman Spectrosc.. 2021;52(4):865-876.
- [CrossRef] [Google Scholar]
- Experimental and computational studies of choline chloride-based deep eutectic solvents. J. Chem. Eng. Data. 2014;59(11):3652-3662.
- [CrossRef] [Google Scholar]
- Molecular mechanism of Overhauser dynamic nuclear polarization in insulating solids. J. Phys. Chem. Lett.. 2017;8(10):2137-2142.
- [CrossRef] [Google Scholar]
- Inversely deducing the initiation mechanism of energetic materials under pressure from possible defect states in nitromethane. Chem. Phys. Lett.. 2020;749:137470
- [CrossRef] [Google Scholar]
- A molecular dynamics study of classical vibrational spectra in hydrostatically compressed crystalline nitromethane. J. Phys. Chem. B. 2010;114(51):17177-17186.
- [CrossRef] [Google Scholar]
- Molecular dynamics study of the crystallization of nitromethane from the melt. J. Chem. Phys.. 2010;133(19):194501
- [CrossRef] [Google Scholar]
- Proper thermal equilibration of simulations with Drude polarizable models: Temperature-grouped dual-Nosé–Hoover thermostat. J. Phys. Chem. Lett.. 2019;10(23):7523-7530.
- [CrossRef] [Google Scholar]
- Competition between hydrogen bonding and dispersion force in water adsorption and epoxy adhesion to boron nitride: from the flat to the curved. Langmuir. 2021;37(38):11351-11364.
- [CrossRef] [Google Scholar]
- How does low temperature coupled with different pressures affect initiation mechanisms and subsequent decompositions in nitramine explosive HMX? Phys. Chem. Chem. Phys.. 2015;17:22823-22831.
- [CrossRef] [Google Scholar]
- Thermal decomposition of solid phase nitromethane under various heating rates and target temperatures based on ab initio molecular dynamics simulations. J. Mol. Model. 2014;20:1-10.
- [CrossRef] [Google Scholar]
- Initial decomposition of HMX energetic material from quantum molecular dynamics and the molecular structure transition of β-HMX to δ-HMX. J. Phys. Chem. C. 2019;123(14):9231-9236.
- [CrossRef] [Google Scholar]
- Theoretical Study on vibrational state-selected rate constants of the reaction C2H2+ +H2—C2H3+ +H. Chem. J. Chin. Univ.. 1995;16:444-448.
- [Google Scholar]
- How well can new-generation density functionals describe the energetics of bond-dissociation reactions producing radicals? Chem. A Eur. J.. 2008;112(6):1095-1099.
- [CrossRef] [Google Scholar]
- Influences of pressure on methyl group, elasticity, sound velocity and sensitivity of solid nitromethane. Eur. Phys. J. B. 2017;90:1-12.
- [CrossRef] [Google Scholar]
- Vibrational properties of layered BiTeCl single crystal. J. Raman Spectrosc.. 2017;48(12):1783-1788.
- [CrossRef] [Google Scholar]
Appendix A
Supplementary material
Supplementary data to this article can be found online at https://doi.org/10.1016/j.arabjc.2023.105579.
Appendix A
Supplementary material
The following are the Supplementary data to this article:Supplementary data 1
Supplementary data 1







