Fractal geometry analysis of chemical structure of natural starch modification as a green biopolymeric product

2.1 Compositions of natural starch

Starch contains two major components: one is amylose, which is a linear polymer, and the other is amylopectin, which is a highly branched polymer. The repeat units in both amylose and amylopectin are identical (so-called α-d-glucosyl residues) but connected in different ways, as given in Fig. 2. Most starches contain 20–30 wt% of amylose, although some waxy starches contain very little amylose. In amylose, α-d-glucosyl residues are linked by an α[1 → 4] bond. Typically, the molecular weights of extracted amylose are in the order of 105–106 g/mol. Amylose generally is recognized as linear macromolecule. However, it has been reported that there is a slight degree of branching (9–20 branch points per molecule) in amylose from various botanical sources. The length of side chains ranges from 4 to over 100 repeat units. There is no effective way of separating the branched amylose from the linear amylose.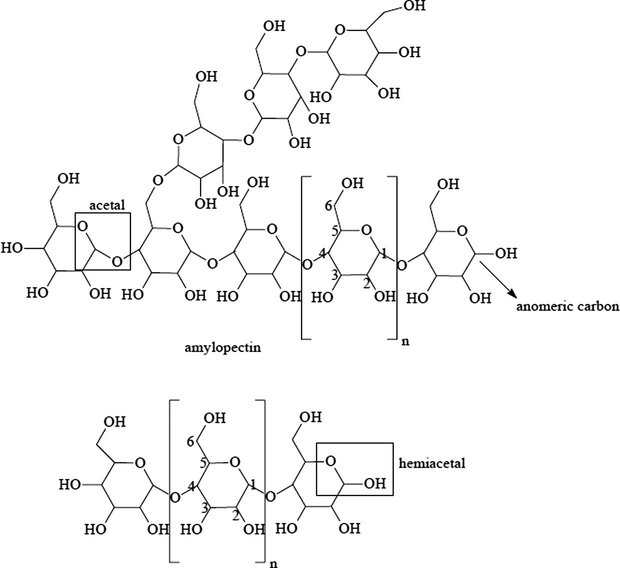

Close

Figure 2

Chemical structures of amylose and amylopectin.

Export to PPT

As described above, the linear polysaccharide chains tend to have helix structure either left-handed or right-handed. The left-handed form is energetically preferred to the right-handed form. There are two ways the helical molecule is packed in the crystalline phases of starch: A-type and B-type, as shown in Fig. 3. In both A- and B-type crystals, the helices are packed parallel. Besides A-type and B-type crystalline structures in natural starches, previous researchers also found Vh-type crystalline structure in starch complex formed between the single helix of amylose molecules with compounds, such as iodine, dimethyl sulfoxide (DMSO), alcohol, and fatty acid. In such complexes, iodine atoms or the hydrocarbon part of alcohol or fatty acid is held by the hydrophobic inner surface in the helix. Then these complexes are packed parallel in an orthorhombic unit cell.

Close

Figure 3

Two major types of crystalline structure in the natural starch granules: A-type and B-type.13 (Reprinted with permission from Elsevier) (Smith et al., 2005).

Export to PPT

2.2 Starch degradation and starch applications

Starch chains are to be phosphorylated in order to be degraded by enzymes. One enzyme type: glucan, water dikinase “GWD” phosphorylates the C-6 position in glucose molecule. Another enzyme: phosphoglucan, water dikinase “PWD” phosphorylates C-3 position. If starch is not phosphorylated, it accumulates in the plastid.

Maltose as the main product of degradation is made by activity of enzyme: beta-amylase “BAM” at non-reduced end of glucose after being phosphorylated.

When the glucose chain has three or less molecules, BAM cannot produce maltose. Another enzyme, disproportionating enzyme-1 “DPE1”, combines two maltotriose molecules and releases glucose molecule. Then BAM releases another maltose molecule from the remaining chain. This process proceeds to completely degrade starch (Smith et al., 2005).

Starch is most widely used as food additive in food industry. On the other hand, Papermaking can be served as the largest non-food application of starches. Starch is also used in making adhesive agent (glues), clothing industry, textile industry, synthetic bioplastic formations, biofuel production via wet milling and so on.

3.1 Geometry, fractal geometry and dimension

In 1623, Galileo expressed that the book of nature was written in mathematic languages and the alphabets of this language is triangles, circles and other geometrical shapes, that human being could not understand it carefully. Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the elements. The Euclidean geometry is the axiomatic study of lines, circles and triangles that shaped form an ideal, therefore approximate basis for understanding geography, mechanics and every real thing. From this perspective, nature is like noisy mathematics and crumpled slightly out of focus.

At 18’th century “Euler” discussed a generalization of Euclidean geometry called “affine geometry”. The 19’th century’s most outstanding progress in geometry occurred when, around 1830, János Bolyai and Nikolai Ivanovich Lobachevsky separately published on non-Euclidean geometry – a newly made realm in that time, in which the parallelism is not right. Einstein’s theory of general relativity shows that the true geometry of spacetime is not Euclidean geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees because of gravity.

At 20th century, controversial works were produced on non-Archimedean models of Euclidean geometry, in which the distance between two points might be infinite or infinitesimal, in the Newton–Leibniz sense.

The name “fractal” in geometry was first invented by mathematician Benoît Mandelbrot in 1975.

Fractal geometry creates an alternative to Euclidean geometry whose elements are not lines and circles but iterations, replications and self-resemblance, whose surfaces are not smooth but jagged, whose features are not perfect but broken. Fractal is a new geometry with capability to understand formerly inexplicable real world phenomena. Fractal provides insight into the distribution of galaxies, the shape of coastlines and growth of crystals. In nature, it can be seen more fractal object such as fern, cauliflowers, clouds, trees and so on.

The fractal objects have distinctive boundaries that occupied the constant volume or space.

Fractals are different from other geometric figures because of the way in which they scale. Doubling the edge lengths of a square scales its area by four, which is two to the power of two, because a square is two-dimensional. Likewise, if the radius of a sphere is doubled, its volume scales by eight, which is two to the power of three, because a sphere is three-dimensional. If a fractal’s one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power of two that is not necessarily an integer (Mandelbrot, 1983).

Fractal dimension can define any changing in the details of object. Until now, many fractal dimensions were introduced with special applications (Mandelbrot, 1983). Generally the fractal dimension is changed between 0 and 3 and takes a real amount. For curve specifically, this varies between one up to two and for surface changes from two to three. The fractal dimension shows freedom’s degree of object. From the perspective of some application and also the concept that is used in present research, fractal dimensions can be used instead of human vision in some systems. So using this concept, it is very useful for object’s pattern investigation. Some of the most important and useful fractal dimensions are box counting, compass and self-similar methods. Although, the applied algorithms differ from method to other, they obey to the same basis summarized by following four steps according to Fig. 4:

1. Prepare the suitable image with adjusted zooming and pixel.

2. Measure the quantities of the object using various step sizes (S and a function of S: f(S)).

3. Plot log (measured quantities) vs. log (step sizes) after calculations.

4. Fit a regression line (like by least-squares) through the data points and estimate FD as the slope of the regression line.

Close

Figure 4

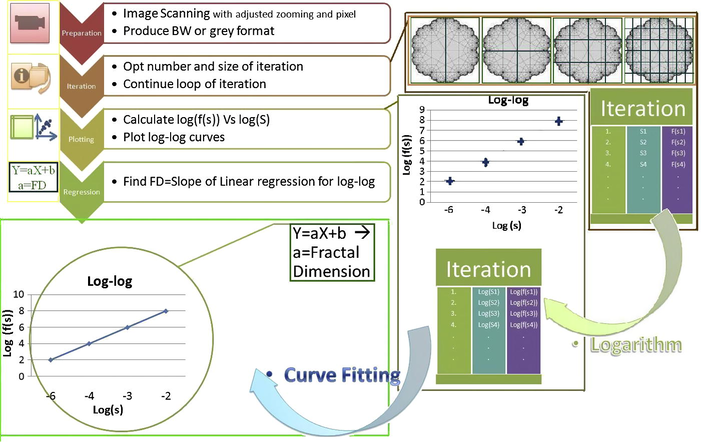
Fractal dimension computing methods’ main algorithm.

Export to PPT

3.2 Box counting dimension (BC)

The box counting method defined by Russel et al. (1980), is the most applied and most popular method in fractal geometry. Box counting dimension used in many applications in different systems. It is related to self-similarity structures, but it can be applied even to the random structure without a conspicuous self-similar unit, like a coastline. For determining box counting dimension (D_B), it is assumed that the object is covered by a square mesh of various sizes “s” and then number of boxes (N(s)) containing part of the image (containing the object) is counted. Because N is the function of the mesh size, N(s) increases as s decreases. The box counting dimension (D_B) is given by the slope of the linear portion of a log(N(s)) vs. log(1/s) graph as expressed by Eq. (1):

Recent studies on box count notes: as the reiteration for different sizes of s can produce various sizes of N(s), the grid should be randomly relocated at each iteration (Appleby, 1996). More recently, Pruess (2007) showed that the computation of the FD is box size sensitive.

3.3 Differential box-counting method (DBCM)

Differential box-counting method (DBCM) proposed by Chaudhuri and Sarkar (1995) is an adaptation or modification of popular box count method. As it aims to solve some of limitations of the BM method, it has tendency to work on gray-scale images instead of binarization of images. The procedure of the method is just like the BC method with difference that the image itself is partitioned into boxes of various size s and N(s) is computed like the difference between the minimum and the maximum gray levels in the (i, j)th box. Then FD is calculated by logarithmic formula (1).

Some limitation in the box-counting methods is the optimization of the box size. Many studies were done to find the upper and lower bounds for the box size. Chen et al. (1993) proposed a theoretical justification for a restriction on the smallest box size inspired by the work of (Pickover and Khorasani, 1986). Also Bisoi and Mishra (2001) established a lower bound of the box size to ensure accurate results.

3.4 Compass dimension

The compass dimension is a relationship between the compass divider setting and measured length. To measure the length of the random fractal curve, a compass divider must divide by a compass divider or ruler with certain ruler setting. If multiplying the ruler length by the number of rulers that is needed to cover the object’s image length, the approximate length of a curve can be expressed as Eq. (2):

By decreasing the length of rulers, the more accurate length of the curve can be obtained, because of the closer measurement to the path of the curve. So if we plot ln (L) against ln (L) for a range value of l, the slope will be an estimation for the compass dimension (D_C).

3.5 Area measurement methods

Area measurement methods upon their name continue the work of box count methods by using some elements (triangle, erosion, dilatation,…) of various scales “s” and compute the area A(s) of the image intensity surface at scale “s” instead of filled box number N(s). In this case FD is the slope of the best fitting line at the points (log(s), log(A(s))) synonymous to BC (log(1/s), log(N(s))). In this method, three algorithms are frequent. Table 1 presents a history of these 3 classes.

4.1 Materials

In present study the sample of structure of natural starch before and after modification was used for investigation and analysis. A microscanner was utilized for taking photograph from natural starch before and after modification at best resolution. The scanning resolution was set to 200 dpi which provides parallel lighting inspection with no shadows on them.

4.2 Computer program, feature extraction

For feature extraction, one MatLab R2013a code is composed to find box count dimension by preparing BW images, rescaling them for some steps and then using linear regression. The size of all the images is the same and is 128 × 128 pixels. Images were covered with boxes then by changing the size of boxes in 30 steps it is found how the number of boxes changes with the size of the boxes. The number of steps are raised up to 30 in order to have more precision. In Fig. 6, the results of transformation are shown. These figures are prepared by a function of MatLab R2013a being Otsu’s method for converting types of images to black and white images illustrating in followings: $$\text{level}=\text{graythresh}(\text{I})\text{;or}:[\text{level EM}]=\text{graythresh}(\text{I})\text{;}$$

The “level = graythresh(I)” computes a global threshold (level) that can be used to convert an intensity image to a binary image with “im2bw”. level is a normalized intensity value that lies in the range [0, 1].

The graythresh function uses Otsu’s method, which chooses the threshold to minimize the intraclass variance of the black and white pixels. By following code the images in Fig. 5 are converted to BW type presented in Fig. 6:

Close

Figure 5

The sample images of natural starch before and after modification: (a), (b) and (c).

Export to PPT

Close

Figure 6

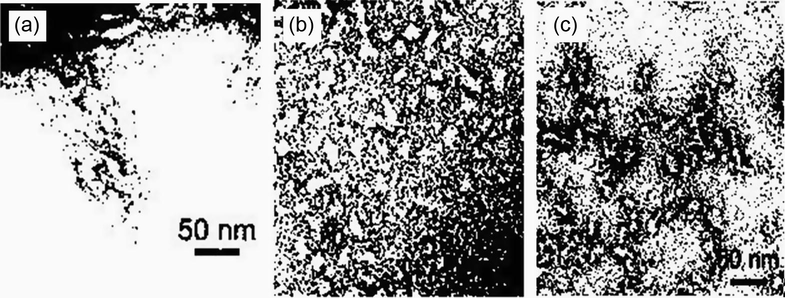
The conversion code and sample images of natural starch for box counting calculation: (a), (b) and (c).

Export to PPT

After converting the images into black and white type, the box counting fractal dimension of each image is defined by horizontal and vertical meshing grid. The array BW of each image is reboxed by averaging via a “for loop” with 30 repetitions. Reboxing performance is schematically shown according to Fig. 7 for 3 steps.

Close

Figure 7

Three steps of meshing for sample b.

Export to PPT

In code, the average amounts of pixel color in each box are calculated which is a real number between 0 and 1. If the number is smaller than 0.5 the box is more black and it is inferred that it is occupied by body otherwise it is empty. Then after each boxing (meshing) and calculation, produced vectors of “vectorS” and “vectorN” are brought to curve fitting tool in MatLab to find the slope of best line passing through naming vectors as following:vectorS = Log(1/s); vectorN = Log(N(s)); vectorN = DB × vectorS;

where:

• “s” is new-meshed array size vector = [S1, S2, …, S30];

• N(s) is the vector of total numbers of filled boxes = [N(S1), N(S2), …, N(S30)];

• vectorS = [Log(1/S1), Log(1/S2), …, Log(1/S30)];

• vectorN = [Log(N(S1)), Log(N(S2)), …, Log(N(S30))];

• DB is box counting dimension being the slope of fit line passing through vectorS and vectorN

4.3 Result and discussion

The graphs of Fig. 8 show the results of applying the fractal algorithm on naming images. They represent the best fit line with slope of DB.

Close

Figure 8

The box counting dimension of images (a), (b) and (c) in study.

Export to PPT

In table No. 2 the results of CF (curve fitting) tool are presented for study images. The second column represents the fit slopes by “Center and scale” method – a method proposed by Matlab CF tool – in which data meet linear regression around mean −4.712 by standard deviation of 1.676. Columns 4 and 5 represent statistical data for pixels of BW images. Color of a binary image is 0 (Black) or 1 (White). Column 4 shows the mean color of pixels in study images and column 5 is the standard deviations of pixel colors.

According to box count results of Table 2 and binary images of Fig. 6, the following notes are perceived: The order of fractal dimensions from low to high is: c < a < b which shows the degree and quality of fractal activity in order such that sample b has the most amount of complexity and replications while sample c has the least amount of fractal presence and iterated divisions. However the fractal dimensions of a and c are approximately close to each other. On the other hand, the order of mean pixel color for samples is: b < c < a which shows sample b is most black and is most filled by body whereas sample a is most white and is most empty. It is inferred that sample b has complex and well-woven texture among the samples as it has more objects and is also more fractal. This matter can be found by a rather high amount of std = 0/4770 because it represents a high amount of distribution of color pixels in figure that means more weight is more dispensed all over the geometry.

Among samples, the modified sample b has FD approximately equal to 2 (a two dimensional case) which is the most suitable pattern for biodegradability based on having a well-distributed structure with more surface area needed for biological and environmental activities. Indeed raising the amount of fractal dimension increases reactivity and so biodegradability. It is noticeable that the samples are classified as distinctive terms: “non-defective” for sample “B” and “thin Spot” for samples “A” and “C” according to neural network algorithm working with 3 parameters naming FD, Mean and Std of processed images (P1, P2 and P3) as shown in Fig. 9.

Close

Figure 9

The structure of neural network.

Export to PPT

Defect detections extracted by Neural Network are classified into four divisions as 1: non-defective, 2: thin Spot, 3: Thick Spot, 4: Neps.

On the other hand about industrial applications of polymers could be stated: different kinds of defects found in an analyzed sample make inability and incapacity of sample texture to play role of container package and contact exposure and hence, qualified product needs for non-defective feature and classification due to design philosophy and quality control. In terms of material mechanics, polymer microstructure must be designed so geometrically that exerted forces and stresses can find suitable equilibrium based on their structure capacity, just as a firm steel structure or a mechanically-designed framework is in statics. Here the importance of fractal geometry is appreciated by providing scientific tool of FD to quantify geometry measurements. The more regularly the microstructure is branched, in a more sophisticated mechanics the structure will sustain loads and forces.