Kosmotropic and chaotropic behavior of hydrated ions in aqueous solutions in terms of expansibility and compressibility parameters

2.1 Materials

Sodium chloride, sodium sulphate, and sodium bicarbonate; product of Sigma-Aldrich were used as received. Doubly distilled and de-ionized water was used for solution preparation. All chemicals exhibit high purity. Specifications of chemicals used in present study have been given in Table 1. Moreover the glassware was carefully washed, cleaned and dried in oven before use.

2.2 Methods

Density (d) and sound velocity (u) of aqueous solutions of electrolytes NaCl (0.0342 mol.kg⁻¹–0.1709 mol.kg⁻¹), Na₂SO₄ (0.0141 mol.kg⁻¹–0.0704 mol.kg⁻¹) and NaHCO₃ (0.0238 mol.kg⁻¹–0.1190 mol.kg⁻¹) were measured at temperatures (293.15 K–313.15 K) and at 101 kPa pressure using Anton Paar DSA 5000 M with high precision vibrating tube digital density meter and ultrasound speed measuring device. The instrument has a built-in thermostat to maintain the temperature. The accuracy and repeatability of DSA 5000 M for density are 5 × 10⁻⁶ gcm⁻³ and 5 × 10⁻⁶ gcm⁻³ respectively. Accuracy in Temperature is ± 0.01 K. The sample density is determined by measuring the oscillation frequency of a U-shaped sample tube completely filled with the sample liquid (Omota et al., 2009). The principle of sound velocity measurement is based on propagation time technique. The sample is sandwiched between two piezoelectric ultrasound transducers. One transducer emits sound waves through the sample-filled cavity (frequency around 3 MHz) and the second transducer receives those waves (Dubey et al., 2019). Thus, the sound velocity is obtained by dividing the known distance between transmitter and receiver by the measured propagation time of the sound waves up to 0.5 m s⁻¹ accuracy and 0.1 ms⁻¹repeatability. The weighing of chemicals was done by Wiggin Hauser electronic balance with a precision of ± 0.001 mg and reproducibility of ± 0.005 mg. During experimental work, molal solutions of different concentrations of electrolytes were prepared using following equation.

In present experiment, water was used a solvent for solution preparation.

3.1 Density and ultrasonic velocity measurements

Density and ultrasonic speed data for water and its comparison with literature reported data at different temperatures has given in Table 2, which showed that measured data is in good agreement with literature data. Measured data of density and sound velocity for aqueous solutions of salts at varying temperatures have given in Table 3 and it is obvious from reported data that density of electrolytic solutions in water is higher than that of pure water at respective temperatures. This difference can be attributed to the fact that presence of charges on electrolytic ions in solutions gathers themselves around the water molecules around them causing solution to become dense (Alvarez et al., 2011). Moreover density increases with increasing concentration of salts because of the fact that water structure developed in the presence of electrolyte becomes more prominent at higher concentrations. Density decreases with rise in temperature because at higher temperatures the kinetic energy of the molecules in solutions increases which dominates over binding energy among solution components and hence solution becomes less denser (Roy et al., 2009).

At higher temperatures kinetic energy of components of solutions increases, which renders the solution less dense and hence sound waves passes through solutions more easily at higher temperature. While at higher concentration of salts in their aqueous solutions, due to greater degree of intermolecular interactions, number of free ions moving in solutions decreases which ultimately reduces their hindrance to the passage of sound waves through solutions and hence speed of sound increases (Kant and Sharma, 2013).

3.2 Apparent and partial molar volume

Apparent molar volume (V_ϕ); a volumetric parameter has been calculated using following mathematical relation (Nain and Pal, 2013) (Adebowale and Adebowale, 2007).

S_v is the slope or pair wise interaction parameter.

Calculated data of V_ϕ, V^o_ϕ and S_v for electrolyte solutions in water at different temperatures has been summarized in Tables 4 and 5. Graphical representation of variation of apparent molar volume (V_ϕ) with concentration (m) of solutions has been shown in Figs. 1-3.

Close

Fig. 1

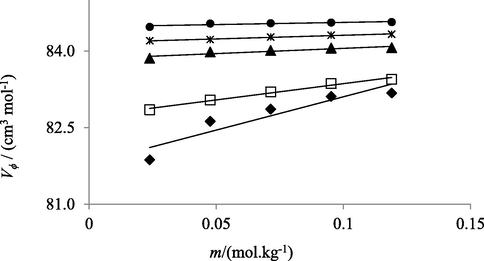
Relation between apparent molar volume (V _ϕ) and concentrations (m) of NaHCO₃ solutions in water at temperatures 293.15 K (♦), 298.15 K (□), 303.15 K (▲), 308.15 K (*) and 313.15 K (●).

Export to PPT

Close

Fig. 2

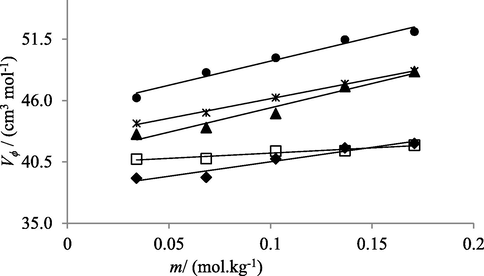
Relation between apparent molar volume (V _ϕ) and concentrations (m) of NaCl solutions in water at temperatures 293.15 K (♦), 298.15 K (□), 303.15 K (▲), 308.15 K (*) and 313.15 K (●).

Export to PPT

Close

Fig. 3

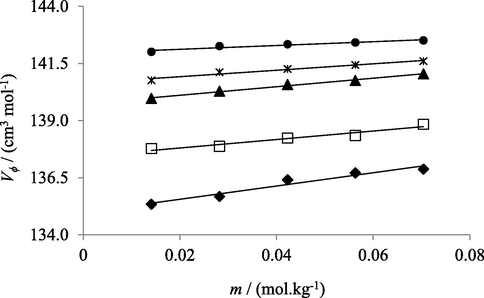
Relation between apparent molar volume (V _ϕ) and various concentrations (m) of Na₂SO₄ solutions in water at temperatures 293.15 K (♦), 298.15 K (□), 303.15 K (▲), 308.15 K (*) and 313.15 K (●).

Export to PPT

Reported data showed that with increasing temperature and concentration of electrolyte in solutions V_ϕ increases. According to co-sphere overlap model, for electrolytic solutions, overlap of co-spheres of two ionic species results an increase in volume of solution (Chadha et al., 2016) (Kumar et al., 2016) (Shamil et al., 1989). V_ϕ values of solutions provide knowledge about molecular interactions present among components of solutions. Greater values of apparent molar volume at higher temperature are also indicative of stronger molecular interactions in solutions. As formation of cavities or voids in solutions contribute positively to apparent molar volume. Solute molecules (electrolytes) at lower temperature don’t find much space to accommodate themselves in water, while at higher temperature cavities become larger in size facilitating the solute molecules to fit in solvent molecules in a much better way. Resultantly, greater interactions of solute molecules with solvent in solutions are observed (Nain and Pal, 2013). Similarly, at higher concentration of electrolytes greater solute–solvent interactions are observed because water molecules don’t directly attach to the surface of solute molecules but are held via strong hydrogen bonding, thus creating a gap in solutions and as a result increase in apparent molar volume of solutions is observed (Kumar and Kaur, 2012).

The observed order of V_ϕ values in salts aqueous solutions with common cation is Na₂SO₄ > NaHCO₃ > NaCl. Such trend showed that in aqueous Na₂SO₄ solutions intermolecular interactions are maximum and least in aqueous NaCl solutions. SO₄²⁻ being highly charged shows strongest interactions with water molecules. HCO₃¹⁻ exhibits lower affinity for water owing to its small charge to size ratio but this attraction is far better than Cl⁻¹. Chlorine is less electronegative as compared oxygen and thus produces weaker bonds (Godhani et al., 2013).

The series: F⁻ ≈ SO₄²⁻ > HPO₄²⁻ > acetate > Cl⁻ > Br⁻ > NO₃^– > ClO₄⁻ > SCN⁻, was proposed by Franz Hofmeister in 1888 (Alkschbirs et al., 2015). Hofmeister related phenomena were interpreted based on specific interactions between the ions and water molecules, and their subsequent influence on water hydrogen-bonding network. It had already been confirmed that ions in water could no longer be considered as point charges because ionic radii, shape, and type (cation or anion) could strongly affect the dynamics and energetic of water molecules in their hydration shell. Ion-specific hydration was therefore addressed by grouping the ions into kosmotropes and chaotropes according to their water affinity. The term kosmotropic describes the behavior of ions of small size and high charge density, which tightly bind adjacent water molecules and immobilize them. In contrast, the term chaotropic represents the effect of large bulky ions of low surface charge density, which bind water less strongly than water molecules bind themselves in bulk solution; thus ‘‘freeing up” the water molecules. Accordingly, the charge density of ions determines their water affinity (Millero, 1970). Different forces involved between all solution components, i.e., ion–water (ion hydration), ion–ion (ion pairing), and water–water molecular (hydrogen bonding) interactions. Each of these interactions can contribute (directly or indirectly) to the stability of water structure in solution and are susceptible to the amount and type of ions present (Moghaddam and Thormann, 2019).

In present study, molecular interactions in aqueous electrolytic solutions can also be explored in terms of kosmotropic and chaotropic behavior of electrolytes. Kosmotropes or ions having high charge density exhibit greater degree of intermolecular interactions with solvent (water) molecules than water with itself and therefore weakens the hydrogen bonding in water molecules. Whereas large single charged ions with low charge density are the chaotropes and they develop comparatively weak interactions with water molecules, and resultantly, don’t have profound effect on hydrogen bonding of water molecules present in their surroundings. Therefore, in present study, among electrolytes with same cation SO₄²⁻ ions exhibit stronger intermolecular interactions(H-bonding) with water molecules and are termed as Kosmotropes while Cl⁻ and HCO₃^– are classified as chaotropes as they develop weaker H-bonding with surrounding water molecules (Lawal 2006).

From Table 5, it is obvious that V^o_ϕ values are positive; these positive values indicate the dominance of solute–solvent interactions in solution (Sharma et al. 2015). The decreasing trend of V^o_ϕ values in salts solutions is Na₂SO₄ > NaHCO₃ > NaCl indicating highest solute–solvent interactions occur in Na₂SO₄. This trend can be justified by the fact that presence of charge on oxygen in case of both salts; NaHCO₃ and Na₂SO₄ makes intermolecular interactions stronger than in aqueous NaCl solutions where charge is present on less electronegative element (Cl⁻). Moreover the SO₄²⁻ bears double negative charge as compared to HCO₃¹⁻. Thus solute–solvent interactions are maximum in Na₂SO₄ and minimum in NaCl (Nain et al., 2013) (Sharma et al. 2015) (Dhondge et al., 2017). Due to greater interactions of SO₄²⁻ ions with water molecules they are termed as structure maker ions as they strengthen the H-bonds with surrounding water molecules. While Cl⁻ and HCO₃^– are structure breaker ions as they have a negative effect on structural arrangement of water molecules (Lawal 2006).

3.3 Partial molar expansibility

Partial molar expansibility or temperature derivative of partial molar volume is another volumetric parameter to determine intermolecular interactions in solutions in terms of the nature of structure making or breaking of solute molecules in solutions (Gheorghe et al., 2016). Following general polynomial equation is used to express the variation of V^ο_ϕ with temperature.

In above Eq. (3) a, b, and c are empirical constants and their values have been given in Table 6. Mathematically, E^o_ϕ is given by following equation (Gheorghe et al., 2016).

Obtained positive values of E^o_ϕ for aqueous salts solutions have been given in Table 7. Reported data showed that partial molar expansibility decreases with rising temperature for both NaCl and NaHCO₃ solutions at all studied temperatures because hydrated water molecules in the outermost shell of both above mentioned salts increases due to stronger electrostatic interactions among ions of salts and water molecules releasing very less water molecules into bulk even at higher temperature and give rise to smaller values of E^o_ϕ, indicative of absence of “caging effect” and predominance of electrostriction changes in solution over structural hydration of solute (NaCl and NaHCO₃) in aqueous solutions (Sharma et al., 2016) (Rafiee and Frouzesh, 2016) (Melinder, 2010). E^o_ϕ values increase with increasing temperature for aqueous Na₂SO₄ solutions which indicates that structural hydrophobic hydration is dominant over hydration of solute molecules with water molecules by strong electrostatic interactions (H-bonding). At higher temperature, water molecules get discharge from loose secondary solvation shell of solute molecules, causing an increase in volume of solution. Therefore, E^o_ϕ values become positive and indicate the presence of ‘caging or packing effect’ of solute (Na₂SO₄) molecules. It means that Na₂SO₄ molecules occupy the interstitial spaces in water molecular network, which shows the structure making/hydrophobic character of Na₂SO₄ solutions.

3.4 Hepler’s constant

Hepler proposed a mathematical relation to determine the tendency of solute molecules to promote or disrupt the structure of solvent molecules surrounding them. Hepler’s constant can be calculated as follows (Melinder, 2010) (Nain and Pal, 2013).

The sign of Hepler’s constant, (∂E^o_ϕ/∂T)_P defines whether a solute in solution is structure maker or breaker. Positive and equal to or close to zero values of (∂E^o_ϕ /∂T)_P indicate the structure promoting tendency of solute molecules. While for structure breaker solutes (∂E^o_ϕ/∂T)_P values are negative. Calculated values of (∂E^o_ϕ/∂T)_P for these salts in their aqueous solutions have been given in Table 7. Results showed that (∂E^o_ϕ/∂T)_P values are negative for aqueous NaCl and NaHCO₃ solutions indicating their ability to break structured water molecule in their surroundings. This can be explained as single charged ions (like Cl⁻ and HCO₃^–) having low charge density develop weaker intermolecular interactions with solvent (water) molecules and affect the network of hydrogen bonding in surrounding water to a very little degree. Such ions are called chaotropes or structure breaker ions (Yan et al., 2016) (Roy et al., 2009). On the other hand, small or multiple-charged ions like SO₄²⁻ ions, develop stronger interactions with water molecules due to their high charge density and are capable to strengthen the H-bonding in water molecules. Also positive value of (∂E^o_ϕ/∂T) for aqueous Na₂SO₄ solutions is indicative of structure making ability of Na₂SO₄ in water. Obtained results are according to classification of ions in Hofmeister series as kosmotropes and chaotropes where Cl⁻ and HCO₃^– are chaotropes while SO₄²⁻ ions are kosmotropes (Miranda‐Quintana and Smiatek, 2020).

3.5 Apparent and partial molar isentropic compressibility

Apparent molar isentropic compressibility (K_ϕ) gives insight about molecular interactions in terms of compressibility of solutions. Mathematical equation for calculating K_ϕ values is as follows (Iloukhani et al., 2005).

β is adiabatic compressibility of salts solutions, β_s^o is adiabatic compressibility of pure solvent, i.e. water and is calculated using following equation.

Calculated K_ϕ values for aqueous salts solutions have been given in Table 8. Results showed that K_ϕ values are negative for all studied solutions which show that portion of solution occupied by hydrated solute molecules is less compressible indicating the presence of strong electrostatic intermolecular interactions than in bulk solution (Iloukhani et al., 2005) (Godhani et al., 2013). Calculated K_ϕ values for presently studied salts in solutions decrease in order i.e. Na₂SO₄ > NaCl > NaHCO₃.

Least compressible structures having greater K_ϕ values shows stronger intermolecular interactions and vice versa. In terms of kosmotropic and chaotropic ions, SO₄²⁻ ions due to their greater hydration and enhanced degree of H-bonding with water molecules are termed as kosmotropes. While, Cl⁻¹ and HCO₃^– ions due to comparatively weaker H- bonding, lose their hydration sheath having less K_ϕ values and are more compressible. Therefore, these ions are known as chaotropes (Godhani et al., 2013).

From the calculated data of K_ϕ, partial molar isentropic compressibility (K^o_ϕ) was calculated using following equation (Sharma et al. 2015)

3.6 Intermolecular free length (L_f)

Another acoustical parameter, i.e. intermolecular free length (L_f) has been calculated using adiabatic compressibility data of salt’s solutions. Variation in intermolecular length of solution components is a direct measure of strength of interactions present in solutions. Following mathematical relation has been used to calculate L_f values (Iloukhani et al., 2005).

L_f = K. β_s^1/2 (10)

In above equation, K is Jacobson temperature-dependent constant {K = (93.875 + 0.375. T)0.10⁻⁸.

Results reported in Table 10 indicated that as the temperature and concentration of salts in solutions increases, L_f values decreases. With increasing concentration of salts in water, the degree of association of solute molecules with water increases, leading to more compact structure of solution, which results in a decrease in L_f values. In other words the structural readjustments in the solution are proceeding in the direction of less compressible phase (closer packing of the molecules) (Roy et al., 2009) (Liu et al., 2007) (Krakowiak, 2011). Ions in solutions cause significant changes in the structural arrangement of solvent (water) molecules. The difference in their effects lies on the relative strength of their bonding with solvent molecules in solutions. From results it is clear that Na₂SO₄ in water exhibits maximum intermolecular interactions (H-bonding). Observed order of strength of intermolecular interactions in different aqueous salts solutions is: Na₂SO₄ > NaCl > NaHCO₃.

Enhanced degree of H-bonding in water molecules structure due to SO₄²⁻ ions shows the structure making ability of SO₄²⁻ ions in aqueous solutions. While, destructive effect of Cl⁻ and HCO₃¹⁻ ions on the structuring in water molecules renders them chaotropes or structure breaker ions. Moreover, obtained results are also in accordance with Hofmeister series about kosmotropes and chaotropes; where Cl⁻ and HCO₃^– are chaotropes while SO₄²⁻ ions are kosmotropes (Smiatek, 2020).