Mechanism investigation of the reaction between triphenylphosphine, dialkyl acetylenedicarboxylates and 2-hydroxybenzimidazole: Experimental and theoretical study

3.1 Calculations

A facile synthesis of the reaction between triphenylphosphine 1, dialkyl acetylenedicarboxylates 2 and 2-hydroxybenzimidazole 3 (as a NH– heterocyclic compound) for the generation of phosphorus ylides 4a–c involving the two geometrical isomers such as Z- and E-isomers has been earlier reported (Maghsoodlou et al., 2006a,b). The reaction is shown in Fig. 1. For assignment of the two Z- and E-isomers as a minor or major form in phosphorus ylides 4a–b containing 2-hydroxybenzimidazole, first the Z- and the E-isomers were optimized for all ylide structures at HF/6–31G(d,p) level of theory by Gaussian98 package program (Frisch et al., 1998). The relative stabilization energies in both the geometrical isomers have been calculated at HF/6–31G(d,p) and B3LYP/6–311++G(d,p) level of theory. Atoms in molecules (AIM) (Bader, 1990), natural population analysis (NPA) methods and CHelpG keyword at HF/6–31G(d,p) level of theory have been employed in order to gain a better understanding of most geometrical parameters of both the E-4(a, b) and the Z-4(a, b) of phosphorus ylides. The numbers of critical points and intramolecular hydrogen bonds as well as the charge of atoms that constructed on the Z- and E-isomers have been recognized. The results altogether reveal the effective factors on stability of the Z- and the E-ylide isomers. In addition, J_x−y, the values of proton and carbon coupling constants and also chemical shifts $({\delta }_{\text{iso}}^{\text{H}}\text{,}{\delta }_{\text{iso}}^{\text{C}})$ have been calculated at mentioned level using SPINSPIN keyword. The relative stabilization energies for the two [Z-4(a, b) and E-4(a, b)] isomers (see Figs. 2 and 3) are reported in Table 1, as can be seen, E-4a and Z-4b isomers are more stable than Z-4a and E-4b forms (0.41 and 0.18 kcal/mol, respectively) at B3LYP level of theory.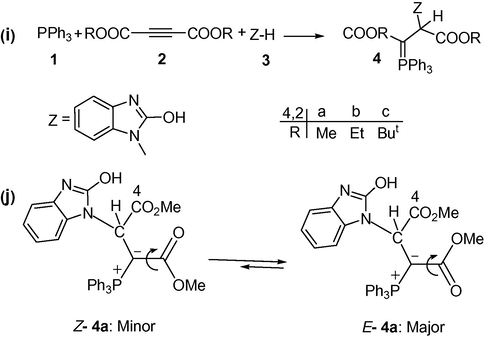

Close

Figure 1

(i) The reaction between triphenylphosphine 1, dialkyl acetylenedicarboxylate 2 (2a or 2b) and 2-hydroxybenzimidazole 3 for generation of stable phosphorus ylides 4 (4a or 4b), (j) The two rotational of isomers E-4a and Z-4a (major and minor, respectively) for ylide 4a.

Export to PPT

Close

Figure 2

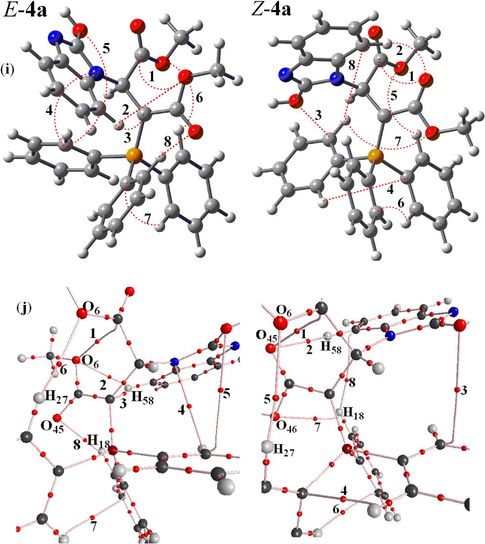
(i) Intramolecular hydrogen bonds (dotted lines) in the two E-4a and Z-4a geometrical isomers of stable ylide 4a, (j) A Part of molecular graphs, including intramolecular hydrogen bond at critical points (BCPs) for the two rotational isomers such as E-4a and Z-4a. Small red spheres, and lines corresponding to BCPs bond paths, respectively.

Export to PPT

Close

Figure 3

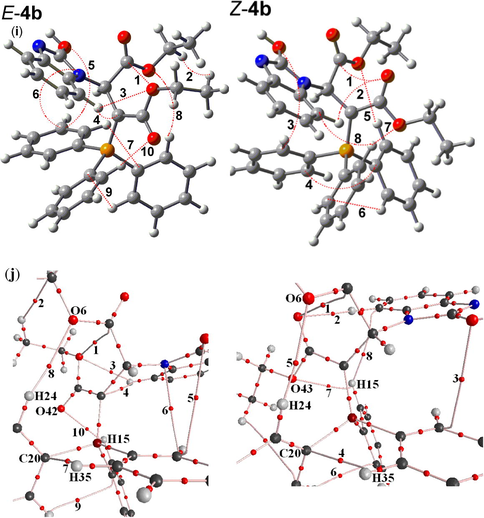
(i) Intramolecular hydrogen bonds (dotted lines) in the two E-4b and Z-4b geometrical isomers of stable ylide 4b, (j) A Part of molecular graphs, including intramolecular hydrogen bond at critical points (BCPs) for the two rotational isomers such as E-4b and Z-4b. Small red spheres, and lines corresponding to BCPs bond paths, respectively.

Export to PPT

Further investigation was undertaken in order to determine more effective factors on the stability of the two Z- and E-isomers on the basis of AIM calculations at HF/6–31G(d,p) level of theory by the AIM2000 program package (Biegler Konig et al., 2001). In recent years, AIM theory has often been applied in the analysis of H-bonds. In this theory, the topological properties of the electron density distribution are derived from the gradient vector field of the electron density ∇ρ(r) and from the Laplacian of the electron density ∇²ρ(r). The Laplacian of the electron density, ∇²ρ(r), identifies regions of space wherein the electronic charge is locally depleted [∇²ρ(r) > 0] or built up [∇²ρ(r) < 0] (Bader, 1990). Two interacting atoms in a molecule form a critical point in the electron density, where ∇ρ (r) = 0, called the bond critical point (BCP). The values of the charge density and its Laplacian at these critical points give useful information regarding the strength of the H-bonds. The ranges of ρ(r) and ∇²ρ(r) are $0.002-0.035\text{e}/{\text{a}}_0^3$ and $0.024-0.139\text{e}/{\text{a}}_0^5$ , respectively, if H-bonds exist (Grabowsk, 2001). The AIM calculation indicates intramolecular hydrogen bond critical points (H-BCP) for the two Z-4(a, b) and E-4(a, b) isomers. Intramolecular H-BCPs along with a part of molecular graphs for the two rotational isomers are shown in Figs. 2 and 3 (dotted line). Most important geometrical parameters involving some H-bonds (bond length and their relevant bond angle) are reported in Table 2. The electron density (ρ) × 10³, Laplacian of electron density ∇²ρ(r) × 10³, and energy density −H(r) × 10⁴ are also reported in Tables 3 and 4. A negative total energy density at the BCP reflects a dominance of potential energy density, which is the consequence of accumulated stabilizing electronic charge (Arnol and Oldfield, 2000). Herein, the number of hydrogen bonds in both categories (E-4a and Z-4a) and (E-4b and Z-4b) are (8 and 8) and also (10 and 8), respectively. The values of ρ and ∇²ρ(r) × 10³ for those are in the ranges (0.002 – 0.014 and 0.003 – 0.014 e/a₀³) and (0.002 – 0.014 and $0.003-0.014\text{e}/a_0^3$ ) and also (12.35 – 61.89 and $10.29-56.88\text{e}/{\text{a}}_0^5$ ) and (8.06 – 59.91 and $10.48-57.15\text{e}/{\text{a}}_0^5$ ), respectively. In addition, the Hamiltonian [−H(r) × 10⁴] are in the ranges (5.78 – 15.09 and 5.79 – 17.16 au) and (5.01 – 18.51 and 5.72 – 17.06 au), respectively (see Tables 3 and 4). These HBs show ∇²ρ(r) > 0 and H(r) < 0, which according to the classification of (Rozas et al., 2000) are medium-strength hydrogen bonds. In both ylides the dipole moment for the two E-4a and E-4b isomers (7.68 and 7.43 D) is smaller than the two Z-4a and Z-4b isomers (10.76 and 10.18 D, respectively) and the value of −H_tot (=Σ−H(r) × 10⁴) for the two E-4a and Z-4b isomers (84.47 and 85.86 au) is smaller than the two Z-4a and E-4b isomers (96.10 and 104.31 au, respectively). Although, −H_tot in the E-4a is lower than the Z-4a and appear as an effective factor on instability of the E-4a, but the values of dipole moment in the E-4a are less than Z-4a and considered as an important fact on stability of E-4a. The results are summarized in Table 5. This difference for the two isomers (E-4b and Z-4b) in ylide 4b involving less dipole moment, large −H_tot and more hydrogen bonds as three dominate factors on stability provides a good chance for E-4b isomer to be a major isomer. On the basis of theoretical calculations (Table 1), the Z-4b has a slight stability with respect to the E-4b (0.18 kcal/mol) isomers and seems to be different from the results of predictable properties of the most important geometrical parameters (Table 5). Perhaps, this slightly different behavior is relevant to the huge structures of the two ylides 4(a, b) involving three large atoms such as the two nitrogen, four oxygen and phosphorus and the large number of other atoms (C and H). This point, made a limitation in application of basis set higher than B3LYP/6–311++G(d,p) for a higher performance to gain more accurate calculations. Nevertheless, the results emerging from the geometrical parameters (dipole moment, −H_tot and number of hydrogen bonds) for the E-4(a, b) category, are compatible with the experiment results from the ¹H, ¹³C, ³¹P NMR spectroscopes [30] which indicate the two isomers of E-4a and E-4b with the experimental abundance percentage of 63% and 71% (major forms) with respect to the Z-4(a, b) (minor forms).

Also, the charge on different atoms which is calculated by AIM and NPA methods and also CHelpG keyword at HF/6–31G(d,p) level is reported in Table 6 for the two Z- and E-isomers of ylides 4a and 4b. There is a good agreement between the results in three methods.

The individual chemical shifts have been characterized by NMR calculations at mentioned level using SPINSPIN keyword. The total spin–spin coupling constant is the sum of four components: the paramagnetic spin–orbit (PSO), diamagnetic spin–orbit (DSO), Fermi-contact (FC) and spin-dipole (SD) terms. The value of chemical shifts (δ) and coupling constants (J_X−Y) is reported in (Tables 7–10) for the two major E-4(a, b) and minor Z-4(a, b) geometrical isomers. As can be seen, there is good agreement between both the experimental (Maghsoodlou et al., 2006a,b) and theoretical chemical shifts (δ) and coupling constants (J_X−Y). In the present work, molecular structures of ylides 4a–b involving three large atoms such as sulfur, phosphorus and nitrogen atoms are huge along with the large numbers of other atoms, for this reason, employment of higher level of theory with basis set higher than HF/6–311++G(d,p) is impossible for a higher performance to gain more accurate calculations. This limitation causes a small difference between both the experimental and theoretical coupling constants in some functional groups.

3.2 Kinetics studies

To gain further insight into the mechanism in the reaction between triphenylphosphine 1, dialkyl acetylenedicarboxylates 2 and 2-hydroxybenzimidazole 3 (as a NH– heterocyclic compound) for generation of phosphorus ylids 4a–c, a kinetics study of the reactions was undertaken by the UV spectrophotometric technique (Aitken et al., 2007; Nielsen et al., 1995; Dash et al., 2011). To find the appropriate wavelength to follow the kinetic study of the reaction, in the first experiment, 3 × 10⁻³ M solution of compounds 1, 2c and 3 was prepared in 1, 2-dichloroethane as solvent and the relevant spectra were recorded over the wavelength range of 200–400 nm. Figs. 4–6 shows the ultraviolet spectra of compounds 1, 2c and 3 respectively. In a second experiment, a 1 mL aliquot from the 3 × 10⁻³ M solutions of each compound of 1 and 3 was pipetted first into a quartz spectrophotometer cell (as there is no reaction between them), later 1 mL aliquot of the 3 × 10⁻³ M solution of reactant 2c was added to the mixture and the reaction monitored by recording scans of the entire spectra every 13 min over the whole reaction time in the presence of 1, 2c and 3 at ambient temperature as shown in Fig. 7 is typical. From this, the appropriate wavelength was found to be 330 nm (corresponding mainly to product 4). The UV–Vis spectra of compound 4c were measured over the concentration range (2 × 10⁻⁴ M ⩽ M_4c ⩽ 10⁻³ M) to check for a linear relationship between absorbance values and concentrations. With the suitable concentration range and wavelength identified, the following procedure was employed.

Close

Figure 4

The UV spectrum of 10⁻³M triphenylphosphine 1 in 1, 2-dichloroethane.

Export to PPT

Close

Figure 5

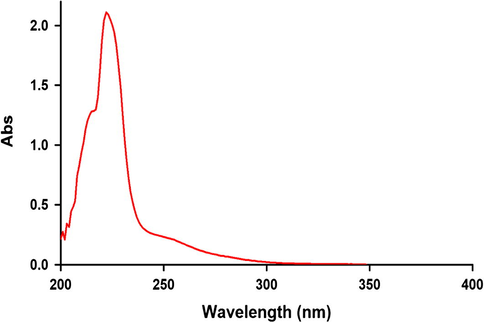
The UV spectrum of 10⁻³M di-tert-butyl acetylenedicarboxylate 2c in 1, 2-dichloroethane.

Export to PPT

Close

Figure 6

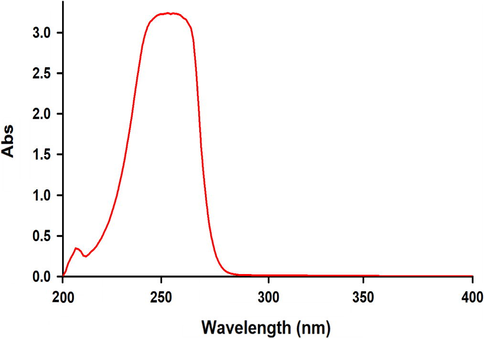
The UV spectrum of 10⁻³M 2-hydroxybenzimidazole 3 in 1, 2-dichloroethane.

Export to PPT

Close

Figure 7

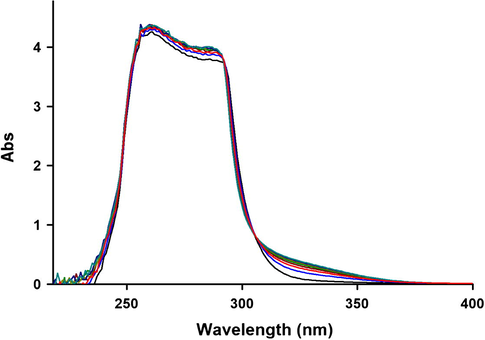
The UV spectra of the reaction between 1, 2c and 3 with 10⁻³M concentration of each compound as reaction proceeds in 1, 2-dichloroethane with 10 mm light-path cell for generation of 4 (4c).

Export to PPT

For each kinetic experiment, the reaction kinetics was followed by plotting UV absorbance against time at 12.0 °C in 1,2-dichloroethane. Fig. 8 shows the absorbance change (dotted line) versus time for the 1:1:1 addition reaction between compounds 1, 2c and 3 at 12.0 °C. Using the original experimental absorbance versus time data provided a second-order fit curve (solid line) by the software associated with the UV instrument (Schwartz and Gelb, 1978) that fits exactly the experimental curve (dotted line) (Fig. 9). This result indicates that the reaction between triphenylphosphine 1, di-tert-butyl acetylenedicarboxylate 2c and 3 follows second-order kinetics. The second-order rate constant (k₂) is then automatically calculated using a standard equation (Schwartz and Gelb, 1978; Okubo et al., 1989) within the program at 12.0 °C. It is reported in Table 11.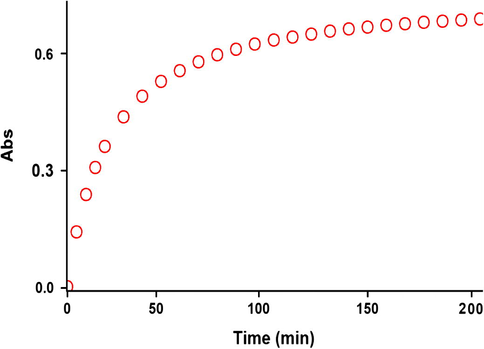

Close

Figure 8

The experimental absorbance changes (dotted line) against time at 330 nm for the reaction between compounds 1, 2c and 3 at 12.0 °C in 1, 2-dichloroethane.

Export to PPT

Close

Figure 9

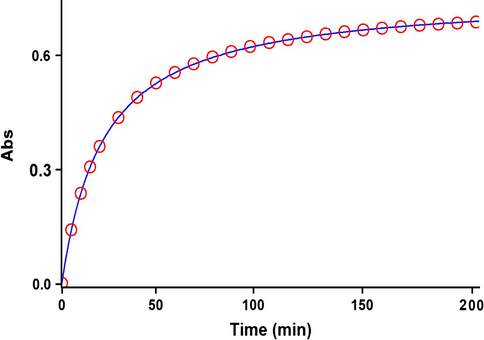
Second order fit curve (solid line) accompanied by the original experimental curve (dotted line) for the reaction between compounds 1, 2c and 3 at 330 nm and 12.0 °C in 1, 2-dichloroethane.

Export to PPT

Furthermore, kinetic studies were carried out in continuation of experiments with different concentrations (5 × 10⁻³ M and 7 × 10⁻³ M). As expected, the second-order rate constant was independent of concentration and its value was the same as in the previous experiment.

3.3 Effect of solvents and temperature

To determine the effect of change in temperature and solvent environment on the rate of reaction, it was elected to perform various experiments at different temperatures and solvent polarities but otherwise under the same conditions as for the previous experiment. For this purpose, ethyl acetate with dielectric constant six was chosen as a suitable solvent since it not only could dissolve all compounds but also did not react with them. The rate constant of the reaction in different solvents and temperatures is given in Table 11. The results show that the rate of reaction in each case was increased at higher temperature. In addition, the rate of reaction between 1, 2c and 3 was accelerated in a higher dielectric constant environment (1, 2-dichloroethane) in comparison with a lower dielectric constant environment (ethyl acetate) at all temperatures investigated. In the temperature range studied, the dependence of the second-order rate constant (ln k₂) on reciprocal temperature is consistent with the Arrhenius equation (Fig. 10), giving activation energy of reaction between 1, 2c and 3 from the slope (Table 12).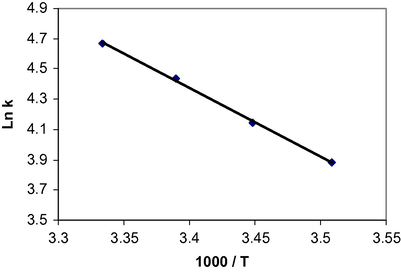

Close

Figure 10

Dependence of second order rate constant (ln k₂) on reciprocal temperature for the reaction between compounds 1, 2c and 3 for generating 4c measured at wavelength 330 nm in 1, 2-dichloroethane in accordance with Arrhenius equation.

Export to PPT

3.4 Effect of concentration

To determine the reaction order with respect to triphenylphosphine 1 and dialkyl acetylene-dicarboxylate 2 (2c), in continuation of experiments, all kinetic studies were carried out in the presence of excess 3. Under this condition, the rate equation may therefore be expressed as:

To determine the reaction order with respect to dialkyl acetylenedicarboxylate 2 (2c), the continuation of experiment was performed in the presence of excess of 1 $(\text{rate}=k_{\text{obs}}^{\prime }{[3]}^{\gamma }{[2]}^{\beta }\text{,}{k}_{\text{obs}}^{\prime }=k_2{[1]}^{\alpha }(2))$ . The original experimental absorbance versus time data provide a pseudo first order fit curve at 330 nm, which exactly fits the experimental curve (dotted line).

As a result since γ = 0 (as determined previously), it is reasonable to accept that the reaction is first order with respect to compound 2 (2c) (β = 1). Because the overall order of reaction is 2 (α + β + γ = 2) it is obvious that α = 1 and the reaction order with respect to triphenylphosphine 1 must be equal to one. This observation was obtained also for reactions between (1, 2b and 3) and (1, 2a and 3) for generating 4b and 4a, respectively. Based on the above results, a simplified proposed reaction mechanism is shown in Fig. 11.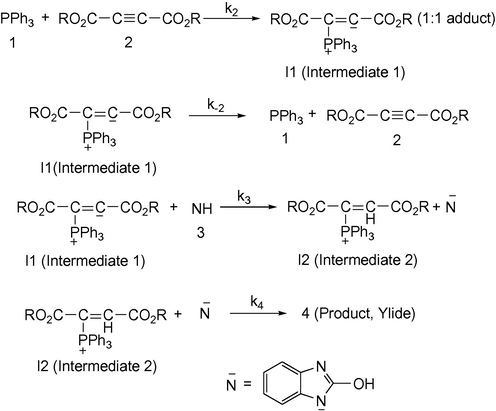

Close

Figure 11

Proposed mechanism for the reaction between 1, 2 (2a, 2b or 2c) and 3 for generation of phosphorus ylides 4a–c.

Export to PPT

The experimental results indicate that the third step (rate constant k₃) is possibly fast. In contrast, it may be assumed that the third step is the rate determining step for the proposed mechanism. In this case the rate law can be expressed as follows:

So the rate of low becomes: $\mathit{rate}=\frac{k_2{k}_3[1][2][3]}{k_{-2}}$

The final equation indicates that the overall order of reaction is three which is not compatible with experimental overall order of reaction (= two). In addition, according to this equation, the order of reaction with respect to 2-hydroxybenzimidazole 3 is one, whereas it was actually shown to be equal to zero. For this reason, it appeared that the third step is fast. If we assume that the fourth step (rate constant k₄) is the rate-determining step for the proposed mechanism, in this case, there are two ionic species to consider in the rate determining step, namely phosphonium ion (I₂) and 2-hydroxybenzimidazole (N⁻). The phosphonium and 2-hydroxybenzimidazole ions, as we see in Fig. 11, have full positive and negative charges and form very powerful ion- dipole bonds to 1,2-dichloroethane, the high dielectric constant solvent. However, the transition state for the reaction between two ions carries a dispersed charge, which here is divided between the attacking 2-hydroxybenzimidazole and the phosphonium ions. Bonding of solvent (1, 2-dichloroethane) to this dispersed charge would be much weaker than to the concentrated charge of 2-hydroxybenzimidazole and phosphonium ions. The solvent thus stabilizes the species ions more than it would the transition state, and therefore E_a would be higher, slowing down the reaction. However, in practice, 1, 2-dichloroethane speeds up the reaction and for this reason, the fourth step, which is independent of the change in the solvent medium, could not be the rate determining step. Furthermore, the rate law of formation of the product (fourth step) for a proposed reaction mechanism with application of steady state assumption can be expressed by: $$\mathit{rate}=k_4[I_2][N^{-}]$$ By application of steady state for [I⁻] and [N⁻], and replacement of their values in the above equation, the following equation is obtained:

4.1 Effect of structure of dialkyl acetylenedicarboxylates

To confirm the above observations, further experiments were performed with diethyl acetylenedicarboxylate 2b and dimethyl acetylenedicarboxylate 2a, respectively, under the same conditions used in the previous experiments. As can be seen from Table 11 the behavior of diethyl acetylenedicarboxylate 2b and dimethyl acetylenedicarboxylate 2a is the same as for the di-tert-butyl acetylenedicarboxylate 2c with respect to the reaction with triphenylphosphine 1 and 2-hydroxybenzimidazole 3. The rate of the former reactions was also accelerated in a higher dielectric constant environment and with higher temperatures; however, these rates under the same condition are approximately 7–12.00 times more than reaction in the presence of di-tert-butyl acetylenedicarboxylate 2c (Tables 11). It seems that both inductive and steric factors for the bulky alkyl groups in 2c tend to reduce the overall reaction rate (see Eq. (9)). In the case of dimetyl acetylenedicarboxylate 2a, the lower steric and inductive effects of the dimethyl groups exert a powerful effect on the rate of reaction.