Translate this page into:
Modeling and computational framework of radiative hybrid nanofluid configured by a stretching surface subject to entropy generation: Using Keller box scheme
⁎Corresponding author. mohamed.reda@fue.edu.eg (Mohamed R. Ali)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract

Abstract
This study examines the characteristics of the velocity, thermal field and entropy profiles for hybrid nanofluid flow passing through a starching sheet with thermal radiation. The carbon nanotube (SWCNT and MWCNT) are used as a nanoparticles with Cattaneo-Christov (C—C) heat flux. Ethylene glycol is utilized as a base fluid in this case. To achieve an improved solution, the fluid flow over the geometric properties is designed using highly non-linear PDEs, and the governing equations must be converted into dimensionless non-similar equation systems using the highly efficient well-known Keller-box scheme in computational software MATLAB. The practical feasibility of these solutions is determined by the range of the controlling parameters. The velocity distribution reduces as the magnetic parameter estimate increases, however, the temperature field and entropy production increase as the magnetic parameter fluctuation esclates. As the slip parameter is increased, the velocity field diminish. The thermal field is enhanced for rising the radiation parameter, and the entropy profile is boosted for increasing Brinkman parameter values. The findings of this research might have a significant impact on industries where local cooling and heating via impingement jets are needed in electronic devices, heat sinks, drying technologies, and so on. To the best of the authors' knowledge, this is the first effort to employ a hybrid nanofluid to analyze entropy formation due to magnetohydrodynamics flow over a starching sheet.
Keywords
Hybrid nanofluid
(Carbon nanotube
Ferro)
Ethylene glycol base fluid
Thermal radiation
Entropy generation
Mathematical physics
Keller Box method
MATLAB
Nomenclature
- Symbols
-
Name with SI Unit
-
Components of velocity
-
Spatial coordinates
-
Mean absorption coefficient
-
Time of hybrid nanofluid
-
Stefan Boltzmann constant
-
Temperature of surface
-
Temperature of fluid
-
Velocity slip factor
-
The density of hybrid nanofluid
-
Initial velocity parameter
-
Porosity of sheet
-
Density
-
Thermal conductivity
-
Thermal conductivity of hybrid nanofluid
-
The viscosity of hybrid nanofluid
-
Dynamic viscosity
-
Heat capacitance
-
Heat capacity of hybrid nanofluid
-
Nanoparticles volume fraction
-
Prandtl number
-
Unsteadiness parameter
-
Magnetic parameter
-
Temperature gradient
-
Mass transfer parameter
-
Thermal diffusivity parameter
-
Thermal radiation parameter
-
Relaxation time parameter
-
Velocity slip parameter
-
Biot number
-
Single-walled carbon nanotube
-
Skin friction coefficient
-
Local Nusselt number
-
Column matrices
-
Row matrices
-
Wall heat flux
-
Shear stress tensor
-
Dimensionless entropy generation
-
Stream function
-
Initial stretching rate
-
Iron oxide (Ferro)
-
Component of deformation rate
-
Multi-walled carbon nanotube
-
Hybrid plastic dynamic viscosity
-
Yield stress
-
Product of deformation rate component
-
Critical value
1 Introduction
Nanoliquid is extremely crucial to researchers because of its increased heat transfer rates, which have substantial technological and manufacturing applications. Hybrid nanofluids are a form of fluid in which two or more metal particles are distributed in the base fluid. When contrasted to typical single-suspended fluids, this novel kind of nanofluid has exhibited intriguing advances in heat-transmitting qualities, in addition to thermo-physical and hydrodynamic properties. Hybrid nanofluids have a wide variety of implimentations in heat transmission, including transport, engineering, and biomedical science. The deferment of multiple nanomaterials in a base fluid mixture can be exploited to generate a hybrid nanofluid. Most natural activities are inextricably linked to nonlinearity, which is exceedingly difficult to resolve. It frequently requires irregular answers utilizing diverse strategies including numerical, approximation, or systematic ways to present an appropriate solution to the problem. Choi (Choi and Eastman, 1995) developed the theory of nanofluid. Kang et al. (Kang et al., 2006) introduced the new area of heat transfer and thermal conductivity is larger than that of single nanomaterials. The effects of a nanofluid along a curved channel containing nanoparticles and compliant walls were examined by Nadeem and Maraj (Nadeem and Maraj, 2014). Shaiq and Maraj (Shaiq and Maraj, 2019) scrutinized the significance of a magnetic field on a curved surface using a carbon nanotube. Maraj et al. (Maraj et al., 2018) studied the outcomes of nanoparticles with nanofluid and viscosity of nanoparticles. Maraj and Nadeem (Maraj and Nadeem, 2016) investigated the theoretical study of nanofluids in the occurence of heat radiation and nanoparticles in a channel. Maraj et al. (Maraj et al., 2022) introduced the MHD flow of a hybrid nanofluid including heat radiation and nanoparticles through a porous media. Li et al. (Li et al., 2020) developed the simulation of nanofluids containing motile microorganisms with bioconvection. Farooq et al. (Farooq et al., 2021) studied the stagnation point of nanoliquid in a rotating cylinder with an electromagnetic field. The free convectional flowing of hybrid Maxwell-based nanofluid via a channel generated by dual vertical plates has been recognized by Ahmad et al. (Ahmad et al., 2020). Hussanan et al. (Hussanan et al., 2020) estimated the enhancement of thermal transmission in non-Newtonian viscous plastics dependent flow across a sheet. Ghalambaz et al. (Ghalambaz et al., 2019) disclosed the movement and thermal transport of hybrid nanofluid in a compound shaped covered through a permeable Chanel. Thermal radiation has also performed a major role in the regulation of the thermal transfer process in the polymer industry. In a rotating phase, Chamkha et al. (Chamkha et al., 2019) witnessed the thermal transfer and the magneto-hydrodynamic motion of a hybrid nanofluid among two sheets. Waqas et al. (Waqas et al., 2023) investigated the thermal transfer of the hybrid nanofluid through the numerical computational impact. Aziz et al. (Aziz et al., 2021) investigated Powell–Eyring water nanofluid, stream, convection thermal transfer, and volumetric entropy production. Zainal et al. (Zainal et al., 2020) investigate the flowing and thermal transmission kinds with a base of water nanofluid on a sheet. Rosca et al. (Roşca et al., 2020) provided the application of mathematical results for problems with the viscous kinematics flow of hybrid nanoparticles over a porous, non-linear, stretching sheet with a non-linear thermal radiation effect. The flow of a nanofluid in the occurence of nanoparticles and heat transfer was scrutinized by Muhammad et al. (Muhammad et al., 2021). Muhammad et al. (Muhammad et al., 2021) observed the numerical structure of a hybrid nanofluid consisting of nanoparticles and base fluid flowing past a curved sheet. Muhammad et al. (Muhammad et al., 2021) looked at the mixed convective flow of a hybrid nanofluid that included heat radiation and a carbon nanotube. Muhammad et al. (Muhammad et al., 2021) investigated the heat transfer of nanofluids and hybrid nanofluids across porous media. Hayat et al. (Hayat et al., 2021) explored hybrid nanofluids formed by combining convective and entropy production over a sheet. MHD focuses on the magnetic properties of electrical current fluids, like salt water, fluid metals, plasmas, and electrolytes. Magnetic fields can generate the force of Lorentz in a spinning fluid. It reduces the mobility of liquids and increases the concentration and temperature of nonmaterial. The role of the electromagnetic field is also important in the delayed separation of boundary layers MHD is also important in fields such as drug storing, manufacturing, mechanics, chemistry, and iron and steel, where it is used to treat cancer, asthma, cardiovascular, gastric drugs, electrodynamics cell division, optical transposable elements, magnetic properties resonance, copper wire stiffening, and optical devices. Nasir et al. (Nasir et al., 2020) compared the importance of heat transfer and thermal production/absorption of a stable MHD stagnation point water-base dater-based nanofluid over the cylinder. Tian et al. (Tian et al., 2021) identified the mixed convective thermal transmission as a combination of forced and natural convection. Biswas et al. (Biswas et al., 2021) illustrated an approach to improve thermal transport via porous materials subjected to thermal radiation during the MHD flow of the nanofluid. Daniel et al. (Daniel et al., 2019) studied the importance of MHD flow with convective properties of nanofluid. Daniel et al. (Daniel et al., 2017) introduced the thermal radiation influence of MHD and hybrid nanofluids. Daniel and Daniel (Daniel and Daniel, 2015) scrutinized the significance of heat radiation on a sheet-based MHD flow nanofluid. Daniel et al. (Daniel et al., 2017) analyzed the significance of entropy framework of nanofluid flow with heat radiation. Daniel et al. (Daniel et al., 2018) studied the upshot of MHD on hybrid nanofluid flow past through a variable thickness sheet. Daniel et al. (Daniel et al., 2017) introduced the nanofluid framework using MHD flow and stretch geometry heat transfer calculations. Using a chemical reaction sheet, Daniel et al. (Daniel et al., 2019) observed the effect of MHD with heat transfer in nanofluid.
The current research's main goal is to assess the relevance of a Ferro-based hybrid nanofluid including nanoparticles such as (SWCNT, MWCNT, and Fe3O4) and the base fluid ethylene glycol across a stretched sheet. The thermal radiation and Cattaneo-Christov (C—C) heat are applied to the current flow problem. To obtain the numerical and graphical results of the current investigation we use Bvp4c solver with the Keller box approach in the computational tool MATLAB. The different graphical outcomes are generated to deliberate the physical trend of prominent physical flow parameters via momentum profile, thermal profile, and entropy generation profile. The velocity field diminshies with rising magnetic parameter estimations, but the thermal field escalates with growing magnetic parameter values. The increasing variations of the velocity slip parameter declined the velocity profile and increased the thermal distribution profile. The current investigation can be expanded in the future to incorporate thermal radiation, entropy production, thermal conductivity, Cattaneo-Christov heat flow theory, and chemical processes. Moreover, the characteristics mentioned above might be added to other non-Newtonian models to examine their influence. There is always the possibility of carrying out practical examinations of such theoretical research. Furthermore, as a recommendation for future research in these domains, physical characteristics like density, viscosity, thermal conductivity, and so on are temperature dependent, which occurs when there is a considerable temperature differential inside the fluid.
2 Mathematical description
The flow of a two-dimensional hybrid nanofluid with thermal radiation and Cattaneo-Christov heat flux across a starching sheet was assumed in the current investigation. We also covered the consequences of entropy creation and slip effects in this section. Here we use the Ethylene Glycol
base fluid
as nanoparticles. Hybrid nanofluid flow is developed by stretching a sheet with
magnetic field strength embedded. The magnetic field is applied in the transverse direction of the surface. The velocity of the fluid is low due to the occurence of a magnetic field, hence the Ohmic dissipation and joule heating impacts are ignored. Here
is effective stretching rate and
indicates the initial stretching rate. Fig. 1a depicts the geometry of flow model.
Flow description of the problem.
The hybrid plastic dynamic viscosity is symbolized by , the yield stress denoted by , are component of deformation rate, which is a product of the deformation rate component and critical value .
The key assumptions of the current flow model are listed here:
-
The problem of the two-dimensional hybrid nanofluid flow with thermal radiation is studied.
-
The nanoparticles and Ethylene Glycol base fluid are used here.
-
The Cattaneo-Christov heat flux theory is highlighted.
-
The entropy generation effect is also investigated here.
-
The stretching surface shape geometry is analyzed.
-
Here we use the Keller box method to obtain numerical and graphical outcomes of prominent parameters
The non-uniform velocity with the surface creates a flow (Jamshed and Aziz, 2018):
As the incompressible Casson nanofluid equation is (Oyelakin et al., 2016; Mukhopadhyay et al., 2013):
The vector forms of the governing equations are addressed as:
The major equations are (Mustafa and Khan, 2015):
Here is constant in thermal relaxation factor is , are velocities components in x-axis and y-axis direction. Here is the time of the hybrid nanofluid; the velocity slip factor here is the initial velocity parameter and the porosity of the sheet.
These are the boundary conditions:
The following formula is used to determine the radiative heat flow (Brewster, 1992):
In equation (9) the Stefan Boltzmann constant
and the mean absorption coefficient are
. The thermal difference inside the flow is assumed that
may be extended as a Taylor series around
. Here we use only linear terms.
From equations (9) and (10):
Solving the main PDEs (05–08), here in analyze stream function as:
Using Eq. (12) and creating Table 1, the main PDEs converted into ODEs:
Properties
Nanofluid
Heat capacity
Thermal conductivity
Viscosity
Density
Properties
Hybrid nanofluid
Heat capacity
Thermal conductivity
Viscosity
Density
With
The prominent flow parameters are:
Parameter values
Parameter name
Notation
Unsteadiness parameter
Magnetic parameter
Relaxation time parameter
Prandtl number
Thermal diffusivity parameter
Thermal radiation parameter
Mass transfer parameter
Velocity slip parameter
Biot number
Brinkman number
Temperature gradient
Reynolds number
3 Outcomes of the problem by Keller-box method
Because Eqs. (13)–(14) are non-linear, closed-form values are difficult to obtain. As a result, using the Keller-box technique, a finite-difference methodology, the equations with (15) are numerically resolved. Keller (Keller, 1971) devised the approach. This approach has been demonstrated to be very effective for parabolic issues. We employed the strategy provided by Cebeci and Pradshaw (Cebeci and Bradshaw, 2012), which has been proven to be particularly suited to dealing with non-linear situations and easily taken to numerically solve any kind of order. Fig. 1b shows the flow pattern of the given problem. The (KBM) Keller box method's main phases for obtaining approximate methods are as follows:
-
Convert the provided first-order ordinary differential equations to a system.
-
Simplified ODEs should be written in finite differences.
-
Linearize the algebraic equations and express them in vector form employing Newton's approach.
-
Use the block upper triangular elimination method to solve the linear system.
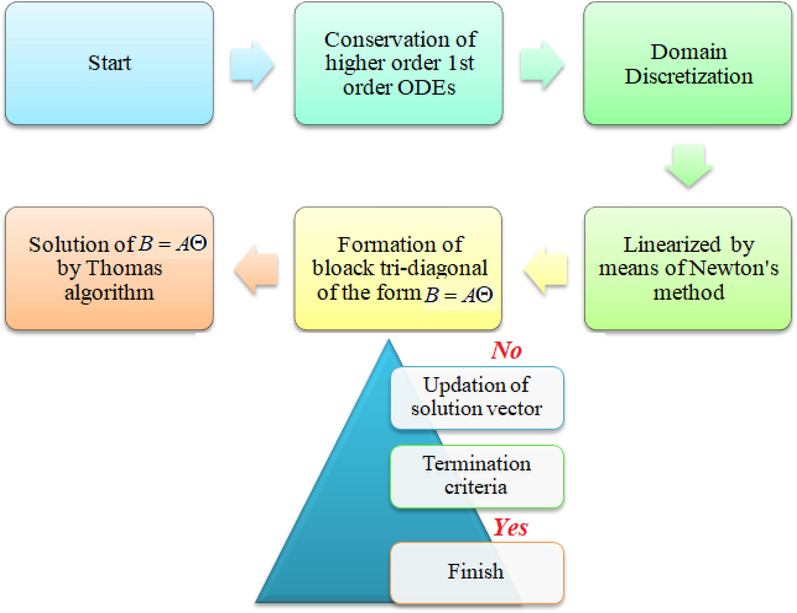
- KBM flow chart.
Here the 1st step of the method is to transfer ODEs (13)–(14) into 1st-order ODEs:
With
As
The ODEs (16)–(18) are transferred into the non-linear algebraic form:
In the above (i + 1) iteration, so
By sub Eqs. (20)–(22) we get
Here
Finally, the boundaries are:
The linear Eqs. (24)–(25) in matrix form:
Here, is the block tri-diagonal matrix which is denoted by the size of the block . The column matrices are symbolized by . The row of matrices is denoted by . To explain the linear scheme the LU factorization method can be used.
The physical quantities are:
Where
The results of physical quantities:
4 Entropy generation analysis
The mathematical model with entropy generation is written as (Keller, 1971):
The dimensionless entropy generation is written as:
The dimensionless form of entropy can be written by using Eq. (12).
Where
5 Results and discussion
In this section, we investigated the graphical and numerical findings of prominent flow parameter via momentum profile, thermal profile, and entropy profile via a well-known numerical approach (KBM) Keller box method in the well Known software computational MATLAB. The significance of the magnetic parameter
via the velocity distribution
is seen in Fig. 2. The dimensionless velocity profile
decreased with the
increases. According to the Lorentz force, the magnetic field introduces a retarding body force that controverts the direction of the external magnetic field. When the magnetic parameter amount is higher, the retarding body is continuously on the rise, and the dimensionless velocity drops. Furthermore, when the magnetic field rises, the extent of the boundary layer declines. Fig. 3 examines the characteristics of
The velocity field
the velocity field
is decreased for the increasing value of the velocity slip parameter
for various shape factors of nanoparticles
. Fig. 4 reveals the characteristics of the volumetric fraction of nanoparticles
via velocity profile
. The velocity field
declined for the increasing magnitude of
for various shape factors of nanoparticles with
and base fluid is
ethylene glycol. Fig. 5 shows the impact of the temperature profile
on the magnetic parameter
. We analyze that the
is enhanced for the booming variations of the
. Fig. 6 characterizes the consequence of slip parameter
against the temperature filed
. This diagram shows how raising the
improves temperature filed
. Fig. 7 deliberates the features of radiation parameter
on the thermal filed
. It is observed that the
rises with an improvement in
various shape factors of nanoparticles with hybrid particles and the base fluid is
ethylene glycol. Fig. 8 includes temperature distribution filed
against
when the curvature parameter is used for various form variables of nanoparticles in both instances with
and base fluid is ethylene glycol. It is found that temperature distribution filed
a curve goes up with enhances in the magnitude of
. Fig. 9 illustrates the impact of
various shape factors of nanoparticles with hybrid particles and base fluid ethylene glycol. The temperature distribution filed
boosted by increment in the values of
.The stimulus of
on
is displayed in Fig. 10. It can be detected from the figure that the enhanced
refuses the temperature distribution filed
for various shape factors of nanoparticles with the base fluid being ethylene glycol.Fig. 11 shows that the thermal profile is a higher magnitude for Lamina
and a low magnitude for the sphere
.The importance of
on
is seen in Fig. 12. As the entropy distribution filed
improves with mounting magnitudes of the magnetic parameter. This is owing to the Lorentz force, which is a resistance force that crosses the fluid motion, causing heat to be produced. As a result, as the magnetic field becomes larger, both the boundary layer thickness and the entropy distribution of filed
boundary layer increase. The outcomes of entropy distribution filed
for larger velocity slip
are addressed in Fig. 13. It is perceived that the entropy distribution filed
dwindles for higher velocity slip parameter
for various shape factors of nanoparticles with hybrid nanofluid and base fluid is ethylene glycol. Inspiration of the volumetric fraction of nanoparticles
on the entropy distribution filed
is disclosed in Fig. 14. It is predicted that the entropy distribution filed
can be lowered by increasing the flow behavior of the volumetric fraction of nanoparticles
for various shape factors of nanoparticles with hybrid particles and base fluid is ethylene glycol. Fig. 15 is prepared to interpret the deviation in entropy distribution filed
for Reynolds number
for various shape factors of nanoparticles with hybrid nanoparticles and base fluid is ethylene glycol. From the curves of entropy, it is depicted that the entropy distribution filed
boosted up with a larger Reynolds number
. The variation of entropy distribution filed
with Brinkman number
is reported in Fig. 16. It is interpreted that the entropy distribution filed
increased for larger Brinkman numbers
for various shape factors of nanoparticles with
and base fluid is ethylene glycol. Fig. 17 shows the variation of streamlines when the
for
. Fig. 18 analyzes the estimations of streamlines when
for
. Fig. 19 studied the impacts of streamlines when the magnetic parameter
for
. Fig. 20 investigates the aspects of streamlines when
for
. Table 1 shows the physical characteristics of nanofluid and hybrid nanofluid like as density, thermal conductivity, viscosity, and heat capacity. Table 2 displays the experimental magnitudes of nanoparticles like Carbon nanotube (SWCNT & MWCNT), Ferro (Fe3O4), and base fluid ethylene glycol. Table 3 analyzed the shape factor including such (brick sphere, cylinder, hexahedron, tetrahedron,column, platelet, and lamina). Table 4 shows the comparison of the Pr over the Nusselt number for the current fluid model. It shows good validations between the old and current frameworks.
Findings of
on velocity field for
.

Findings of
on velocity field for
.

Findings of
on velocity field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on heat field for
.

Findings of
on entropy field for
.

Findings of
on entropy field for
.

Findings of
on entropy field for
.

Findings of
on entropy field for
.

Findings of
on entropy field for
.

Variation of streamlines when
for
.

Variation of streamlines when
for
.

Variation of streamlines when
for
.

Variation of streamlines when
for
.
Properties
Density
Heat Capacity
Thermal Conductivity
Electrical Conductivity

5180
670
9.7

2600
425
6600
–

1600
796
3000
–

1114
2415
0.2525
Geometrical appearance
Shape Factor

(Brick)3.7

(Sphere)3.0

(Cylinder)4.9

(Hexahedron)3.7221

(Tetrahedron)4.0613

(Column)6.3598

(Platelet)5.7

(Lamina)16.1576
Pr
Ishak et al. (Ishak et al., 2009)
Abolbashari et al. (Abolbashari et al., 2014)
Das et al. (Das et al., 2015)
Jamshed & Aziz (Jamshed and Aziz, 2018)
Current work
0.7
0.8086
0.80863135
0.80876122
0.80876181
0.80876182
1.0
1.0000
1.00000000
1.00000000
1.00000000
1.00000000
3.0
1.9236
1.92368259
1.92357431
1.92357420
1.92357421
7.0
3.0722
3.07225021
3.07314679
3.07314651
3.07314652
10.0
3.7006
3.72067390
3.72055436
3.72055429
3.72055430
6 Concluding remarks
In the current computational and numerical investigation we investigated the significance of thermal radiation on hybrid nanofluid having nanoparticles and base fluid ethylene glycol passing through a starching sheet. The outcomes of Cattaneo–Christov heat theory and entropy generation are also studied here. We use the Keller box numerical technique in the computational tool MATLAB to find the outcomes of prominent flow parameters via momentum profile, thermal field, and entropy profile. The main results of the current framework are listed here.
-
The velocity field is declined when the velocity slip parameter is enhanced.
-
For an enhanced magnitude of magnetic parameter and a volumetric proportion of nanoparticles, the velocity distribution field decreases.
-
The temperature distribution field is improved for the advanced values of the thermal radiation parameter and .
-
The thermal field is increased for the growing estimations of thermal relaxation parameter.
-
The entropy generation field is reduced for the raising magnitude of and velocity slip parameter.
-
The entropy generation field is boosted up for the growing magnitudes of both parameters Brinkman number and .
-
The main application of the currently analyzed hybrid nanofluid in neurological diseases is because carbon nanotubes are more useful for this.
-
Because of the particle's use in engineering and manufacturing for expanding and contracting shells, such as packaging, sheet polymerization, glass fiber production, bundle wrapping, hot roll, metallic packages, and aluminum bottles industrial production, wire roll, parabolic difficult surface collectors, cooling of thermal reactors, and so on, the investigation oftwo-dimentional flowing over a sheet has been conducted. The proposed problem findings are used to increase heat transfer in a variety of liquids by utilizing nanoparticles and phenomena such as nonlinear thermal radiation and Cattaneo-Christov heat flux.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol.. 2014;267:256-267.
- [Google Scholar]
- Mathematical modeling of (Cu− Al2O3) water-based Maxwell hybrid nanofluids with Caputo-Fabrizio fractional derivative. Adv. Mech. Eng.. 2020;12(9) 1687814020958841
- [Google Scholar]
- Entropy analysis of Powell-Eyring hybrid nanofluid including the effect of linear thermal radiation and viscous dissipation. J. Therm. Anal. Calorim.. 2021;143(2):1331-1343.
- [Google Scholar]
- Effects of half-sinusoidal nonuniform heating during MHD thermal convection in Cu–Al2O3/water hybrid nanofluid saturated with porous media. J. Therm. Anal. Calorim.. 2021;143(2):1665-1688.
- [Google Scholar]
- Thermal radiative transfer and properties. John Wiley & Sons; 1992.
- Physical and computational aspects of convective heat transfer. Springer Science & Business Media; 2012.
- Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv.. 2019;9(2):025103
- [Google Scholar]
- Choi, S.U., Eastman, J.A., 1995. Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne National Lab.(ANL), Argonne, IL (United States).
- Numerical study of Entropy analysis for the electrical unsteady natural magnetohydrodynamic flow of nanofluid and heat transfer. Chin. J. Phys.. 2017;55(5):1821-1848.
- [Google Scholar]
- Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys.. 2017;55(3):630-651.
- [Google Scholar]
- Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alex. Eng. J.. 2015;54(3):705-712.
- [Google Scholar]
- Entropy analysis in electrical magnetohydrodynamic (MHD) flow of nanofluid with effects of thermal radiation, viscous dissipation, and chemical reaction. Theor. Appl. Mech. Lett.. 2017;7(4):235-242.
- [Google Scholar]
- Impact of thermal radiation on electrical MHD flow of nanofluid over a nonlinear stretching sheet with variable thickness. Alex. Eng. J.. 2018;57(3):2187-2197.
- [Google Scholar]
- Stratified electron magnetohydrodynamic flow of nanofluid supporting convective role. Korean J. Chem. Eng.. 2019;36(7):1021-1032.
- [Google Scholar]
- Thermal radiation on unsteady electrical MHD flow of nanofluid over a stretching sheet with chemical reaction. Journal of King Saud University-Science. 2019;31(4):804-812.
- [Google Scholar]
- Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl. Math. Mech.. 2015;36(12):1593-1610.
- [Google Scholar]
- Thermally radioactive bioconvection flow of Carreau nanofluid with modified Cattaneo-Christov expressions and exponential space-based heat source. Alex. Eng. J.. 2021;60(3):3073-3086.
- [Google Scholar]
- Investigation on thermophysical properties of Tio2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol.. 2017;322:428-438.
- [Google Scholar]
- Free convection heat transfer of MgO-MWCNTs/EG hybrid nanofluid in a porous complex-shaped cavity with MHD and thermal radiation effects. Int. J. Numer. Meth. Heat Fluid Flow 2019
- [Google Scholar]
- FDM analysis for nonlinear mixed convective nanofluid flow with entropy generation. Int. Commun. Heat Mass Transfer. 2021;126:105389
- [Google Scholar]
- Heat transfer enhancement in sodium alginate-based magnetic and non-magnetic nanoparticles mixture hybrid nanofluid. Physica A. 2020;550:123957
- [Google Scholar]
- Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica. 2009;44(4):369-375.
- [Google Scholar]
- Cattaneo-Christov based study of $${\text {TiO}} _2 $$ TiO 2–CuO/EG Casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl. Nanosci.. 2018;8(4):685-698.
- [Google Scholar]
- Estimation of thermal conductivity of nanofluid using experimental effective particle volume. Exp. Heat Transfer. 2006;19(3):181-191.
- [Google Scholar]
- A new difference scheme for parabolic problems. In: Numerical Solution of Partial Differential Equations–II. Academic Press; 1971. p. :327-350.
- [Google Scholar]
- A numerical exploration of modified second-grade nanofluid with motile microorganisms, thermal radiation, and Wu’s slip. Symmetry. 2020;12(3):393.
- [Google Scholar]
- The extraordinary role of hydrogen possessions and viscosity variation in electrically conducting copper and silver nanoparticles inspired by mixed convection. Int. J. Hydrogen Energy. 2018;43(24):10915-10925.
- [Google Scholar]
- MHD Carbon Nanotubes Gravity-Driven Flow Along a Thermal Sensitive Porous Surface. Arab. J. Sci. Eng. 2022:1-11.
- [Google Scholar]
- Theoretical analysis of entropy generation in peristaltic transport of nanofluid in an asymmetric channel. Int. J. Exergy. 2016;20(3):294-317.
- [Google Scholar]
- Numerical study of Newtonian heating in the flow of hybrid nanofluid (SWCNTs+ CuO+ Ethylene glycol) past a curved surface with viscous dissipation. J. Therm. Anal. Calorim.. 2021;143(2):1291-1302.
- [Google Scholar]
- A comparative study for the convective flow of base fluid (gasoline oil), nanomaterial (SWCNTs), and hybrid nanomaterial (SWCNTs+ MWCNTs) Appl. Nanosci.. 2021;11(1):9-20.
- [Google Scholar]
- Mixed convective slip flow of hybrid nanofluid (MWCNTs+ Cu+ Water), nanofluid (MWCNTs+ Water) and base fluid (Water): a comparative investigation. J. Therm. Anal. Calorim.. 2021;143(2):1523-1536.
- [Google Scholar]
- Melting heat transfer in squeezing flow of base fluid (water), nanofluid (CNTs+ water), and hybrid nanofluid (CNTs+ CuO+ water) J. Therm. Anal. Calorim.. 2021;143(2):1157-1174.
- [Google Scholar]
- Casson fluid flow and heat transfer at an exponentially stretching permeable surface. J. Appl. Mech.. 2013;80(5)
- [Google Scholar]
- Model for the flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv.. 2015;5(7):077148
- [Google Scholar]
- The mathematical analysis for peristaltic flow of a nanofluid in a curved channel with compliant walls. Appl. Nanosci.. 2014;4(1):85-92.
- [Google Scholar]
- MHD stagnation point flow of hybrid nanofluid over a permeable cylinder with homogeneous and heterogeneous reaction. Phys. Scr.. 2020;96(3):035201
- [Google Scholar]
- Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective, and slip boundary conditions. Alex. Eng. J.. 2016;55(2):1025-1035.
- [Google Scholar]
- Inspection of thermal jump conditions on nanofluids with nanoparticles and multiple slip effects. Sci. Rep.. 2022;12(1):1-14.
- [Google Scholar]
- The axisymmetric flow of hybrid nanofluid due to a permeable non-linearly stretching/shrinking sheet with radiation effect. Int. J. Numer. Meth. Heat Fluid Flow 2020
- [Google Scholar]
- Flow and heat transport phenomenon for dynamics of Jeffrey nanofluid past stretchable sheet subject to Lorentz force and dissipation effects. Sci. Rep.. 2021;11(1):1-15.
- [Google Scholar]
- Role of the induced magnetic field on dispersed CNTs in propylene glycol transportation toward a curved surface. Arab. J. Sci. Eng.. 2019;44(9):7515-7528.
- [Google Scholar]
- A techno-economic investigation of 2D and 3D configurations of fins and their effects on heat sink efficiency of MHD hybrid nanofluid with slip and non-slip flow. Int. J. Mech. Sci.. 2021;189:105975
- [Google Scholar]
- Numerical and Computational simulation of blood flow on hybrid nanofluid with heat transfer through a stenotic artery: Silver and gold nanoparticles. Results Phys.. 2023;44:106152
- [Google Scholar]
- MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Meth. Heat Fluid Flow 2020
- [Google Scholar]







