Refractometric study of systems water-poly(ethylene glycol) for preparation and characterization of Au nanoparticles dispersion

1 Introduction

Poly(ethylene glycol), PEG, is a neutral, nonionic, linear polymer that has a well-defined molecular structure and consists of hydrophilic oxygen and hydrophobic ethylene units (Zulauf and Rosenbusch, 1983; Mitchell et al., 1983; Sasahara et al., 1998). PEG of molecular weights of 200–600 g mol⁻¹ is transparent or slightly yellow liquids at room temperature. PEG of molecular weights 1000 and more g mol⁻¹ is white or almost white solids of a wax or paraffin appearance or as a dry powder. They exhibit a high solubility over a wide range of temperatures in water as well as in different types of organic solvents (Aucouturier et al., 1999). Liquid PEG is very hygroscopic, and a hygroscopicity decreases with increasing molecular weight. Density of liquid PEG at 25 °C is in the range from 1.11 to 1.14 g cm⁻³ and density of solid PEG at 25 °C is 1.15 to 1.21 g cm⁻³ (Rowe et al., 2006). Liquid PEG is an important industrial organic solvent and in medical usage because of its favorable properties, such as low vapor pressure, low toxicity, high chemical stability, and low melting temperature (Zhang et al., 2012). PEG has found a wide variety of applications in numerous industrial processes from petroleum, textiles to pharmaceutical and biochemical technologies (Moosavi et al., 2013; Rajulu and Sab, 1998; Yasmin et al., 2011). The possibility of having a wide range of polymers of increasing molar mass makes these compounds particularly interesting for the correlation of thermodynamic properties of polymer solutions or mixtures and the prediction of phase diagrams (Aucouturier et al., 1999). PEG has an important clinical usage due to their low toxicity, too. They are stable, hydrophilic substances that are essentials and nonirritant to the skin. Due to this they are widely used in a variety of pharmaceutical formulations including parenteral, topical, ophthalmic, oral and rectal preparations (Rowe et al., 2006).

Solutions of PEG in water have been used in biochemistry and biochemical engineering to separate and purify biological products, biomaterials, proteins, and enzymes from the complex mixtures in which they are produced (Albertsson, 1986; Hariri et al., 1989; Soane, 1992; Laurence, 1994). PEG of different molecular weights, especially its binary systems with water, is also applied in tissue engineering (Kim et al., 2016; Neumann et al., 2016). They are used as grafting solutions for grafting of new chemical functional groups to surfaces of plasma modified polymer foils (Švorčík et al., 2012). This modification significantly changes surface properties of polymer foils, as a surface chemistry, wettability, polarity, roughness and morphology, which can improve a subsequent adhesion and proliferation of rat vascular smooth muscle cells (Švorčík et al., 2012). Binary systems such as water-glycerin or water-PEG can serve as a dispersion surrounding for preparation of colloidal solution of gold or silver nanoparticles (Siegel et al., 2012; Slepička et al., 2015a).

Some studies of these systems have been already presented (Maisano et al., 1993; Jannelli et al., 1994; Muller and Rasmussen, 1991; Douheret et al., 1997) but only for limited range of temperature or mole fraction. The physical and transport properties of liquid mixtures are very important in understanding the nature of molecular interactions between the molecules of mixtures (Zafarani-Moattar and Tohidifar, 2008) and also affect most separation procedures, such as liquid-liquid extraction, gas adsorption/absorption, and distillation (Zhang et al., 2011; Deng et al., 2006).

Refractive index of binary system water-PEG was studied only sporadic up to now, either for only one molecular weight of PEG, or for only one temperature (Moosavi et al., 2013; Rajulu and Sab, 1998; Silva et al., 2007). But in fact refractive index is an important parameter which can serve as input data for calculation of other physico-chemical properties, like reflectivity or polarizability and molar refraction (Tariq et al., 2009; Jeong et al., 2015). Some parameters of binary systems water-PEG, as refractive index, are important input data for analysis of nanoparticles’ colloidal systems, e.g. for dynamic light scattering (DLS) of dispersion systems, for zeta potential determination and for determination of size and distribution of metal nanoparticles dispersed in solution composed from water and PEG.

Therefore in this work we have studied binary systems of water-PEG of different molecular weights (200, 300, 400, 600, and 1000 g mol⁻¹) and present new data of refractive index as a function of PEG mole fraction and molecular weight in temperature range 283.15–363.15 K. Obtained data were used as a basis for zeta potential analysis and size and distribution determination of gold nanoparticles (AuNPs) dispersed in water-PEG system. The optical properties of AuNPs have been studied by UV–vis spectroscopy (UV–vis), and dimensions of the nanoparticles were studied with transmission electron microscopy (TEM) for comparison of nanoparticle size obtained by DLS method.

2 Material and methods

3 Results and discussion

Obtained results are presented in Figs. 1–4 and Tables 1–6. Fig. 1 represent dependence of average refractive index (n_589.3) for binary systems water-PEG of molecular weights 200 g mol⁻¹ (left) and 600 g mol⁻¹ (right) on the mole fraction of PEG (x₁) in temperature range 283.15–363.15 K as a representative of the lowest and the highest molecular weights measured in all concentration and temperature range. Empty points represent experimental data obtained in this work. The curves in Fig. 1 are correlations of these experimental data by Eq. (3). From Fig. 1 it is clear that the refractive index increases with increasing mole fraction of PEG. It is evident that the dependence is not linear, which proves a strongly non-ideal behavior of this system. This non-ideal behavior of system water-PEG can be caused by the following four effects (Chen et al., 2013; Moosavi et al., 2013; Rajulu and Sab, 1998): (i) approaches during solving, which is for these systems accompanied with volume and enthalpy changes (excess molar volume and excess molar enthalpy); (ii) hygroscopicity of PEG; (iii) interactions between molecules of PEG and water, especially due to the strong H-bond and (iv) molecules of water are “much” smaller in comparison with molecules of PEG because the polymer chains do not stay as linear and strain but it is flexible and creates the “ball” and the water molecules can be placed in cavity in PEG structure (Chen et al., 2013; Moosavi et al., 2013; Rajulu and Sab, 1998). It is also clear from Fig. 1, that the curve for a dependence of refractive index on the mole fraction of PEG (x₁) varies for individual molecular weight of PEG, the higher molecular PEG weight, and the steeper curve. Refractive index (n_589.3) of individual samples decreases with increasing temperature. The curve for system water-PEG 600 for T = 283.15 K does not cover all the concentration ranges due to solidification of samples of higher mole fraction of PEG in measuring cell.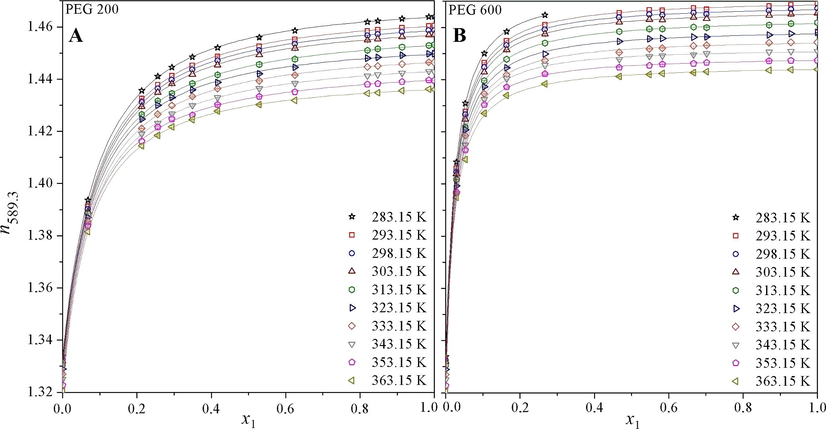

Close

Figure 1

Dependence of refractive index (n_589.3) of system water-PEG of molecular weight (A) 200 g mol⁻¹ (PEG 200) and (B) 600 g mol⁻¹ (PEG 600) on concentration (x₁ means the mole fraction of PEG) in temperature range of 283.15–363.15 K. Individual points are experimental data, and the curves present correlation obtained by Eq. (3).

Export to PPT

Close

Figure 2

Dependence of refractive index (n_589.3) of systems water-PEG of molecular weights 200 g mol⁻¹ (PEG 200), 300 g mol⁻¹ (PEG 300), 400 g mol⁻¹ (PEG 400), 600 g mol⁻¹ (PEG 600) and 1000 g mol⁻¹ (PEG 1000) on concentration (x₁ means the mole fraction of PEG) at temperature 298.15 K. Individual points are experimental data, and the lines present curve obtained by Eq. (3).

Export to PPT

Close

Figure 3

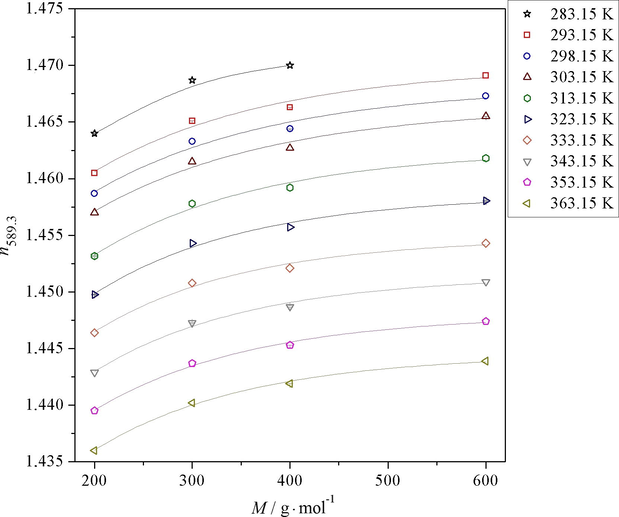
Dependence of refractive index (n_589.3) of systems water-PEG of molecular weight 200 g mol⁻¹ (PEG 200), 300 g mol⁻¹ (PEG 300), 400 g mol⁻¹ (PEG 400) and 600 g·mol⁻¹ (PEG 600) on molecular weight of PEG (M) in temperature range of 283.15–363.15 K. Individual points are experimental data, and the lines present curve obtained by Eq. (4).

Export to PPT

Close

Figure 4

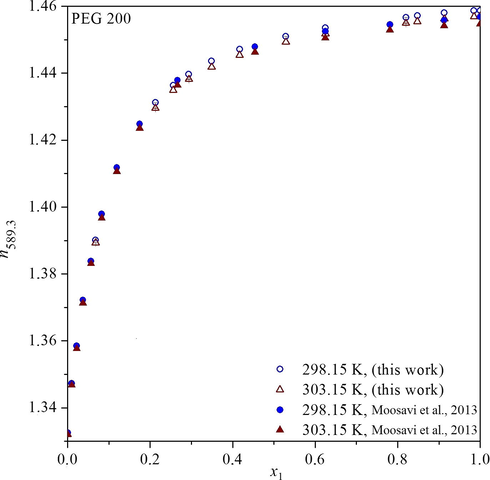
Comparison of refractive index (n_589.3) of system water-PEG of molecular weight 200 g mol⁻¹ for T = 298.15 and 303.15 K. Empty symbols are dated from this work, and full symbols are previously published data (Moosavi et al., 2013).

Export to PPT

Tables 1–5 include parameters A, B, C and D of Eq. (3) which enable to calculate refractive index of tested binary systems at any mole fraction of PEG (x₁) in temperature range of 283.15–363.15 K. The accuracies of these descriptions are presented by their standard deviation (STD) and determination coefficient R² for individual temperatures. Due to the solidification of system water-PEG 1000 in the measuring cell only parameters A, B, C and D of Eq. (3) are presented for interpolation of refractive index (n_589.3) in a very narrow concentration range. All these results confirmed the trend that refractive index increases with increasing concentration of PEG and decreases with increasing temperature.

Study of dependence of refractive index (n_589.3) on molecular weight of PEG (M) was also performed. Fig. 2 shows dependence of refractive index of systems water-PEG of molecular weights of 200 g mol⁻¹ (PEG 200), 300 g mol⁻¹ (PEG 300), 400 g mol⁻¹ (PEG 400), 600 g mol⁻¹ (PEG 600) and 1000 g mol⁻¹ (PEG 1000) on mole fraction of PEG (x₁) at temperature 298.15 K. Individual points are experimental data, and the line presents curve obtained by 3-parameter Eq. (4) (x₁ means the mole fraction of PEG). Fig. 2 clearly shows the strong dependence of refractive index on molecular weight of PEG. Refractive index increases with increasing PEG molecular weight. From Fig. 3 it is clear that dependence is not linear. Parameters a, b and c of Eq. (4) for individual temperatures are summarized in Table 6.

We have also compared experimental data on refractive index obtained in this work with data presented earlier (Moosavi et al., 2013). Fig. 4 shows a very good agreement of the data (empty points) with those published previously by other authors (Moosavi et al., 2013, full points).

Obtained data on refractive index have been employed for determination of size and zeta potential AuNPs dispersed in systems water-PEG by DLS method. When we have inputted the correct and accurate experimental data on refractive index (obtained in this work), we obtain the following data on AuNPs size, d (nm) and zeta potential, ζ (mV): for water-PEG 200: d₁ (first fraction) = 0.86 ± 0.04 nm and d₂ (second fraction) = 10.07 ± 0.21 nm, ζ₁ (first fraction) = −10.84 ± 0.56 mV and ζ₂ (second fraction) = −54.40 ± 1.38 mV; for water-PEG 300: d = 13.62 ± 5.67 nm, ζ₁ (first fraction) = −11.35 ± 1.88 mV and ζ₂ (second fraction) = −55.57 ± 9.38 mV; for water-PEG 400: d₁ (first fraction) = 0.98 ± 0.28 nm and d₂ (second fraction) = 7.97 ± 2.92 nm, ζ₁ (first fraction) = −15.61 ± 5.14 mV and ζ₂ (second fraction) = −42.40 ± 3.26 mV. These data correspond with data presented earlier (Slepička et al., 2015a). When the correct and accurate data on refractive index are not input, values for zeta potential are also incorrect and inaccurate, they vary from correct data and have a higher error: for water-PEG 200: ζ = −9.65 ± 6.99 mV; for water-PEG 300: ζ = −6.64 ± 1.28 mV and for water-PEG 400: ζ = −10.36 ± 10.44 mV. These data do not correspond with data presented earlier (Slepička et al., 2015a). Therefore, it is necessary to operate only with correct and accurate input data for determination of properties of AuNPs dispersions.

As stated above, the physico-chemical behavior of water-PEG solutions has a significant influence on the consequent properties of metal nanoparticles (NPs) solutions (Slepička et al., 2015a) and accurate input data are very important for the solution preparation. Therefore after detailed physico-chemical analysis of water-PEG solution we have continued with particular application, the preparation of noble metal-PEG-water solutions and their optical and morphological analysis. For the series of experiments the system of water-PEG 400 was chosen and the direct sputtering into PEG with consequent dilution into water with different ratio water-PEG was applied. The colloidal solutions of prepared gold NPs (AuNPs) showed a significant absorption peak maximum in UV–vis spectra. Noble metal nanoparticle solutions may have a significant application in tissue engineering (Slepička et al., 2015b; Kim et al., 2016; Neumann et al., 2016), as promoters of cell growth (Slepičková Kasálková et al., 2012) or as antibacterial substrates for inhibition of bacteria growth (Slepička et al., 2016; Siegel et al., 2013).

For all prepared samples the changes of absorption peaks (position and size) were observed and analyzed (see Fig. 5). Particle size distribution was increased as it is obvious from the increasing width of the peak. The height of the peak depends on the solution concentration and the characteristics of AuNPs (Slepička et al., 2015a). The optical properties of AuNPs in water-PEG solutions determined with UV spectroscopy for different PEG (200, 400 and 600 g mol⁻¹) are introduced in Fig. 5. The colloidal solutions of prepared AuNPs showed the significant absorption peak maxima in UV–vis spectra by ca 530 nm. The height of the peak depends on the solution concentration (Slepička et al., 2015a). It was proved that the water-PEG concentration affects the size of NPs immediately after preparation (during preparation resp. mixing) significantly, even at the beginning the solutions exhibit similar UV–vis absorbances (Slepička et al., 2015a). As it can be seen from Fig. 5, peak positions for solutions with ratio PEG:H₂O = 1:9 remain stable, and the value of absorbance increases as expected with increasing concentration of AuNPs. The AuNPs concentration increases with increasing exposure (sputtering) time. In this case we have also tried to find the correlation between molecular weights of PEG and sizes of nanoparticles. But our previous and also current results show there is no effect of molecular weight of PEG on nanoparticle size. As we can see the same size of nanoparticles in system water-PEG independently of molecular weight of PEG (Slepička et al., 2015a) has been prepared. It can be caused by two effects: (i) firstly, PEG serves as a steric stabilizer of nanoparticles (Zhang et al., 2016) and its chain length does not play role on nanoparticle size because this chain does not stay straight but they create the ball or clusters around NPs and coated them and these clusters (coatings) seem to be independent on molecular weight of PEG; (ii) the second effect is a concentration of PEG in water which play much important role, because molecules of water play role for electrostatic stabilization of nanoparticles. When water is not present, the colloidal samples of nanoparticles (in only PEG) have got a violet color which presents much more particle size (Slepička et al., 2015a).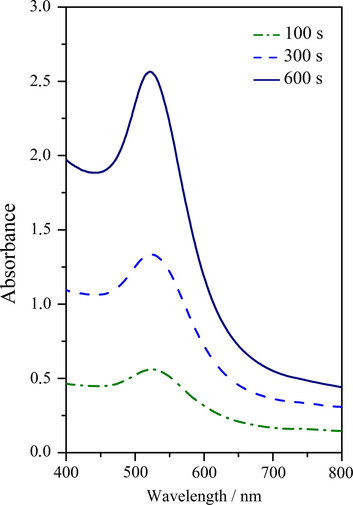

Close

Figure 5

The UV–vis absorption spectra for AuNPs dispersion in water-PEG of molecular weight 400 g mol⁻¹ at a ratio of 1:9. Sputtering times varied in the interval 100–600 s and the samples were prepared at 30 mA.

Export to PPT

The NPs size may be altered by changing of input parameters of plasma device as has been demonstrated earlier (Hatakeyama et al., 2011; Kaneko et al., 2014). Hatakeyama et al., 2011 reported that the working distance does not affect the size and size distribution of AuNPs generated in the capture medium (Hatakeyama et al., 2011). Different approaches for noble metal nanocluster deposition were applied as discussed earlier (Slepička et al., 2015a). Selected TEM images of the NPs prepared under different conditions are shown in Fig. 6. We have chosen two different ratios of water-PEG (1:1, see Fig. 6A and 1:9, Fig. 6B). It is obvious that water-PEG ratio has a significant influence of stability of AuNPs-water-PEG solution and the number of larger agglomerates. These agglomerates of AuNPs larger than 100 nm can be seen in Fig. 6A (ratio 1:1). In Fig. 6B, on the contrary, AuNPs have a spherical shape with uniform distribution. As it is clear from Fig. 6, size of AuNPs prepared in system water-PEG 400 determined by DLS (discussed above) and TEM is in a very good agreement.

Close

Figure 6

TEM images of AuNPs dispersion in the water-PEG of molecular weight 400 g mol⁻¹ obtained by sputtering, prepared at 30 mA and 300 s with ratio of water-PEG: (A) −1:1 and (B) −1:9.

Export to PPT

4 Conclusions

Refractive index of several systems of water-PEG of different molecular weights (M = 200, 300, 400, 600, 1000 g mol⁻¹) was measured. Experiments were performed in temperature range from 298.15 to 363.15 K at atmospheric pressure and at all mole fraction range except PEG of M = 1000 g mol⁻¹. Refractive index increases with increasing mole fraction and with increasing molecular weight of PEG. Refractive index decreases with increasing temperature. Data have been also described by (i) four parameters’ relationship for dependence of refractive index on mole fraction of PEG and (ii) three parameters’ relationship for dependence on molecular weight of PEG. Experimental data obtained in this work were compared with data published previously with a very good agreement. Binary systems of water-PEG show non-ideal behavior. The dependence of refractive index on molar fraction is not linear. This non-ideal behavior of this system can be caused by approaches during solving, by interactions between molecules of water and PEG, especially due to the strong H-bond. Obtained data on refractive index served as an input data for subsequent study of the colloidal systems of AuNPs in dispersion surrounding inclusive water and PEG. It was confirmed that only correct and accurate experimental data on refractive index can yield the correct determination of size and zeta potential of AuNPs in dispersion. The colloidal solutions of prepared AuNPs showed a significant absorption peak maximum in UV–vis spectra by ca 530 nm. The height of the peak depended on the solution concentration and ratio of water-PEG. The size of AuNPs determined by DLS method was confirmed by TEM measurement with very good agreement and for water-PEG ratio 1:9 did not exceed 11 nm. Nanoparticle size is independent of molecular weight of PEG but it is strongly depended on PEG concentration.