Regio- and stereoselectivity of the 1,3-dipolar cycloaddition of azomethine ylides to (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-ones: A combined experimental and theoretical study
⁎Corresponding authors at: Department of Chemistry, Faculty of Applied Science, Umm Al-Qura University, 21955 Makkah, Saudi Arabia. amhfarghaly@uqu.edu.sa (Essam M. Hussein), essam.hussein78@yahoo.com (Essam M. Hussein), saahmed@uqu.edu.sa (Saleh A. Ahmed) saleh_63@hotmail.com (Saleh A. Ahmed)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Functionalized oxindoles and pyrrolizidines form the central structural framework for numerous natural products with extensive biological and pharmacological applications. The requirement for high regio- and stereoselectivity is the main obstacle in the synthesis of such five-membered heterocycles. Multicomponent cycloaddition reactions often provide an efficient and straightforward approach for the preparation of specific regio- and stereoisomers. In this article, the regio- and stereochemistry of the polar [3 + 2]-cycloaddition (32CA) reaction of azomethine ylides prepared by the reaction of isatin derivatives and L-proline with a series of (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-ones was investigated by experimental and theoretical methods. Among the isatin and (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one derivatives, a remarkable inversion of regioselectivity was observed in the 32CA reaction of azomethine ylide generated by the reaction of L-proline and 5-chloroisatin or N-methyl-5-chloroisatin with (E)-5-chloro-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one. The regio- and stereochemical assignment of the structures of the cycloaddition products was determined by one- and two-dimensional (1D&2D) homonuclear and heteronuclear correlation nuclear magnetic resonance spectroscopy. The molecular mechanism as well as the regio- and stereoselectivity of the cycloaddition were investigated by means of global and local reactivity indices and a density functional theory (DFT) and explained in detail on the basis of the transition state stabilities of the reactants.
Keywords
Natural product scaffold
Multicomponent [3 + 2] cycloaddition
DFT
Transition state
Local reactivity
- 1
-
1,3-dipolar cycloaddition
- 2
-
azomethine ylides
- 3
-
stereoselectivity
- 4
-
regioselectivity
- 5
-
DFT-theory
Abbreviations
1 Introduction
The [3 + 2]-cycloaddition (32CA) reactions provide an efficient and straightforward approach to the construction of five-membered heterocycles and very often proceed with high regio- and stereoselectivity (Padwa and Pearson, 2002). Therefore, the intermolecular 32CA reaction of unstabilized azomethine ylides with electron deficient olefins serves as a convenient and efficient protocol for the synthesis of highly functionalized heterocycles such as pyrrolidines and pyrrolizidines containing multiple stereogenic centers in a single step (Dondas et al., 2004).
Functionalized oxindoles and pyrrolizidines serve as the central scaffold for several natural products and represent a class of compounds that exhibit significant biological activity (Monlineux, 1987). Spiropyrrolizidine oxindole species have recently attracted considerable attention due to their abundance in many natural products as well as their broad biological and pharmacological applications (Rajeswaran et al., 1999). In addition, the pyrene moiety is one of the most valuable building blocks for the construction of fluorogenic chemosensors (Weng et al., 2012).
In the last decades, the understanding of the mechanism and underlying principles of the polar 32CA process in addition to selectivity has grown through several studies that have investigated the interplay between theoretical and experimental aspects, although it remains a challenge to this day (Merino et al., 2003). Several mechanisms have been proposed to explain the [3 + 2] cycloadddition (32CA) reaction which has experienced a recent resurgence as indicated by the incredible volume of recent studies reported on the subject (Rios-Gutierrez et al., 2019). First, the 32CA reaction consists of an addition reaction between a three-atom component (TAC) and a multiple bond system and the transformation may proceed under metal-free or metal-assisted conditions (Rios-Gutierrez et al., 2019). The former is a neutral species whose core structure is composed from three nuclei sharing at least 8 electrons. TACs can be geometrically categorized into two types: linear (L-TAC) and bent (B-TAC) geometries. Mechanistically, Huisgen originally proposed that three mechanisms were plausible (i) the positive end of the TAC may react first, and the negative end would then complete the addition; (ii) the negative pole may attack first and then the positive end would complete the addition; or (iii) both charged ends of the dipole may be added concurrently. While mechanisms i and ii proceed via octet 1,2-dipoles and involve zwitterionic intermediate, mechanism iii takes place via sextet 1,3-dipoles and is concerted. Firestone proposed, an alternative stepwise radical mechanism via formation of a diradical intermediate (Rios-Gutierrez et al., 2019). It has been established that the regio- and stereochemistry of 32CA reactions can be controlled either by selecting the appropriate dipole and/or dipolarophile or by controlling the reaction with a catalyst (Yan et al., 2006). Electronic and steric effects are two key factors that can influence the outcome of the regio- and stereoselectivity of such reactions (Bakthadoss and Sivakumar, 2009). Recently, the molecular mechanism and underlying factors affecting regio- and chemoselectivity in 32CA processes have been theoretically investigated using reactivity indices of density functional theory (DFT) (Domingo et al., 2002) and molecular electron density theory (MEDT) (Domingo, 2016).
As a further extension of our ongoing research on 32CA reactions and their utility for the synthesis of novel spiroheterocycles (Hussein and Abdel-Monem, 2011), we now report the results of experimental and theoretical studies on the regio- and stereoselectivity of the 32CA reaction of azomethine ylides (AYs) 3a-c (generated in situ from isatins 1a-c and L-proline (2) with a series of (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one derivatives 4a-d, in order to obtain a series of hitherto unknown new 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidin-2′,3″-indoline]-2,2″-diones and/or 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidin-1′,3″-indoline]-2,2″-diones.
2 Results and discussion
2.1 Synthetic approach
The [3 + 2]-cycloaddition reaction of azomethine ylides (AYs) 3a-c, generated in situ from the reaction of isatin derivatives 1a-c and L-proline (2) in absolute ethanol under reflux, with (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one derivatives 4a-d prepared as dipolarophiles, gave a new series of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones 5a-l and/or 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones 6a-l (Scheme 1).
![Synthesis of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones 5a-l and 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones 6a-l.](/content/184/2022/15/6/img/10.1016_j.arabjc.2022.103855-fig1.png)
- Synthesis of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones 5a-l and 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones 6a-l.
The regioisomeric molar ratio was determined by 1H NMR spectroscopy using C1′—H and C2′—H as distinctive signals for regioisomer 5 and 6, respectively. The reaction was found to be relatively regioselective and stereospecific at the stereogenic centers. The regiochemistry of the reaction was found to be dependent on the chemical structure of both the dipole and the dipolarophile (Table 1). It can be seen from Table 1 that in most cases, regioisomers 5 were obtained as the major products (Table 1, entries 1–7 & 10–12). Surprisingly, in the case of the 32CA reaction of dipoles 3b (generated in situ by the reaction of 5-chloroisatin 1b and L-proline) and 3c (generated in situ by the reaction of N-methyl-5-chloroisatin 1c and L-proline) with (E)-5-chloro-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one (4c), the regiochemistry was reversed and the cycloadducts 6h (Table 1, entry 8) and 6i (Table 1, entry 9) were obtained as the major products. It should be mentioned that the pure regioisomers 5a, 5b, 5d, 5e, 5j, 5l and 6i were obtained by recrystallizing the crude reaction mixture from absolute ethanol. Unfortunately, compounds 5c, 5f, 5g, 5h, 5k and their corresponding regioisomers could not be separated by either recrystallization or column chromatography because they have similar Rf values in different organic solvents.
| Entry | Reactants | Products | Time (h) | Yielda (%) |
Diastereomeric ratio (%) | Regioisomeric ratiob (5:6) |
|---|---|---|---|---|---|---|
| 1 | 1a+2+4a | 5a | 3.5 | 97 | 100 | >95:5 |
| 2 | 1b+2+4a | 5b | 5.5 | 88 | 100 | >95:5 |
| 3 | 1c+2+4a | 5c+6c | 5 | 86 | 100 | 70:30 |
| 4 | 1a+2+4b | 5d | 3 | 81 | 100 | >95:5 |
| 5 | 1b+2+4b | 5e | 5 | 75 | 100 | >95:5 |
| 6 | 1c+2+4b | 5f+6f | 5 | 71 | 100 | 83:17 |
| 7 | 1a+2+4c | 5g+6g | 2.5 | 95 | 100 | 59:41 |
| 8 | 1b+2+4c | 5h+6h | 5 | 91 | 100 | 27:73 |
| 9 | 1c+2+4c | 6i | 4.5 | 78 | 100 | 0:100 |
| 10 | 1a+2+4d | 5j | 2.5 | 83 | 100 | >95:5 |
| 11 | 1b+2+4d | 5k+6k | 4.5 | 84 | 100 | 66:34 |
| 12 | 1c+2+4d | 5l | 4 | 67 | 100 | >95:5 |
2.2 Regio- and stereoselectivity
To confirm the chemical structures and regio/stereochemistry of the isolated products for each pair of reacting substrates, we performed multiple one-dimensional (1D) (proton, carbon-13, CRAPT, DEPT-135 NMR) and two-dimensional (2D) homo- and heteronuclear correlation nuclear magnetic resonance spectrometry measurements (gDQFCOSY, gHSQCAD, HMBCAD, ROESYAD) as well as decoupling experiments on several compounds (Figs. S1–S97). The determination of relative and absolute configuration of organic compounds by various NMR techniques is being frequently used and is a growing field of research as it offers an alternative approach, besides single crystal X-ray crystallography, to determine structure (Bifulco et al., 2007). The NMR technique is useful for non-crystalline samples that resist all type of crystallization into suitable X-ray grade crystals. Therefore, the selection of 5-chloro-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5b) and 5,5″-dichloro-1-methyl-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones (6i) as representative models for the remaining derivatives in the series, the relevant spectra used for regiochemical determination and stereochemical assignment are shown in Figs. 1–4.
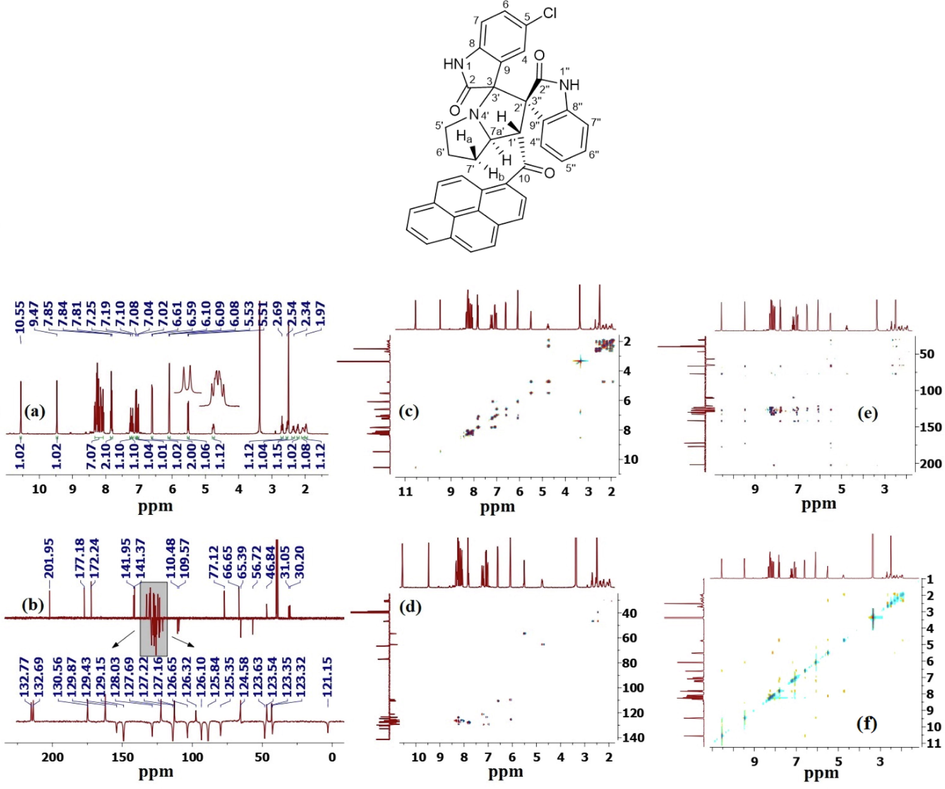
- (a) 1H NMR spectrum of (5b); (b) 13C CRAPT-NMR spectrum; (c) 1H–1H-COSY-NMR spectrum; (d) 1H–13C-HSQC-NMR spectrum; (e) 1H–13C-HMBC-NMR spectrum; (f) 1H–1H-ROESY-NMR spectrum.
-
1H–1H decoupling experiments of 5b: (a) non-decoupled spectrum; (b) irrad. of C7′—Hb; (c) irrad. of C6′—H; (d) irrad. of C6′—H; (e) irrad. of C7′—Ha; (f) irrad. of C5′—H; (g) irrad. of C5′—H; (h) irrad. of C7a′—H; (i) irrad. of C1′—H; (j) multiple-frequency irrad. of C4-H & C7″—H; (k) irrad. of C7″—H; (l) irrad. of C4-H; (m) irrad. of C7-H; (n) irrad. of C6-H; (o) irrad. of 1Hpyrene; (p) irrad. of C6″—H; (q) irrad. of C5″—H; (r) irrad. of C4″—H & 1Hpyrene.
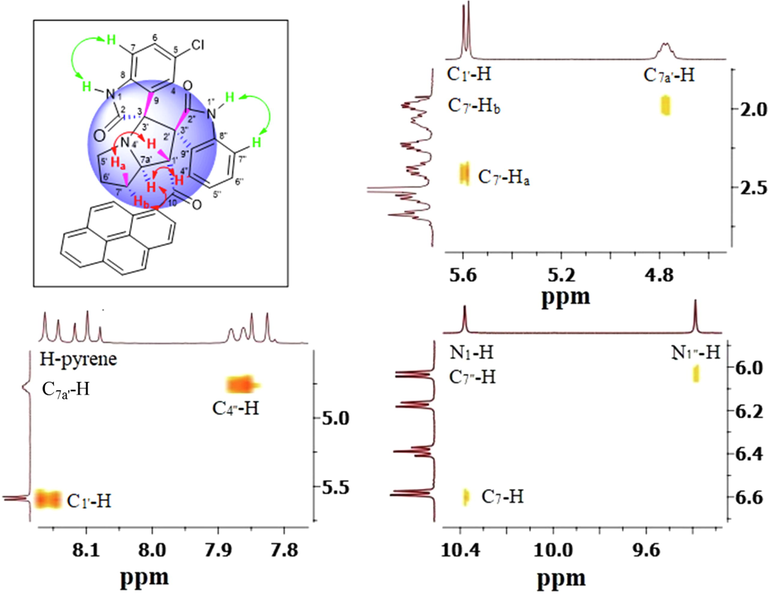
- (a) Overview of pertinent correlations observed in the 1H–1H-ROESYAD spectrum of 5b showing truncated signals stemming from C1′—H, C7a′—H, C7′—Ha and C7′—Hb, N1-H, N1″—H, C7-H, and C7″—H.
- (a) Relevant signals and correlations observed in the (a) 1H, (b) 1H–13C-HMBCAD, and (c) 1H–1H-ROESYAD NMR spectra of 6i showing truncated signals stemming from C2′—H and C7a′—H.
2.2.1 Regiochemical assignment of 5b as a model example
Examination of the 13C-CRAPT (Fig. 1, spectrum b) and 13C NMR spectra (Fig. S33) revealed the presence of 38 signals (16 aromatic CH's, 12 aromatic quaternary carbons, three carbonyl carbons, two spiro carbons, three methylene and two methine carbons, consistent with all carbon atoms being magnetically nonequivalent. The three carbonyl carbons of the pyrene and oxindole rings absorb at δ 202.0 (C10), 177.2 (C2, identified via 1H–13C-HMBCAD long-term coupling with N1—H; Fig. 1, spectrum e), and 172.2 (C2″, identified via 1H–13C-HMBCAD long-term coupling with N1″—H) ppm, respectively. The two spirocyclic carbon atoms of the pyrrolizidine ring C3′/C3 (δ 77.1 ppm) and C2′/C3″ (δ 66.7 ppm) exhibit the broadest chemical shifts compared to the remaining carbon atoms of this particular ring. The chemical shifts and signals of these quaternary carbons were identified by comparing the 13C NMR (Fig. S33) and 13C-CRAPT spectra (Fig. 1, spectrum b). While the 13C chemical shifts of the two methine carbons (C1′/δ 56.7 & C7a'/δ 65.4 ppm) were clearly identified as the only signals with negative phases in the aliphatic region of the 1H–13C-HSQCAD spectrum (Fig. 1, spectrum d), the attached protons C1′—H and C7a′—H appear as d and ddd [δ 5.52 (d, J = 8.0 Hz, 1H, C1′—H), 4.76 (ddd, 1H, J = 10, 8.0, 5.6 Hz, C7a′—H) ppm, respectively] (Fig. 1, spectrum a) and were correlated in the 1H–13C-HSQCAD NMR spectrum by two contours with the corresponding C1′ and C7a' carbons at 56.7 (C1′—H) and 65.4 (C7a′—H) ppm, respectively (Fig. 1, spectrum d). In particular, the C1′—H proton resonance of methine (δ 5.52), which is the lowest aliphatic signal in the 1H NMR spectrum due to diamagnetic anisotropy, shows strong 1H–13C HMBC correlations (Fig. 1, spectrum e) with the neighboring carbonyl group (C10, δ 202 ppm, 2JCH), the C2′/C3″ carbon of the spirocenter (66.7 ppm, 2JCH), and the oxindole carbonyl C2″ carbon (δ 172.2 ppm, 3JCH), C7′—CH2 (31.1 ppm, 3JCH), and C9″ carbon (126.3 ppm, 3JCH), (Fig. 1, spectrum e). The 1H–13C-HMBC data of N1″—H of the oxindole ring was key in assigning the chemical shift values of all the carbon atoms associated with the 5-membered oxindole ring (C2″, C3″, C8″ & C9″), while the observed 1H–1H-ROESYAD correlation contours between N1″—H and C7″—H (Fig. 1, spectrum f) assigned the chemical shift of the latter and prompted a partial assignment of the C4″—C7″ protons. Consequently, based on the 1H–1H-gCOSYAD correlation of C7″—H (outside the diagonal contour at δ 6.09/7.19) (Fig. 1, spectrum c), the triplet at δ 7.19 was correlated with the neighboring proton C6″—H. The most diagnostic resonance peaks for distinguishing the regioisomers were those associated with the methine groups (C1′—H & C7a′—H) and their corresponding multiplicities. Based on the demonstrated vicinal correlations between C1′—H and C7a′—H in the 1H–1H-gCOSYAD (Fig. 1, spectrum c), it is evident that the methine groups are spin-coupled. This obviously supports the suggested structure 5b (Scheme 1) and rules out the regioisomer 6b, in which the two groups are in separate spin systems. Literature evidence in line with our findings and supporting the regiochemical outcome of the above transformation stems from the work of Velikorodov et al. who described a similar cycloaddition to the one discussed herein using L-proline and isatin, although they utilized methyl 4-[2-(2-oxo-1,2-dihydro-3H-indol-3-ylidene)acetyl]phenylcarbamate as the dipolarophile (Velikorodov et al., 2011). Using unsubstituted isatin, the group reported the same regioisomeric outcome presented herein for the formation of the pyrrolizidine core, although the study was severely limited in substrate scope, reporting only one regioisomeric pyrrolizidine product without any stereochemical analysis. Later, the same group described an intriguing cycloaddition regioselectivity reversal associated with the same reaction when 5,7-dimethylisatin was used to generate the dipole instead of isatin (Velikorodov et al., 2013). The reversal observed was attributed to steric factors related to the hindered nature of 5,7-dimethylisatin. It is noted that the study reported only one regioisomeric product of this reversed type and the study was mostly focused on the preparation of other spiro cycloadducts like isoxazoline and pyrazole fragments. The stereochemical outcome was not discussed either. Another similar strategy to prepare the related octahydroindolizine through a 1,3-dipolar cycloaddition reaction of heteroaromatic N-ylides with 3-[(E)-2-aryl(hetaryl)-2-oxoethylidene]indolin-2-ones also produced the same regiochemical outcome observed in our case (Serov et al., 2005). Although in their study the general structure of the dipolarophile offered similar electronic environment to the one utilized herein, both the dipolarophile and dipole are significantly different that those employed in our current study.
Although at the moment a more fundamental and tangible understanding of the reasons behind the selectivity observed could not be provided in a complete convincing manner, the current regiospecific cycloaddition reaction reported herein of the dipole generated from isatin and L-proline to (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-ones demonstrated consistent attack of the electron-rich carbon atom of the dipole upon the α-carbon of the enone. It is conceivable that a combination of electronic (formation of a highly delocalized enolate anion following the addition of the dipole to the α-carbon of the enone) and steric factors (preferential attack of the dipole at the secondary α-carbon as opposed to the more hindered β tertiary carbon) work together to dictate the preferential formation of the observed regioisomeric product as the sole product.
2.2.2 Stereochemical assignment of 5b as a model example
It was crucial to assign at least all chemical shifts of the aromatic protons of the oxindole and pyrrolizidine rings before attempting any kind of stereochemical assignment. Overlaps between the signals warranted extensive 2D, 3D, and homonuclear decoupling studies. As expected, the C7a′—H (δ 4.76 ppm) multiplicity was a doublet of a doublet of a doublet (ddd) due to coupling with C1′—H and the neighboring nonequivalent diastereotopic C7′—Ha and C7′—Hb protons. The C1′—H proton resonated significantly further downfield and appeared as a doublet at δ 5.52 ppm (d, J = 8.0 Hz) due to scalar coupling with the neighboring C7a′—H. The six non-equivalent pyrrolizidine methylene protons C7′—H2—C5′—H2 were correlated to each other and to the same spin system of C7a′—H and C1′—H by 1H–1H-gDQFCOSY (Fig. 1, spectrum c), and the chemical shifts of carbon-13 were also verified by 1H–13C-gHSQCAD correlations (Fig. 1, spectrum d). Clearly, the magnetic anisotropy and inherent diastereotopic nature of the methylenes affected the chemical shifts of their carbon atoms, and the effect was even greater on the shift of their protons, offsetting the effect of the local atomic environment that justified the detailed NMR studies mentioned above. Fortunately, the N1-H group (δ 10.55 ppm) of the oxindole moiety (Figs. 1, 1H NMR spectrum a) was the crucial access point that finally led to the unambiguous assignment of the relative stereochemistry of the four stereogenic centers of the isolated regioisomer. In the ROESYAD NMR spectrum (Fig. 1, spectrum f), there is a strongly correlated cross peak between the N1-H proton (δ 10.55 ppm) and C7-H (d, J = 8.0 Hz, δ 6.60 ppm) and the recognition of the latter triggered the partial assignment of C7-H and C6-H of the protons of the oxindole ring. The N1-H proton also showed strong 1H–13C-HMBCAD correlation contours with C7 (3JCH), C2 (2JCH) and the C3/C3′ spirocenter (3JCH)), providing further evidence for the previous assignment and creating a perfect match between the previous signals and the corresponding oxindole ring atoms. It was expected that the presence of Cl would facilitate the assignment of the corresponding chemical shifts to the corresponding oxindole ring protons, as it produces a known distinct splitting pattern of the three aromatic protons as d (∼J = 8.0 Hz), dd (∼J = 8.0, 2.4 Hz) and d (∼J = 2.4 Hz). Based on the 1H–1H-gCOSY correlation of C7-H (contour at δ 6.60/7.02) (Fig. 1, spectrum c), the dd at δ 7.02 (J = 8.0, 2.4 Hz) was aligned with the neighboring C6-H. Thus, it appears that the two overlapping signals between δ 6.12–6.07 ppm are from 2 protons belonging to two different aromatic oxindole rings, and that the overlapping signals in the δ 7.88–7.80 region belong to 2 protons from the oxindole and pyrenoyl rings (vide infra). From the ROESYAD NMR spectrum (Fig. 1, spectrum f), the strong correlation contour between the N1″—H proton (δ 9.47 ppm) and δ 6.09 ppm C7″—H (d, J = 8.0 Hz) exposes it as one of the overlapping signals in the δ 6.12–6.07 region and prompts a partial assignment of the C6″—H and C5″—H protons. As can be seen from the contours at δ 7.19/6.09 and δ 7.19/7.25, the two triplet doubles at δ 7.19 and δ 7.25 ppm were assigned to C6″—H and C5″—H, respectively.
Unfortunately, the most informative 1H NMR signals of C4″—H and C4-H, which incidentally have been previously used in related systems (Hussein and Abdel-Monem, 2011) as keys to assign the relative stereochemistry of all chiral centers, were part of the overlapping signals at δ 6.12–6.07 and δ 7.86–7.80 ppm, respectively, and eluded unambiguous identification because the 2D and 3D NMR data were insufficient to verify which signal belonged to which oxindole ring. Therefore, further advanced NMR studies were required, which could only be performed by 1H–1H homonuclear uncoupling NMR experiments (vide infra).
Of note is the overlap between the two resonances at δ 7.80–7.84 ppm and two other signals at δ 6.08–6.09 ppm. 1H–1H-gDQFCOSY correlations were insufficient to fully correlate the C4-H—C7-H spin system and distinguish between 1H NMR signals associated with the latter and those originating from the other oxindole C4″—H—C7″—H spin system. Therefore, homonuclear uncoupling experiments (Fig. 2) were performed to assign the chemical shifts of the oxindole protons to their respective positions on the aromatic oxindole rings. Moreover, these experiments were of utmost importance in assigning the chemical shifts of the 6 aliphatic signals (δ 2.69–1.93 ppm) to their corresponding methylene protons. Thus, the irradiation of C7′—Hb (Fig. 2, spectrum b), C6′—H (Fig. 2, spectrum c), C7″—H (Fig. 2, spectrum d), C7′—Ha (Fig. 2, spectrum e), C5′—H (Fig. 2, spectrum f), C5′—H (Fig. 2, spectrum g), C7a′—H (Fig. 2, spectrum h), C1′—H (Fig. 2, spectrum i), C7″—H (Fig. 2, spectrum k), C4-H (Fig. 2, spectrum l), C7-H (Fig. 2, spectrum m), C6-H (Fig. 2, spectrum n), C6″—H (Fig. 2, spectrum p), C5″—H (Fig. 2, spectrum q), C4″—H & 1Hpyrene (Fig. 2, spectrum r), resulted in the collapse of prominent signals, including C5′—H, which collapsed to a doublet (spectrum c), C7a′—H to a doublet of doublets (spectrum i), and C1′—H/C4-H/C7-H/C7″—H/C4″—H to singlet (spectrum h, n, p, & q, respectively). These experiments led to a clear assignment of chemical shifts for the oxindoles and pyrrolizidine protons as well as for the overlapping resonances between δ 6.12–6.07 and δ 7.86–7.80 ppm. In particular, irradiation of the characteristic C6-H dd (Fig. 2, spectrum n) collapsed both signals of C4-H, C7-H into singlets and indicated that the overlapping resonances in the δ 6.12–6.07 region comprise a doublet with small scalar coupling value (C4-H, J = 2.0 Hz) that overlaps with another doublet with much larger coupling constant (C7″—H, J = 8.0 Hz). Similarly, irradiation of the characteristic C5″—H td (δ 7.25 ppm) and 1Hpyrene d (δ 7.09 ppm) suggests that the overlapping resonances in the δ 7.86–7.80 region comprise two doublets (C5″—H & 1Hpyrene). Accordingly, the C4″—H—C7″—H protons were associated with δ 7.84, 7.25, 7.19 and 6.09 ppm, respectively, and the C4-H, C7-H and C6-H protons were associated with δ 6.08, 6.60 and 7.02 ppm, respectively. As expected, the first proton spin system showed two triplets and two doublets, while the second one comprised two doublets and one doublet of doublets, further supporting the above assignments.
Having identified and assigned chemical shifts in the proton spectrum for each H atom in the three aforementioned autonomous spin systems (oxindole and pyrrolizidine ring systems), we needed to examine the ROESYAD spectrum (Fig. 1, spectrum F) closely for notable spatial correlations that could be used to determine the relative stereochemistry of the four stereogenic centers. A strong contour at δ 7.84/4.76 ppm indicates a proximity of C4″—H and C7a′—H to each other (Fig. 3), suggesting that a syn-stereochemical relationship exists between the aromatic oxindole ring and C7a′—H, determining the relative stereochemistry for the C2′/C3″-spirocenter and C7a′—H. Based on the trans geometry of the dipole, C1′—H is expected to be trans to both flanking groups, the adjacent aromatic oxindole ring and C7a′—H. The trans-stereochemical relationship between C1′—H and C7a′—H is evident from the lack of a cross-peak between their signals in the ROESYAD spectrum (Fig. 1, spectrum F). While C7a′—H showed a strong ROESY correlation with cis C7′—Hb and no correlation with trans C7′—Ha, C1′—H correlated strongly with C7′—Ha and showed no correlation with C7′—Hb. The diastereotopic protons C7′—Ha and C7′—Hb were identified via 1H–13C-HSQCAD NMR (Fig. 1, spectrum d), as they were both traced to a common carbon atom (δ 31.3 ppm), and their relative position with respect to C6′—H2 and C5′—H2 was determined via gDQFCOSY NMR (Fig. 1, spectrum c). Finally, the trans geometry of the oxindole rings was evident from the complete absence of relevant contours between the two groups of aromatic spin systems. Except for two cases (Table 1, entries 8 and 9), regioisomer 5 was obtained exclusively as pure (Table 1, entries 1, 2, 4, 5, 10, and 12) or as the major product (Table 1, entries 3, 6, 7, and 11), and regioisomer 6 was observed as a minor product. However, regioisomer 6 was obtained in pure form in one case (Table 1, entry 9) and as the major isomer (73%) in another example (Table 1, entry 8).
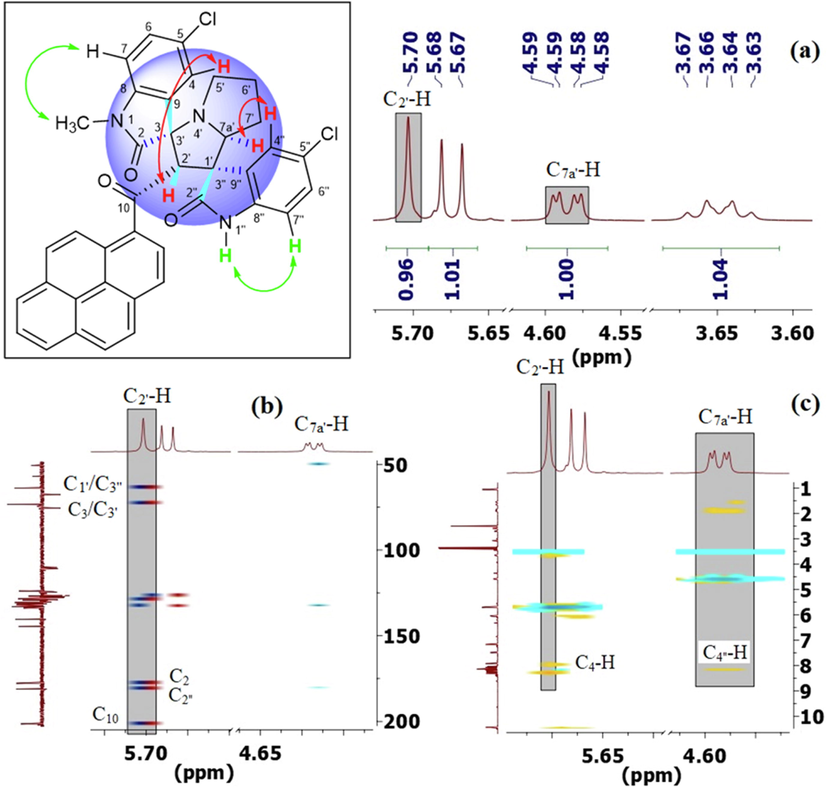
The regiochemistry of the cycloadduct 6i was readily established due to the lack of correlation between C2′—H (s) and C7a′—H (dd) in the 1H–1H-gDQFCOSY and the pronounced multiplicity of C2′—H (s) (Fig. 4, spectrum a), which, as expected, appears as the only singlet in the entire 1H NMR spectrum (δ 5.70 ppm), being the only isolated aliphatic spin system in the entire molecule. Further evidence for the assignment of C2′—H in cycloadduct 6i is provided by a strong 1H–13C-HMBCAD correlation of C2′—H with the three flanking carbons at δ 72.1 (C3/C3′, 2JCH), 62.7 (C1′/C3″), and 200.3 (q, C10), and with the two indoline carbonyls at 179.9 (C2″, 3JCH) and 176.6 (C2, 3JCH) (Fig. 4, spectrum b). In the 1H–1H-ROESYAD spectrum (Fig. 4, spectrum c), a strong correlation between the N1″—H and the C7″—H triggered the assignment of C7″—H—C4″—H using 1H–1H-gDQFCOSY. Similarly, a strong correlation between N1—CH3 and C7-H in the 1H–1H-ROESYAD triggered the assignment of C7-H—C4-H using 1H–1H-gDQFCOSY. After the identification of the H NMR chemical shifts for each proton in the above four autonomous spin systems (oxindole and pyrrolizidine ring systems), it only remained to look for significant spatial proximity contours in the 1H–1H-ROESYAD spectrum (Fig. 4, spectrum c) to clarify the relative stereochemistry of the four chiral centers. Certainly, a characteristic contour at δ 7.92/5.70 ppm indicated the spatial proximity of C4-H and C2′—H to each other (Fig. 3), suggesting that a syn-stereochemical relationship exists between the oxindole aromatic ring of C7-H—C4-H and C2′—H and determines the relative stereochemistry for the C3/C3′-spirocenter and C2′—H. Based on the trans-stereochemical geometry of the dipole, the aromatic ring C7″—H—C4″—H is expected to be trans to C2′—H. The stereochemistry of C7a′—H was determined from a strong 1H–1H-ROESYAD cross-peak (at δ 8.14/4.59 ppm) between C4″—H and C7a′—H as syn to the aromatic ring C7″—H—C4″—H.
2.3 Reaction mechanism
As suggested in Scheme 2 below, the regio- and stereochemistry for the formation of dispiropyrrolizidine oxindoles 5a-l and 6a-l are described in terms of electronic factor and the repulsion force. The formation of regioisomer 5 occurs via “pathway A”, in which the nucleophilic carbon atom of the azomethine ylide (AY) attacks the α-carbon of ethylene derivative 4 through an “exo” transition state (exo-TS5, Scheme 2). In this case, exo-TS5 is more stable because the corresponding “endo” transition state (endo-TS5) requires more free activation energy than exo-TS5 due to the electrostatic repulsion between the cis-carbonyl groups, which increases the free activation energy. On the other hand, the formation of the other regioisomer 6 occurs via “pathway B”, in which the nucleophilic carbon atom of the azomethine ylide (AY) attacks the β-carbon of the ethylene derivatives 4 also via an “exo” transition state (exo-TS6, Scheme 2).
![Plausible mechanism for the formation of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizine-2′,3″-indoline]-2,2″-diones 5a-l and 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizine-1′,3″-indoline]-2,2″-diones 6a-l.](/content/184/2022/15/6/img/10.1016_j.arabjc.2022.103855-fig6.png)
- Plausible mechanism for the formation of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizine-2′,3″-indoline]-2,2″-diones 5a-l and 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizine-1′,3″-indoline]-2,2″-diones 6a-l.
Moreover, the regiochemistry of this type of 32CA reaction can be illustrated by the secondary orbital interaction (SOI) of the carbonyl group orbitals of dipolarophiles 4a-d with those of ylides 3a-c, as shown in Scheme 2.
2.4 Theoretical studies
Hypothetically, the reaction could proceed via pathway A (α-attack) or pathway B (β-attack) and in both cases the orientation of the reactants could be endo or exo. Therefore, a theoretical study was carried out to determine the energetics of reaction pathways A and B through the exo and endo transition states for the formation of compounds 5a and 6a starting from 3a and 4a. The calculated free energy profile of the exo and endo transition states (exo-TS and endo-TS) and the products of reaction pathway A are shown in Fig. 5A. Fig. 5B shows the same for reaction pathway B. The calculated activation energies (Ea) and free energy values (ΔG) are listed in Table 2.

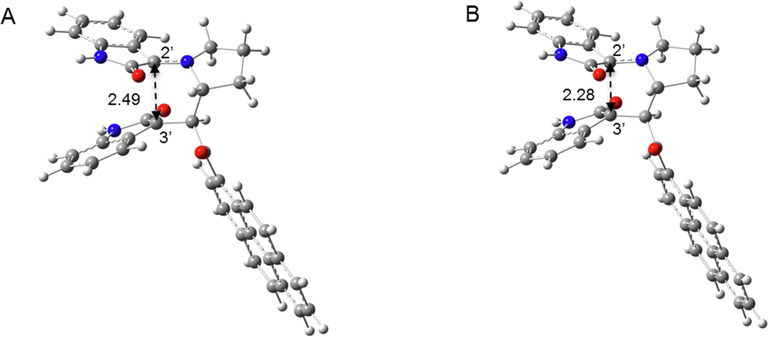
- Computed free energy profiles of the possible reaction paths for (3a+4a). (A) Free energies of α-attack (path A) for the formation of 5a via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (B) Free energies of β-attack (path B) for the formation of 6a via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. Optimized geometries and global electron density transfer (GEDT) at exo-TS in α-attack (C) and β-attack (D). The 5′⋯4′ and 2′⋯3′ bond distances are shown with black dotted arrows. The gray arrow indicates the direction of GEDT.
| Reactants | Products | Ea | ΔG | Reactants | Products | Ea | ΔG |
|---|---|---|---|---|---|---|---|
| 3a+4a | endo-5a | 8.35 | −6.71 | 3b+4c | endo-5h | 8.72 | −5.93 |
| exo-5a | 4.82 | −10.57 | exo-5h | 4.99 | −9.30 | ||
| endo-6a | 20.45 | −7.58 | endo-6h | 20.45 | −6.47 | ||
| exo-6a | 10.14 | −15.14 | exo-6h | 10.05 | −14.58 | ||
| 3a+4c | endo-5g | 7.10 | −7.17 | 3c+4c | endo-5i | 7.58 | −6.48 |
| exo-5g | 3.85 | −10.56 | exo-5i | 4.60 | −9.86 | ||
| endo-6g | 19.03 | −8.03 | endo-6i | 19.71 | −6.93 | ||
| exo-6g | 8.80 | −15.80 | exo-6i | 9.45 | −15.16 | ||
The stereoselectivity of the reaction can be explained on the basis of the activation energies for the formation of 5a and 6a via exo- and endo- TS. The activation energy for the formation of exo-5a is lower than that of endo-5a (Fig. 5A). Similarly, the activation energy for the formation of exo-6a is lower than that of endo-6a (Fig. 5B). Therefore, all reactions are stereospecific and yield the exo adduct as a single product in all cases. To explain the regioselectivity, we compared the activation energies for exo-5a and exo-6a. From the activation energies (Fig. 5, Table 2), it is evident that the reaction is regiospecific and yields only cycloadduct-5 as a single product. It should be noted that the exo-6a isomer was energetically more stable than exo-5a, but due to the higher activation energy barrier, it could not form. For reactions (3a + 4a), (3a + 4b), (3a + 4d), (3b + 4a), (3b + 4b) and (3c + 4d), the reaction proved to be regiospecific and gave only cycloadduct-5 as the sole product. Thus, the computational results agree well with the experimental results. The optimized geometries of the exo-transition state (exo-TS) in pathways A and B are shown in Fig. 5C and 5D, respectively. Global electron density transfer (GEDT) calculations were performed on the transition states. The GEDT value of 0.15e at 5a-exo-TS is consistent with a polar nature of the reaction.
Experimentally, it was observed that in the case of reactions (3a + 4c), (3b + 4d), (3c + 4a) and (3c + 4b), the reaction was regioselective and cycloadduct-5 was obtained as the major product and cycloadduct-6 as the minor product in each case. To explain this observation, we calculated the free energy profile for reaction (3a + 4c) as shown in Fig. 6. It is evident that the activation energy (Table 2) is lowest for the formation of cycloadduct-5, indicating that the formation of 5g would be most favorable. The difference between the activation energies for the formation of exo-5g and exo-6g is 4.95 kcal/mol, which is less than the difference between the activation energies (5.32 kcal/mol) for the formation of exo-5a and exo-6a, which could be a reason for the formation of cycloadduct-6 as a by-product.
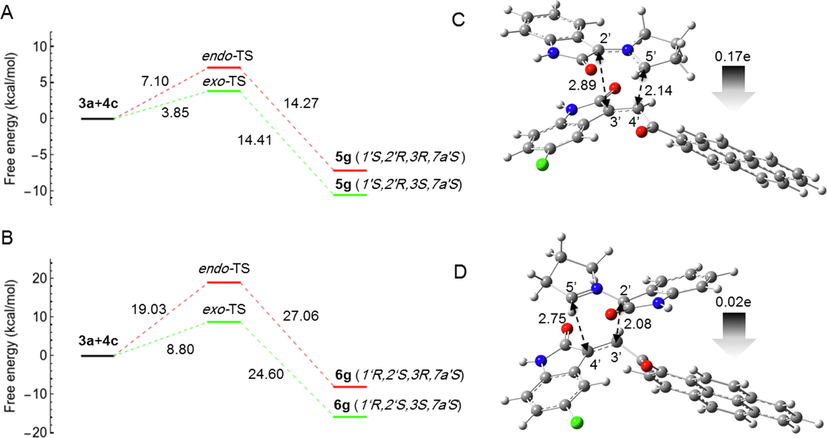
- Computed free energy profiles of the possible reaction paths for (3a + 4c). (A) Free energies of α-attack (path A) for the formation of 5g via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (B) Free energies of β-attack (path B) for the formation of 6g via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (C) Optimized geometry of 5g-exo-TS. (D) Optimized geometry of 6g-exo-TS. The 5′⋯4′ and 2′⋯3′ bond distances are indicated with black dotted arrows. The gray arrow shows the direction of GEDT.
In the case of (3b + 4c) and (3c + 4c), experiments have shown that the regiochemistry is reversed and the reaction is regioselective, yielding the cycloadduct-6 (6h) as the major product in the case of (3b + 4c), whereas in the case of (3c + 4c) it is regiospecific, yielding only the cycloadduct-6 (6i) as the single product. To explain this unique observation, the free energy profiles for both reactions were calculated (Figs. 7 and 8) and the activation energies are listed in Table 2.
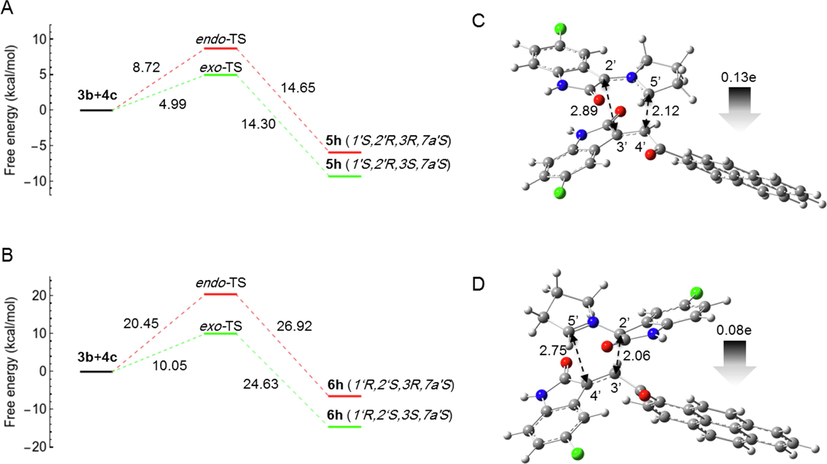
- Computed free energy profiles of the possible reaction paths for (3b + 4c). (A) Free energies of α-attack (path A) for the formation of 5h via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (B) Free energies of β-attack (path B) for the formation of 6h via exo and endo TS, respectively. Relative free energies are given in kcal/mol. (C) Optimized geometry of 5h-exo-TS. (D) Optimized geometry of 6h-exo-TS. The 5′⋯4′ and 2′⋯3′ bond distances are indicated with black dotted arrows. The gray arrow shows the direction of GEDT.
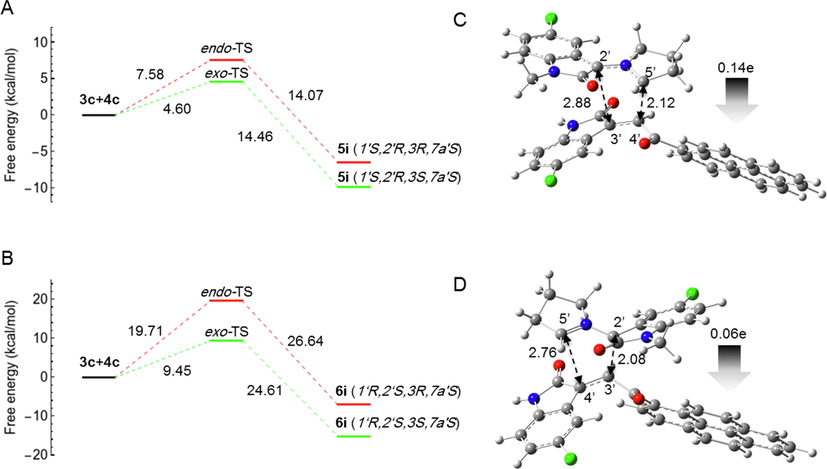
- Computed free energy profiles of the possible reaction paths for (3c + 4c). (A) Free energies of α-attack (path A) for the formation of 5i via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (B) Free energies of β-attack (path B) for the formation of 6i via exo- and endo-TS, respectively. Relative free energies are given in kcal/mol. (C) Optimized geometry of 5i-exo-TS. (D) Optimized geometry of 6i-exo-TS. The 5′⋯4′ and 2′⋯3′ bond distances are indicated with black dotted arrows. The gray arrow shows the direction of GEDT.
However, the calculated activation energies for the formation of cycloadduct-5 (5h and 5i) are 4.99 and 4.60 kcal/mol, respectively, which are much lower than the activation energies for the formation of cycloadduct-6 (10.05 and 9.45 kcal/mol for 6h and 6i, respectively). Thus, the calculated free energy profile could not explain the switching of regioselectivity in the case of (3b + 4c) and (3c + 4c). However, in all cases, the computational results confirmed that all reactions were stereospecific and, in all cases, gave the exo-adduct as a single product.
The optimized transition state geometries in the α-attack pathway show that the C4′≡C5′ distance is smaller than the C2′≡C3′ distance, indicating that the C4′≡C5′ bond is formed first, followed by the formation of the C2′≡C3′ bond. Similarly, the optimized transition state geometries in the β-attack pathway show that the C2′≡C3′ distance is smaller than the C4′≡C5′ distance, indicating that the formation of the C2′≡C3′ bond is followed by the C4′≡C5′ bond. To investigate whether there are stable intermediates, the C2′≡C3′ distance in the α-attack pathway and the C4′≡C5′ distance in the β-attack pathway were perturbed and the potential energy was plotted in Fig. 9. From the scan of the potential energy (PES), it can be seen that there is no stable intermediate in the β-attack and that after the formation of the C2′≡C3′ bond, the C4′≡C5′ bond is formed in a barrierless and concerted manner.
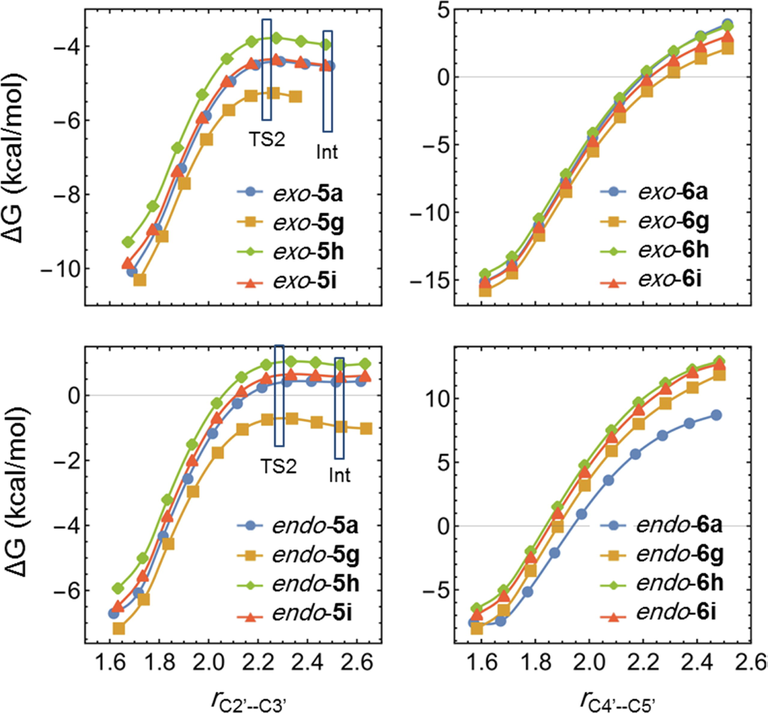
- Potential energy diagram for the C2′···C3′ bond length perturbation in cycloadduct-5 and the C4′···C5′ bond length perturbation in cycloadduct-6. Thermodynamically stable intermediate (Int) and the second transition state (TS2) are marked.
On the other hand, the α-attack pathway shows thermodynamically stable intermediates and a second transition state (Fig. 10). However, the activation energy required to form the intermediate is in the range of 0.1–0.3 kcal/mol, which is much less than the kBT at room temperature (0.59 kcal/mol), indicating that the intermediate is not stable at room temperature (as well as at the reaction temperature) and the α-attack also occurs in a concerted manner.
- Optimized geometry of the thermodynamically stable intermediate (A) and the second transition state (B) in the exo-5a formation path. C2′⚌C3′ distances are shown with back dotted arrows.
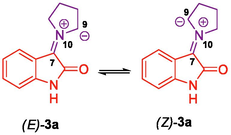
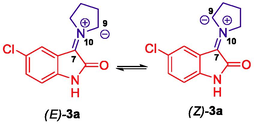
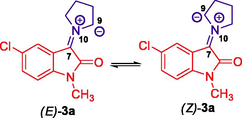
As described in our previous publication (Hussein et al., 2011), global and local reactivity descriptors such as chemical potential μ, chemical hardness η, and global electrophilicity ω, defined in the framework of density functional theory, have proven to be very useful for the interpretation of reactivity and regioselectivity in polar reactions. The calculated values of μ and η, ω are given in Table 3. From the data, it is evident that the electronic chemical potentials μ of 3a-c are higher than those of 4a-d. Moreover, the E configuration of 3a-c has higher electronic chemical potential than its Z configuration and E configurations are energetically more favorable than the Z configurations. This suggests that electrons flow from the (E)-3a-c to the 4a-d, which act as electrophiles due to their larger ω-values (3.53 < ω < 3.93) compared to the ω-values (1.52 < ω < 1.87) of the 3a-c. On the electrophilicity scale (strong, ω > 1.5 eV, moderate, 0.8 < ω < 1.5 eV, and marginal ω < 0.8 eV) as described by Domingo et al. (Domingo et al., 2002), our ethylene derivatives 4a-d can be counted among the strong molecules on this scale of electrophilicity. However, 3a-c are also strong electrophiles, but their electrophilicity is lower than that of 4a-d. On the other hand, the nucleophilicity N index described by Jaramillo et al. (2008) classifies molecules as strong, N > 3.00 eV, moderate, 2.00 eV < N < 3.00 eV, and marginal nucleophilic, N < 2.00 eV. The calculated nucleophilicity descriptor N, as listed in Table 3, shows that all reactants can be classified as strong nucleophilic and (E)-3a is the best nucleophile in this series. These results confirm the expected reactivity pattern.
| Comp. | E(HOMO) | E(LUMO) | μ | η | ω | N |
|---|---|---|---|---|---|---|
| TCE | −9.41 | −5.25 | −7.33 | 4.16 | 6.47 | 0.00 |
| 4c | −5.89 | −3.24 | −4.57 | 2.65 | 3.93 | 3.52 |
| 4d | −5.87 | −3.19 | −4.53 | 2.68 | 3.82 | 3.54 |
| 4a | −5.82 | −3.09 | −4.45 | 2.74 | 3.62 | 3.59 |
| 4b | −5.80 | −3.04 | −4.42 | 2.76 | 3.53 | 3.61 |
| (Z)-3b | −5.15 | −1.86 | −3.51 | 3.29 | 1.87 | 4.26 |
| (Z)-3c | −5.10 | −1.81 | −3.46 | 3.29 | 1.81 | 4.31 |
| (E)-3b | −5.05 | −1.72 | −3.39 | 3.33 | 1.72 | 4.36 |
| (E)-3c | −5.00 | −1.68 | −3.34 | 3.32 | 1.68 | 4.41 |
| (Z)-3a | −4.93 | −1.65 | −3.29 | 3.28 | 1.65 | 4.48 |
| (E)-3a | −4.82 | −1.52 | −3.17 | 3.30 | 1.52 | 4.59 |
In order to rationalize and understand the regioselectivity observed in this work, we calculated the local reactivity indices, including the electrophilic and nucleophilic Parr and Fukui functions. The local electrophilicity parameter is defined by ωk = ωPk+, to reveal the reactive behavior of the atoms forming a molecule. From Table 4, the highest values of Pk− in 3a-c at carbon atom C7 are 0.388, 0.364 and 0.356, respectively. Moreover, the carbon C1 in 4a represents the electrophilic site with a local electrophilicity value of ωk = 0.54 eV. Therefore, the interaction takes place between the C7 center of 3a-c and the C1 center of 4a, which facilitates the α-attack. Interestingly, in the case of 4c, the C2 carbon represents the electrophilic site with a local electrophilicity value of ωk = 0.65 eV, suggesting that the C7 center of 3a-c can align with the C2 center of 4c, facilitating β-attack. Although the activation energies could not clarify why cycloadduct-6 was formed in some cases, the calculated descriptors for the local electrophilicity/nucleophilicity of the reactants could elucidate the mechanism of regioselectivity.
| Comp. | Site k | fk− | fk+ | Pk− | Pk+ | ||
|---|---|---|---|---|---|---|---|
|
(Z)-3a | 7 | C | 0.235 | 0.047 | 0.362 | −0.102 |
| 9 | C | 0.216 | 0.496 | 0.351 | 0.796 | ||
| 10 | N | 0.007 | 0.166 | −0.124 | 0.164 | ||
| (E)-3a | 7 | C | 0.244 | 0.054 | 0.388 | −0.095 | |
| 9 | C | 0.203 | 0.513 | 0.328 | 0.824 | ||
| 10 | N | 0.006 | 0.160 | −0.118 | 0.133 | ||
|
(Z)-3b | 7 | C | 0.229 | 0.034 | 0.349 | −0.108 |
| 9 | C | 0.199 | 0.503 | 0.315 | 0.803 | ||
| 10 | N | 0.006 | 0.169 | −0.116 | 0.162 | ||
| (E)-3b | 7 | C | 0.241 | 0.040 | 0.364 | −0.113 | |
| 9 | C | 0.191 | 0.517 | 0.300 | 0.826 | ||
| 10 | N | 0.006 | 0.163 | −0.111 | 0.133 | ||
|
(Z)-3c | 7 | C | 0.219 | 0.033 | 0.327 | −0.109 |
| 9 | C | 0.195 | 0.501 | 0.312 | 0.801 | ||
| 10 | N | 0.006 | 0.170 | −0.113 | 0.165 | ||
| (E)-3c | 7 | C | 0.236 | 0.038 | 0.356 | −0.124 | |
| 9 | C | 0.189 | 0.517 | 0.300 | 0.824 | ||
| 10 | N | 0.006 | 0.163 | −0.111 | 0.134 | ||
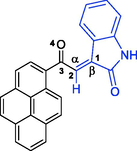
|
4a | 1 | C | 0.005 | 0.139 | −0.004 | 0.149 |
| 2 | C | 0.006 | 0.155 | 0.031 | 0.144 | ||
| 3 | C | 0.003 | 0.136 | −0.018 | 0.124 | ||
| 4 | O | 0.022 | 0.126 | −0.001 | 0.192 | ||
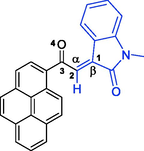
|
4b | 1 | C | 0.006 | 0.140 | −0.007 | 0.150 |
| 2 | C | 0.006 | 0.148 | 0.023 | 0.133 | ||
| 3 | C | 0.001 | 0.139 | −0.018 | 0.122 | ||
| 4 | O | 0.020 | 0.127 | −0.003 | 0.192 | ||
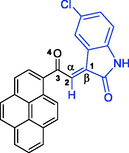
|
4c | 1 | C | 0.006 | 0.139 | 0.002 | 0.147 |
| 2 | C | 0.005 | 0.168 | 0.015 | 0.166 | ||
| 3 | C | 0.003 | 0.133 | −0.018 | 0.117 | ||
| 4 | O | 0.024 | 0.124 | 0.002 | 0.193 | ||
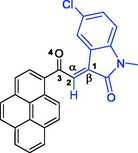
|
4d | 1 | C | 0.006 | 0.140 | −0.003 | 0.137 |
| 2 | C | 0.005 | 0.161 | 0.010 | 0.159 | ||
| 3 | C | 0.003 | 0.137 | −0.016 | 0.119 | ||
| 4 | O | 0.023 | 0.125 | −0.0001 | 0.193 | ||
3 Conclusion
In conclusion, one-pot three-component regio- and stereoselective polar 32CA reactions of azomethine ylides with (E)-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one derivatives were carried out. The experimental results showed that the regiochemistry in these reactions is influenced by the chemical structure of both the dipole and the dipolarophile. A remarkable reversal of regioselectivity was carried out in the reaction of azomethine ylide generated by the reaction of L-proline and 5-chloroisatin or N-methyl-5-chloroisatin with (E)-5-chloro-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one. The chemical structures and stereochemistry of the obtained regioselective products were confirmed by 1D and 2D NMR spectroscopy.
Computational free energy profile studies clearly show that for both α-attack and β-attack, product formation via exo-TS always follows a lower energy pathway than the pathway via endo-TS, confirming the stereospecificity of the reactions and justifying the observation of the exo-adduct as a single product in all cases.
Generally, the reaction is regioselective affording adduct-5 as major product via α-attack and the computational results agree well with the experimental observations. However, the calculated free energy profile could not explain the switching of regioselectivity in the case of dipole/dipolarophile interaction of 1-(5-chloro-2-oxoindolin-3-ylidene)pyrrolidinium ylide/(E)-5-chloro-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one and 1-(5-chloro-1-methyl-2-oxoindolin-3-ylidene)pyrrolidinium ylide/(E)-5-chloro-3-(2-oxo-2-(pyren-1-yl)ethylidene)indolin-2-one yielding the cycloadduct-6 as the major product via β-attack.
Analysis of the optimized transition state geometries indicates that in the case of α-attack, the C4′⚌C5′ bond is formed first, followed by the formation of the C2′⚌C3′ bond, while in the case of β-attack, the C2′⚌C3′ bond is formed first, followed by the formation of the C4′⚌C5′ bond. PES analysis, as obtained by the C2′⚌C3′ bond length perturbation in the case of α-attack, revealed the existence of an intermediate and a second transition state. However, the activation energy barrier for the second transition state is well below kBT at room temperature, indicating that the formation of the second bond in the α-attack is indeed barrierless at reaction temperature and the entire reaction proceeds in a concerted manner. PES analysis for the C4′⚌C5′ bond length disorder in the β-attack showed that the formation of the C4′⚌C5′ bond in the β-attack is barrierless and the reaction mechanism proceeds in a concerted manner, with a single transition state existing. Analysis of the global and local electrophilicity and nucleophilicity further elucidates the alignment of dipolarophiles 4a-d with dipoles 3a-c and highlights the regioselectivity of the reactions.
4 Experimental
4.1 Chemical synthesis
All solvents used in this work were purchased from Sigma-Aldrich. They were all spectroscopic grade and used without additional purifications. Melting points of solids reported herein are uncorrected and were obtained using a Stuart SMP3 melting point apparatus. All NMR spectra were recorded on a Varian NMR machine (at 400 MHz for 1H, 100 MHz for 13C) in DMSO‑d6 as solvent. The known dipolarophiles 4a-d were synthesized according to literature procedure (Domingo, 2016).
4.1.1 Typical procedure for the preparation of 1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones 5a-l and 2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones 6a-l.
An ethanolic mixture (10 mL absolute ethanol) of isatin 1 (1.2 mmol), L-proline 2 (138 mg, 1.2 mmol) and 4 (1.0 mmol) was refluxed for 3–6 h, followed by cooling to room temperature. The resulting solid formed during the reaction was isolated by filtration to afford the corresponding regioisomers 5a-l and 6a-l. The molar ratio of 5a-l/6a-l was determined by 1H NMR spectroscopy. The pure cycloadducts 5a, 5b, 5d, 5e, 5j, 5l, and 6i were obtained by recrystallization from absolute ethanol.
4.1.1.1 (1'S,2'R,3S,7a'S)-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5a)
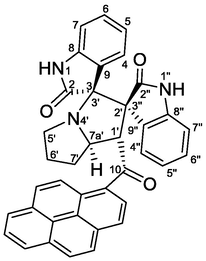
Buff crystals, mp 251–252 °C; yield 0.556 g (97%) from 176 mg (1.2 mmol) of 1a and 373 mg (1.0 mmol) of 4a. 1H NMR (DMSO‑d6, 400 MHz) δ 10.40 (s, 1H, N1-H), 9.41 (s, 1H, N1″—H), 8.34 (d, J = 8.0 Hz, 1Hpyrene), 8.30–8.25 (m, 3Hpyrene), 8.22 (d, J = 8.0 Hz, 1Hpyrene), 8.15 (d, J = 8.0 Hz, 1Hpyrene), 8.10 (t, J = 8.0 Hz, 1Hpyrene), 7.87 (d, J = 7.2 Hz, 1H, C4″—H), 7.84 (d, J = 9.2 Hz, 1Hpyrene), 7.24 (td, J = 7.6, 0.8 Hz, 1H, C5″—H), 7.17 (td, J = 7.6, 1.2 Hz, 1H, C6″—H), 7.09 (d, J = 9.2 Hz, 1Hpyrene), 6.98 (td, J = 7.6, 1.2 Hz, 1H, C6-H), 6.61 (d, J = 7.6 Hz, 1H, C7-H), 6.42 (td, J = 7.6, 1.2 Hz, 1H, C5-H), 6.20 (d, J = 7.2 Hz, 1H, C4-H), 6.06 (d, J = 7.1 Hz, 1H, C7″—H), 5.59 (d, J = 8.0 Hz, 1H, C1′—H), 4.82–4.73 (m, 1H, C7a′—H), 2.71–2.64 (m, 1H, C5′—H), 2.60–2.54 (m, 1H, C5′—H), 2.45–2.34 (m, 1H, C7′—Ha), 2.28–2.20 (m, 1H, C6′—H), 2.13–2.02 (m, 1H, C6′—H), 2.01–1.94 (m, 1H, C7′—Hb) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 202.2 (q, C10), 177.6 (q, C2), 172.5 (q, C2″), 142.5 (q, C8″), 142.0 (q, C8), 133.0 (q, Cpyrene), 132.7 (q, Cpyrene), 130.6 (q, Cpyrene), 129.9 (q, Cpyrene), 129.3 (C6H), 129.2 (CHpyrene), 129.1 (C6″H), 128.0 (CHpyrene), 127.7 (q, Cpyrene), 127.3 (CHpyrene), 127.2 (CHpyrene), 126.7 (q, C9″), 126.6 (CHpyrene), 126.1 (CHpyrene), 125.8 (CHpyrene), 125.7 (C4H), 125.3 (CHpyrene), 125.2 (q, C9), 123.6 (q, Cpyrene and CHpyrene), 123.5 (C4″H), 123.4 (q, Cpyrene), 121.1 (C5″H), 120.5 (C5H), 109.4 (C7″H), 109.1 (C7H), 77.0 (C3/C3′), 66.7 (C2′/C3″), 65.3 (C7a'H), 56.9 (C1′H), 46.9 (C5′—CH2), 31.0 (C7′—CH2), 30.2 (C6′—CH2).
4.1.1.2 (1'S,2'R,3S,7a'S)-5-chloro-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5b)
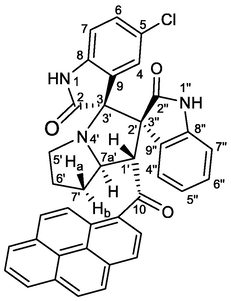
Pink crystals, mp 258–259 °C; yield 0.533 g (88%) from 218 mg (1.2 mmol) of 1b and 373 mg (1.0 mmol) of 4a. 1H NMR (DMSO‑d6, 400 MHz) δ 10.55 (s, 1H, N1-H), 9.47 (s, 1H, N1″—H), 8.33 (d, J = 8.0 Hz, 1Hpyrene), 8.29–8.24 (m, 3Hpyrene), 8.20 (d, J = 8.8 Hz, 1Hpyrene), 8.15 (d, J = 8.0 Hz, 1Hpyrene), 8.08 (t, J = 8.0 Hz, 1Hpyrene,) 7.84 (d, J = 6.8 Hz, 1H, C4″—H), 7.81 (d, J = 9.6 Hz, 1Hpyrene), 7.25 (td, J = 7.6, 0.8 Hz, 1H, C5″—H), 7.19 (td, J = 7.6, 1.2 Hz, 1H, C6″—H), 7.09 (d, J = 9.2 Hz, 1Hpyrene), 7.02 (dd, J = 8.0, 2.4 Hz, 1H, C6-H), 6.60 (d, J = 8.0 Hz, 1H, C7-H), 6.09 (d, J = 8.0 Hz, 1H, C7″—H), 6.08 (d, J = 2.0 Hz, 1H, C4-H), 5.52 (d, J = 8.0 Hz, 1H, C1′—H), 4.76 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 2.69 (t, J = 8.0 Hz, 1H, C5′—H), 2.58–2.52 (m, 1H, C5′—H), 2.42–2.30 (m, 1H, C7′—Ha), 2.28–2.17 (m, 1H, C6′—H), 2.14–2.01 (m, 1H, C6′—H), 2.01–1.93 (m, 1H, C7′—Hb) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 202.0 (q, C10), 177.2 (q, C2), 172.2 (q, C2″), 141.9 (q, C8″), 141.4 (q, C8), 132.8 (q, Cpyrene), 132.7 (q, Cpyrene), 130.6 (q, Cpyrene), 129.9 (q, Cpyrene), 129.4 (C6″H), 129.2 (C6H & CHpyrene), 128.0 (C4″H), 127.7 (C—Cl), 127.2 (2xCHpyrene), 127.1 (q, Cpyrene), 126.7 (CHpyrene), 126.3 (q, C9″), 126.1 (CHpyrene), 125.8 (2xCHpyrene), 125.4 (C4H), 124.6 (q, C9), 123.6 (CHpyrene), 123.5 (q, Cpyrene), 123.4 (q, Cpyrene), 123.3 (CHpyrene), 121.2 (C5″H), 110.5 (C7H), 109.6 (C7″H), 77.1 (C3/C3′), 66.7 (C2′/C3″), 65.4 (C7a'H), 56.7 (C1′H), 46.9 (C5′—CH2), 31.1 (C7′—CH2), 30.2 (C6′—CH2).
4.1.1.3 (1'S,2'R,3S,7a'S)-5-chloro-1-methyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5c) and (1′R,2′S,3S,7a'S)-1-methyl-5-chloro-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones (6c)
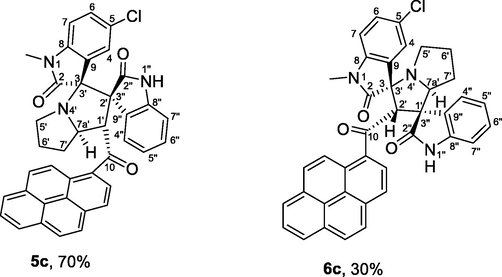
Buff crystals, mp 177–178 °C; 5c: yield 0.374 g (60%) from 235 mg (1.2 mmol) of 1c and 373 mg (1.0 mmol) of 4a. 1H NMR (DMSO‑d6, 400 MHz) δ 9.39 (s, 1H, N1″—H), 8.41–8.02 (m, 7Hpyrene), 7.85 (d, J = 6.8 Hz, 1H, C4″—H), 7.79 (d, J = 9.6 Hz, 1Hpyrene), 7.24 (td, J = 7.6, 0.8 Hz, 1H, C5″—H), 7.17 (td, J = 7.6, 1.2 Hz, 1H, C6″—H), 7.11 (dd, J = 8.0, 2.4 Hz, 1H, C6-H), 7.05 (d, J = 9.2 Hz, 1Hpyrene), 6.81 (d, J = 8.0 Hz, 1H, C7-H), 6.03 (d, J = 8.0 Hz, 1H, C7″—H), 6.14 (d, J = 2.0 Hz, 1H, C4-H), 5.52 (d, J = 8.0 Hz, 1H, C1′—H), 4.78 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 3.05 (s, 3H, N1—CH3), 2.65 (t, J = 8.0 Hz, 1H, C5′—H), 2.59–1.45 (m, 5H, C5′—H, C6′—H2, C7′—H2) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 202.9 (q, C10), 181.2 (q, C2), 177.1 (q, C2″), 143.9 (q), 140.7 (q), 133.6 (q), 133.0 (q), 132.1 (q), 130.8 (q), 130.6 (q), 130.2 (q), 130.1 (CH), 129.9 (q), 129.8 (CH), 128.6 (q), 127.9 (CH), 127.4 (CH), 127.3 (CH), 127.2 (CH), 127.1 (CH), 126.9 (CH), 126.8 (CH), 126.7 (CH), 126.6 (q), 125.8 (CH), 124.7 (CH), 124.5 (CH), 122.3 (CH), 110.3 (CH), 108.4 (C7-H), 75.4 (CH), 72.5 (q), 67.0 (CH), 63.2 (q), 49.9 (CH2), 26.6 (N1—CH3), 26.3 (CH2), 24.5 (CH2). 6c: Yield (0.160 g, 26%) from 235 mg of 1c and 373 mg of 4a. 1H NMR (DMSO‑d6, 400 MHz) δ 10.32 (s, 1H, N1″—H), 8.41–8.02 (m, 7Hpyrene), 7.87 (d, J = 2.0 Hz, 1H, C4-H), 7.79 (d, J = 9.6 Hz, 1Hpyrene), 7.46 (dd, J = 8.0, 2.4 Hz, 1H, C6-H), 7.14 (d, J = 8.0 Hz, 1H, C4″—H), 7.05 (d, J = 9.2 Hz, 1Hpyrene), 6.42 (td, J = 7.6, 1.2 Hz, 1H, C5″—H), 6.13 (td, J = 7.6, 1.2 Hz, 1H, C6″—H), 5.76 (d, J = 8.0, 1H, C7-H), 5.67 (s, 1H, C2′—H), 4.61 (dd, J = 8.4, 2.0 Hz, 1H, C7a′—H), 3.69–3.61 (m, 1H, C5′—H), 2.87 (s, 3H, N1—CH3), 2.59–1.45 (m, 5H, C5′—H, C6′—H2, C7′—H2) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 200.7 (q, C10), 176.0 (q, C2), 172.6 (q, C2″), 142.8 (q), 142.0 (q), 133.2 (q), 132.8 (q), 131.3 (q), 130.7 (q), 130.3 (q), 130.0 (q), 129.8 (CH), 129.6 (CH), 129.5 (CH), 128.7 (q), 128.4 (CH), 128.1 (q), 126.5 (CH), 126.4 (CH), 126.3 (q), 126.2 (CH), 125.9 (CH), 125.7 (CH), 125.2 (CH), 123.9 (CH), 123.7 (CH), 123.4 (CH), 123.2 (q), 121.7 (CH), 109.9 (CH), 109.7 (CH), 77.1 (q), 67.3 (q), 65.7 (CH), 57.1 (CH), 47.1 (CH2), 31.2 (CH2), 30.4 (CH2), 26.2 (N1—CH3).
4.1.1.4 (1'S,2'R,3S,7a'S)-1″-methyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5d)
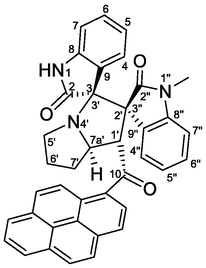
Yellow crystals, mp 183–184 °C; yield 0.475 g (81%) from 176 mg (1.2 mmol) of 1a and 387 mg (1.0 mmol) of 4b. 1H NMR (DMSO‑d6, 400 MHz) δ 10.39 (s, 1H, N1-H), 8.32 (d, J = 7.2 Hz, 1Hpyrene), 8.29–8.23 (m, 3Hpyrene), 8.20 (d, J = 8.0 Hz, 1Hpyrene), 8.11 (d, J = 8.0 Hz, 1Hpyrene), 8.06 (t, J = 8.0 Hz, 1Hpyrene), 7.91 (d, J = 7.2 Hz, 1H, C4″—H), 7.82 (d, J = 9.2 Hz, 1Hpyrene), 7.28 (td, J = 7.6, 0.8 Hz, 1H, C5″—H), 7.16 (td, J = 7.6, 1.2 Hz, 1H, C6″—H), 7.05 (d, J = 9.2 Hz, 1Hpyrene), 6.92 (td, J = 7.6, 1.2 Hz, 1H, C6-H), 6.56 (d, J = 7.6 Hz, 1H, C7-H), 6.38 (td, J = 8.0, 1.2 Hz, 1H, C5-H), 6.24 (d, J = 7.2 Hz, 1H, C4-H), 6.01 (d, J = 7.6 Hz, 1H, C7″—H), 5.52 (d, J = 8.0 Hz, 1H, C1′—H), 4.79–4.72 (m, 1H, C7a′—H), 3.24 (s, 3H, N1″—CH3), 2.71–2.63 (m, 1H, C5′—H), 2.62–2.53 (m, 1H, C5′—H), 2.43–2.30 (m, 1H, C7′—Ha), 2.29–2.20 (m, 1H, C6′—H), 2.15–2.07 (m, 1H, C6′—H), 2.06–1.98 (m, 1H, C7′—Hb) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.8 (q, C10), 177.4 (q, C2), 170.9 (q, C2″), 142.7 (q, C8″), 142.2 (q, C8), 132.4 (q, Cpyrene), 132.1 (q, Cpyrene), 130.5 (q, Cpyrene), 129.2 (C6-H), 129.1 (CHpyrene), 129.0 (C6″H), 127.9 (CHpyrene), 127.2 (q, Cpyrene), 127.1 (CHpyrene), 127.0 (CHpyrene), 126.9 (q, Cpyrene), 126.7 (CHpyrene), 126.2 (CHpyrene), 125.9 (CHpyrene), 125.7 (C4-H), 125.6 (q, C9″), 125.1 (CHpyrene), 124.8 (q, C9), 124.0 (CHpyrene), 123.9 (q, Cpyrene), 123.2 (C4″H), 123.0 (q, Cpyrene), 121.8 (C5″H), 120.4 (C5-H), 109.1 (C7″—H″—H), 108.1 (C7-H), 76.03 (C3/C3′), 65.9 (C2′/C3″), 65.0 (C7a′—H), 57.3 (C1′—H), 46.6 (C5′—CH2), 30.8 (C7′—CH2), 30.0 (C6′—CH2), 26.1 (N1″—CH3).
4.1.1.5 (1'S,2'R,3S,7a'S)-5-chloro-1″-methyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5e)
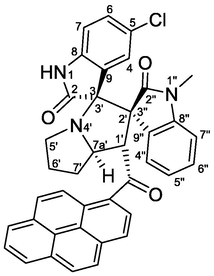
Yellow crystals, mp 239–240 °C; yield 0.466 g (75%) from 218 mg (1.2 mmol) of 1b and 387 mg (1.0 mmol) of 4b. 1H NMR (DMSO‑d6, 400 MHz) δ 10.54 (s, 1H, N1-H), 8.32–8.15 (m, 5Hpyrene), 8.11–8.01 (m, 2Hpyrene), 7.87 (d, J = 7.2 Hz, 1H, C4″—H), 7.80 (d, J = 9.2 Hz, 1Hpyrene), 7.28 (td, J = 7.6, 0.4 Hz, 1H, C5″—H), 7.16 (td, J = 8.0, 1.2 Hz, 1H, C6″—H), 7.04 (d, J = 9.2 Hz, 1Hpyrene), 6.95 (dd, J = 8.4, 2.0 Hz, 1H, C6-H), 6.55 (d, J = 8.4 Hz, 1H, C7-H), 6.14 (d, J = 2.0 Hz, 1H, C4-H), 6.03 (d, J = 7.6 Hz, 1H, C7″—H), 5.44 (d, J = 8.0 Hz, 1H, C1′—H), 4.73 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a'-H), 2.68 (t, J = 8.4 Hz, 1H, C5′—H), 2.56–2.50 (m, 1H, C5′—H), 2.38–2.26 (m, 1H, C7′—Ha), 2.28–2.17 (m, 1H, C6′—H), 2.12–2.04 (m, 1H, C6′—H), 2.04–1.98 (m, 1H, C7′—Hb), 1.60 (s, 3H, N1″—CH3) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.4 (q, C10), 176.8 (q, C2), 170.4 (q, C2″), 142.6 (q, C8″), 141.0 (q, C8), 132.3 (q, Cpyrene), 131.8 (q, Cpyrene), 130.2 (q, Cpyrene), 129.5 (q, Cpyrene), 129.3 (CH), 128.9 (CH), 127.8 (CH), 127.1 (q, Cpyrene), 126.8 (q, Cpyrene), 126.7 (CH), 126.5 (CH), 126.4 (CH), 126.4 (CH), 125.8 (CH), 125.6 (CH), 125.1 (q, Cpyrene), 125.1 (CH), 124.2 (C—Cl), 123.8 (q, Cpyrene), 123.1 (CH), 122.9 (q, Cpyrene), 122.8 (CH), 122.1 (CH), 121.7 (CH), 110.3 (C7-H), 108.2 (C7″—H), 76.3 (C3/C3′), 65.8 (C2′/C3″), 65.0 (C7a′—H), 57.1 (C1′—H), 46.5 (C5′—CH2), 30.8 (C7′—CH2), 29.9 (C6′—CH2), 26.0 (N1″—CH3).
4.1.1.6 (1'S,2'R,3S,7a'S)-5-chloro-1,1″-dimethyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2′'-diones (5f) and (1'R,2'S,3S,7a'S)-5-chloro-1,1″-dimethyl-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones (6f)
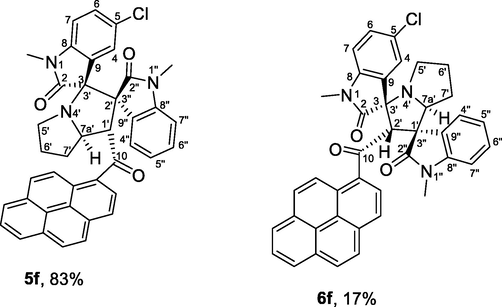
Yellow crystals, mp 155–156 °C; yield 0.451 g (71%) from 235 mg (1.2 mmol) of 1c and 387 mg (1.0 mmol) of 4b. 1H NMR (DMSO‑d6, 400 MHz) δ 8.61–5.97 (23.5H, Ar-H, both isomers), 5.66 (s, 0.47H, minor isomer), 5.49 (d, J = 8.0 Hz, 1H), 4.80 (ddd, J = 10, 8.0, 5.6 Hz, 1H), 4.66 (dd, J = 8.4, 2 Hz, 0.47H, minor isomer), 3.76–3.67 (m, 0.47H, minor isomer), 3.24 (s, 3H, CH3, major isomer), 3.08 (s, 1.42H, CH3, minor isomer), 2.75–1.60 (m, 8.33H, both isomers), 2.84 (s, 1.42H, CH3, minor isomer), 1.53 (s, 3H, CH3, major isomer) ppm; 13C NMR (DMSO‑d6, 100 MHz) major isomer: δ 201.5 (q, C10), 175.5 (q, C2), 170.5 (q, C2″), 142.8 (q), 142.6 (q), 132.7 (q), 132.0 (q), 130.5 (q), 129.8 (q), 128.2 (CH), 128.1 (CH), 127.4 (q), 127.0 (CH), 126.9 (CH), 126.8 (CH), 126.2 (CH), 126.0 (CH), 125.9 (CH), 125.3 (q), 125.1 (q), 125.1 (CH), 124.9 (CH), 124.1 (q), 123.4 (CH), 123.2 (q), 123.0 (CH), 122.9 (q), 122.6 (CH), 122.1 (CH), 109.6 (CH), 108.6 (CH), 76.3 (q), 72.2 (q), 65.3 (CH), 57.3 (CH), 49.8 (CH2), 31.0 (CH2), 30.3 (CH2), 26.1 (N1—CH3), 24.9 (N1″—CH3).
4.1.1.7 (1'S,2'R,3S,7a'S)-5″-chloro-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5g) and (1'R,2'S,3S,7a'S)-5″-chloro-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones (6g)
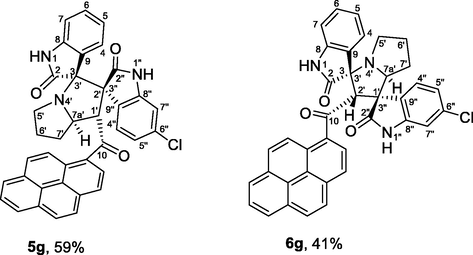
Pink crystals, mp 243–244 °C; yield 0.577 g (95%) from 176 mg (1.2 mmol) of 1a and 408 mg (1.0 mmol) of 4c. 1H NMR (DMSO‑d6, 400 MHz) δ 10.64 (s, 0.69H, N1″—H, minor), 10.44 (s, 1H, N1″—H, major), 10.40 (s, 0.69H, N1′—H, minor), 9.62 (s, 1H, N1′—H, major), 8.66–6.98 (m, 22H, Ar-H), 6.62 (d, J = 7.6 Hz, 1H, major), 6.50 (t, J = 7.6 Hz, 1H, C6-H, major), 6.22 (d, J = 7.2 Hz, 0.69H, C7-H, minor), 6.12 (dd, J = 8.0, 2.0 Hz, 0.69H, C5″—H, minor), 6.11 (d, J = 8.4 Hz, 1H, C4″—H, major), 5.71 (d, J = 8.4 Hz, 0.69H, C4″—H, minor), 5.57 (s, 0.69H, C2′—H, minor), 5.58 (d, J = 8.0 Hz, 1H, C1′—H, major), 4.66 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H, major), 4.60 (dd, J = 8.4, 2 Hz, 0.69H, C7a′—H, minor), 3.69–3.64 (m, 0.69H, minor), 2.69 (t, J = 8.4 Hz, 1H, C5′—H, major), 2.60 (t, J = 8.4 Hz, 0.69H, C5′—H, minor), 2.45–1.52 (m, 7.5H, both isomers) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 202.2 (q, C10, major), 200.4 (q, C10, minor), 180.4 (q, C2″), 178.9 (q, C2″), 177.2 (q C2), 172.2 (q, C2), 143.5 (q), 142.5 (q), 140.9 (q), 139.6 (q), 132.9, 132.7, 132.5, 132.2, 131.4, 129.9, 129.8, 129.7, 129.5 (2xC), 129.4, 129.3, 129.2, 128.9, 128.8, 128.2, 128.0 (2xC), 127.7, 127.6, 127.4, 127.2, 126.9 (2xC), 126.7, 126.6, 126.3, 126.2, 126.0, 125.9 (2xC), 126.2, 126.1, 126.0, 125.9 (2xC), 125.8, 125.6, 125.3, 125.1, 124.9, 124.7, 123.7, 123.6, 123.5, 123.4 (2xC), 123.0 (2xC), 121.2, 120.6, 110.7 (CH), 109.7 (CH), 109.3 (CH), 109.2 (CH), 76.8 (q, major), 74.7 (CH, minor), 72.6 (q, minor), 66.8 (q, major), 66.7 (CH, minor), 65.3 (CH, major), 63.1 (q, minor), 56.9 (CH, major), 49.6 (CH2, minor), 46.38 (CH2, major), 31.0 (CH2, major), 30.0 (CH2, major), 26.2 (CH2, minor), 24.2 (CH2, minor).
4.1.1.8 (1'S,2'R,3S,7a'S)-5,5″-dichloro-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5h) and (1'R,2'S,3S,7a'S)-5,5″-dichloro-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3′'-indoline]-2,2″-diones (6h)
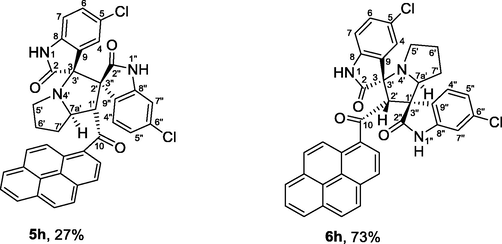
Buff crystals, mp 241–242 °C; 5h: yield (0.158 g, 25%) from 218 mg (1.2 mmol) of 1b and 408 mg (1.0 mmol) of 4c. 1H NMR (DMSO‑d6, 400 MHz) δ 10.61 (s, 1H, NH), 9.70 (s, 1H, NH), 8.40–6.00 (m, 15H, Ar-H), 5.68 (d, J = 8.0 Hz, 0.1H, C1′—H), 4.68 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 2.72 (t, J = 8.4 Hz, 1H, C5′—H), 2.42–1.50 (m, 5H, C5′—H, C6′—H2, C7′—H2) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 202.5 (q, C10), 177.3 (q), 172.5 (q), 141.9 (q), 140.4 (q), 133.2 (q), 132.9 (q), 131.0 (q), 130.9 (q), 129.8 (CH), 129.7 (q, CH), 129.6 (CH), 129.0 (q), 128.1 (CH), 128.0 (q), 127.1 (CH), 127.1 (CH), 126.7 (CH), 126.6 (q, CH), 126.4 (q, CH), 126.3 (CH), 125.9 (q), 125.6 (q, CH), 124.1 (CH), 124.0 (q), 123.8 (CH), 123.4 (CH), 111.4 (CH), 111.2 (CH), 77.3 (q), 67.3 (q), 65.9 (CH), 57.3 (CH), 47.3 (CH2), 31.5 (CH2), 30.5 (CH2). 6h: Yield (0.426 g, 66%) from 218 mg of 1b and 408 mg of 4c. 1H NMR (DMSO‑d6, 400 MHz) δ 10.80 (s, 1H, NH), 10.43 (s, 1H, NH), 8.40–6.00 (m, 15H, Ar-H), 5.66 (s, 1H, C2′—H), 4.57 (dd, J = 8.4, 2 Hz, 1H, C7a′—H), 3.67–3.59 (m, 1H, C5′—H), 2.61 (t, J = 8.4 Hz, 1H, C5′—H), 2.42–1.50 (m, 4H, C6′—H2, C7′—H2) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.1 (C10, q), 180.7 (q), 179.1 (q), 142.8 (q), 140.1 (q), 133.3 (q), 132.7 (q), 131.8 (q), 130.2 (q), 130.0 (CH), 129.8 (CH), 129.7 (q, CH), 128.7 (CH), 128.5 (CH), 127.4 (CH), 127.3 (CH), 128.1 (q), 126.7 (CH), 126.6 (q, CH,), 126.4 (q, CH), 126.2 (CH), 126.0 (CH), 125.6 (q, CH), 124.2 (CH), 123.8 (q), 123.7 (CH), 123.5 (q), 111.4 (CH), 109.6 (CH), 75.0 (CH), 73.2 (q), 67.2 (CH), 65.9 63.4 (q), 50.1 (CH2), 26.6 (CH2), 24.7 (CH2).
4.1.1.9 (1'R,2'S,3S,7a'S)-5,5″-dichloro-1-methyl-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3″-indoline]-2,2″-diones (6i)
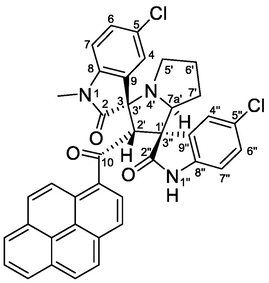
Yellow crystals, mp 230–231 °C; yield 0.512 g (78%) from 235 mg (1.2 mmol) of 1c and 408 mg (1.0 mmol) of 4c. 1H NMR (DMSO‑d6, 400 MHz) δ 10.43 (s, 1H, N1″—H), 8.30 (d, J = 8.0 Hz, 2Hpyrene), 8.26 (d, J = 8.0 Hz, 1Hpyrene), 8.20 (d, J = 6.0 Hz, 1Hpyrene), 8.16 (d, J = 6.4 Hz, 1Hpyrene), 8.14 (d, J = 1.6 Hz, 1H, C4″—H), 8.12–8.11 (m, 2Hpyrene), 8.07 (t, J = 4.8 Hz, 1Hpyrene), 8.04 (d, J = 6.0 Hz, 1Hpyrene), 7.92 (d, J = 1.2 Hz, 1H, C4-H), 7.48 (dd, J = 5.6, 1.2 Hz, 1H, C6-H), 7.17 (d, J = 5.6 Hz, 1H, C7-H), 6.05 (dd, J = 5.6, 1.6 Hz, 1H, C6″—H), 5.70 (s, 1H, C2′—H), 5.68 (d, J = 5.6 Hz, 1H, C7″—H), 4.59 (dd, J = 6.0, 1.6 Hz, 1H, C7a′—H), 3.65 (dd, J = 8.0, 4.0 Hz, 1H, C5′—H), 3.39 (s, 3H, N1—CH3), 2.59 (t, J = 8.0 Hz, 1H, C5′—H), 1.95–1.88 (m, 1H, C7′—H), 1.87–1.80 (m, 1H, C6′—H), 1.69–1.60 (m, 1H, C6′—H), 1.59–1.50 (m, 1H, C7′—H) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 200.3 (q, C10), 179.9 (q, C2″), 176.6 (q, C2), 143.4 (q, C8), 139.3 (q, C8″), 132.6 (q, C9″), 131.8 (q, Cpyrene), 130.9 (C—Cl), 130.1 (C—Cl), 129.5 (q, Cpyrene), 129.4 (C6H), 129.1 (CHpyrene), 128.1 (q, Cpyrene), 127.8 (CHpyrene), 127.3 (q, Cpyrene), 126.7 (CHpyrene), 126.6 (CHpyrene), 126.4 (C6″H), 126.0 (CHpyrene), 125.9 (CHpyrene), 125.8 (q, C9″), 125.7 (C4H), 125.6 (q, Cpyrene), 125.5 (CHpyrene), 125.4 (C4″H), 123.5 (CHpyrene), 123.0 (q, Cpyrene), 122.9 (CHpyrene), 122.73 (q, Cpyrene), 109.7 (C7H), 108.9 (C7″H), 74.4 (C7a'H), 72.1 (C3/C3′), 66.5 (C2′H), 62.7 (C1′/C3″), 49.4 (C5′—CH2), 26.1 (N1—CH3), 25.9 (C6′—CH2), 24.0 (C6′—CH2).
4.1.1.10 (1'S,2'R,3S,7a'S)-5″-chloro-1″-methyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5j)
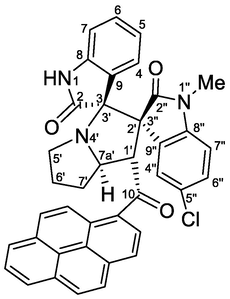
Pale yellow crystals, mp 262–263 °C; yield 0.516 g (83%) from 176 mg (1.2 mmol) of 1a and 422 mg (1.0 mmol) of 4d. 1H NMR (DMSO‑d6, 400 MHz) δ 10.45 (s, 1H, N1-H), 8.37–8.01 (m, 7Hpyrene), 7.92 (d, J = 9.6 Hz, 1Hpyrene), 7.84 (d, J = 2.4 Hz, 1H, C4″—H), 7.22 (d, J = 9.6 Hz, 1Hpyrene), 7.19 (dd, J = 8.4, 2.4 Hz, 1H, C6″—H), 6.95 (td, J = 7.6, 0.8 Hz, 1H, C6-H), 6.59 (d, J = 7.6 Hz, 1H, C7-H), 6.46 (td, J = 7.6, 1.2 Hz, 1H, C5-H), 6.22 (d, J = 7.2 Hz, 1H, C4-H), 6.05 (d, J = 8.4 Hz, 1H, C7″—H), 5.52 (d, J = 8.0 Hz, 1H, C1′—H), 4.67 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 2.71–2.64 (m, 1H, C5′—H), 2.60–2.54 (m, 1H, C5′—H), 2.45–2.34 (m, 1H, C7′—Ha), 2.28–2.20 (m, 1H, C6′—H), 2.13–2.02 (m, 1H, C6′—H), 2.01–1.94 (m, 1H, C7′—Hb), 1.68 (s, 3H, N1″—CH3) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.7 (q, C10), 176.9 (q, C2), 170.4 (q, C2″), 142.1 (q, C8″), 141.6 (q, C8), 132.4 (q), 131.6 (q), 130.2 (q), 129.5 (q), 129.3 (CH), 129.0 (CH), 128.8 (CH), 128.0 (CH), 127.6 (q), 127.0 (q), 126.7 (CH), 126.4 (CH), 126.1 (CH), 126.0 (CH), 126.0 (q), 125.7 (CH), 125.6 (CH), 124.6 (CH), 124.3 (q), 123.1 (CH), 122.9 (2xq), 122.4 (C5″H), 120.4 (C5H), 109.4 (C7″H), 109.1 (C7H), 76.1 (C3/C3′), 65.9 (C2′/C3″), 65.0 (C7a'H), 57.2 (C1′H), 46.6 (C5′—CH2), 30.8 (C7′—CH2), 29.8 (C6′—CH2), 24.9 (N1″—CH—CH3).
4.1.1.11 (1'S,2'R,3S,7a'S)-5,5″-dichloro-1″-methyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5k) and (1'R,2'S,3S,7a'S)-5,5″-dichloro-1″-methyl-2′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-1′,3′'-indoline]-2,2″-diones (6k)
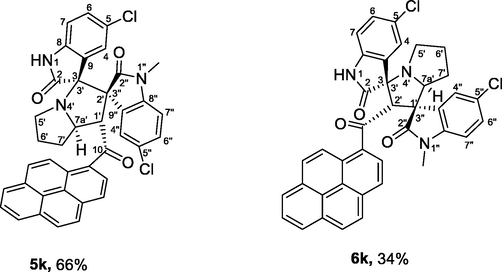
Yellow crystals, mp 159–160 °C; 5k: yield (0.364 g, 55%) from 218 mg (1.2 mmol) of 1b and 422 mg (1.0 mmol) of 4d. 1H NMR (DMSO‑d6, 400 MHz) δ 10.60 (s, 1H, N1-H, major), 8.35–8.03 (m, 7Hpyrene), 7.92 (d, J = 9.2 Hz, 1Hpyrene), 7.85 (d, J = 2.4 Hz, 1H, C4″—H), 7.24 (dd, J = 8.4, 2.0 Hz, 1H, C6″—H), 7.22 (d, J = 9.2 Hz, 1Hpyrene), 7.01 (dd, J = 8.4, 2.0 Hz, 1H, C6-H), 6.60 (d, J = 8.4 Hz, 1H, C7-H), 6.16 (d, J = 2.2 Hz, 1H, C4-H), 6.10 (d, J = 8.4 Hz, 1H, C7″—H), 5.47 (d, J = 8.0 Hz, 1H, C1′—H), 4.69 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 2.72 (t, 1H, J = 8.4 Hz, C5′—H), 2.44–2.34 (m, 2H, C5′—H & C7′—Ha), 2.26–1.98 (m, 3H, C6′—CH2 & C7′—Hb), 1.72 (s, 3H, N1″—CH3) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.5 (q, C10), 176.6 (q, C2), 170.2 (q, C2″), 141.6 (q, C8″), 141.0 (q, C8), 132.5 (q), 131.5 (q), 130.3 (q), 129.5 (q), 129.2 (CH), 129.1 (CH), 128.1 (CH), 126.8 (CH), 127.3 (q), 127.0 (q), 126.8 (CH), 126.5 (CH), 126.3 (q), 126.1 (q), 126.0 (CH), 126.0 (2CH), 125.7 (CH), 125.6 (CH), 124.8 (CH), 124.3 (q), 123.1 (CH), 122.9 (q, 2xC), 122.4 (CH), 110.5 (C7″H), 109.7 (C7H), 76.2 (C3/C3′), 65.9 (C2′/C3″), 65.1 (C7a′—H), 57.2 (C1′—H), 46.5 (C5′—CH2), 30.8 (C7′—CH2), 29.8 (C6′—CH2), 25.0 (N1″—CH3). 6k: Yield (0.188 g, 29%) from 218 mg of 1b and 422 mg of 4d. 1H NMR (DMSO‑d6, 100 MHz) δ 10.78 (s, 1H, N1-H), 8.30 (d, J = 8.0 Hz, 2Hpyrene), 8.20 (d, J = 8.8 Hz, 1Hpyrene), 8.15 (d, J = 8.8 Hz, 1Hpyrene), 8.14 (d, J = 1.6 Hz, 1H, C4″—H), 8.12–8.00 (m, 5Hpyrene), 7.83 (d, J = 2.4 Hz, 1H, C4-H), 7.36 (dd, J = 8.4, 2.0 Hz, 1H, C6-H), 6.96 (d, J = 8.4 Hz, 1H, C7-H), 5.94 (dd, J = 8.0, 2.0 Hz, 1H, C6″—H), 5.67 (d, J = 8.4 Hz, 1H, C7″—H), 5.61 (s, 1H, C2′—H, minor), 4.55 (dd, J = 8.8, 3.6 Hz, 1H, C7a′—H), 3.63 (dd, J = 8.0, 4.0 Hz, 1H, C5′—H), 2.80 (s, 3H, N1″—CH3), 2.60 (t, J = 8.0 Hz, 1H, C5′—H), 1.90–1.76 (m, 2H, C6′—H & C7′—H), 1.69–1.57 (m, 1H, C7′—H), 1.46–1.38 (m, 1H, C6′—H) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 200.2 (q, C10), 178.3 (q, C2), 178.0 (q, C2″), 142.1 (q, C8″), 140.6 (q, C8), 132.7 (q), 131.0 (q), 130.7 (q), 130.1 (q), 129.4 (q), 129.3 (CH), 129.0 (CH), 128.9 (q), 127.9 (CH), 127.2 (q), 126.7 (CH), 126.6 (q), 126.4 (2xCH), 126.0 (CH), 126.1 (CH), 125.9 (CH), 125.2 (CH), 125.1 (CH), 124.9 (q), 123.3 (CH), 123.0 (q), 122.7 (q), 122.2 (CH), 110.7 (C7″H), 107.7 (C7-H), 73.5 (C7a′—H), 72.5 (C3/C3′), 67.3 (C2′—H), 62.1 (C1′/C3″), 49.5 (C5′—CH2), 26.1 (N1″—CH3), 25.9 (C7′—CH2), 24.0 (C6′—CH2).
4.1.1.12 (1'S,2'R,3S,7a'S)-5,5″-dichloro-1,1″-dimethyl-1′-(1-pyrenoyl)-dispiro[indoline-3,3′-pyrrolizidine-2′,3″-indoline]-2,2″-diones (5l)
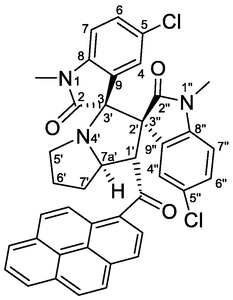
Yellow crystals, mp 206–208 °C; yield 0.449 g (67%) from 235 mg (1.2 mmol) of 1c and 422 mg (1.0 mmol) of 4d. 1H NMR (DMSO‑d6, 400 MHz) δ 8.36–8.17 (m, 5Hpyrene), 8.12–8.05 (m, 2Hpyrene), 7.92 (d, J = 9.2 Hz, 1Hpyrene), 7.86 (d, J = 2.4 Hz, 1H, C4″—H), 7.24 (dd, J = 8.4, 2.0 Hz, 1H, C6″—H), 7.22 (d, J = 9.2 Hz, 1Hpyrene), 7.12 (dd, J = 8.4, 2.0 Hz, 1H, C6-H), 6.82 (d, J = 8.4 Hz, 1H, C7-H), 6.22 (d, J = 2.2 Hz, 1H, C4-H), 6.06 (d, J = 8.4 Hz, 1H, C7″—H), 5.49 (d, J = 8.0 Hz, 1H, C1′—H), 4.73 (ddd, J = 10, 8.0, 5.6 Hz, 1H, C7a′—H), 3.08 (s, 3H, N1″—CH3), 2.70 (t, 1H, J = 8.4 Hz, C5′—H), 2.47–2.35 (m, 2H, C5′—H & C7′—Ha), 2.26–2.00 (m, 3H, C6′—CH—CH2 & C7′—Hb), 1.60 (s, 3H, N1—CH3) ppm; 13C NMR (DMSO‑d6, 100 MHz) δ 201.5 (q, C10), 175.2 (q, C2), 170.3 (q, C2″), 142.6 (q, C8″), 141.8 (q, C8), 132.8 (q, Cpyrene), 131.7 (q, Cpyrene), 130.5 (q, Cpyrene), 129.8 (q, Cpyrene), 129.5 (CH), 129.4 (2xCH), 128.4 (CH), 127.3 (q, Cpyrene), 127.2 (q, Cpyrene), 127.0 (CH), 126.8 (CH), 126.5 (q, Cpyrene), 126.3 (2xCH), 126.1 (CH), 126.0 (CH), 125.9 (q, Cpyrene), 125.4 (q, Cpyrene), 124.7 (CH), 123.5 (CH), 123.2 (2xC—Cl), 122.6 (CH), 110.1 (C7H), 109.8 (C7″H), 76.2 (C3/C3′), 65.5 (C2′/C3″), 65.4 (C7a'H), 57.4 (C1′H), 46.9 (C5′—CH2), 31.0 (C7′—CH2), 30.2 (C6′—CH2), 26.1 (N1″—CH3), 25.2 (N1—CH3).
4.2 Computational details
Quantum chemical calculations were performed to obtain cycloaddition free energy profiles following a previously published protocol (Domingo, 2016). Geometry optimizations were performed in vacuum with density functional theory (DFT) using the B3LYP exchange correlation functional (Miehlich et al., 1989) and the People's double-zeta basis set (6-31G) with additional polarization function and diffuse function on the heavy atoms (B3LYP/6-31G+(d)) as implemented in Gaussian 16 software. Frequency calculations were performed with the optimized ground-state and transition-state geometries at the same level of theory. Relative energies were calculated with respect to the sum of the energies of the reactants. The energy values were converted to kcal/mol by Hartree per particle, using 627.509467 as the conversion factor.
The global electronic properties of series 3a-c and compounds 4a-d were estimated according to the equations of Parr and Domingo (Velikorodov et al., 2011; Domingo et al., 2002). The electronic chemical potential μ and chemical hardness η were both determined from the one-electron energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), EHOMO and ELUMO, as μ = (EHOMO + ELUMO)/2 and η = (ELUMO − EHOMO), respectively. Then, the global electrophilicity (ω) was calculated using the electronic chemical potential (μ) and chemical hardness (η) according to the formula ω = μ2/2η. Then, the global nucleophilicity (N) is expressed as follows: N = EHOMO − EHOMO(TCE), where tetracyanoethylene (TCE) was used as a reference because it provides the lowest HOMO energy of many organic molecules previously studied in polar cycloadditions.
Regional Fukui functions for electrophilic (fk−) and nucleophilic (fk+) attacks were obtained from a one-point calculation on the optimized ground state structures of the molecules, as described in the literature (Miehlich et al., 1989). The electrophilic (Pk+) and nucleophilic (Pk−) Parr functions were obtained by analyzing the Mulliken atomic spin densities of the radical anion and radical cation, respectively, by one-point energy calculations over the optimized neutral geometries using the unrestricted B3LYP formalism for radical species (Parr et al., 1999).
CRediT authorship contribution statement
Essam M. Hussein: Conceptualization, Methodology, Data curation, Validation, Investigation, Visualization, Project administration, Supervision, Funding acquisition, Writing – review & editing. Ziad Moussa: Data curation, Validation, Funding acquisition, Visualization. Uttam Pal: Software, Visualization. Reem I. Alsantali: Data curation, Validation, Investigation, Funding acquisition. Abdullah Y.A. Alzahrani: Data curation, Validation, Investigation, Funding acquisition. Rami J. Obaid: Data curation, Validation, Investigation, Funding acquisition. Fawaz M. Alzahrani: Methodology, Data curation, Validation, Investigation. Munirah M. Al-Rooqi: Data curation, Validation, Investigation, Funding acquisition. Meshari A. Alsharif: Data curation, Validation, Investigation, Funding acquisition. Nizar El Guesmi: Validation, Data curation, Investigation. Rabab S. Jassas: Data curation, Validation, Investigation, Funding acquisition. M. Shaheer Malik: . Hatem M. Altass: . Samir K. Pal: Validation. Tanusri Saha Dasgupta: Validation. Saleh A. Ahmed: Conceptualization, Methodology, Data curation, Validation, Investigation, Visualization, Project administration, Supervision, Funding acquisition, Writing – review & editing.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Small Research Project under grant number (RGP.1/124/42). The authors would like to acknowledge the Deanship of Scientific Research at Umm Al-Qura University, for supporting this work by Grant code: 22UQU4350067DSR01. Also, the authors would like to extend their sincere appreciation to Taif University Researchers Supporting Project number (TURSP-2020/312), Taif University, Taif, Saudi Arabia. Dr. Ziad Moussa is grateful to the United Arab Emirates University (UAEU) of Al-Ain and to the Research Office for supporting the research developed in his laboratory (Grant no. G00003291).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Novel regio- and stereoselective synthesis of functionalized 3-spiropyrrolidines and 3-spiropyrrolizidines using the Baylis-Hillman adducts derived from nitroolefins. Synlett 2009:1014-1018.
- [Google Scholar]
- (a) G. Bifulco, P. Dambruoso, L. Gomez-Paloma, R. Riccio, Determination of relative configuration in organic compounds by NMR spectroscopy and computational methods, Chem. Rev. 2007, 107, 3744-3779; (b) X. Zhang, K-Z. Lu, H-W. Yan, Z-M. Feng, Y-N. Yang, J.-S. Jiang, P-C. Zhang, An ingenious method for the determination of the relative and absolute configurations of compounds containing aryl-glycerol fragments by 1H NMR spectroscopy RSC Adv., 2021, 11, 8107; (c) X. Li, K.H. Hopmann, J. Hudecová, J. Isaksson, J. Novotná, W. Stensen, V. Andrushchenko, M. Urbanová, J-S. Svendsen, P. Bouř, K. Ruud, Determination of absolute configuration and conformation of a cyclic dipeptide by NMR and chiral spectroscopic methods, J. Phys. Chem. A, 2013, 117, 1721-1736; (d) Y. Takeuchi, H. Fujisawa, R. Noyori, A very reliable method for determination of absolute configuration of chiral secondary alcohols by 1H NMR spectroscopy, Org. Lett., 2004, 6, 4607-4610; (e) T. J. Wenzel, Strategies for using NMR spectroscopy to determine absolute configuration, Tetrahedron: Asymmetry, 2017, 28, 1212-1219. (f) Y-N. Yang, B. Han, P-F. Yang, Z-M. Feng, J-S. Jiang, P-C. Zhang, A concise approach for determining the relative configuration of H-7 and H-8 in 8,4′-oxyneolignans by 1H NMR spectroscopy, Org. Chem. Front., 2019,6, 886-891.
- (a) Contreras, R. R.; Fuentealba, P.; Galván, M.; Pérez, P. A direct evaluation of regional Fukui functions in molecules. Chem. Phys. Lett. 1999, 304, 405–413. (b) Fuentealba, P.; Pérez, P.; Contreras, R. On the condensed Fukui function. The J. Chem. Phys. 2000, 113, 2544–2551.
- Molecular electron density theory: A Modern View of Reactivity in Organic Chemistry. Molecules. 2016;21:1319.
- [Google Scholar]
- Quantitative characterization of the local electrophilicity of organic molecules. Understanding the regioselectivity on Diels−Alder reactions. J. Phys. Chem. A.. 2002;106:6871-6875.
- [Google Scholar]
- (a) Domingo, L. R.; Aurell, M. J.; Perez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions Tetrahedron 2002, 58, 4417-4423. (b) Pérez, P.; Domingo, L. R.; Aurell, M. J.; Contreras, R. Quantitative characterization of the global electrophilicity pattern of some reagents involved in 1,3-dipolar cycloaddition reactions Tetrahedron 2003, 59, 3117-3125. (c) Arroyo, P.; Picher, M. T.; Domingo, L. R. The domino reaction between 4, 6-dinitrobenzofuroxan and cyclopentadiene. Insights on the nature of the molecular mechanism J. Mol. Struct. 2004, 709, 45-52. (d) Arroyo, P.; Picher, M. T.; Domingo, L. R.; Terrier, F. A DFT study of the polar Diels–Alder reaction between 4-aza-6-nitrobenzofuroxan and cyclopentadiene Tetrahedron 2005, 61, 7359-7365.
- (a) H.A. Dondas, C.W.G. Fishwick, R. Grigg, C. Kilner, 1,3-Dipolar cycloaddition of stabilised and non-stabilised azomethine ylides derived from uracil polyoxin C (UPoC): access to nikkomycin analogues, Tetrahedron 2004, 60, 3473; (b) M. Poornachandran, R. Raghunathan, Synthesis of spirooxindolo/spiroindano nitro pyrrolizidines through regioselective azomethine ylide cycloaddition reaction, Synth. Commun., 2007, 37, 2507; (c) M. Boruah, D. Konwar, S.D. Sharma, KF/Al2O3 mediated 1,3-dipolar cycloaddition of azomethine ylides: a novel and convenient procedure for the synthesis of highly substituted pyrrolidines, Tetrahedron Lett. 2007, 48, 4535; (d) K. Kawashima, A. Kakehi, M. Noguchi, Generation of functionalized azomethine ylides and their application to stereoselective heterocycle synthesis: an equivalent process of C-unsubstituted nitrile ylide cycloaddition reaction, Tetrahedron 2007, 63, 1630.
- (a) Hussein, E. M.; Abdel-Monem, M. I. Regioselective synthesis and anti-inflammatory activity of novel dispiro[pyrazolidine-4,3'-pyrrolidine-2',3“-indoline]-2”,3,5-triones Arkivoc 2011, 10, 85-98. (b) Hussein, E. M.; Ahmed, S. A.; El Guesmi, N.; Khairou, K. S. 1,3-Dipolar cycloaddition approach to novel dispiro[pyrazolidine-4,3'-pyrrolizidine-2',3''-indoline]-2'',3,5-triones J. Chem. Res. 2017, 41, 346–351. (c) Hussein, E. M.; Ahmed, S. A.; Althagafi, I. I. A convenient regioselective synthesis of novel spirooxindolinopyrrolizidines incorporating the pyrene moiety through [3 + 2]-cycloaddition reaction Heterocycl. Commun. 2017, 23, 379–384. (d) Hussein, E. M.; Moussa, Z.; Ahmed, S. A. Exclusive regioselective 1,3-dipolar cycloaddition of 9-diazo-9H-fluorene and diphenyldiazomethane to 2-arylideneindane-1,3-diones: new approach toward effective synthesis of novel spiropyrazole derivatives Monatsh. Chem. 2018, 149, 2021–2030. (e) Hussein, E. M.; Moussa, Z.; El Guesmi, N.; Ahmed, S. A. Facile access to regio- and stereoselective synthesis of highly functionalized spiro[indoline-3,2'-pyrrolidines] incorporating a pyrene moiety: experimental, photophysical and theoretical approach. RSC Adv. 2018, 8, 24116-24127. (f) Hussein, E. M.; El Guesmi, N.; Moussa, Z.; Pal, U.; Pal, S. K.; Saha-Dasgupta, T.; Ahmed, S. A. Unprecedented regio- and stereoselective synthesis of pyrene-grafted dispiro[indoline-3,2'-pyrrolidine-3,3“-indolines]: expedient experimental and theoretical insights into polar [3 + 2] cycloaddition. ACS Omega , 2020, 5, 24081−24094.
- A further exploration of a nucleophilicity index based on the gas-phase ionization potentials. J. Mol. Struct. THEOCHEM.. 2008;865:68-72.
- [Google Scholar]
- (a) P. Merino, J. Revuelta, T. Tejero, U. Chiacchio, A. Rescifinab, G. Romeoc, A DFT study on the 1,3-dipolar cycloaddition reactions of C-(methoxycarbonyl)-N-methyl nitrone with methyl acrylate and vinyl acetate, Tetrahedron, 2003, 59, 3581; (b) W. Benchouk, S.M. Mekelleche, M.J. Aurell, L.R. Domingo, Understanding the regio-and chemoselective polar [3 + 2] cycloaddition of the Padwa carbonyl ylides with α-methylene ketones. A DFT study, Tetrahedron, 2009, 65, 4644; (c) G. Bentabed-Ababsa, A. Derdour, T. Roisnel, J.A. Saez, P. Perez, E. Chamorro, L.R. Domingo, F.A. Mongin, A combined experimental and theoretical study of the polar [3+2] cycloaddition of electrophilically activated carbonyl ylides with aldehydes and imines, J. Org. Chem. 2009, 74, 2120; (d) A.K. Nacereddine, W. Yahia, S. Bouacha, A. Djerourou, A theoretical investigation of the regio- and stereoselectivities of the 1,3-dipolar cycloaddition of C-diethoxyphosphoryl-N-methylnitrone with substituted alkenes, Tetrahedron Lett. 2010, 51, 2617; (e) A. R. Suresh Babu and R. Raghunathan, Ultrasonic assisted-silica mediated [3+2] cycloaddition of azomethine ylides—a facile multicomponent one-pot synthesis of novel dispiroheterocycles, Tetrahedron 2007, 48, 6809.
- (a) Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. (b) Becke, A. D. Density‐functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652.
- (a) R.J. Monlineux, In Alkaloids: Chemical and biological perspective; Pelletier, S. W., Ed.; Wiley: New York, NY, 1987; Chapter 1; (b) S. Fujimori, Jap. Pat. Appl. 88-2912; Chem. Abstr. 1990, 112, 98409.
- Synthetic Applications of 1,3 Dipolar Cycloaddition Chemistry toward Heterocycles and Natural Products. John Wiley & Sons Inc.; 2002.
- (a) Parr, R. G.; Szentpály, L.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. (b) Pérez, P.; Toro-Labbé, A.; Aizman, A.; Contreras, R. Comparison between experimental and theoretical scales of electrophilicity in benzhydryl cations. J. Org. Chem. 2002, 4747–4752. (c) Domingo, L. R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. (d) Domingo, L. R.; Pérez, P. The nucleophilicity N index in organic chemistry. Org. Biomol. Chem. 2011, 9, 7168–7175. (e) Chattaraj, K.; Duley, P. S.; Domingo, L. R. Understanding local electrophilicity/nucleophilicity activation through a single reactivity difference index. Org. Biomol. Chem. 2012, 10, 2855–2861. (f) Domingo, L. R.; Pérez, P.; Sáez, J. A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. (g) Domingo, L. R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules. 2016, 21, 748.
- (a) W.G. Rajeswaran, R.B. Labroo, E.A. Cohen, Synthesis of 5-[(indol-2-on-3-yl)methyl]-2,2-dimethyl-1,3- dioxane-4,6-diones and spirocyclopropyloxindole derivatives. Potential aldose reductase inhibitors, J. Org. Chem. 64 (1999) 1369; (b) J.F.M. da Silva, S.J. Garden, A.C. Pinto, The Chemistry of Isatins: a Review from 1975 to 1999, J. Braz. Chem. Soc. 2001, 12, 273; (c) C.V. Galliford, K.V. Scheidt, Pyrrolidinyl-spirooxindole natural products as inspirations for the development of potential therapeutic agents, Angew. Chem. Int. Ed. 2007, 46, 8748; (d) P. Shanmugam, B. Viswambharan, K. Selvakumar, S. Madhavan, A facile and efficient synthesis of highly functionalised 3,3′-dispiropyrrolidine- and 3,3′-dispiropyrrolizidine bisoxindoles via [3+2] cycloaddition, Tetrahedron Lett. 2008, 49, 2611.
- (a) M. Rios-Gutierrez, L.R. Domingo, Unravelling the mysteries of the [3+2] cycloaddition reactions, Eur. J. Org. Chem., 2019, 267; (b) R. Jasiński, A new insight on the molecular mechanism of the reaction between (Z)-C,N-diphenylnitrone and 1,2-bismethylene-3,3,4,4,5,5-hexamethylcyclopentane, J. Mol. Graphics Modell. 2019, 94, 107461; (c) R. Jasiński, In the searching for zwitterionic intermediates on reaction paths of [3 + 2] cycloaddition reactions between 2,2,4,4-tetramethyl-3-thiocyclobutanone S-methylide and polymerizable olefins, RSC Adv. 2015, 5, 101045; (d) R. Jasiński, Competition between one-step and two-step mechanism in polar [3 + 2] cycloadditions of (Z)-C-(3,4,5-trimethoxyphenyl)-N-methyl-nitrone with (Z)-2-EWG-1-bromo-1-nitroethenes, Comput. Theor. Chem. 2018, 1125, 77; (e) R. Jasiński, M. Ziółkowska, O. Demchuk, A. Maziarka, Regio- and stereoselectivity of polar [2+3] cycloaddition reactions between (Z)-C-(3,4,5-trimethoxyphenyl)-N-methylnitrone and selected (E)-2-substituted nitroethenes, Cent. Eur. J. Chem. 2014, 12, 586; (f) R. Jasiński, A stepwise, zwitterionic mechanism for the 1,3-dipolar cycloaddition between (Z)-C-4-methoxyphenyl-N-phenylnitrone and gem-chloronitroethene catalysed by 1-butyl-3-methylimidazolium ionic liquid cations, Tetrahedron Lett. 2015, 56, 532; (g) B. Braida, C. Walter, B. Engels, P. C. Hiberty, A clear correlation between the diradical character of 1,3-dipoles and their reactivity toward ethylene or acetylene, J. Am. Chem. Soc. 2010, 132, 7631; (h) L.R. Domingo, M. Ríos-Gutiérrez, A molecular electron density theory study of the reactivity of azomethine imine in [3+2] cycloaddition reactions, Molecules, 2017, 22, 750; (i) M. Ríos-Gutiérrez, L. Nasri, N. A. Khorief, A. Djerourou, L. R. Domingo, A molecular electron density theory study of the [3 + 2] cycloaddition reaction between an azomethine imine and electron deficient ethylenes, J. Phys. Org. Chem. 2018, 31, e3830; (j) D. H. Ess, K. N. Houk, Theory of 1,3-dipolar cycloadditions: distortion/interaction and frontier molecular orbital models, J. Am. Chem. Soc. 2008, 130, 10187–10198; (k) R. A. Firestone, The low energy of concert in many symmetry-allowed cycloadditions supports a stepwise-diradical mechanism, Int. J. Chem. Kinet. 2013, 45, 415–428. (l) L. R. Domingo, M. Rios-Gutierrez, P. Perez, A molecular electron density theory study of the role of the copper metalation of azomethine ylides in [3 + 2] cycloaddition reactions, J. Org. Chem. 2018, 83, 2182–219(m) A. S. Novikov; M. L. Kuznetsov. Theoretical study of Re(IV) and Ru(II) bis-isocyanide complexes and their reactivity in cycloaddition reactions with nitrones, Inorg. Chim. Acta, 2012, 380, 78-89. (n) A.S. Novikov; M.L. Kuznetsov; A.J.L. Pombeiro. Theory of the formation and decomposition of n-heterocyclic aminooxycarbenes through metal-assisted [2+3]-dipolar cycloaddition/retro-cycloaddition. Chem. Eur. J., 2013, 19, 2874-2888. (o) M.A. Kinzhalov, A.S. Novikov, K.V. Luzyanin, M. Haukka, A.J. Pombeiro, V.Y. Kukushkin. Pd II-mediated integration of isocyanides and azide ions might proceed via formal 1, 3-dipolar cycloaddition between RNC ligands and uncomplexed azide. New J. Chem. 2016, 19, 521-52(p) M.A. Kinzhalov, A.S. Legkodukh, T.B. Anisimova, A.S. Novikov, V.V. Suslonov, K.V. Luzyanin, V.Y. Kukushkin. Tetrazol-5-ylidene gold (III) complexes from sequential [2+ 3] cycloaddition of azide to metal-bound Isocyanides and N4 alkylation. Organometallics 2017, 36, 3974-3980. (q) A. A. Melekhova, A. S. Smirnov, A. S. Novikov, T. L. Panikorovskii, N. A. Bokach, V. Y. Kukushkin. Copper(I)-catalyzed 1,3-dipolar cycloaddition of ketonitrones to dialkylcyanamides: a step toward sustainable generation of 2,3-dihydro-1,2,4-oxadiazoles, ACS Omega 2017, 2, 1380-1391. (r) A.Y. Dubovtsev, V.V. Zvereva, N.V. Shcherbakov, D.V. Dar'in, A.S. Novikov, V.Y. Kukushkin. Acid-catalyzed [2+ 2+ 2] cycloaddition of two cyanamides and one ynamide: highly regioselective synthesis of 2, 4, 6-triaminopyrimidines. Org. Biomol. Chem. 2021, 19, 4577-4584. (s) E.V. Sirotkina, M.M. Efremova, A.S. Novikov, V.V. Zarubaev, I.R. Orshanskaya , G.L. Starova, R.R. Kostikov, A.P. Molchanov. Regio-and diastereoselectivity of the cycloaddition of aldonitrones with benzylidenecyclopropane: An experimental and theoretical study. Tetrahedron. 2017, 73, 3025-3030. (t) M.M. Efremova, A.S. Novikov, R.R. Kostikov, T.L. Panikorovsky, A.V. Ivanov, A.P. Molchanov. Regio-and diastereoselectivity of the cycloaddition of nitrones with N-propadienylindole and pyrroles. Tetrahedron. 2018, 74, 174-183. (u) Dmitriev VA, Efremova MM, Novikov AS, Zarubaev VV, Slita AV, Galochkina AV, Starova GL, Ivanov AV, Molchanov AP. Highly efficient and stereoselective cycloaddition of nitrones to indolyl-and pyrrolylacrylates. Tetrahedron Lett. 2018, 59, 2327-2331. Teterina PS, Efremova MM, Sirotkina EV, Novikov AS, Khoroshilova OV, Molchanov AP. A highly efficient and stereoselective cycloaddition of nitrones to N-arylitaconimides. Tetrahedron Lett. 2019, 60, 151063. (v) Efremova MM, Molchanov AP, Novikov AS, Starova GL, Muryleva AA, Slita AV, Zarubaev VV. 1, 3-Dipolar cycloaddition of N-allyl substituted polycyclic derivatives of isoindole-1, 3-dione with nitrones and nitrile oxides: An experimental and theoretical investigation. Tetrahedron. 2020, 76, 131104. (w) Efremova MM, Makarova AA, Novikov AS, Kryukova MA, Kuznetsov MA, Molchanov AP. Regio-and stereoselective (3+ 2)-cycloaddition reactions of nitrones with cyclic allenes. Org. Biomol. Chem. 2021, 19, 9773-9784. (x) Chen HX, Zhang Y, Zhang Y, He X, Zhang ZW, Liang H, He W, Jiang X, Chen X, Qiu L. Synthesis of six-membered spirooxindoles via a chiral Brønsted acid-catalyzed asymmetric intramolecular Friedel–Crafts reaction. RSC advances. 2018, 8, 37035-37039. (y) Liang H, He X, Zhang Y, Chen B, Ouyang JS, Li Y, Pan B, Reddy CV, Chan WT, Qiu L. Copper-catalyzed (4+ 1) and (3+ 2) cyclizations of iodonium ylides with alkynes. Chem. Commun. 2020, 56, 11429-114232.
- 1,3-Dipolar cycloaddition reaction of heteroaromatic N-ylides with 3-[(E)-2-aryl(hetaryl)-2-oxoethylidene]indolin-2-ones. Russ. Chem. Bull.. 2005;54:2432-2436.
- [Google Scholar]
- Three-component synthesis of spiro compounds with a carbamate functionality. Russ. J. Org. Chem.. 2011;47:402-404.
- [Google Scholar]
- Synthesis and Antimicrobial and Antifungal Activity of Carbamate-Functionized Spiro Compounds. Pharm. Chem. J.. 2013;46:715-719.
- [Google Scholar]
- A new colorimetric and fluorescent ratiometric sensor for Hg2+ based on 4-pyren-1-yl-pyrimidine. Tetrahedron. 2012;68:3129.
- [Google Scholar]
- (a) Yan, X.-X.; Peng, Q.; Zhang, Y.; Zhang, K.; Hong, W.; Hou, X.-L.; Wu, Y.-D. A highly enantio- and diastereoselective Cu-catalyzed 1,3-dipolar cycloaddition of azomethine ylides with nitroalkenes Angew. Chem. Int. Ed. 2006, 45, 1979-1983. (b) Li, W.; Shi, M. Brønsted acid TfOH-mediated [3 + 2] cycloaddition reactions of diarylvinylidenecyclo-propanes with nitriles J. Org. Chem. 2008, 73, 4151-4154. (c) Tsubogo, T.; Saito, S.; Seki, K.; Yamashita, Y.; Kobayashi, S. Development of catalytic asymmetric 1, 4-addition and [3 + 2] cycloaddition reactions using chiral calcium complexes J. Am. Chem. Soc. 2008, 130, 13321-13332. (d) Ghandi, M.; Yari, A.; Rezaei, S. J. T.; Taheri, A. Synthesis of novel spiropyrrolidine/pyrrolizine-oxindole scaffolds through 1,3-dipolar cycloadditions Tetrahedron Lett. 2009, 50, 4724-4726. (e) Yamashita, Y.; Guo, X.-X.; Takashita, R.; Kobayashi, S. Chiral silver amide-catalyzed enantioselective [3 + 2] cycloaddition of α-aminophosphonates with olefins J. Am. Chem. Soc. 2010, 132, 3262-3263.
Appendix A
Supplementary material
NMR spectra of the synthesized compounds; Coordinates of the optimized geometries. Supplementary data to this article can be found online at https://doi.org/10.1016/j.arabjc.2022.103855.
Appendix A
Supplementary material
The following are the Supplementary data to this article:
Supplementary data 1
Supplementary data 1







