Structural effects and thermal decomposition kinetics of chalcones under non-isothermal conditions

2.1 Materials

All the chemicals were of AnalaR grade, purchased from Sd fine chemicals and were used as such without further purifications.

2.2 Instruments

Elemental analyzes were performed on a Carlo Analyzer at Central Drug Research Institute (CDRI), Lucknow, India. FT-IR spectra were recorded in a KBr-pellet on an Avatar-330 spectrometer (with resolution 2 cm⁻¹). The mass spectra were recorded on a JEOL Gcmate, at the Indian Institute of Technology, Chennai, India. The NMR spectra were recorded on a Bruker AMX 400 MHz for ¹H and 100 MHz for ¹³C NMR with TMS as an internal standard at the Indian Institute of Science, Bangalore, India. The simultaneous TGA and DTA curves were obtained with the thermal analysis system model Perkin Elmer TAC 7/DX Thermal Analysis Controller TAC-7. The TG and DTA analyzes of BHMPD and BHMBC were carried out under dynamic nitrogen atmosphere (100 mL min⁻¹), in an alumina crucible with a sample mass around 10 mg with heating rates of 10, 15 and 20 K min⁻¹ from 35 to 700 °C. The kinetic parameters E_a and ln A were calculated using Microsoft® Excel Software. The sample temperature, which is controlled by a thermocouple, did not exhibit any systematic deviation from the preset linear temperature program.

2.3 Synthesis of BHMPD

Dry HCl gas was passed through a solution containing vanillin (1 mmol) and acetone (0.5 mmol) in dry methanol. The solution turned dark pink and yellow precipitate was obtained after the addition of water. It was purified by crystallization from methanol medium (m.p. = 99 °C; lit. = 98–99 °C) (Du et al., 2006).

Elemental analysis: Calculated = C, 70.13; H, 5.19. Found = C, 70.48; H, 5.17. FT-IR (KBr disk, cm⁻¹): ${\nu }_{\mathrm{C}\text{⚌}\mathrm{O}}=1667$ , ${\nu }_{\mathrm{C}\text{⚌}\mathrm{C}}=1591\text{,}1511$ , ${\nu }_{\mathrm{C}\text{—}\mathrm{H}}=1428$ and ${\nu }_{\mathrm{OH}}=3177$ . ¹H NMR (CDCl₃, δ ppm): 3.82 (methoxy proton), 6.94–7.38 (aromatic protons), 7.40, 9.73 (vinyl protons of the α,β-unsaturated arylidene system), 10.26 (phenolic —OH). ¹³C NMR (CDCl₃, δ ppm): 55.46 (methoxy carbon), 110–148 (aromatic carbons and vinyl carbons), 152.97 (C—O carbons of the α,β-unsaturated arylidene system, 190.86 (carbonyl carbon of arylidene keto moiety).

2.4 Synthesis of BHMBC

Vanillin (1 mmol) and cyclopentanone (0.5 mmol) were heated in a water bath (45–50 °C) until a clear solution was obtained, concentrated hydrochloric acid was then added followed by 2 h stirring. After standing overnight, the mixture was treated with cold aqueous acetic acid (1:1) and filtered. The solid material was washed first with cold ethanol, then with hot water and dried in vacuum. The yellow substance was recrystallized from ethanol (m.p. = 212 °C; lit. = 212–214 °C) (Du et al., 2006).

Elemental analysis: Calculated = C, 71.59; H, 6.68. Found: C, 71.23; H, 6.57. FT-IR (KBr disk, cm⁻¹): ${\nu }_{\mathrm{C}\text{⚌}\mathrm{O}}=1667\text{,}{\nu }_{\mathrm{C}\text{⚌}\mathrm{C}}=1617\text{,}{\nu }_{\mathrm{C}\text{—}\mathrm{H}}=3005\text{,}{\nu }_{\mathrm{C}\text{⚌}\mathrm{C}}=1519$ and ${\nu }_{\mathrm{C}\text{—}\mathrm{H}}=1421$ . ¹H NMR (CDCl₃ and DMSO-d₆, δ ppm): 7.31 (2H, —OH protons), 6.97–6.98 (2H, aromatic hydrogen), 7.52 (2H, —CH⚌), 3.94 (6H, OCH₃ protons), 2.15–2.17 (4H, —H₂C—CH₂—). ¹³C NMR (CDCl₃, δ ppm): 195.89 (C⚌O), 148.06–147.32 (CH, C⚌C, C—O), 113–134.66 (aromatic carbons), 55.77 (OCH₃), 26.32 (CH₂).

3.1 Model fitting method

The integral method of Coats and Redfern has been most successfully used for studying the kinetics of dehydration and decomposition of different solid substances (Horowitz and Metzger, 1963; Coats and Redfern, 1964; Wendlandt, 1974; Sestak, 1984). The kinetic parameters can be derived from modified Coats and Redfern equation:

3.2 Model free methods

Friedman method (Friedman, 1963) is a different method and was one of the first isoconversion methods. The logarithm of the non-isothermal rate law:

The plots of ln (βdα/dT) Vs 1/T (Eq. (3)), ln β Vs 1/T (Eq. (4)) and ln (β/T²) Vs 1/T (Eq. (5)) have been shown to give the values of apparent activation energies for the decomposition of BHMPD and BHMBC at different values of α. According to these equations, the reaction mechanism and shape of g(α) function do not affect the values of the activation energies of the decomposition stage.

3.3 Invariant kinetic parameters (IKP) method

The invariant kinetic parameters were obtained by the method of Lesnikovich and Levchik (1983). The straight lines obtained for the plots of ln A_β Vs E_β for several constant heating rates should intersect at a point (Lesnikovich and Levchik, 1985) which corresponds to the true values of activation energy and pre-exponential factor, which are called invariant kinetic parameters (E_inv, A_inv). The evaluation of the invariant kinetic parameters is performed using the supper correlation equation:

The plot of a_β Vs b_β, obtained for three constant heating rates, is a straight line (Flynn, 1997) whose parameters allow the determination of ln A_inv and E_inv.

3.4 Thermodynamic parameters

The kinetic parameters, energy of activation and pre-exponential factor obtained from Kissinger single point (Kissinger, 1957, 1956; Patel and Chaudhri, 1978; Whelan et al., 1984) kinetic method uses the Eq. (7):

Based on the values of activation energy and pre-exponential factor for the decomposition stage, the values of $\mathrm{\Delta }{S}^{\ne }\text{,}\mathrm{\Delta }{H}^{\ne }\text{,}\mathrm{\Delta }{G}^{\ne }$ for the formation of activated complex from the reactant were calculated according (Malek, 1989; Bamford and Tipper, 1980; Cordes, 1968) to, equations:

4.1 Non-isothermal TG and DTA

The TG and DTA thermograms of pure BHMPD and BHMBC were recorded in a dynamic nitrogen atmosphere at different heating rates of 10, 15 and 20 K min⁻¹ and presented in Figs. S1 and S2 and show those two distinct endothermic peaks on account of melting and decomposition. The thermal decomposition process of BHMPD and BHMBC in one stage was observed from the TG curves. The decomposition processes of BHMPD and BHMBC are completed 99.2% and 67% with endothermic peaks, respectively. The decomposition process of BHMPD starts from 180 °C and ends at 280 °C whereas that for BHMBC starts from 300 °C and ends at 480 °C.

4.2 Non-isothermal decomposition reaction kinetics

The heating rates 10, 15 and 20 K min⁻¹ were selected to study the decomposition process of chalcones. The values of α ranging from 0.22 to 0.80 for BHMPD and 0.20 to 0.70 for BHMBC with an increment of 0.02 were chosen for kinetic calculations.

The values of energy of activation corresponding to the values of α for the decomposition procedure obtained by Friedman (Friedman, 1963), Kissinger–Akahira–Sunose (Kissinger, 1957; Akahira and Sunose, 1971) and Flynn–Wall–Ozawa (Flynn and Wall, 1966; Ozawa, 1965) are shown in Fig. 1. It is clear that the value of E_a increases with α values and remains constant from 0.20 to 0.80 for BHMPD and 0.2 to 0.70 for BHMBC the increases with increasing α indicating removal of gaseous products from solid mass. Therefore, the decomposition stage could be recorded as a single step process (Vyazovkin and Wight, 1997). The apparent activation energy varied with increasing conversions and the average value is 100.71 ± 0.14 kJ mol⁻¹ for BHMPD and 128.99 ± 0.25 kJ mol⁻¹ for BHMBC (Friedman method). The meager dependence of activation energy on the extent of conversion suggests that the decomposition took place in a single step for BHMPD and BHMBC. BHMBC compound has higher energy of activation than BHMPD, which indicates cyclic compound thermally more stable than acyclic compound. The mass spectral data of these compounds show that compounds are decomposed instead of sublimation.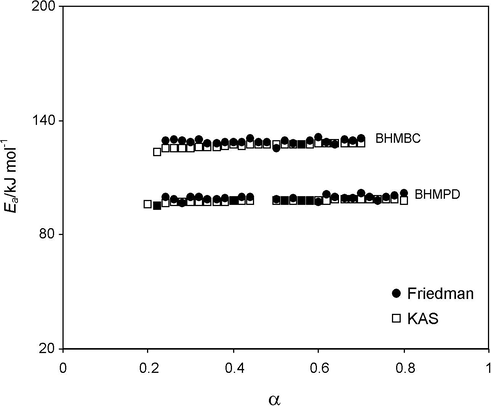

Close

Figure 1

E_a versus α plot for the decomposition of BHMPD and BHMBC under non-isothermal condition.

Export to PPT

4.3 Invariant kinetic parameters (IKP) analysis

The invariant kinetic parameter method was applied to the data calculated for the heating rates of 10, 15 and 20 K min⁻¹. The evaluation of the kinetic parameters was performed using Coats–Redfern method. For these kinetic models in the range 0.2 ⩽ α ⩽ 0.8 for BHMPD and 0.2 ⩽ α ⩽ 0.7 for BHMBC, the straight lines corresponding to Coats–Redfern method is characterized by correlation coefficient values close to unity. The values of E_a and ln A depend on the kinetic model as well as on the heating rate, as shown in Tables 1 and 2.

For several groups of apparent activation parameters, obtained by different kinetic models, we tried to establish the best combination (r → 1), a better resolution in determining the invariant kinetic parameters and the closest value to the mean isoconversional activation energies (Budrugeac and Segal, 2007; Vyazovkin and Lesnikovich, 1988; Pratap et al., 2007). For (all kinetics models) AKM–{F2; F3; D1; D2; D3; D4}, the plot of ln A Vs E_a has the highest correlation coefficient (r = 0.988) and is a true straight line for BHMPD whereas for AKM–{F2; F3; D1; D2; D3; D4; R2; R3}, the plot of ln A Vs E_a has the highest correlation coefficient (r = 0.999) and is a true straight line for BHMBC. Depending on the choice of kinetic models, the compensation effect parameters are obtained with different accuracies, their values and derived invariant activation parameters varying substantially.

For AKM–{F2; F3; D1; D2; D3; D4}, the invariant kinetic parameters are E_inv = 91.02 kJ mol⁻¹ and ln A_inv = 19.41 (Table S1) obtained with r = 0.988 for BHMPD and AKM–{F2; F3; D1; D2; D3; D4; R2; R3}, the invariant kinetic parameters are E_inv = 128.75 kJ mol⁻¹ and ln A_inv = 22.05 (Table S2) obtained with r = 0.999 for BHMBC, respectively. For these groups, the invariant activation energy is slightly above 103.06 kJ mol⁻¹, close to 99.06 ± 0.28 kJ mol⁻¹, 97.69 ± 0.14 kJ mol⁻¹ obtained by Friedman and KAS method for BHMPD and for BHMBC is slightly above 128.77 kJ mol⁻¹, close to 126.80 ± 0.24 kJ mol⁻¹ obtained by KAS method (Tables S1 and S2). The higher E_a value for BHMBC may be due to the ring system that influences the stability of the compound and also BHMBC is thermally more stable, because of decomposition that starts at >320 °C at all heating rates (Fig. S2).

The most probable kinetic model for decomposition process of BHMPD and BHMBC is R2 and F1 models, respectively. By introducing the derived reaction model for BHMPD, g(α) = [1 − (1 − α)^1/2], the following Eq. (11) is obtained:

The plot of [1 − (1 − α)^1/2] against (E_a p(x)/Rβ) at the different heating rates is constructed in Fig. S3, and for BHMBC is, g(α) = −ln (1 − α), the following Eq. (12) is obtained:

The plot of −ln (1 − α) against (E_a/Rβ) p(x) at different heating rates is constructed and is similar to Fig. S3.

By using the above equations, the A value was determined from the slope of the fitted line shown in Fig. S3. For contracting area model (R2) and E_a = 99.06 ± 0.28 kJ mol⁻¹, the pre-exponential (frequency) factor was found to be A = 8.92 × 10⁸ min⁻¹ (ln A = 20.60) for BHMPD and for power law (F1) and E_a = 128.99 ± 0.25 kJ mol⁻¹, the pre-exponential (frequency) factor was found to be A = 3.94 × 10⁹ min⁻¹ (ln A = 22.09) for BHMBC, respectively. The obtained value of ln A is in good agreement with average value of Friedman isoconversional intercept ln [A f(α)] = 20.92 for BHMPD and 21.47 for BHMBC, respectively.

4.4 Thermodynamic parameters

From the DTA curves, the peak temperatures for BHMPD are 542.6, 548.3 and 557.6 K and for BHMBC are 676.58, 686.31 and 696.21 K. These peak temperatures are used to evaluate single point kinetic parameters. The obtained values are 103.71 and 124.32 kJ mol⁻¹ for BHMPD and BHMBC, respectively. The obtained values are in good agreement with values obtained by Friedman method for both compounds.

The thermodynamic parameters, $\mathrm{\Delta }{S}^{\ne }$ , $\mathrm{\Delta }{H}^{\ne }$ and $\mathrm{\Delta }{G}^{\ne }$ were calculated at the peak temperature T_m in the DTA curves for the corresponding stage, since the temperature characterizes the higher rate of decomposition and therefore, it is an important parameter.

As can be seen from the Table 3, the value of $\mathrm{\Delta }{S}^{\ne }$ for the decomposition stage is negative for both the compounds. It means that the corresponding activated complexes were with high degree of arrangement than the initial state. The positive values of $\mathrm{\Delta }{H}^{\ne }$ and $\mathrm{\Delta }{G}^{\ne }$ for both the compounds show that they are connected with absorption of heat and they are non-spontaneous processes (Criado et al., 2005; Sokolskii and Druz, 1981). The obtained E_a values are coincided with invariant parameters. Energy of activation of BHMBC has a higher value than that of BHMPD which indicates that BHMBC is thermally more stable than BHMPD.