10.8
CiteScore
 
5.3
Impact Factor
Generic selectors
Exact matches only
Search in title
Search in content
Post Type Selectors
Search in posts
Search in pages
Filter by Categories
Corrigendum
Current Issue
Editorial
Erratum
Full Length Article
Full lenth article
Letter to Editor
Original Article
Research article
Retraction notice
Review
Review Article
SPECIAL ISSUE: ENVIRONMENTAL CHEMISTRY
10.8
CiteScore
5.3
Impact Factor
Generic selectors
Exact matches only
Search in title
Search in content
Post Type Selectors
Search in posts
Search in pages
Filter by Categories
Corrigendum
Current Issue
Editorial
Erratum
Full Length Article
Full lenth article
Letter to Editor
Original Article
Research article
Retraction notice
Review
Review Article
SPECIAL ISSUE: ENVIRONMENTAL CHEMISTRY
View/Download PDF

Translate this page into:

Original article
12 (
8
); 3847-3862
doi:
10.1016/j.arabjc.2015.12.009

Interactions in the mixed micelles of monomeric and gemini surfactants: Influence of some co-solvents as a function of temperature

, ,
 Department of Chemistry, Guru Nanak Dev University, Amritsar 143 005, Punjab, India

⁎Corresponding author. Tel.: +91 (0183) 2258802 09x3319; fax: +91 (0183) 2258819 20. tsbanipal@yahoo.com (Tarlok Singh Banipal)

Received: , Accepted: ,
© The Author(s) 2015
Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Mixed micellar behavior of a series of m-2-m cationic gemini surfactants (where m = 10, 12 and 14) with monomeric surfactants (dodecyltrimethylammonium bromide, tetradecyltrimethyl-ammonium bromide and cetyltrimethylammonium bromide) has been studied in aqueous and in aqueous n-propanol, n-butanol, tertiary butanol, propylene glycol and glycerol solutions using conductivity, surface tension, viscosity and dynamic light scattering techniques at 298.15, 308.15 and 318.15 K, respectively. In mixtures of 10–2–10 with monomeric surfactants, the synergistic interactions increase with the chain length of monomeric surfactants whereas the mixtures with 12–2–12 and 14–2–14 exhibit the opposite trends. However, the synergistic interactions decrease with the increase in temperature of all the mixtures. The thermodynamic and surface parameters have been evaluated and the influence of the variations in hydrophobic chain length of the surfactants and the type of the co-solvent on these parameters has been discussed. The hydrodynamic diameter increases with the chain length of the surfactants.

Keywords

Mixed micelles
Co-solvents
Conductivity
Surface tension
Viscosity
Dynamic light scattering
1

1 Introduction

In recent years, interfacial and micellar properties of mixed surfactant systems have attracted significant attention in the area of surface science and solution chemistry (Pan et al., 2012; Khan et al., 2014; Bielawska et al., 2014). Extensive investigations on binary mixtures of cationic–cationic, cationic–anionic, and cationic–nonionic systems have also been reported (Rosen and Hua, 1982; Moulik et al., 1996; Vora et al., 1999; Bakshi et al., 2002; Chakraborty et al., 2005; Svanedal et al., 2014), but nowadays studies involving gemini surfactant as one of the components in the mixed systems have attained special attention from both academic and industrial view points (Koya and Kabir-ud-Din, 2011; Martín et al., 2013; Khan et al., 2014; Fatma et al., 2015). Gemini surfactant is a family of surfactants possessing two polar/ionic head groups, covalently connected by a spacer group at the level of the head groups. Due to their enhanced self-assembling ability, these surfactants are superior to the conventional surfactants in characteristic features such as high surface activity, lower critical micelle concentration and Krafft temperature, unusual rheological properties and better wetting ability (Menger and Littau, 1993; Gull et al., 2009; Lu et al., 2012). In addition, the difference in the tail and the head groups of the gemini surfactants in the mixed systems may result in composition dependent micellar properties (Zana and Xia, 2004).

Many pharmaceutical formulations often require the addition of surfactants to regulate the physical properties of the product or improve its stability. The environmental factors such as temperature, pressure and the presence of co-solvents also affect the micellar, interfacial and thermodynamic parameters of these mixtures (Das and Ismail, 2008; Michele et al., 2011; Chakraborty et al., 2011). Thus, mixed surfactants serve as carrier of active ingredients and co-solvents help to improve this property by modifying the solvent characteristics which in turn influence the critical micellar concentration of these mixtures. It provides an opportunity to study the role of solvophobic effect in micellization. For instance, ethylene glycol is the most commonly used industrial co-solvent because it possesses high cohesive energy and dielectric constant and has many characteristics similar to that of water (Das and Das, 2009). Some studies have also been devoted on the mixed micellar properties of surfactants in the presence of ethylene glycol (Javadian et al., 2010; Tikariha et al., 2011; Koya and Kabir-ud-Din, 2011).

Further, short chain alcohols especially ethanol are also industrially important co-solvents because of their vital role in the preparation of microemulsions (Chavda and Bahadur, 2011; Kumar et al., 2012; Bielawska et al., 2013). But, to the best of our knowledge, the reports on the effect of presently used alcohols and glycols on the mixed micellar behavior of ionic gemini and monomeric surfactant mixtures are rare and limited only to conventional ionic/non-ionic surfactant mixtures (Gil and Lee, 2008; Park and Lee, 2012; Bielawska et al., 2014). The addition of alcohols can strongly influence the behavior of mixed micelles consisting of conventional monomeric/gemini ionic surfactants and increase or decrease micellar size depending upon the hydrophilic/hydrophobic character and thus can fine-tune the surfactant micelles template for the fabrication of nanomaterials (Kumar et al., 2012).

Therefore, we have investigated the effect of some short chain alcohols and glycols (2.5 and 5.0% v/v) on the mixed micellar and interfacial properties involving series of m-2-m gemini and alkyltrimethylammonium bromide (CnTAB) monomeric surfactants using conductivity and viscosity measurements at 298.15, 308.15 and 318.15 K. These systems have also been evaluated by surface tension and dynamic light scattering techniques at 298.15 K. The monomeric surfactants used for this purpose are dodecyltrimethylammonium bromide (DTAB), tetradecyltrimethylammonium bromide (TTAB) and cetyltrimethylammonium bromide (CTAB) whereas the co-solvents selected are n-propanol (PrOH), n-butanol (BuOH), tertiary butanol (tert BuOH), propylene glycol (PG) and glycerol (Gly). An attempt has been made to (i) find out the conditions for synergism in the bulk phase and at the air/water interface, (ii) evaluate the effect of various factors such as temperature, type of the co-solvent and chain length of monomeric or gemini surfactant on the interactions in the mixed micellar solutions and (iii) study the effect of alcohols and glycols on the variation in relative viscosity and the size of the mixed micelles.

2

2 Materials and methods

2.1

2.1 Materials

The dimethylene bis(alkyldimethyl ammonium bromide), denoted as ‘m-2-m’ (where m = 10, 12 and 14) gemini surfactants was synthesized by the reaction of N1,N1,N2,N2-tetramethylene-1,2-diamine with the corresponding alkyl bromides in extrapure alcohols by refluxing till the diamine present is completely consumed (Zana et al., 1991) as shown in Scheme 1. Once the reaction is complete, the solvent was removed by evaporation. The impure surfactants were recrystallized twice in 50:50 ethyl acetate/acetone mixtures. The final product thus recovered was then dried and kept in desiccator. All the other chemicals were more than 99% pure and used as such without further purification. The structure, sources and purity of the chemicals used are listed in Table 1. Double distilled and degassed water was used for the preparation of all the solutions.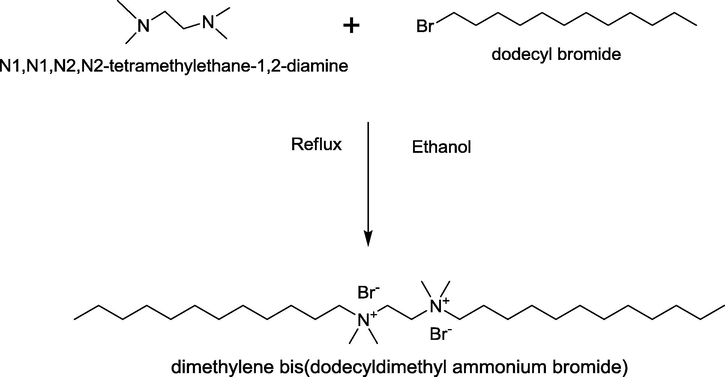

Scheme 1
Table 1 Name, structure and sources of chemicals used in the study.
S. no. Compound Structure Source Purity/grade
1. DTAB Lancaster Synthesis, UK >99%
2. TTAB Acros Organics, Germany >99%
3. CTAB Acros Organics, Germany >99%
4. 10–2–10 Synthesized in Laboratory Characterized by 1H NMR and Elemental analysis
5. 12–2–12 Synthesized in Laboratory Characterized by 1H NMR and Elemental analysis
6. 14–2–14 Synthesized in Laboratory Characterized by 1H NMR and Elemental analysis
7. PrOH CH3(CH2)2OH S.D. Fine, Mumbai Extrapure AR
8. BuOH CH3(CH2)3OH S.D. Fine, Mumbai Extrapure AR
9. tert BuOH (CH3)3COH S.D. Fine, Mumbai Extrapure AR
10. PG CH3CHOHCH2OH S.D. Fine, Mumbai Extrapure AR
11. Gly CH2OHCHOHCH2OH S.D. Fine, Mumbai Extrapure AR

2.2

2.2 Methods

2.2.1

2.2.1 Conductivity measurements

The conductivity measurements were carried out with a digital conductivity meter (Systronics-306) using a dip-type cell with double walled glass jacket. The temperature of the conductivity cell was maintained within ±0.01 K using temperature bath (Model: MV 25F Julabo, Germany). The concentration of the solution was varied by aliquot addition of a stock surfactant solution of known concentration to a known volume of solvent in the vessel using a micropipette (Finnpipette Labsystems, Finland). The reproducibility in the measurement of critical micelle concentration (CMC) was calculated to be always within ±1%.

2.2.2

2.2.2 Surface tension measurements

The CMC values of the surfactants were determined at 298.15 K by the surface tension (γ) measurements made by ring detachment method using Krüss Easy Dyne (K20) tensiometer (Krüss Gmbh, Hamburg, Germany) based upon duNoűy principle. For each set of experiments, the ring was washed thoroughly by double distilled water and then heated in alcohol flame. The readings were taken in triplicate to ensure the reproducibility in CMC measurements within ±2%.

2.2.3

2.2.3 Viscosity measurements

The relative viscosity of individual surfactants and their binary mixtures were determined by using an Ubbelohde type suspended level capillary viscometer. Water was circulated through the glass jacket surrounding the viscometer at constant temperature using thermostat. From the ratio of the efflux time of test solution, t, to that of the reference solvent, to, the relative viscosity (ηr) was calculated by ignoring the density correction factor in case of dilute solutions (Ozeki and Ikeda, 1980). For each measurement, 3–5 readings were taken and mean of three nearest values has been reported. The reproducibility in each reading is within ±2%.

2.2.4

2.2.4 Dynamic light scattering measurements

The size of the micelle has been obtained (Cai et al., 2013) by measuring the hydrodynamic diameter of the micelle (Dh) using Stokes–Einstein equation:

(1)
D h = kT 3 π η D where k = Boltzmann constant, D = diffusion coefficient, T = Absolute temperature, and η = viscosity of the solution. The DLS measurements were performed using Malvern Zetasizer Nano ZS (Malvern, UK) apparatus with He-Ne laser (λ = 632 nm) at 298.15 K (Naskar et al., 2012). All the experimental solutions were passed through 0.2 μm filters (Whatman™, GE Healthcare, UK). The mean values of three measurements of each sample have been reported and the reproducibility in each reading is within ±3%.

3

3 Results and discussion

3.1

3.1 Conductivity studies

3.1.1

3.1.1 Mixed micellar interactions in aqueous solutions

The CMC values of the studied gemini and monomeric surfactants in aqueous solutions at different temperatures have been obtained by intersection of specific conductance (κ) versus concentration of the surfactant (C) plots in the pre-micellar and post-micellar regions as shown in Fig. 1 and were found to agree well with the literature (Bakshi et al., 2005; Modaressi et al., 2007; Das and Das, 2009; Akbas et al., 2012; Dubey, 2013). The CMC values of binary mixtures of these surfactants (Cm) over the whole mole fraction (α) range of monomeric surfactants have also been determined. The ideal CMC values of these mixtures (Ci) have been obtained from the Clint equation (Clint, 1975):

(2)
1 C i = α C 1 + 1 - α C 2 where C1 and C2 represent the CMC of monomeric and gemini surfactant respectively. The values of Cm and Ci thus determined for the mixtures of DTAB and gemini surfactants at 298.15 K in aqueous and in aqueous co-solvent solutions are given in Table 2. The remaining data at different temperatures have been provided in Tables S1–S3 (Supplementary Information). In case of 10–2–10 + DTAB mixtures, the Cm values are more than corresponding Ci values showing slight repulsive interactions between these two surfactants. But Cm becomes lower than Ci as the chain length of gemini surfactants is increased. It suggests that improved hydrophobic environment for the mixed micelle formation results in attractive interactions between the two surfactants. However, the difference between Cm and Ci values increases with temperature in 10–2–10 + DTAB mixture showing that the repulsive interactions increase whereas a decrease in the attractive interactions has been noticed in mixtures of 12–2–12/14–2–14 with DTAB. It is due to disruption of water structure surrounding the hydrophobic groups which delays the mixed micellization (Mehta et al., 2007; Yan et al., 2011; Moradi et al., 2013).
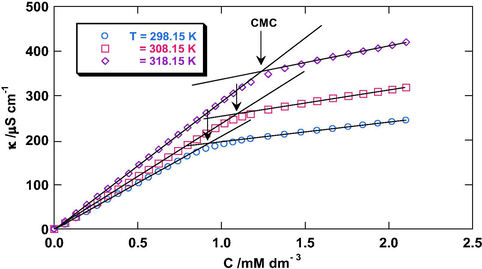
κ versus C plots for 12–2–12 in aqueous solutions at different temperatures.
Figure 1
κ versus C plots for 12–2–12 in aqueous solutions at different temperatures.
Table 2 Experimental and ideal CMC (Cm, Ci), degree of dissociation (g), mixed micellar mole fractions (X1, Xi), Excess free energy (gM,E), interaction parameter (β), Standard Gibbs free energy, enthalpy and entropy (ΔGom, ΔHom, ΔSom) of micellization for the mixtures of DTAB and gemini surfactants in aqueous solutions at 298.15 K using conductivity measurements at different mole fractions (α) of DTAB.
α Cm (mmol dm−3) Ci (mmol dm−3) X1 gM,E (kJ mol−1) Xi β g ΔGom (kJ mol−1) ΔHom (kJ mol−1) ΔSom (J mol−1 K−1)
10–2–10 + DTAB
0.000 6.33 (6.63)a 6.33 0.15 −60.35 −6.35 181.14
0.128 7.42 6.96 – – – – 0.32 −52.05 −15.72 122.05
0.268 7.78 7.74 0.14 – 0.14 0.02 0.22 −56.09 −17.62 129.17
0.449 8.78 8.71 – – – – 0.26 −53.81 −13.83 134.32
0.604 10.35 9.96 0.35 – 0.37 0.23 0.25 −53.15 −11.63 139.47
0.753 12.33 12.31 – – – – 0.27 −51.39 −13.18 128.18
0.902 14.21 14.65 – – – – 0.25 −51.47 −10.54 103.01
1.000 16.10 (16.00)b 16.10 0.27 −34.87 −5.17 99.89
12–2–12 + DTAB
0.000 0.92 (0.90)b 0.92 0.20 −70.76 −28.60 141.46
0.128 0.85 1.01 0.15 −2.09 0.01 −3.50 0.30 −66.15 −41.52 80.25
0.268 1.06 1.21 0.13 −1.74 0.02 −2.48 0.31 −64.20 −44.10 65.35
0.449 1.21 1.51 0.18 −2.09 0.04 −2.49 0.29 −64.25 −29.56 112.14
0.604 1.57 2.01 0.21 −2.11 0.07 −2.05 0.42 −55.78 −28.60 88.47
0.753 1.93 3.58 0.36 −1.89 0.18 −3.22 0.61 −45.02 −15.81 95.61
0.902 2.98 6.11 0.34 −2.10 0.23 −2.64 0.63 −44.07 −17.62 89.24
1.000 16.10 16.10 0.27 −34.87 −5.17 99.89
14–2–14 + DTAB
0.000 0.15 (0.16)b 0.15 0.24 −82.46 −36.21 148.25
0.128 0.16 0.17 0.06 −2.67 0.00 −4.12 0.27 −77.58 −57.02 67.62
0.268 0.18 0.21 0.12 −3.33 0.00 −4.61 0.41 −68.28 −49.06 62.25
0.449 0.23 0.27 0.12 −2.89 0.01 −3.78 0.36 −70.16 −39.95 98.31
0.604 0.28 0.37 0.16 −2.88 0.01 −3.83 0.45 −63.62 −47.96 49.47
0.753 0.46 0.71 0.24 −3.56 0.03 −4.02 0.56 −54.26 −19.69 112.21
0.902 0.44 0.77 0.23 −4.14 0.02 −4.04 0.57 −44.27 −14.53 103.41
1.000 16.10 16.10 0.27 −34.87 −5.17 99.89

The degree of micellar dissociation (g) has also been calculated by taking the ratio of slopes of post-micellar region to those of pre-micellar region (Kumar et al., 2012). In 10–2–10 + DTAB mixture, the values of g remain almost constant (Table 2) throughout the whole mole fraction. However, in 12–2–12/14–2–14 + DTAB mixtures, the g values increase with α whereas a decrease in these values has been observed in mixtures with TTAB/CTAB (Tables S2–S3, Supplementary Information). Therefore, the degree of dissociation depends upon not only the head groups but also the chain lengths of the two surfactants. Moreover, the values of g increase with temperature for these mixtures due to electrostatic repulsions between the charged ion species leading to more dissociation at higher temperatures (Mehta and Kaur, 2013).

A quantitative interpretation of the experimental results can be obtained by Rubingh’s treatment, based on the regular solution theory (Rubingh, 1979). The micellar mole fraction of monomeric surfactant (X1) as well as interaction parameter (β) can be calculated using the following equations:

(3)
X 1 2 ln ( C m α / C 1 X 1 ) ( 1 - X 1 ) 2 ln C m ( 1 - α ) C 2 ( 1 - X 1 ) = 1
(4)
β = ln ( C m α / C 1 X 1 ) ( 1 - X 1 ) 2

The activity coefficients f1 and f2 of surfactants 1 and 2 are related to β as

(5)
f 1 = e β ( 1 - x 1 ) 2
(6)
f 2 = e β x 1 2

The β values for the mixtures of 10–2–10 with DTAB at 298.15 K are slightly positive showing repulsive interactions (antagonism) between the two surfactants (Table 2). These values could not be calculated at certain α values and are shown as “–” in the tables. However, in 12–2–12 + DTAB mixtures, the negative β values show synergistic interactions between the two surfactants which increase with chain length of gemini surfactants as shown in Fig. 2a by the decrease in the average values of β (βavg). It may be due to longer hydrophobic twin tails of gemini surfactant which interact more favorably with DTAB to form the core of mixed micelles. The negative βavg decrease slightly with increase in temperature (Table S1, Supplementary Information) as a result of an increase in the Cm values due to disruption of water structure surrounding the hydrophobic groups as mentioned earlier.

Variation in βavg with temperature for different mixtures in aqueous solutions.
Figure 2
Variation in βavg with temperature for different mixtures in aqueous solutions.

Synergistic interactions have been observed gemini + TTAB mixtures at 298.15 and 308.15 K (Table S2, Supplementary Information). These interactions increase with hydrophobic chain length of the gemini surfactants (Fig. 2b) as expected. At 318.15 K, the mixtures of 10–2–10/12–2–12 + TTAB show antagonistic behavior although synergism is exhibited in mixture of 14–2–14. In mixtures of gemini + CTAB at 298.15 and 308.15 K (Table S3, Supplementary Information), the synergistic interactions become antagonistic with the increase in chain length of the gemini surfactants from 10 to 12 and with further increase in the chain length from 12 to 14, these interactions show synergistic effect (Fig. 2c). Similar synergistic effect in 14–2–14 + CTAB mixture has been reported by Mirgorodskaya et al. (2014). The study also shows that with the increase in spacer length of the gemini surfactant from 2 to 4, the mixture exhibits antagonistic effect and with further increase in spacer length to 6, the mixture behaves almost ideally. These comparisons indicate that mixed micellar behavior is not governed only by the hydrophobicity of side chains but also by the spacer length. Moreover, it has been noted that in mixtures of 10–2–10, the synergistic interactions increase with chain length of monomeric surfactants whereas in mixtures of 12–2–12/14–2–14, opposite is true. In the literature, an increase in the synergistic interactions in the mixtures of 10–2–10/12–2–12 with the hydrophobic chain length of a series of zwitterionic surfactants has been reported whereas no trend was followed in the mixtures with 14–2–14 (Bakshi and Singh, 2005).

The mole fraction of monomeric surfactant in the mixed micelles in the ideal state (Xi) has been obtained using Motomura theory (Motomura and Aratono, 1993) based on excess thermodynamic quantities from Eq. (7):

(7)
X i = α C 2 α C 2 + ( 1 - α ) C 1

In 10–2–10 + DTAB mixtures at 298.15 K (Table 2), the calculated X1 and Xi values are almost same at all α values. But with the increase in hydrophobic chain length of gemini surfactant, the X1 values become more than Xi indicating that the contribution of DTAB in the mixed micelles increases. However, the difference between these two values decreases with the increase in temperature. For 10–2–10 + TTAB mixtures, the X1 and Xi values are almost same at all α values (Fig. 3a). But, with the increase in chain length of gemini surfactant i.e. 12–2–12, the X1 values are slightly more than Xi in 12–2–12 rich region (α < 0.268) and become less in TTAB rich region as shown in Fig. 3b. However, in mixtures with 14–2–14, the X1 values are always lower than Xi (Fig. 3c). This shows that the contribution of TTAB decreases with increase in chain length of gemini surfactant. Almost similar behavior is exhibited by the mixtures of CTAB with gemini surfactants (Table S3, Supplementary Information).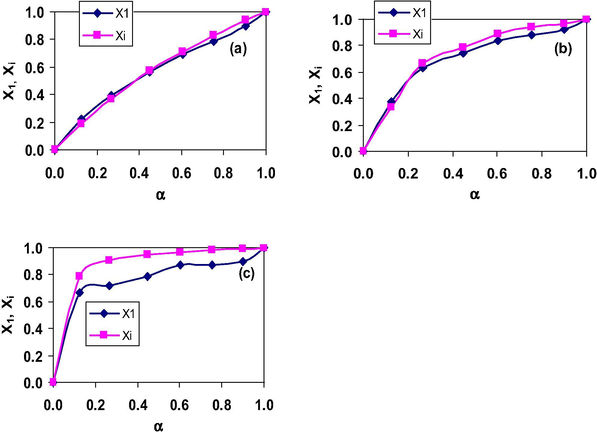

Plots of ( ) X1 and ( ) Xi versus α for the binary mixtures of TTAB with (a) 10–2–10 (b) 12–2–12 and (c) 14–2–14 in aqueous solutions at 298.15 K.
Figure 3
Plots of ( ) X1 and ( ) Xi versus α for the binary mixtures of TTAB with (a) 10–2–10 (b) 12–2–12 and (c) 14–2–14 in aqueous solutions at 298.15 K.

The excess free energy of micelle formation (gM,E) describes the deviation from ideal mixing and has been calculated as follows based upon the Motomura theory (Motomura and Aratono, 1993):

(8)
g M , E = RT ( X 1 M ln f 1 M + X 2 M ln f 2 M ) where f1M and f2M are the activities of surfactant 1 (i.e. monomeric) and surfactant 2 (i.e. gemini). The values of f1M and f2M have been evaluated by
(9)
C m X 1 = C 1 f 1 M X 1 M
(10)
C m X 2 = C 2 f 2 M X 2 M where X1M and X2M are the micelle mole fractions of monomeric and gemini surfactants, respectively. The values of X2M are evaluated by
(11)
X 2 M = X 2 - ( X 1 X 2 / C m ) ( ∂ C m / ∂ X 2 ) T , P

The values of gM,E were found to be negative (Table 2) when the mixed micelles formed by the two surfactants show synergistic behavior whereas these values could not be determined when the two surfactants showed antagonistic behavior (Singh and Marangoni, 2007). The negative values of gM,E increase with the hydrophobic chain length of the surfactants and decrease with the increase in temperature. In general, these values follow almost similar trends as followed by β values.

3.1.2

3.1.2 Mixed micellar interactions in the presence of aqueous co-solvent solutions

Mixed micellar properties of m-2-m gemini surfactants with series of monomeric surfactants have also been studied in aqueous solutions containing 2.5 and 5.0% (v/v) of n-propanol (PrOH), n-butanol (BuOH), tertiary butanol (tert BuOH), propylene glycol (PG) and glycerol (Gly). The presence of various co-solvents modifies the dissociation of the surface groups as well as alters the hydrogen bonded structure of water (Ruiz, 1999). The addition of co-solvents results in the increase in the degree of dissociation (Tables S1–S3, Supplementary Information). It is due to reduction in ionic head group repulsions leading to decrease in surface charge density at the mixed micellar surface (Tiwari et al., 2014). For the present studied systems the increase in g is more in the presence of linear chain alcohols i.e. PrOH and BuOH as the incorporation of these alcohol molecules in the micelle is expected to cause a greater reduction among the charged groups at the micellar surface (Chavda and Bahadur, 2011). Further, the g values show a sharp increase at higher mole fractions of monomeric surfactant in the mixtures indicating that the presence of small amount of gemini surfactant in the micelles of monomeric surfactants tends to reduce the repulsions among the hydrophilic head groups to a greater extent than in pure gemini or monomeric surfactant solutions. This is because in pure surfactant solutions, the ability to bind counter ions is related to the charge density on the head group. But in surfactant mixtures, it is also related to the ability of the two different molecules to pack closely at the surface, thus making a compact micellar surface (Kabir-ud-Din et al., 2013).

In order to compare the effect of various co-solvents on interactions between the studied surfactants, the βavg values for some mixtures are given in Fig. 4 at 298.15 K. For the mixture of 10–2–10 + DTAB, βavg values in the presence of all the co-solvents were negative (except with Gly) as compared to positive values in aqueous solutions, showing that the presence of all these co-solvents increases the hydrophobic interactions between these surfactants. The negative values of βavg follow the sequence BuOH > tert BuOH > PrOH > PG. The influence of these co-solvents on the mixed micellar properties of surfactants can be explained on the basis of several different roles of alcohols (Kabir-ud-Din et al., 2007). On the one hand, the short chain alcohol molecules (up to three carbons) are miscible with water. They are located in the bulk phase of the micellar solution and replace water in the bulk solvent sphere that surrounds the hydrocarbon chain of surfactant and thus bind to the surfactant molecule. However, on the other hand, the alcohols with more than four carbon atoms are solubilized in such a way that their –OH group remains at the micellar surface whereas the hydrophobic part intercalates among the hydrophobic portions of the surfactants. The BuOH molecule is grouped with either short chain or long chain alcohols depending upon its solubility in the surfactant solution (Chavda et al., 2011; Dharaiya et al., 2013). Therefore, the locus of solubilization of BuOH is the most significant criteria in determining the physicochemical characteristics of the mixed micelles. In our case, the presence of both BuOH and tert BuOH increases the hydrophobic interactions more in comparison with those by PrOH and PG. It is due to higher octanol–water partition coefficient (Po/w) of BuOH and tert BuOH (Chavda and Bahadur, 2011). This results in reduction of ionic repulsions among the positively charged head groups at the micellar surface as the average distance between the ionic head groups belonging to the different molecules increases and thus the micellar charge density decreases (Graciani et al., 2010). Moreover, the increase in hydrophobic interactions is smaller in the presence of tert BuOH as compared to BuOH since the polar –OH group in tert BuOH is located such that it divides nonpolar region into smaller regions which decrease Po/w or increase its solubility and thus it remains relatively more in the aqueous phase and thus incorporation in the mixed micelles is less. A comparison between the effect of PrOH and PG shows that the presence of additional –OH group in PG tends to decrease the number of ordered water molecules around the hydrophobic chain, thereby, decreasing the hydrophobic effect. Similar results have been obtained by Chavda and Bahadur (2011) for the effect of BuOH and 1,4 butadiene on the micellar behavior of 12–4–12 gemini surfactant using NMR studies. Gly, having three –OH groups, cannot penetrate into the micellar core and is located at the hydrophilic shell of the micelles. Moreover, Po/w value of Gly is the least (−2.55) among the studied co-solvents (Alexandridis and Yang, 2000) indicating strong affinity for water causing modification in solvent properties. Therefore, the solubility of surfactant tail increases resulting in higher Cm as compared to Ci values leading to positive β values.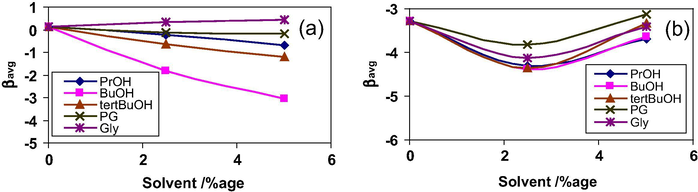

Variation of βavg versus solvent composition for (a) 10–2–10 + DTAB, (b) 10–2–10 + TTAB, (c) 10–2–10 + CTAB, (d) 12–2–12 + DTAB, (e) 12–2–12 + TTAB, (f) 12–2–12 + CTAB, (g) 14–2–14 + DTAB, (h) 14–2–14 + TTAB and (i) 14–2–14 + CTAB mixtures at 298.15 K.
Figure 4
Variation of βavg versus solvent composition for (a) 10–2–10 + DTAB, (b) 10–2–10 + TTAB, (c) 10–2–10 + CTAB, (d) 12–2–12 + DTAB, (e) 12–2–12 + TTAB, (f) 12–2–12 + CTAB, (g) 14–2–14 + DTAB, (h) 14–2–14 + TTAB and (i) 14–2–14 + CTAB mixtures at 298.15 K.

In the presence of co-solvents too, the synergistic interactions increase with chain length of monomeric surfactants in mixtures with 10–2–10 and decrease in case of 12–2–12/14–2–14. Further, in certain mixtures, the synergistic interactions are more in 2.5% co-solvent solutions as compared to those in aqueous solutions and become less in 5% aqueous co-solvent solutions (Fig. 4b). It can be understood by considering that the distribution of the co-solvent between bulk phase and the pseudo micellar phase has two possible effects on Cm. Firstly, at low concentrations, it partitions more in micellar phase and the intercalation between surfactant molecules results in decrease in electrostatic repulsions leading to decrease in Cm and hence the synergism increases (Thimons et al., 1997). Secondly, at higher concentrations, water + co-solvent mixtures act like a better solvent for surfactant alkyl tail and hence increase the Cm which results in the decrease of synergetic interactions (Ruiz, 1999). The effect of temperature on these interactions in water + co-solvent system is similar to that in aqueous solutions.

At 298.15 K, the presence of BuOH and tert BuOH in 10–2–10 + DTAB mixtures shows higher X1 than the corresponding Xi values whereas these two values remain almost same in aqueous solutions of the remaining co-solvents (Table S1, Supplementary Information). This indicates that the presence of longer chain alcohols increases the contribution of DTAB in the mixed micelles. However, the presence of these alcohols in 12–2–12/14–2–14 mixtures with DTAB has no affect on the X1 and Xi values. Further, the relative difference between X1 and Xi values remains almost same with the increase in co-solvent concentration and decreases with increase in temperature. The presence of alcohols in 10–2–10 + TTAB mixtures increases the contribution of TTAB in 10–2–10 rich region (α < 0.449) although a decrease in TTAB contribution has been seen in TTAB rich region (α > 0.604). However, the X1 and Xi values remain almost same at all α values in the presence of PG and Gly. The presence of studied co-solvents in 12–2–12/14–2–14 + TTAB/CTAB mixtures exhibits almost similar variations in X1 and Xi values as in aqueous solutions. From these observations it may be concluded that the presence of alcohols in short chain gemini and monomeric surfactant mixtures increases the contribution of monomeric surfactant whereas no significant variation is observed in mixtures of long chain surfactants. Similarly, the presence of glycols has no effect on the relative contribution of the two surfactants in all the mixtures. The effect of temperature on the g values of the mixtures depends upon the relative effect of the columbic and thermal forces (Zana, 1996). The former attracts surfactant head groups while the latter disperses the surfactant head groups. The thermal forces predominate the columbic forces and this leads to the separation between the counter ions and the head groups, hence increase the g values (Tables S1–S3, Supplementary Information).

3.1.3

3.1.3 Thermodynamics of Micellization

The standard Gibbs free energy of micellization (ΔGom) can be calculated on the basis of phase separation model for ionic surfactants using Eqs. (12) and (13):

(12)
Δ G m o = ( 2 - g ) RT ln X CMC for ionic monomeric surfactants
(13)
Δ G m o = ( 3 - 2 g ) RT ln X CMC for gemini surfactants and their mixtures

From the temperature dependence of CMC, the standard enthalpy change for the mixed micellization process, ΔHom can be obtained as

(14)
Δ H m o = - ( 2 - g ) RT 2 d ( ln X CMC ) dT for ionic monomeric surfactants
(15)
Δ H m o = - ( 3 - 2 g ) RT 2 d ( ln X CMC ) dT for gemini surfactants and their mixtures

The entropy change associated with the micellization process ΔSom is obtained by using the following relationship:

(16)
Δ S m o = Δ H m o - Δ G m o T

The process of mixed micellization becomes less spontaneous with the increase in co-solvent concentration and temperature as indicated by decrease in ΔGom values (Tables S1–S3, Supplementary Information). However, among the studied co-solvents, the process is more spontaneous in mixtures containing alcohols than glycols. The negative values of ΔHom in all the mixtures indicate that the process is exothermic in nature and becomes more so with the increase in temperature and chain length. It is due to possible interactions between surfactant–solvent and solvent–solvent molecules and change in the hydration of head groups of cationic amphiphiles with temperature (Batigöç et al., 2011; Koya et al., 2013). These values decrease with the increase in additive concentration because of decrease in energy required to break up the iceberg structure surrounding the hydrophobic part of the mixture (Tikariha et al., 2012). The more negative values of ΔHom in the mixtures than those in case of pure components further show that the mixed micellization is enthalpically more favorable. ΔSom values decrease with increase in temperature as the aggregation becomes poor at higher temperatures due to enhanced molecular motions (Banipal et al., 2011; Sood et al., 2012). These values roughly show a decrease with increase in percentage of additives implying that the ordering of the randomly oriented cationic surfactants from the solvated form to the micellar structure is more pronounced than the destruction of the water structure. As the enthalpy of micellization is negative and becomes more negative with the rise in temperature accordingly positive entropy becomes less positive and therefore there is entropy–enthalpy compensation in all the studied systems (Mehta et al., 2007).

3.2

3.2 Surface tension studies

The CMC values for the mixtures of gemini and monomeric surfactants in aqueous and aqueous co-solvent solutions at 298.15 K were obtained from the break in surface tension (γ) versus concentration plots as shown in Fig. 5. Since there is not much change in the γ values for 0 < α < 0.48, therefore only representative data (at α = 0.356) have been plotted. Moreover, the considerable decrease in the CMC from α = 1.000 to 0.903 is due to the incorporation of gemini in the micelles of monomeric surfactants causing enhancement in the hydrophobic interactions (Azum et al., 2008). These CMC values (C′m) for DTAB + gemini surfactant mixtures, along with their ideal values (C′i), calculated by Clint Eq. (1), are given in Table 3 whereas C′m and C′i values for the remaining mixtures are included in Table S4 (Supplementary Information).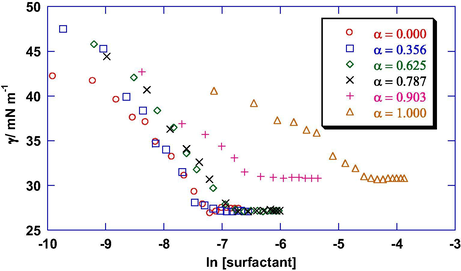

Plot of surface tension (γ) versus total concentration for 12–2–12 and DTAB mixtures in aqueous solutions at different mole fractions of DTAB (α) at 298.15 K.
Figure 5
Plot of surface tension (γ) versus total concentration for 12–2–12 and DTAB mixtures in aqueous solutions at different mole fractions of DTAB (α) at 298.15 K.
Table 3 Experimental and ideal CMC (C′m, C′i), mixed micellar mole fractions (X′1, Xγ1, X′i), interaction parameters (β′, βγ) for the mixtures of DTAB and gemini surfactant systems in aqueous solutions at 298.15 K using surface tension measurements at different mole fractions of DTAB (α).
α C′m (mmol dm−3) C′i (mmol dm−3) X′1 Xγ1 X′i β′ βγ
10–2–10 + DTAB
0.000 5.86 5.86
0.156 6.90 6.26 – – – – –
0.356 7.46 7.12 – 0.14 – – 0.63
0.480 7.99 7.47 0.22 0.19 0.26 0.41 0.59
0.625 8.96 8.25 0.35 0.36 0.39 0.47 0.24
0.787 10.25 9.43 0.56 0.52 0.58 0.68 0.99
0.903 12.66 10.62 0.75 0.62 0.78 3.49 0.87
1.000 13.94 13.94
12–2–12 + DTAB
0.000 0.80 0.80
0.156 0.60 0.91 0.20 0.21 0.01 −5.34 −5.54
0.356 0.71 1.11 0.22 0.22 0.01 −3.84 −4.65
0.480 0.79 1.33 0.26 0.26 0.04 −4.04 −3.88
0.625 1.21 1.72 0.25 0.31 0.08 −2.56 −3.98
0.787 1.21 2.58 0.36 0.38 0.16 −3.83 −4.43
0.903 1.32 4.61 0.46 0.46 0.34 −5.30 −5.40
1.000 13.94 13.94
14–2–14 + DTAB
0.000 0.15 0.15
0.156 0.08 0.17 0.23 0.25 0.00 −9.24 −10.02
0.356 0.11 0.21 0.24 0.26 0.01 −7.24 −8.56
0.480 0.14 0.24 0.23 0.29 0.01 −6.61 −8.97
0.625 0.20 0.33 0.23 0.29 0.01 −5.36 −7.45
0.787 0.32 0.54 0.25 0.32 0.03 −4.50 −6.93
0.903 0.38 1.02 0.37 0.39 0.07 −5.75 −8.85
1.000 13.94 13.94

Regular solution theory (Rubingh, 1979) has been used to obtain interaction parameter (β′) and mole fraction of monomeric surfactant (X′1) as explained in the previous section. The average values of β′(β′avg) are negative for all the mixtures (except 10–2–10 + DTAB) as shown in Fig. 6a. Moreover, β′avg values for 10–2–10 + monomeric surfactant mixtures decrease with increase in chain length (m) of monomeric surfactants although an increase in these values has been seen in mixtures with 12–2–12/14–2–14. These results agree well with those obtained by conductivity measurements although β′avg were slightly more negative than βavg. The micellar mole fraction of monomeric surfactant (Xγ1) and interaction parameter (βγ) at the mixed adsorbed monolayer has also been obtained from Rosen Model (Rosen and Zhou, 2001) using the following equations:

(17)
( X 1 γ ) 2 ln ( C 12 α / C 1 o X 1 γ ) ( 1 - X 1 γ ) 2 ln ( C 12 ( 1 - α ) / C 2 o ( 1 - X 1 γ ) ) = 1 where Co1, Co2 and C12 are the molar concentrations in the solution phase of surfactant 1 (monomeric), surfactant 2 (gemini) and their mixtures, respectively. The values of Xγ1 can be used to calculate the interfacial molecular interaction parameter (βγ) as
(18)
β γ = ln ( C 12 α / C 1 o X 1 γ ) ( 1 - X 1 γ ) 2
Variations of β′avg and βγavg for the mixtures of gemini surfactants with chain length (m) of monomeric surfactants in aqueous solutions at 298.15 K.
Figure 6
Variations of β′avg and βγavg for the mixtures of gemini surfactants with chain length (m) of monomeric surfactants in aqueous solutions at 298.15 K.

The synergistic interactions in the surfactant mixtures are not governed only by the β values but also by the relevant properties of the individual surfactant in the mixture (Rosen and Zhou, 2001). The conditions for synergism in a mixture of two surfactants are as follows:

  1. β must be negative

  2. |β| > |ln (C1/C2)|

  3. |βγ − β| >  [ | ln ( C 1 o / C 2 o ) | - | ln ( C 1 / C 2 ) | ]

The calculations based upon the data shown in Tables 2 and 3 reveal that the mixtures of 12–2–12/14–2–14 with DTAB satisfy all the three conditions and thus exhibit synergism whereas 10–2–10 + DTAB mixture does not follow these conditions and show antagonism.

Similar to the mixed micelle formation, the conditions for synergism in mixed monolayer formation are as follows:

  1. βγ must be negative

  2. |βγ| > | ln ( C 1 o / C 2 o ) |

It can be seen from the data in Table 3 that both these conditions are fulfilled by the mixtures of 12–2–12/14–2–14 whereas the mixture of 10–2–10 with DTAB does not obey these conditions.

Motomura theory (Motomura and Aratono, 1993) has been used to calculate the mole fraction of the monomeric surfactant (X′i) in ideal state. The Xγ1 values are in general smaller than X′i (Table S4, Supplementary Information) showing that contribution of monomeric surfactant is more in mixed micelle formation than in mixed monolayer. Further, Xγ1 values increase with the chain length of ionic surfactants. The average values of βγ (βγavg) are more negative than those of β′avg in most of the mixtures which indicate stronger interactions at the air–solution interface (Fig. 6b). The negative magnitude of βγ values increases in the presence of alcohols because the intercalation of these alcohols in the mixed micelles causes screening of electrostatic repulsions between head groups of the two types of surfactants and increases hydrophobic interactions (Mohammad et al., 2011).

The maximum excess concentration (Γmax) and minimum area per surfactant molecule (Amin) at the air–water interface can be obtained from Eqs. (19) and (20), respectively:

(19)
Γ max = - 1 nRT d γ d ln [ surfactant ]
(20)
A min = 10 20 N A Γ max where R is the gas constant (8.314 J mol−1 K−1), T is temperature in Kelvin, [surfactant] is the concentration of the surfactant in solution and NA is the Avogadro number (6.023 × 1023 molecules mol−1). The constant n (prefactor) has been taken as 2 for these surfactants and their mixtures (Mohammad et al., 2011). The Γmax and Amin values for the studied gemini surfactants and DTAB mixtures are given in Table 4 whereas data for the remaining mixtures are summarized in Table S5 (Supplementary Information). The lower Γmax values in case of pure gemini as compared to monomeric surfactants are due to the fact that these molecules, having two hydrophobic head groups covalently bonded with the help of a spacer and thus occupy more area. Moreover, with the increase in chain length of these surfactants, the surface area occupied by each molecule increases further and hence Γmax decreases (Table S5, Supplementary Information). In 2.5% alcohol solutions, these Γmax values increase whereas Amin decrease due to intercalation of alcohol molecules between aqueous and micellar phase which results in decrease in polar head group repulsions leading to tight packing (Khan et al., 2014). The increase in Γmax is more in case of gemini than monomeric surfactants. However, the Γmax values decrease with further increase in alcohol percentage (5.0%) as these alcohols act as better co-solvents at higher concentrations (Ruiz, 1999). In case of glycol solutions, Γmax decreases (Amin increases) with the increase in glycol concentration because glycols are more soluble in the aqueous phase and therefore, tend to keep the surfactant molecules far apart from any association, resulting in decrease in compactness (Sohrabi et al., 2010). Moreover, in case of gemini surfactants, the increase in Amin is more in comparison with that in monomeric surfactants because the spacer gets extended and thus the distance between the head groups increases in the presence of glycols (Batigöç et al., 2011).
Table 4 Maximum surface excess concentration (Γmax), experimental and ideal values of minimum area per molecule (Amin, Aidmin), CMC and surface concentration ratio (C′m/C20) and surface pressure at CMC (ΠCMC), Standard free energies of micellization, adsorption and at the air–water interface (ΔG′om, ΔGoad, G(s)min) and packing parameter (P∗) for the mixtures of DTAB and gemini surfactants in aqueous solutions at 298.15 K using surface tension measurements at different mole fractions of DTAB (α).
α Γmax · 106 (mol m−2) Amin (Å2 molecule−1) Aidmin (Å2 molecule−1) C′m/C20 ПCMC (mN m−1) G(s)min (kJ mol−1) ΔG′om (kJ mol−1) ΔGoad (kJ mol−1) P∗
10–2–10 + DTAB
0.000 1.30 127.59 3.76 44.48 23.90 −22.69 −61.46 0.32
0.156 0.78 213.16 – 3.65 45.08 34.56 −22.29 −80.16 -
0.356 0.89 196.32 148.23 3.14 44.15 28.24 −21.59 −72.12 0.23
0.480 1.09 151.70 155.45 2.86 44.15 25.26 −21.92 −62.26 0.20
0.625 0.94 176.70 165.06 2.51 43.80 29.16 −21.64 −68.26 0.26
0.787 0.73 225.28 174.10 3.36 42.21 39.74 −21.31 −78.58 0.35
0.903 0.66 250.51 144.72 2.61 40.60 46.77 −20.78 −82.04 0.44
1.000 1.57 105.81 2.54 40.67 37.24 −20.93 −70.22 0.20
12–2–12 + DTAB
0.000 1.19 139.55 4.42 45.39 20.28 −27.63 −62.50 0.30
0.156 1.11 149.43 143.01 6.67 44.38 24.41 −28.34 −68.28 0.34
0.356 1.24 136.35 144.24 6.64 45.01 21.28 −28.01 65.41 0.39
0.480 1.34 123.78 146.70 6.10 45.11 20.04 −27.65 −61.28 0.44
0.625 1.52 108.82 150.38 6.71 44.76 17.78 −26.61 −55.94 0.40
0.787 1.16 143.10 155.54 4.84 44.88 23.20 −26.60 −65.28 0.39
0.903 1.61 103.11 161.43 5.81 43.65 17.48 −26.39 −53.50 0.37
1.000 1.57 105.81 2.54 40.67 37.24 −20.93 −70.22 0.20
14–2–14 + DTAB
0.000 1.15 144.50 10.06 29.98 33.59 −31.76 −55.82 0.29
0.156 0.79 210.68 150.21 4.96 44.68 34.41 −33.20 −89.90 0.24
0.356 0.91 171.25 150.94 5.73 44.59 28.56 −32.41 −80.46 0.33
0.480 1.10 150.31 152.93 6.13 45.11 24.34 −31.93 −72.77 0.25
0.625 0.84 197.55 152.93 4.86 44.76 32.29 −31.02 −84.27 0.25
0.787 0.90 183.87 154.97 6.15 44.88 29.81 −29.85 −79.55 0.26
0.903 1.10 150.45 159.73 5.39 43.65 25.51 −29.45 −69.01 0.34
1.000 1.57 105.81 2.54 40.67 37.24 −20.93 −70.22 0.20

P∗ stands for P or Peff.

The value of surface pressure at the CMC (ПCMC) is obtained from the equation ПCMC = γo − γCMC, where γo is the surface tension of aqueous solution of co-solvent and γCMC is the surface tension at CMC. The γo values among the studied co-solvents follow the sequence of PG > PrOH > tert BuOH > Gly > BuOH. Moreover, ПCMC values in the presence of studied co-solvents are much lower than those in aqueous solutions and decrease with increase in concentration of co-solvent. ПCMC values are the least in the presence of Gly among these co-solvents (Table S5, Supplementary Information) indicating significant reduction in the effectiveness of the surfactants in lowering the surface tension.

The standard Gibbs free energies of micellization and adsorption (ΔG′om, ΔGoad) have been calculated as per the following equations:

(21)
Δ G m ′ o = RT ln X CMC ′
(22)
Δ G ad o = Δ G m ′ o - π CMC Γ max where X′ is the CMC in mole fraction units obtained from surface tension studies. The more negative values of ΔGoad than ΔG′om (Tables 4 and S5, Supplementary Information) confirm that micellization is secondary in nature as compared to surface adsorption; therefore, work has to be done to transfer the molecules from the monomeric form to the micelle form (Khan et al., 2012). The magnitude of both ΔG′om and ΔGoad increases with the chain length of ionic surfactant and the effect is more in case of gemini surfactants. ΔG′om values were more negative in the presence of PrOH and BuOH than in aqueous solution whereas no significant variation is observed in case of remaining studied co-solvents. However, the magnitude of ΔGoad values is smaller in the presence of co-solvents than in aqueous solutions. It shows that the second term (ΠCMC/Γmax) in Eq. (22) plays a significant role in determining the adsorption tendency.

The C′m/C20 ratio measures reduction in the surface tension of water by the presence of additional surfactant or co-solvents. It has been observed that the ratio decreases in the presence of co-solvents and increases with the chain length of monomeric/gemini surfactants (Table S5, Supplementary Information). The decrease in the ratio is more in case of alcohols as compared to glycols. Sugihara et al. (2003) have proposed a thermodynamic quantity, and the minimum free energy at the air–solution interface, G(s)min, for evaluating synergism in mixing and is given as

(23)
G min ( s ) = A min γ CMC N A G(s)min is regarded as the work needed to make an interface per mole or the free energy change accompanied by the transition from the bulk phase to the interface of the components in the solution. In other words, the lower the value of G(s)min, the more thermodynamically stable surface is formed. It can be seen from Table S5 (Supplementary Information), that the G(s)min values are lower in the presence of alcohols at lower concentrations (2.5%) in comparison with those in aqueous solutions and become higher in 5.0% alcohol solutions. However, these values decrease with the increase in the amount of glycols (PG and Gly) in the solution.

According to Israelachvili et al. (1976), the nature of amphiphile packing in micelles and their structural geometry can be predicted by packing parameter (P) defined by the relation,

(24)
P = V A l c where V is the volume of the micelle which can be considered as fluid and incompressible, A is the surface area of the head group and lc is the maximum effective length of the hydrophobic chain of the monomer.

The critical or effective length for a saturated hydrocarbon chain with Cn number of carbon atoms can be obtained from Tanford formula (Tanford, 1980):

(25)
l c ⩽ l max ≈ ( 0.154 + 0.1265 C n ) nm where lmax is the maximum length of the chain. The volume of the micelle can be obtained from
(26)
V = ( 0.0274 + 0.0269 C n ) nm 3

Since the exact determination of the head group area A is comparatively difficult, therefore Amin values have been used instead of A in the above calculations (Kabir-ud-Din et al., 2010; Rodríguez et al., 2008; Ray et al., 2007). In the mixed micelles, the aggregation can be evaluated in terms of the effective packing parameter (Peff) as (Ray et al., 2007)

(27)
P eff = ∑ V i x i mic ∑ A i x i mic l c where ximic and Ai are the micellar mole fraction and area of the ith component in the mixed micelles, respectively. The shape and type of amphiphile aggregates can be predicted from the magnitude of P or Peff so that, for spherical assemblies, P ⩽ 0.333; for non spherical shape, 0.333 < P < 0.5; for vesicles and bilayer, 0.5 < P < 1 and for inverted structures P > 1. Thus all the studied ionic surfactants produce spherical or non spherical micelles in aqueous solutions as shown in Tables 4 and S5 (Supplementary Information). The values of Peff, in general, are more in mixed micellar solutions than pure monomeric surfactant solutions which indicate transformations to vesicles and bilayers. It is because, in case of mixed systems, the presence of gemini surfactant with spacer group weakens the strong electrostatic effect between the head groups which decreases the area per molecule (Amin) significantly, thereby increasing Peff values, leading to the formation of vesicles (Shang et al., 2007). In addition, as the mole fraction of the gemini component increases in the mixtures, the net surface charge increases along with the hydrophobicity. This net charge discourages the aggregation but on the other hand, the stronger hydrophobicity promotes the aggregation and makes them come close to each other to form micelles. The values of Peff increase in the presence of co-solvents and are more in alcohols than in glycols. With the increase in hydrophobic chain length of the gemini surfactant and alcohols, the hydrophobic volume V increases, causing increase in Peff, leading to changes in the micellar shapes.

3.3

3.3 Viscosity studies

3.3.1

3.3.1 Relative viscosity in aqueous solutions

The relative viscosity (ηr) of the studied mixed micellar systems has been calculated at different temperatures and the data are summarized in Table S6 (Supplementary Information). The ηr values increase with the chain length of both types of surfactants but the effect is more in case of gemini as compared to monomeric surfactants. It can be explained by considering that in aqueous solutions of monomeric surfactants, the head groups are randomly distributed on the surface separating the aqueous and the micellar hydrophobic core. Due to the opposite forces involved in micellization, the distribution of distance between the head groups is more at thermodynamic equilibrium distance (Zana, 2002). In contrast, the distribution of distance between head groups in gemini surfactants is bimodal. This bimodal distribution of head group distances and the effect of chemical linkage between head groups on packing of the surfactant alkyl chains in the micellar core affect the curvature of the surfactant layers and thus the micellar shape which influences the properties in the solutions.

In mixtures of 10–2–10 + monomeric surfactants, the ηr values decrease with the increase in mole fraction (α) of monomeric surfactants (Fig. 7a) although an increase in ηr has been seen with the hydrophobic chain length of monomeric surfactants. It can be explained by considering two opposing factors (Kabir-ud-Din et al., 1996; Patel et al., 2009) which are responsible for the variation in the ηr values; one is the electrostatic repulsion term originating from intermicellar and intramicellar columbic interactions which result in micelle formation with higher surface area per head group i.e. spherical micelles and the other is due to hydrophobic interactions between the hydrocarbon part of the micelles/monomers which tries to achieve aggregates with tightly packed chains i.e. rods or disks. Therefore, the increased hydrophobic interactions in case of longer chain monomeric surfactants are mainly responsible for the pronounced micellar growth and a distinct rise in viscosity (Wang et al., 2008). Similar results have been observed with the increase in chain length of gemini surfactants as shown in Fig. 7b. A sudden increase in ηr at α = 0.356 for the mixture of 12–2–12 + DTAB may be due to breakdown of 12–2–12 micelles to incorporate similar hydrophobic chain length DTAB resulting in increase in ηr (Bakshi et al., 2006). The ηr values decrease with the increase in α in mixture of 12–2–12/14–2–14 with TTAB/CTAB (Table S6, Supplementary Information). Moreover, the ηr values in all the studied mixtures decrease with increase in temperature. It is because at higher temperatures, the hydrophobic interactions among the surfactant molecules decrease resulting in the decrease in the size of the micellar aggregates (Patel et al., 2009).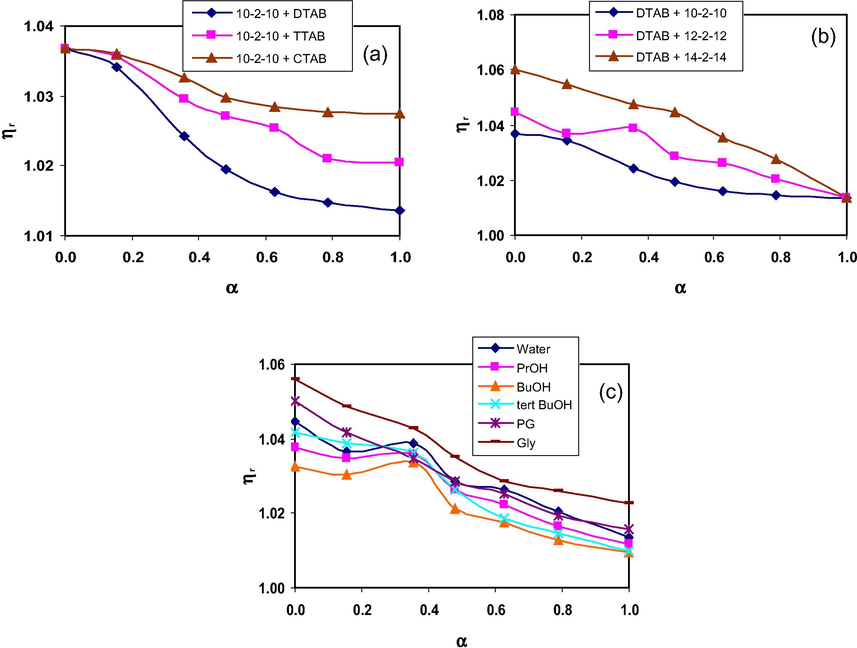

Effect of hydrophobic chain length of (a) monomeric (b) gemini surfactants on the variation of ηr with α in mixed micellar aqueous solutions; (c) variation of ηr with α for the mixture of 12–2–12 + DTAB in the presence 2.5% of different co-solvents at 298.15 K.
Figure 7
Effect of hydrophobic chain length of (a) monomeric (b) gemini surfactants on the variation of ηr with α in mixed micellar aqueous solutions; (c) variation of ηr with α for the mixture of 12–2–12 + DTAB in the presence 2.5% of different co-solvents at 298.15 K.

3.3.2

3.3.2 Effect of co-solvents on relative viscosity

The presence of studied alcohols and glycols (at low concentrations) has marginal affect on the mixed micellar solutions of gemini and monomeric surfactants. For instance, the ηr values are slightly lower in case of PrOH and BuOH whereas slightly higher values have been observed in PG and Gly solutions as compared to those in aqueous solutions (Fig. 7c). The lower values of ηr in the presence of short chain alcohols are due to higher solubility in water and consequently lower solubility in the micelles (Siddiqui et al., 2012). However, an increase in the ηr values has also been reported in case of medium chain length alcohols (C6-, C7- and C8OH) due to their tendency to be embedded among the monomers forming micelles resulting in the significant change in the shape of the micelles (Ansari et al., 2012). Moreover, it has been suggested by Mukerjee (1979) that a solvent is mainly solubilized at the micellar surface. This increases the effective volume V of the hydrophobic chain in Eq. (25) leading to increase in P. It leads to micellar growth and increase in ηr. The sudden rise in ηr for 12–2–12 + DTAB mixture at α = 0.356 in the presence of the studied alcohols is more as compared to that in Gly solutions as shown in Fig. 7c. It is due to partitioning of alcohols among the similar hydrophobic chain length monomer units of mixed micelles which leads to reduction in electrostatic repulsions and hence promotes micellar growth.

3.4

3.4 Dynamic light scattering measurements

DLS measurements have been carried out to obtain further information on the physicochemical properties of the mixed surfactant systems. The size of the micelles formed in aqueous and aqueous co-solvent solutions has been determined by measuring hydrodynamic diameter (Dh) of the micelle using Stokes–Einstein Eq. (1). The Dh values for the studied mixtures at different α values are summarized in Table S7 (Supplementary Information). These Dh values increase with the hydrophobic chain length of the surfactants as shown in Fig. 8a due to the decrease in aggregation number which results in the formation of loose micelles (Varade et al., 2004; Kamboj et al., 2014). These trends are supported by the variation in ηr values with chain length of these surfactants. Moreover, it is evident from the literature that the decrease in electrostatic repulsions between polar head groups of surfactant molecules favors the micellar growth (Li et al., 2010). In aqueous solutions of 10–2–10 + DTAB, Dh values decrease with increase in mole fraction of DTAB. When the hydrophobic chain length of the gemini is increased from 10 to 12, Dh values increase up to α ≈ 0.480 and then decrease with further increase in α (Fig. 8a). Similar effect on ηr values has been seen from viscosity studies at α ≈ 0.356. This shows that there are structural transitions of the micelles at these α values which are further supported by the Peff values. A slight rise in Dh values has been seen in mixtures of gemini surfactants with TTAB at α ≈ 0.625 (Fig. 8b). Similarly, in gemini + CTAB mixtures, the Dh values increase initially with α and then decrease with further increase in α (Table S7, Supplementary Information).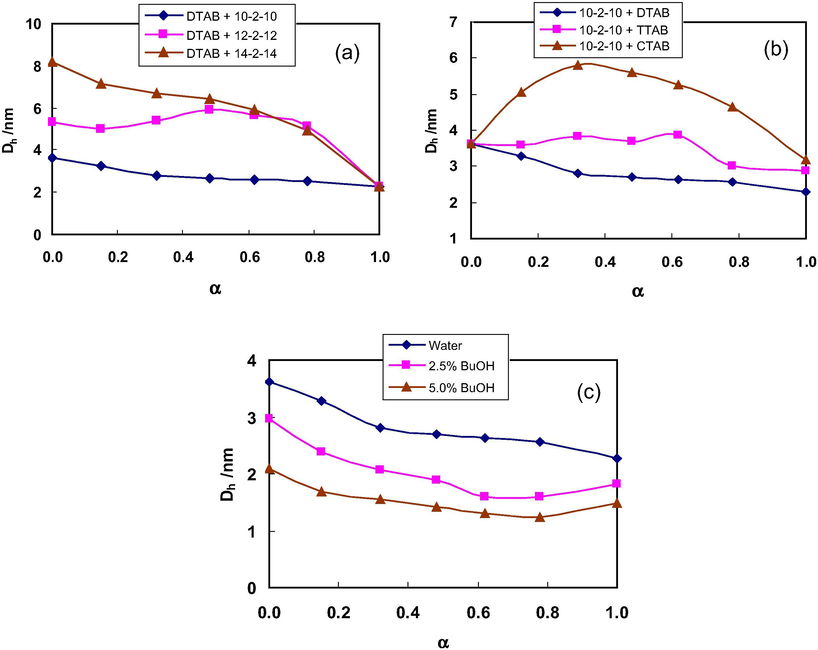

Effect of hydrophobic chain length of (a) gemini and (b) monomeric surfactants on the variation of Dh with α in aqueous mixed micellar solutions; (c) n-butanol (BuOH) on the Dh on the mixed micellar solutions of 10–2–10 + DTAB at 298.15 K.
Figure 8
Effect of hydrophobic chain length of (a) gemini and (b) monomeric surfactants on the variation of Dh with α in aqueous mixed micellar solutions; (c) n-butanol (BuOH) on the Dh on the mixed micellar solutions of 10–2–10 + DTAB at 298.15 K.

The presence of alcohols decreases the Dh values for the mixtures (Fig. 8c) whereas glycols have the opposite effects. These observations are well supported by the variation in the ηr values. The decrease in Dh values in the presence of alcohols is due to penetration of alcohol molecules in the micellar system which results in small mixed aggregates (Tomi et al., 2009; Kuperkar et al., 2011). Further, the decrease is more in case of longer chain alcohol i.e. BuOH which is in accordance with the results obtained from conductivity and surface tension studies. In case of tert BuOH, the polar –OH group is positioned so that it divides the nonpolar organic region into smaller regions that increase its solubility in water i.e. it remains relatively more in aqueous bulk phase and incorporation with micelles is less. Dh values of surfactant mixtures decrease with increase in alcohol percentage (Table S7, Supplementary Information) and are more significant in mixtures with smaller chain length surfactants. Moreover, the relative variation in the Dh with α in the presence of co-solvents follows the similar trends as in aqueous solutions.

In case of glycols, the additional hydroxyl groups tend to decrease number of ordered water molecules around surfactant hydrophobic chain thereby decreasing the hydrophobic effect and hence Dh increases. These observations are further supported by the difference in the partition coefficients of glycols in comparison with that of alcohols as reported by Mullally et al. (2004). Further, the presence of these glycols in the palisade layer of micelles decreases the entropy and the results are in good agreement with those from the conductivity studies. Apart from this, the alkyl chain between the two hydroxyl groups may not be of sufficient length for a favorable interaction with the hydrophobic core of mixed micelles. Hence, the presence of either PG or Gly causes an increase in the Dh values of the studied surfactants and their mixtures.

4

4 Conclusions

The studies on the mixed micellar characteristics of a series of monomeric and gemini surfactants in aqueous solutions show that in the mixtures of 10–2–10 with monomeric surfactants, the synergistic interactions increase with chain length of monomeric surfactants whereas the mixtures with 12–2–12 and 14–2–14 follow the opposite trend. However, these synergistic interactions decrease with increase in temperature due to disruption of water structure surrounding the hydrophobic groups. Further, the contribution of monomeric surfactant in the mixed micelles decreases with increase in chain length of gemini surfactants as well as temperature.

In 2.5% co-solvents, the synergistic interactions increase and are strongest in case of BuOH among the studied co-solvents. However, in certain mixtures, the synergistic interactions decrease at higher (5.0%) concentration of these co-solvents. The presence of alcohols in mixtures of short chain gemini and monomeric surfactants increases the contribution of monomeric surfactant in the mixed micelles whereas no significant effect is seen in mixtures consisting of longer chain surfactant mixtures. The presence of short chain linear alcohols (PrOH and BuOH) decreases the ηr values of the mixed micelles whereas slight increase in the ηr values has been observed in case of glycols (PG and Gly). The hydrodynamic diameter (Dh) increases with chain length of these surfactants. The alcohols decrease the Dh values of the surfactant mixtures whereas glycols show the opposite effect. The DLS results support the observations from the viscosity studies.

Acknowledgments

Dynamic Light Scattering facility under the “University with Potential for Excellence” scheme of University Grants Commission, New Delhi, is thankfully acknowledged.

References

  1. , , , . Aggregation and thermodynamic properties of some cationic gemini surfactants. J. Surfact. Deterg.. 2012;15:33.
    [Google Scholar]
  2. , , . SANS investigation of polyether block copolymer micelle structure in mixed solvents of water and formamide, ethanol, or glycerol. Macromolecules. 2000;33:5574.
    [Google Scholar]
  3. , , , , . Micellar growth of m-2-m type gemini surfactants (m = 10, 12, 14) with higher chain length alcohols/amines (C6–C8) in the absence and presence of organic salts (sodium salicylate, sodium tosylate) J. Mol. Liq.. 2012;174:5.
    [Google Scholar]
  4. , , , , . Studies of mixed micelle formation between cationic gemini and cationic conventional surfactants. J. Colloid Interface Sci.. 2008;328:429.
    [Google Scholar]
  5. , , . Synergistic interactions in the mixed micelles of cationic gemini with zwitterionic surfactants: fluorescence and Krafft temperature studies. J. Colloid Interface Sci.. 2005;287:288.
    [Google Scholar]
  6. , , , , , , , , . Mixed-micelle formation by strongly interacting surfactant binary mixtures: effect of head-group modification. Colloid Polym. Sci.. 2002;280:990.
    [Google Scholar]
  7. , , , , . Mixed micelle behavior of Pluronic L64 and Triton X-100 with conventional and dimeric cationic surfactants. J. Colloid Interface Sci.. 2005;286:369.
    [Google Scholar]
  8. , , , , , . Synergistic mixing of L64 with various surfactants of identical hydrophobicity under the effect of temperature. Colloids Surf. A. 2006;278:218.
    [Google Scholar]
  9. , , , . Micellization behavior of 14–2–14 gemini surfactant with some conventional surfactants at different temperatures. J. Surfact. Deterg.. 2011;14:235.
    [Google Scholar]
  10. , , , . Micellization behaviour and thermodynamic parameters of 12–2–12 gemini surfactant in (water + organic solvent) mixtures. J. Chem. Thermodynam.. 2011;43:1349.
    [Google Scholar]
  11. , , , . Behavior of cetyltrimethylammonium bromide, tert-octylphenol (9.5 EO) ethoxylate and ethanol mixtures at the water–air interface. Surf. Deterg.. 2013;16:203.
    [Google Scholar]
  12. , , , . Behavior of cetyltrimethylammonium bromide and Triton X-100 mixture at solution–air interface in presence of short-chain alcohols. Colloids Surf. A. 2014;454:65.
    [Google Scholar]
  13. , , , , , , . Adsorption and micellization of gemini surfactants with pyrrolidinium head groups: effect of the spacer length. Soft Matter. 2013;9:7637.
    [Google Scholar]
  14. , , , . Micellization and related behavior of binary and ternary surfactant mixtures in aqueous medium: cetyl pyridinium chloride (CPC), cetyl trimethyl ammonium bromide (CTAB), and polyoxyethylene (10) cetyl ether (Brij-56) derived system. J. Phys. Chem. B. 2005;109:14813.
    [Google Scholar]
  15. , , , . The methods of determination of critical micellar concentrations of the amphiphilic systems in aqueous medium. Arab. J. Chem.. 2011;4:265.
    [Google Scholar]
  16. , , . Micellization of a cationic gemini surfactant in aqueous solutions with different alkanols and alkanediols as additives: Effect of nonpolar chain and position of hydroxyl groups. J. Mol. Liq.. 2011;161:72.
    [Google Scholar]
  17. , , , , , , . Quantitative analysis and subsequent effects of partitioning of a mono-and dihydric C4 alcohols into the micelles of cationic surfactants. Colloids Surf. A. 2011;378:79.
    [Google Scholar]
  18. , . Micellization of mixed nonionic surface active agents. J. Chem. Soc. Faraday Trans.. 1975;71:1327.
    [Google Scholar]
  19. , , , , , . Light scattering and NMR studies of Triton X-100 micelles in the presence of short chain alcohols and ethoxylates. Colloids Surf. A. 2013;436:252.
    [Google Scholar]
  20. , , . Thermodynamic and interfacial adsorption studies on the micellar solutions of alkyltrimethylammonium bromides in ethylene glycol (1) + water (2) mixed solvent media. J. Chem. Eng. Data. 2009;54:559.
    [Google Scholar]
  21. , , . Aggregation and adsorption properties of sodium dodecyl sulfate in water–acetamide mixtures. J. Colloid Interface Sci.. 2008;327:198.
    [Google Scholar]
  22. , . CTAB aggregation in solutions of higher alcohols: Thermodynamic and spectroscopic studies. J. Mol. Liq.. 2013;184:60.
    [Google Scholar]
  23. , , , , . Environment-friendly ester bonded gemini surfactant: mixed micellization of 14–E2–14 with ionic and nonionic conventional surfactants. J. Mol. Liq.. 2015;211:247.
    [Google Scholar]
  24. , , . Effects of butanol isomers on the mixed micellization of TTAB/Brij 35 mixed surfactant systems. J. Korean Chem. Soc.. 2008;52:111.
    [Google Scholar]
  25. , , , , . Micellization and micellar growth of alkanediyl-α, ω-bis(dimethyldodecylammonium bromide) surfactants in the presence of medium-chain linear alcohols. J. Colloid Interface Sci.. 2010;342:382.
    [Google Scholar]
  26. , , , , . Interaction of bovine (BSA), rabbit (RSA), and porcine (PSA) serum albumins with cationic single-chain/gemini surfactants: a comparative study. Langmuir. 2009;25:11686.
    [Google Scholar]
  27. , , , . Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J. Chem. Soc. Faraday Trans.. 1976;2(72):1525.
    [Google Scholar]
  28. , , , . Adsorption and micellar properties of binary ionic/nonionic surfactant mixtures in ethylene glycol + water. J. Chem. Eng. Data. 2010;55:1122.
    [Google Scholar]
  29. , , , , . 1H NMR and viscometric studies on cationic gemini surfactants in presence of aromatic acids and salts. J. Phys. Chem. B. 2007;111:8860.
    [Google Scholar]
  30. , , , , . Micellar growth in presence of alcohols and amines: a viscometric study. Langmuir. 1996;12:1490.
    [Google Scholar]
  31. , , , , , . Ion-dipole induced interaction between cationic gemini/TTAB and nonionic (Tween) surfactants: interfacial and microstructural phenomena. RSC Adv.. 2013;3:6945.
    [Google Scholar]
  32. , , , . Analysis of mixed micellar and interfacial behavior of cationic gemini hexanediyl-1,6-bis(dimethylcetylammonium bromide) with conventional ionic and nonionic surfactants in aqueous medium. J. Phys. Chem. B. 2010;114:6023.
    [Google Scholar]
  33. , , , . Synthesis, characterization and surface properties of N-(2-hydroxyalkyl)-N′-(2-hydroxyethyl) imidazolium surfactants. Colloids Surf. A. 2014;41:233.
    [Google Scholar]
  34. , , , , . Physicochemical study of cationic gemini surfactant butanediyl-1,4-bis(dimethyldodecylammonium bromide) with various counterions in aqueous solution. Colloids Surf. A. 2012;394:46.
    [Google Scholar]
  35. , , , , , . Micellization and interfacial properties of cationic gemini surfactant (12–4–12) in the presence of additives in aqueous electrolyte solution: a tensiometric study. J. Mol. Liq.. 2014;191:29.
    [Google Scholar]
  36. , , , , . Influence of 1,4-dioxane on the aggregation of bis(tetradecyldimethylammonium) butane dibromide gemini surfactant. J. Mol. Liq.. 2013;177:288.
    [Google Scholar]
  37. , , . Studies on the mixed micelles of alkyltrimethylammonium bromides and butanediyl-1,4-bis(alkyldimethylammonium bromide) dimeric surfactants in the presence and absence of ethylene glycol at different temperatures. J. Colloid Interface Sci.. 2011;360:175.
    [Google Scholar]
  38. , , , , . Effect of short chain length alcohols on micellization behavior of cationic gemini and monomeric surfactants. J. Mol. Liq.. 2012;172:81. (and references therein)
    [Google Scholar]
  39. , , , . Effect of 1-alkanols/salt on the cationic surfactant micellar aqueous solutions – a dynamic light scattering study. Colloids Surf. A. 2011;380:60.
    [Google Scholar]
  40. , , , , , , , . Aggregation behavior of a chiral long-chain ionic liquid in aqueous solution. J. Colloid Interface Sci.. 2010;343:94.
    [Google Scholar]
  41. , , , , , . Surface properties, aggregation behavior and micellization thermodynamics of a class of gemini surfactants with ethyl ammonium headgroups. J. Colloid Interface Sci.. 2012;377:222.
    [Google Scholar]
  42. , , , , . Role of the spacer in the non ideal behavior of alkanedyil-α, ω-bis(dodecyldimethylammonium) bromide-MEGA10 binary mixtures. Colloids Surf. A. 2013;418:139.
    [Google Scholar]
  43. , , , , , . Conductometric and spectroscopic studies of sodium dodecyl sulfate in aqueous media in the presence of organic chalcogen. Colloids Surf. A. 2007;304:88.
    [Google Scholar]
  44. , , . Self-aggregation and solution behavior of synthesized organo transition metal (Co, Fe, Zn) amphiphilic complexes. J. Colloid Interface Sci.. 2013;393:219.
    [Google Scholar]
  45. , , . Gemini surfactants: a new class of self-assembling molecules. J. Am. Chem. Soc.. 1993;115:10083.
    [Google Scholar]
  46. , , , , , , . Effect of head group size, temperature and counterion specificity on cationic micelles. J. Colloid Interface Sci.. 2011;358:160.
    [Google Scholar]
  47. , , , , , , , , . Aggregation behavior and interface properties of mixed surfactant systems gemini 14-s-14/CTABr. Colloids Surf. A. 2014;457:425.
    [Google Scholar]
  48. , , , , , , . CTAB aggregation in aqueous solutions of ammonium based ionic liquids; conductimetric studies. Colloids Surf. A. 2007;296:104.
    [Google Scholar]
  49. , , , , . Mixed micellization and interfacial properties of alkanediyl-α, ω-bis(dimethylcetylammonium bromide) in the presence of alcohols. J. Mol. Liq.. 2011;162:113.
    [Google Scholar]
  50. , , , , . Adsorption and micellar phase properties of anionic surfactant in the presence of electrolyte and oil at different temperatures. Fluid Phase Equilib.. 2013;337:370.
    [Google Scholar]
  51. , , . , , eds. Mixed surfactant systems. Vol vol. Surfactant Science Series. New York: Marcel Dekker; . (46)
  52. , , , , . Micellar properties of cationic surfactants in pure and mixed states. J. Phys. Chem.. 1996;100:701.
    [Google Scholar]
  53. , . , ed. Solution chemistry of surfactants. New York: Plenum; .
  54. , , , . The partitioning of alkanediols into SDS and DTAB micelles from NMR-PRE experiments. Colloid Polym. Sci.. 2004;283:335.
    [Google Scholar]
  55. , , , . Solution behavior of normal and reverse triblock copolymers (Pluronic L44 and 10R5) individually and in binary mixture. Langmuir. 2012;28:7134.
    [Google Scholar]
  56. , , . The viscosity behavior of aqueous NaCI solutions of dodecyldimethylammonium chloride and the flexibility of its rod-like micelle. J. Colloid Interface Sci.. 1980;77:219.
    [Google Scholar]
  57. , , , , , , , . Amphiphile behavior in mixed solvent media I: self-aggregation and ion association of sodium dodecylsulfate in 1,4-dioxane–water and methanol–water media. Langmuir. 2012;28:13830.
    [Google Scholar]
  58. , , . Mixed micellization of sodium dodecylbenzene sulfonate with polyoxyethylene lauryl ether surfactants (POLE4and POLE23) in n-butanol aqueous solution. J. Surfact. Deterg.. 2012;15:41.
    [Google Scholar]
  59. , , , , . Structural characteristics of the aqueous mixed nonionic–cationic surfactants: effect of chain length, head group and temperature. Colloids Surf. A. 2009;333:145.
    [Google Scholar]
  60. , , , , , , , . Studies on binary and ternary amphiphile combinations of tetradecyltrimethylammonium bromide (C14TAB), tetradecyltriphenylphosphonium bromide (C14TPB), and tetradecylpyridinium bromide (c14pb): a critical analysis of their interfacial and bulk behaviors. J. Phys. Chem. B. 2007;111:9828.
    [Google Scholar]
  61. , , , , . Mixtures of monomeric and dimeric surfactants: hydrophobic chain length and spacer group length effects on non ideality. J. Phys. Chem. B. 2008;112:11942.
    [Google Scholar]
  62. , , . Surface concentrations and molecular interactions in binary mixtures of surfactants. J. Colloid Interface Sci.. 1982;86:164.
    [Google Scholar]
  63. , , . Surfactant–surfactant interactions in mixed monolayer and mixed micelle formation. Langmuir. 2001;17:3532.
    [Google Scholar]
  64. , . , ed. Solution chemistry of surfactants. New York: Plenum; .
  65. , . Thermodynamics of micellization of tetradecyltrimethylammonium bromide in ethylene glycol–water binary mixtures. Colloid Polym. Sci.. 1999;277:701.
    [Google Scholar]
  66. , , , , . Phase behavior and microstructures of the Gemini (12-3-12,2Br−)–SDS–H2O ternary. Colloids Surf. A. 2007;294:203.
    [Google Scholar]
  67. , , , , . Morphological changes of cationic gemini surfactants 14-s-14 (s = 4, 5, 6) in the presence of additives. J. Solution Chem.. 2012;41:1133.
    [Google Scholar]
  68. , , . Synergistic interactions in the mixed micelles of cationic gemini with zwitterionic surfactants: the pH and spacer effect. J. Colloid Interface Sci.. 2007;315:620.
    [Google Scholar]
  69. , , , . Effect of ethylene glycol on micellization and surface properties of gemini surfactant solutions. Colloids Surf. A. 2010;364:87.
    [Google Scholar]
  70. , , , , . Mixed micellization behavior of m-2-m gemini surfactants with some conventional surfactants at different temperatures. J. Surfact. Deterg.. 2012;15:327.
    [Google Scholar]
  71. , , , , , , . Adsorption and micelle formation of mixed surfactant systems in water II – a combination with cationic gemini surfactant with Mega-10. J. Oleo Sci.. 2003;52:449.
    [Google Scholar]
  72. , , , , . Interactions in mixed micellar systems of an amphoteric chelating surfactant and ionic surfactants. Langmuir. 2014;30:1250.
    [Google Scholar]
  73. , . The Hydrophobic Effect: Formation of Micelles and Biological Membranes. New York: John Wiley & Sons; .
  74. , , , , . Effects of pentanol isomers on the growth of SDS micelles in 0.5 M NaCl. J. Phys. Chem. B. 1997;101:11087.
    [Google Scholar]
  75. , , , , , . Micellization properties of mixed cationic gemini and cationic monomeric surfactants in aqueous-ethylene glycol mixture. Colloids Surf. A. 2011;381:61.
    [Google Scholar]
  76. , , , , , , . Physicochemical characterization of cationic gemini surfactants and their effect on reaction kinetics in ethylene glycol–water medium. Colloids Surf. A. 2012;411:1.
    [Google Scholar]
  77. , , , . Aggregation properties and thermodynamics of micellization of gemini surfactants with diethyl ether spacer in water and water–organic solvent mixed media. J. Chem. Thermodynam.. 2014;70:24.
    [Google Scholar]
  78. , , , , . Micelle formation of a cationic surfactant in the presence of 1, n-alkanediol and the miscibility of alcohols in micelles. Colloids Surf. A. 2009;346:28.
    [Google Scholar]
  79. , , , , . Effect of salt and alkyl chain length on the structure of bile salt–cationic mixed surfactant system. Colloids Surf. A. 2004;251:161.
    [Google Scholar]
  80. , , , , . Mixed micelles of some anionic–anionic, cationic–cationic, and ionic–nonionic surfactants in aqueous media. J. Surf. Deterg.. 1999;2:213.
    [Google Scholar]
  81. , , , . Monolayers of gemini surfactants and their catanionic mixtures with sodium dodecyl sulfate at the air–water interface: chain length and composition effects. Thin Solid Films. 2008;516:7458.
    [Google Scholar]
  82. , , , , , . Effect of glycyl dipeptides on the micellar behavior of gemini surfactant: a conductometric and fluorescence spectroscopic study. J. Mol. Liq.. 2011;161:49.
    [Google Scholar]
  83. , . Critical micellization concentration of surfactants in aqueous solution and free energy of micellization. Langmuir. 1996;12:1208.
    [Google Scholar]
  84. , . Dimeric and oligomeric surfactants. Behavior at interfaces and in aqueous solution: a review. Adv. Colloid Interface Sci.. 2002;97:205.
    [Google Scholar]
  85. , , , . Alkanediyl-α, ω-bis(dimethylalky1ammonium bromide) critical micelle concentration and micelle ionization degree. Langmuir. 1991;7:1072.
    [Google Scholar]
  86. , , . Gemini Surfactants: Synthesis, Interfacial and Solution-Phase Behavior and Applications. New York: Marcel Dekker; .

Appendix A

Supplementary material

Tables containing mixed micellar, surface, thermodynamic, relative viscosity and hydrodynamic diameter data of the mixtures in aqueous and aqueous co-solvent solutions are included. Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.arabjc.2015.12.009.

Appendix A

Supplementary material

Supplementary data 1

Supplementary data 1


Fulltext Views
64

PDF downloads
36
View/Download PDF
Download Citations
BibTeX
RIS
Show Sections

Suggested read for related articles:

© Copyright 2025 – Arabian Journal of Chemistry.

Published by Scientific Scholar on behalf of King Saud University together with Saudi Chemical Society, Riyadh, Saudi Arabia.

ISSN (Print): 1878-5352
ISSN (Online): 1878-5379
Scientific Scholar CrossRef Creative Commons Open Acess Portico