Kinetic parameters underlying hematite-assisted decomposition of tribromophenol

2.1 Thermogravimetric analysis (TGA) runs

The pyrolytic and combustion reactions were performed using TGA Q500 V20.10 of TA instruments. The oxygen and nitrogen of 60 ml/min flow rates were used as the carrier gas, and the analysis was performed in the temperature range of 25–600 °C at the heating rate of 10 °C/min. The peak degradation temperature (T_d), and kinetic and thermodynamic parameters were obtained from the TGA data. A sample weighing approximately 8–10 mg was taken to run the experiments, and for the mixture, the sample weight was considered a 1:1 mass ratio (hematite:TBP).

2.2 Model-Free or isoconversional methods

The thermokinetic studies of the samples were done by the model-free method, also known as the isoconversional technique, from the acquired TGA data for different heating rates. The basic concept of this technique is at a specific conversion; the rate of reaction depends only on the temperature (Dhyani and Bhaskar, 2018). This method delivers the characteristic kinetics parameters from the conversion plot against temperature (Vyazovkin, 2000). Moreover, model-free approaches do not require an assumption of any reaction models like the Coats-Redfern method (Naqvi et al., 2018). The studies are conducted on three well-known isoconversional models: Starink, Kissinger Akahira Sunose (KAS), and Flynn-Wall-Ozawa (FWO). This model provides an opportunity to investigate the deviations in the activation energy (Ea, kJ/mol) as a function of conversion (α) throughout the different reactions (Stančin et al., 2021). The pre-exponential or frequency factor (A, min⁻¹) and the linear regression (R²) are also calculated from the characteristic equation for each model. The fundamental state of the equation for the thermal decomposition of the solid state can be generalized, as shown in Eq. (1).

TBP + Fe₂O₃ (with/without) → Char (solid) + Condensate (liquid) + Volatile (gas)

There are commonly two different methods of isoconversional technique such as differential and integral approaches. The equation is known as the differential method, which has the Friedman method of determining kinetics, whereas the integral form for the model-free approach that obtained by separating the variables α and T, followed by the integration, which gives the following Eq. (7).

Below the onset temperature T_i, the extent of conversion is negligible; hence the equation will be zero between 0 and T_i (Ozawa, 1965; Soria-Verdugo et al., 2020), as illustrated in Eq. (8). Therefore, the final $g\left(\alpha \right)$ is obtained in Eq. (9), which is referred as Integral method under which the Straink (Starink, 2003), KAS (Akahira and Sunose, 1971), and FWO (Flynn and Wall, 1966) are covered. In this research work, we are deriving the kinetic parameters by using the isoconversional integral method because it is considered less sensitive. Hence, the possibility of error will be less in this method (Naqvi et al., 2018).

The difference between the models mainly depends upon their assumption in the approximation of the temperature integrals. In the FWO model, as shown in Eq. (10), the approximation of Doyle is used, whereas, the KAS model is focused on improving the FWO model by changing the approximation from Doyle to Murray and White, as shown in Eq. (11) (Doyle, 1962; Murray, 1955). The final Starink model is represented in Eq. (12). The comprehensive details of the mathematical derivation of the following models are reported elsewhere (Soria-Verdugo et al., 2018; Starink, 2003).

From the following derived equations, the characteristic plots are created using each model for the combustion, pyrolysis, catalytic combustion, and catalytic pyrolysis. In our considered notation, we refer to the degradation of the hematite:TBP mixture as a catalytic-assisted process that operates in the decomposition of the latter. The linear plots will be obtained for $ln\left(\frac{\beta }{T^{1.92}}\right)$ vs $\frac{1}{T}$ in Starink model, $\mathrm{l}\mathrm{n}(\frac{\beta }{T^2})$ vs $\frac{1}{T}$ in KAS, and $\mathrm{l}\mathrm{n}(\beta )$ vs $\frac{1}{T}$ for the FWO model, respectively. The slope and intercept are found from the obtained linear curves by which it can calculate the Ea and A values for the required conversions. The mean squared error (MSE) for the determined kinetic parameters was calculated using Eq. (13).

2.3 Model fitting method

The reaction mechanism involved at different temperature ranges for each heating rate analyzed was determined by using the model fitting method. The model fitting method is also known as the Coat-Redfern integral method represented as Eq. (14). This approach derives the different kinetic parameters utilizing the data obtained from the TGA.

The thermodynamic variables such as the enthalpy change $\mathrm{\Delta }H$ , entropy change $\mathrm{\Delta }S,$ and Gibbs free energy change $\mathrm{\Delta }G$ are extracted from the findings of kinetic triplets using the model-free method (Xu and Chen, 2013). The $\mathrm{\Delta }H$ evaluates the energy required for the bond dissociation while undergoing the decomposition reactions. The $\mathrm{\Delta }H$ values enable to determine the condition of reaction either exothermic or endothermic (Arabkhani et al., 2021). $\mathrm{\Delta }S$ measures the degree of disorderness of the formed products from reactants in a system, in which lower $\mathrm{\Delta }S$ values resemble the lower reactivity than high $\mathrm{\Delta }S$ values. The maximum mechanical work that can be attained by a substance for a specific task is called as Gibbs Free energy and hence $\mathrm{\Delta }\mathrm{G}$ signifies the viability of energy on undergoing the reactions. The equation related to each thermodynamic parameter are illustrated in Eq. (15), Eq. (16), and Eq. (17).

2.4 Computational methodology

3.1 Thermogravimetric analysis

The TGA data were acquired for the samples with and without Fe₂O₃ in the presence of oxygen and nitrogen at four different heating rates 5, 10, 15, and 20 °C, respectively. The pure TBP sample exhibited only a single decomposition stage in both pyrolysis and combustion due to the absence of any other impurities, whereas the mixture sample exposed two stages in which the second stage was minor. In all the TGA plots for the samples, as shown in Fig. 1, the first stage is considered the active zone where the major devolatilization of TBP occurs, and the second stage is known to be the passive zone. There was no significant fluctuation in the initial and final temperatures for all the samples in both environments. The onset temperature for all the processes was 95–100 °C, and the endpoint was around 200 °C. The differential thermogravimetric (DTG) curves were also plotted for the following TGA curves, which have their own characteristic plot for each sample. The DTG curve detects the T_d at which the maximum mass loss occurs. An increasing trend of temperature in the TGA plot for the T_d was noticed by increasing the heating rate, which was a similar pattern reported in previous studies (Kaur et al., 2018; Liu et al., 2021; Müsellim et al., 2018). The T_d value increased for the combustion process compared to the pyrolysis for the samples. The T_d had a significant hike from 154 to 183 °C to 166–180 °C in catalytic combustion, whereas a relatively small increment was observed in normal combustion from 152 to 180 °C to 158–185 °C compared to the pyrolysis reaction at the four different heating rates. Apart from this, the appearance of the second decomposition stage with a T_d value around 400 °C in both catalytic reactions can be attributed to two reasons. The first possibility could be the detachment of oxygen from the oxygenated compounds that form during the decomposition of TBP with the help of Fe₂O₃ in the second stage (Jayashree et al., 2019). The formation of oxygenated compounds is already reported in the previous study of TBP and Fe₂O₃ (Mousa et al., 2022). The second possibility for this slight curve can also rise due to char oxidation, which appeared only in catalytic reactions (Ali et al., 2023; Bai et al., 2014).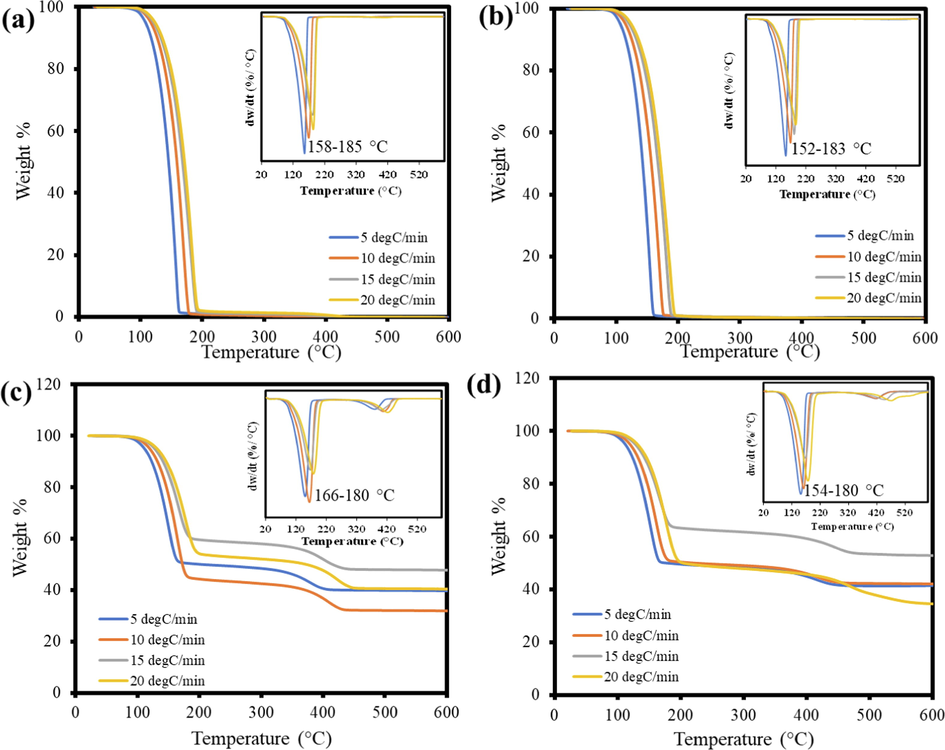

Close

Fig. 1

TGA and DTG curves for (a) Pure TBP combustion, (b) Pure TBP pyrolysis, (c) Catalytic combustion (TBP + Fe₂O₃), and (d) Catalytic pyrolysis (TBP + Fe₂O₃).

Export to PPT

The formation of char was noticed in the catalytic reactions only. Pyrolysis of pure TBP did not result in the formation of char. But in catalytic reactions, due to the presence of Fe₂O₃, the emitted volatile gases during the degradation of TBP will be reacting with the Fe₂O₃ resulting in the bond dissociation and formation of FeBr₃ (Chen et al., 2018), which is verified by the results obtained in XRD, FTIR, and SEM-EDX. In addition to the FeBr₃, the char consists of carbon ashes and other inorganics. The char formation was more in the catalytic pyrolysis with 45 %, whereas it was around 35 % for the catalytic combustion. The char mass was varied according to the heating rates for the catalytic reactions.

3.2 Thermo-kinetic analysis by model-free/isoconversional method

The thermo-kinetic parametric analysis was carried out using the model-free approach using the obtained TGA data for the four processes: combustion, pyrolysis, catalytic pyrolysis, and catalytic combustion. The isoconversional curves were plotted for the Starink, KAS, and FWO model as a function of conversion for combustion and pyrolysis processes in the presence and absence of Fe₂O₃ at four different heating rates to determine the linearity, as shown in Fig. S.1 and Fig. S.2 in the Supplementary Materials (SM). The conversion range was selected from 0.05 to 0.95 for normal reactions and 0.05–0.5 for catalytic reactions with a step size of 0.05. The slope obtained from the curves was used to calculate the dependency of E_a on calculated R² values. All the models gave a correlation coefficient of above 0.95 for most of the investigated conversions. This indicates that the selected models were reliable in calculating E_a and A values from the derived characteristic equations of each model. However, poor regression was obtained in the experiments run in the presence of the Fe₂O₃, and this reduced correlation was found only at the termination stage of the reaction. This could arise due to the experimental error in observing the minor mass changes at the end of the reaction, which is common in the TGA experiments (Liu et al., 2020).

The calculated Ea for the Starink and KAS model was identical in the four processes, but a slight variation was observed in both Ea and A values for the FWO model. This variation can be attributed to the assumption made for each model in the approximation of temperature integrals. Comparing the combustion and pyrolysis reaction of pure TBP, the Ea values were found to be approximately in the range of 65–105 kJ/mol and 60–93 kJ/mol, respectively, as enlisted in the Supplementary Material Table S.1 and Table S.2 (Supplementary Material, SM). The Ea values obtained for the pure TBP were comparable with the previous literature studies (Wang and Hsieh, 1993). The combustion reaction incurs a more Ea value with a 10 kJ/mol difference from the pyrolysis reaction. In both cases, a significant drop was reflected when the conversion range was 0.05–0.15. This explains that the decomposition of TBP into other unsaturated and saturated compounds is initiated in the early stage of the reaction itself. Further conversions also followed the decreasing pattern in Ea value up to 95 % but at a minimal level. The A values for the combustion process were in the range of 10¹³-10⁹ min⁻¹, whereas for the pyrolysis reaction, it was reported in 10¹¹-10⁸ min⁻¹. From the A values, both processes followed simple reactions or surface reactions (Ali et al., 2022b). Further higher A values indicated a high rate of molecular collision, which requires more reaction energy, in agreement with the values obtained for Ea (Liu et al., 2020).

Comparing the Ea and A values for the combustion and pyrolysis in the presence of Fe₂O₃ perceived a reverse trend. The estimated Ea values for catalytic combustion were 47–80 kJ/mol and for the pyrolysis reaction was 57–82 kJ/mol, excluding the conversion with poor regression as tabulated in Table 2 and Table 3. It was interesting to notice the decrease in the E_a values of combustion compared to pyrolysis in the presence of oxygen. The exact reverse trend was also shown in the A values for the catalytic process. The estimated A values for the catalytic combustion and catalytic pyrolysis were in the range of 10¹⁰-10⁷ min⁻¹ and 10¹¹-10⁹ min⁻¹, respectively. Overall, both processes indicated a simple reaction but, for a small conversion range at the end of the reaction in catalytic combustion, the A value reduces below 10⁹ min⁻¹, which explains that the reaction was tight complex during this conversion (Turmanova et al., 2008). The E_a and A values showed in the α range of 45 %, and 50 % were not reliable due to poor regression, and this could happen due to the experimental error in the minor changes of weight towards the end of the reaction.

The plot of Ea as a conversion function for different models on the four processes is illustrated in Fig. 2. The calculated Ea values of Starink and KAS models were identical, but a slight variation was observed in the FWO model. As discussed in the TGA curves, it was seen that there was a sudden drop in the Ea values in the presence of a Fe₂O₃. This is because the reaction ended with 50 % conversion, as discussed in the TGA plots. It is seen that the Ea was the least for the catalytic combustion reaction. Moreover, concerning the Ea values, the corresponding A values also showed a difference of two or three orders of magnitude when catalytic combustion compared to other processes, which indicated the simplicity and fastness of the catalytic reaction in the presence of oxygen.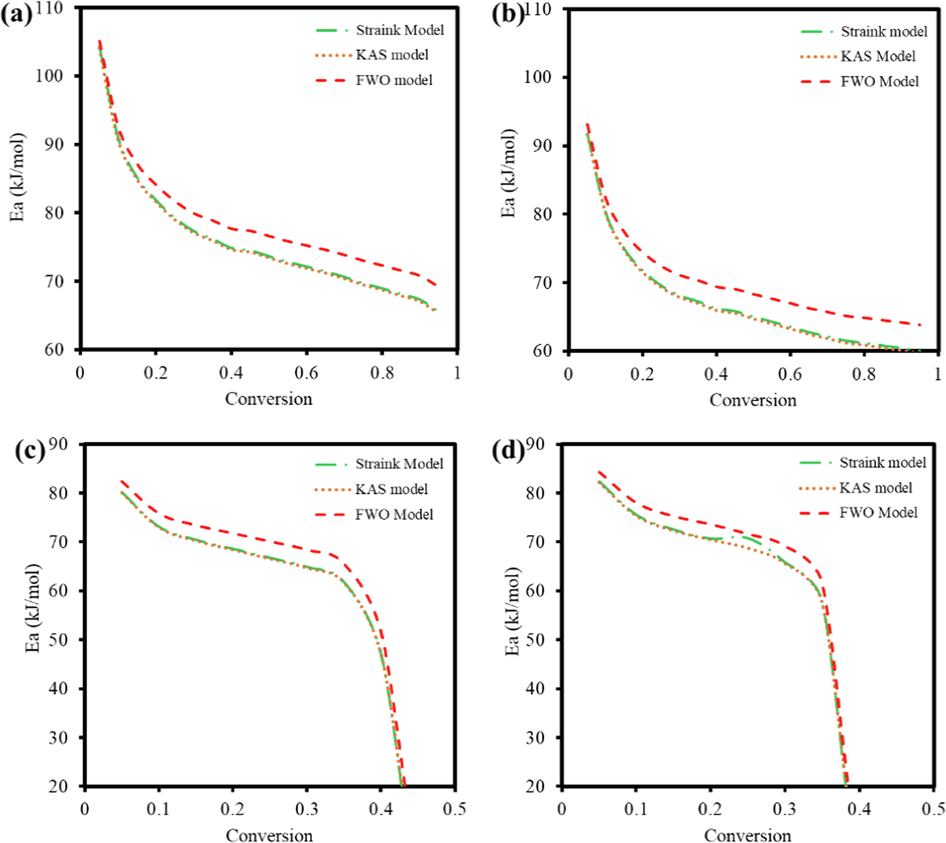

Close

Fig. 2

Plot of Ea as a function of α for TBP (a) combustion, (b) pyrolysis, (c) catalytic combustion, (d) catalytic pyrolysis.

Export to PPT

From the TGA analysis for both pyrolysis and combustion, it was observed that the decomposition takes place via a single-stage degradation in the temperature window 100–200 °C. On the contrary, degradation of the mixture features three regions of 100–200 °C, 200 – 400 °C, and 400–500 °C. From the derived 15 mechanisms and based on the R² values, the best-fitted mechanism for the reactions at different heating rates were determined as enlisted in Table 4 and Table 5 for pyrolysis and combustion reactions. After comparing the values of activation energies obtained from the model-free kinetic approach with Coats and Redfern approach, the reaction mechanism in pyrolysis and combustion of pure TBP follows a 1st and half order reaction, spherical and cylindrical contraction and Avarami Erofeev A1. While mixing the TBP with Fe₂O₃ in both pyrolysis and combustion exhibits a rather very complex nature of the reaction mechanism with 1st, ½ order reaction, geometrical contraction, and Avarami Eroveef A1 with the addition of one-dimensional diffusion and power law. In case of pyrolysis, both pure and mixtures - except the random nucleation and power law (P3) -, all deployed models provide very well-fitting at low-temperature regions. In the mixture at a high-temperature region most models (except tone-dimensional diffusion, contracting sphere, and Avarami Erofeev A1), entail R² values close to 1.0 for the heating rate of 10 and 15 °C/min. For the combustion process, one-dimensional diffusion exhibited a good fitting correlation in both pure and blend samples. In the case of reaction-order mechanisms for the mixture, first and ½ order reactions afford excellent fitting across the high-temperature zone utilizing a 15 °C/min heating rate. The same pattern of reaction mechanism was observed for the contracting sphere and cylinder models. Overall, Power law model P2 proved to be the best-fitted model for all the temperature ranges and different heating rates for both combustion and pyrolysis reactions.

3.3 Thermodynamic analysis

The thermodynamic parameters were calculated from kinetic data obtained from the model-free approach. The values obtained for the parameters $\mathrm{\Delta }H$ , $\mathrm{\Delta }G$ , $\mathrm{\Delta }S$ , were identical in the Starink and KAS models, but a slight difference was noticed in the FWO model, which could be due to the different assumptions made for each model in the approximation of temperature integrals. The $\mathrm{\Delta }H$ value indicates the amount of energy required for converting the TBP into value-added products in the form of condensate and volatiles during the degradation. It represents the energy difference between reactant consumption and the formation of activated complexes. $\mathrm{\Delta }H$ values for the proposed three models in all the techniques were found to be positive, resembling the endothermic reactions. This indicate that during all the reactions, the samples are undergoing the breakage of lower energy bonds resulting in the formation of higher energy bonds. The highest and lowest values for the $\mathrm{\Delta }H$ were found to be in the combustion and catalytic combustion with a value of 100.86 and 75.77 kJ/mol as indicated in Table 6 and enlisted in Table S.3, Table S.4, Table S.5 of Supplementary Material. The pyrolysis and catalytic pyrolysis values for $\mathrm{\Delta }H$ were lying between the other two processes. This indicated the least energy was required for the bond dissociation of TBP organic compound in the presence of Fe₂O₃ and oxygen atmosphere. Further, another estimation was done using the $\mathrm{\Delta }H$ value to determine the favourability of forming products by calculating the difference between $\mathrm{\Delta }H$ and Ea. The feasibility of the reaction was preferred if the difference value was lower (Moine et al., 2016; Müsellim et al., 2018).

The obtained values for the combustion and pyrolysis in the presence of Fe₂O₃ were 4.4 and 4.8 kJ/mol, indicating a thermodynamic driving force of the catalytic combustion reaction. $\mathrm{\Delta }G$ calculates the increment of the total energy of the system, which was also found to be hold a lower value in catalytic combustion compared to all other processes. $\mathrm{\Delta }S$ signifies the degree of randomness of the product formed. If the $\mathrm{\Delta }S$ value is negative, it resembles that the disorderness of the products is lower than that of the reactants, and it favors the state of thermodynamic equilibrium (Stančin et al., 2021). On the other side, if the value is positive, it points toward high product reactivity. The $\mathrm{\Delta }S$ values were initiated from −0.05 kJ/mol in catalytic combustion, whereas in all other processes, the value started from −0.02 kJ/mol, which supports the catalytic combustion reaction. For all models in different techniques, the $\mathrm{\Delta }G$ has a positive value and $\mathrm{\Delta }S$ with a negative value, which refers to the non-spontaneous process (Naqvi et al., 2018).

3.4 Mechanistic pathway

Via surface characterization techniques (Fig. S.3, SM), our previous investigation established organic bromine transfer from the TBP ring into the hematite surface (Mousa et al., 2022). The portrayed reaction mainly ensues via direct abstraction of the aromatic bromine by the hematite (Altarawneh et al., 2016b). However, dissociative addition through the fission of the hydroxyl’s OH bond also takes place. Fig. 3 portrays steps that characterize ring-opening pathways that proceed following the scission of the O—H bond over the Lewis acid-base sites in hematite (M1 → M2). Ring-opening along the step M2 → M3 requires a sizable activation enthalpy of 200 kJ/mol whereas the reaction is noticeably endothermic at 193 kJ/mol. Calculated Mayer’s bond orders characterize the bonding nature in the produced C₆ adduct. A Mayer’s bond order at 0.31 infers a genuine bonding between the fragment and the cluster. As shown in the structure of M3, an ortho bromine atom is expelled upon ring opening. The following steps feature the departure of C₂BrH molecules without encountering activation energies via endothermic reactions. Values of bond orders remain largely unchanged with the shortening of the hydrocarbon chain in the M5 intermediate. The formation of carbon monoxide moieties in the final step is in accord with the evolution of CO and the observed reduction cycle Fe₂O₃ → Fe₃O₄ → FeO → Fe (Oleszek et al., 2013).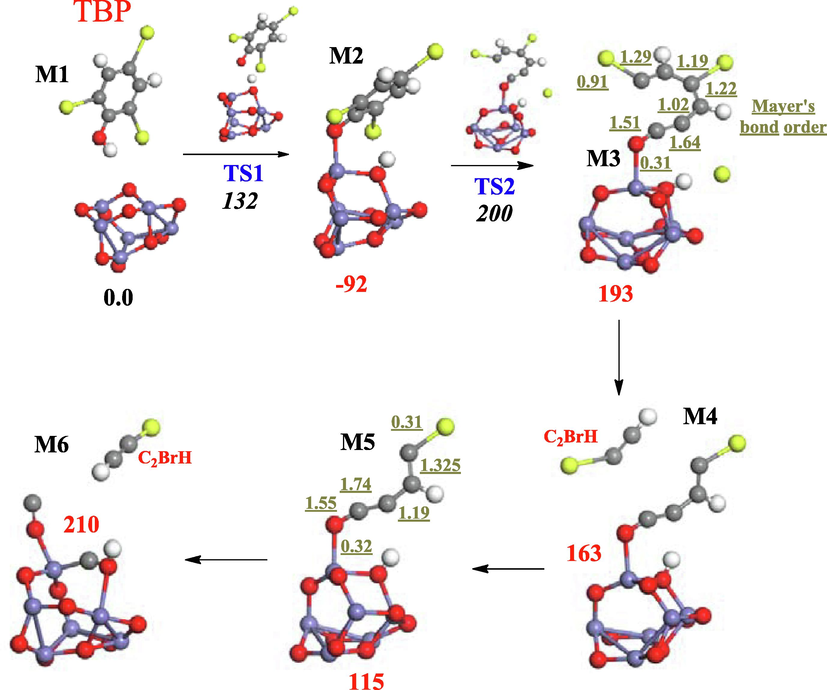

Close

Fig. 3

Decomposition of TBP over hematite. Values (in kJ/mol) in bold and italic fonts represent reaction and activation energies respectively. Red, white, grey, blue, and yellow sphere denote oxygen, hydrogen, carbon, iron, and bromine atoms respectively.

Export to PPT

In a recent study, we reported products that arise from co-pyrolysis of hematite with TBP in the temperature window from 150 to 500 °C using GCMS (Mousa et al., 2022). We have also investigated interaction between an evaporated stream of TBP with hematite (Ali et al., 2022c). Alkylated benzenes were found to dominate the gas fraction. A wide product distribution was observed in the condensable products (Mousa et al., 2022). The major constituents in the gas phase were toluene with a relative area of 50.88 % followed by p-xylene (22 %), 3-methyl butanone (16.64 %), ethylbenzene (4.99 %), and mesitylene (3.78 %) in our study (Mousa et al., 2022). Hematite proved to be a good debromination agent during the thermal degradation of TBP releasing zero brominated compounds in the gaseous phase (Ali et al., 2022c; Ma et al., 2018). Mechanistically, Fe³⁺ cations fixed evolved HBr gases through a dissociative adsorption reaction forming FeBr₂. In addition to these gases, the presence of Fe particles also enhanced the production of H₂, CO, and CH₄ (Ma and Kamo, 2019).